Radiation Pattern Prediction for Metasurfaces: A Neural Network-Based Approach
Abstract
1. Introduction
- We develop an NN-based radiation pattern predictor, which, through our analysis, is established to be nearly as accurate as a full-wave simulation but with the computational complexity of an analytical method.
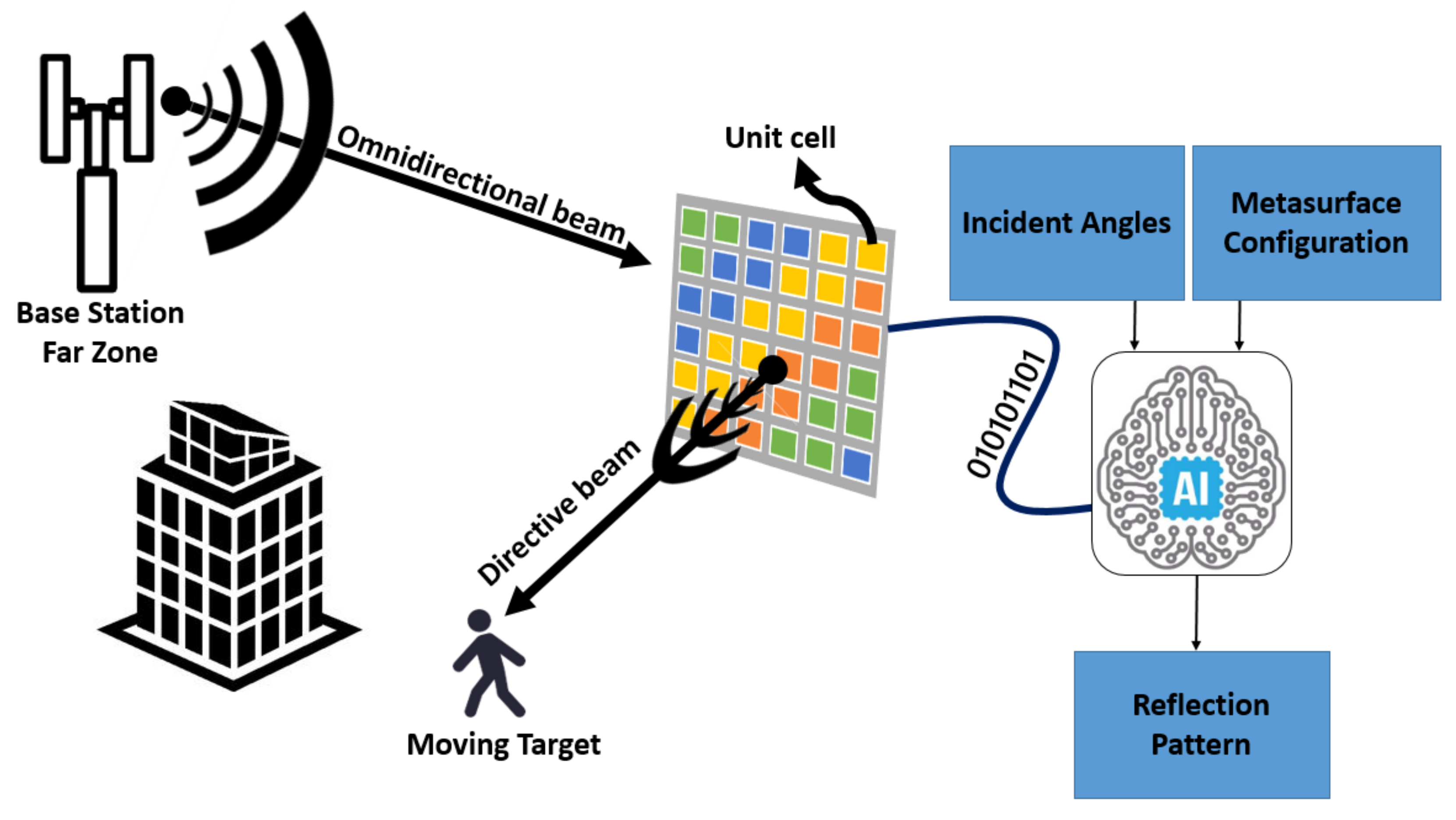
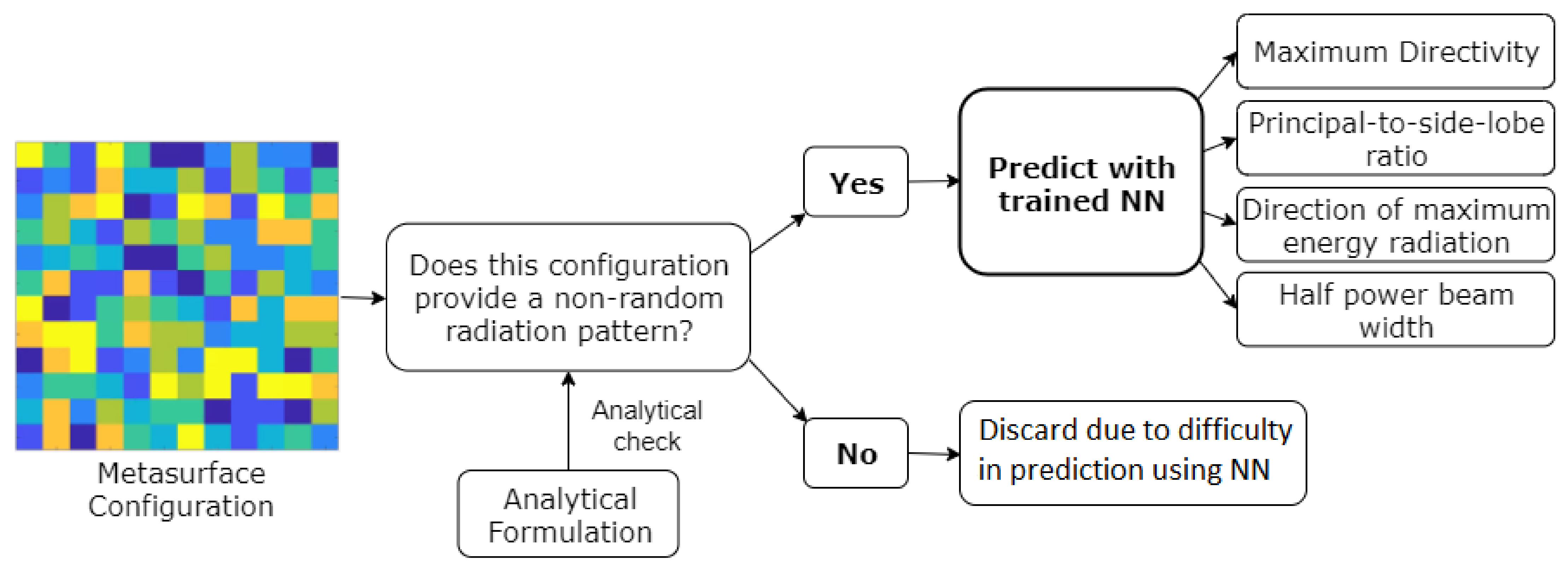
- To the best of our knowledge, this is the first method wherein certain important features of the reflected beam radiation pattern for a given MSF, i.e., Directivity, Principal-to-side-lobe ratio, Direction of maximum energy radiation and Half power beam width, have been predicted and effectively utilized for the complete characterization of the reflected beam radiation pattern. Consequently, this also provisions the capacity of our methodology in 6G networks (Figure 1).
- We provide an analysis based on the accuracy of prediction of the aforesaid parameters, for the locally tunable MSF scenario. Through the incremental design methodology, we establish a concrete framework and benchmark towards the selection of a CNN-based predictor for the reflected beam radiation pattern. Specifically, we compare the performance of a CNN-based predictor with an MLP based predictor. The comparative study reveals that the CNN predictor provisions an accuracy similar to the MLP predictor. It is imperative to state here that a CNN incurs significantly lower computational complexity as compared to an MLPNN. To this end, we have also provided a short discussion on the computational complexity of the NN models, analytical method, and the CST full-wave simulator in Appendix B.
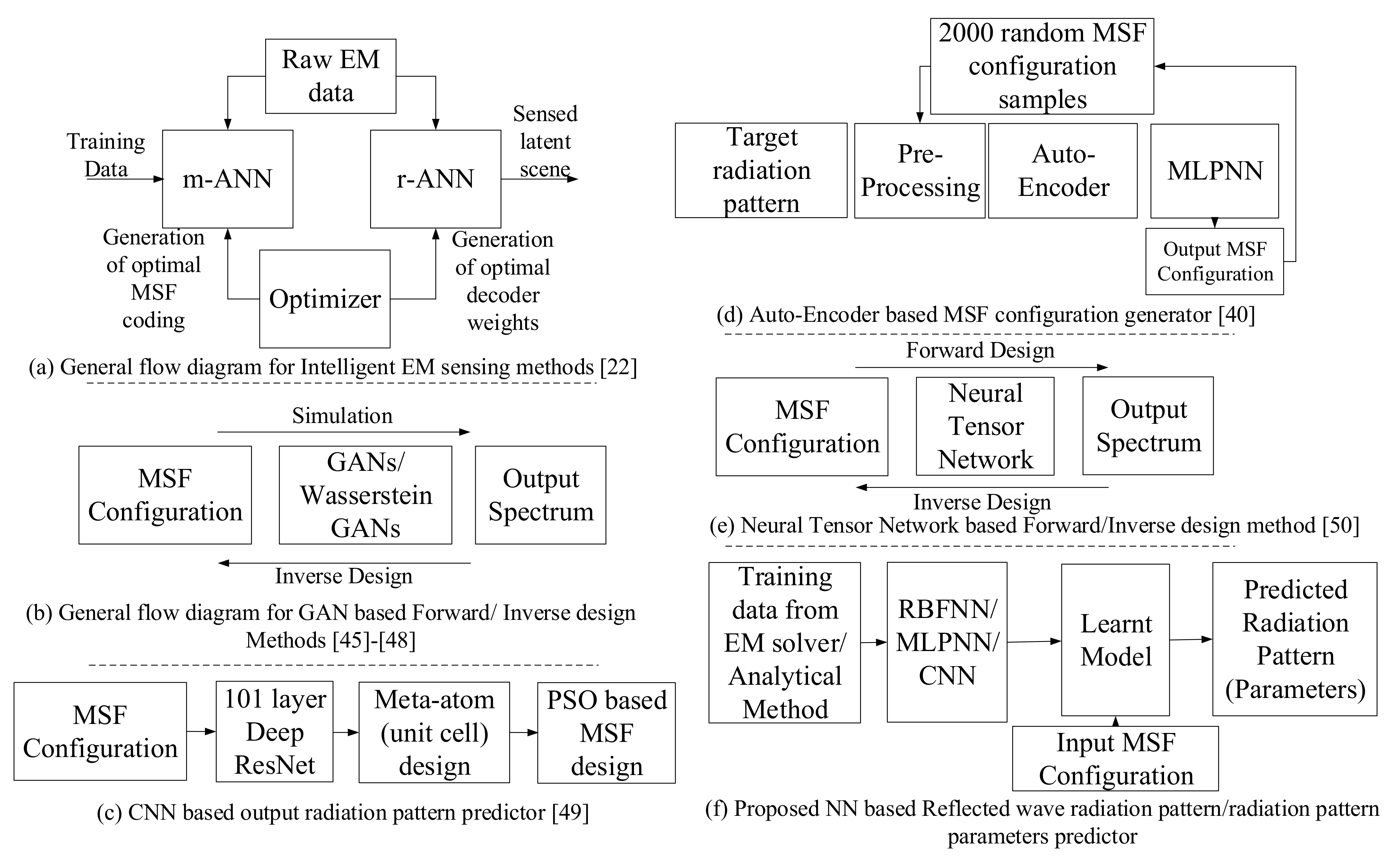
2. State of the Art
2.1. Forward Design Approaches
2.2. Inverse/MSF Design Approaches
3. Incremental Design Framework
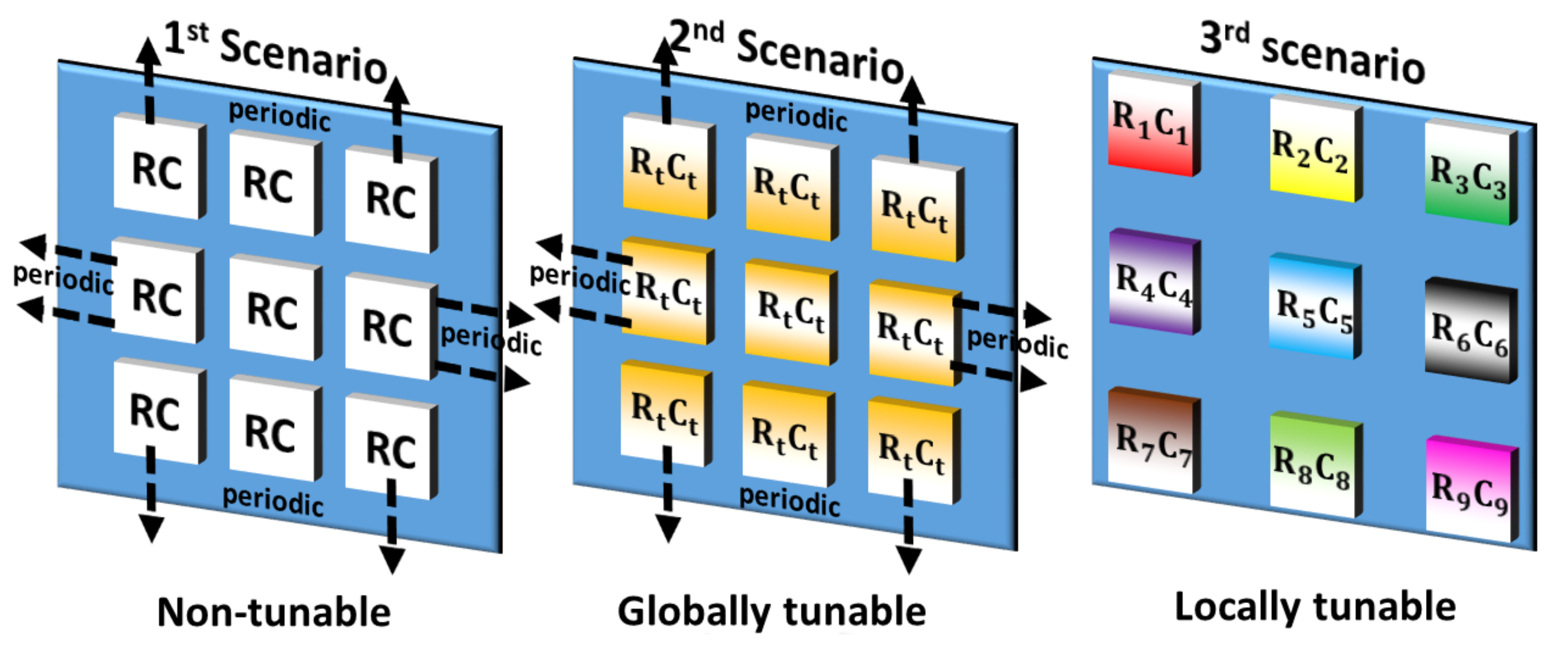
- The non-tunable scenario consists of a non-tunable unit cell configuration across the MSF. Such a configuration is termed a non-tunable MSF.
- The globally tunable scenario consists of a matrix of unit cells across the MSF, wherein the unit cells have the same values for the tunable resistance R and capacitance C. Such a configuration is termed a globally tunable MSF.
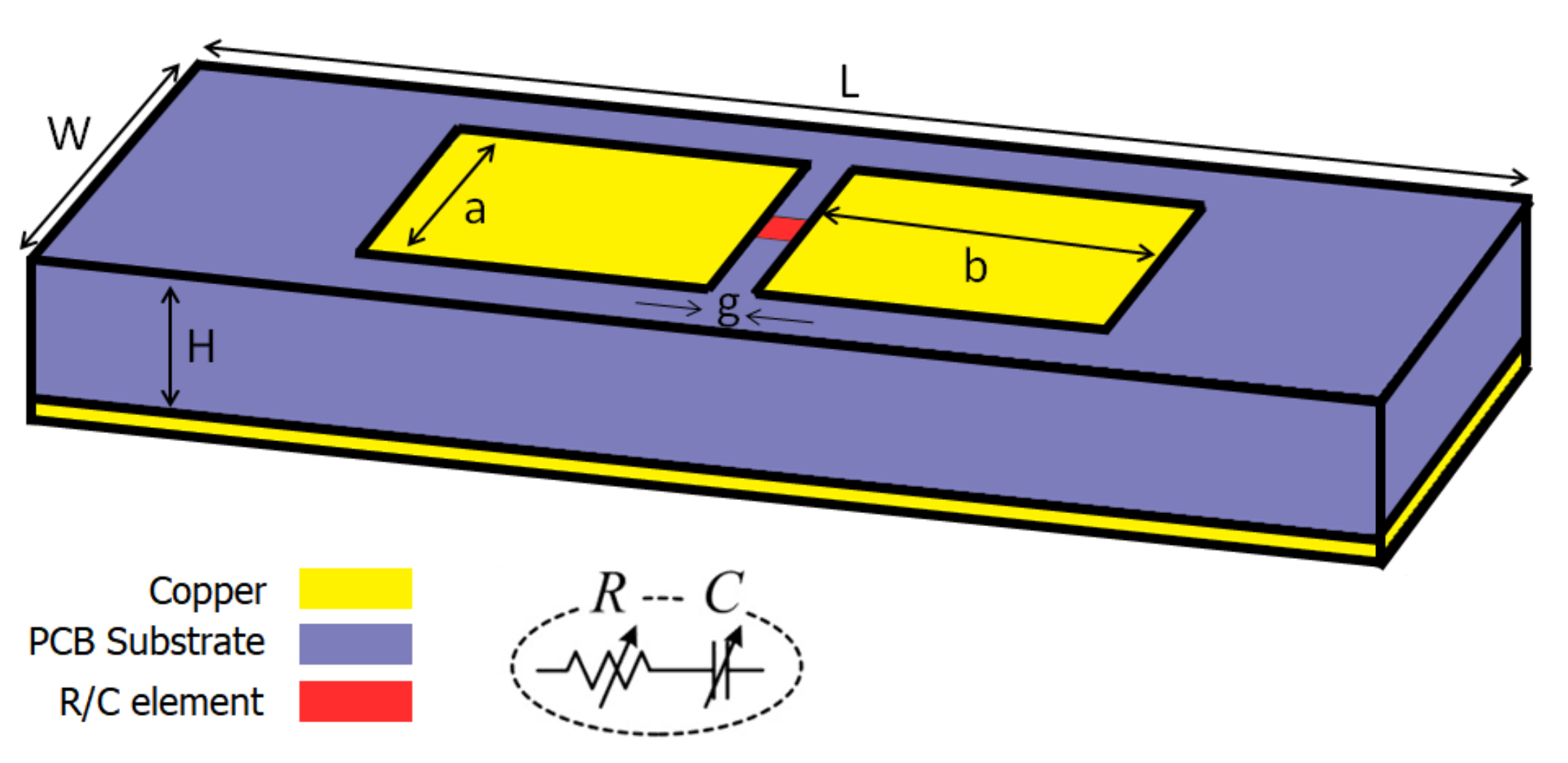
3.1. Homogeneous MSF Configuration
3.1.1. Non-Tunable Scenario (Non-Tunable, Single Unit Cell/Full Radiation Pattern Estimation)
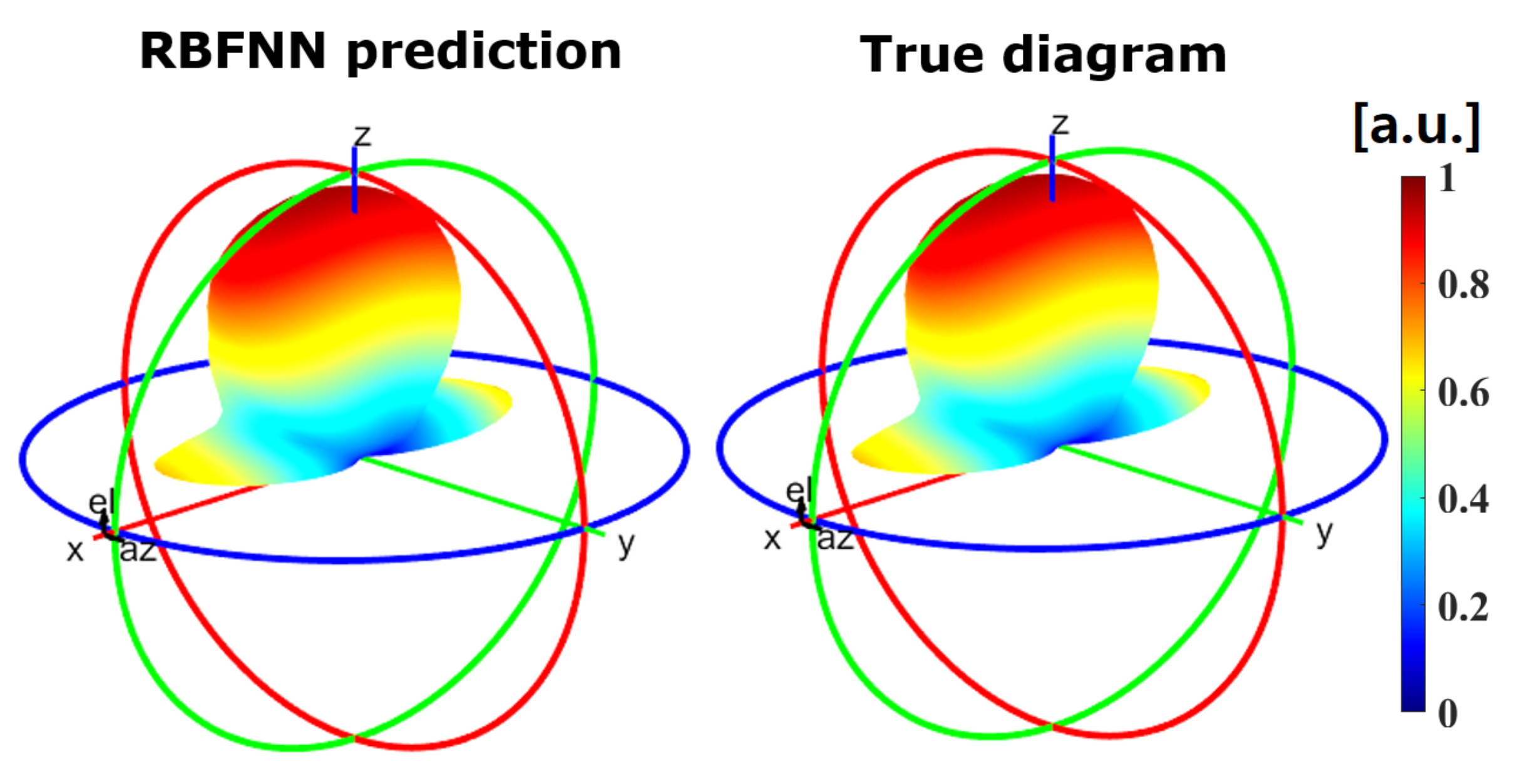
3.1.2. Globally Tunable Scenario (Tunable Single Unit Cell/Full Radiation Pattern Estimation)
3.2. Heterogeneous MSF Configuration
3.2.1. Locally Tunable Scenario (Tunable Full Surface/Radiation Pattern Attribute Estimation)
4. Methodology
4.1. Homogeneous MSF Configuration
4.1.1. Non-Tunable Scenario
4.1.2. Globally Tunable Scenario
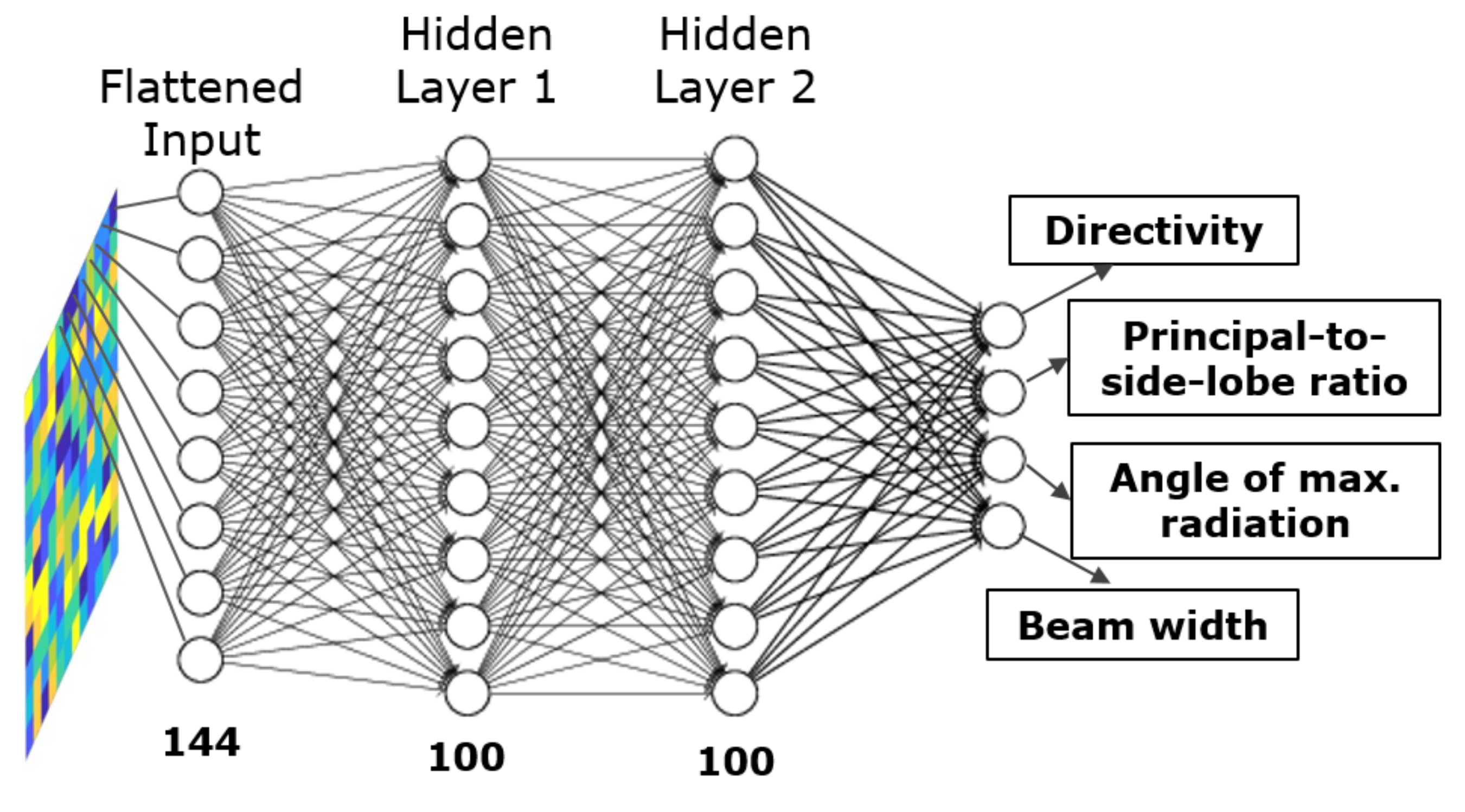
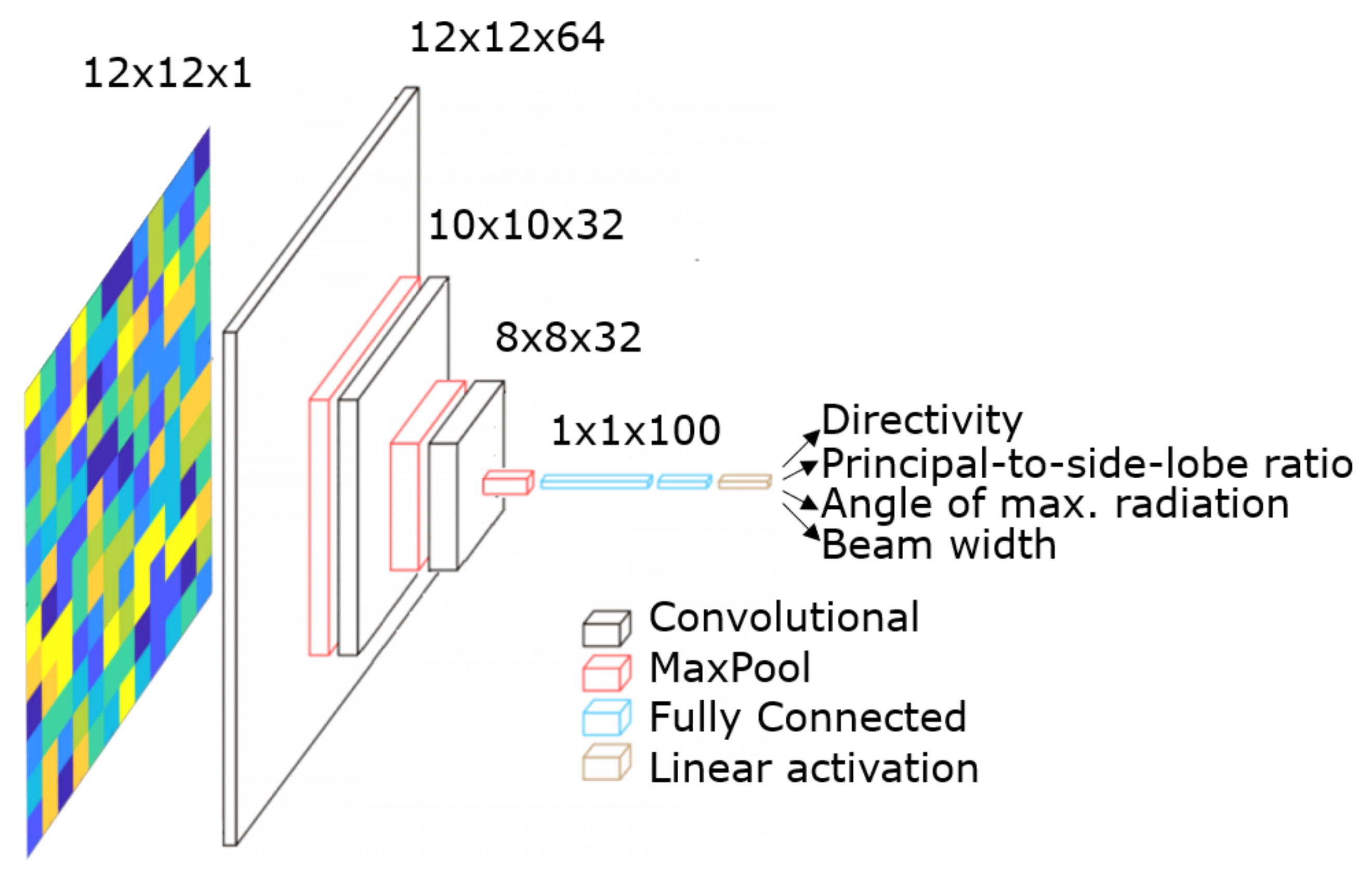
4.2. Heterogeneous MSF Configuration (Locally Tunable Scenario)
- Our ML approach predicts the measures of the reflected beam pattern accurately.
- Provided that there is enough computational power, we can extrapolate the same model and methodology to the scenario where we have more samples from an EM solver.
4.2.1. Multi-Layer Perceptron Neural Network
4.2.2. Convolutional Neural Network
5. Evaluation
5.1. Homogeneous MSF Configuration
5.1.1. Non-Tunable Scenario
5.1.2. Globally Tunable Scenario
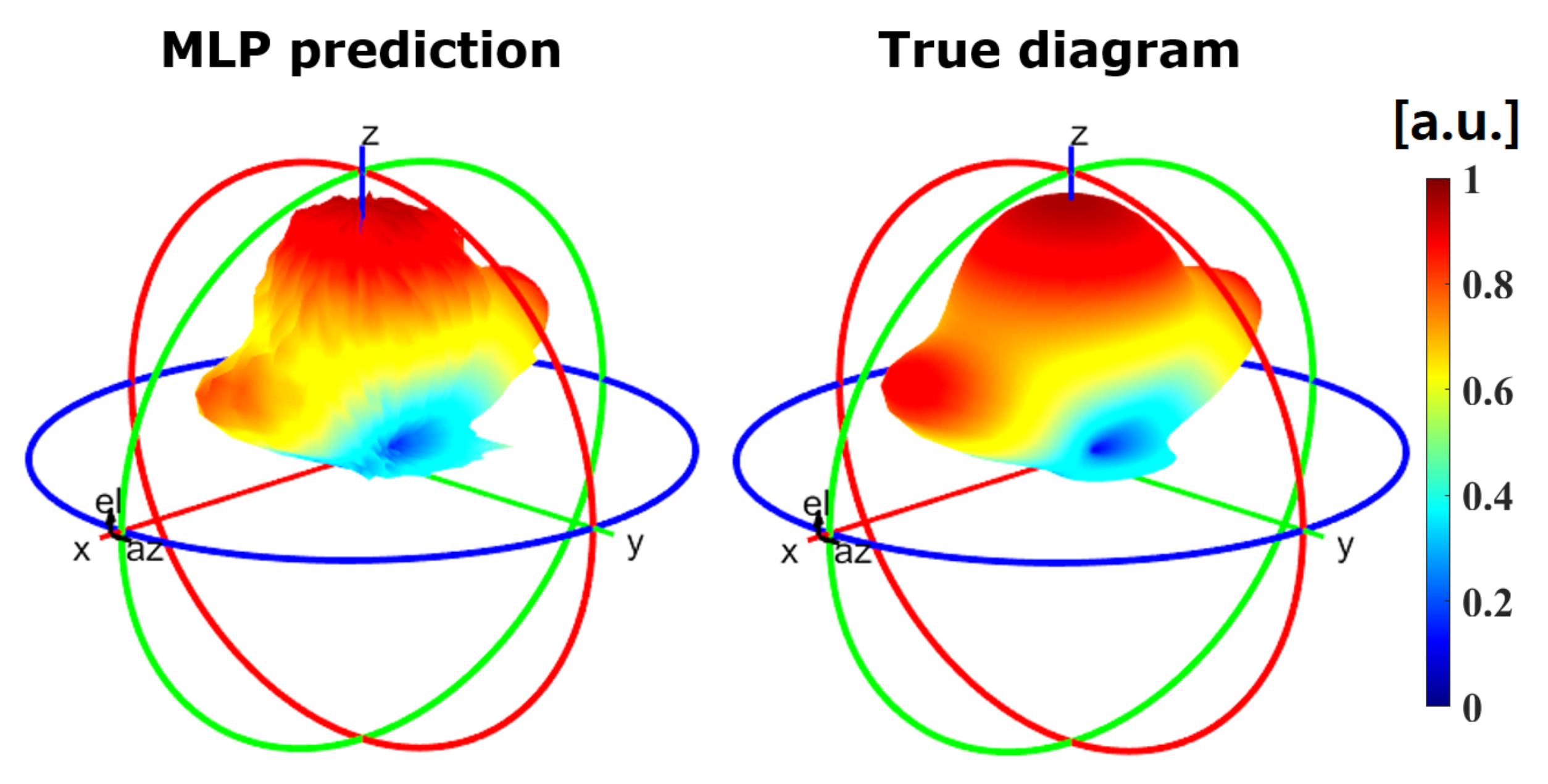
5.2. Heterogeneous MSF Configuration (Locally Tunable Scenario)
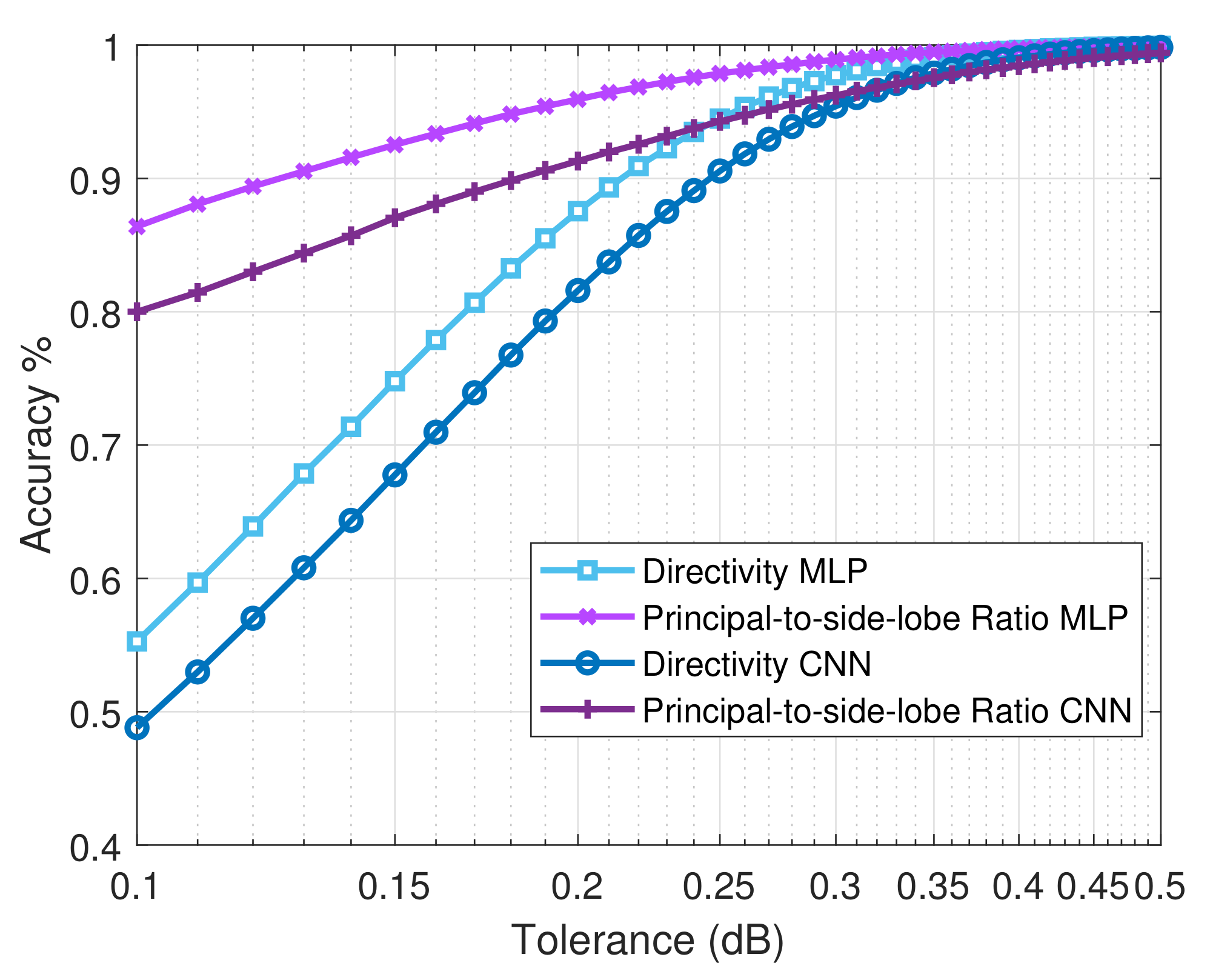
5.2.1. Directivity
5.2.2. Principle-to-Side Lobe Ratio
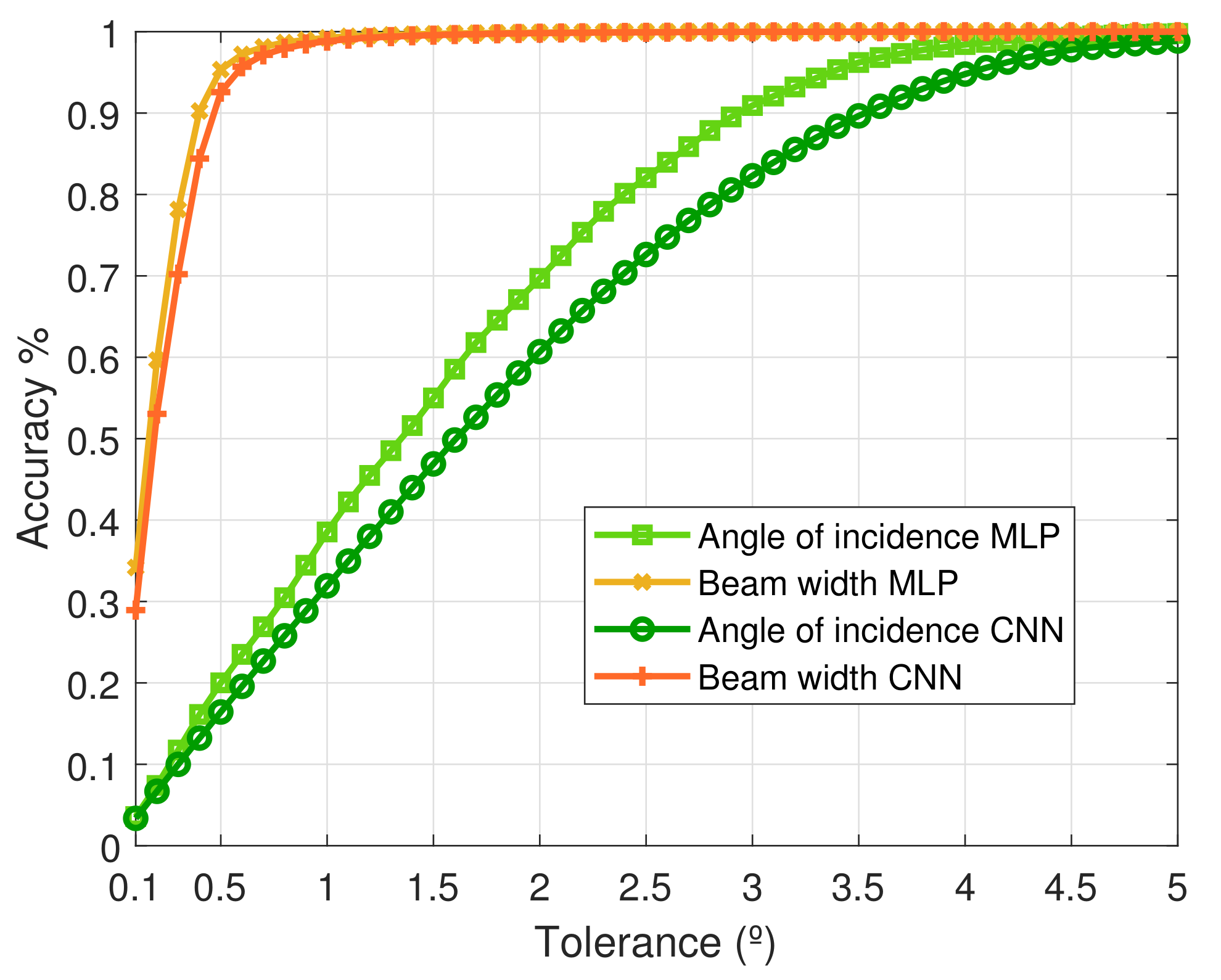
5.2.3. Angle of Maximum Radiation
5.2.4. Half Power Beam Width
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Zhang, Z.; Xiao, Y.; Ma, Z.; Xiao, M.; Ding, Z.; Lei, X.; Karagiannidis, G.K.; Fan, P. 6G Wireless Networks: Vision, Requirements, Architecture, and Key Technologies. IEEE Veh. Technol. Mag. 2019, 14, 28–41. [Google Scholar] [CrossRef]
- Saad, W.; Bennis, M.; Chen, M. A Vision of 6G Wireless Systems: Applications, Trends, Technologies, and Open Research Problems. IEEE Netw. 2020, 34, 134–142. [Google Scholar] [CrossRef]
- Calvanese Strinati, E.; Barbarossa, S.; Gonzalez-Jimenez, J.L.; Ktenas, D.; Cassiau, N.; Maret, L.; Dehos, C. 6G: The Next Frontier: From Holographic Messaging to Artificial Intelligence Using Subterahertz and Visible Light Communication. IEEE Veh. Technol. Mag. 2019, 14, 42–50. [Google Scholar] [CrossRef]
- Haas, H.; Yin, L.; Wang, Y.; Chen, C. What is LiFi? J. Light. Technol. 2016, 34, 1533–1544. [Google Scholar] [CrossRef]
- Basar, E.; Di Renzo, M.; De Rosny, J.; Debbah, M.; Alouini, M.; Zhang, R. Wireless communications through reconfigurable intelligent surfaces. IEEE Access 2019, 7, 116753–116773. [Google Scholar] [CrossRef]
- Renzo, M.D.; Debbah, M.; Phan-Huy, D.T.; Zappone, A.; Alouini, M.S.; Yuen, C.; Sciancalepore, V.; Alexandropoulos, G.C.; Hoydis, J.; Gacanin, H.; et al. Smart radio environments empowered by reconfigurable AI meta-surfaces: An idea whose time has come. Eurasip J. Wirel. Commun. Netw. 2019, 129. [Google Scholar] [CrossRef]
- Di Renzo, M.; Habibi Danufane, F.; Xi, X.; de Rosny, J.; Tretyakov, S. Analytical Modeling of the Path-Loss for Reconfigurable Intelligent Surfaces—Anomalous Mirror or Scatterer? In Proceedings of the 2020 IEEE 21st International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Atlanta, GA, USA, 26–29 May 2020; pp. 1–5. [Google Scholar]
- Papazafeiropoulos, A.; Kourtessis, P.; Renzo, M.D.; Chatzinotas, S.; Senior, J.M. Performance Analysis of Cell-Free Massive MIMO Systems: A Stochastic Geometry Approach. IEEE Trans. Veh. Technol. 2020, 69, 3523–3537. [Google Scholar] [CrossRef]
- Liaskos, C.; Nie, S.; Tsioliaridou, A.; Pitsillides, A.; Ioannidis, S.; Akyildiz, I. A New Wireless Communication Paradigm through Software-Controlled Metasurfaces. IEEE Commun. Mag. 2018, 56, 162–169. [Google Scholar] [CrossRef]
- Elmeadawy, S.; Shubair, R.M. Enabling Technologies For 6g Future Wireless Communications: Opportunities And Challenges. arXiv 2020, arXiv:2002.06068. [Google Scholar]
- Rajatheva, N.; Atzeni, I.; Bjornson, E.; Bourdoux, A.; Buzzi, S.; Doré, J.; Erkucuk, S.; Fuentes, M.; Guan, K.; Hu, Y.; et al. White Paper on Broadband Connectivity in 6G. arXiv 2020, arXiv:2004.14247. [Google Scholar]
- Ammari, H.; Kang, H.; Lee, H.; Lim, M.; Yu, S. Enhancement of Near Cloaking for the Full Maxwell Equations. Siam J. Appl. Math. 2013, 73, 2055–2076. [Google Scholar] [CrossRef]
- Alitalo, P.; Tretyakov, S. Electromagnetic cloaking with metamaterials. Mater. Today 2009, 12, 22–29. [Google Scholar] [CrossRef]
- Sievenpiper, D.F.; Schaffner, J.H.; Song, H.J.; Loo, R.Y.; Tangonan, G. Two-dimensional beam steering using an electrically tunable impedance surface. IEEE Trans. Antennas Propag. 2003, 51, 2713–2722. [Google Scholar] [CrossRef]
- Shalaev, M.I.; Sun, J.; Tsukernik, A.; Pandey, A.; Nikolskiy, K.; Litchinitser, N.M. High-Efficiency All-Dielectric Metasurfaces for Ultracompact Beam Manipulation in Transmission Mode. Nano Lett. 2015, 15, 6261–6266. [Google Scholar] [CrossRef] [PubMed]
- Del Hougne, P.; Fink, M.; Lerosey, G. Optimally diverse communication channels in disordered environments with tuned randomness. Nat. Electron. 2019, 2, 36–41. [Google Scholar] [CrossRef]
- Tang, W.; Dai, J.Y.; Chen, M.Z.; Wong, K.K.; Li, X.; Zhao, X.; Jin, S.; Cheng, Q.; Cui, T.J. MIMO Transmission Through Reconfigurable Intelligent Surface: System Design, Analysis, and Implementation. IEEE J. Sel. Areas Commun. 2020, 38, 2683–2699. [Google Scholar] [CrossRef]
- Zhao, H.; Shuang, Y.; Wei, M.; Cui, T.J.; Hougne, P.d.; Li, L. Metasurface-Assisted Passive Wireless Communication with Commodity Wi-Fi Signals. Sci. Rep. 2020, 11. [Google Scholar] [CrossRef]
- Wymeersch, H.; He, J.; Denis, B.; Clemente, A.; Juntti, M. Radio Localization and Mapping With Reconfigurable Intelligent Surfaces: Challenges, Opportunities, and Research Directions. IEEE Veh. Technol. Mag. 2020, 15, 52–61. [Google Scholar] [CrossRef]
- Del Hougne, P.; Imani, M.F.; Fink, M.; Smith, D.R.; Lerosey, G. Precise localization of multiple noncooperative objects in a disordered cavity by wave front shaping. Phys. Rev. Lett. 2018, 121. [Google Scholar] [CrossRef]
- Del Hougne, P. Robust position sensing with wave fingerprints in dynamic complex propagation environments. Phys. Rev. Res. 2020, 2, 043224. [Google Scholar] [CrossRef]
- Li, H.Y.; Zhao, H.T.; Wei, M.L.; Ruan, H.X.; Shuang, Y.; Cui, T.J.; del Hougne, P.; Li, L. Intelligent Electromagnetic Sensing with Learnable Data Acquisition and Processing. Patterns 2020, 1, 100006. [Google Scholar] [CrossRef] [PubMed]
- Taghvaee, H.R.; Zarrinkhat, F.; Abrishamian, M.S. Terahertz Kerr nonlinearity analysis of a microribbon graphene array using the harmonic balance method. J. Phys. Appl. Phys. 2017, 50, 255104. [Google Scholar] [CrossRef]
- Del Hougne, P.; Imani, M.F.; Diebold, A.V.; Horstmeyer, R.; Smith, D.R. Learned Integrated Sensing Pipeline: Reconfigurable Metasurface Transceivers as Trainable Physical Layer in an Artificial Neural Network. Adv. Sci. 2020, 7, 1901913. [Google Scholar] [CrossRef] [PubMed]
- Qian, C.; Zheng, B.; Shen, Y.; Jing, L.; Li, E.; Shen, L.; Chen, H. Deep-learning-enabled self-adaptive microwave cloak without human intervention. Nat. Photonics 2020, 14. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Esselle, K.P. Directivity improvement of a Fabry-Perot cavity antenna by enhancing near field characteristic. In Proceedings of the 2016 17th International Symposium on Antenna Technology and Applied Electromagnetics (ANTEM), Montreal, QC, Canada, 10–13 July 2016; pp. 1–2. [Google Scholar]
- Das, P.; Mandal, K.; Lalbakhsh, A. Single-layer polarization-insensitive frequency selective surface for beam reconfigurability of monopole antennas. J. Electromagn. Waves Appl. 2020, 34, 86–102. [Google Scholar] [CrossRef]
- Paul, G.S.; Mandal, K.; Lalbakhsh, A. Single-layer ultra-wide stop-band frequency selective surface using interconnected square rings. Aeu Int. J. Electron. Commun. 2021, 132, 153630. [Google Scholar] [CrossRef]
- Hayat, T.; Afzal, M.U.; Lalbakhsh, A.; Esselle, K.P. 3-D-Printed Phase-Rectifying Transparent Superstrate for Resonant-Cavity Antenna. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1400–1404. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P.; Smith, S.L. Low-Cost Nonuniform Metallic Lattice for Rectifying Aperture Near-Field of Electromagnetic Bandgap Resonator Antennas. IEEE Trans. Antennas Propag. 2020, 68, 3328–3335. [Google Scholar] [CrossRef]
- Liu, F.; Pitilakis, A.; Mirmoosa, M.S.; Tsilipakos, O.; Wang, X.; Tasolamprou, A.C.; Abadal, S.; Cabellos-Aparicio, A.; Alarcón, E.; Liaskos, C.; et al. Programmable Metasurfaces: State of the Art and Prospects. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Liaskos, C.; Nie, S.; Tsioliaridou, A.; Pitsillides, A.; Ioannidis, S.; Akyildiz, I. Realizing Wireless Communication Through Software-Defined HyperSurface Environments. In Proceedings of the 2018 IEEE 19th International Symposium on “A World of Wireless, Mobile and Multimedia Networks” (WoWMoM), Chania, Greece, 12–15 June 2018; pp. 14–15. [Google Scholar]
- Taghvaee, H.; Abadal, S.; Pitilakis, A.; Tsilipakos, O.; Tasolamprou, A.C.; Liaskos, C.; Kafesaki, M.; Kantartzis, N.V.; Cabellos-Aparicio, A.; Alarcón, E. Scalability Analysis of Programmable Metasurfaces for Beam Steering. IEEE Access 2020, 8, 105320–105334. [Google Scholar] [CrossRef]
- Hosseininejad, S.E.; Rouhi, K.; Neshat, M.; Faraji-Dana, R.; Cabellos-Aparicio, A.; Abadal, S.; Alarcón, E. Reprogrammable Graphene-based Metasurface Mirror with Adaptive Focal Point for THz Imaging. Sci. Rep. 2019, 9, 2868. [Google Scholar] [CrossRef]
- Lagaris, I.E.; Likas, A.; Fotiadis, D.I. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 1998, 9, 987–1000. [Google Scholar] [CrossRef]
- Hosseininejad, S.E.; Rouhi, K.; Neshat, M.; Cabellos-Aparicio, A.; Abadal, S.; Alarcón, E. Digital Metasurface Based on Graphene: An Application to Beam Steering in Terahertz Plasmonic Antennas. IEEE Trans. Nanotechnol. 2019, 18, 734–746. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Shi, Z.; Zhu, A.Y.; Chen, W.T.; Sanjeev, V.; Zaidi, A.; Capasso, F. Achromatic Metalens over 60 nm Bandwidth in the Visible and Metalens with Reverse Chromatic Dispersion. Nano Lett. 2017, 17, 1819–1824. [Google Scholar] [CrossRef]
- Valasoulis, K.; Fotiadis, D.L.; Lagaris, I.E.; Likas, A. Solving differential equations with neural networks: Implementation on a DSP platform. In Proceedings of the 2002 14th International Conference on Digital Signal Processing, DSP 2002 (Cat. No.02TH8628), Santorini, Greece, 1–3 July 2002; pp. 1265–1268. [Google Scholar]
- Tsoulos, I.G.; Gavrilis, D.; Glavas, E. Solving differential equations with constructed neural networks. Neurocomputing 2009, 72, 2385–2391. [Google Scholar] [CrossRef]
- Inampudi, S.; Mosallaei, H. Neural network based design of metagratings. Appl. Phys. Lett. 2018, 112, 241102. [Google Scholar] [CrossRef]
- Qiu, T.; Shi, X.; Wang, J.; Li, Y.; Qu, S.; Cheng, Q.; Cui, T.; Sui, S. Deep Learning: A Rapid and Efficient Route to Automatic Metasurface Design. Adv. Sci. 2019, 6, 1900128. [Google Scholar] [CrossRef] [PubMed]
- Taghvaee, H.; Cabellos-Aparicio, A.; Georgiou, J.; Abadal, S. Error Analysis of Programmable Metasurfaces for Beam Steering. IEEE J. Emerg. Sel. Top. Circuits Syst. 2020, 10, 62–74. [Google Scholar] [CrossRef]
- Santos, A.; Figueiredo, E.; Silva, M.; Sales, C.; Costa, J. Machine learning algorithms for damage detection: Kernel-based approaches. J. Sound Vib. 2016, 363, 584–599. [Google Scholar] [CrossRef]
- Libbrecht, M.W.; Noble, W.S. Machine learning applications in genetics and genomics. Nat. Rev. Genet. 2015, 16, 321–332. [Google Scholar] [CrossRef] [PubMed]
- Mullainathan, S.; Spiess, J. Machine learning: An applied econometric approach. J. Econ. Perspect. 2017, 31, 87–106. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, D.; Rodrigues, S.P.; Lee, K.T.; Cai, W. Generative Model for the Inverse Design of Metasurfaces. Nano Lett. 2018, 18, 6570–6576. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Sell, D.; Hoyer, S.; Hickey, J.; Yang, J.; Fan, J.A. Free-Form Diffractive Metagrating Design Based on Generative Adversarial Networks. Acs Nano 2019, 13, 8872–8878. [Google Scholar] [CrossRef] [PubMed]
- Hodge, J.A.; Mishra, K.V.; Zaghloul, A.I. Joint Multi-Layer GAN-Based Design of Tensorial RF Metasurfaces. In Proceedings of the 2019 IEEE 29th International Workshop on Machine Learning for Signal Processing (MLSP), Pittsburgh, PA, USA, 13–16 October 2019; pp. 1–6. [Google Scholar]
- An, S.; Zheng, B.; Tang, H.; Shalaginov, M.Y.; Zhou, L.; Li, H.; Kang, M.; Richardson, K.A.; Gu, T.; Hu, J.; et al. Multifunctional Metasurface Design with a Generative Adversarial Network. Adv. Opt. Mater. 2021, 9, 2001433. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, C.; Wan, X.; Zhang, L.; Liu, S.; Yang, Y.; Cui, T.J. Machine-Learning Designs of Anisotropic Digital Coding Metasurfaces. Adv. Theory Simulat. 2019, 2, 1800132. [Google Scholar] [CrossRef]
- An, S.; Fowler, C.; Shalaginov, M.Y.; Zhang, Y.; Su, P.; Kang, M.; Zheng, B.; Tang, H.; Li, H.; Agarwal, A.M.; et al. Modeling of All-Dielectric Metasurfaces Using Deep Neural Networks. In Proceedings of the 2019 International Applied Computational Electromagnetics Society Symposium (ACES), Miami, FL, USA, 14–19 April 2019; pp. 1–2. [Google Scholar]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P. Multiobjective Particle Swarm Optimization to Design a Time-Delay Equalizer Metasurface for an Electromagnetic Band-Gap Resonator Antenna. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 912–915. [Google Scholar] [CrossRef]
- Wiecha, P.R.; Muskens, O.L. Deep Learning Meets Nanophotonics: A Generalized Accurate Predictor for Near Fields and Far Fields of Arbitrary 3D Nanostructures. Nano Lett. 2020, 20, 329–338. [Google Scholar] [CrossRef]
- Taghvaee, H.; Abadal, S.; Georgiou, J.; Cabellos-Aparicio, A.; Alarcón, E. Fault Tolerance in Programmable Metasurfaces: The Beam Steering Case. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar]
- Saeed, T.; Abadal, S.; Liaskos, C.; Pitsillides, A.; Taghvaee, H.; Cabellos-Aparicio, A.; Lestas, M.; Alarcón, E. Workload Characterization of Programmable Metasurfaces. In Proceedings of the Sixth Annual ACM International Conference on Nanoscale Computing and Communication, Association for Computing Machinery, New York, NY, USA, 25–27 September 2019. [Google Scholar] [CrossRef]
- Ashraf, N.; Lestas, M.; Saeed, T.; Taghvaee, H.; Abadal, S.; Pitsillides, A.; Liaskos, C. Extremum Seeking Control for Beam Steering using Hypersurfaces. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Liu, F.; Tsilipakos, O.; Pitilakis, A.; Tasolamprou, A.C.; Mirmoosa, M.S.; Kantartzis, N.V.; Kwon, D.H.; Georgiou, J.; Kossifos, K.; Antoniades, M.A.; et al. Intelligent Metasurfaces with Continuously Tunable Local Surface Impedance for Multiple Reconfigurable Functions. Phys. Rev. Appl. 2019, 11, 044024. [Google Scholar] [CrossRef]
- Yazdi, M.; Albooyeh, M. Analysis of Metasurfaces at Oblique Incidence. IEEE Trans. Antennas Propag. 2017, 65, 2397–2404. [Google Scholar] [CrossRef]
- Chu, H.; Qi, J.; Xiao, S.; Qiu, J. A thin wideband high-spatial-resolution focusing metasurface for near-field passive millimeter-wave imaging. Appl. Phys. Lett. 2018, 112, 174101. [Google Scholar] [CrossRef]
- HShah, S.M.Q.A.; Shoaib, N.; Ahmed, F.; Alomainy, A.; Quddious, A.; Nikolaou, S.; Imran, M.A.; Abbasi, Q.H. A multiband circular polarization selective metasurface for microwave applications. Sci. Rep. 2021, 11. [Google Scholar]
- Bakır, M.; Karaaslan, M.; Dincer, F.; Sabah, C. Metamaterial characterization by applying different boundary conditions on triangular split ring resonator type metamaterials. Int. J. Numer. Model. Electron. Netw. Devices Fields 2017, 30, e2188. [Google Scholar] [CrossRef]
- Lei, M.; Feng, N.; Wang, Q.; Hao, Y.; Huang, S.; Bi, K. Magnetically tunable metamaterial perfect absorber. J. Appl. Phys. 2016, 119, 244504. [Google Scholar] [CrossRef]
- Kim, H.K.; Lee, D.; Lim, S. Frequency-tunable metamaterial absorber using a varactor-loaded fishnet-like resonator. Appl. Opt. 2016, 55, 4113–4118. [Google Scholar] [CrossRef] [PubMed]
- Zhu, B.; Feng, Y.; Zhao, J.; Huang, C.; Jiang, T. Switchable metamaterial reflector/absorber for different polarized electromagnetic waves. Appl. Phys. Lett. 2010, 97, 051906. [Google Scholar] [CrossRef]
- Tao, Z.; Wan, X.; Pan, B.C.; Cui, T.J. Reconfigurable conversions of reflection, transmission, and polarization states using active metasurface. Appl. Phys. Lett. 2017, 110, 121901. [Google Scholar] [CrossRef]
- Najafi, M.; Schober, R. Intelligent Reflecting Surfaces for Free Space Optical Communications. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–7. [Google Scholar]
- Kisseleff, S.; Martins, W.A.; Al-Hraishawi, H.; Chatzinotas, S.; Ottersten, B. Reconfigurable Intelligent Surfaces for Smart Cities: Research Challenges and Opportunities. IEEE Open J. Commun. Soc. 2020, 1, 1781–1797. [Google Scholar] [CrossRef]
- Di Renzo, M.; Ntontin, K.; Song, J.; Danufane, F.H.; Qian, X.; Lazarakis, F.; De Rosny, J.; Phan-Huy, D.T.; Simeone, O.; Zhang, R.; et al. Reconfigurable Intelligent Surfaces vs. Relaying: Differences, Similarities, and Performance Comparison. IEEE Open J. Commun. Soc. 2020, 1, 798–807. [Google Scholar] [CrossRef]
- Di Renzo, M.; Zappone, A.; Debbah, M.; Alouini, M.S.; Yuen, C.; de Rosny, J.; Tretyakov, S. Smart Radio Environments Empowered by Reconfigurable Intelligent Surfaces: How It Works, State of Research, and The Road Ahead. IEEE J. Sel. Areas Commun. 2020, 38, 2450–2525. [Google Scholar] [CrossRef]
- Masini, B.M.; Silva, C.M.; Balador, A. The Use of Meta-Surfaces in Vehicular Networks. J. Sens. Actuator Netw. 2020, 9, 15. [Google Scholar] [CrossRef]
- Yang, L.; Meng, F.; Zhang, J.; Hasna, M.O.; Renzo, M.D. On the Performance of RIS-Assisted Dual-Hop UAV Communication Systems. IEEE Trans. Veh. Technol. 2020, 69, 10385–10390. [Google Scholar] [CrossRef]
- Liu, J. Radial Basis Function (RBF) Neural Network Control for Mechanical Systems: Design, Analysis and Matlab Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kasiviswanathan, K.; Agarwal, A. Radial basis function artificial neural network: Spread selection. Int. J. Adv. Comput. Sci. 2012, 2, 394–398. [Google Scholar]
- Møller, M.F. A scaled conjugate gradient algorithm for fast supervised learning. Elsevier Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Cui, T.; Liu, S.; Li, L. Information entropy of coding metasurface. Light Sci. Appl. 2016, 5, e16172. [Google Scholar] [CrossRef]
- Pulido-Mancera, L.; Bowen, P.T.; Imani, M.F.; Kundtz, N.; Smith, D. Polarizability extraction of complementary metamaterial elements in waveguides for aperture modeling. Phys. Rev. B 2017, 96, 235402. [Google Scholar] [CrossRef]
- Yoo, I.; Smith, D.R. Analytic Model of Coax-Fed Printed Metasurfaces and Analysis of Antenna Parameters. IEEE Trans. Antennas Propag. 2020, 68, 2950–2964. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Tsilipakos, O.; Tasolamprou, A.C.; Koschny, T.; Kafesaki, M.; Economou, E.N.; Soukoulis, C.M. Pairing Toroidal and Magnetic Dipole Resonances in Elliptic Dielectric Rod Metasurfaces for Reconfigurable Wavefront Manipulation in Reflection. Adv. Opt. Mater. 2018, 6, 1800633. [Google Scholar] [CrossRef]
- Yang, H.; Cao, X.; Yang, F.; Gao, J.; Xu, S.; Li, M.; Chen, X.; Zhao, Y.; Zheng, Y.; Li, S. A programmable metasurface with dynamic polarization, scattering and focusing control. Sci. Rep. 2016, 6, 1–11. [Google Scholar]
- CS231n Convolutional Neural Networks for Visual Recognition. Available online: https://cs231n.github.io/convolutional-networks/ (accessed on 2 October 2020).

| Methods | Computation Time |
|---|---|
| Analytical Methods | ∼1 s |
| Full-Wave Simulators | ∼1 h |
| Neural Networks | ∼1 min |
| Design Approach | Application | Year | Reference |
|---|---|---|---|
| Optimizer | Time-delay equalizer | 2017 | [52] |
| Two Deep NN and optimizer | Smart sensing | 2020 | [22] |
| GAN and CNN | Frequency response prediction | 2018 | [46] |
| GAN | Inverse design | 2019 | [47] |
| GAN and CNN | MSF design | 2019 | [48] |
| GAN | MSF design | 2021 | [49] |
| CNN | Reflection phase prediction | 2019 | [50] |
| Auto-encoder | MSF design | 2019 | [41] |
| MLP and NTN | MSF design | 2019 | [51] |
| Encoder-decoder | Field prediction | 2020 | [53] |
| Parameter Name | Value |
|---|---|
| Regularization type | L2 |
| 0.8 | |
| Training algorithm | scaled conjugate gradient |
| Number of hidden layers | 2 |
| Neurons of 1st hidden layer | 100 |
| Neurons of 2nd hidden layer | 100 |
| Parameter Name | Value |
|---|---|
| Regularization type | Dropout |
| Dropout factor 3rd conv. layer | 0.2 |
| Dropout factor FC layer | 0.25 |
| Training algorithm | Stochastic Gradient Descent |
| Learning rate | 0.001 |
| ineMomentum | 0.9 |
| Decay | |
| Num. of conv. layers | 3 |
| Num. of FC layers | 1 |
| Parameter | MLPNN | CNN | ||
|---|---|---|---|---|
| Tolerance | Accuracy | Tolerance | Accuracy | |
| Directivity | 0.5 dB | 0.999 | 0.5 dB | 0.998 |
| 0.25 dB | 0.950 | 0.25 dB | 0.906 | |
| 0.1 dB | 0.563 | 0.1dB | 0.488 | |
| Principle-to-side lobe ratio | 0.5 dB | 0.999 | 0.5 dB | 0.994 |
| 0.25 dB | 0.983 | 0.25 dB | 0.943 | |
| 0.1 dB | 0.861 | 0.1 dB | 0.801 | |
| Angle of maximum radiation | 5 | 0.998 | 5 | 0.989 |
| 2 | 0.727 | 2 | 0.607 | |
| 1 | 0.406 | 1 | 0.319 | |
| Half Power Beam Width | 1 | 0.995 | 1 | 0.988 |
| 0.5 | 0.973 | 0.5 | 0.926 | |
| 0.25 | 0.792 | 0.25 | 0.618 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taghvaee, H.; Jain, A.; Timoneda, X.; Liaskos, C.; Abadal, S.; Alarcón, E.; Cabellos-Aparicio, A. Radiation Pattern Prediction for Metasurfaces: A Neural Network-Based Approach. Sensors 2021, 21, 2765. https://doi.org/10.3390/s21082765
Taghvaee H, Jain A, Timoneda X, Liaskos C, Abadal S, Alarcón E, Cabellos-Aparicio A. Radiation Pattern Prediction for Metasurfaces: A Neural Network-Based Approach. Sensors. 2021; 21(8):2765. https://doi.org/10.3390/s21082765
Chicago/Turabian StyleTaghvaee, Hamidreza, Akshay Jain, Xavier Timoneda, Christos Liaskos, Sergi Abadal, Eduard Alarcón, and Albert Cabellos-Aparicio. 2021. "Radiation Pattern Prediction for Metasurfaces: A Neural Network-Based Approach" Sensors 21, no. 8: 2765. https://doi.org/10.3390/s21082765
APA StyleTaghvaee, H., Jain, A., Timoneda, X., Liaskos, C., Abadal, S., Alarcón, E., & Cabellos-Aparicio, A. (2021). Radiation Pattern Prediction for Metasurfaces: A Neural Network-Based Approach. Sensors, 21(8), 2765. https://doi.org/10.3390/s21082765







