Sensitivity of Field-Effect Transistor-Based Terahertz Detectors
Abstract
:1. Introduction
2. Commonly Used Methods for the Estimation of THz Detector Area
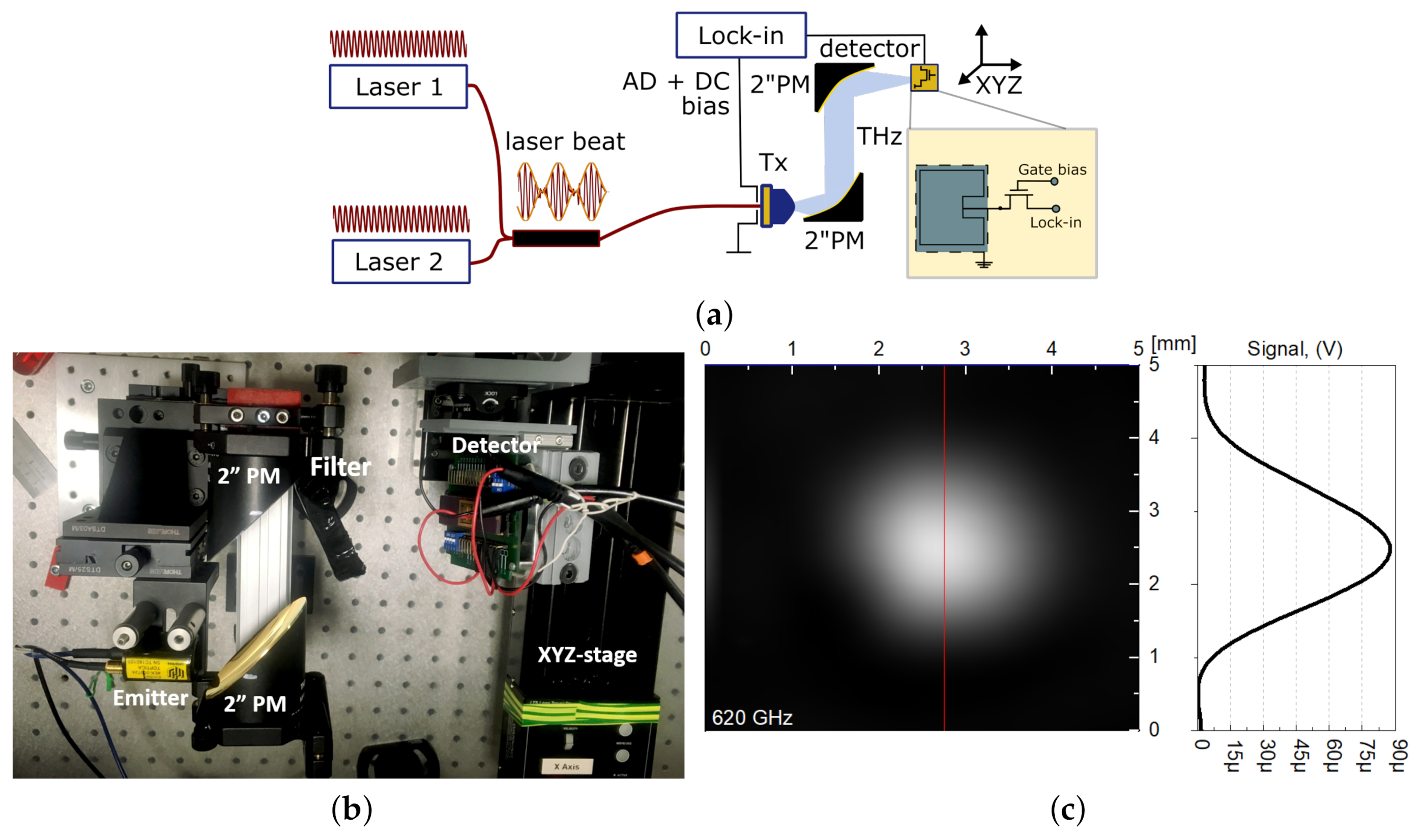
3. Samples and Measurement Setup
3.1. Detector Array Design
3.2. THz Characterisation Setup
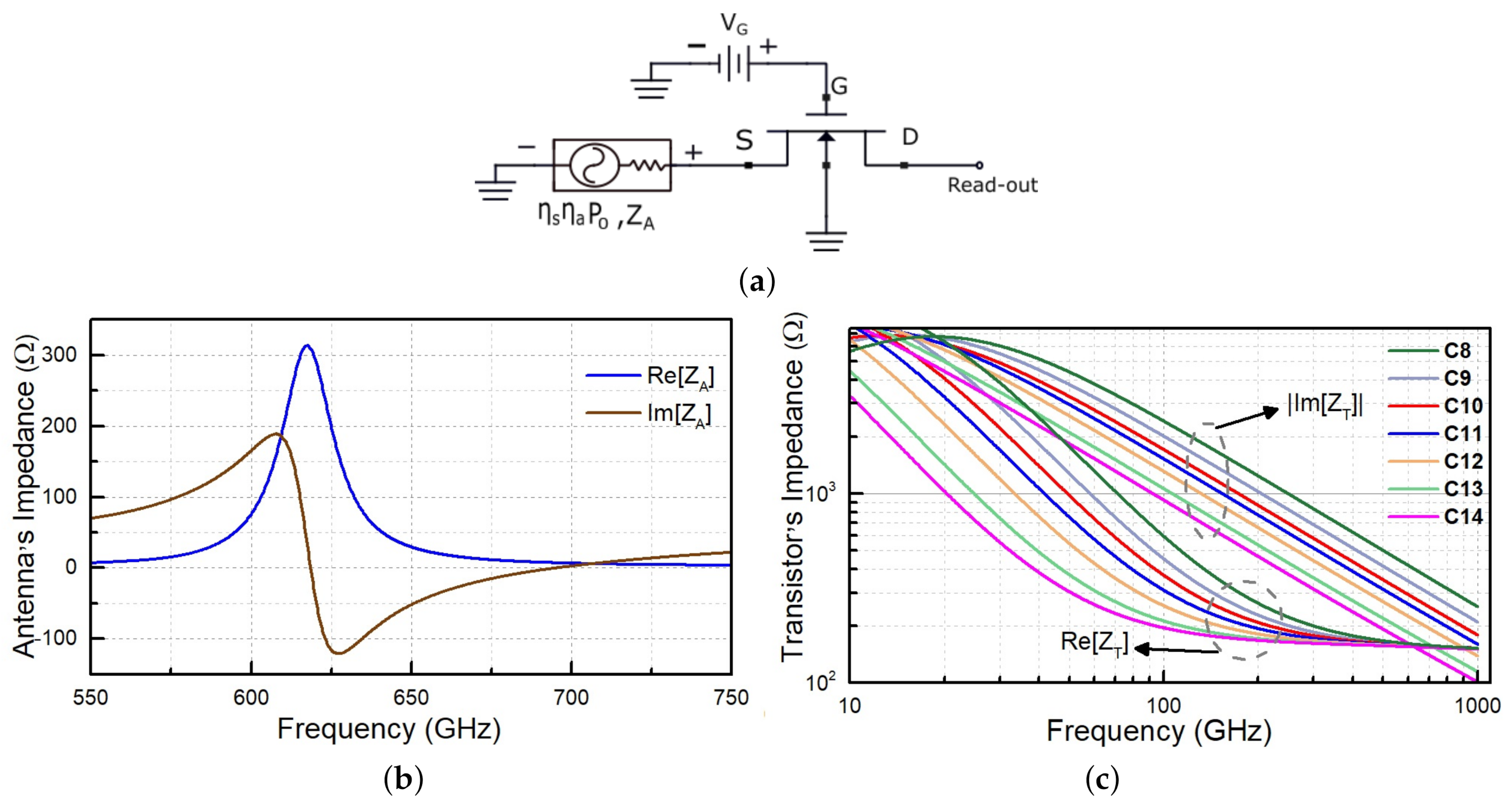
4. Modelling
4.1. Circuit Level Modelling of Detector
4.2. Electromagnetic Simulations of Antenna
5. Experimental Results
5.1. Methodology of Measuring Device’s Effective Area and Determining Input Power
5.2. Terahertz Responsivity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| III–V | III–V compound semiconductor |
| BiCMOS | Bipolar CMOS |
| BL-GFET | Bi-layer graphene field-effect transistor |
| BLG | Bi-layer GFET (see BL-GFET) |
| BP-based FET | Black phosphorus-based field-effect transistor |
| CAD | Computer-aided design |
| CMOS | Complementary metal–oxide–semiconductor |
| CSDRA | Chip scale dielectric resonator antenna |
| DGG-HEMT | Dual-grating-gate high-electron-mobility transistor |
| DGG-GFET | Dual-grating-gate graphene field-effect transistor |
| FD-SOI | Fully depleted silicon on insulator |
| FDTD | Finite-difference time-domain |
| FET | Field-effect transistor |
| FWHM | Full width at half maximum |
| GFET | Graphene field-effect transistor |
| HBT | Heterojunction bipolar transistor |
| HEMT | High-electron-mobility transistor |
| HFET | Heterostructure FET |
| MOSFET | Metal–oxide–semiconductor field-effect transistor |
| Nanowire-FET | Nanowire-based field-effect transistor |
| NEP | Noise equivalent power |
| P–N diode | P–N junction diode |
| SSD | Self-switching device |
| SBD | Schottky barrier diode |
| SL-GFET | Single-layer graphene field-effect transistor |
| SLG | Single-layer GFET (see SL-GFET) |
| SNR | Signal-to-noise ratio |
| SOI | Silicon on insulator |
| THz | Terahertz |
References
- Desmaris, V.; Rashid, H.; Pavolotsky, A.; Belitsky, V. Design, simulations and optimization of micromachined Golay-cell based THz sensors operating at room temperature. Procedia Chem. 2009, 1, 1175–1178. [Google Scholar] [CrossRef] [Green Version]
- Müller, R.; Bohmeyer, W.; Kehrt, M.; Lange, K.; Monte, C.; Steiger, A. Novel Detectors for Traceable THz Power Measurements. J. Infrared, Millim. Terahertz Waves 2014, 35, 659–670. [Google Scholar] [CrossRef] [Green Version]
- Simoens, F.; Meilhan, J. Terahertz real-time imaging uncooled array based on antenna- and cavity-coupled bolometers. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20130111. [Google Scholar] [CrossRef] [Green Version]
- Brown, E.R.; Young, A.C.; Zimmerman, J.; Kazerni, H.; Gossard, A.C. Advances in Schottky rectifier performance. IEEE Microw. Mag. 2007, 8, 54–59. [Google Scholar] [CrossRef]
- Hesler, J.L.; Crowe, T.W. Responsivity and noise measurements of zero-bias Schottky diode detectors. In Proceedings of the 18th International Symposium Space Terahertz Technology (ISSTT 2007), Pasadena, CA, USA, 21–23 March 2007; pp. 89–92. [Google Scholar]
- Sydlo, C.; Cojocari, O.; Schçnherr, D.; Goebel, T.; Meissner, P.; Hartnagel, H. Fast THz detectors based on InGaAs Schottky diodes. Frequenz 2008, 62, 107–110. [Google Scholar] [CrossRef]
- Al Hadi, R.; Sherry, H.; Grzyb, J.; Zhao, Y.; Forster, W.; Keller, H.M.; Cathelin, A.; Kaiser, A.; Pfeiffer, U.R. A 1 k-Pixel Video Camera for 0.7-1.1 Terahertz Imaging Applications in 65-nm CMOS. IEEE J. Solid-State Circuits 2012, 47, 2999–3012. [Google Scholar] [CrossRef]
- Lisauskas, A.; Bauer, M.; Boppel, S.; Mundt, M.; Khamaisi, B.; Socher, E.; Venckevičius, R.; Minkevičius, L.; Kašalynas, I.; Seliuta, D.; et al. Exploration of Terahertz Imaging with Silicon MOSFETs. J. Infrared Millim. Terahertz Waves 2014, 35, 63–80. [Google Scholar] [CrossRef]
- Boukhayma, A.; Dupret, A.; Rostaing, J.P.; Enz, C. A low-noise CMOS THz imager based on source modulation and an in-pixel high-Q passive switched-capacitor N-path filter. Sensors 2016, 16, 325. [Google Scholar] [CrossRef]
- Zdanevičius, J.; Bauer, M.; Boppel, S.; Palenskis, V.; Lisauskas, A.; Krozer, V.; Roskos, H.G. Camera for High-Speed THz Imaging. J. Infrared Millim. Terahertz Waves 2015, 36, 986–997. [Google Scholar] [CrossRef]
- Yokoyama, S.; Ikebe, M.; Kanazawa, Y.; Ikegami, T.; Ambalathankandy, P.; Hiramatsu, S.; Sano, E.; Takida, Y.; Minamide, H. 5.8 A 32 × 32-Pixel 0.9 THz Imager with Pixel-Parallel 12b VCO-Based ADC in 0.18 µm CMOS. In Proceedings of the 2019 IEEE International Solid- State Circuits Conference—(ISSCC), San Francisco, CA, USA, 17–21 February 2019; pp. 108–110. [Google Scholar] [CrossRef]
- Knap, W.; Kachorovskii, V.; Deng, Y.; Rumyantsev, S.; Lü, J.Q.; Gaska, R.; Shur, M.S.; Simin, G.; Hu, X.; Khan, M.A.; et al. Nonresonant detection of terahertz radiation in field effect transistors. J. Appl. Phys. 2002, 91, 9346. [Google Scholar] [CrossRef]
- Knap, W.; Teppe, F.; Meziani, Y.M.; Dyakonova, N.; Lusakowski, J.; Boeuf, F.; Skotnicki, T.; Maude, D.K.; Rumyantsev, S.; Shur, M.S. Plasma wave detection of sub-terahertz and terahertz radiation by silicon field-effect transistors. Appl. Phys. Lett. 2004, 85, 675. [Google Scholar] [CrossRef] [Green Version]
- Lisauskas, A.; Pfeiffer, U.; Öjefors, E.; Bolìvar, P.H.; Glaab, D.; Roskos, H.G. Rational design of high-responsivity detectors of terahertz radiation based on distributed self-mixing in silicon field-effect transistors. J. Appl. Phys. 2009, 105, 114511. [Google Scholar] [CrossRef]
- Dyakonov, M.I. Generation and detection of Terahertz radiation by field effect transistors. Comptes Rendus Phys. 2010, 11, 413–420. [Google Scholar] [CrossRef] [Green Version]
- Preu, S.; Kim, S.; Verma, R.; Burke, P.G.; Sherwin, M.S.; Gossard, A.C. An improved model for non-resonant terahertz detection in field-effect transistors. J. Appl. Phys. 2012, 111, 024502. [Google Scholar] [CrossRef]
- Boppel, S.; Lisauskas, A.; Mundt, M.; Seliuta, D.; Minkevičius, L.; Kašalynas, I.; Valusis, G.; Mittendorff, M.; Winnerl, S.; Krozer, V.; et al. CMOS Integrated Antenna-Coupled Field-Effect Transistors for the Detection of Radiation From 0.2 to 4.3 THz. IEEE Trans. Microw. Theory Tech. 2012, 60, 3834–3843. [Google Scholar] [CrossRef]
- Rudin, S.; Rupper, G.; Gutin, A.; Shur, M. Theory and measurement of plasmonic terahertz detector response to large signals. J. Appl. Phys. 2014, 115, 064503. [Google Scholar] [CrossRef]
- Zdanevičius, J.; Čibiraitė, D.; Ikamas, K.; Bauer, M.; Matukas, J.; Lisauskas, A.; Richter, H.; Hagelschuer, T.; Krozer, V.; Hübers, H.; et al. Field-Effect Transistor Based Detectors for Power Monitoring of THz Quantum Cascade Lasers. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 613–621. [Google Scholar] [CrossRef]
- Lu, J.Q.; Shur, M.; Hesler, J.; Sun, L.; Weikle, R. Terahertz detector utilizing two-dimensional electronic fluid. IEEE Electron Device Lett. 1998, 19, 373–375. [Google Scholar] [CrossRef]
- Tauk, R.; Teppe, F.; Boubanga, S.; Coquillat, D.; Knap, W.; Meziani, Y.M.; Gallon, C.; Boeuf, F.; Skotnicki, T.; Fenouillet-Beranger, C.; et al. Plasma wave detection of terahertz radiation by silicon field effects transistors: Responsivity and noise equivalent power. Appl. Phys. Lett. 2006, 89, 253511. [Google Scholar] [CrossRef] [Green Version]
- Javadi, E.; Lisauskas, A.; Shahabadi, M.; Masoumi, N.; Zhang, J.; Matukas, J.; Roskos, H.G. Terahertz Detection With a Low-Cost Packaged GaAs High-Electron-Mobility Transistor. IEEE Trans. Terahertz Sci. Technol. 2019, 9, 27–37. [Google Scholar] [CrossRef]
- Öjefors, E.; Baktash, N.; Zhao, Y.; Hadi, R.A.; Sherry, H.; Pfeiffer, U.R. Terahertz imaging detectors in a 65-nm CMOS SOI technology. In Proceedings of the 2010 Proceedings of ESSCIRC, Seville, Spain, 14–16 September 2010; pp. 486–489. [Google Scholar]
- Bauer, M.; Venckevičius, R.; Kašalynas, I.; Boppel, S.; Mundt, M.; Minkevičius, L.; Lisauskas, A.; Valušis, G.; Krozer, V.; Roskos, H.G. Antenna-coupled field-effect transistors for multi-spectral terahertz imaging up to 4.25 THz. Opt. Express 2014, 22, 19235. [Google Scholar] [CrossRef]
- Ferreras-Mayo, M.; Čibiraitė-Lukenskienė, D.; Lisauskas, A.; Grajal, J.; Krozer, V. Broadband sensing around 1 THz via a novel biquad-antenna-coupled low-NEP detector in CMOS. IEEE Trans. Terahertz Sci. Technol. 2020, 11, 16–27. [Google Scholar] [CrossRef]
- Ikamas, K.; Čibiraitė, D.; Lisauskas, A.; Bauer, M.; Krozer, V.; Roskos, H.G. Broadband Terahertz Power Detectors Based on 90-Nm Silicon CMOS Transistors with Flat Responsivity up to 2.2 THz. IEEE Electron Device Lett. 2018, 39. [Google Scholar] [CrossRef]
- Virginia Diodes, Inc. VDI Zero Bias Detector Specifications. Available online: https://www.vadiodes.com/en/products/detectors (accessed on 22 February 2021).
- Auton, G.; But, D.B.; Zhang, J.; Hill, E.; Coquillat, D.; Consejo, C.; Nouvel, P.; Knap, W.; Varani, L.; Teppe, F.; et al. Terahertz Detection and Imaging Using Graphene Ballistic Rectifiers. Nano Lett. 2017, 17, 7015–7020. [Google Scholar] [CrossRef]
- Zak, A.; Andersson, M.A.; Bauer, M.; Matukas, J.; Lisauskas, A.; Roskos, H.G.; Stake, J. Antenna-Integrated 0.6 THz FET Direct Detectors Based on CVD Graphene. Nano Lett. 2014, 14, 5834–5838. [Google Scholar] [CrossRef]
- Bauer, M.; Andersson, M.; Zak, A.; Sakalas, P.; Čibiraitė, D.; Lisauskas, A.; Schröter, M.; Stake, J.; Roskos, H.G. The potential for sensitivity enhancement by the thermoelectric effect in carbon-nanotube and graphene Tera-FETs. J. Phys. Conf. Ser. 2015, 647, 012004. [Google Scholar] [CrossRef] [Green Version]
- Viti, L.; Purdie, D.G.; Lombardo, A.; Ferrari, A.C.; Vitiello, M.S. HBN-Encapsulated, Graphene-based, Room-temperature Terahertz Receivers, with High Speed and Low Noise. Nano Lett. 2020, 20, 3169–3177. [Google Scholar] [CrossRef]
- Sizov, F.; Rogalski, A. THz detectors. Prog. Quantum Electron. 2010. [Google Scholar] [CrossRef]
- Sizov, F. Terahertz radiation detectors: The state-of-the-art. Semicond. Sci. Technol. 2018, 33, 123001. [Google Scholar] [CrossRef]
- Sizov, F.; Golenkov, A.; But, D.; Sakhno, M.; Reva, V. Sub-THz radiation room temperature sensitivity of long-channel silicon field effect transistors. Opto-Electron. Rev. 2012, 20, 194–199. [Google Scholar] [CrossRef]
- Sakhno, M.; Golenkov, A.; Sizov, F. Uncooled detector challenges: Millimeter-wave and terahertz long channel field effect transistor and Schottky barrier diode detectors. J. Appl. Phys. 2013, 114, 164503. [Google Scholar] [CrossRef]
- But, D.B.; Drexler, C.; Sakhno, M.V.; Dyakonova, N.; Drachenko, O.; Sizov, F.F.; Gutin, A.; Ganichev, S.D.; Knap, W. Nonlinear photoresponse of field effect transistors terahertz detectors at high irradiation intensities. J. Appl. Phys. 2014, 115, 164514. [Google Scholar] [CrossRef]
- Jain, R.; Zatta, R.; Grzyb, J.; Harame, D.; Pfeiffer, U.R. A Terahertz Direct Detector in 22 nm FD-SOI CMOS. In Proceedings of the 2018 13th European Microwave Integrated Circuits Conference (EuMIC), Madrid, Spain, 23–25 September 2018; IEEE: Madrid, Spain, 2018; pp. 25–28. [Google Scholar] [CrossRef]
- Volakis, J.L. (Ed.) Antenna Engineering Handbook, 4th ed.; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- Al Hadi, R.; Grzyb, J.; Heinemann, B.; Pfeiffer, U.R. A Terahertz Detector Array in a SiGe HBT Technology. IEEE J. Solid-State Circuits 2013, 48, 2002–2010. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Liu, L.Y.; Yang, J.; Wu, N.J. A CMOS fully integrated 860-GHz terahertz sensor. IEEE Trans. Terahertz Sci. Technol. 2017, 7, 455–465. [Google Scholar] [CrossRef]
- Han, R.; Zhang, Y.; Kim, Y.; Kim, D.Y.; Shichijo, H.; Afshari, E.; Kenneth, K.O. Active terahertz imaging using Schottky diodes in CMOS: Array and 860-GHz pixel. IEEE J. Solid-State Circuits 2013, 48, 2296–2308. [Google Scholar] [CrossRef]
- Javadi, E.; Delgado-Notario, J.A.; Masoumi, N.; Shahabadi, M.; Velázquez-Pérez, J.E.; Meziani, Y.M. Continuous Wave Terahertz Sensing Using GaN HEMTs. Phys. Status Solidi 2018, 215, 1700607. [Google Scholar] [CrossRef]
- Ahmad, Z.; Kenneth, K.O. THz Detection Using p+/n-Well Diodes Fabricated in 45-nm CMOS. IEEE Electron Device Lett. 2016, 37, 823–826. [Google Scholar] [CrossRef]
- But, D.B.; Javadi, E.; Knap, W.; Ikamas, K.; Lisauskas, A. Silicon based resonant power detector for 620 GHz. In Proceedings of the 2020 23rd International Microwave and Radar Conference (MIKON), Warsaw, Poland, 5–8 October 2020; pp. 305–308. [Google Scholar] [CrossRef]
- Karolyi, G.; Gergelyi, D.; Foldesy, P. Sub-THz Sensor Array With Embedded Signal Processing in 90 nm CMOS Technology. IEEE Sens. J. 2014, 14, 2432–2441. [Google Scholar] [CrossRef]
- Shaulov, E.; Jameson, S.; Socher, E. A Zero Bias J-Band Antenna-Coupled Detector in 65-nm CMOS. IEEE Trans. Terahertz Sci. Technol. 2021, 11, 62–69. [Google Scholar] [CrossRef]
- Fang, T.; Liu, Z.Y.; Liu, L.Y.; Li, Y.Y.; Liu, J.Q.; Liu, J.; Wu, N.J. Detection of 3.0 THz wave with a detector in 65 nm standard CMOS process. In Proceedings of the 2017 IEEE Asian Solid-State Circuits Conference (A-SSCC), Seoul, Korea, 6–8 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 189–192. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory: Analysis and Design, 4th ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Pfeiffer, U.; Grzyb, J.; Sherry, H.; Cathelin, A.; Kaiser, A. Toward low-NEP room-temperature THz MOSFET direct detectors in CMOS technology. In Proceedings of the 38th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Mainz, Germany, 1–6 September 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–2. [Google Scholar]
- Jain, R.; Rücker, H.; Pfeiffer, U.R. Zero gate-bias terahertz detection with an asymmetric NMOS transistor. In Proceedings of the 2016 41st International Conference on Infrared, Millimeter, and Terahertz waves (IRMMW-THz), Copenhagen, Denmark, 25–30 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–2. [Google Scholar]
- Sherry, H.; Al Hadi, R.; Grzyb, J.; Öjefors, E.; Cathelin, A.; Kaiser, A.; Pfeiffer, U.R. Lens-integrated THz imaging arrays in 65 nm CMOS technologies. In Proceedings of the 2011 IEEE Radio Frequency Integrated Circuits Symposium, Baltimore, MD, USA, 5–7 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–4. [Google Scholar]
- Kim, D.Y.; Park, S.; Han, R.; Kenneth, K. Design and demonstration of 820-GHz array using diode-connected NMOS transistors in 130-nm CMOS for active imaging. IEEE Trans. Terahertz Sci. Technol. 2016, 6, 306–317. [Google Scholar] [CrossRef]
- Ojefors, E.; Pfeiffer, U.R.; Lisauskas, A.; Roskos, H.G. A 0.65 THz Focal-Plane Array in a Quarter-Micron CMOS Process Technology. IEEE J. Solid-State Circuits 2009, 44, 1968–1976. [Google Scholar] [CrossRef]
- Sengupta, K.; Seo, D.; Yang, L.; Hajimiri, A. Silicon Integrated 280 GHz Imaging Chipset With 4 × 4 SiGe Receiver Array and CMOS Source. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 427–437. [Google Scholar] [CrossRef]
- Watanabe, T.; Tombet, S.B.; Tanimoto, Y.; Wang, Y.; Minamide, H.; Ito, H.; Fateev, D.; Popov, V.; Coquillat, D.; Knap, W.; et al. Ultrahigh sensitive plasmonic terahertz detector based on an asymmetric dual-grating gate HEMT structure. Solid-State Electron. Pergamon 2012, 78, 109–114. [Google Scholar] [CrossRef]
- Giliberti, V.; Di Gaspare, A.; Giovine, E.; Boppel, S.; Lisauskas, A.; Roskos, H.G.; Ortolani, M. Heterodyne and subharmonic mixing at 0.6 THz in an AlGaAs/InGaAs/AlGaAs heterostructure field effect transistor. Appl. Phys. Lett. 2013, 103, 093505. [Google Scholar] [CrossRef]
- Sun, J.D.; Sun, Y.F.; Wu, D.M.; Cai, Y.; Qin, H.; Zhang, B.S. High-responsivity, low-noise, room-temperature, self-mixing terahertz detector realized using floating antennas on a GaN-based field-effect transistor. Appl. Phys. Lett. 2012, 100, 013506. [Google Scholar] [CrossRef]
- Rumyantsev, S.; Fobelets, K.; Veksler, D.; Hackbarth, T.; Shur, M. Strained-Si modulation doped field effect transistors as detectors of terahertz and sub-terahertz radiation. Semicond. Sci. Technol. 2008, 23, 105001. [Google Scholar] [CrossRef] [Green Version]
- Spirito, D.; Coquillat, D.; De Bonis, S.L.; Lombardo, A.; Bruna, M.; Ferrari, A.C.; Pellegrini, V.; Tredicucci, A.; Knap, W.; Vitiello, M.S. High performance bilayer-graphene terahertz detectors. Appl. Phys. Lett. 2014, 104, 061111. [Google Scholar] [CrossRef] [Green Version]
- Delgado-Notario, J.; Clericò, V.; Diez, E.; Velázquez-Pérez, J.; Taniguchi, T.; Watanabe, K.; Otsuji, T.; Meziani, Y. Asymmetric dual-grating gates graphene FET for detection of terahertz radiations. APL Photonics 2020, 5, 066102. [Google Scholar] [CrossRef]
- Vicarelli, L.; Vitiello, M.; Coquillat, D.; Lombardo, A.; Ferrari, A.C.; Knap, W.; Polini, M.; Pellegrini, V.; Tredicucci, A. Graphene field-effect transistors as room-temperature terahertz detectors. Nat. Mater. 2012, 11, 865–871. [Google Scholar] [CrossRef]
- Vitiello, M.S.; Coquillat, D.; Viti, L.; Ercolani, D.; Teppe, F.; Pitanti, A.; Beltram, F.; Sorba, L.; Knap, W.; Tredicucci, A. Room-temperature terahertz detectors based on semiconductor nanowire field-effect transistors. Nano Lett. 2012, 12, 96–101. [Google Scholar] [CrossRef]
- Viti, L.; Hu, J.; Coquillat, D.; Politano, A.; Knap, W.; Vitiello, M.S. Efficient terahertz detection in black-phosphorus nano-transistors with selective and controllable plasma-wave, bolometric and thermoelectric response. Sci. Rep. 2016, 6, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Romeo, L.; Coquillat, D.; Pea, M.; Ercolani, D.; Beltram, F.; Sorba, L.; Knap, W.; Tredicucci, A.; Vitiello, M. Nanowire-based field effect transistors for terahertz detection and imaging systems. Nanotechnology 2013, 24, 214005. [Google Scholar] [CrossRef]
- Viti, L.; Hu, J.; Coquillat, D.; Knap, W.; Tredicucci, A.; Politano, A.; Vitiello, M.S. Black phosphorus terahertz photodetectors. Adv. Mater. 2015, 27, 5567–5572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grzyb, J.; Andree, M.; Jain, R.; Heinemann, B.; Pfeiffer, U.R. A Lens-Coupled On-Chip Antenna for Dual-Polarization SiGe HBT THz Direct Detector. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2404–2408. [Google Scholar] [CrossRef]
- Andree, M.; Grzyb, J.; Jain, R.; Heinemann, B.; Pfeiffer, U.R. A Broadband Antenna-Coupled Terahertz Direct Detector in a 0.13-μm SiGe HBT Technology. In Proceedings of the 14th European Microwave Integrated Circuits Conference (EuMIC), Paris, France, 30 September–1 October 2019; IEEE: Paris, France, 2019; pp. 168–171. [Google Scholar] [CrossRef]
- Andree, M.; Grzyb, J.; Jain, R.; Heinemann, B.; Pfeiffer, U.R. A Broadband Dual-Polarized Terahertz Direct Detector in a 0.13-μm SiGe HBT Technology. In Proceedings of the IEEE MTT-S International Microwave Symposium (IMS), Boston, MA, USA, 2–7 June 2019; IEEE: Boston, MA, USA, 2019; pp. 500–503. [Google Scholar] [CrossRef]
- De Vroede, A.; Reynaert, P. 23.3 A 605 GHz 0.84 mW Harmonic Injection-Locked Receiver Achieving 2.3 pW/Hz NEP in 28 nm CMOS. In Proceedings of the IEEE International Solid- State Circuits Conference (ISSCC), San Francisco, CA, USA, 13–22 February 2021; IEEE: San Francisco, CA, USA, 2021; pp. 328–330. [Google Scholar] [CrossRef]
- Hillger, P.; Grzyb, J.; Jain, R.; Pfeiffer, U.R. Terahertz Imaging and Sensing Applications With Silicon-Based Technologies. IEEE Trans. Terahertz Sci. Technol. 2019, 9, 1–19. [Google Scholar] [CrossRef]
- Generalov, A.A.; Andersson, M.A.; Yang, X.; Vorobiev, A.; Stake, J. A 400-GHz Graphene FET Detector. IEEE Trans. Terahertz Sci. Technol. 2017, 7, 614–616. [Google Scholar] [CrossRef]
- Bauer, M.; Rämer, A.; Chevtchenko, S.A.; Osipov, K.Y.; Čibiraitė, D.; Pralgauskaitė, S.; Ikamas, K.; Lisauskas, A.; Heinrich, W.; Krozer, V.; et al. A high-sensitivity AlGaN/GaN HEMT terahertz detector with integrated broadband bow-tie antenna. IEEE Trans. Terahertz Sci. Technol. 2019, 9, 430–444. [Google Scholar] [CrossRef]
- Bandurin, D.A.; Svintsov, D.; Gayduchenko, I.; Xu, S.G.; Principi, A.; Moskotin, M.; Tretyakov, I.; Yagodkin, D.; Zhukov, S.; Taniguchi, T.; et al. Resonant terahertz detection using graphene plasmons. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bauer, M.; Rämer, A.; Boppel, S.; Chevtchenko, S.; Lisauskas, A.; Heinrich, W.; Krozer, V.; Roskos, H.G. High-sensitivity wideband THz detectors based on GaN HEMTs with integrated bow-tie antennas. In Proceedings of the 2015 10th European Microwave Integrated Circuits Conference (EuMIC), Paris, France, 7–8 September 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–4. [Google Scholar]
- Sangaré, P.; Ducournau, G.; Grimbert, B.; Brandli, V.; Faucher, M.; Gaquière, C.; De-La-Torre, A.Í.; De-La-Torre, I.Í.; Millithaler, J.F.; Mateos, J.; et al. Experimental demonstration of direct terahertz detection at room-temperature in AlGaN/GaN asymmetric nanochannels. J. Appl. Phys. 2013, 113, 034305. [Google Scholar] [CrossRef] [Green Version]
- Blin, S.; Teppe, F.; Tohme, L.; Hisatake, S.; Arakawa, K.; Nouvel, P.; Coquillat, D.; Pénarier, A.; Torres, J.; Varani, L.; et al. Plasma-wave detectors for terahertz wireless communication. IEEE Electron Device Lett. 2012, 33, 1354–1356. [Google Scholar] [CrossRef]
- Bandurin, D.; Gayduchenko, I.; Cao, Y.; Moskotin, M.; Principi, A.; Grigorieva, I.; Goltsman, G.; Fedorov, G.; Svintsov, D. Dual origin of room temperature sub-terahertz photoresponse in graphene field effect transistors. Appl. Phys. Lett. 2018, 112, 141101. [Google Scholar] [CrossRef] [Green Version]
- Degl’Innocenti, R.; Xiao, L.; Jessop, D.S.; Kindness, S.J.; Ren, Y.; Lin, H.; Zeitler, J.A.; Alexander-Webber, J.A.; Joyce, H.J.; Braeuninger-Weimer, P.; et al. Fast room-temperature detection of terahertz quantum cascade lasers with graphene-loaded bow-tie plasmonic antenna arrays. ACS Photonics 2016, 3, 1747–1753. [Google Scholar] [CrossRef] [Green Version]
- Elkhatib, T.A.; Kachorovskii, V.Y.; Stillman, W.J.; Veksler, D.B.; Salama, K.N.; Zhang, X.C.; Shur, M.S. Enhanced plasma wave detection of terahertz radiation using multiple high electron-mobility transistors connected in series. IEEE Trans. Microw. Theory Tech. 2010, 58, 331–339. [Google Scholar] [CrossRef]
- Wiecha, M.M.; Kapoor, R.; Chernyadiev, A.V.; Ikamas, K.; Lisauskas, A.; Roskos, H.G. Antenna-coupled field-effect transistors as detectors for terahertz near-field microscopy. Nanoscale Adv. 2021. [Google Scholar] [CrossRef]
- Schuster, F.; Coquillat, D.; Videlier, H.; Sakowicz, M.; Teppe, F.; Dussopt, L.; Giffard, B.; Skotnicki, T.; Knap, W. Broadband terahertz imaging with highly sensitive silicon CMOS detectors. Opt. Express 2011, 19, 7827. [Google Scholar] [CrossRef] [PubMed]
- Nahar, S.; Gutin, A.; Muraviev, A.; Wilke, I.; Shur, M.; Hella, M.M. Terahertz detection using on chip patch and dipole antenna-coupled GaAs High Electron Mobility Transistors. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS2014), Tampa, FL, USA, 1–6 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–4. [Google Scholar]
- Kurita, Y.; Ducournau, G.; Coquillat, D.; Satou, A.; Kobayashi, K.; Boubanga Tombet, S.; Meziani, Y.; Popov, V.; Knap, W.; Suemitsu, T.; et al. Ultrahigh sensitive sub-terahertz detection by InP-based asymmetric dual-grating-gate high-electron-mobility transistors and their broadband characteristics. Appl. Phys. Lett. 2014, 104, 251114. [Google Scholar] [CrossRef] [Green Version]
- Ryu, M.W.; Kim, K.S.; Lee, J.S.; Park, K.; Yang, J.R.; Han, S.T.; Kim, K.R. Performance Enhancement of Plasmonic Sub-Terahertz Detector Based on Antenna Integrated Low-Impedance Silicon MOSFET. IEEE Electron Device Lett. 2015, 36, 220–222. [Google Scholar] [CrossRef]
- Castilla, S.; Terrés, B.; Autore, M.; Viti, L.; Li, J.; Nikitin, A.Y.; Vangelidis, I.; Watanabe, K.; Taniguchi, T.; Lidorikis, E.; et al. Fast and sensitive terahertz detection using an antenna-integrated graphene pn junction. Nano Lett. 2019, 19, 2765–2773. [Google Scholar] [CrossRef]
- Perenzoni, M. Measurement of spatial response of CMOS antenna-coupled FET detector at 325 GHz. In Proceedings of the 2014 39th International Conference on Infrared, Millimeter, and Terahertz waves (IRMMW-THz), Tucson, AZ, USA, 14–19 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–2. [Google Scholar]
- Ali, M.; Perenzoni, M.; Stoppa, D. A methodology to measure input power and effective area for characterization of direct THz detectors. IEEE Trans. Instrum. Meas. 2016, 65, 1225–1231. [Google Scholar] [CrossRef]
- Martín-Mateos, P.; Čibiraitė Lukenskienė, D.; Barreiro, R.; de Dios, C.; Lisauskas, A.; Krozer, V.; Acedo, P. Hyperspectral terahertz imaging with electro-optic dual combs and a FET-based detector. Sci. Rep. 2020, 10, 1–7. [Google Scholar] [CrossRef]
- Hou, H.; Liu, Z.; Teng, J.; Palacios, T.; Chua, S.J. A sub-terahertz broadband detector based on a GaN high-electron-mobility transistor with nanoantennas. Appl. Phys. Express 2016, 10, 014101. [Google Scholar] [CrossRef]
- Regensburger, S.; Preu, S.; Mukherjee, A.K.; Schonhuber, S.; Kainz, M.A.; Winnerl, S.; Klopf, J.M.; Lu, H.; Gossard, A.C.; Unterrainer, K. Broadband Terahertz Detection With Zero-Bias Field-Effect Transistors Between 100 GHz and 11.8 THz With a Noise Equivalent Power of 250 pW/Hz at 0.6 THz. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 465–471. [Google Scholar] [CrossRef]
- Qin, H.; Li, X.; Sun, J.; Zhang, Z.; Sun, Y.; Yu, Y.; Li, X.; Luo, M. Detection of incoherent terahertz light using antenna-coupled high-electron-mobility field-effect transistors. Appl. Phys. Lett. 2017, 110, 171109. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Vorobiev, A.; Generalov, A.; Andersson, M.A.; Stake, J. A flexible graphene terahertz detector. Appl. Phys. Lett. 2017, 111, 021102. [Google Scholar] [CrossRef] [Green Version]
- Roggenbuck, A.; Schmitz, H.; Deninger, A.; Mayorga, I.C.; Hemberger, J.; Güsten, R.; Grüninger, M. Coherent broadband continuous-wave terahertz spectroscopy on solid-state samples. New J. Phys. 2010, 12, 043017. [Google Scholar] [CrossRef]
- TOPTICA Photonics, Inc. TeraScan 780/1550 Brochure. Available online: https://www.toptica.com/fileadmin/Editors_English/11_brochures_datasheets/01_brochures/toptica_BR_THz_TeraScan.pdf (accessed on 21 February 2021).
- Deninger, A.J.; Roggenbuck, A.; Schindler, S.; Preu, S. 2.75 THz tuning with a triple-DFB laser system at 1550 nm and InGaAs photomixers. J. Infrared Millim. Terahertz Waves 2015, 36, 269–277. [Google Scholar] [CrossRef] [Green Version]
- Brown, E.R.; Smith, F.W.; McIntosh, K.A. Coherent millimeter-wave generation by heterodyne conversion in low-temperature-grown GaAs photoconductors. J. Appl. Phys. 1993, 73, 1480–1484. [Google Scholar] [CrossRef] [Green Version]
- Stephenson, D.; Strauch, R. Water vapor spectrum near 600 GHz. J. Mol. Spectrosc. 1970, 35, 494–495. [Google Scholar] [CrossRef]
- Andersen, J.; Frandsen, A. Absorption efficiency of receiving antennas. IEEE Trans. Antennas Propag. 2005, 53, 2843–2849. [Google Scholar] [CrossRef] [Green Version]
- Socher, E.; Shannan, H.; Kastner, R. On the physical aperture and the power that exits a surface enclosing a receiving antenna. E-FERMAT 2015, 7, 1–6. [Google Scholar]
- Coquillat, D.; Marczewski, J.; Kopyt, P.; Dyakonova, N.; Giffard, B.; Knap, W. Improvement of terahertz field effect transistor detectors by substrate thinning and radiation losses reduction. Opt. Express 2016, 272–281. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sakhno, M.; Gumenjuk-Sichevska, J.; Sizov, F. Modeling of the substrate influence on multielement THz detector operation. J. Infrared Millim. Terahertz Waves 2014, 35, 703–719. [Google Scholar] [CrossRef]
- Sakhno, M.; Gumenjuk-Sichevska, J.; Sizov, F. Modeling of THz detector antenna on conductive substrate. In Proceedings of the 2016 9th International Kharkiv Symposium on Physics and Engineering of Microwaves, Millimeter and Submillimeter Waves (MSMW), Kharkiv, Ukraine, 20–24 June 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Čibiraitė, D.; Bauer, M.; Lisauskas, A.; Krozer, V.; Roskos, H.G.; Rämer, A.; Krozer, V.; Heinrich, W.; Pralgauskaitė, S.; Zdanevičius, J.; et al. Thermal noise-limited sensitivity of FET-based terahertz detectors. In Proceedings of the 2017 International Conference on Noise and Fluctuations (ICNF), Vilnius, Lithuania, 20–23 June 2017; pp. 1–4. [Google Scholar] [CrossRef]








| Method for calculation of | Comment | Ref. |
|---|---|---|
| I. From the antenna gain | This is a widely accepted method in the field of microwave antennas, which has been described in textbooks and simulation tools. It accounts for the power loss due to antenna efficiency and allows for estimating the power which is applied to the detector circuit. | [34,35,36,37], [38] (pp. 1–10) |
| II. From the maximal directivity | This definition describes the maximum antenna effective aperture. Therefore, it is best suited for the determination and comparison of optical characteristics of detectors. | [17,19,24,39,40,41,42,43,44,45,46,47], [48] (p. 92) |
| III. Physical area | In multipixel imaging arrays with overlapping effective areas, the detector pixel size can be approximated by the pitch between devices. However, it must be assured that the devices do not form a dielectric antenna structure. In some works, the physical area has been specified as the aperture of the substrate lens. | [9,10,11,23,39,49,50,51,52,53,54,55,56,57] |
| IV. Area of the diffraction-limited spot | This area is often used for devices without dedicated antennas. It has been claimed to be a conservative estimate; however, in most cases, it leads to the substantial overestimation of detector performance. | [31,58,59,60,61,62,63,64,65] |
| V. Normalised for the omnidirectional antenna case | This area is used for devices with known (simulated or measured) directivity, by normalising it to unity for the omnidirectional antenna case (in other words, the antenna gain is de-embedded) and, for devices without dedicated antennas, it is interpreted as a circular-shaped diffraction-limited spot. | [28,66,67,68,69,70] |
| VI. Without any normalisation | The optical performance without normalisation of the incident power is relevant for a wide range of applications, such as raster-scan imaging, spectroscopy, and other systems exploiting point-to-point configurations. The performance values obtained in this way can be compared with that of commercially available devices, such as bolometers, Golay cells, pyroelectric sensors, or quasioptically coupled Schottky diode detectors. | [26,29,71,72,73,74,75,76,77,78,79,80] |
| Technology | Freq. | Antenna | NEP | Responsivity | Single or Array | Method-Ology * | Ref. |
|---|---|---|---|---|---|---|---|
| GHz | pW/ | V/W | |||||
| MOSFET, 90 nm CMOS | 250 | Slot + Si lens | 21 | 408 | Single | VI | [80] |
| MOSFET, 90 nm CMOS | 250–750 | Various | 40 | 185 k ** | Single | II | [45] |
| HBT, 130 nm SiGe | 292 | Wire ring + Si lens | 1.9 | 9 k | Single | V | [67] |
| MOSFET, 90 nm CMOS | 300 | Slot + Si lens | 20.8 | 55 k ** | Single | VI | [88] |
| MOSFET, 90 nm CMOS | 300–1500 | Bow-tie + Si lens | 48–70 | 45 | Single | VI | [26] |
| MOSFET, 65 nm CMOS | 315 | CSDRA | 3.5 | 2 k | Single | II | [46] |
| HBT, 130 nm SiGe | 430 | Wire-ring +Si lens | 2.7 | 5 k | Single | V | [68] |
| MOSFET, 90 nm CMOS | 590 | Patch | 20 | - | Single | II | [24] |
| MOSFET, 150 nm CMOS | 595 | Patch | 42 | 350 | Single | II | [17] |
| MOSFET, 130 nm CMOS | 600 | Bow-tie | 25.9 | 216 k ** | Array 31 × 31 | III | [9] |
| MOSFET, 150 nm CMOS | 600 | Patch | 43 | 300 | Array 24 × 24 | III | [10] |
| MOSFET, 22 nm FD-SOI CMOS | 605 | Double-folded dipole + Si lens | 2.3 | 32 k | Single | V | [69] |
| MOSFET, 65 nm SOI CMOS | 650 | Folded dipole + Si lens | 17 | 1930 | Array 3 × 5 | III | [51] |
| MOSFET, 130 nm SiGe BiCMOS | 650 | Ring + Si lens | 80 | 450 | Single | III | [50] |
| MOSFET, 250 nm CMOS | 650 | Patch | 300 | 80 k ** | Array 3 × 5 | III | [53] |
| HBT, 250 nm SiGe | 700 | Ring + Si lens | 50 | 1 A/W | Array 3 × 5 | II | [39] |
| MOSFET, 65 nm Si CMOS | 724 | Ring + Si lens | 14 | 2200 | Single | III | [49] |
| P-N diode, 45 nm CMOS | 781 | Patch | 56 | 558 | Single | II | [43] |
| Diode-connected MOSFET, 130 nm CMOS | 823 | Patch | 36.2 | 2560 | Array 8 × 8 | III | [52] |
| MOSFET, 22 nm FD-SOI CMOS | 855 | Ring + Si lens | 12 | 0.180 [A/W] | Single | I | [37] |
| MOSFET, 180 nm CMOS | 860 | Patch | 106 | 3300 | Array 3 × 5 | II | [40] |
| SBD, 130 nm CMOS | 860 | Patch | 42 | 273 | Single | II | [41] |
| MOSFET, 65 nm CMOS | 1000 | Bi-quad + Si lens | 25 | 765 | Single | VI | [25] |
| MOSFET, 90 nm CMOS | 2520 3110 4250 | Patch | 63 85 110 | 336 308 230 | Single | II | [8] |
| MOSFET, 65 nm CMOS | 3000 | Patch | 73 | 526 | Array 12 × 9 | II | [47] |
| MOSFET, 65 nm CMOS | 620 | Patch | 19.2 | 1400 | Array 2 × 7 | II | This work |
| Technology | Freq. | Antenna | Min. NEP | Responsivity | Single or Array | Method-Ology | Ref. |
|---|---|---|---|---|---|---|---|
| GHz | pW/ | V/W | |||||
| GaN HEMT | 140 | Nano-antenna | 0.58 | 15.5 k | Single | III ** | [89] |
| DGG-HEMT, InAlAs/ InGaAs/InP | 200 | Grating coupling | 0.48 | 22.7 | Single | III | [83] |
| GaAs HEMT | 271, 632 | - | 135, 1250 | 42, 1.6 | Single | II | [42] |
| AlGaN/GaN SSD | 300 | - | 280 | 100 | Array | VI | [75] |
| GaAs HEMT | 300 | Dipole | 9.1 | 8.5 k | Single | III | [82] |
| GaAs/AlGaAs FET | 305 | - | 1330 | 11 | Single | VI | [76] |
| AlGaN/GaN HEMT | 490–645 | Bow-tie + Si lens | 25–31 | 104 [mA/W] | Single | VI | [72] |
| InGaAs/AlGaAs HFET | 592 | Bow-tie + Si lens | 500 | 20 | Single | III | [56] |
| AlGaAs/GaAs HEMT | 600 | Log-spiral + Si lens | 250 | 20–40 [mA/W] | Single | VI | [90] |
| AlGaN/GaN HEMT | 700–925 | Assym. dipole + Si lens | 30 | - | Single | III | [91] |
| AlGaN/GaN HEMT | 897 | Assym. dipole | 40 | 3.6 k | Single | III | [57] |
| AlGaN/GaN HEMT | 900 | Bow-tie + Si lens | 57 | 48 [mA/W] | Single | VI | [74] |
| DGG-HEMT, InAlAs/InGaAs/InP | 1000 | Grating coupling | 15 | 2.2 k | Single | III | [55] |
| InGaAs/GaAs | 1630 | - | 170 | Single | VI | [79] |
| Technology | Freq. | Antenna | Min. NEP | Responsivity | Single or Array | Method-Ology * | Ref. |
|---|---|---|---|---|---|---|---|
| GHz | pW/ | V/W | |||||
| GFET | 130–450 | logarithmic spiral | 600 | 20 | Single | VI | [77] |
| BL-GFET | 290–380 | – | 2000 | 1.2 | Single | IV | [59] |
| BP-based FET | 300 | Bow-tie | - | Single | IV | [63] | |
| BP-based FET | 300 | Bow-tie | 0.15 | Single | IV | [65] | |
| DGG-GFET | 300 | - | - | Single | IV | [60] | |
| Graphene Ballistic Rectifier | 300 | Bow-tie | 34 | 764 | Single | V | [28] |
| Nanowire-FET | 300 | Bow-tie | 1.5 | Single | IV | [62] | |
| Nanowire-FET | 300 | Bow-tie | 1000 | 100 | Single | IV | [64] |
| SL-GFET, BL-GFET | 300 | a log-periodic circular-toothed | (SLG) (BLG) | - | Single | IV | [61] |
| GFET | 400 | Bow-tie | 130 | 74 | Single | VI | [71] |
| GFET | 487 | Bow-tie | 3000 | 2 | Single | VI | [92] |
| GFET | 600 | Bow-tie | 515 | 14 | Single | VI | [29] |
| Graphene | 2000 | Bow-tie | - | Array | VI | [78] | |
| GFET | 2800 | Bow-tie | 160 | - | Single | IV | [31] |
| D | D | |||||
|---|---|---|---|---|---|---|
| Detector | Meas. | Meas. | Sim. | Sim. | ||
| (deg) | (deg) | (dBi) | (mm) | (dBi) | (mm) | |
| C | 87 | 47 | 8.70 | 0.138 | 8.65 | 0.136 |
| C | 93 | 38 | 8.58 | 0.134 | 8.43 | 0.130 |
| C | 94 | 35 | 8.59 | 0.134 | 8.65 | 0.136 |
| C | 93 | 32 | 8.76 | 0.140 | 8.45 | 0.130 |
| C | 93 | 36 | 8.60 | 0.136 | 8.73 | 0.139 |
| C | 90 | 38 | 8.82 | 0.142 | 8.59 | 0.134 |
| C | 85 | 46 | 8.90 | 0.145 | 7.83 | 0.113 |
| Method | Max. Responsivity | Min.NEP | |
|---|---|---|---|
| (mm) | (V/W) | (pW/) | |
| Measured directivity of the detector in array D = 8.7 dBi) | 0.138 | 1414 | 19.2 |
| Simulated directivity of single detector D = 6 dBi | 0.074 | 2651 | 10.28 |
| Physical area defined by the pitch between devices | 0.077 | 2545 | 10.7 |
| Area of diffraction limited spot | 0.058 | 3368 | 8.09 |
| From the antenna gain () | 0.069 | 2828 | 9.6 |
| Normalised for the omnidirectional antenna case | 0.018 | 10.8 K | 2.5 |
| Without any normalisation (Optical performance) | 63.6 | 428 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javadi, E.; But, D.B.; Ikamas, K.; Zdanevičius, J.; Knap, W.; Lisauskas, A. Sensitivity of Field-Effect Transistor-Based Terahertz Detectors. Sensors 2021, 21, 2909. https://doi.org/10.3390/s21092909
Javadi E, But DB, Ikamas K, Zdanevičius J, Knap W, Lisauskas A. Sensitivity of Field-Effect Transistor-Based Terahertz Detectors. Sensors. 2021; 21(9):2909. https://doi.org/10.3390/s21092909
Chicago/Turabian StyleJavadi, Elham, Dmytro B. But, Kęstutis Ikamas, Justinas Zdanevičius, Wojciech Knap, and Alvydas Lisauskas. 2021. "Sensitivity of Field-Effect Transistor-Based Terahertz Detectors" Sensors 21, no. 9: 2909. https://doi.org/10.3390/s21092909
APA StyleJavadi, E., But, D. B., Ikamas, K., Zdanevičius, J., Knap, W., & Lisauskas, A. (2021). Sensitivity of Field-Effect Transistor-Based Terahertz Detectors. Sensors, 21(9), 2909. https://doi.org/10.3390/s21092909







