The 20k Samples-Per-Second Real Time Detection of Acoustic Vibration Based on Displacement Estimation of One-Dimensional Laser Speckle Images
Abstract
:1. Introduction
2. Materials and Methods
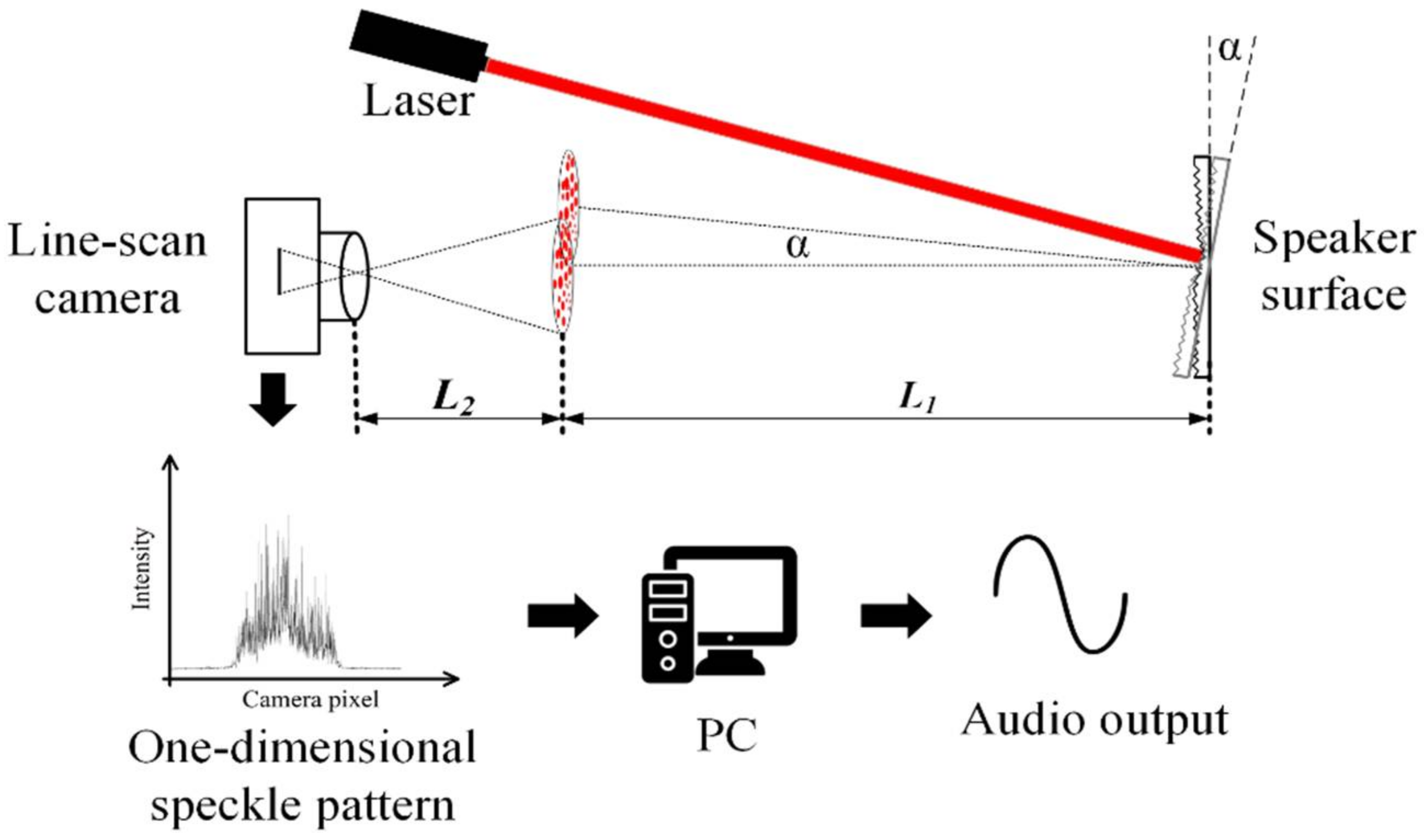
2.1. Speckle Sensing Model
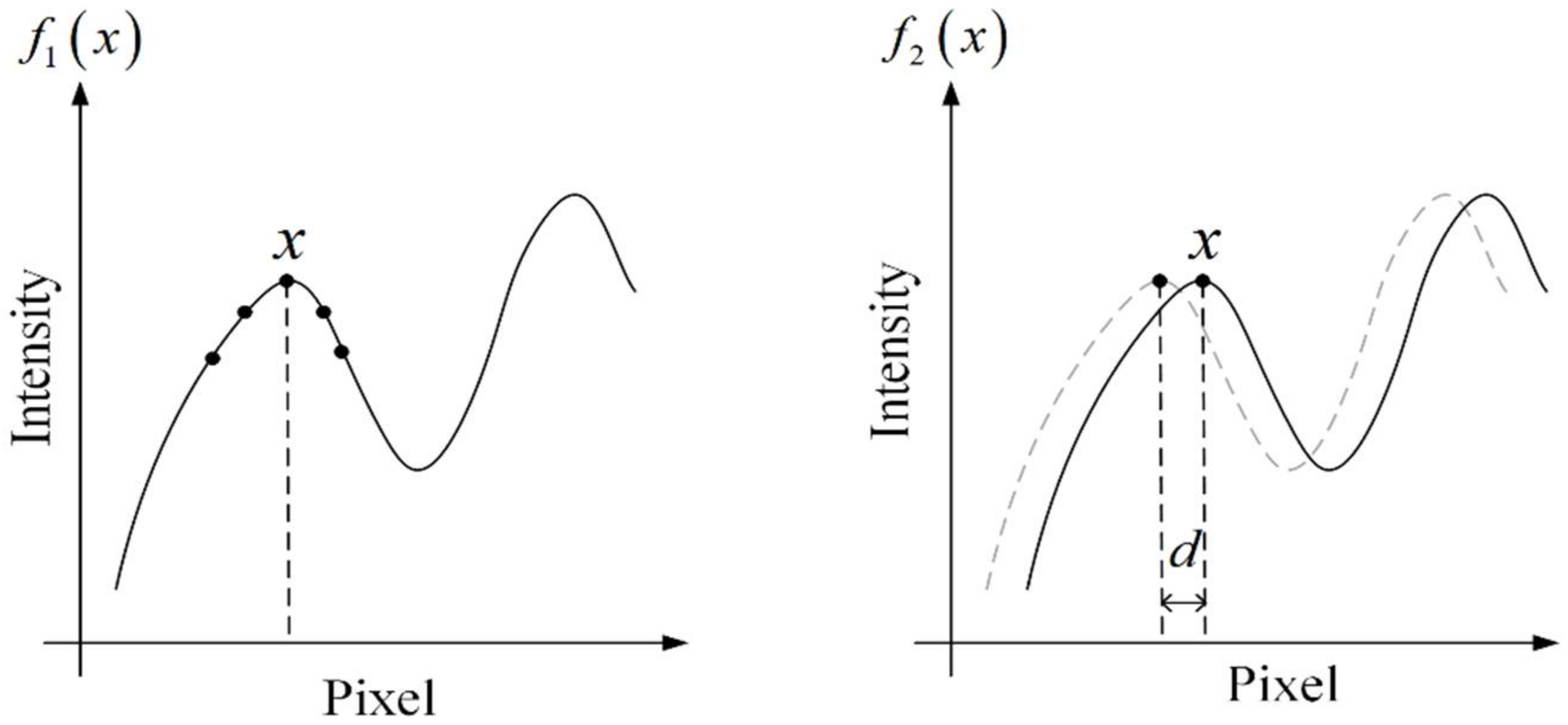
2.2. Explanation of 1D Optical Flow Algorithm for Displacement Estimation
3. Experiment Results
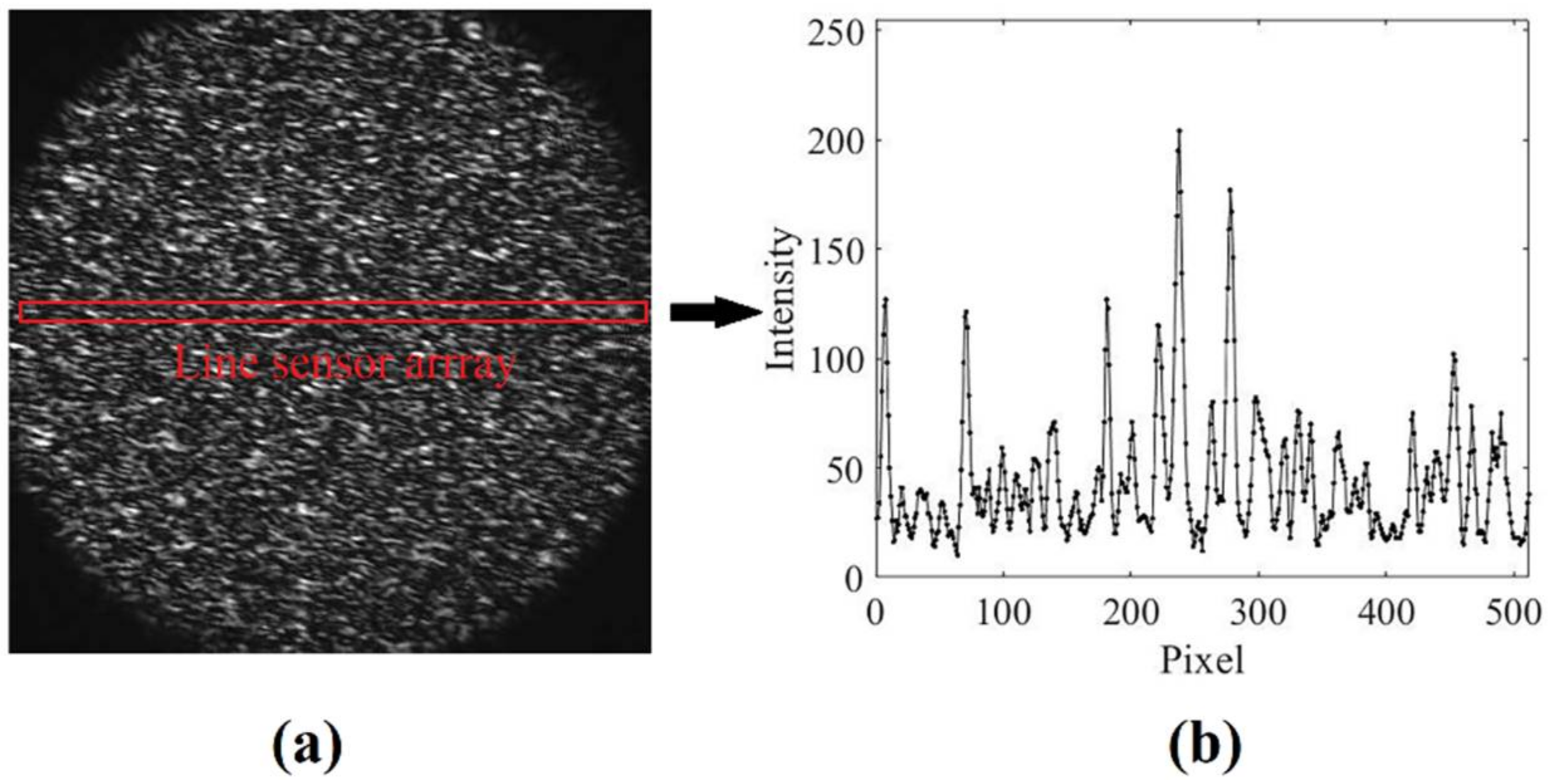
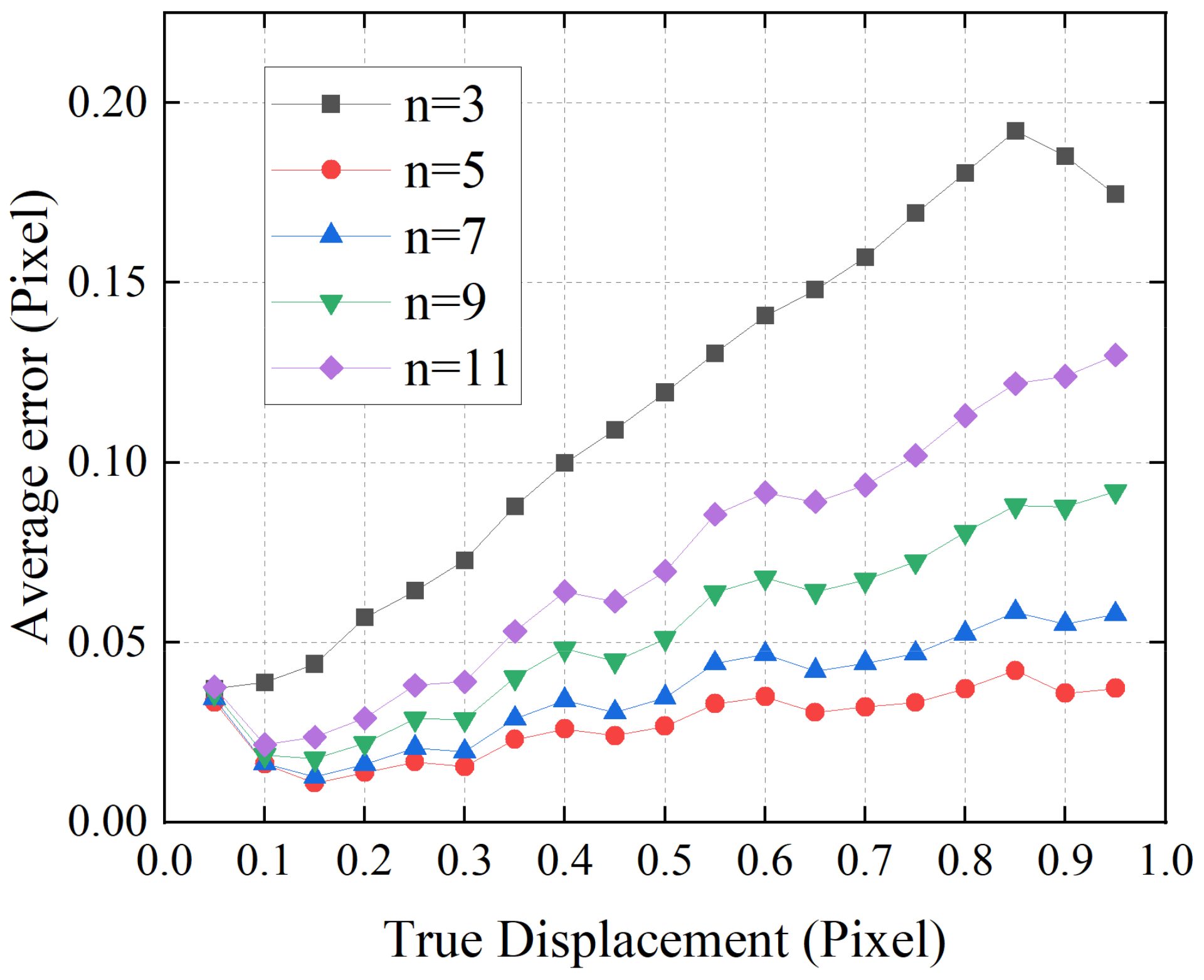
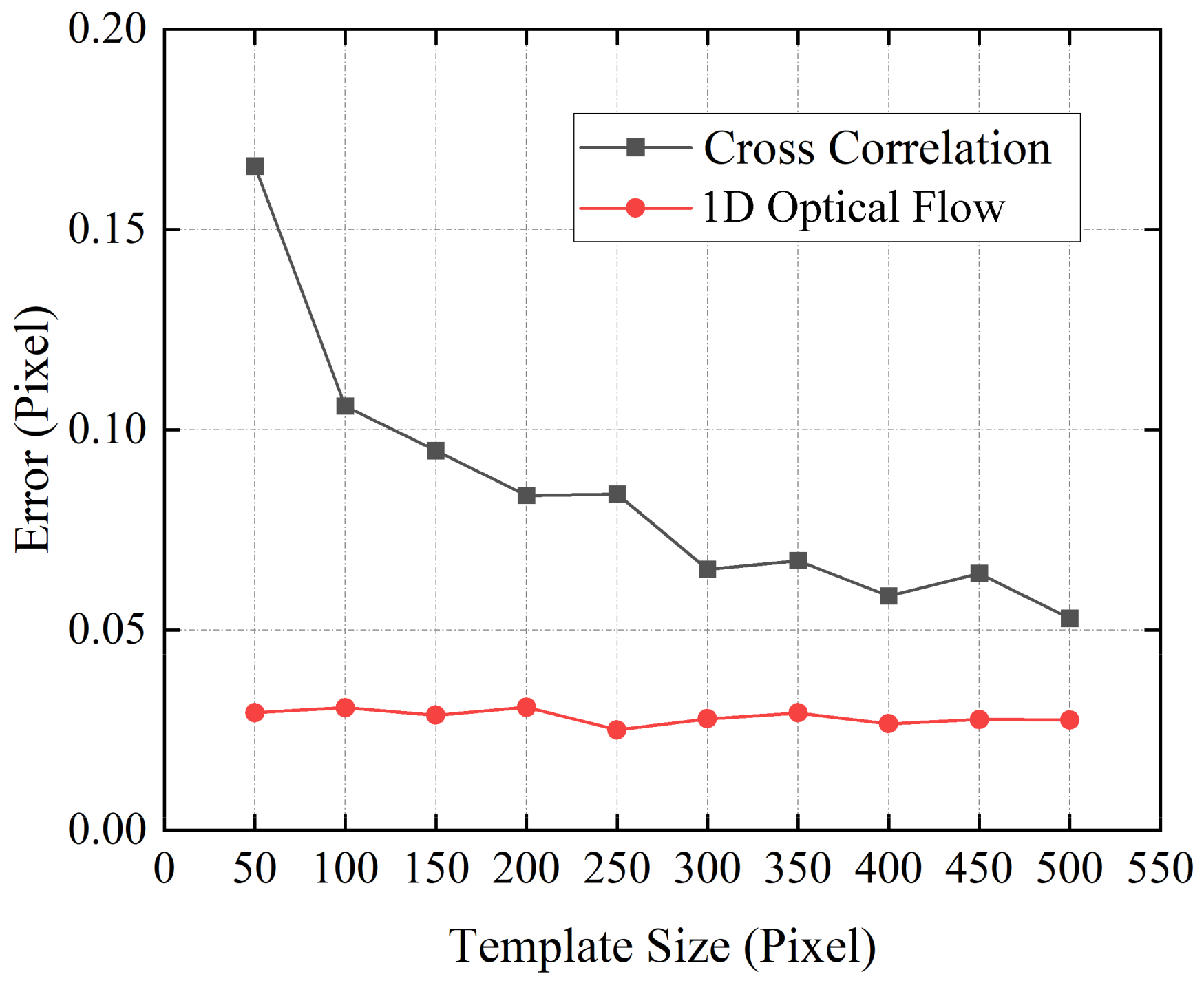
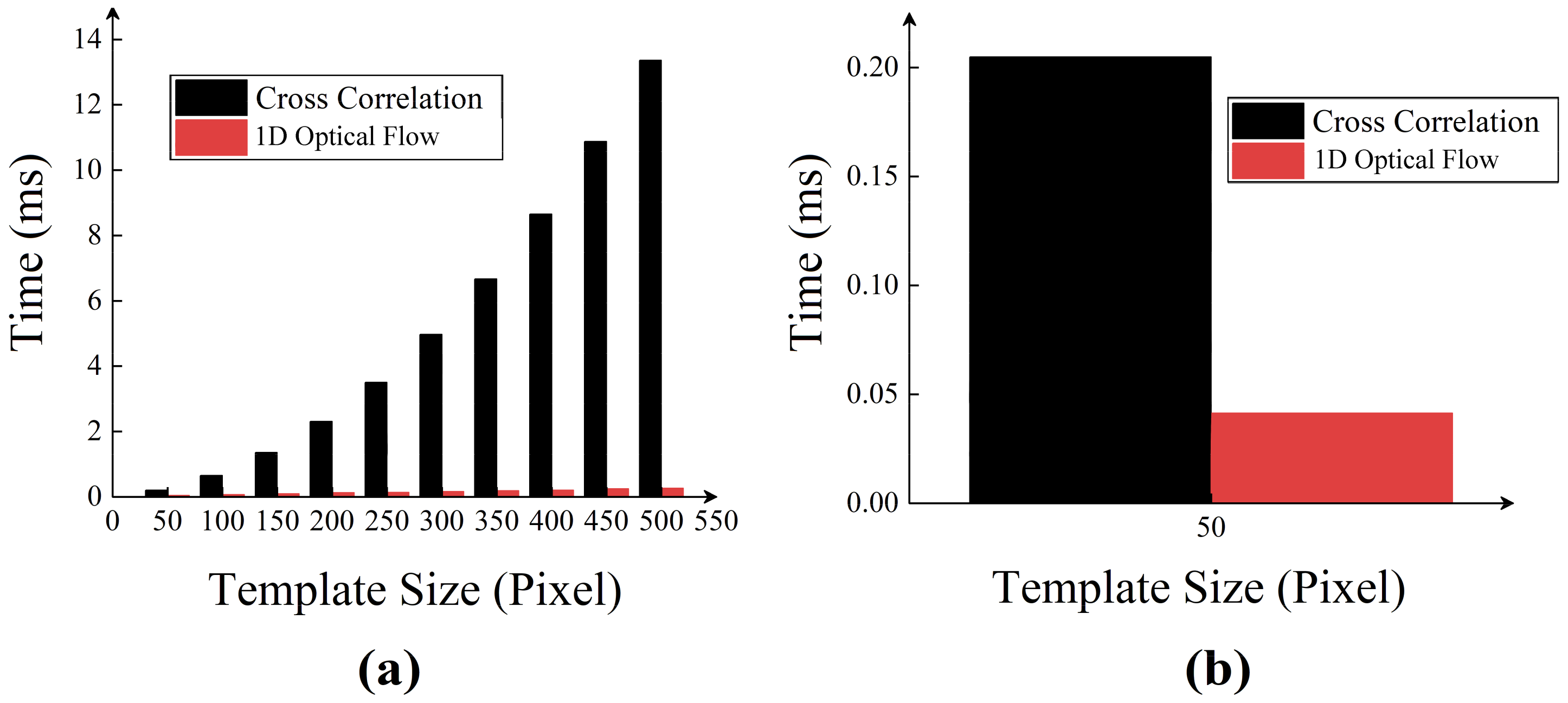
3.1. Performance Test of 1D Optical Flow Algorithm
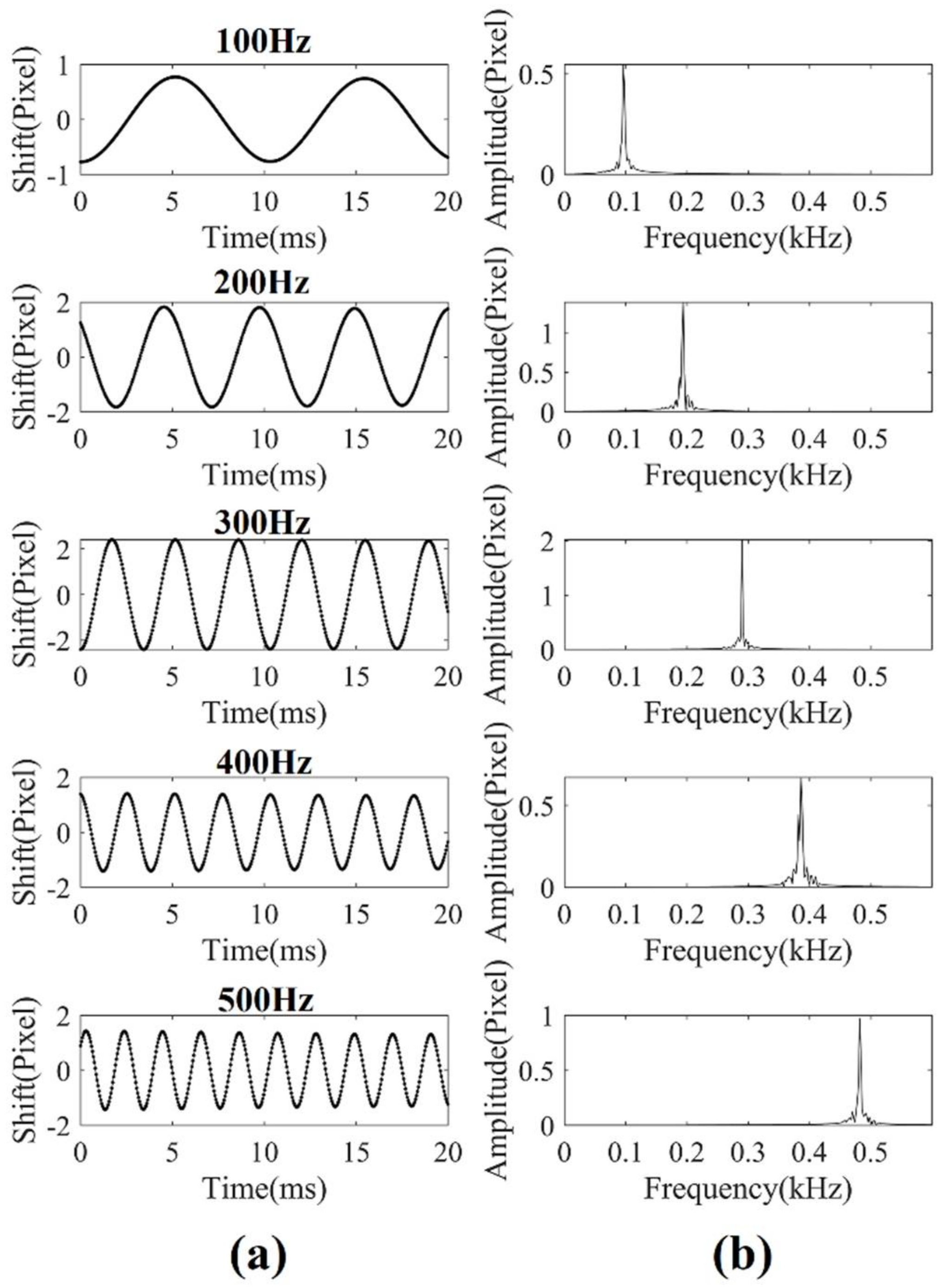
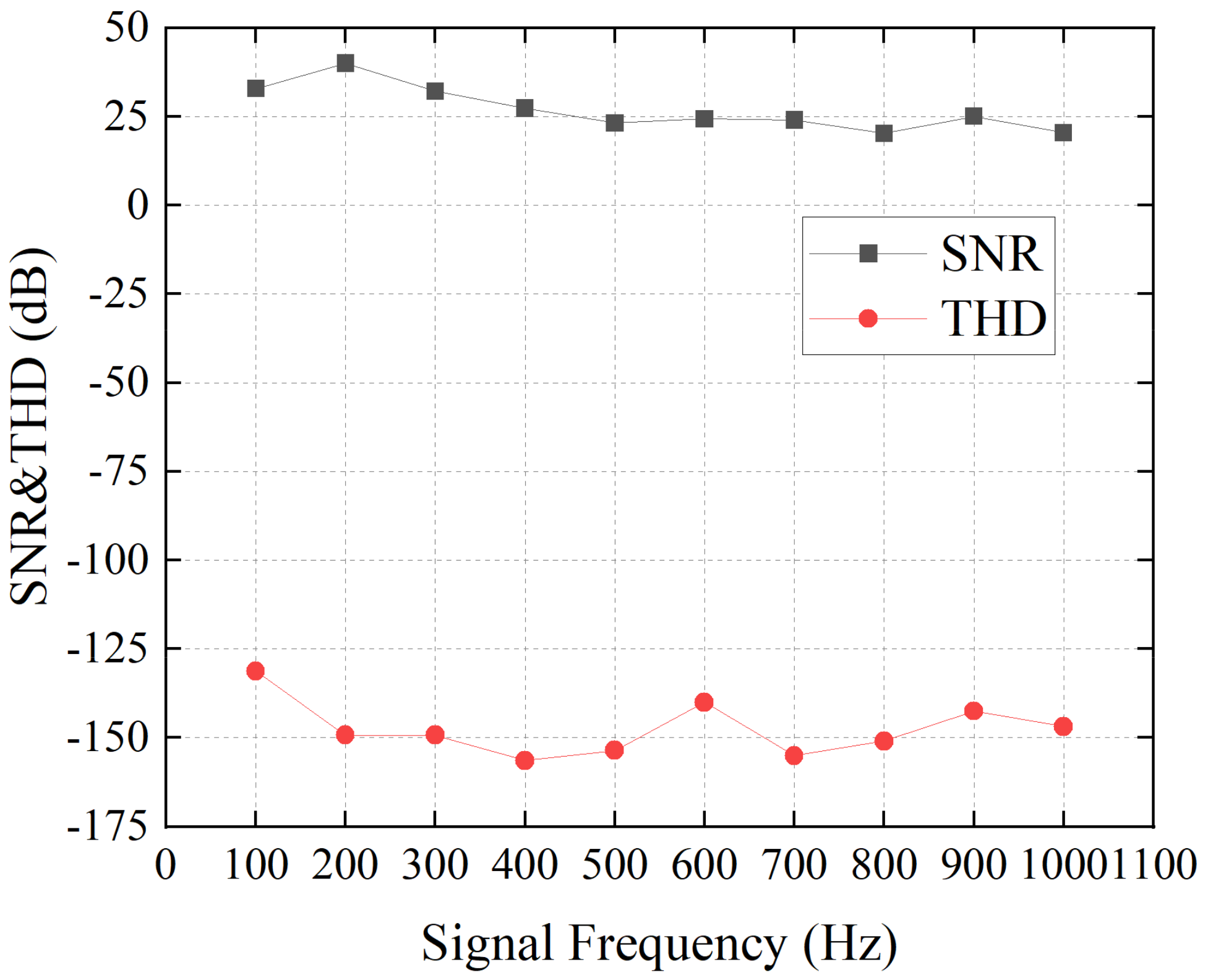
3.2. Result of Real Time Audio Signal Extraction
3.3. Further Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, C.C.; Trivedi, S.; Jin, F.; Swaminathan, V.; Rodriguez, P.; Prasad, N.S. High sensitivity pulsed laser vibrometer and its application as a laser microphone. Appl. Phys. 2009, 94, 051112. [Google Scholar] [CrossRef]
- Bakhoum, E.G.; Cheng, M.H.M. Advanced Optical Microphone. IEEE Sens. J. 2014, 14, 7–14. [Google Scholar] [CrossRef]
- Wan, Q.; Wang, C.; Xu, K.; Kang, J.; Wu, Y.; Trivedi, S.B.; Gehlbach, P.; Boctor, E. Ultrasound Signal Detection with Multi-bounce Laser Microphone. In Proceedings of the 2020 IEEE International Ultrasonics Symposium (IUS), Las Vegas, NV, USA, 7–11 September 2020; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Lv, T.; Zhang, H.Y.; Yan, C.H. Double mode surveillance system based on remote audio/video signals acquisition. Appl. Acoust. 2009, 129, 316–321. [Google Scholar] [CrossRef]
- Han, X.; Lv, T.; Wu, S.; Li, Y.; He, B. A remote human activity detection system based on partial-fiber LDV and PTZ camera. Opt. Laser Technol. 2019, 111, 575–584. [Google Scholar] [CrossRef]
- Chandrakala, S.; Jayalakshmi, S.L. Environmental audio scene and sound event recognition for autonomous surveillance: A survey and comparative studies. ACM Comput. Surv. 2019, 52, 1–34. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Yang, W.; Xiong, X.; Wang, Z.; Zou, X. Viaxl: A Solution of a Low-Cost Real-Time Visual Accelerometer Based on Laser Speckle Optical Flow Detection. Sensors 2020, 20, 7033. [Google Scholar] [CrossRef]
- Li, R.; Wang, T.; Zhu, Z.; Xiao, W. Vibration characteristics of various surfaces using an LDV for long-range voice acquisition. IEEE Sens. J. 2010, 11, 1415–1422. [Google Scholar] [CrossRef]
- Li, R.; Madampoulos, N.; Zhu, Z.; Xie, L. Performance comparison of an all-fiber-based laser Doppler vibrometer for remote acoustical signal detection using short and long coherence length lasers. Appl. Opt. 2012, 51, 5011–5018. [Google Scholar] [CrossRef]
- Wu, S.S.; Lv, T.; Han, X.Y.; Yan, C.H.; Zhang, H.Y. Remote audio signals detection using a partial-fiber laser Doppler vibrometer. Appl. Acoust. 2018, 130, 216–221. [Google Scholar] [CrossRef]
- Matoba, O.; Inokuchi, H.; Nitta, K.; Awatsuji, Y. Optical voice recorder by off-axis digital holography. Opt. Lett. 2014, 39, 6549–6552. [Google Scholar] [CrossRef]
- Ishikawa, K.; Tanigawa, R.; Yatabe, K.; Oikawa, Y.; Onuma, T.; Niwa, H. Simultaneous imaging of flow and sound using high-speed parallel phase-shifting interferometry. Opt. Lett. 2018, 43, 991–994. [Google Scholar] [CrossRef]
- Bianchi, S. Vibration detection by observation of speckle patterns. Appl. Opt. 2014, 53, 931–936. [Google Scholar] [CrossRef]
- Davis, A.; Rubinstein, M.; Wadhwa, N.; Mysore, G.J.; Durand, F.; Freeman, W.T. The visual microphone: Passive recovery of sound from video. ACM Trans. Graph. 2014, 33, 1–10. [Google Scholar] [CrossRef]
- Zalevsky, Z.; Beiderman, Y.; Margalit, I.; Gingold, S.; Teicher, M.; Mico, V.; Garcia, J. Simultaneous remote extraction of multiple speech sources and heart beats from secondary speckles pattern. Opt. Express 2009, 17, 21566–21580. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, L.; Gubarev, F.A.; Klenovskii, M.S.; Bloshkina, A.I. Vibration measurement by means of digital speckle correlation. In Proceedings of the 2016 International Siberian Conference on Control and Communications (SIBCON), Moscow, Russia, 12–14 May 2016; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Hu, W.; Miao, H. Sub-pixel displacement algorithm in temporal sequence digital image correlation based on correlation coefficient weighted fitting. Opt. Lasers Eng. 2018, 110, 410–414. [Google Scholar] [CrossRef]
- Duadi, D.; Ozana, N.; Shabairou, N.; Wolf, M.; Zalevsky, Z.; Primov-Fever, A. Non-contact optical sensing of vocal fold vibrations by secondary speckle patterns. Opt. Express 2020, 28, 20040–20050. [Google Scholar] [CrossRef]
- Liushnevskaya, Y.D.; Gubarev, F.A.; Li, L.; Nosarev, A.V.; Gusakova, V.S. Measurement of whole blood coagulation time by laser speckle pattern correlation. Biomed. Eng. 2020, 54, 262–266. [Google Scholar] [CrossRef]
- Shen, L.; Li, D.G.; Luo, F. Study on laser speckle correlation method applied in triangulation displacement measurement. J. Opt. Technol. 2013, 80, 604–610. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, C.; Huang, C.; Fu, H.; Luo, H.; Wang, H. Audio signal reconstruction based on adaptively selected seed points from laser speckle images. Opt. Commun. 2014, 331, 6–13. [Google Scholar] [CrossRef]
- Zhu, G.; Yao, X.R.; Qiu, P.; Mahmood, W.; Yu, W.K.; Sun, Z.B.; Zhai, G.J.; Zhao, Q. Sound recovery via intensity variations of speckle pattern pixels selected with variance-based method. Opt. Eng. 2018, 57, 026117. [Google Scholar] [CrossRef]
- Zhu, G.; Yao, X.-R.; Sun, Z.-B.; Qiu, P.; Wang, C.; Zhai, G.-J.; Zhao, Q. A High-Speed Imaging Method Based on Compressive Sensing for Sound Extraction Using a Low-Speed Camera. Sensors 2018, 18, 1524. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, N.; Haruyama, S. Real-time sound detection and regeneration based on optical flow algorithm of laser speckle images. In Proceedings of the 2019 28th Wireless and Optical Communications Conference (WOCC), Beijing, China, 9–10 May 2019; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Wu, N.; Haruyama, S. Real-time audio detection and regeneration of moving sound source based on optical flow algorithm of laser speckle images. Opt. Express 2020, 28, 4475–4488. [Google Scholar] [CrossRef] [PubMed]
- Barcellona, C.; Halpaap, D.; Amil, P.; Buscarino, A.; Fortuna, L.; Tiana-Alsina, J.; Masoller, C. Remote recovery of audio signals from videos of optical speckle patterns: A comparative study of signal recovery algorithms. Opt. Express 2020, 28, 8716–8723. [Google Scholar] [CrossRef] [PubMed]
- Gregory, D.A. Basic physical principles of defocused speckle photography: A tilt topology inspection technique. Opt. Laser Technol. 1976, 8, 201–213. [Google Scholar] [CrossRef]
- Tiziani, H.J. A study of the use of laser speckle to measure small tilts of optically rough surfaces accurately. Opt. Commun. 1972, 5, 271–276. [Google Scholar] [CrossRef] [Green Version]
- Reu, P.L. Experimental and numerical methods for exact subpixel shifting. Exp. Mech. 2010, 51, 443–452. [Google Scholar] [CrossRef]
- Guizar-Sicairos, M.; Thurman, S.T.; Fienup, J.R. Efficient subpixel image registration algorithms. Opt. Lett. 2008, 33, 156–158. [Google Scholar] [CrossRef] [Green Version]




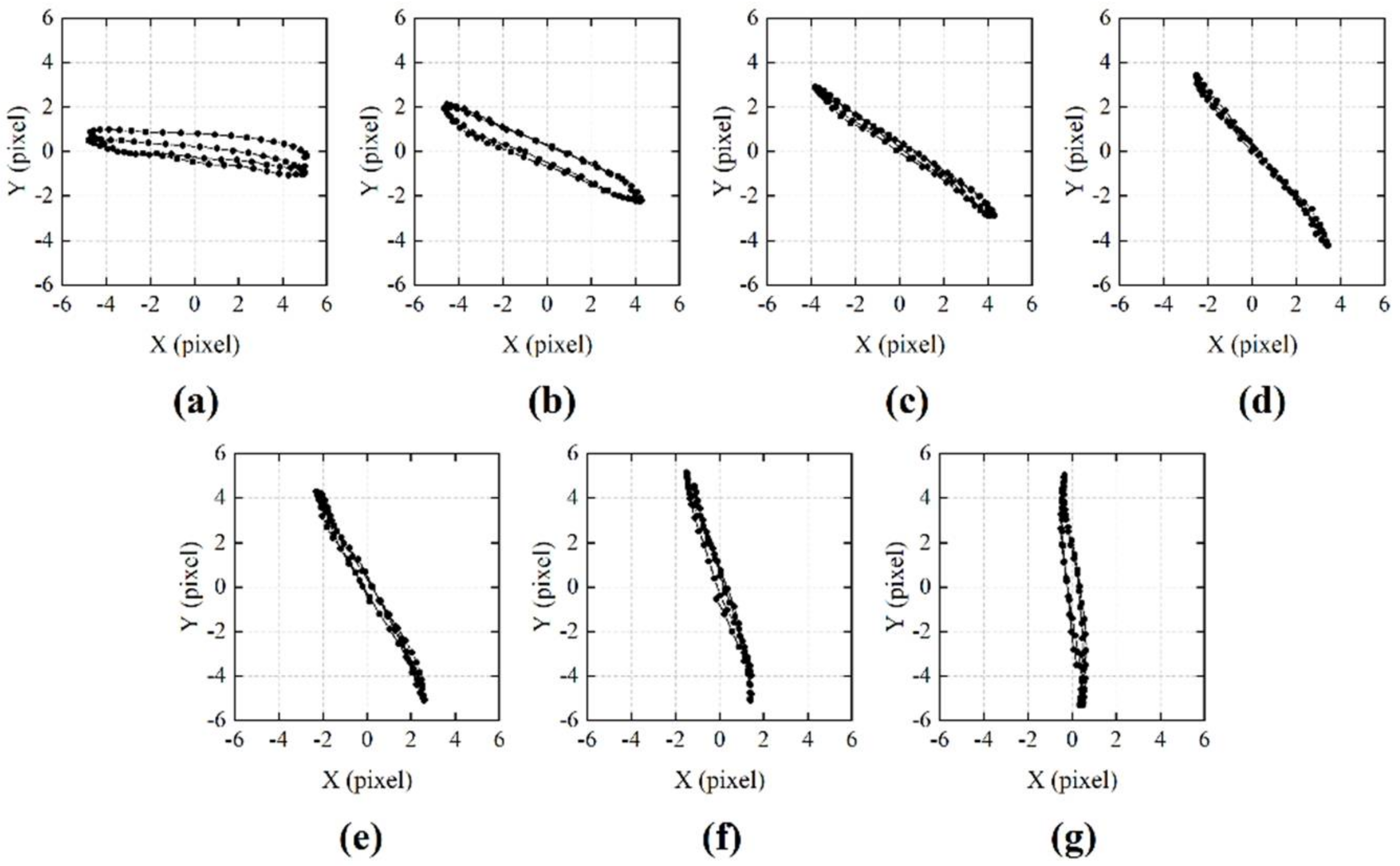

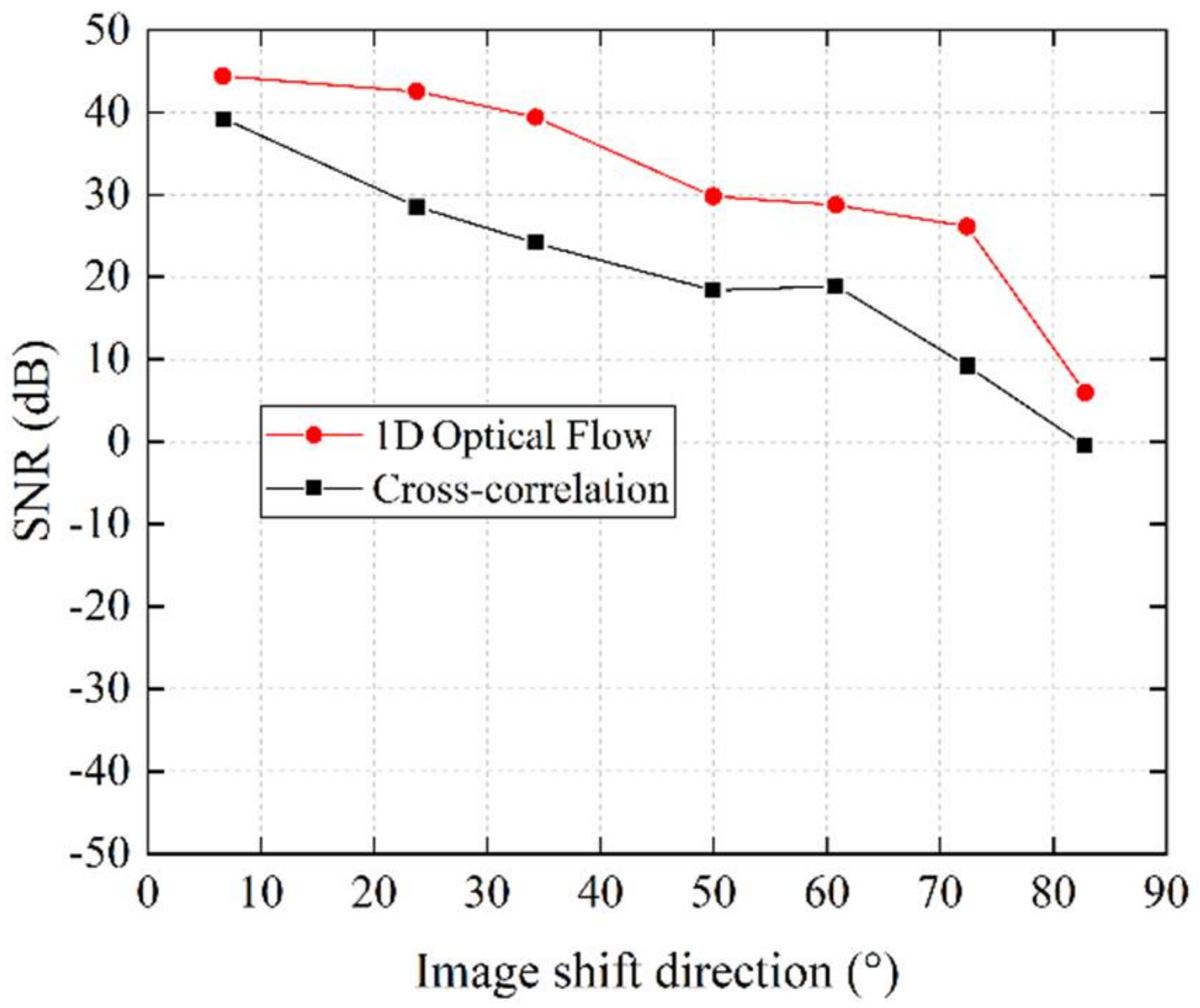

| Stage angle (°) | 60 | 75 | 90 | 105 | 120 | 135 | 150 |
| 2D image shift angle (°) | 6.6577 | 23.7615 | 34.2741 | 49.9582 | 60.7933 | 72.3964 | 82.8111 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, N.; Haruyama, S. The 20k Samples-Per-Second Real Time Detection of Acoustic Vibration Based on Displacement Estimation of One-Dimensional Laser Speckle Images. Sensors 2021, 21, 2938. https://doi.org/10.3390/s21092938
Wu N, Haruyama S. The 20k Samples-Per-Second Real Time Detection of Acoustic Vibration Based on Displacement Estimation of One-Dimensional Laser Speckle Images. Sensors. 2021; 21(9):2938. https://doi.org/10.3390/s21092938
Chicago/Turabian StyleWu, Nan, and Shinichiro Haruyama. 2021. "The 20k Samples-Per-Second Real Time Detection of Acoustic Vibration Based on Displacement Estimation of One-Dimensional Laser Speckle Images" Sensors 21, no. 9: 2938. https://doi.org/10.3390/s21092938
APA StyleWu, N., & Haruyama, S. (2021). The 20k Samples-Per-Second Real Time Detection of Acoustic Vibration Based on Displacement Estimation of One-Dimensional Laser Speckle Images. Sensors, 21(9), 2938. https://doi.org/10.3390/s21092938






