Bhattacharyya Parameter of Monomial Codes for the Binary Erasure Channel: From Pointwise to Average Reliability
Abstract
:1. Introduction
1.1. Polar Codes Are Strongly Decreasing Monomial Codes
- given two monomials in such that , then, for any multiples with and we have where denotes the greatest common divisor of .
- two particular monomials are the key ingredients in the proof, We show that for all , and in general that any pair of monomials of degree 2 , satisfying that has the property for all
1.2. Average Reliability of Synthetic Channels
Threshold Points for Sharp Transitions
1.3. Outline of the Article
2. Background and Preliminary Results
2.1. Monomial Codes
- monomials: where
- support of a monomial: , where and
- a subset of the support of a monomial:
- the set of monomials:
2.2. Polar Codes
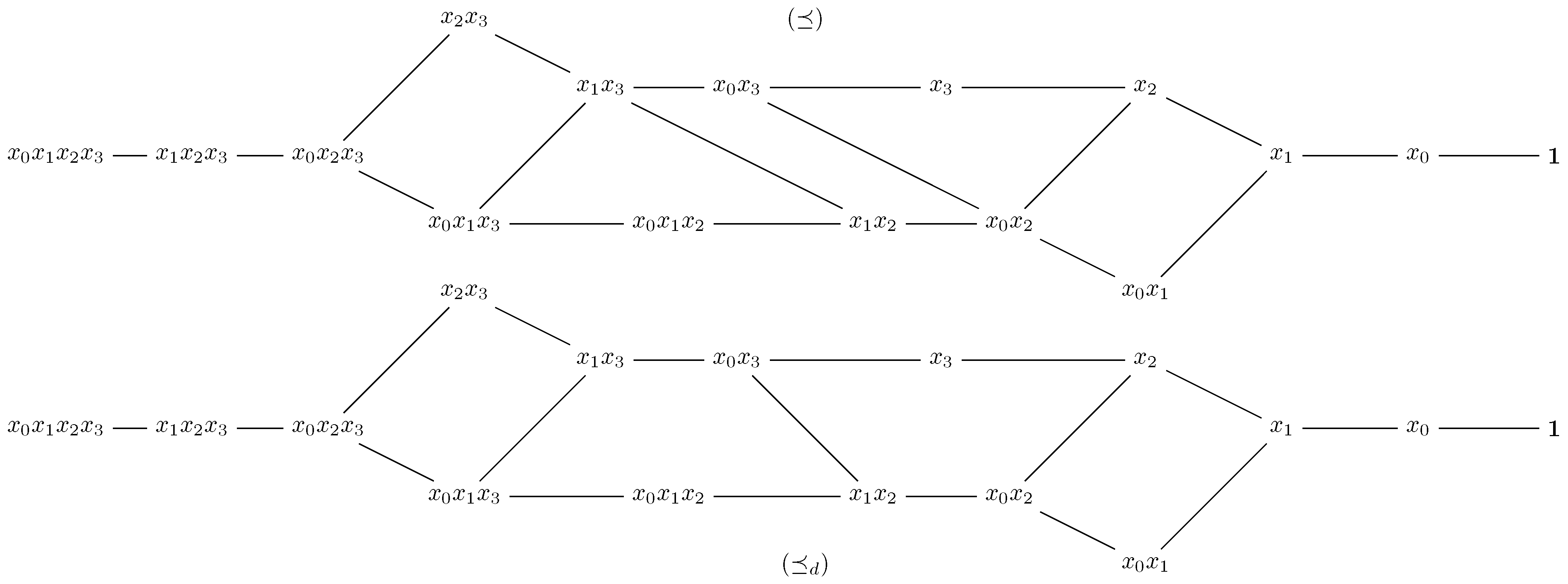
2.3. Weakly Decreasing and Decreasing Monomial Codes
- The order between f and g is defined as
- The ⪯ order between f and g is defined as
- -
- when and , we have
- -
- when we have
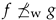 . We also remark that is the smallest element both for ⪯ and for , and we have
. We also remark that is the smallest element both for ⪯ and for , and we have
- We define the closed interval
- is called a decreasing set if and only if ( and ) implies .
- Let be a decreasing set. Then, is called a decreasing monomial code.
2.4. Two-Terminal Networks
Reliability Polynomial
2.5. Bhattacharyya Parameters and Reliability Polynomials
3. Polar Codes Are Strongly Decreasing Monomial Code Over the BEC
3.1. Definitions and Results
- when and , we have
- when we have
- We define the closed interval
- is called a strongly decreasing set if, and only if, ( and ) implies .
- Let be a strongly decreasing set. Then, is called strongly decreasing monomial code.
 and
and 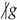 . Then, we have
. Then, we have3.2. Perspectives of Application of in the Construction of Polar Codes
3.2.1. Reducing the Number of Non-Comparable Monomials
Simulations
3.2.2. Reducing the Number of Codes
Simulations
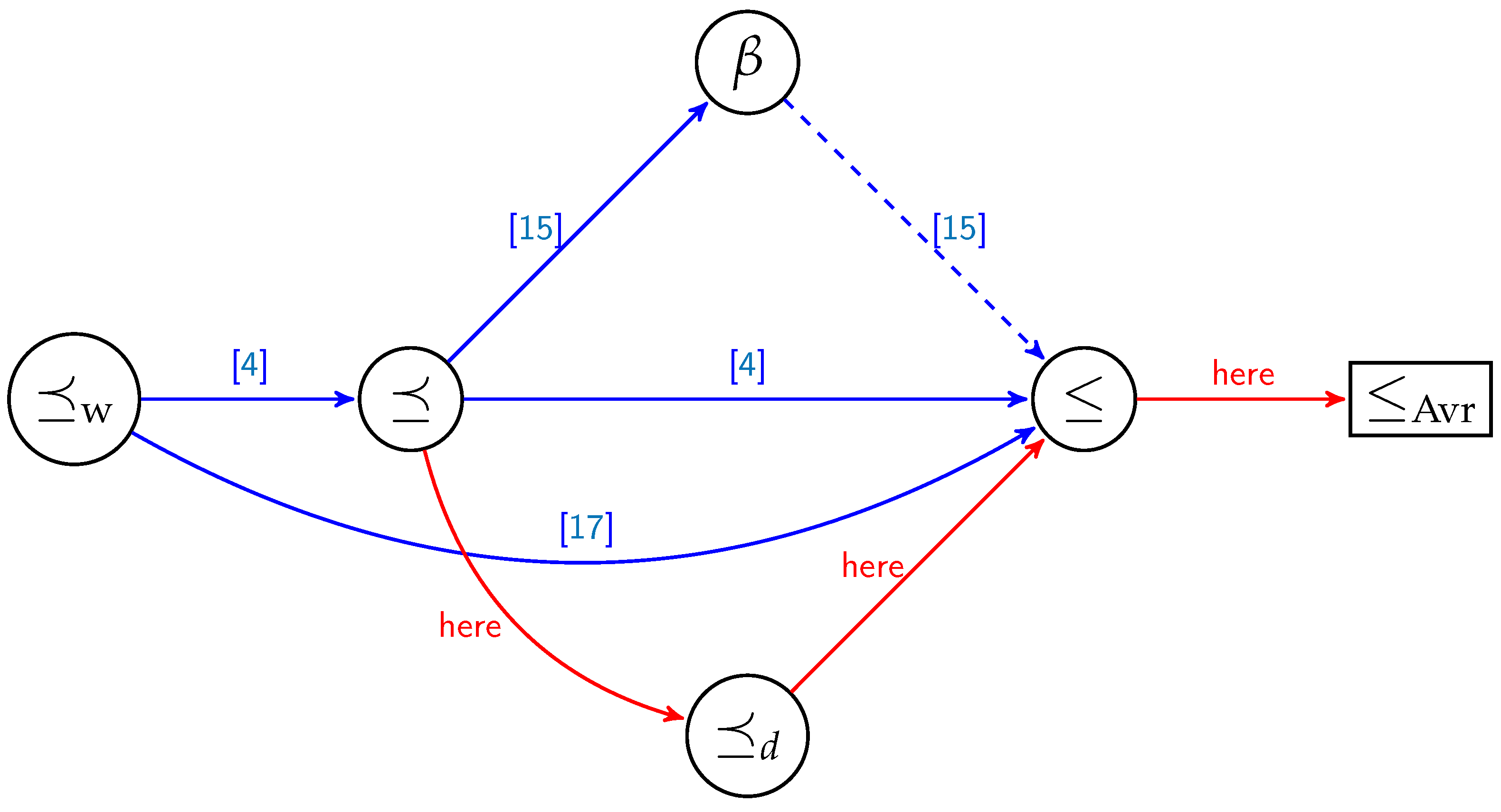
4. Average Reliability of the Synthetic Channels
4.1. Properties
4.2. Relation to -Expansion
4.3. Threshold Points of the Binary Erasure Polarization Sub-Channels
- for any we have and
- for any we have and
5. Conclusions and Perspectives
- the number of non-comparable monomials in the middle of is significantly reduced by means of ,
- the number of strongly decreasing monomial codes is less than the number of decreasing monomial codes for fixed length and dimension.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proofs of Results from Section 3
Appendix A.1. Proof of Proposition 6
 and
and 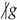 . Then we have
. Then we have- If or then the relation can easily be verified by using the definition of
- If there is an integer s.t. and then the relation can easily be verified as in the previous step.
- If there are two distinct integers s.t. and then two cases have to be considered.
- -
- If then we have and , which implies the following orderingCombining Equation (A2) with the definition of we obtain the desired result, i.e.,
- -
- then we have and which implies the following orderingNow, since it might be possible to have , which implies a violation of the partial sum conditions in the definition of If the next partial sum changes the sign, i.e., , by setting we have the following inequalitiesThis impliesHowever, since the Equation A6) becomes impossible, which completes the proof.
Appendix A.2. Proof of Lemma 2
Appendix A.3. Proof of Theorem 5
- and thus
- and thus
- ⋯
- and thus
- by definition of and thus
- ⋯
- If then we have and Since we have by the induction hypothesis
- Else, by the definition of the order we necessary have We also have thatWhich implies that In the same time notice that and Therefore we obtain
References
- Arıkan, E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inform. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Bioglio, V.; Condo, C.; Land, I. Design of Polar Codes in 5G New Radio. IEEE Commun. Surv. Tutor. 2020, 23, 29–40. [Google Scholar] [CrossRef] [Green Version]
- Dragoi, V. Algebraic Approach for the Study of Algorithmic Problems Coming from Cryptography and the Theory of Error Correcting Codes. Ph.D. Thesis, Université de Rouen, Normandie, France, 2017. [Google Scholar]
- Bardet, M.; Dragoi, V.; Otmani, A.; Tillich, J. Algebraic properties of polar codes from a new polynomial formalism. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 230–234. [Google Scholar] [CrossRef] [Green Version]
- Rengaswamy, N.; Calderbank, R.; Newman, M.; Pfister, H.D. Classical Coding Problem from Transversal T Gates, 2020. In Proceedings of the 2020 IEEE International Symposium on Information Theory (ISIT), Los Angeles, CA, USA, 21–26 June 2020; pp. 1891–1896. [Google Scholar] [CrossRef]
- Rengaswamy, N. Classical Coding Approaches to Quantum Applications. arXiv 2020, arXiv:2004.06834. [Google Scholar]
- Krishna, A.; Tillich, J.P. Magic state distillation with punctured polar codes. arXiv 2019, arXiv:1811.03112. [Google Scholar]
- Bardet, M.; Chaulet, J.; Dragoi, V.; Otmani, A.; Tillich, J.P. Cryptanalysis of the McEliece Public Key Cryptosystem Based on Polar Codes. In Post-Quantum Cryptography, PQCrypto 2016; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 9606, pp. 118–143. [Google Scholar] [CrossRef] [Green Version]
- Drăgoi, V.; Beiu, V.; Bucerzan, D. Vulnerabilities of the McEliece Variants Based on Polar Codes. In Innovative Security Solutions for Information Technology and Communications, SecITC 2018; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 11359, pp. 376–390. [Google Scholar] [CrossRef]
- Bucerzan, D.; Dragoi, V.; Kalachi, H.T. Evolution of the McEliece Public Key Encryption Scheme. In Innovative Security Solutions for Information Technology and Communications, SecITC 2017; Lecture Notes in Computer Science; Springer: Cham, Switzerland; Volume 10543, pp. 129–149. [CrossRef]
- Drăgoi, V.F.; Beiu, V. Fast Reliability Ranking of Matchstick Minimal Networks. arXiv 2019, arXiv:1911.01153. [Google Scholar]
- Dragoi, V.; Cowell, S.; Beiu, V. Ordering series and parallel compositions. In Proceedings of the 2018 IEEE 18th International Conference on Nanotechnology (IEEE-NANO), Cork, Ireland, 23–26 July 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Beiu, V.; Cowell, S.R.; Drăgoi, V.F. On Posets for Reliability: How Fine Can They Be? In Soft Computing Applications SOFA 2018, Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2021; Volume 1221, pp. 115–129. [Google Scholar] [CrossRef]
- Mondelli, M.; Hassani, S.H.; Urbanke, R. Construction of polar codes with sublinear complexity. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 1853–1857. [Google Scholar] [CrossRef] [Green Version]
- He, G.; Belfiore, J.; Land, I.; Yang, G.; Liu, X.; Chen, Y.; Li, R.; Wang, J.; Ge, Y.; Zhang, R.; et al. Beta-Expansion: A Theoretical Framework for Fast and Recursive Construction of Polar Codes. In Proceedings of the GLOBECOM 2017-2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Tal, I.; Vardy, A. How to Construct Polar Codes. IEEE Trans. Inform. Theory 2013, 59, 6562–6582. [Google Scholar] [CrossRef] [Green Version]
- Mori, R.; Tanaka, T. Performance and construction of polar codes on symmetric binary-input memoryless channels. In Proceedings of the 2009 IEEE International Symposium on information theory, Seoul, Korea, 28 June–3 July 2009; pp. 1496–1500. [Google Scholar] [CrossRef] [Green Version]
- Mahdavifar, H.; El-Khamy, M.; Lee, J.; Kang, I. On the construction and decoding of concatenated polar codes. In Proceedings of the 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013; pp. 952–956. [Google Scholar] [CrossRef] [Green Version]
- Korada, S.B.; Sasoglu, E.; Urbanke, R.L. Polar Codes: Characterization of Exponent, Bounds, and Constructions. IEEE Trans. Inform. Theory 2010, 56, 6253–6264. [Google Scholar] [CrossRef] [Green Version]
- Afşer, H.; Deliç, H. On the Channel-Specific Construction of Polar Codes. IEEE Commun. Lett. 2015, 19, 1480–1483. [Google Scholar] [CrossRef]
- Trifonov, P.; Trofimiuk, G. A randomized construction of polar subcodes. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 1863–1867. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Zhang, H.; Li, R.; Ge, Y.; Wang, J. AI Coding: Learning to Construct Error Correction Codes. IEEE Trans. Commun. 2020, 68, 26–39. [Google Scholar] [CrossRef] [Green Version]
- Romano, G.; Ciuonzo, D. Minimum-Variance Importance-Sampling Bernoulli Estimator for Fast Simulation of Linear Block Codes over Binary Symmetric Channels. IEEE Trans. Wirel. Commun. 2014, 13, 486–496. [Google Scholar] [CrossRef]
- Minja, A.; Šenk, V. Quasi-Analytical Simulation Method for Estimating the Error Probability of Star Domain Decoders. IEEE Trans. Commun. 2019, 67, 3101–3113. [Google Scholar] [CrossRef]
- Wu, W.; Siegel, P.H. Generalized Partial Orders for Polar Code Bit-Channels. IEEE Trans. Inf. Theory 2019, 65, 7114–7130. [Google Scholar] [CrossRef]
- Saptharishi, R.; Shpilka, A.; Volk, B.L. Efficiently Decoding Reed–Muller Codes From Random Errors. IEEE Trans. Inf. Theory 2017, 63, 1954–1960. [Google Scholar] [CrossRef] [Green Version]
- Kudekar, S.; Kumar, S.; Mondelli, M.; Pfister, H.D.; Sasoglu, E.; Urbanke, R. Reed-Muller Codes Achieve Capacity on Erasure Channels. IEEE Trans. Inf. Theory 2017, 63, 4298–4316. [Google Scholar] [CrossRef]
- Kumar, S.; Calderbank, R.; Pfister, H.D. Beyond double transitivity: Capacity-achieving cyclic codes on erasure channels. In Proceedings of the 2016 IEEE Information Theory Workshop (ITW), Cambridge, UK, 11–14 September 2016; pp. 241–245. [Google Scholar] [CrossRef]
- Ordentlich, E.; Roth, R.M. On the Pointwise Threshold Behavior of the Binary Erasure Polarization Subchannels. IEEE Trans. Inf. Theory 2019, 65, 6044–6055. [Google Scholar] [CrossRef]
- Drăgoi, V.F.; Beiu, V. Studying the Binary Erasure Polarization Subchannels Using Network Reliability. IEEE Commun. Lett. 2020, 24, 62–66. [Google Scholar] [CrossRef]
- Stanley, R.P. Enumerative Combinatorics; Cambridge University Press: Cambridge, NY, USA, 2012. [Google Scholar]
- Cristescu, G.; Drăgoi, V.F. Cubic Spline Approximation of the Reliability Polynomials of Two Dual Hammock Networks. Transylv. J. Math. Mech. 2019, 11, 77–90. [Google Scholar]
- Cristescu, G.; Drăgoi, V.F. Efficient approximation of two-terminal networks reliability polynomials using cubic splines. IEEE Trans. Reliab. 2021, 1–11. [Google Scholar] [CrossRef]
- Mondelli, M. From Polar to Reed-Muller Codes: Unified Scaling, Non-standard Channels, and a Proven Conjecture. Ph.D. Thesis, Ecole Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2016. [Google Scholar]
- Richardson, T.; Urbanke, R. Modern Coding Theory; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Roth, R.M. Introduction to Coding Theory; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Carlet, C. Boolean functions for cryptography and error correcting codes. In Boolean Models and Methods in Mathematics, Computer Science, and Engineering; Cambridge University Press: Cambridge, NY, USA, 2010; Chapter 8; pp. 257–397. [Google Scholar]
- Moore, E.F.; Shannon, C.E. Reliable circuits using less reliable relays - Part I. J. Frankl. Inst. 1956, 262, 191–208. [Google Scholar] [CrossRef]
- Drăgoi, V.; Cowell, S.R.; Beiu, V.; Hoară, S.; Gaşpar, P. How Reliable are Compositions of Series and Parallel Networks Compared with Hammocks? Int. J. Comput. Commun. Control 2018, 13, 772–791. [Google Scholar] [CrossRef] [Green Version]
- Colbourn, C.J. The Combinatorics of Network Reliability; Oxford University Press: New York, NY, USA, 1987. [Google Scholar]
- Dăuş, L.; Jianu, M. The shape of the reliability polynomial of a hammock network. In Intelligent Methods in Computing, Communication and Control. ICCC 2020, Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2021; Volume 1243, pp. 93–105. [Google Scholar] [CrossRef]
- Brown, J.; Cox, D.; Ehrenborg, R. The average reliability of a graph. Discret. Appl. Math. 2014, 177, 19–33. [Google Scholar] [CrossRef]

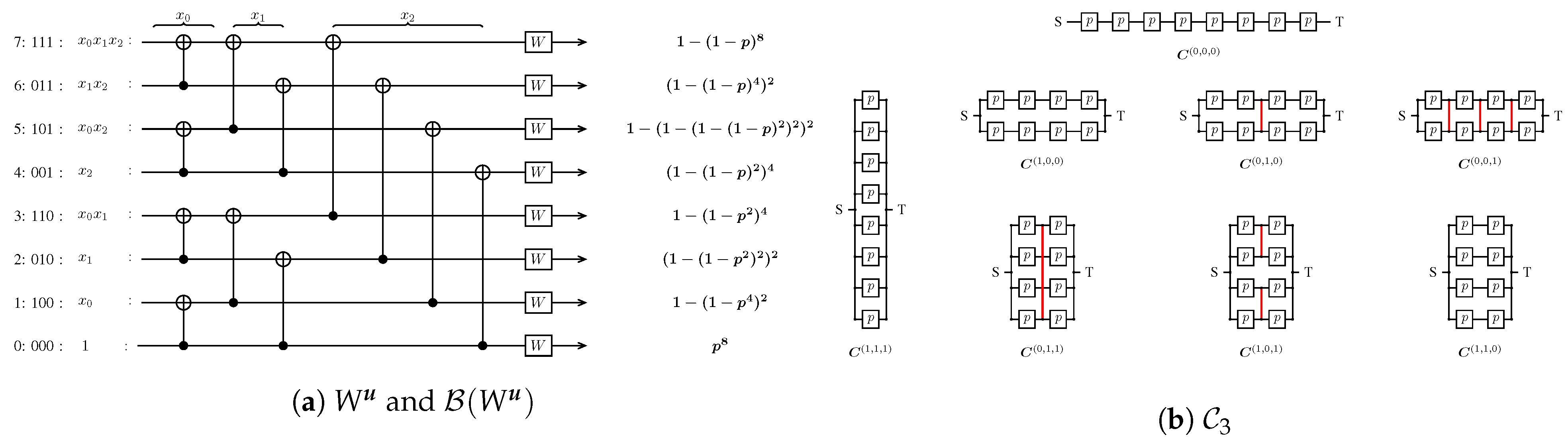

| ⪯ | |||
| ⪯ | |||
| ⪯ | |||
| k | ind(I) for ⪯ | ind(J) for |
|---|---|---|
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 0 | 1 | 2 | 3 | ||||||||||||
| 0 | 1 | 2 | 4 | 3 | 5 | 6 | 7 | ||||||||
| 0 | 1 | 2 | 4 | 8 | 3 | 5 | 6 | 9 | 10 | 12 | 7 | 11 | 13 | 14 | 15 |
| m | [/10-/10+] | |||||
|---|---|---|---|---|---|---|
| 5 | 2 | 3 | 4 | 4 | 3 | |
| 6 | 5 | 7 | 6 | 8 | 6 | |
| 7 | 11 | 13 | 14 | 13 | 13 | |
| 8 | 23 | 25 | 27 | 27 | 26 | |
| 9 | 49 | 51 | 50 | 55 | 51 | |
| 10 | 99 | 104 | 98 | 107 | 104 | |
| 11 | 199 | 209 | 204 | 204 | 208 |
 s.t.
s.t. | m | Number of Incompatible Pair of Elements | ||
|---|---|---|---|
| 4 | – | 16 | |
| 5 | – | 32 | |
| 6 | 2 | 64 | |
| 7 | 10 | 128 | |
| 8 | 36 | 256 | |
| 9 | 99 | 512 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drăgoi, V.-F.; Cristescu, G. Bhattacharyya Parameter of Monomial Codes for the Binary Erasure Channel: From Pointwise to Average Reliability. Sensors 2021, 21, 2976. https://doi.org/10.3390/s21092976
Drăgoi V-F, Cristescu G. Bhattacharyya Parameter of Monomial Codes for the Binary Erasure Channel: From Pointwise to Average Reliability. Sensors. 2021; 21(9):2976. https://doi.org/10.3390/s21092976
Chicago/Turabian StyleDrăgoi, Vlad-Florin, and Gabriela Cristescu. 2021. "Bhattacharyya Parameter of Monomial Codes for the Binary Erasure Channel: From Pointwise to Average Reliability" Sensors 21, no. 9: 2976. https://doi.org/10.3390/s21092976
APA StyleDrăgoi, V.-F., & Cristescu, G. (2021). Bhattacharyya Parameter of Monomial Codes for the Binary Erasure Channel: From Pointwise to Average Reliability. Sensors, 21(9), 2976. https://doi.org/10.3390/s21092976






