Human Motion Tracking with Less Constraint of Initial Posture from a Single RGB-D Sensor
Abstract
:1. Introduction
- We propose a human volumetric capture method based on human priors, which can effectively reduce the strict requirements of the initial posture and keep accurate motion tracking.
- To overcome the self-scan constraint, we propose a new optimization pipeline that combines human priors with volume fusion only using the front-view input.
2. Related Research
2.1. Data Accumulation Based Approaches
2.2. Learning-Based Approaches
2.3. Template-Based Approaches
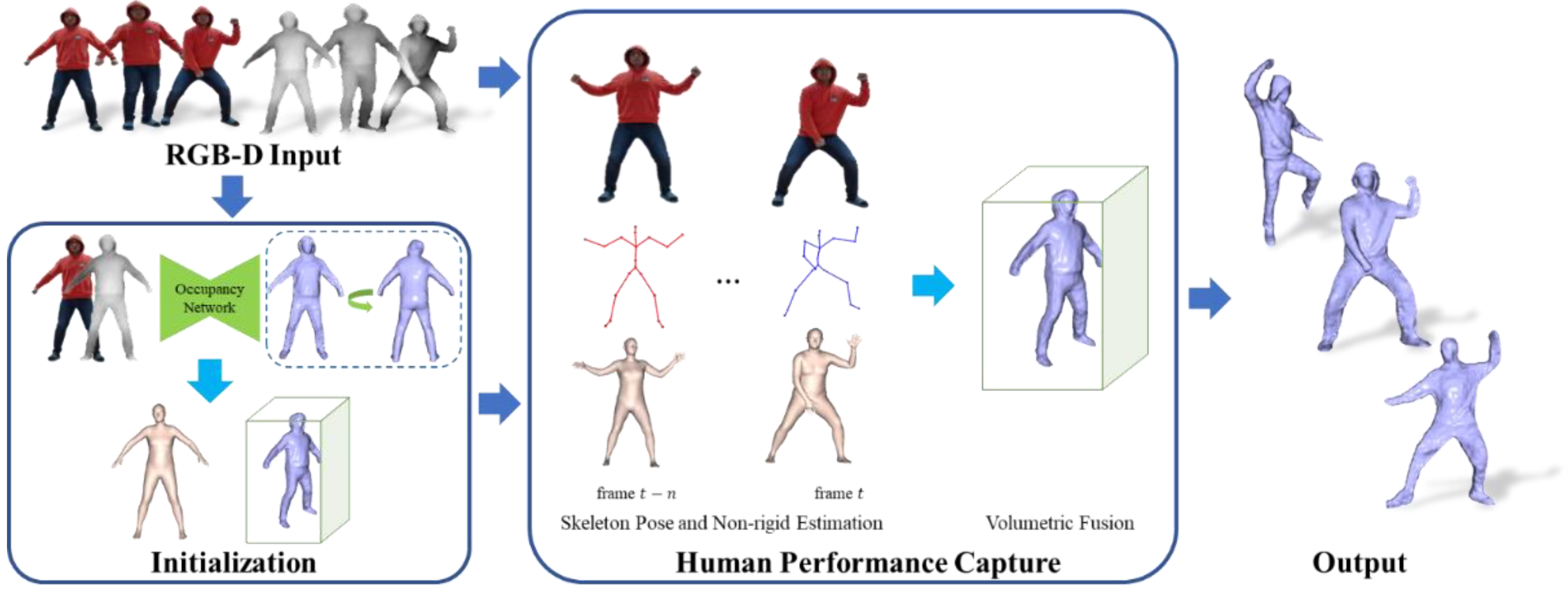
3. Method
3.1. Initialization
3.1.1. Volume Alignment
3.1.2. Inner Body Alignment
3.2. Human Performance Capture
3.2.1. Skeleton Pose Estimation
3.2.2. Non-Rigid Estimation
3.2.3. Volumetric Fusion
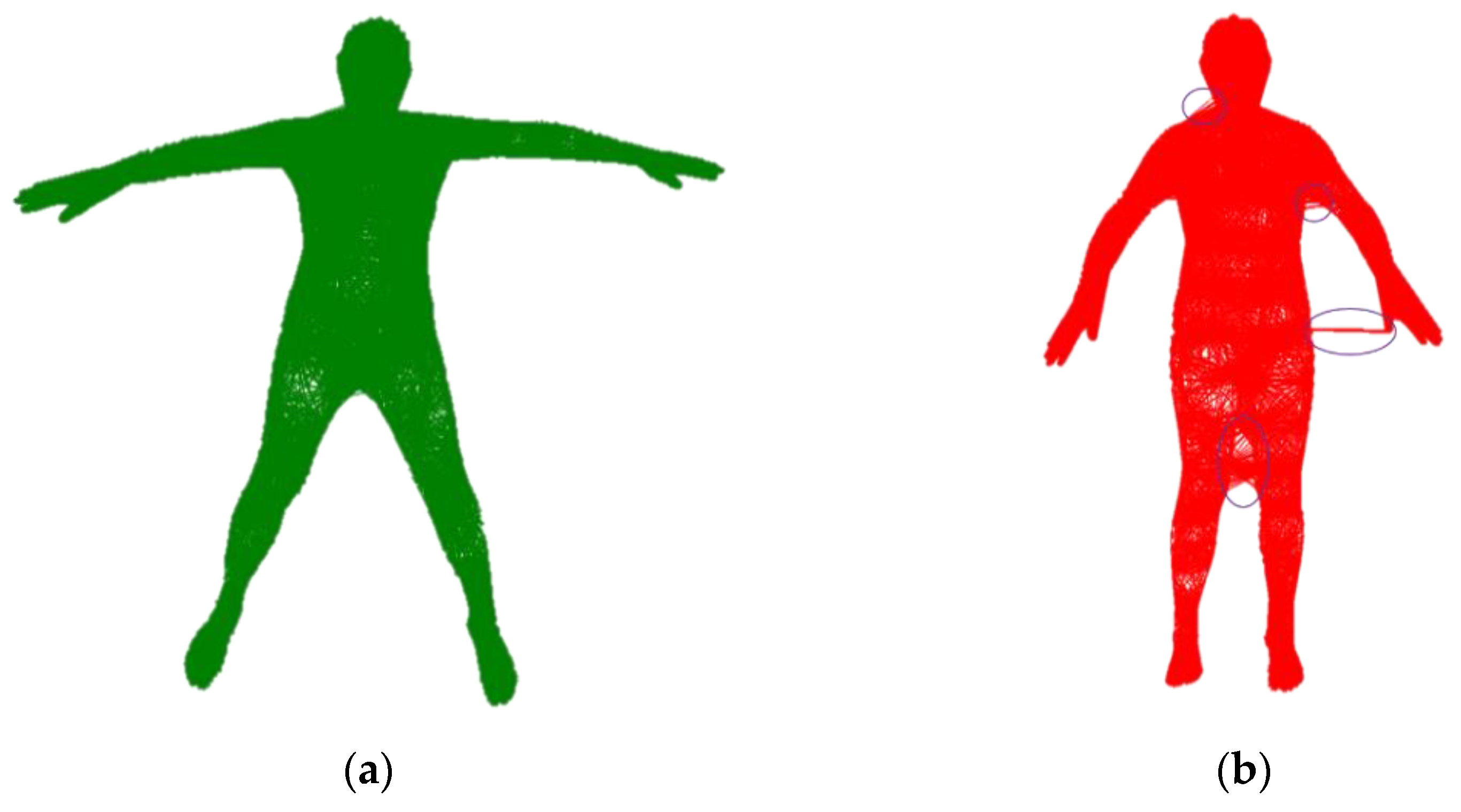
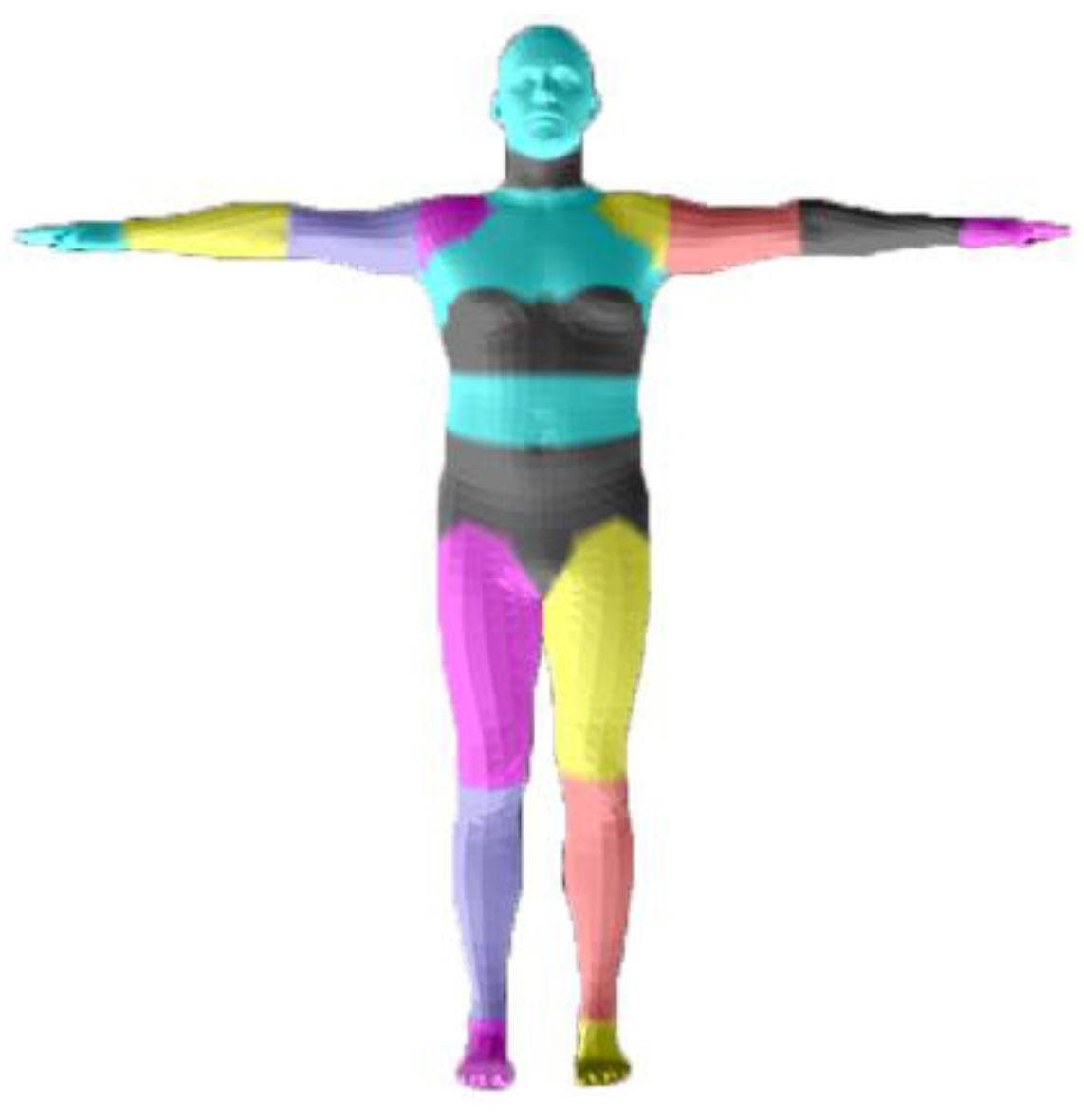
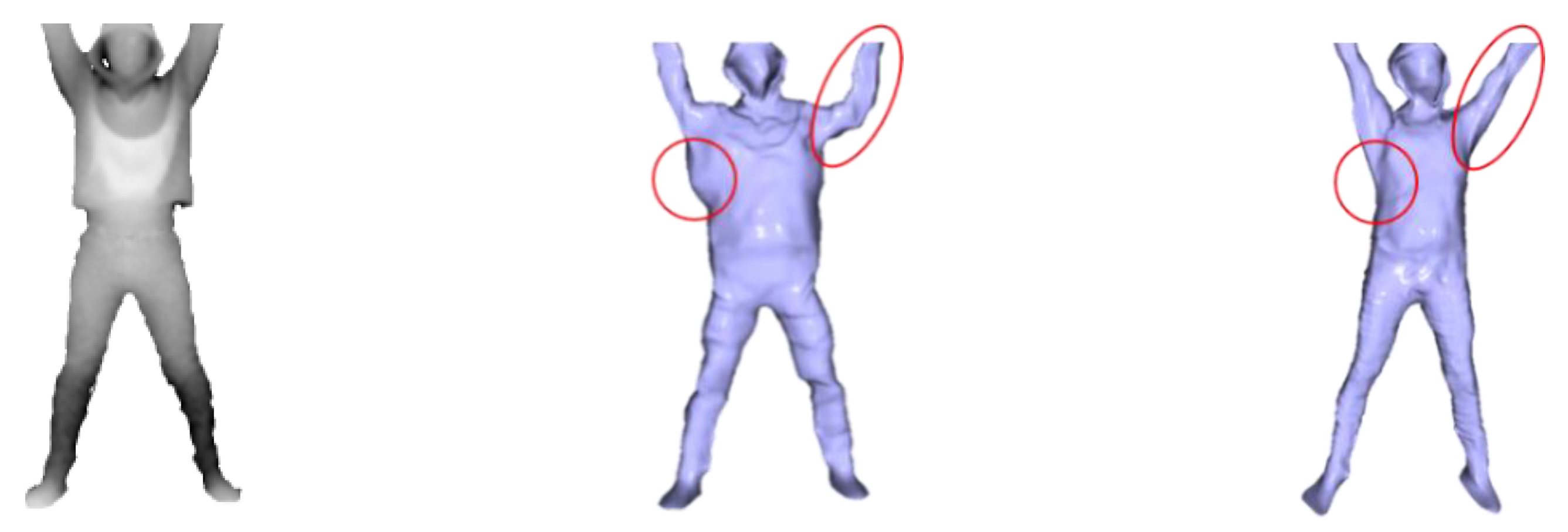
4. Experiment
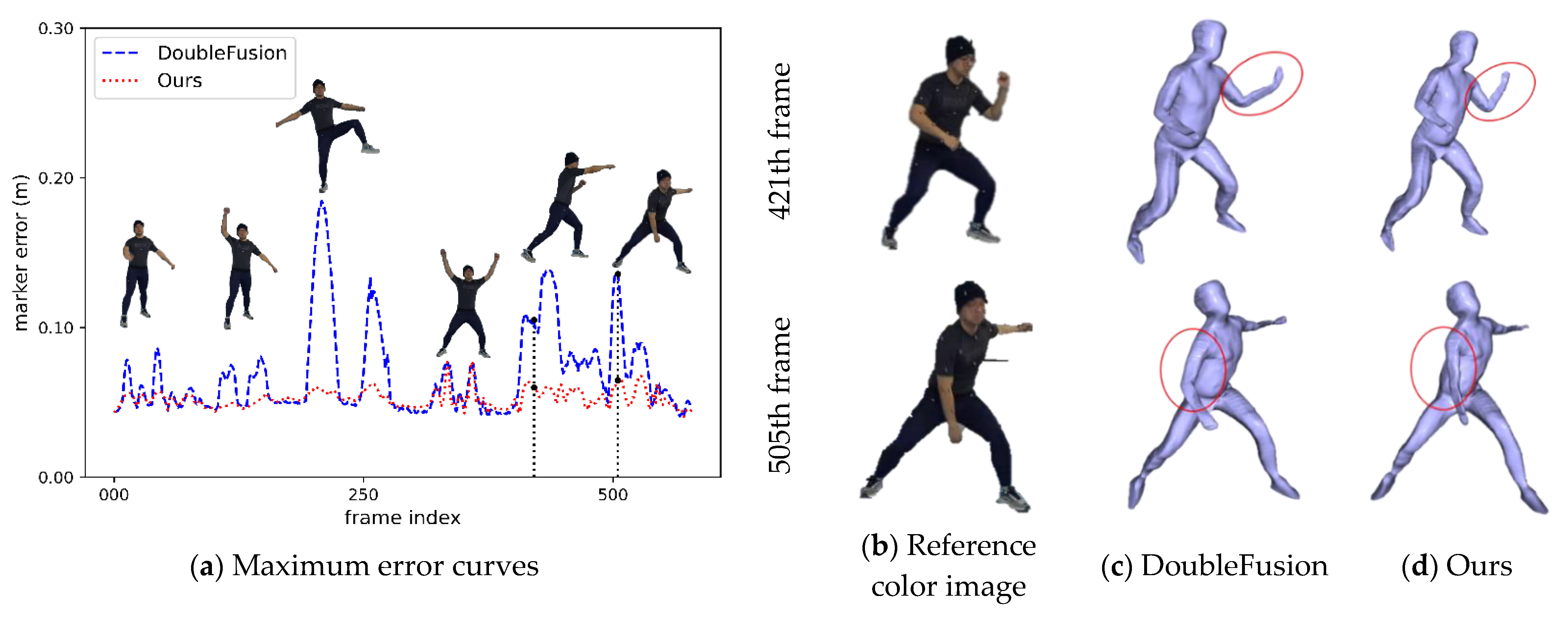
4.1. Qualitative Evaluation
4.2. Quantitative Evaluation
5. Discussion
5.1. Limitations
5.2. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Izadi, S.; Kim, D.; Hilliges, O.; Molyneaux, D.; Newcombe, R.A.; Kohli, P.; Shotton, J.; Hodges, S.; Freeman, D.; Davison, A.J. KinectFusion: Real-Time 3D Reconstruction and Interaction Using a Moving Depth Camera. In Proceedings of the 24th ACM Symposium on User Interface Software & Technology, Santa Barbara, CA, USA, 16–19 October 2011; Association for Computing Machinery: New York, NY, USA, 2011. [Google Scholar]
- Newcombe, R.A.; Davison, A.J.; Izadi, S.; Kohli, P.; Hilliges, O.; Shotton, J.; Molyneaux, D.; Hodges, S.; Kim, D.; Fitzgibbon, A. KinectFusion: Real-time dense surface mapping and tracking. In Proceedings of the 2011 10th IEEE International Symposium on Mixed and Augmented Reality, Basel, The Switzerland, 26–29 October 2011; IEEE: New York, NY, USA; pp. 127–136. [Google Scholar]
- Newcombe, R.A.; Fox, D.; Seitz, S.M. DynamicFusion: Reconstruction and Tracking of Non-rigid Scenes in Real-Time. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–13 June 2015; pp. 343–352. [Google Scholar]
- Dou, M.S.; Taylor, J.; Fuchs, H.; Fitzgibbon, A.; Izadi, S. 3D Scanning Deformable Objects with a Single RGBD Sensor. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–13 June 2015; pp. 493–501. [Google Scholar]
- Innmann, M.; Zollhofer, M.; Niessner, M.; Theobalt, C.; Stamminger, M. VolumeDeform: Real-Time Volumetric Non-rigid Reconstruction. Lect. Notes Comput. Sci. 2016, 9912, 362–379. [Google Scholar]
- Dou, M.; Taylor, J.; Kohli, P.; Tankovich, V.; Izadi, S.; Khamis, S.; Degtyarev, Y.; Davidson, P.; Fanello, S.R.; Kowdle, A.; et al. Fusion4D. ACM Trans. Graph. 2016, 35, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Slavcheva, M.; Baust, M.; Cremers, D.; Ilic, S. KillingFusion: Non-rigid 3D Reconstruction without Correspondences. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5474–5483. [Google Scholar]
- Zhang, J.; Li, W.; Ogunbona, P.O.; Wang, P.; Tang, C. RGB-D-based action recognition datasets: A survey. Pattern Recognit. 2016, 60, 86–105. [Google Scholar] [CrossRef] [Green Version]
- Hao, L.; Adams, B.; Guibas, L.J.; Pauly, M. Robust Single-View Geometry and Motion Reconstruction. In Proceedings of the ACM Siggraph Asia, Yokohama, Japan, 16–19 December 2009; Association for Computing Machinery: New York, NY, USA, 2009. [Google Scholar]
- Vlasic, D.; Baran, I.; Matusik, W.; Popovic, J. Articulated mesh animation from multi-view silhouettes. ACM Trans. Graph. 2008, 27, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Dou, M.; Fuchs, H.; Frahm, J.-M. Scanning and Tracking Dynamic Objects with Commodity Depth Cameras. In Proceedings of the 2013 IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Adelaide, Australia, 1–4 October 2013; IEEE: New York, NY, USA, 2013; pp. 99–106. [Google Scholar]
- Tong, J.; Zhou, J.; Liu, L.; Pan, Z.; Yan, H. Scanning 3d full human bodies using kinects. IEEE Trans. Vis. Comput. Graph. 2012, 18, 643–650. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alexiadis, D.S.; Zarpalas, D.; Daras, P. Real-time, full 3-D reconstruction of moving foreground objects from multiple consumer depth cameras. IEEE Trans. Multimed. 2012, 15, 339–358. [Google Scholar] [CrossRef]
- Dou, M.S.; Davidson, P.; Fanello, S.R.; Khamis, S.; Kowdle, A.; Rhemann, C.; Tankovich, V.; Izadi, S. Motion2Fusion: Real-time Volumetric Performance Capture. ACM Trans. Graph. 2017, 36, 1–16. [Google Scholar] [CrossRef]
- Joo, H.; Simon, T.; Sheikh, Y. Total Capture: A 3d Deformation Model for Tracking Faces, Hands, and Bodies. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; IEEE: New York, NY, USA, 2018; pp. 8320–8329. [Google Scholar]
- Xu, L.; Su, Z.; Han, L.; Yu, T.; Liu, Y.; Lu, F. UnstructuredFusion: Realtime 4D Geometry and Texture Reconstruction using Commercial RGBD Cameras. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 2508–2522. [Google Scholar] [CrossRef]
- Guo, K.; Taylor, J.; Fanello, S.; Tagliasacchi, A.; Dou, M.; Davidson, P.; Kowdle, A.; Izadi, S. TwinFusion: High Framerate Non-rigid Fusion through Fast Correspondence Tracking. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 596–605. [Google Scholar]
- Xu, L.; Cheng, W.; Guo, K.; Han, L.; Liu, Y.; Fang, L. Flyfusion: Realtime dynamic scene reconstruction using a flying depth camera. IEEE Trans. Vis. Comput. Graph. 2019, 27, 68–82. [Google Scholar] [CrossRef]
- Yu, T.; Zheng, Z.R.; Guo, K.W.; Zhao, J.H.; Dai, Q.H.; Li, H.; Pons-Moll, G.; Liu, Y.B. DoubleFusion: Real-time Capture of Human Performances with Inner Body Shapes from a Single Depth Sensor. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 7287–7296. [Google Scholar]
- Zheng, Z.; Yu, T.; Li, H.; Guo, K.; Dai, Q.; Fang, L.; Liu, Y. HybridFusion: Real-Time Performance Capture Using a Single Depth Sensor and Sparse IMUs. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Springer: Berlin, Germany, 2018; pp. 384–400. [Google Scholar]
- Varol, G.; Ceylan, D.; Russell, B.; Yang, J.; Yumer, E.; Laptev, I.; Schmid, C. Bodynet: Volumetric Inference of 3d Human Body Shapes. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Springer: Berlin, Germany, 2018; pp. 20–36. [Google Scholar]
- Saito, S.; Simon, T.; Saragih, J.; Joo, H. PIFuHD: Multi-Level Pixel-Aligned Implicit Function for High-Resolution 3D Human Digitization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; IEEE: New York, NY, USA, 2020; pp. 84–93. [Google Scholar]
- Zheng, Z.; Yu, T.; Wei, Y.; Dai, Q.; Liu, Y. DeepHuman: 3D Human Reconstruction from a Single Image. arXiv 2019, arXiv:1903.06473. [Google Scholar]
- Ma, Q.; Tang, S.; Pujades, S.; Pons-Moll, G.; Ranjan, A.; Black, M.J. Dressing 3D Humans using a Conditional Mesh-VAE-GAN. arXiv 2019, arXiv:1907.13615. [Google Scholar]
- Alldieck, T.; Pons-Moll, G.; Theobalt, C.; Magnor, M. Tex2Shape: Detailed Full Human Body Geometry from a Single Image. arXiv 2019, arXiv:1904.08645. [Google Scholar]
- Zheng, Z.; Yu, T.; Liu, Y.; Dai, Q. PaMIR: Parametric Model-Conditioned Implicit Representation for Image-based Human Reconstruction. arXiv 2020, arXiv:2007.03858. [Google Scholar]
- Onizuka, H.; Hayirci, Z.; Thomas, D.; Sugimoto, A.; Uchiyama, H.; Taniguchi, R.-i. TetraTSDF: 3D human reconstruction from a single image with a tetrahedral outer shell. arXiv 2020, arXiv:2004.10534. [Google Scholar]
- Huang, Z.; Xu, Y.; Lassner, C.; Li, H.; Tung, T. ARCH: Animatable Reconstruction of Clothed Humans. arXiv 2020, arXiv:2004.04572. [Google Scholar]
- Habermann, M.; Xu, W.; Zollhoefer, M.; Pons-Moll, G.; Theobalt, C. DeepCap: Monocular Human Performance Capture Using Weak Supervision. arXiv 2020, arXiv:2003.08325. [Google Scholar]
- Wang, L.; Zhao, X.; Yu, T.; Wang, S.; Liu, Y. NormalGAN: Learning Detailed 3D Human from a Single RGB-D Image. arXiv 2020, arXiv:2007.15340. [Google Scholar]
- Chibane, J.; Alldieck, T.; Pons-Moll, G. Implicit Functions in Feature Space for 3d Shape Reconstruction and Completion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; IEEE: New York, NY, USA, 2020; pp. 6970–6981. [Google Scholar]
- Bogo, F.; Kanazawa, A.; Lassner, C.; Gehler, P.; Romero, J.; Black, M.J. Keep It SMPL: Automatic Estimation of 3D Human Pose and Shape from a Single Image. Lect. Notes Comput. Sci. 2016, 9909, 561–578. [Google Scholar]
- Kanazawa, A.; Black, M.J.; Jacobs, D.W.; Malik, J. End-to-End Recovery of Human Shape and Pose. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; IEEE: New York, NY, USA, 2018; pp. 7122–7131. [Google Scholar]
- Pavlakos, G.; Kolotouros, N.; Daniilidis, K. TexturePose: Supervising Human Mesh Estimation with Texture Consistency. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, Seoul, Korea, 27–28 October 2019; IEEE: New York, NY, USA, 2019; pp. 803–812. [Google Scholar]
- Kocabas, M.; Athanasiou, N.; Black, M.J. VIBE: Video Inference for Human Body Pose and Shape Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; IEEE: New York, NY, USA, 2020; pp. 5253–5263. [Google Scholar]
- Choi, H.; Moon, G.; Lee, K.M. Pose2Mesh: Graph Convolutional Network for 3D Human Pose and Mesh Recovery from a 2D Human Pose. In Proceedings of the ECCV, Glasgow, UK, 23–28 August 2020; Springer: Berlin, Germany, 2020. [Google Scholar]
- Zhu, H.; Zuo, X.; Wang, S.; Cao, X.; Yang, R. Detailed Human Shape Estimation from a Single Image by Hierarchical Mesh Deformation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seoul, Korea, 27–28 October 2019; IEEE: New York, NY, USA, 2019; pp. 4491–4500. [Google Scholar]
- Kolotouros, N.; Pavlakos, G.; Black, M.J.; Daniilidis, K. Learning to Reconstruct 3D Human Pose and Shape via Model-fitting in the Loop. arXiv 2019, arXiv:1909.12828. [Google Scholar]
- Omran, M.; Lassner, C.; Pons-Moll, G.; Gehler, P.; Schiele, B. Neural body fitting: Unifying deep learning and model based human pose and shape estimation. In Proceedings of the International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; IEEE: New York, NY, USA, 2018; pp. 484–494. [Google Scholar]
- Yoshiyasu, Y.; Gamez, L. Learning Body Shape and Pose from Dense Correspondences. arXiv 2019, arXiv:1907.11955. [Google Scholar]
- Pavlakos, G.; Choutas, V.; Ghorbani, N.; Bolkart, T.; Osman, A.A.; Tzionas, D.; Black, M.J. Expressive body capture: 3d hands, face, and body from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seoul, Korea, 27–28 October 2019; IEEE: New York, NY, USA, 2019; pp. 10975–10985. [Google Scholar]
- Li, H.; Vouga, E.; Gudym, A.; Luo, L.J.; Barron, J.T.; Gusev, G. 3D Self-Portraits. Acm Trans. Graph. 2013, 32, 1–9. [Google Scholar] [CrossRef]
- Zhang, Q.; Fu, B.; Ye, M.; Yang, R.G. Quality Dynamic Human Body Modeling Using a Single Low-cost Depth Camera. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; IEEE: New York, NY, USA, 2014; pp. 676–683. [Google Scholar]
- Guo, K.; Xu, F.; Wang, Y.; Liu, Y.; Dai, Q. Robust Non-Rigid Motion Tracking and Surface Reconstruction Using $ L_0 $ Regularization. IEEE Trans. Vis. Comput. Graph. 2018, 24, 1770. [Google Scholar] [CrossRef]
- Slavcheva, M.; Baust, M.; Ilic, S. SobolevFusion: 3D Reconstruction of Scenes Undergoing Free Non-rigid Motion. Proc. Cvpr. IEEE 2018, 2646–2655. [Google Scholar]
- Zhuo, S.L.X.; Zerong, Z.; Tao, Y.; Yebin, L.; Lu, F. RobustFusion: Human Volumetric Capture with Data-driven Visual Cues using a RGBD Camera. In Proceedings of the ECCV, Glasgow, UK, 23–28 August 2020; Springer: Berlin, Germany, 2020. [Google Scholar]
- Bogo, F.; Black, M.J.; Loper, M.; Romero, J. Detailed Full-Body Reconstructions of Moving People from Monocular RGB-D Sequences. In Proceedings of the IEEE International Conference on Computer Vision, Las Vegas, NV, USA, 27–30 June 2016; IEEE: New York, NY, USA, 2016. [Google Scholar]
- Sun, S.; Li, C.; Guo, Z.; Tai, Y. Parametric Human Shape Reconstruction via Bidirectional Silhouette Guidance. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Seoul, Korea, 27–28 October 2019; IEEE: New York, NY, USA, 2019; pp. 4004–4013. [Google Scholar]
- Lorensen, W.E.; Cline, H.E. Marching cubes: A high resolution 3D surface construction algorithm. ACM Siggraph Comput. Graph. 1987, 21, 163–169. [Google Scholar] [CrossRef]
- Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; Black, M.J. SMPL: A skinned multi-person linear model. ACM Trans. on Graph. (TOG) 2015, 34, 1–16. [Google Scholar] [CrossRef]
- Rong, Y.; Shiratori, T.; Joo, H. FrankMocap: Fast Monocular 3D Hand and Body Motion Capture by Regression and Integration. arXiv 2020, arXiv:2008.08324. [Google Scholar]
- Ravi, N.; Reizenstein, J.; Novotny, D.; Gordon, T.; Lo, W.-Y.; Johnson, J.; Gkioxari, G. Accelerating 3d deep learning with pytorch3d. arXiv 2020, arXiv:2007.08501. [Google Scholar]
- Lassner, C. Fast Differentiable Raycasting for Neural Rendering using Sphere-based Representations. arXiv 2020, arXiv:2004.07484. [Google Scholar]




| Joint | DoubleFusion [2] | Ours |
|---|---|---|
| Chest | 0.0495 | 0.0516 |
| Left wrist | 0.1078 | 0.0321 |
| Left elbow | 0.0507 | 0.0513 |
| Left shoulder | 0.1211 | 0.0459 |
| Left hip | 0.0822 | 0.0662 |
| Left knee | 0.1845 | 0.0582 |
| Left ankle | 0.0515 | 0.0492 |
| Left foot | 0.0633 | 0.0402 |
| Right wrist | 0.0896 | 0.0429 |
| Right elbow | 0.0471 | 0.0513 |
| Right shoulder | 0.1381 | 0.0514 |
| Right hip | 0.0755 | 0.0770 |
| Right knee | 0.1336 | 0.0604 |
| Right ankle | 0.0454 | 0.0457 |
| Right foot | 0.0423 | 0.0379 |
| Method | DoubleFusion | Ours |
|---|---|---|
| Maximum Error (m) | 0.0689 | 0.0526 |
| Average Error (m) | 0.0362 | 0.0316 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Wang, A.; Bu, C.; Wang, W.; Sun, H. Human Motion Tracking with Less Constraint of Initial Posture from a Single RGB-D Sensor. Sensors 2021, 21, 3029. https://doi.org/10.3390/s21093029
Liu C, Wang A, Bu C, Wang W, Sun H. Human Motion Tracking with Less Constraint of Initial Posture from a Single RGB-D Sensor. Sensors. 2021; 21(9):3029. https://doi.org/10.3390/s21093029
Chicago/Turabian StyleLiu, Chen, Anna Wang, Chunguang Bu, Wenhui Wang, and Haijing Sun. 2021. "Human Motion Tracking with Less Constraint of Initial Posture from a Single RGB-D Sensor" Sensors 21, no. 9: 3029. https://doi.org/10.3390/s21093029
APA StyleLiu, C., Wang, A., Bu, C., Wang, W., & Sun, H. (2021). Human Motion Tracking with Less Constraint of Initial Posture from a Single RGB-D Sensor. Sensors, 21(9), 3029. https://doi.org/10.3390/s21093029






