Identification of the Optimal Season and Spectral Regions for Shrub Cover Estimation in Grasslands
Abstract
:1. Introduction
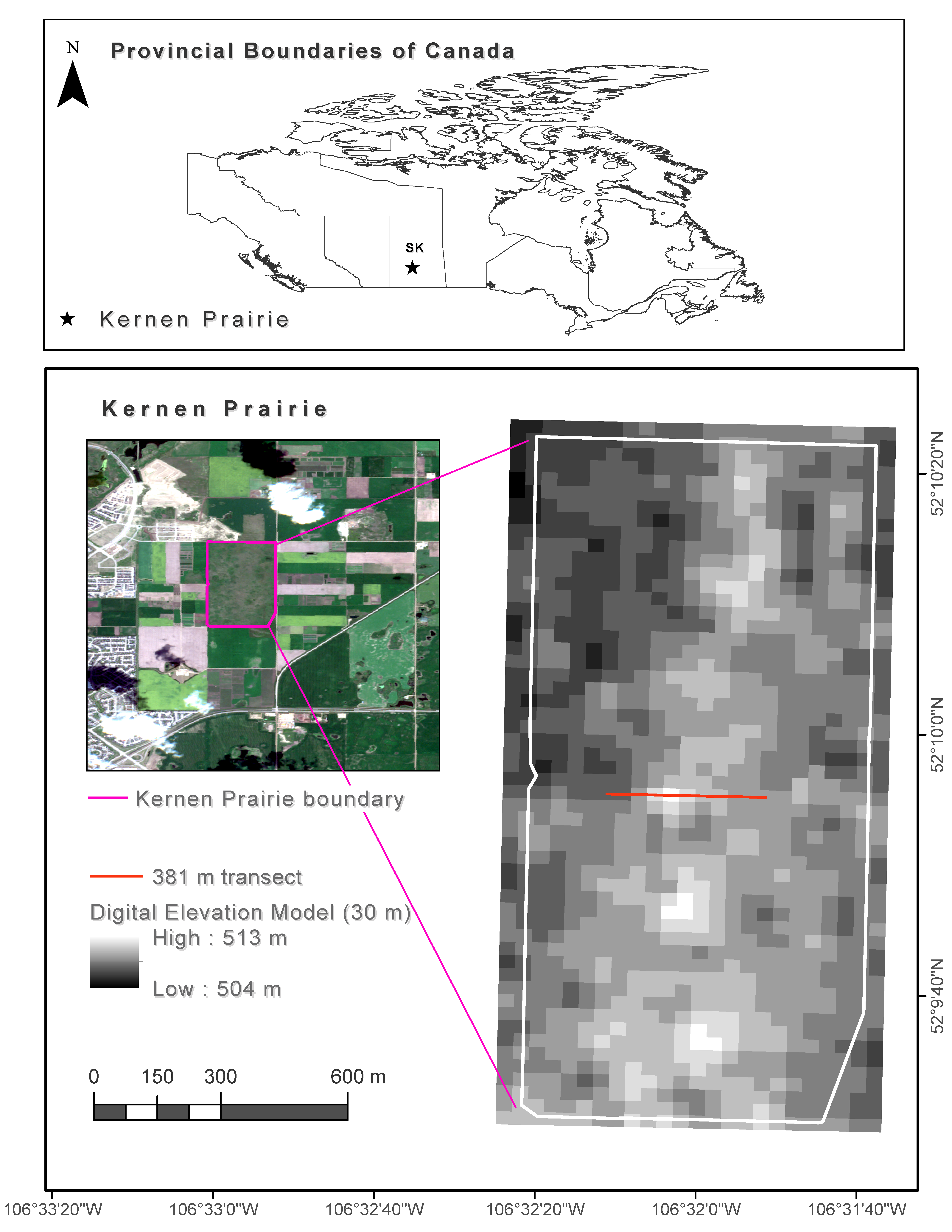
2. Study Area
3. Methods
3.1. Field Design and Data Collection
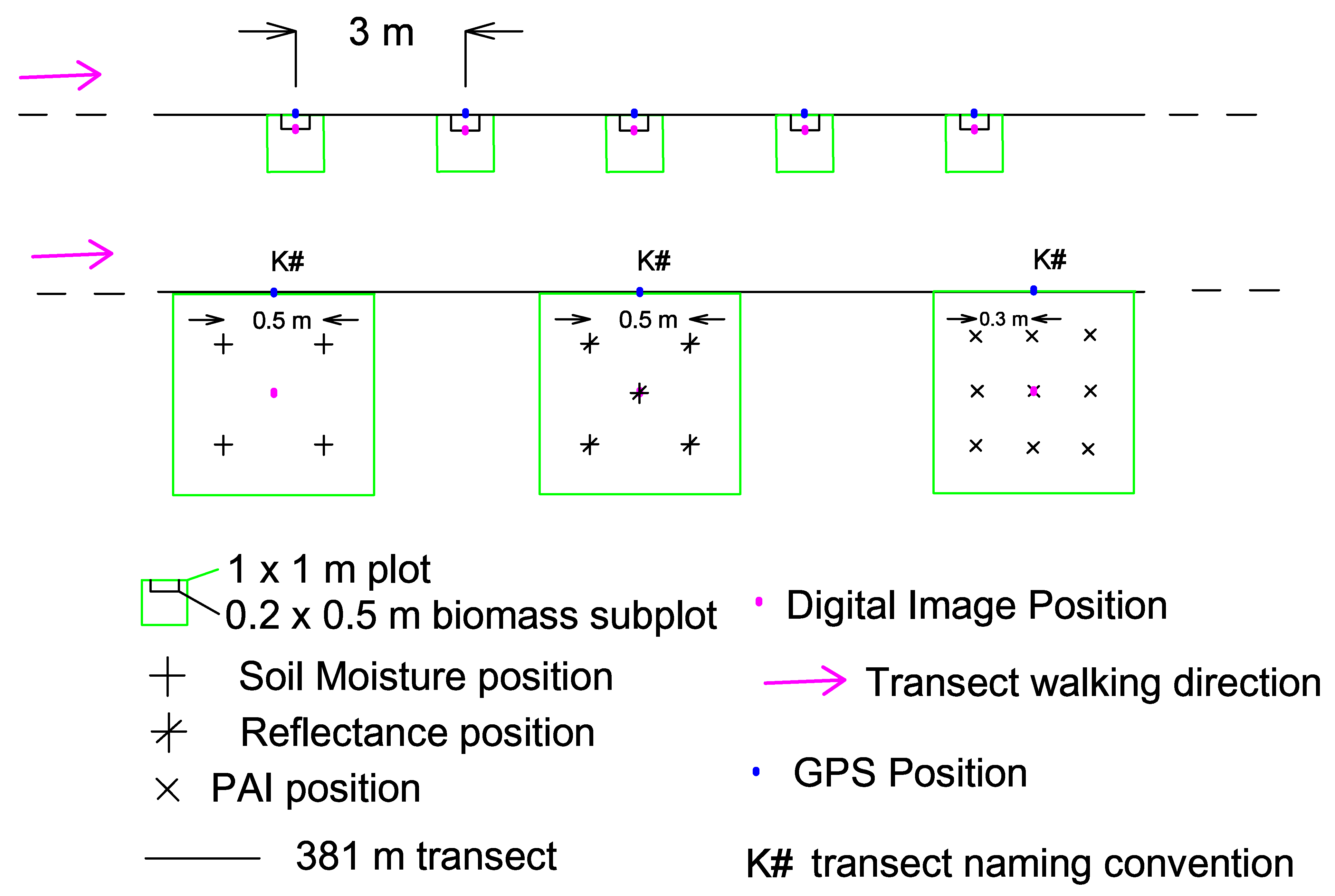
3.1.1. Field Design
3.1.2. Data Collection
3.2. Data Processing
3.3. Seasonal Variation of Biophysical Measurements
3.4. Correlation Analysis between Wavelengths and Shrub Cover
3.5. Shrub Cover Spectral Separability Analysis
3.5.1. Calculation of Separability Metrics
3.5.2. Thresholding and Selection of Important Wavelength Regions
3.6. Broadband Simulation and Shrub Cover Spectral Difference
3.6.1. Broadband Simulation
3.6.2. Broadband Spectral Difference between Shrub Cover Groups
4. Results
4.1. Seasonal Variation of Biophysical and Spectral Measurements
4.2. Relationships between Wavelengths and Shrub Cover
4.3. Shrub Cover Spectal Separation Groups
4.4. Performance of Separability Metrics
4.5. Broadband Simulation and Shrub Cover Spectral Difference
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| B | Bhattacharyya distance |
| D | Divergence |
| JM | Jeffries-Matusita distance |
| LIT | Line Intercept Transect |
| M | M-Statistic |
| NIR | Near Infrared |
| PAI | Plant Area Index |
| SWIR | Shortwave Infrared |
| TD | Transformed Divergence |
| HSD | Honestly Significant Difference |
| WPE | Woody Plant Encroachment |
References
- Bengtsson, J.; Bullock, J.M.; Egoh, B.; Everson, C.; Everson, T.; O’Connor, T.; O’Farrell, P.J.; Smith, H.G.; Lindborg, R. Grasslands—more important for ecosystem services than you might think. Ecosphere 2019, 10. [Google Scholar] [CrossRef]
- Kulshreshtha, S.; Undi, M.; Zhang, J.; Ghorbani, M.M.; Karin, W.; Stewart, A.; Salvano, E.; Kebreab, E.; Ominski, K.K.; Wittenberg, K.; et al. Challenges and Opportunities in Estimating the Value of Goods and Services in Temperate Grasslands—A Case Study of Prairie Grasslands in Manitoba, Canada; InTech Open Access Publisher: Rijeka, Croatia, 2015; Chapter 6; pp. 147–169. [Google Scholar]
- Gang, C.; Zhou, W.; Chen, Y.; Wang, Z.; Sun, Z.; Li, J.; Qi, J.; Odeh, I. Quantitative assessment of the contributions of climate change and human activities on global grassland degradation. Environ. Earth Sci. 2014, 72, 4273–4282. [Google Scholar] [CrossRef]
- Archer, S.R.; Andersen, E.M.; Predick, K.I.; Schwinning, S.; Steidl, R.J.; Woods, S.R. Woody Plant Encroachment-Causes and Concequences. In Rangeland Systems-Processes, Management and Challenges; Briske, D., Ed.; Springer Series on Environmental Management; Springer: Cham, Switzerland, 2017; pp. 25–84. [Google Scholar]
- Heisler, J.L.; Briggs, J.M.; Knapp, A.K. Long-Term Patterns of Shrub Expansion in a C4-Dominated Grassland: Fire Frequency and the Dynamics of Shrub Cover and Abundance. Am. J. Bot. 2003, 90, 423–428. [Google Scholar] [CrossRef] [PubMed]
- Lett, M.S.; Knapp, A.K.; Briggs, J.M.; Blair, J.M. Influence of shrub encroachment on aboveground net primary productivity and carbon and nitrogen pools in a mesic grassland. Can. J. Bot. 2004, 82, 1363–1370. [Google Scholar] [CrossRef]
- Abreu, R.C.R.; Hoffmann, W.A.; Vasconcelos, H.L.; Pilon, N.A.; Rossatto, D.R.; Durigan, G. The biodiversity cost of carbon sequestration in tropical savanna. Sci. Adv. 2017, 3, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zinnert, J.C.; Shiflett, S.A.; Vick, J.K.; Young, D.R. Plant functional traits of a shrub invader relative to sympatric native shrubs. Ecosphere 2013, 4. [Google Scholar] [CrossRef]
- Schreiner-McGraw, A.P.; Vivoni, E.R.; Ajami, H.; Sala, O.E.; Throop, H.L.; Peters, D.P.C. Woody Plant Encroachment has a Larger Impact than Climate Change on Dryland Water Budgets. Sci. Rep. 2020, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kwon, H.-Y.; Nkonya, E.; Johnson, T.; Graw, V.; Kato, E.; Kihiu, E. Global estimates of the impacts of grassland degradation on livestock productivity from 2001 to 2011. In Economics of Land Degradation and Improvement-A Global Assessment for Sustainable Development; Nkonya, E., Mirzabaev, A., von Braun, J., Eds.; Springer: Cham, Switzerland, 2016; pp. 197–214. ISBN 9783319191683. [Google Scholar]
- Goslee, S.C.; Havstad, K.M.; Peters, D.P.C.; Rango, A.; Schlesinger, W.H. High-resolution images reveal rate and pattern of shrub encroachment over six decades in New Mexico, U.S.A. J. Arid Environ. 2003, 54, 755–767. [Google Scholar] [CrossRef]
- Liu, N.; Guan, L. Linkages between woody plant proliferation dynamics and plant physiological traits in southwestern North America. J. Plant Ecol. 2012, 5, 407–416. [Google Scholar] [CrossRef] [Green Version]
- Tong, A.; He, Y. Estimating and mapping chlorophyll content for a heterogeneous grassland: Comparing prediction power of a suite of vegetation indices across scales between years. ISPRS J. Photogramm. Remote Sens. 2017, 126, 146–167. [Google Scholar] [CrossRef]
- Becker, R.H.; Zmijewski, K.A.; Crail, T. Seeing the forest for the invasives: Mapping buckthorn in the Oak Openings. Biol. Invasions 2013, 15, 315–326. [Google Scholar] [CrossRef]
- Köchy, M.; Wilson, S.D. Competitive Effects of Shrubs and Grasses in Prairie. OIKOS 2000, 91, 385–395. [Google Scholar] [CrossRef] [Green Version]
- Gates, D.M.; Keegan, H.J.; Schleter, J.C.; Weidner, V.R. Spectral Properties of Plants. Appl. Opt. 1965, 4, 11. [Google Scholar] [CrossRef]
- Ustin, S.L.; Jacquemoud, S. How the Optical Properties of Leaves Modify the Absorption and Scattering of Energy and Enhance Leaf Functionality BT-Remote Sensing of Plant Biodiversity; Cavender-Bares, J., Gamon, J.A., Townsend, P.A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 349–384. ISBN 978-3-030-33157-3. [Google Scholar]
- Sinclair, T.R.; Hoffer, R.M.; Schreiber, M.M. Reflectance and Internal Structure of Leaves from Several Crops During a Growing Season. Agron. J. 1971, 63, 864–868. [Google Scholar] [CrossRef]
- Ross, J. The Radiation Regime and Architecture of Plant Stands. Q. Rev. Biol. 1982, 57, 96–99. [Google Scholar]
- Norman, J.M.; Welles, J.M.; Walter, E.A. Contrasts Among Bidirectional Reflectance of Leaves, Canopies, and Soils. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 659–667. [Google Scholar] [CrossRef]
- Myneni, R.B.; Williams, D.L. On the relationship between FAPAR and NDVI. Remote Sens. Environ. 1994, 49, 200–211. [Google Scholar] [CrossRef]
- Fitter, A.; Hay, R. Environmental Physiology of PLANTS, 3rd ed.; Academic Press-A Division of Harcourt, Inc.: Lodon, UK; San Diego, CA, USA, 2002; ISBN 0-12-257766-3. [Google Scholar]
- Oldeland, J.; Dorigo, W.; Wesuls, D.; Jürgens, N. Mapping bush encroaching species by seasonal differences in hyperspectral imagery. Remote. Sens. 2010, 2, 1416–1438. [Google Scholar] [CrossRef] [Green Version]
- Ng, W.T.; Rima, P.; Einzmann, K.; Immitzer, M.; Atzberger, C.; Eckert, S. Assessing the potential of sentinel-2 and pléiades data for the detection of prosopis and vachellia spp. In Kenya. Remote. Sens. 2017, 9, 74. [Google Scholar] [CrossRef] [Green Version]
- Somers, B.; Asner, G.P. Invasive species mapping in hawaiian rainforests using multi-temporal hyperion spaceborne imaging spectroscopy. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2013, 6, 351–359. [Google Scholar] [CrossRef] [Green Version]
- Kopeć, D.; Zakrzewska, A.; Halladin-Dąbrowska, A.; Wylazłowska, J.; Kania, A.; Niedzielko, J. Using Airborne Hyperspectral Imaging Spectroscopy to Accurately Monitor Invasive and Expansive Herb Plants: Limitations and Requirements of the Method. Sensors 2019, 19, 2871. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niphadkar, M.; Nagendra, H. Remote sensing of invasive plants: Incorporating functional traits into the picture. Int. J. Remote. Sens. 2016, 37, 3074–3085. [Google Scholar] [CrossRef]
- Mori, N. Composition and Structure of Fescue Prairie Respond to Burning and Environmental Conditions More Than to Grazing or Burning Plus Grazing in the Short Term; University of Saskatchewan: Saskatoon, SK, Canada, 2009. [Google Scholar]
- Archibold, O.W.; Ripley, E.A.; Bretell, D.L. Comparison of the Microclimates of a Small Aspen Grove and Adjacent Prairie in Saskatchewan. Am. Midl. Nat. 1996, 136, 248. [Google Scholar] [CrossRef]
- Baines, G.B.K. Plant Distribution on a Saskatchewan Prairie. Vegetatio 1973, 28, 99–123. [Google Scholar] [CrossRef]
- Slopek, J.I.; Lamb, E.G. Long-Term Efficacy of Glyphosate for Smooth Brome Control in Native Prairie. Invasive Plant Sci. Manag. 2017, 10, 350–355. [Google Scholar] [CrossRef]
- Pylypec, B. The Kernen Prairie–a relict fescue grassland near Saskatoon, Saskatchewan. Blue JAY 1986, 44, 222–231. [Google Scholar] [CrossRef]
- Acton, D.F.; Ellis, J.G. The Soils of the Saskatoon Map Area 73-B Saskatchewan; No. 306; Extension Division, University of Saskatchewan: Saskatoon, SK, Canada, 1978. [Google Scholar]
- Sanderson, M. Drought in the Canadian Northwest. Geogr. Rev. 1948, 38, 289–299. [Google Scholar] [CrossRef]
- Government of Canada Canadian Climate Normals 1981–2010 Station Data-Saskatoon SRC. Available online: https://climate.weather.gc.ca/climate_normals/results_1981_2010_e.html?searchType=stnProx&txtRadius=25&optProxType=city&selCity=52%7C9%7C106%7C39%7CSaskatoon&selPark=&txtCentralLatDeg=&txtCentralLatMin=0&txtCentralLatSec=0&txtCentralLongDeg=&txtCentralLon (accessed on 23 April 2020).
- Statistics Canada 2016 Census-Boundary Files. Available online: https://www12.statcan.gc.ca/census-recensement/2011/geo/bound-limit/bound-limit-2016-eng.cfm (accessed on 20 January 2021).
- ESA Copernicus Open Access Hub. Available online: https://scihub.copernicus.eu/dhus/#/home (accessed on 8 March 2021).
- USGS USGS EROS Archive-Digital Elevation-Shuttle Radar Topography Mission (SRTM) 1 Arc-Second Global. Available online: https://www.usgs.gov/centers/eros/science/usgs-eros-archive-digital-elevation-shuttle-radar-topography-mission-srtm-1-arc?qt-science_center_objects=0#qt-science_center_objects (accessed on 8 May 2020).
- Souster, W.E. Soils of the Kernen Crop Research Farm; Saskatchewan Institute of Pedology: Saskatoon, SK, Canada, 1979. [Google Scholar]
- Meyer, T.; Holloway, P.; Christiansen, T.B.; Miller, J.A.; D’Odorico, P.; Okin, G.S. An assessment of multiple drivers determining woody species composition and structure: A case study from the Kalahari, Botswana. Land 2019, 8. [Google Scholar] [CrossRef] [Green Version]
- Yusuf, H.M.; Treydte, A.C.; Sauerborn, J. Managing semi-arid rangelands for carbon storage: Grazing and woody encroachment effects on soil carbon and nitrogen. PLoS ONE 2015, 10, e0109063. [Google Scholar] [CrossRef]
- Wilfong, B.N.; Gorchov, D.L.; Henry, M.C. Detecting an Invasive Shrub in Deciduous Forest Understories Using Remote Sensing. Weed Sci. 2009, 57, 512–520. [Google Scholar] [CrossRef]
- McNickle, G.G.; Lamb, E.G.; Lavender, M.; Cahill, J.F.; Schamp, B.S.; Siciliano, S.D.; Condit, R.; Hubbell, S.P.; Baltzer, J.L. Checkerboard score–area relationships reveal spatial scales of plant community structure. Oikos 2018, 127, 415–426. [Google Scholar] [CrossRef]
- Hiernaux, P.; Diarra, L.; Trichon, V.; Mougin, E.; Soumaguel, N.; Baup, F. Woody plant population dynamics in response to climate changes from 1984 to 2006 in Sahel (Gourma, Mali). J. Hydrol. 2009, 375, 103–113. [Google Scholar] [CrossRef] [Green Version]
- Michalsky, S.J.; Ellis, R.A. Vegetation of Grasslands National Park; DA Westworth and Associates: Calgary, AB, Canada, 1994. [Google Scholar]
- Camacho, F. Standards for in situ LAI and biophysical variables measurements. In Proceedings of the JECAM/GOEGLAM Science Meeting, Brussels, Belgium, 16–17 November 2015. [Google Scholar]
- LI-COR. LAI-2000 Pland Canopy Analyzer-Instruction Manual; LI-COR, Inc.: Lincoln, NE, USA, 1992. [Google Scholar]
- Li, Z.; Guo, X. A suitable NDVI product for monitoring spatiotemporal variations of LAI in semiarid mixed grassland. Can. J. Remote. Sens. 2013, 38, 683–694. [Google Scholar] [CrossRef]
- Jain, A.; Dubes, R. Algorithms for Clustering Data; Prentice Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Murtagh, F.; Legendre, P. Ward’s Hierarchical Agglomerative Clustering Method: Which Algorithms Implement Ward’s Criterion? J. Classif. 2014, 31, 274–295. [Google Scholar] [CrossRef] [Green Version]
- Wu, J. Cluster Analysis and K-means Clustering: An Introduction 1.1 The Emergence of Data Mining. Adv. K-Means Clust. 2012, 1–16. [Google Scholar] [CrossRef]
- Charrad, M.; Ghazzali, N.; Boiteau, V.; Niknafs, A. NbClust: An R Package for Determining the Relevant Number of Clusters in a Data Set. J. Stat. Softw. 2014, 61, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1987, 100, 441–471. [Google Scholar] [CrossRef] [PubMed]
- Zar, J.H. Significance testing of the spearman rank correlation coefficient. J. Am. Stat. Assoc. 1972, 67, 578–580. [Google Scholar] [CrossRef]
- Evans, J.S.; Murphy, M.A.; Ram, K. Package ‘ Spatialeco ’-Spatial Analysis and Modelling Utilities; Version 1.3-5; CRAN. Available online: https://github.com/jeffreyevans/spatialEco (accessed on 20 February 2021).
- Kaufman, Y.J.; Remer, L.A. Detection of Forests Using Mid-IR Reflectance: An Application for Aerosol Studies. IEEE Trans. Geosci. Remote. Sens. 1994, 32, 672–683. [Google Scholar] [CrossRef]
- Bhattacharyya, A. On a Measure of Divergence between Two Multinomial Populations. Indian J. Stat. 1946, 7, 401–406. [Google Scholar]
- Bruzzone, L.; Roli, F.; Serpico, S.B. An Extension of the Jeffreys-Matusita Distance to Multiclass Cases for Feature Selection. IEEE Trans. Geosci. Remote. Sens. 1995, 33, 1318–1321. [Google Scholar] [CrossRef] [Green Version]
- Jeffreys, H. Theory of Probability, 2nd ed.; Oxford, Clarendon Press: Oxford, UK, 1948. [Google Scholar]
- Jeffreys, H. An Invariant Form for the Prior Probability in Estimation Problems. R. Soc. Lond. Ser. A Math. Phys. Sci. 1946, 186, 453–461. [Google Scholar]
- Swain, P.H.; Davis, S.M. Remote sensing: The quantitative approach. Remote. Sens. Quant. Approach. 1978, 3, 713–714. [Google Scholar] [CrossRef]
- Gunal, S.; Edizkan, R. Subspace based feature selection for pattern recognition. Inf. Sci. 2008, 178, 3716–3726. [Google Scholar] [CrossRef]
- Kailath, T. The Divergence and Bhattacharyya Distance Measures in Signal Selection. IEEE Trans. Commun. Technol. 1967, 15, 52–60. [Google Scholar] [CrossRef]
- Bindel, M.; Hese, S.; Berger, C.; Schmullius, C. Feature selection from high resolution remote sensing data for biotope mapping. ISPRS-Int. Arch. Photogramm. Remote.Sens. Spat. Inf. Sci. 2012, XXXVIII-4/W19, 39–44. [Google Scholar] [CrossRef] [Green Version]
- Matusita, K. A distance and related statistics in multivariate analysis. In Multivariate Analysis; Krishnaiah, P.R., Ed.; Academic: New York, NY, USA, 1966; pp. 178–200. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591. [Google Scholar] [CrossRef]
- Mohd Razali, N.; Bee Wah, Y. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Huang, H.; Roy, D.P.; Boschetti, L.; Zhang, H.K.; Yan, L.; Kumar, S.S.; Gomez-Dans, J.; Li, J. Separability analysis of Sentinel-2A Multi-Spectral Instrument (MSI) data for burned area discrimination. Remote. Sens. 2016, 8, 873. [Google Scholar] [CrossRef] [Green Version]
- Campbell, J.E.; Harris, J.R.; Huntley, D.H.; McMartin, I.; Wityk, U.; Dredge, L.A.; Eagles, S. Remote Predictive Mapping of Surficial Earth Materials: Wager Bay North Area, Nunavut-NTS 46-E (N), 46-K (SW), 46-L, 46-M (SW), 56-H (N), 56-I and 56-J (S); Geological Survey of Canada: Ottawa, ON, Canada, 2013. [Google Scholar]
- NASA Spectral Response of the Operational Land Imager In-Band, Band-Average Relative Spectral Response. Available online: https://landsat.gsfc.nasa.gov/landsat-8/spectral-response-operational-land-imager-band-band-average-relative-spectral-response (accessed on 26 March 2021).
- ESA Sentinel-2 Spectral Response Functions (S2-SRF). Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-2-msi/document-library/-/asset_publisher/Wk0TKajiISaR/content/sentinel-2a-spectral-responses (accessed on 26 March 2021).
- Lehnert, L.W.; Meyer, H.; Obermeier, W.A.; Silva, B.; Regeling, B.; Thies, B.; Bendix, J. Hyperspectral data analysis in R: The hsdar package. J. Stat. Softw. 2019, 89, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Holechek, J.J.; Pieper, R.D.; Herbel, C.H. Range Management-Principles and Practices, 6th ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2011; ISBN 978-0-13-501416-5. [Google Scholar]
- Ratliff, L.F.; Ritchie, J.T.; Cassel, D.K. Field-Measured Limits of Soil Water Availability as Related to Laboratory-Measured Properties. Soil Sci. Soc. Am. J. 1983, 47, 770–775. [Google Scholar] [CrossRef]
- ESA Sentinel Online-Radiometric Resolutions. Available online: https://sentinels.copernicus.eu/web/sentinel/user-guides/sentinel-2-msi/resolutions/radiometric (accessed on 6 March 2021).
- USGS Landsat 8 Band Designations. Available online: https://www.usgs.gov/media/images/landsat-8-band-designations (accessed on 6 March 2021).
- Lafleur, P.M.; Hember, R.A.; Admiral, S.W.; Roulet, N.T. Annual and seasonal variability in evapotranspiration and water table at a shrub-covered bog in southern Ontario, Canada. Hydrol. Process. 2005, 19, 3533–3550. [Google Scholar] [CrossRef]
- Wang, P.; Li, X.Y.; Wang, L.; Wu, X.; Hu, X.; Fan, Y.; Tong, Y. Divergent evapotranspiration partition dynamics between shrubs and grasses in a shrub-encroached steppe ecosystem. New Phytol. 2018, 219, 1325–1337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ouyang, Z.T.; Gao, Y.; Xie, X.; Guo, H.Q.; Zhang, T.T.; Zhao, B. Spectral Discrimination of the Invasive Plant Spartina alterniflora at Multiple Phenological Stages in a Saltmarsh Wetland. PLoS ONE 2013, 8, e67315. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Liu, Y.; Cui, X.; Chen, J.; Chen, X. Mechanisms, monitoring and modeling of shrub encroachment into grassland: A review. Int. J. Digit. Earth 2019, 12, 625–641. [Google Scholar] [CrossRef]
- Shivakanth, G.; Tanwar, P.S. Review On Conventional and Advanced Classification Approaches in Remote Sensing Image Processing. Int. J. Comput. Sci. Eng. 2018, 6, 871–879. [Google Scholar] [CrossRef]
- Hennessy, A.; Clarke, K.; Lewis, M. Hyperspectral Classification of Plants: A Review of Waveband Selection Generalisability. Remote. Sens. 2020, 12, 113. [Google Scholar] [CrossRef] [Green Version]
- Thenkabail, P.S.; Gumma, M.K.; Teluguntla, P.; Irshad, A.M. Hyperspectral Remote Sensing of Vegetation and Agricultural Crops. Photogramm. Eng. Remote Sens. 2014, 80, 697–709. [Google Scholar]
- Hank, T.B.; Berger, K.; Bach, H.; Clevers, J.G.P.W.; Gitelson, A.; Zarco-Tejada, P.; Mauser, W. Spaceborne Imaging Spectroscopy for Sustainable Agriculture: Contributions and Challenges. Surv. Geophys. 2019, 40, 515–551. [Google Scholar] [CrossRef] [Green Version]
- Homer, C.G.; Meyer, D.K.; Aldridge, C.L.; Schell, S.J. Detecting annual and seasonal changes in a sagebrush ecosystem with remote sensing-derived continuous fields. J. Appl. Remote. Sens. 2013, 7, 073508. [Google Scholar] [CrossRef] [Green Version]
- Rajah, P.; Odindi, J.; Mutanga, O. Evaluating the potential of freely available multispectral remotely sensed imagery in mapping american bramble (Rubus cuneifolius). S. Afr. Geogr. J. 2018, 100, 291–307. [Google Scholar] [CrossRef]
- Manske, L.L. Western Snowberry Biology, 2006 Annual Report, Grassland Section; Dickinson Research Extension Center: Dickinson, ND, USA, 2006. [Google Scholar]
- Timenstein, D.; Festuca Altaica, F.; Campestris, F. Hallii. In Fire Effects Information System; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station, Fire Sciences Laboratory (Producer), 2000; Available online: https://www.fs.fed.us/database/feis/plants/graminoid/fesspp/all.html (accessed on 30 January 2021).
- He, Y.; Yang, J.; Guo, X. Green vegetation cover dynamics in a heterogeneous grassland: Spectral unmixing of landsat time series from 1999 to 2014. Remote. Sens. 2020, 12, 3826. [Google Scholar] [CrossRef]
- Dormaar, J.F. Susceptibility of organic matter of chernozemic ah horizons to biological decomposition. Can. J. Soil Sci. 1975, 55, 473–480. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Guo, X. Monitoring northern mixed prairie health using broadband satellite imagery. Int. J. Remote. Sens. 2008, 29, 2257–2271. [Google Scholar] [CrossRef]
- Proy, C.; Tanré, D.; Deschamps, P.Y. Evaluation of topographic effects in remotely sensed data. Remote. Sens. Environ. 1989, 30, 21–32. [Google Scholar] [CrossRef]
- Hao, D.; Wen, J.; Xiao, Q.; Wu, S.; Lin, X.; You, D.; Tang, Y. Modeling Anisotropic Reflectance over Composite Sloping Terrain. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 3903–3923. [Google Scholar] [CrossRef]
- Si, B.C.; Kachanoski, R.G.; Reynolds, W.D. Analysis of Soil Variability. In Soil Sampling and Methods of Analysis; Carter, M.R., Gregorich, E.G., Eds.; CRC Press: Boca Raton, FL, USA, 2003; pp. 1–32. [Google Scholar]




| Separability Statistic | Threshold Value | Separability Class |
|---|---|---|
| M-Statistic | >1 | Good |
| ≤1 | Poor | |
| Transformed Divergence and Jeffries-Matusita Distance | ≥1.8 | Good |
| 1.51–1.79 | Moderate | |
| ≤1.5 | Poor |
| Spring | Summer | Fall | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| M | SD | Min–Max | M | SD | Min–Max | M | SD | Min–Max | ||
| Cover (%) | Green grass | 25.5 | 8.6 | 5–65 | 30.2 | 7.7 | 5–55 | 23.5 | 6.3 | 10–40 |
| Shrub | 20.0 | 19.3 | 0–75 | 18.0 | 17.2 | 0–80 | 17.4 | 16.5 | 0–75 | |
| Forb | 14.4 | 11.0 | 0–50 | 15.0 | 9.9 | 0–40 | 13.8 | 8.3 | 0–40 | |
| Standing dead | 30.5 | 11.3 | 0–60 | 30.4 | 9.0 | 0–50 | 41.9 | 12.8 | 0–80 | |
| Litter | 8.2 | 7.2 | 0–40 | 5.9 | 4.9 | 0–25 | 2.9 | 5.1 | 0–25 | |
| Bare ground | 0.7 | 3.1 | 0–25 | 0.3 | 2.2 | 0–20 | 0.1 | 1.3 | 0–15 | |
| Rock | 0.5 | 2.6 | 0–20 | 0.2 | 1.3 | 0–10 | 0.3 | 1.9 | 0–20 | |
| Other | 0.1 | 1.32 | 0–15 | 0.1 | 0.9 | 0–10 | 0.1 | 0.6 | 0–5 | |
| PAI | 1.69 | 0.50 | 0.29–3.15 | 2.37 | 0.70 | 0.37–4.26 | 1.96 | 0.57 | 0.97–3.41 | |
| Soil moisture (m³/m³) | 0.148 | 0.035 | 0.068–0.212 | 0.183 | 0.026 | 0.076–0.225 | 0.189 | 0.019 | 0.144–0.248 | |
| Biomass (g/m²) | Green grass | 123.8 | 53.9 | 11–314 | ||||||
| Forb | 21.1 | 24.0 | 1–126 | |||||||
| Shrub | 97.5 | 139.0 | 1–888 | |||||||
| Non-photosynthetic vegetation | 422.8 | 194.1 | 84–931 | |||||||
| Moss | 3.8 | 7.3 | 1–40 | |||||||
| Total | 669.0 | |||||||||
| Average Shrub Cover (%) | Shrub Density Per 1 m | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Total Shrub | W. Snowb. | Prairie R. | Total Shrub | W. Snowb. | Prairie R. | |||||
| Estimation method | M | SD | M | SD | M | SD | M | M | M | |
| LIT | 28.1 | - | 25.4 | - | 2.7 | - | 1.3 | 1.09 | 0.23 | |
| Quadrat | 20.2 | 19.2 | 18.8 | 19.1 | 1.4 | 2.2 | - | - | - | |
| Season | Shrub Cover Groups (%) | Number of Quadrats per Group |
|---|---|---|
| Spring | 0, <10, <35, <50, <75, <100 | 18, 35, 53, 12, 10, 32 |
| Summer | 0, <10, <25, <40, <80, <100 | 19, 35, 41, 22, 11, 11 |
| Fall | 0, <20, <40, <75, <100 | 19, 61, 38, 10, 20 |
| Season | Shrub Sensitive Wavelength Regions | |||
|---|---|---|---|---|
| Moderate | Good | |||
| Spectral Bands (nm) | Spectral Region | Spectral Bands (nm) | Spectral Region | |
| Spring | 380–466 | B | 467–509 | B |
| 604–617 | R | 618–694 | R | |
| 723–883 | NIR | |||
| 1485–1518 | SWIR-1 | 1431–1484 | SWIR-1 | |
| 2105–2329 | SWIR-2 | 1981–2104 | SWIR-2 | |
| Summer | 1981–2061 | SWIR-2 | 718–979 | NIR |
| 980–1122 | NIR | |||
| Fall | 580–597 | G | 525–579 | G |
| 1183–1314 | NIR | 704–1182 | NIR | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soubry, I.; Guo, X. Identification of the Optimal Season and Spectral Regions for Shrub Cover Estimation in Grasslands. Sensors 2021, 21, 3098. https://doi.org/10.3390/s21093098
Soubry I, Guo X. Identification of the Optimal Season and Spectral Regions for Shrub Cover Estimation in Grasslands. Sensors. 2021; 21(9):3098. https://doi.org/10.3390/s21093098
Chicago/Turabian StyleSoubry, Irini, and Xulin Guo. 2021. "Identification of the Optimal Season and Spectral Regions for Shrub Cover Estimation in Grasslands" Sensors 21, no. 9: 3098. https://doi.org/10.3390/s21093098
APA StyleSoubry, I., & Guo, X. (2021). Identification of the Optimal Season and Spectral Regions for Shrub Cover Estimation in Grasslands. Sensors, 21(9), 3098. https://doi.org/10.3390/s21093098






