Robust Texture Mapping Using RGB-D Cameras
Abstract
:1. Introduction
2. Related Work
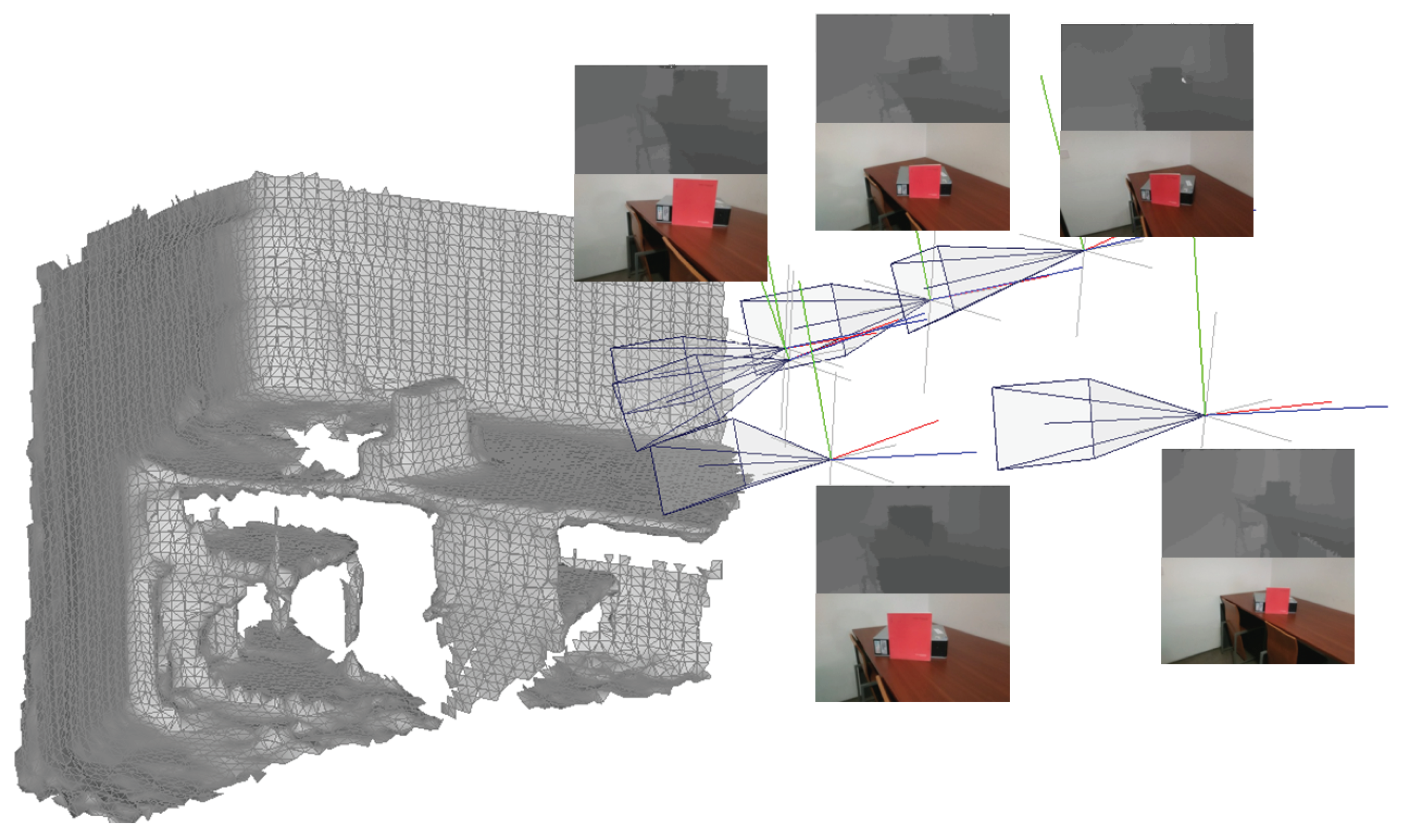
3. Problem Formulation
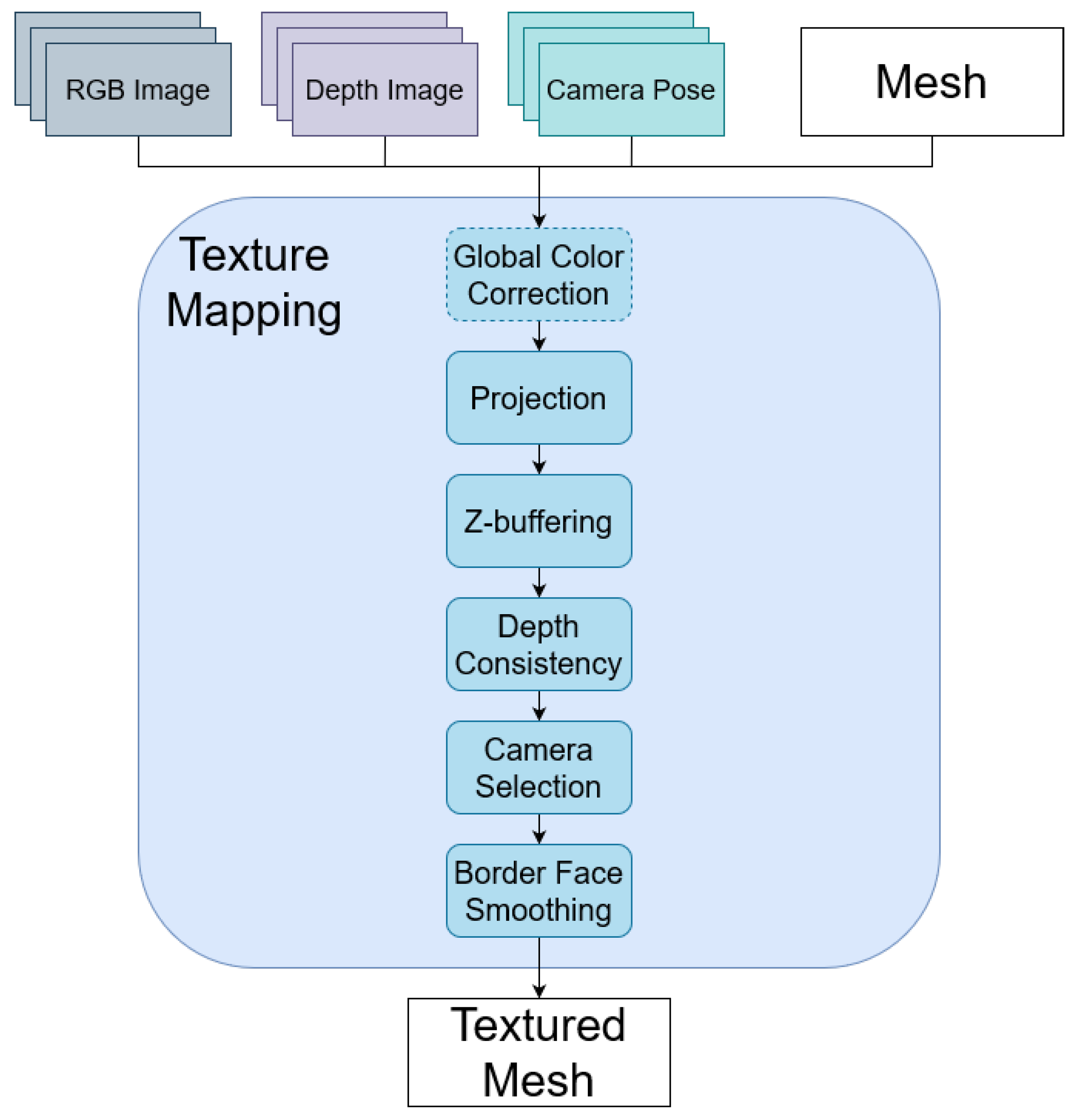
4. Proposed Approach
4.1. Projection
4.2. Z-Buffering
4.3. Depth Consistency
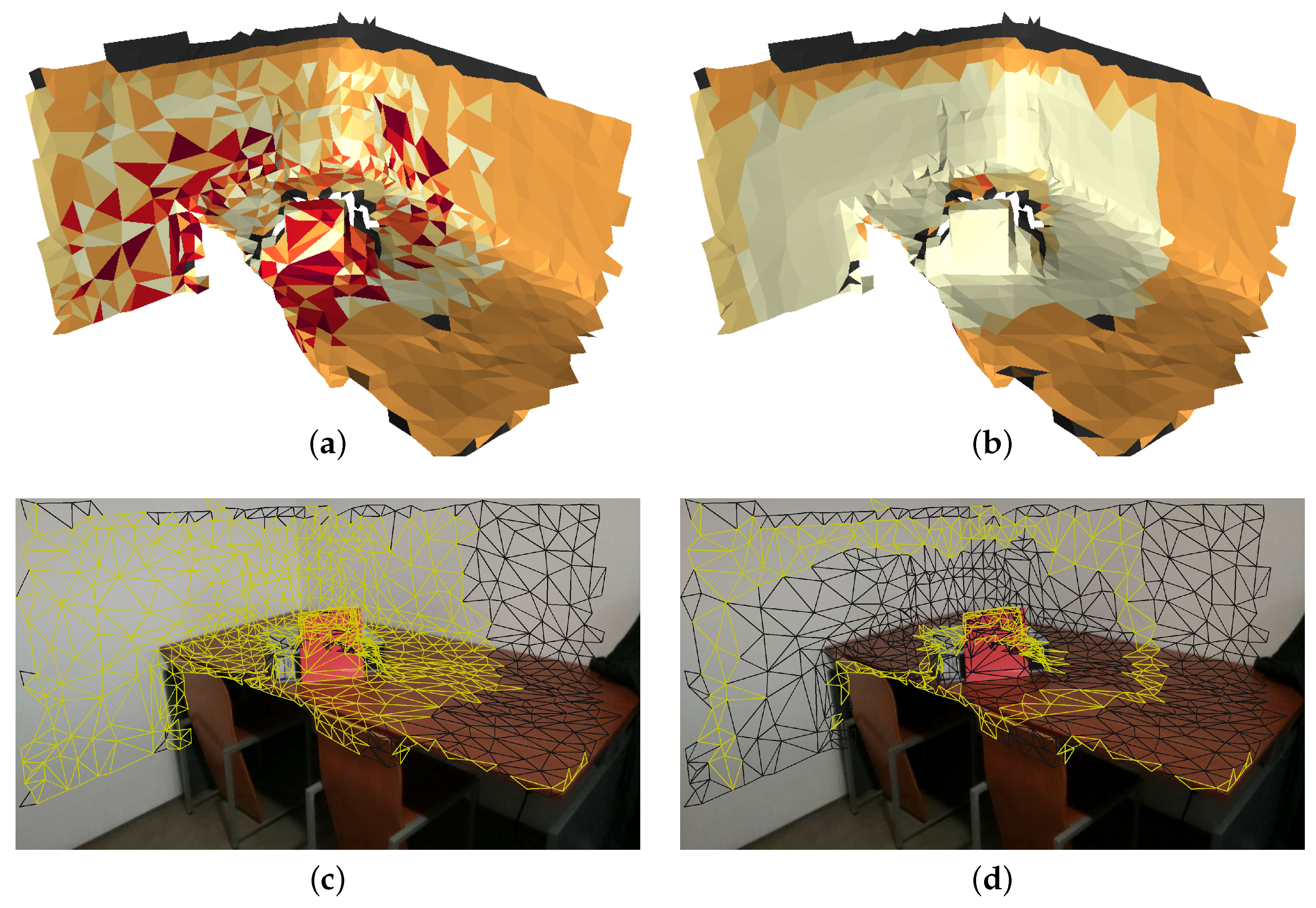
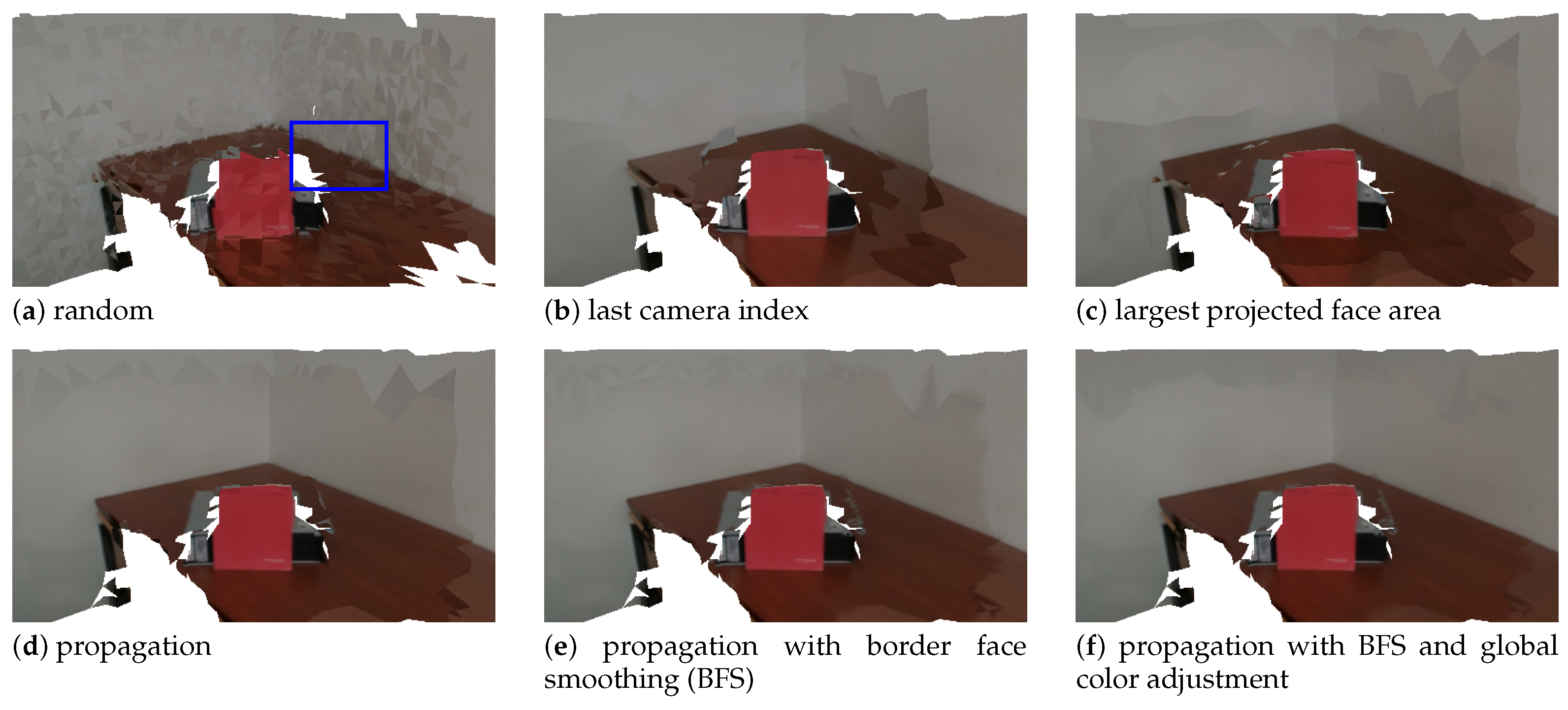
4.4. Camera Selection
4.5. Border Face Smoothing
4.6. Global Color Adjustment
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, H.; Li, H.; Liu, X.; Luo, J.; Xie, S.; Sun, Y. A Novel Method for Extrinsic Calibration of Multiple RGB-D Cameras Using Descriptor-Based Patterns. Sensors 2019, 19, 349. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, C.; Yang, B.; Song, S.; Tian, M.; Li, J.; Dai, W.; Fang, L. Calibrate Multiple Consumer RGB-D Cameras for Low-Cost and Efficient 3D Indoor Mapping. Remote Sens. 2018, 10, 328. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z. Microsoft kinect sensor and its effect. IEEE Multimed. 2012, 19, 4–10. [Google Scholar] [CrossRef] [Green Version]
- Morell-Gimenez, V.; Saval-Calvo, M.; Azorin-Lopez, J.; Garcia-Rodriguez, J.; Cazorla, M.; Orts-Escolano, S.; Fuster-Guillo, A. A Comparative Study of Registration Methods for RGB-D Video of Static Scenes. Sensors 2014, 14, 8547–8576. [Google Scholar] [CrossRef] [PubMed]
- Munaro, M.; Menegatti, E. Fast RGB-D people tracking for service robots. Auton. Robot. 2014, 37, 227–242. [Google Scholar] [CrossRef]
- Andújar, D.; Dorado, J.; Fernández-Quintanilla, C.; Ribeiro, A. An Approach to the Use of Depth Cameras for Weed Volume Estimation. Sensors 2016, 16, 972. [Google Scholar] [CrossRef] [Green Version]
- Osroosh, Y.; Khot, L.R.; Peters, R.T. Economical thermal-RGB imaging system for monitoring agricultural crops. Comput. Electron. Agric. 2018, 147, 34–43. [Google Scholar] [CrossRef]
- Yan, Y.; Mao, Y.; Li, B. SECOND: Sparsely Embedded Convolutional Detection. Sensors 2018, 18, 3337. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, M.; Santos, V.; Sappa, A.D.; Dias, P.; Moreira, A.P. Incremental texture mapping for autonomous driving. Robot. Auton. Syst. 2016, 84, 113–128. [Google Scholar] [CrossRef]
- Pham, H.H.; Salmane, H.; Khoudour, L.; Crouzil, A.; Velastin, S.A.; Zegers, P. A Unified Deep Framework for Joint 3D Pose Estimation and Action Recognition from a Single RGB Camera. Sensors 2020, 20, 1825. [Google Scholar] [CrossRef] [Green Version]
- Lim, G.H.; Pedrosa, E.; Amaral, F.; Lau, N.; Pereira, A.; Dias, P.; Azevedo, J.L.; Cunha, B.; Reis, L.P. Rich and robust human-robot interaction on gesture recognition for assembly tasks. In Proceedings of the International Conference on Autonomous Robot Systems and Competitions (ICARSC), Coimbra, Portugal, 26–28 April 2017; pp. 159–164. [Google Scholar]
- Liu, Z.; Zhao, C.; Wu, X.; Chen, W. An Effective 3D Shape Descriptor for Object Recognition with RGB-D Sensors. Sensors 2017, 17, 451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oliveira, M.; Lopes, L.S.; Lim, G.H.; Kasaei, S.H.; Tomé, A.M.; Chauhan, A. 3D object perception and perceptual learning in the RACE project. Robot. Auton. Syst. 2016, 75, 614–626. [Google Scholar] [CrossRef]
- Su, P.C.; Shen, J.; Xu, W.; Cheung, S.C.S.; Luo, Y. A Fast and Robust Extrinsic Calibration for RGB-D Camera Networks. Sensors 2018, 18, 235. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Yan, Q.; Yang, L.; Liao, J.; Xiao, C. Texture Mapping for 3D Reconstruction With RGB-D Sensor. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Sui, W.; Wang, L.; Fan, B.; Xiao, H.; Wu, H.; Pan, C. Layer-Wise Floorplan Extraction for Automatic Urban Building Reconstruction. IEEE Trans. Vis. Comput. Graph. 2016, 22, 1261–1277. [Google Scholar] [CrossRef]
- Klingensmith, M.; Dryanovski, I.; Srinivasa, S.; Xiao, J. Chisel: Real Time Large Scale 3D Reconstruction Onboard a Mobile Device. In Proceedings of the Robotics Science and Systems 2015, Rome, Italy, 13–17 July 2015. [Google Scholar]
- Garcia-Hernando, G.; Yuan, S.; Baek, S.; Kim, T.K. First-Person Hand Action Benchmark With RGB-D Videos and 3D Hand Pose Annotations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Luo, R.; Sener, O.; Savarese, S. Scene semantic reconstruction from egocentric rgb-d-thermal videos. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 593–602. [Google Scholar]
- Mueller, F.; Mehta, D.; Sotnychenko, O.; Sridhar, S.; Casas, D.; Theobalt, C. Real-time hand tracking under occlusion from an egocentric rgb-d sensor. In Proceedings of the International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; Volume 10. [Google Scholar]
- Rogez, G.; Supancic, J.S.; Ramanan, D. Understanding everyday hands in action from rgb-d images. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 3889–3897. [Google Scholar]
- Koniaris, C.; Cosker, D.; Yang, X.; Mitchell, K. Survey of texture mapping techniques for representing and rendering volumetric mesostructure. J. Comput. Graph. Tech. 2014, 3, 18–60. [Google Scholar]
- Zollhöfer, M.; Patrick Stotko, A.G.; Theobalt, C.; Nießner, M.; Klein, R.; Kolb, A. State of the Art on 3D Reconstruction with RGB-D Cameras. Comput. Graph. Forum 2018, 37, 625–652. [Google Scholar] [CrossRef]
- Zhou, K.; Gong, M.; Huang, X.; Guo, B. Data-Parallel Octrees for Surface Reconstruction. IEEE Trans. Vis. Comput. Graph. 2011, 17, 669–681. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Ye, M.; Manocha, D.; Yang, R. 3D Reconstruction in the Presence of Glass and Mirrors by Acoustic and Visual Fusion. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1785–1798. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Hartley, R.; Salzmann, M. Mirror Surface Reconstruction from a Single Image. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 760–773. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Funkhouser, T. Deep Depth Completion of a Single RGB-D Image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Liu, L.; Chan, S.H.; Nguyen, T.Q. Depth Reconstruction From Sparse Samples: Representation, Algorithm, and Sampling. IEEE Trans. Image Process. 2015, 24, 1983–1996. [Google Scholar] [CrossRef] [PubMed]
- Canelhas, D.R.; Stoyanov, T.; Lilienthal, A.J. A Survey of Voxel Interpolation Methods and an Evaluation of Their Impact on Volumetric Map-Based Visual Odometry. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 3637–3643. [Google Scholar]
- Oleynikova, H.; Taylor, Z.; Fehr, M.; Siegwart, R.; Nieto, J. Voxblox: Incremental 3D Euclidean Signed Distance Fields for on-board MAV planning. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1366–1373. [Google Scholar]
- Werner, D.; Al-Hamadi, A.; Werner, P. Truncated Signed Distance Function: Experiments on Voxel Size. In Proceedings of the International Conference Image Analysis and Recognition (ICIAR 2014), Vilamoura, Portugal, 22–24 October 2014; pp. 357–364. [Google Scholar]
- Rouhani, M.; Sappa, A.D.; Boyer, E. Implicit B-Spline Surface Reconstruction. IEEE Trans. Image Process. 2015, 24, 22–32. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Lai, S. An Orientation Inference Framework for Surface Reconstruction From Unorganized Point Clouds. IEEE Trans. Image Process. 2011, 20, 762–775. [Google Scholar] [CrossRef] [PubMed]
- Marques, B.; Carvalho, R.; Dias, P.; Oliveira, M.; Ferreira, C.; Santos, B.S. Evaluating and enhancing google tango localization in indoor environments using fiducial markers. In Proceedings of the 2018 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Torres Vedras, Portugal, 25–27 April 2018; pp. 142–147. [Google Scholar]
- Liu, L.; Wang, Y.; Zhao, L.; Huang, S. Evaluation of different SLAM algorithms using Google tangle data. In Proceedings of the 12th IEEE Conference on Industrial Electronics and Applications (ICIEA), Siem Reap, Cambodia, 18–20 June 2017; pp. 1954–1959. [Google Scholar]
- Nguyen, K.A.; Luo, Z. On assessing the positioning accuracy of Google Tango in challenging indoor environments. In Proceedings of the 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; pp. 1–8. [Google Scholar]
- Roberto, R.; Lima, J.P.; Araújo, T.; Teichrieb, V. Evaluation of Motion Tracking and Depth Sensing Accuracy of the Tango Tablet. In Proceedings of the 2016 IEEE International Symposium on Mixed and Augmented Reality (ISMAR-Adjunct), Merida, Mexico, 19–23 September 2016; pp. 231–234. [Google Scholar]
- Lefloch, D.; Kluge, M.; Sarbolandi, H.; Weyrich, T.; Kolb, A. Comprehensive Use of Curvature for Robust and Accurate Online Surface Reconstruction. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2349–2365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, Q.; Xu, D.; Zou, W. A survey on three-dimensional modeling based on line structured light scanner. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 7439–7444. [Google Scholar]
- Zhou, Q.Y.; Koltun, V. Color Map Optimization for 3D Reconstruction with Consumer Depth Cameras. ACM Trans. Graph. 2014, 33, 155. [Google Scholar] [CrossRef]
- Maier, R.; Kim, K.; Cremers, D.; Kautz, J.; Nießner, M. Intrinsic3D: High-Quality 3D Reconstruction by Joint Appearance and Geometry Optimization with Spatially-Varying Lighting. In Proceedings of the International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Plötz, T.; Roth, S. Automatic Registration of Images to Untextured Geometry Using Average Shading Gradients. Int. J. Comput. Vis. 2017, 125, 65–81. [Google Scholar] [CrossRef]
- Guo, Y.; Wan, J.; Zhang, J.; Xu, K.; Lu, M. Efficient registration of multiple range images for fully automatic 3D modeling. In Proceedings of the 2014 International Conference on Computer Graphics Theory and Applications (GRAPP), Lisbon, Portugal, 5–8 January 2014; pp. 1–8. [Google Scholar]
- Guo, Y.; Sohel, F.; Bennamoun, M.; Wan, J.; Lu, M. An Accurate and Robust Range Image Registration Algorithm for 3D Object Modeling. IEEE Trans. Multimed. 2014, 16, 1377–1390. [Google Scholar] [CrossRef]
- Marroquim, R.; Pfeiffer, G.; Carvalho, F.; Oliveira, A.A.F. Texturing 3D models from sequential photos. Vis. Comput. 2012, 28, 983–993. [Google Scholar] [CrossRef]
- Pintus, R.; Gobbetti, E. A Fast and Robust Framework for Semiautomatic and Automatic Registration of Photographs to 3D Geometry. J. Comput. Cult. Herit. 2015, 7, 23. [Google Scholar] [CrossRef]
- Liu, L.; Nguyen, T.Q. A Framework for Depth Video Reconstruction From a Subset of Samples and Its Applications. IEEE Trans. Image Process. 2016, 25, 4873–4887. [Google Scholar] [CrossRef]
- Neugebauer, P.J.; Klein, K. Texturing 3D Models of Real World Objects from Multiple Unregistered Photographic Views. Comput. Graph. Forum 2001, 18, 245–256. [Google Scholar] [CrossRef]
- Callieri, M.; Cignoni, P.; Corsini, M.; Scopigno, R. Masked Photo Blending: Mapping dense photographic dataset on high-resolution 3D models. Comput. Graph. 2008, 32, 464–473. [Google Scholar] [CrossRef] [Green Version]
- Kehl, W.; Navab, N.; Ilic, S. Coloured signed distance fields for full 3D object reconstruction. In Proceedings of the British Machine Vision Conference, Nottingham, UK, 1–5 September 2014. [Google Scholar]
- Lempitsky, V.S.; Ivanov, D.V. Seamless Mosaicing of Image-Based Texture Maps. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–6. [Google Scholar]
- Allène, C.; Pons, J.P.; Keriven, R. Seamless image-based texture atlases using multi-band blending. In Proceedings of the 19th International Conference on Pattern Recognition, Tampa, FL, USA, 8–11 December 2008; pp. 1–4. [Google Scholar]
- Gal, R.; Wexler, Y.; Ofek, E.; Hoppe, H.; Cohen-Or, D. Seamless Montage for Texturing Models. Eurographics 2010 2010, 29, 479–486. [Google Scholar] [CrossRef] [Green Version]
- Pérez, P.; Gangnet, M.; Blake, A. Poisson Image Editing. ACM Trans. Graph. 2003, 22, 313–318. [Google Scholar] [CrossRef]
- Chang, A.; Dai, A.; Funkhouser, T.; Halber, M.; Niessner, M.; Savva, M.; Song, S.; Zeng, A.; Zhang, Y. Matterport3D: Learning from RGB-D Data in Indoor Environments. In Proceedings of the International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017. [Google Scholar]
- Oxholm, G.; Nishino, K. Shape and Reflectance Estimation in the Wild. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 376–389. [Google Scholar] [CrossRef]
- Lombardi, S.; Nishino, K. Reflectance and Illumination Recovery in the Wild. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 129–141. [Google Scholar] [CrossRef]
- Zheng, Y.; Lin, S.; Kambhamettu, C.; Yu, J.; Kang, S.B. Single-image vignetting correction. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 2243–2256. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.J.; Pollefeys, M. Robust radiometric calibration and vignetting correction. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 562–576. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, M.; Sappa, A.D.; Santos, V. Unsupervised local color transfer for coarsely registered images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 201–208. [Google Scholar]
- Xu, W.; Mulligan, J. Performance evaluation of color correction approaches for automatic multi-view image and video stitching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 263–270. [Google Scholar]
- Oliveira, M.; Sappa, A.D.; Santos, V. A Probabilistic Approach for Color Correction in Image Mosaicking Applications. IEEE Trans. Image Process. 2015, 24, 508–523. [Google Scholar] [CrossRef] [PubMed]
- Wyman, C.; Hoetzlein, R.; Lefohn, A. Frustum-traced irregular Z-buffers: Fast, sub-pixel accurate hard shadows. IEEE Trans. Vis. Comput. Graph. 2016, 22, 2249–2261. [Google Scholar] [CrossRef] [PubMed]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, M.; Lim, G.-H.; Madeira, T.; Dias, P.; Santos, V. Robust Texture Mapping Using RGB-D Cameras. Sensors 2021, 21, 3248. https://doi.org/10.3390/s21093248
Oliveira M, Lim G-H, Madeira T, Dias P, Santos V. Robust Texture Mapping Using RGB-D Cameras. Sensors. 2021; 21(9):3248. https://doi.org/10.3390/s21093248
Chicago/Turabian StyleOliveira, Miguel, Gi-Hyun Lim, Tiago Madeira, Paulo Dias, and Vítor Santos. 2021. "Robust Texture Mapping Using RGB-D Cameras" Sensors 21, no. 9: 3248. https://doi.org/10.3390/s21093248
APA StyleOliveira, M., Lim, G.-H., Madeira, T., Dias, P., & Santos, V. (2021). Robust Texture Mapping Using RGB-D Cameras. Sensors, 21(9), 3248. https://doi.org/10.3390/s21093248








