A Two Joint Neck Model to Identify Malposition of the Head Relative to the Thorax
Abstract
:1. Introduction
1.1. Neck Pain
1.2. Identifying Malposition
1.3. Contribution
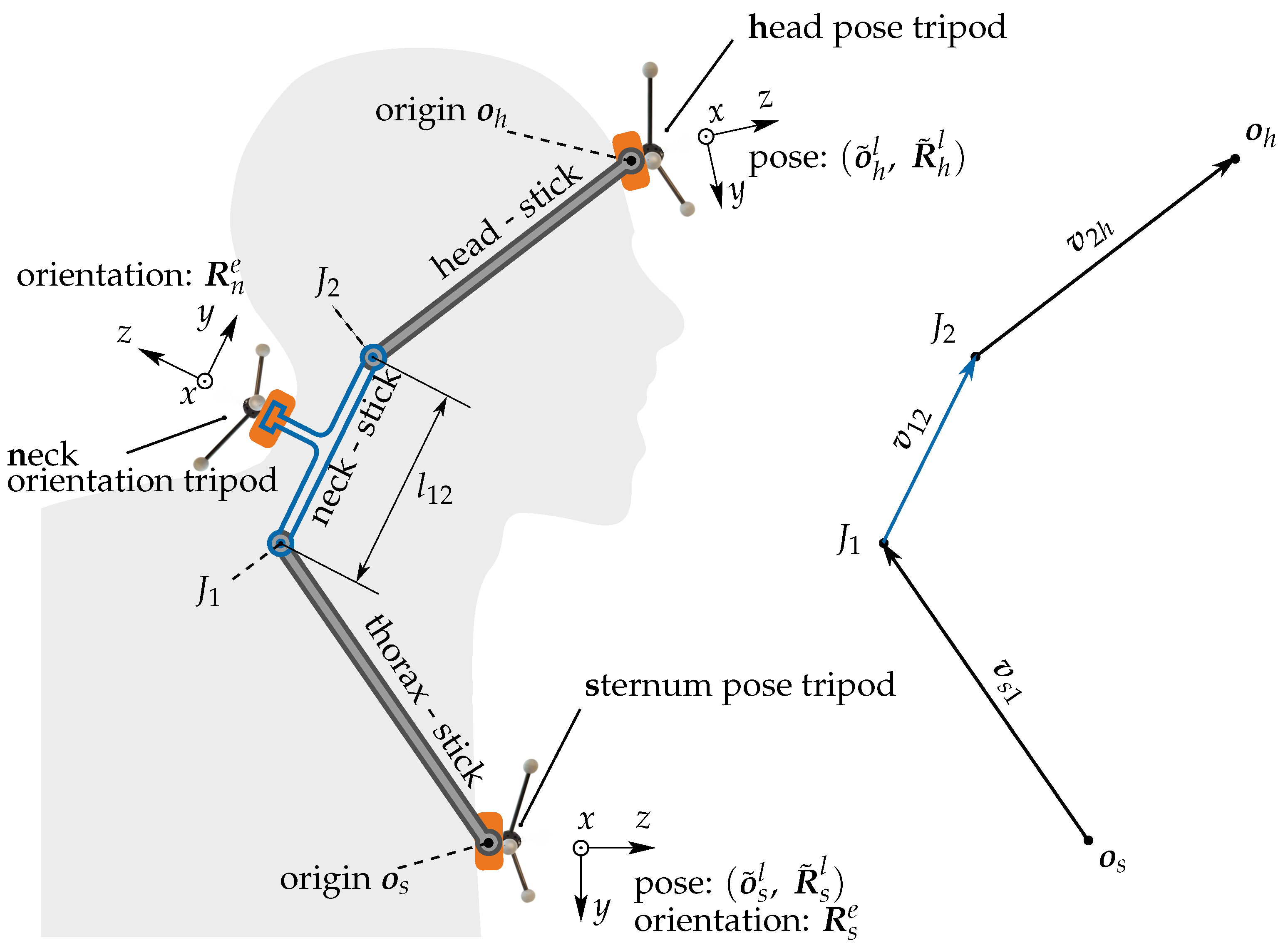
2. Neck Model
2.1. Coordinate Frames
2.2. Model Parameter Identification
2.2.1. Predicted Head Position
2.2.2. Measured Head Position
2.2.3. Parameter Fitting
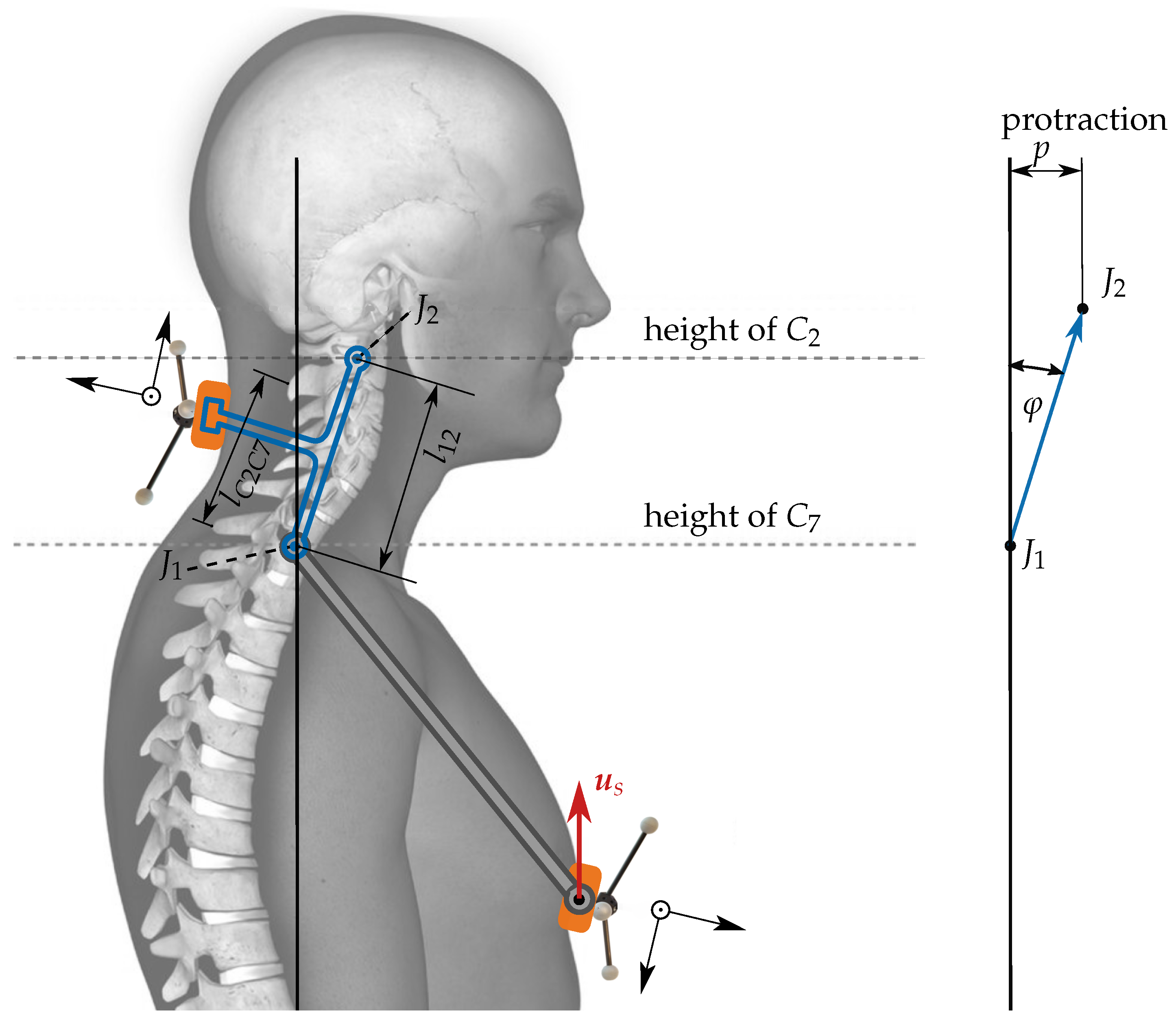
2.3. Calibration Procedure
2.4. Measuring Protraction
3. Materials and Methods
3.1. Participants
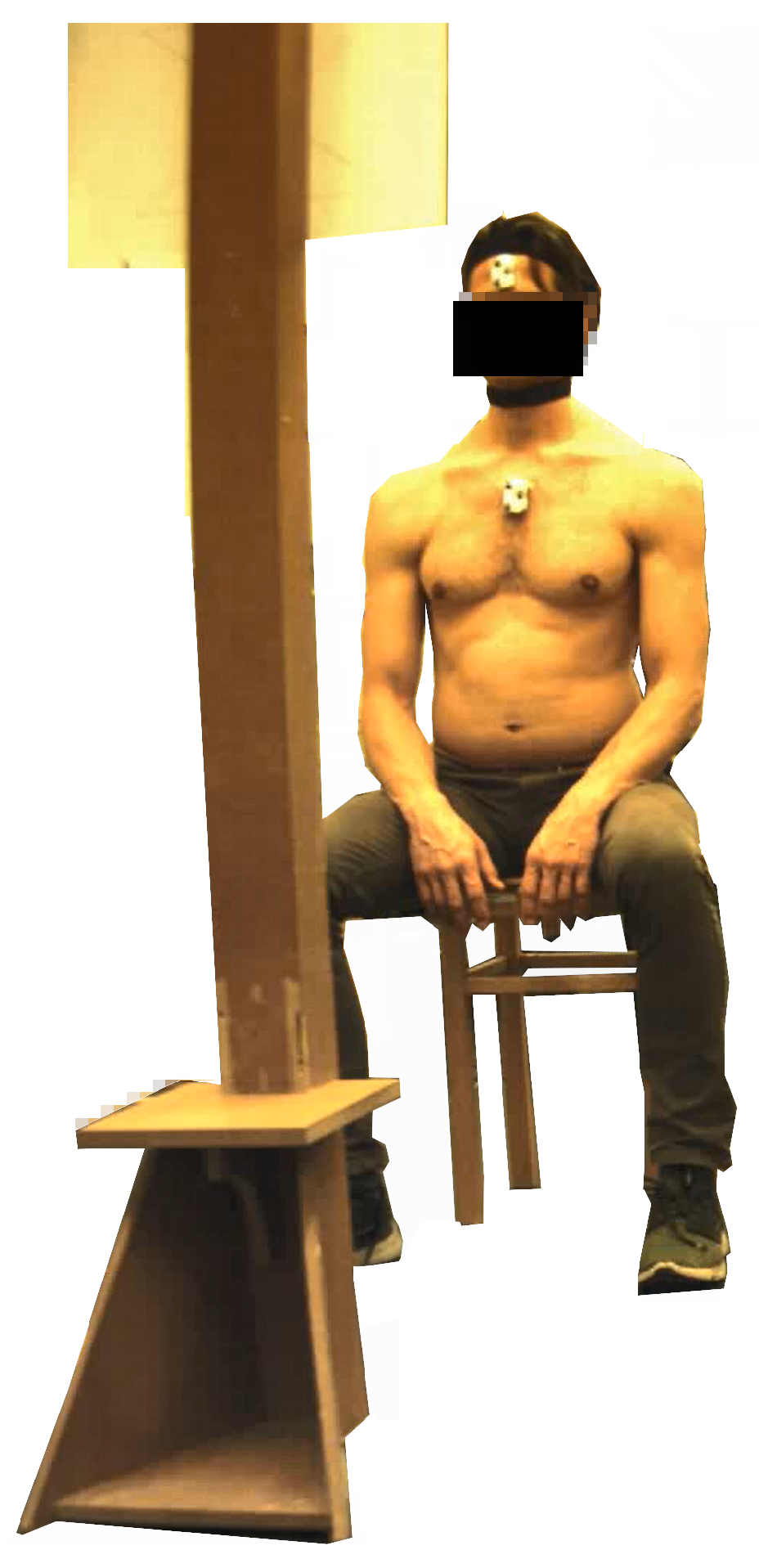
3.2. Equipment
3.3. Measurement Procedure
3.4. Data Analysis
3.4.1. Neck Length Estimates
3.4.2. Real-World Model Validation
3.4.3. Noise Sensitivity
3.4.4. Video Analysis
4. Results
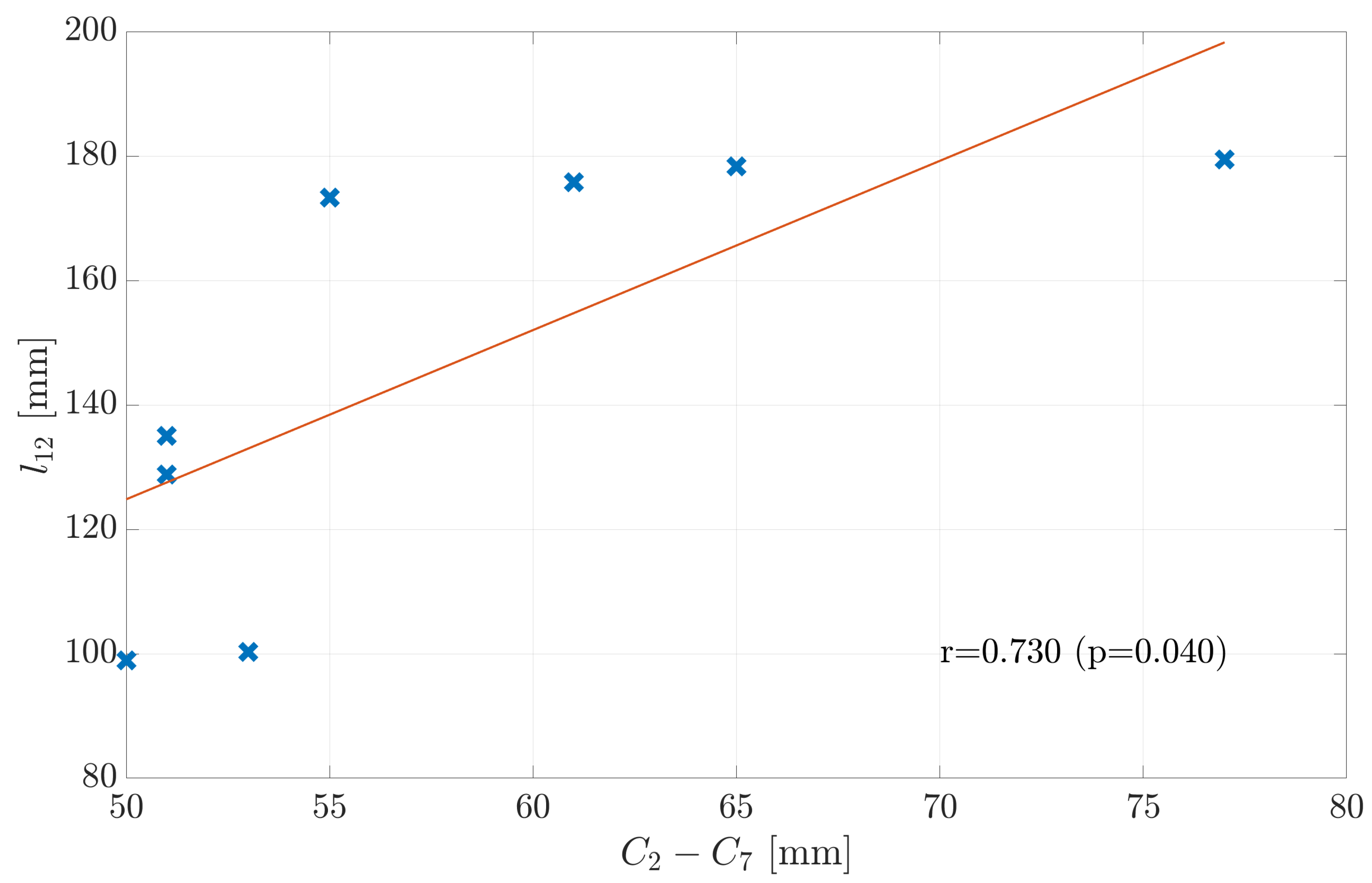
4.1. Neck Length Estimates
4.2. Real-World Model Validation
4.3. Noise Sensitivity
4.4. Video Analysis
4.5. Outlook
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Global Burden of Disease Study Collaborators. Global, regional, and national incidence, prevalence, and years lived with disability for 301 acute and chronic diseases and injuries in 188 countries, 1990–2013: A systematic analysis for the Global Burden of Disease Study 2013. Lancet 2015, 386, 743–800. [Google Scholar] [CrossRef] [Green Version]
- Hoy, D.G.; Protani, M.; De, R.; Buchbinder, R. The epidemiology of neck pain. Best Pract. Res. Clin. Rheumatol. 2010, 24, 783–792. [Google Scholar] [CrossRef]
- Kocur, P.; Wilski, M.; Lewandowski, J.; Łochyński, D. Female office workers with moderate neck pain have increased anterior positioning of the cervical spine and stiffness of upper trapezius myofascial tissue in sitting posture. Pm&r 2019, 11, 476–482. [Google Scholar]
- Persson, P.R.; Hirschfeld, H.; Nilsson-Wikmar, L. Associated sagittal spinal movements in performance of head pro- and retraction in healthy women: A kinematic analysis. Man. Ther. 2007, 12, 119–125. [Google Scholar] [CrossRef]
- Coban, G.; Çöven, I.; Çifçi, B.E.; Yıldırım, E.; Yazıcı, A.C.; Horasanlı, B. The importance of craniovertebral and cervicomedullary angles in cervicogenic headache. Diagn. Interv. Radiol. 2014, 20, 172. [Google Scholar] [CrossRef]
- Liang, Z.; Galea, O.; Thomas, L.; Jull, G.; Treleaven, J. Cervical musculoskeletal impairments in migraine and tension type headache: A systematic review and meta-analysis. Musculoskelet. Sci. Pract. 2019, 42, 67–83. [Google Scholar] [CrossRef] [PubMed]
- Brink, Y.; Crous, L.C.; Louw, Q.A.; Grimmer-Somers, K.; Schreve, K. The association between postural alignment and psychosocial factors to upper quadrant pain in high school students: A prospective study. Man. Ther. 2009, 14, 647–653. [Google Scholar] [CrossRef]
- Cagnie, B.; Danneels, L.; Van Tiggelen, D.; De Loose, V.; Cambier, D. Individual and work related risk factors for neck pain among office workers: A cross sectional study. Eur. Spine J. 2007, 16, 679–686. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jun, D.; Zoe, M.; Johnston, V.; O’Leary, S. Physical risk factors for developing non-specific neck pain in office workers: A systematic review and meta-analysis. Int. Arch. Occup. Environ. Health 2017, 90, 373–410. [Google Scholar] [CrossRef] [PubMed]
- Thigpen, C.A.; Padua, D.A.; Michener, L.A.; Guskiewicz, K.; Giuliani, C.; Keener, J.D.; Stergiou, N. Head and shoulder posture affect scapular mechanics and muscle activity in overhead tasks. J. Electromyogr. Kinesiol. 2010, 20, 701–709. [Google Scholar] [CrossRef]
- Ha, S.Y.; Sung, Y.H. A temporary forward head posture decreases function of cervical proprioception. J. Exerc. Rehabil. 2020, 16, 168. [Google Scholar] [CrossRef]
- Kang, J.H.; Park, R.Y.; Lee, S.J.; Kim, J.Y.; Yoon, S.R.; Jung, K.I. The effect of the forward head posture on postural balance in long time computer based worker. Ann. Rehabil. Med. 2012, 36, 98. [Google Scholar] [CrossRef] [Green Version]
- Moustafa, I.M.; Walton, L.M.; Raigangar, V.; Shousha, T.M.; Harrison, D. Reduction of Posture Hyperkyphosis Improves Short and Long Term Outcomes in Patients with Neck Pain. In Proceedings of the 2020 Combined Sections Meeting (CSM), APTA, Denver, CO, USA, 12–15 February 2020. [Google Scholar]
- Nucci, P.; Curiel, B.; Lembo, A.; Serafino, M. Anomalous head posture related to visual problems. Int. Ophthalmol. 2015, 35, 241–248. [Google Scholar] [CrossRef]
- Dunleavy, K.; Goldberg, A. Comparison of cervical range of motion in two seated postural conditions in adults 50 or older with cervical pain. J. Man. Manip. Ther. 2013, 21, 33–39. [Google Scholar] [CrossRef] [Green Version]
- Edmondston, S.; Björnsdóttir, G.; Pálsson, T.; Solgård, H.; Ussing, K.; Allison, G. Endurance and fatigue characteristics of the neck flexor and extensor muscles during isometric tests in patients with postural neck pain. Man. Ther. 2011, 16, 332–338. [Google Scholar] [CrossRef]
- Park, S. Kinematic analysis of the lower cervical spine in the protracted and retracted neck flexion positions. J. Phys. Ther. Sci. 2015, 27, 135–137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ernst, M.J.; Crawford, R.J.; Schelldorfer, S.; Rausch-Osthoff, A.K.; Barbero, M.; Kool, J.; Bauer, C.M. Extension and flexion in the upper cervical spine in neck pain patients. Man. Ther. 2015, 20, 547–552. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ordway, N.R.; Seymour, R.J.; Donelson, R.G.; Hojnowski, L.S.; Edwards, W.T. Cervical flexion, extension, protrusion, and retraction. A radiographic segmental analysis. Spine 1999, 24, 240–247. [Google Scholar] [CrossRef] [PubMed]
- Straker, L.M.; O’Sullivan, P.B.; Smith, A.J.; Perry, M.C. Relationships between prolonged neck/shoulder pain and sitting spinal posture in male and female adolescents. Man. Ther. 2009, 14, 321–329. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Straker, L.M.; O’Sullivan, P.B.; Smith, A.; Perry, M. Computer use and habitual spinal posture in Australian adolescents. Public Health Rep. 2007, 122, 634–643. [Google Scholar] [CrossRef]
- Brink, Y.; Louw, Q.; Grimmer, K.; Jordaan, E. The spinal posture of computing adolescents in a real-life setting. BMC Musculoskelet. Disord. 2014, 15, 212. [Google Scholar] [CrossRef] [Green Version]
- Lemeunier, N.; Jeoun, E.B.; Suri, M.; Tuff, T.; Shearer, H.; Mior, S.; Wong, J.J.; da Silva-Oolup, S.; Torres, P.; D’Silva, C.; et al. Reliability and validity of clinical tests to assess posture, pain location, and cervical spine mobility in adults with neck pain and its associated disorders: Part 4. A systematic review from the cervical assessment and diagnosis research evaluation (CADRE) collaboration. Musculoskelet. Sci. Pract. 2018, 38, 128–147. [Google Scholar] [CrossRef] [PubMed]
- Walmsley, R.P.; Kimber, P.; Culham, E. The effect of initial head position on active cervical axial rotation range of motion in two age populations. Spine 1996, 21, 2435–2442. [Google Scholar] [CrossRef] [PubMed]
- Kuo, Y.L.; Wang, P.S.; Ko, P.Y.; Huang, K.Y.; Tsai, Y.J. Immediate effects of real-time postural biofeedback on spinal posture, muscle activity, and perceived pain severity in adults with neck pain. Gait Posture 2019, 67, 187–193. [Google Scholar] [CrossRef] [PubMed]
- Richards, J. The measurement of human motion: A comparison of commercially available systems. Hum. Mov. Sci. 1999, 18, 589–602. [Google Scholar] [CrossRef]
- Hanten, W.; Olson, S.; Russell, J.; Lucio, R.; Campbell, A. Total Head Excursion and Resting Head Posture: Normal and Patient Comparisons. Arch. Phys. Med. Rehabil. 2000, 81, 62–66. [Google Scholar] [CrossRef]
- Lee, H.; Nicholson, L.; Adams, R. Cervical Range of Motion Associations With Subclinical Neck Pain. Spine 2004, 29, 33–40. [Google Scholar] [CrossRef]
- Sohn, J.; Choi, H.C.; Lee, S.; Jun, A. Differences in cervical musculoskeletal impairment between episodic and chronic tension-type headache. Cephalalgia 2010, 30, 1514–1523. [Google Scholar] [CrossRef]
- Rudolfsson, T.; Björklung, M.; Djupsjöbacka, M. Range of motion in the upper and lower cervical spine in people with chronic neck pain. Man. Ther. 2012, 17, 53–59. [Google Scholar] [CrossRef]
- Fernández-de-las Peñas, C.; Alonso-Blanco, C.; Cuadrado, M.; Pareja, J. Forward Head Posture and Neck Mobility in Chronic Tension-Type Headache: A Blinded, Controlled Study. Cephalalgia 2006, 26, 314–319. [Google Scholar] [CrossRef]
- Pürckhauer, H.; Rast, F.M.; Nicoletti, C.; Ernst, M.J. Joint position error after neck protraction-retraction movements in healthy office workers: A cross-sectional study. Hum. Mov. Sci. 2020, 72, 102633. [Google Scholar] [CrossRef]
- Yeom, H.; Lim, J.; Yoo, S.; Lee, W. A new posture-correcting system using a vector angle model for preventing forward head posture. Biotechnol. Biotechnol. Equip. 2014, 28, 6–13. [Google Scholar] [CrossRef]
- Hesby, B.B.; Hartvigsen, J.; Rasmussen, H.; Kjaer, P. Electronic measures of movement impairment, repositioning, and posture in people with and without neck pain—a systematic review. Syst. Rev. 2019, 8, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Aranda-Valera, I.C.; Cuesta-Vargas, A.; Garrido-Castro, J.L.; Gardiner, P.V.; López-Medina, C.; Machado, P.M.; Condell, J.; Connolly, J.; Williams, J.M.; Muñoz-Esquivel, K.; et al. Measuring Spinal Mobility Using an Inertial Measurement Unit System: A Validation Study in Axial Spondyloarthritis. Diagnostics 2020, 10, 426. [Google Scholar] [CrossRef] [PubMed]
- O’Grady, M.; O’Dwyer, T.; Connolly, J.; Condell, J.; Esquivel, K.M.; O’Shea, F.D.; Gardiner, P.; Wilson, F. Measuring Spinal Mobility Using an Inertial Measurement Unit System: A Reliability Study in Axial Spondyloarthritis. Diagnostics 2021, 11, 490. [Google Scholar] [CrossRef]
- Sommer, B.; Weisenhorn, M.; Ernst, M.; Meichtry, A.; Rast, F.; Kleger, D.; Schmid, P.; Lünenburger, L.; Bauer, C. Concurrent validity and reliability of a mobile tracking technology to measure angular and linear movements of the neck. J. Biomech. 2019, 96. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Whitmire, E.; Salemi Parizi, F.; Patel, S. Aura: Inside-out electromagnetic controller tracking. In Proceedings of the 17th Annual International Conference on Mobile Systems, Applications, and Services, Seoul, Korea, 17–21 June 2019; pp. 300–312. [Google Scholar]
- Theobald, P.; Jones, M.; Williams, J. Do inertial sensors represent a viable method to reliably measure cervical spine range of motion? Man. Ther. 2012, 17, 92–96. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.; Li, H.; Li, A.; Zhang, H. Wearable IMU-based real-time motion warning system for construction workers’ musculoskeletal disorders prevention. Autom. Constr. 2017, 74, 2–11. [Google Scholar] [CrossRef]
- Wang, J.; Hsu, Y.; Liu, J. An inertial-measurement-unit-based pen with a trajectory reconstruction algorithm and its applications. IEEE Trans. Ind. Electron. 2010, 57, 3508–3521. [Google Scholar] [CrossRef]
- Cappozzo, A.; Della Croce, U.; Leardini, A.; Chiari, L. Human movement analysis using stereophotogrammetry: Part 1: Theoretical background. Gait Posture 2005, 21, 186–196. [Google Scholar] [PubMed]
- Chiari, L.; Della Croce, U.; Leardini, A.; Cappozzo, A. Human movement analysis using stereophotogrammetry: Part 2: Instrumental errors. Gait Posture 2005, 21, 197–211. [Google Scholar] [CrossRef]
- Leardini, A.; Chiari, L.; Della Croce, U.; Cappozzo, A. Human movement analysis using stereophotogrammetry: Part 3. Soft tissue artifact assessment and compensation. Gait Posture 2005, 21, 212–225. [Google Scholar] [CrossRef]
- Della Croce, U.; Leardini, A.; Chiari, L.; Cappozzo, A. Human movement analysis using stereophotogrammetry: Part 4: Assessment of anatomical landmark misplacement and its effects on joint kinematics. Gait Posture 2005, 21, 226–237. [Google Scholar] [CrossRef] [PubMed]
- Seo, S.; Hwang-Bo, G.; Yuk, G.; Han, J.; Kim, J.; Park, S. Dynamic Intervertebral Body Angle of the Lower Spine during Protracted Head Extension Using Measured by Fluoroscopy. J. Phys. Ther. Sci. 2013, 25, 237–239. [Google Scholar] [CrossRef] [Green Version]
- Björck, Å. Numerical Methods for Least Squares Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1996. [Google Scholar]
- Bauer, C.; Rast, F.; Ernst, M.; Kool, J.; Oetiker, S.; Rissanen, S.; Suni, J.; Kankaanpää, M. Concurrent validity and reliability of a novel wireless inertial measurement system to assess trunk movement. J. Electromyogr. Kinesiol. 2015, 25, 782–790. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ernst, M.J.; Rast, F.M.; Bauer, C.M.; Marcar, V.L.; Kool, J. Determination of thoracic and lumbar spinal processes by their percentage position between C7 and the PSIS level. BMC Res. Notes 2013, 6, 1–6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ernst, M.J.; Sommer, B.B.; Meichtry, A.; Bauer, C.M. Intra-rater reliability of determining positions of cervical spinous processes and measuring their relative distances. BMC Res. Notes 2019, 12, 1–4. [Google Scholar] [CrossRef]



| Participant | Length C7–S2 (cm) | Length C2–C7 (cm) | Height (m) | BMI (kg/m2) | Age (Years) |
|---|---|---|---|---|---|
| Mean (standard deviation) | 50.7 (2.2) | 5.8 (0.9) | 1.73 (0.09) | 24.0 (2.4) | 41.1 (11.9) |
| Participant 1 | 49.5 | 6.1 | 1.61 | 23.3 | 30 |
| Participant 2 | 52.0 | 5.1 | 1.81 | 23.4 | 52 |
| Participant 3 | 48.8 | 5.3 | 1.65 | 20.5 | 31 |
| Participant 4 | 53.2 | 7.7 | 1.81 | 27.8 | 28 |
| Participant 5 | 51.0 | 5.5 | 1.72 | 23.9 | 52 |
| Participant 6 | 53.8 | 6.5 | 1.87 | 25.5 | 53 |
| Participant 7 | 47.5 | 5.1 | 1.69 | 21.2 | 31 |
| Participant 8 | 49.5 | 5.0 | 1.68 | 26.1 | 52 |
| Task | Instructions | Illustration |
|---|---|---|
| Static sitting | Sit up straight and straighten up the pelvis. Loosely put your arms on your lap and look straight ahead. Hold this position. | |
| Zigzag in neutral head position | Follow the zigzag pattern on the wall with your head, keeping as close as possible to the middle line. Start moving to the top left. Repeat this movement three times. | 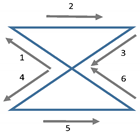 |
| Zigzag in protracted head position | Follow the zigzag pattern on the wall with your head, keeping as close as possible to the middle line. Start moving to the top left. Repeat this movement three times. Hold your head forward. | 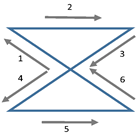 |
| Cross in neutral head position | Follow the cross pattern on the wall with your head, keeping as close as possible to the middle line. Start moving to the top. Repeat this movement three times. | 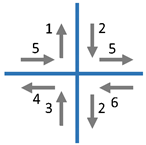 |
| Cross in protracted head position | Follow the cross pattern on the wall with your head, keeping as close as possible to the middle line. Start moving to the top. Hold your head forward. Repeat this movement three times. | 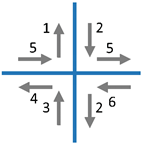 |
| Free movement | Now move your head completely free, at your comfortable speed, for 30 s. |
| Participant | ME X [mm] | X Percent. [mm] | ME Y [mm] | Y Percent. [mm] | ME Z [mm] | Z Percent. [mm] | |||
|---|---|---|---|---|---|---|---|---|---|
| 5% | 95% | 5% | 95% | 5% | 95% | ||||
| 1 | −0.52 | −8.45 | 3.83 | −0.85 | −6.96 | 5.07 | 1.42 | −4.41 | 8.67 |
| 2 | −2.62 | −10.51 | 2.83 | −0.26 | −6.93 | 5.37 | −2.24 | −8.36 | 3.68 |
| 3 | −1.03 | −5.99 | 3.07 | −0.28 | −3.95 | 3.49 | −2.48 | −7.27 | 1.92 |
| 4 | 0.98 | −3.43 | 4.88 | −3.10 | −12.48 | 1.91 | −0.99 | −4.86 | 3.27 |
| 5 | −3.59 | −10.05 | 2.52 | −1.22 | −6.74 | 3.27 | 1.22 | −3.79 | 6.13 |
| 6 | −4.96 | −11.73 | 0.71 | 0.16 | −6.15 | 6.27 | 2.64 | −2.50 | 7.76 |
| 7 | −1.34 | −5.17 | 2.39 | −2.21 | −7.97 | 6.46 | 2.41 | −3.09 | 7.31 |
| 8 | −1.97 | −9.76 | 4.20 | −2.81 | −9.97 | 3.84 | 1.47 | −6.31 | 12.81 |
| Participant | ME X [mm] | X Percent. [mm] | ME Y [mm] | Y Percent. [mm] | ME Z [mm] | Z Percent. [mm] | |||
|---|---|---|---|---|---|---|---|---|---|
| 5% | 95% | 5% | 95% | 5% | 95% | ||||
| 1 | 18.04 | 15.76 | 19.51 | 3.11 | 2.72 | 3.59 | 9.50 | 6.71 | 13.20 |
| 2 | 6.75 | 5.81 | 7.29 | 0.21 | −0.25 | 0.70 | 2.78 | 1.42 | 4.61 |
| 3 | −27.62 | −29.29 | −25.22 | −4.70 | −5.83 | −3.92 | −16.86 | −20.34 | −14.16 |
| 4 | −14.11 | −16.58 | −10.64 | −1.82 | −2.65 | −1.08 | −12.57 | −15.86 | −9.69 |
| 5 | 28.80 | 25.31 | 31.27 | 3.91 | 2.54 | 4.83 | 18.71 | 14.62 | 23.67 |
| 6 | 11.20 | 10.09 | 11.75 | 0.64 | 0.21 | 0.99 | 5.22 | 4.01 | 7.26 |
| 7 | 0.94 | 0.82 | 1.01 | −0.03 | −0.09 | 0.03 | 0.70 | 0.60 | 0.84 |
| 8 | −15.38 | −19.73 | −9.81 | −2.39 | −4.55 | −1.05 | −20.37 | −23.91 | −16.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmid, P.M.; Bauer, C.M.; Ernst, M.J.; Sommer, B.; Lünenburger, L.; Weisenhorn, M. A Two Joint Neck Model to Identify Malposition of the Head Relative to the Thorax. Sensors 2021, 21, 3297. https://doi.org/10.3390/s21093297
Schmid PM, Bauer CM, Ernst MJ, Sommer B, Lünenburger L, Weisenhorn M. A Two Joint Neck Model to Identify Malposition of the Head Relative to the Thorax. Sensors. 2021; 21(9):3297. https://doi.org/10.3390/s21093297
Chicago/Turabian StyleSchmid, Philipp M., Christoph M. Bauer, Markus J. Ernst, Bettina Sommer, Lars Lünenburger, and Martin Weisenhorn. 2021. "A Two Joint Neck Model to Identify Malposition of the Head Relative to the Thorax" Sensors 21, no. 9: 3297. https://doi.org/10.3390/s21093297
APA StyleSchmid, P. M., Bauer, C. M., Ernst, M. J., Sommer, B., Lünenburger, L., & Weisenhorn, M. (2021). A Two Joint Neck Model to Identify Malposition of the Head Relative to the Thorax. Sensors, 21(9), 3297. https://doi.org/10.3390/s21093297






