Analysis of Heart-Sound Characteristics during Motion Based on a Graphic Representation
Abstract
1. Introduction
2. Experimental Platform and Method
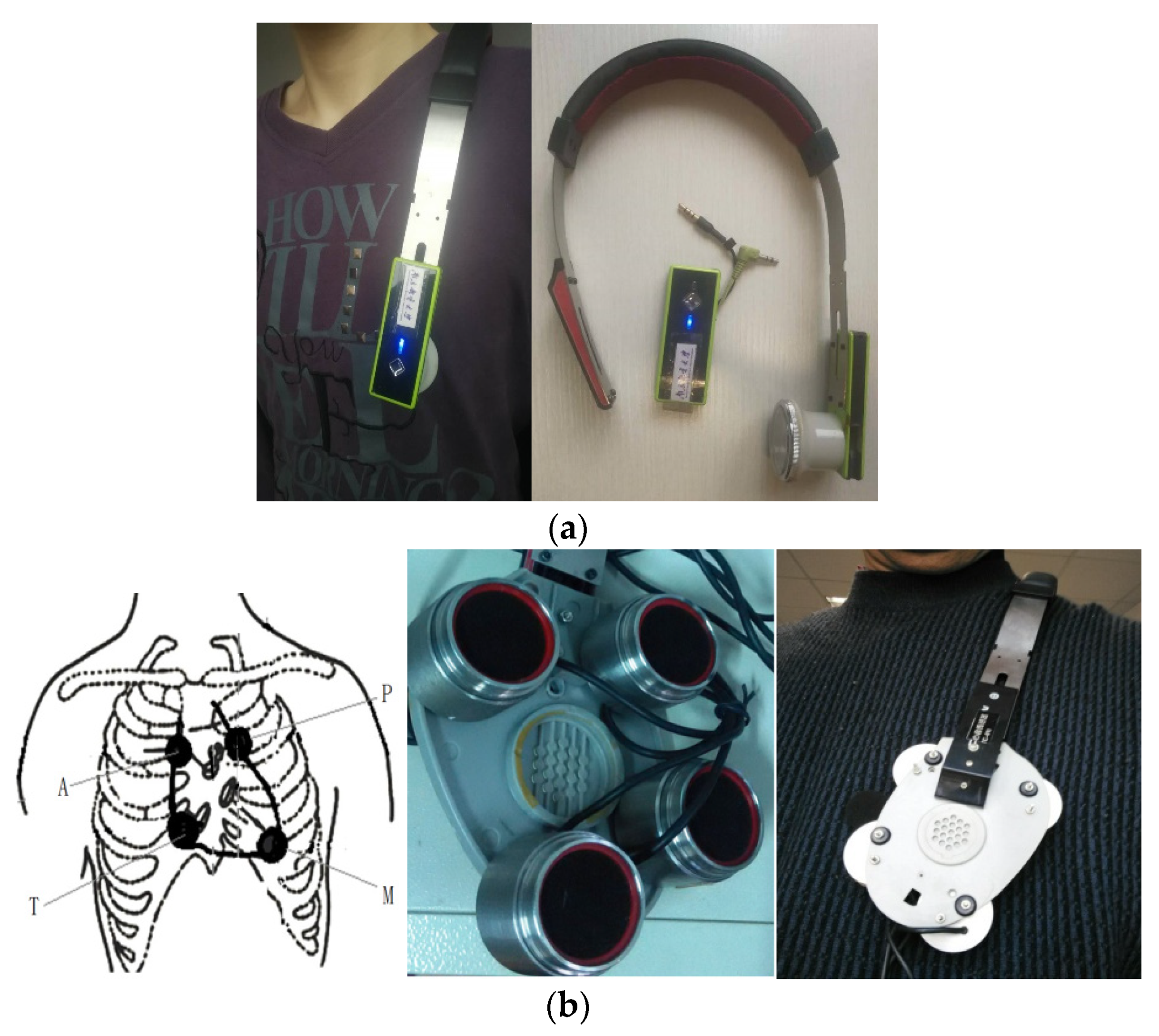
2.1. Heart-Sound Collector
2.2. Data Collection Methods
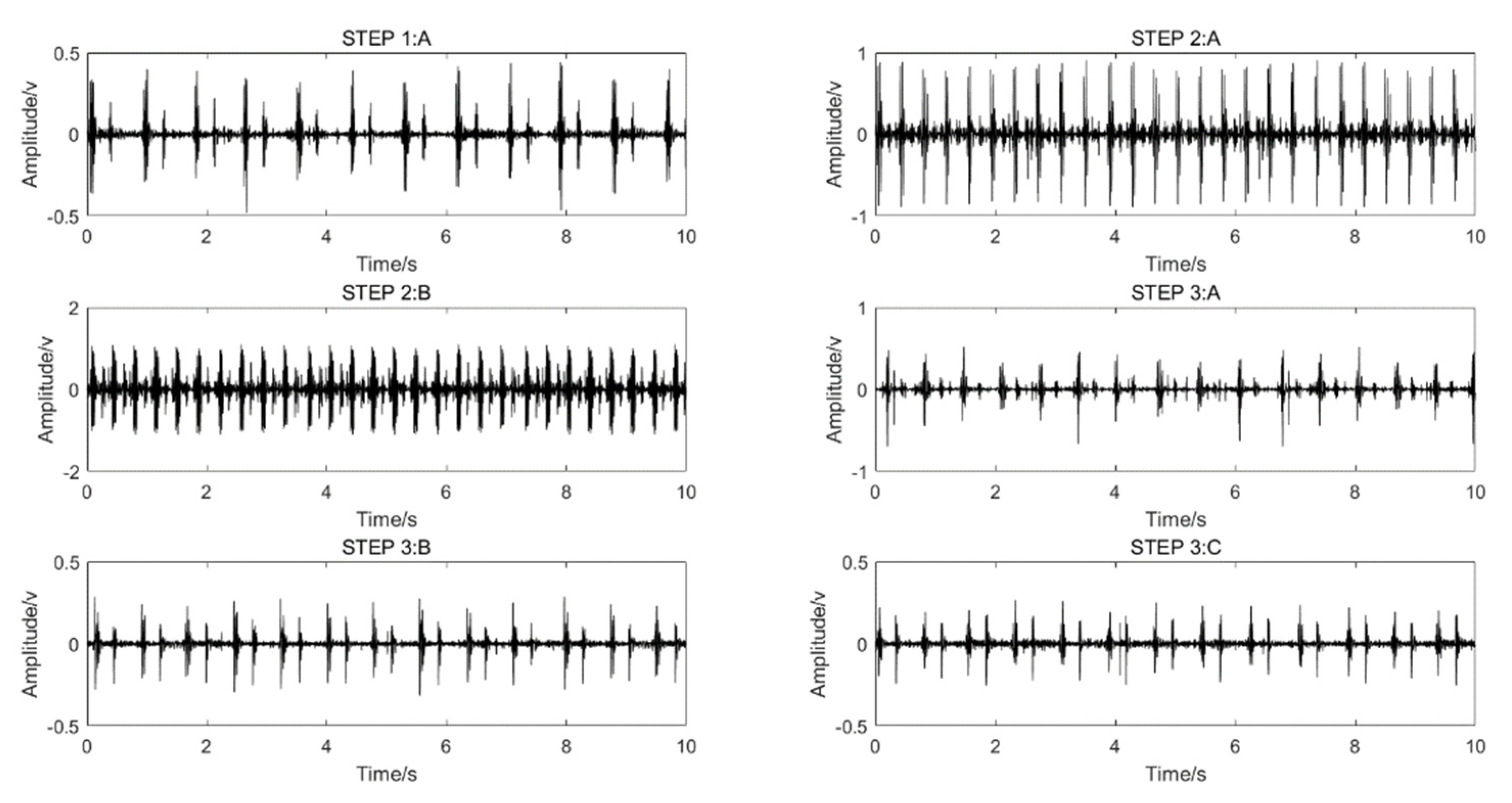
3. Analysis Results for the Characteristics of Heart Sounds in Motion
3.1. Basic Model and Characteristics of Heart-Sound Signals
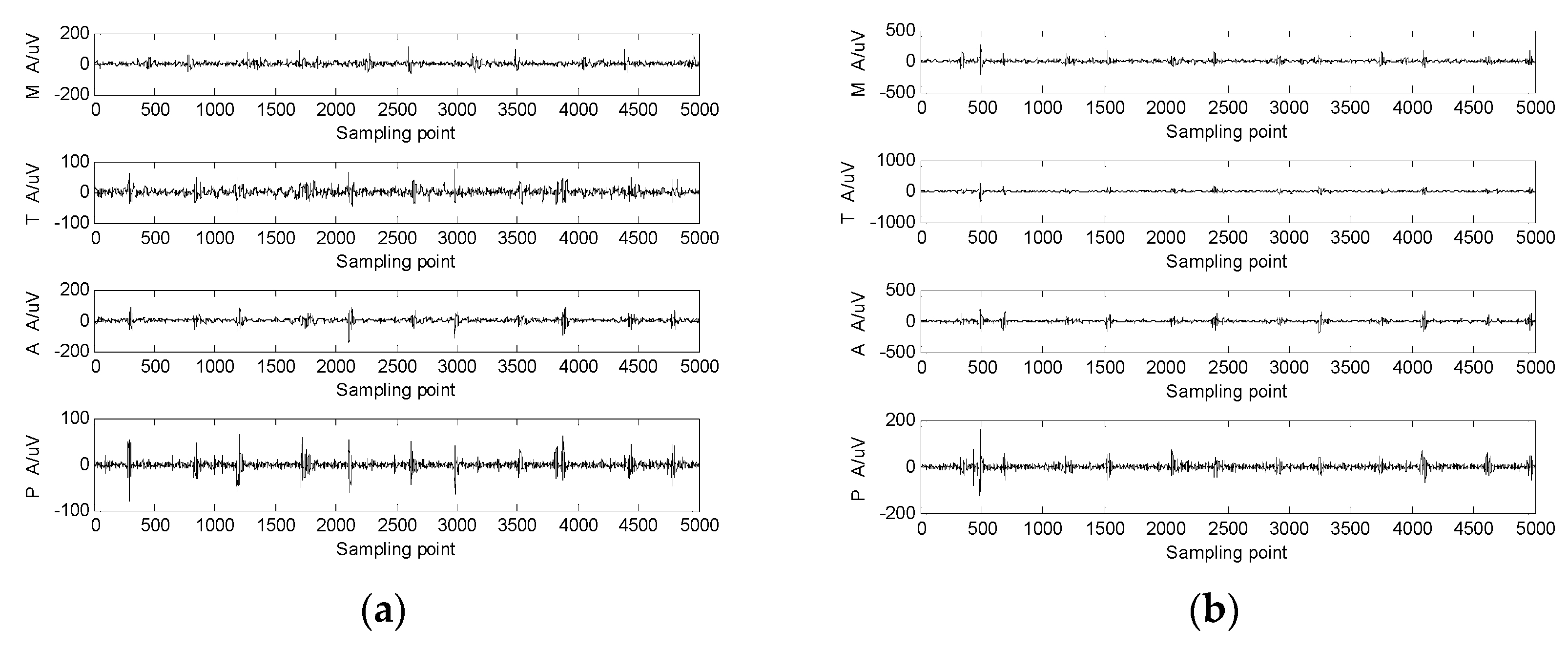
3.2. Influence of Motion on the Sound-Direction Vector of Heart Sounds
3.3. Influence of Motion on the Time-Domain Characteristics of Heart Sounds and Blood Pressure
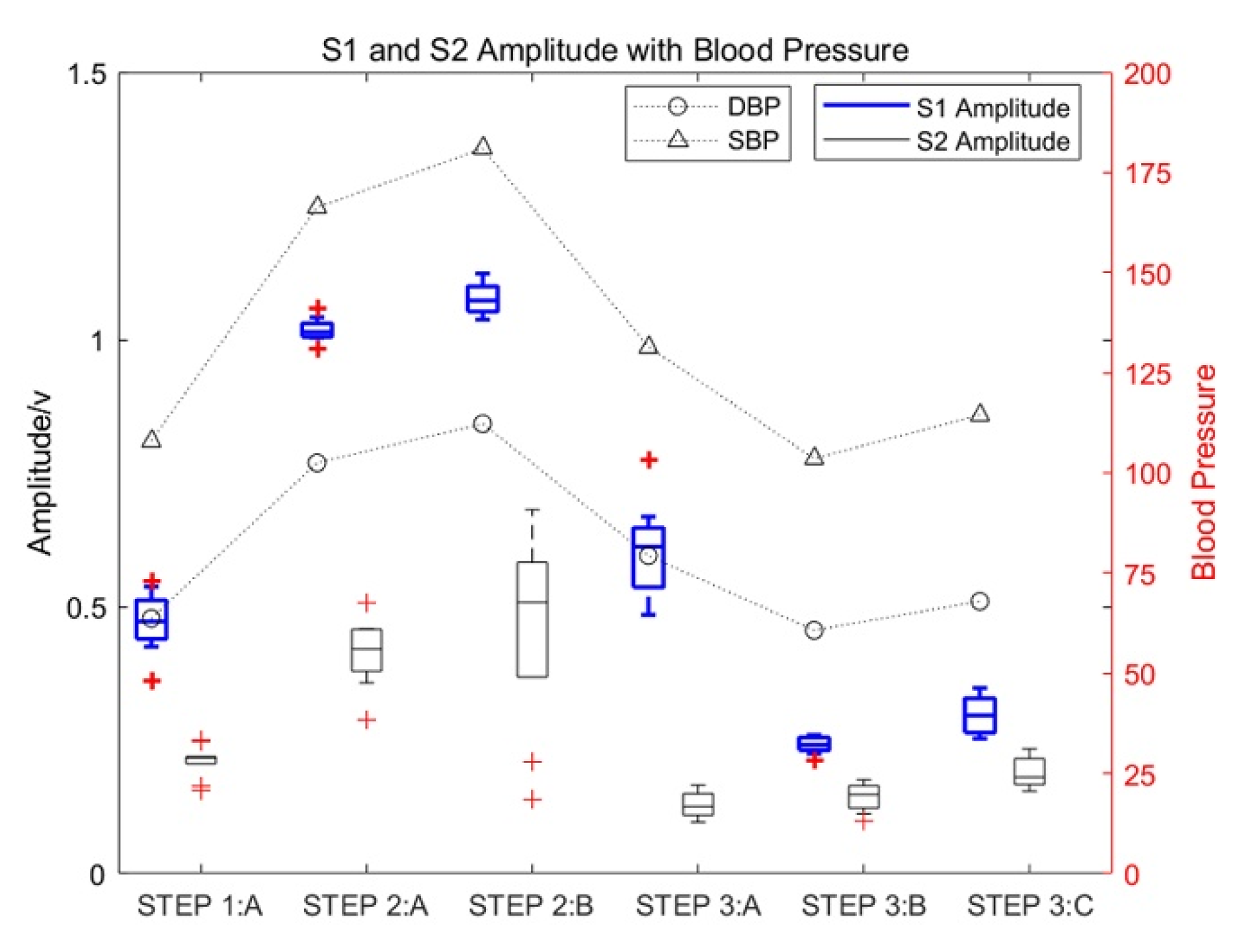
3.3.1. Influence of Motion on Heart-Sound Amplitude and the Corresponding Change Rule of Blood Pressure
3.3.2. Influence of Motion on the Diastolic and Systolic Duration of Heart Sounds and the Corresponding Change Rules of Blood Pressure
3.4. Influence of Motion on the Nonlinear Characteristics of Heart Sounds
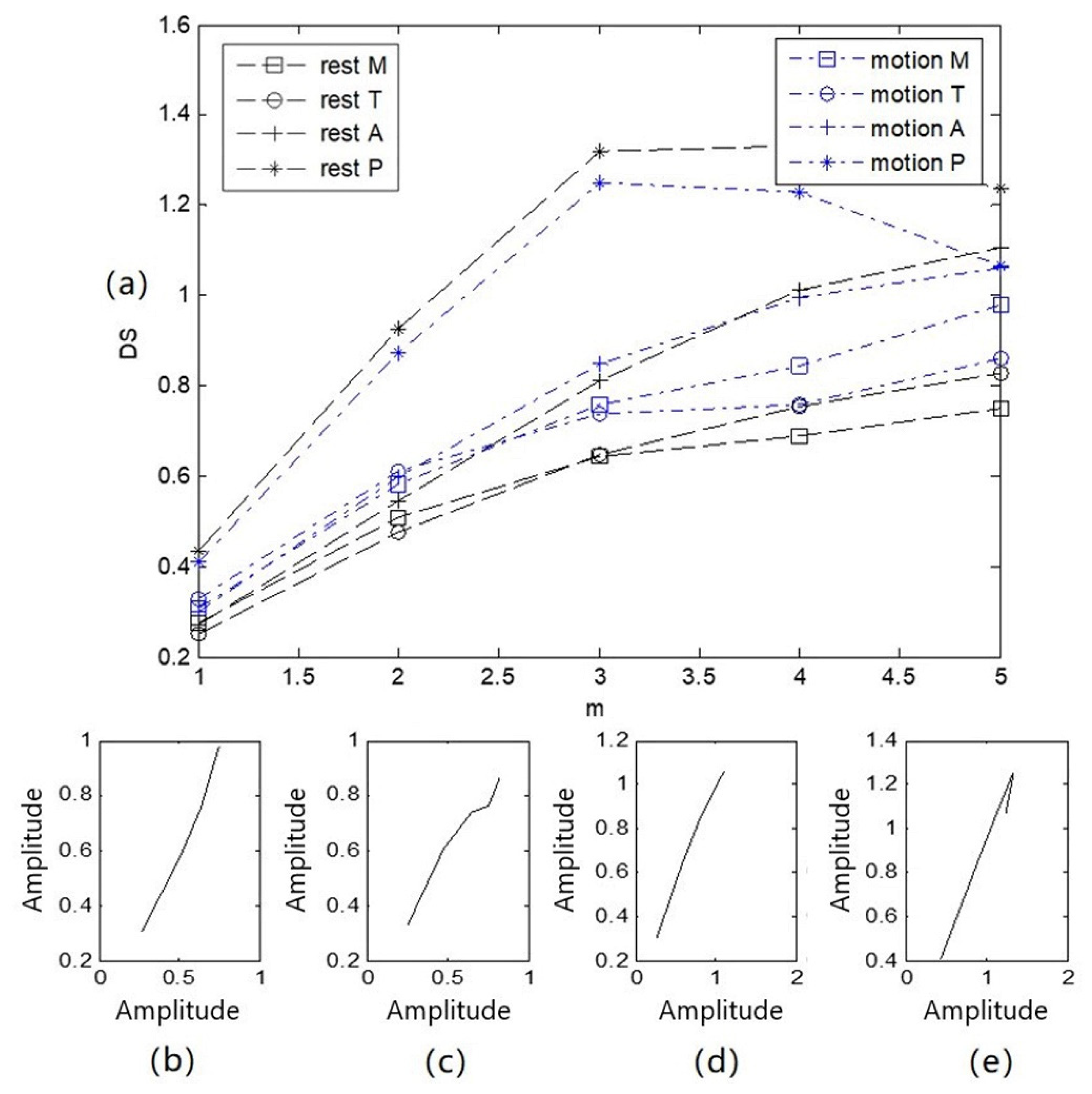
3.4.1. State-Change Trend Diagram of Heart-Sound Signals
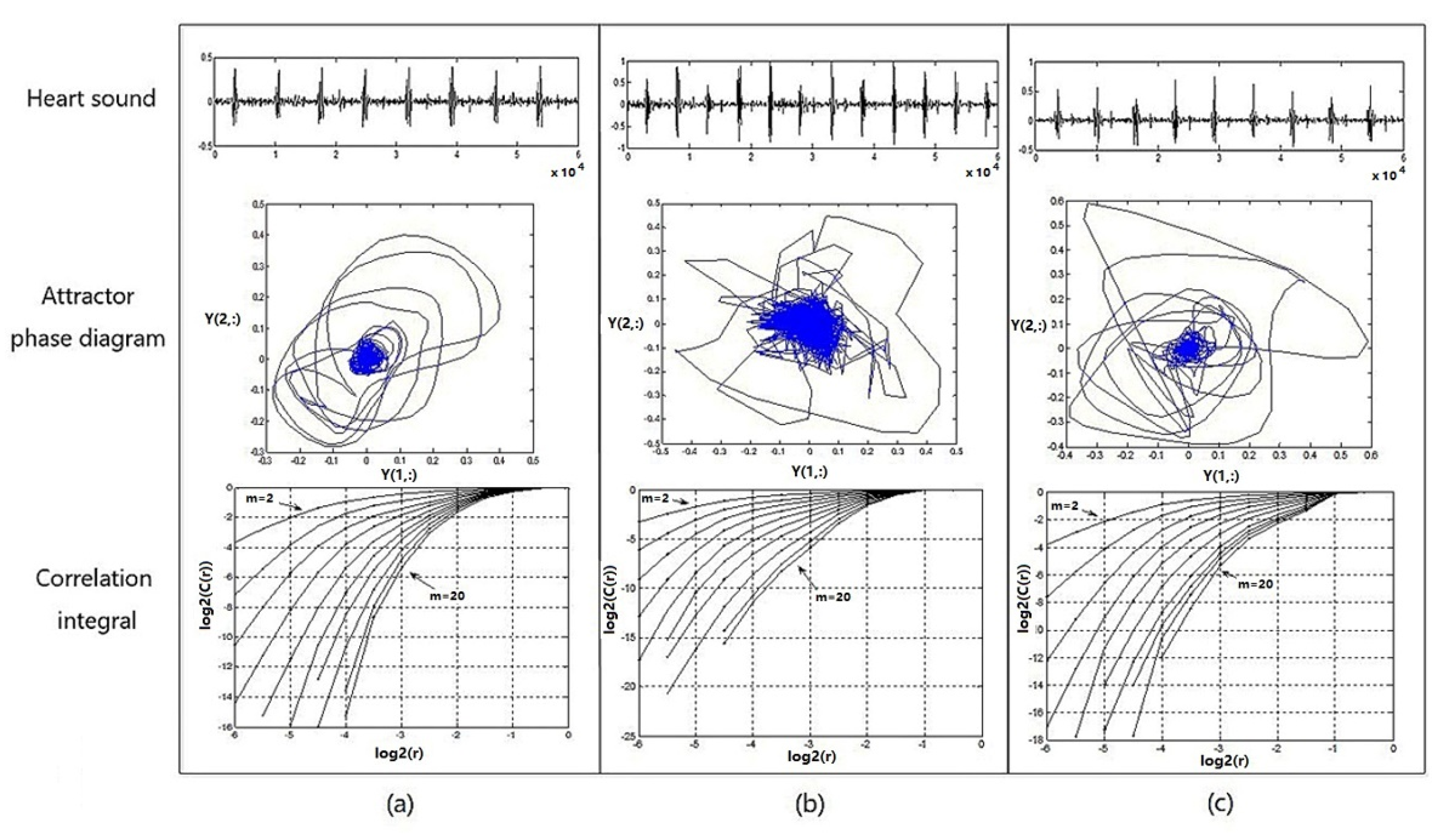
3.4.2. Attractor Phase Diagrams of Three States of Heart-Sound Signals
4. Conclusions
- (1)
- According to our experiment, when the heart-sound signal changed from a resting state to a state of motion, the sound-direction vector remained basically unchanged, and the similarity distance between the two was very small (=0.0038), which indicates that the heart, as a sound source, had no effect on the acoustic physical characteristics of the sound source itself;
- (2)
- The change of the heart-sound signal from a resting state to a state of motion had little effect on the state-change-trend chart and the difference value of the state change. In the signal of the P channel, the similarity distance between Rest P and Motion P was 0.0011; in the signal of the M channel, the similarity distance between Rest M and Motion M was 0.0006; in the signal of the T channel, the similarity distance between Rest T and Motion T was 0.0038; in the signal of the A channel, the similarity distance between Rest A and Motion A was 0.0013. This result indicates that the difference between similar distances was 0.0032;
- (3)
- The change from a rest to a state of motion can be observed through the amplitude of heart sound, the diastolic heart sound, the systolic period, the frequency characteristics, and the fluctuation of blood pressure. Heart sound amplitude and blood pressure are directly proportional to the heart load, while the diastolic/systolic period of heart sound decreased with an increase in exercise intensity;
- (4)
- Because the size of a heart is clearly greater than the distance from the auscultation point to the heart, the heart as a whole cannot be equivalent to the point source. Thus, only the corresponding local cardiac auscultation area is considered equivalent to the point source, making the four corresponding cardiac auscultation areas equivalent to four different point sources. Consequently, some of the characteristics of heart-sound signals present obvious differences. In the later stage, we will carry out relevant research on heart sound during motion from the perspective of physiology and clinical medicine.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, X.F.; Ma, Y.; Liu, C. Research on heart sound identification technology. Sci. China Inf. Sci. 2012, 55, 281–292. [Google Scholar] [CrossRef]
- Varghees, V.N.; Ramachandran, K. A novel heart sound activity detection framework for automated heart sound analysis. Biomed. Signal Process. Control 2014, 13, 174–188. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, P.; She, C. Biometric Identification Method for Heart Sound Based on Multimodal Multiscale Dispersion Entropy. Entropy 2020, 22, 238. [Google Scholar] [CrossRef]
- Liu, C.; Springer, D.; Clifford, G. Performance of an open-source heart sound segmentation algorithm on eight independent databases. Physiol. Meas. 2017, 38, 1730–1745. [Google Scholar] [CrossRef]
- Wang, J.-K.; Chang, Y.-F.; Tsai, K.-H.; Wang, W.-C.; Tsai, C.-Y.; Cheng, C.-H.; Tsao, Y. Automatic recognition of murmurs of ventricular septal defect using convolutional recurrent neural networks with temporal attentive pooling. Sci. Rep. 2020, 10, 21797. [Google Scholar] [CrossRef] [PubMed]
- Beritelli, F.; Spadaccini, A. Human identity verification based on Mel frequency analysis of digital heart sounds. In Proceedings of the Radar Conference, EuRAD 2009, Santorini, Greece, 5–7 July 2009. [Google Scholar]
- Abo-Zahhad, M.; Farrag, M.; Abbas, S.N.; Ahmed, S.M. A comparative approach between cepstral features for human authentication using heart sounds. Signal Image Video Process. 2016, 10, 843–851. [Google Scholar] [CrossRef]
- Chen, T.E.; Yang, S.I.; Ho, L.T.; Tsai, K.H.; Chen, Y.H.; Chang, Y.F.; Lai, Y.H.; Wang, S.S.; Tsao, Y.; Wu, C.C. S1 and S2 Heart Sound Recognition using Deep Neural Networks. IEEE Trans. Biomed. Eng. 2016, 64, 372–380. [Google Scholar]
- Abbas, S.N.; Abo–Zahhad, M.; Ahmed, S.M.; Farrag, M. Heart-ID: Human identity recognition using heart sounds based on modifying mel-frequency cepstral features. IET Biom. 2016, 5, 284–296. [Google Scholar] [CrossRef]
- Xiong, L.; Xiao, S.; Zhou, Q.; Wu, X.; Xiao, Z.; Guo, X.; Lu, D.; Zhao, W.; Wu, X.; Yan, X.; et al. Multi-center pragmatic studies evaluating the time indicator of cardiac perfusion reserve. J. Biomed. Sci. Eng. 2013, 6, 1–7. [Google Scholar] [CrossRef][Green Version]
- Wang, K.; Cheng, X.; Chen, Y.; She, C.; Sun, K.; Zhao, P. Heart Sound Model Based on Cascaded and Lossless Acoustic Tubes. J. Mech. Med. Biol. 2019, 19, 1950031. [Google Scholar] [CrossRef]
- Al-Shamma, S.D.; Al-Noaemi, M.C. Heart sound as a physiological biometric signature. In Proceedings of the 5th Cairo International Biomedical Engineering Conference, Cairo, Egypt, 16–18 December 2010. [Google Scholar]
- Zhong, M.; Yang, Y.; Zhou, Y.; Postolache, M.O.; Chandrasekar, M.; Babu, G.V.; Manikandan, C.; Balaji, V.S.; Saravanan, S.; Elamaran, V. Advanced Digital Signal Processing Techniques on the Classification of the Heart Sound Signals. J. Med. Imaging Health Inform. 2020, 10, 2010–2015. [Google Scholar] [CrossRef]
- Elamaran, V.; Arunkumar, N.; Hussein, A.F.; Solarte, M.; Ramirez-Gonzalez, G. Spectral Fault Recovery Analysis Revisited With Normal and Abnormal Heart Sound Signals. IEEE Access 2018, 6, 62874–62879. [Google Scholar] [CrossRef]
- Kamson, A.P.; Sharma, L.N.; Dandapat, S. Multi-centroid diastolic duration distribution based HSMM for heart sound segmentation. Biomed. Signal Process. Control 2019, 48, 265–272. [Google Scholar] [CrossRef]
- Zhao, Z.D.; Shen, Q.Q.; Ren, F.Q. Heart sound biometric system based on marginal spectrum analysis. J. Sens. 2013, 13, 2530–2551. [Google Scholar] [CrossRef] [PubMed]
- Phua, K.; Chen, J.; Dat, T.H.; Shue, L. Heart sound as a biometric. J. Pattern Recognit. 2008, 41, 906–919. [Google Scholar] [CrossRef]
- She, C.; Cheng, X.; Wang, J. Study on chaotic characteristics of heart sound based on correlation dimension and K entropy. AIP Adv. 2019, 9, 075021. [Google Scholar] [CrossRef]
- Castro, A.; Gomes, P.; Mattos, S.S.; Coimbra, M.T. Comparison between Users of a New Methodology for Heart Sound Auscultation. In Proceedings of the 38th Annual International Conference of the IEEE-Engineering-in-Medicine-and-Biology-Society, Orlando, FL, USA, 16–20 August 2016; pp. 5388–5391. [Google Scholar]
- Guo, X.; Xiao, S.; Jing, P.; Yan, Y.; Xin, T. Heart sound recognition algorithm based on Probabilistic neural network for evaluating cardiac contractility change trend. In Proceedings of the 2007 IEEE/ICME International Conference on Complex Medical Engineering, Beijing, China, 23–27 May 2007. [Google Scholar]
- Wu, W.Z.; Guo, X.M.; Xie, M.L.; Xiao, Z.F.; Yang, Y.; Xiao, S.Z. Research on First Heart Sound and Second Heart Sound Amplitude Variability and Reversal Phenomenon—A New Finding in Athletic Heart Study. J. Med. Biol. Eng. 2009, 29, 202–205. [Google Scholar]
- Li, S.-S. Effect of cardiopulmonary exercise test on cardiopulmonary reserve function and prognosis of patients with coronary heart disease. Chin. J. Med. Eng. 2020, 28, 94–96. [Google Scholar]
- Zeng, H. Study on Monitoring and Evaluation Method of Population Cardiac Reserve Based on Heart Sound; Chongqing University: Chongqing, China, 2017. [Google Scholar]
- Cheng, X.; Feng, S.; Li, Y.; Gui, G. Research on Parallel Compressive Sensing and Application of Multi-channel Synchronous Acquisition of Heart Sound Signals. IEEE Access 2019, 7, 30033–30041. [Google Scholar] [CrossRef]
- Cheng, X.-F.; Dai, S.-C.; Zhao, P.-J. Blood pressure estimation based on heart sound signals. Acta Phys. Sin. 2020, 69, 148701. [Google Scholar] [CrossRef]
- Glass, L. Introduction to controversial topics in nonlinear science: Is the normal heart rate chaotic? Chaos 2009, 19, 028501. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.-R.; Guo, X.-M.; Zhong, L.-S. Nonlinear dynamic analysis of heart sound signals based on chaos theory. J. Vib. Shock 2012, 31, 55–59. [Google Scholar]
- Cheng, X.; Chen, H.; Ji, H.; Guo, Y.; Zhang, S. A study of lumped-parameter cardiovascular simulation model and heart sound mechanism. Sci. China 2014, 44, 1121–1139. [Google Scholar]

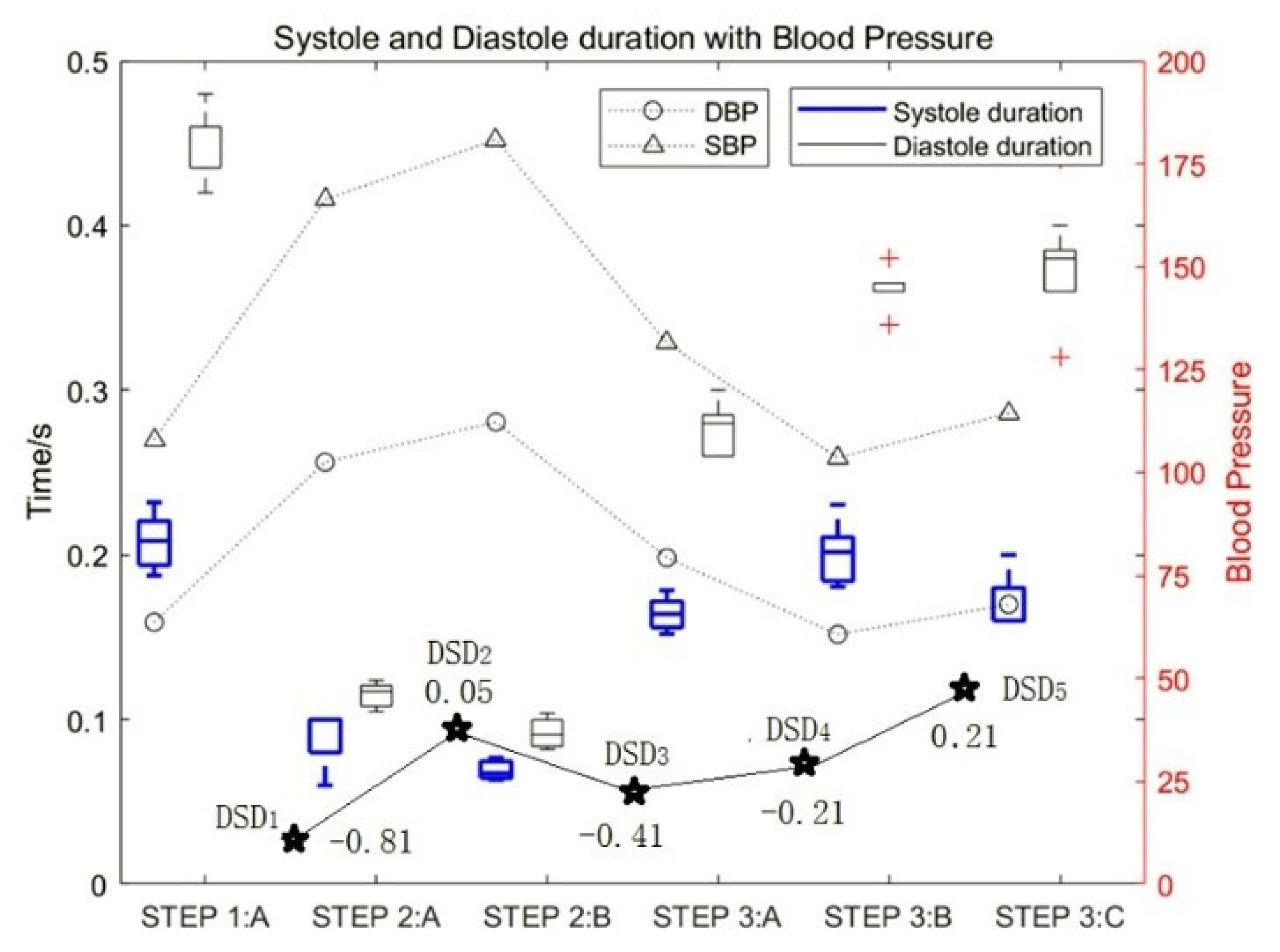
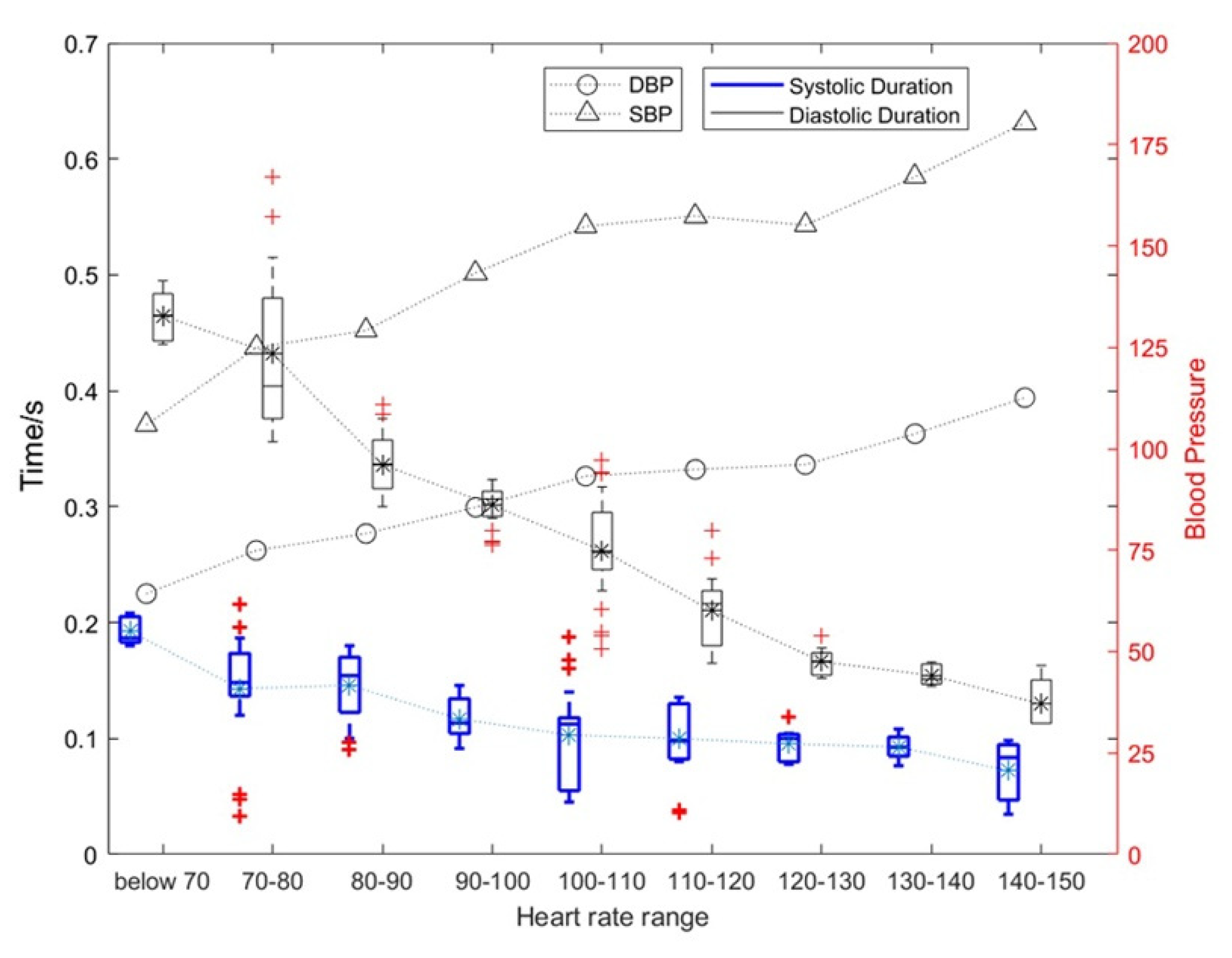
| Heart rate (beats/min) | 70–80 | 80–90 | 90–100 | 100–110 | 110–120 | 120+ |
| Mean systolic period (s) | 0.1421 | 0.1335 | 0.1171 | 0.1012 | 0.0838 | 0.0571 |
| relative rate of systole | - | 6.03% | 12.27% | 13.58% | 17.16% | 31.89% |
| Mean diastolic period (s) | 0.3909 | 0.3502 | 0.2991 | 0.2544 | 0.2371 | 0.2008 |
| Relative rate of diastole | - | 10.41% | 14.60% | 14.93% | 6.79% | 15.34% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
She, C.-J.; Cheng, X.-F.; Wang, K. Analysis of Heart-Sound Characteristics during Motion Based on a Graphic Representation. Sensors 2022, 22, 181. https://doi.org/10.3390/s22010181
She C-J, Cheng X-F, Wang K. Analysis of Heart-Sound Characteristics during Motion Based on a Graphic Representation. Sensors. 2022; 22(1):181. https://doi.org/10.3390/s22010181
Chicago/Turabian StyleShe, Chen-Jun, Xie-Feng Cheng, and Kai Wang. 2022. "Analysis of Heart-Sound Characteristics during Motion Based on a Graphic Representation" Sensors 22, no. 1: 181. https://doi.org/10.3390/s22010181
APA StyleShe, C.-J., Cheng, X.-F., & Wang, K. (2022). Analysis of Heart-Sound Characteristics during Motion Based on a Graphic Representation. Sensors, 22(1), 181. https://doi.org/10.3390/s22010181





