Wind Tunnel Performance Tests of the Propellers with Different Pitch for the Electric Propulsion System †
Abstract
:1. Introduction
- —air density [kg/m3],
- —drag force coefficient [-],
- —lift force coefficient [-],
- —resultant air velocity [m/s],
- —blade width [m],
- c—blade chord [m].
2. Methodology
3. Research Object
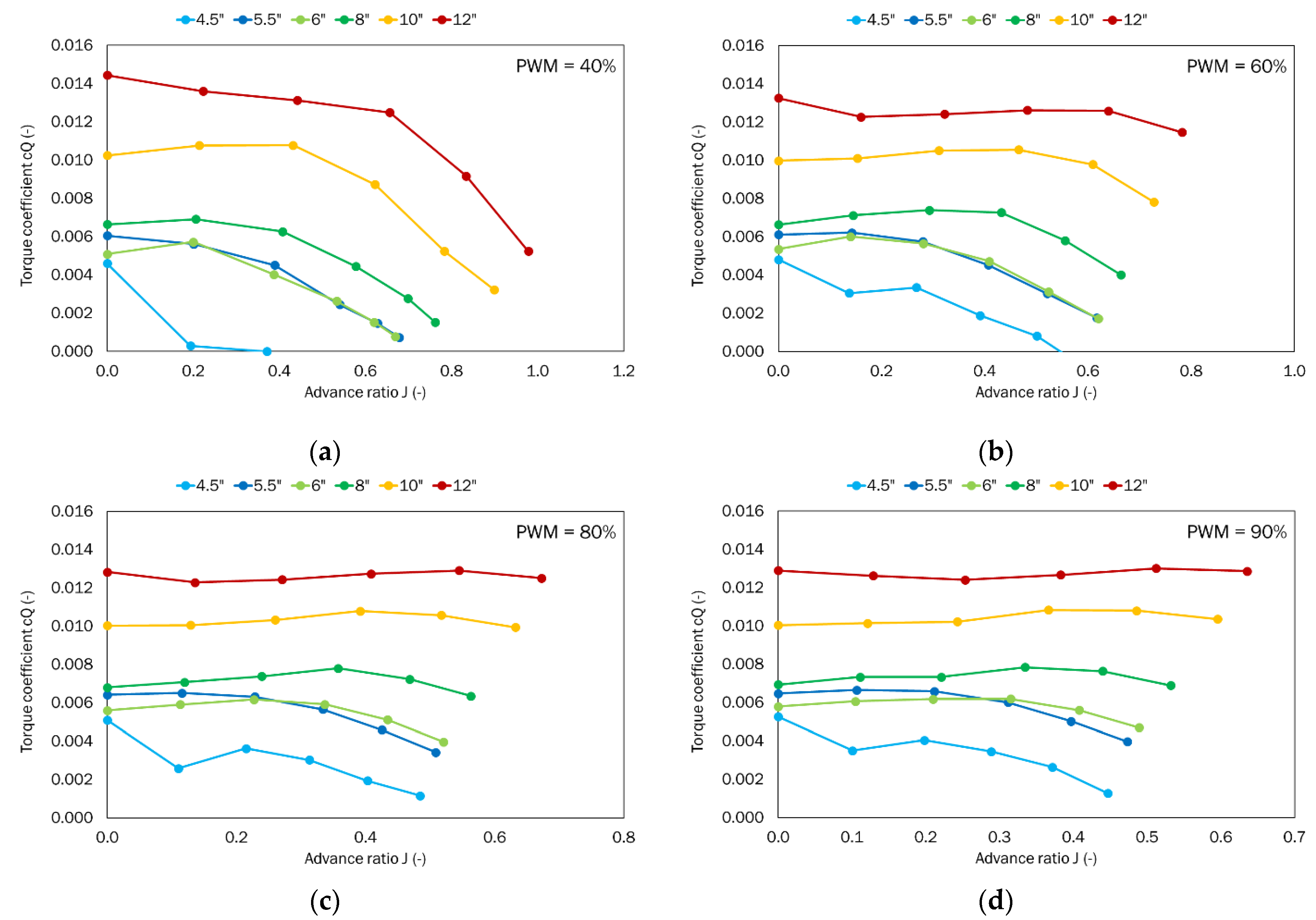
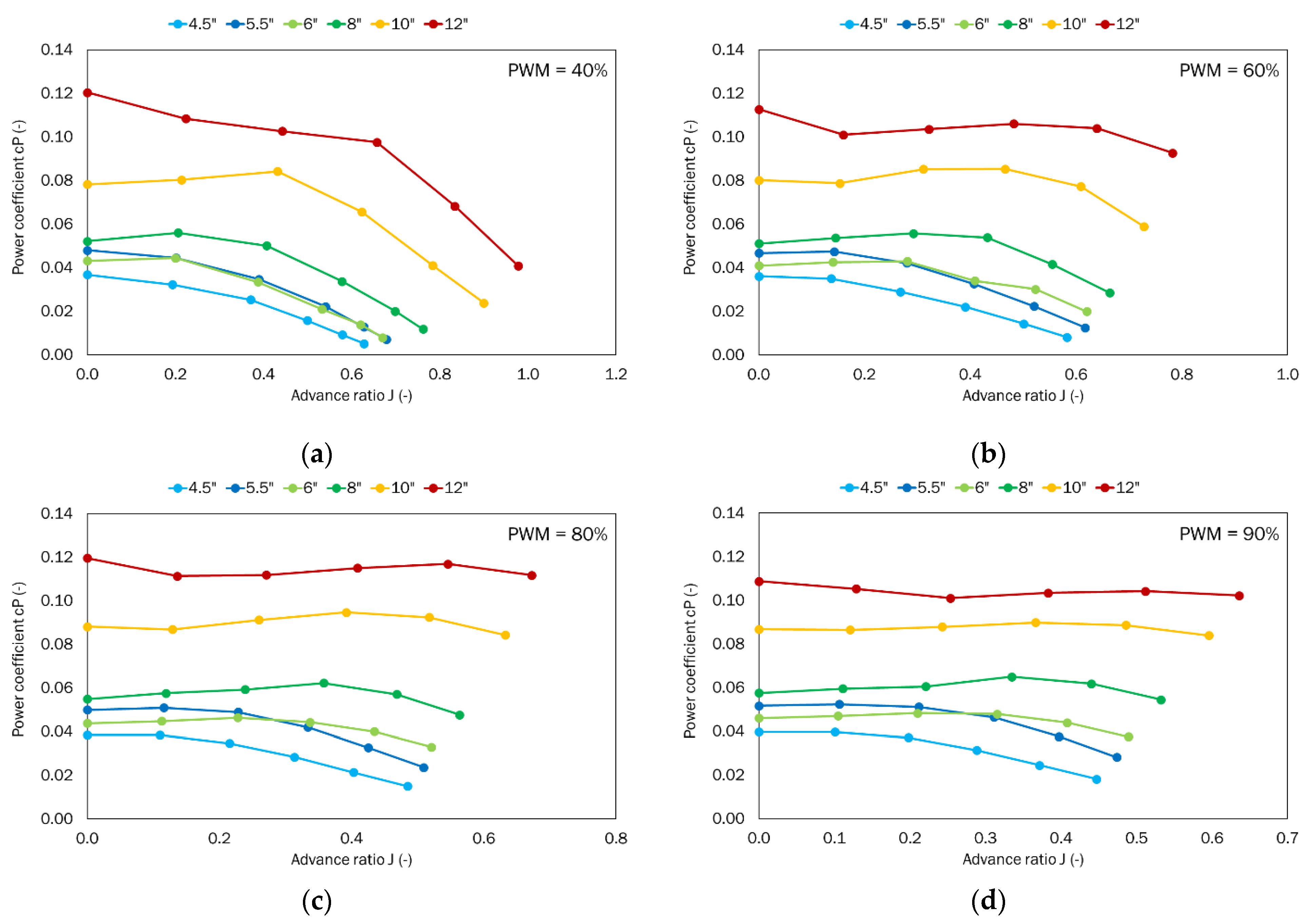
4. Results and Analysis
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Podsędkowski, M.; Konopiński, R.; Obidowski, D.; Koter, K. Variable pitch propeller for UAV-experimental tests. Energies 2020, 13, 5264. [Google Scholar] [CrossRef]
- Avanzini, G.; Di Nisio, A.; Lanzolla, A.; Stigliano, D. A testbench for battery-motor-propeller assemblies designed for multirotor vehicles. In Proceedings of the 2020 IEEE International Workshop on Metrology for AeroSpace, Pisa, Italy, 22–24 June 2020; pp. 600–605. [Google Scholar] [CrossRef]
- Islami, Z.S.; Hartono, F. Development of small propeller test bench system. IOP Conf. Ser. Mater. Sci. Eng. 2019, 645, 012017. [Google Scholar] [CrossRef]
- Scanavino, M.; Vilardi, A.; Guglieri, G. An experimental analysis on propeller performance in a climate-controlled facility. J. Intell. Robot. Syst. 2020, 100, 505–517. [Google Scholar] [CrossRef]
- Pieniazek, J.; Ciecinski, P. Measurement system for small propeller propulsion. In Proceedings of the 2021 IEEE International Workshop on Metrology for AeroSpace, Naples, Italy, 23–25 June 2021; pp. 687–691. [Google Scholar] [CrossRef]
- Hossain, M.R.; Krouglicof, N. Propeller dynamometer for small unmanned aerial vehicle. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Calgary, AB, Canada, 2–5 May 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Speck, S.; Herbst, S.; Kim, H.; Stein, F.-G.; Hornung, M. Development, startup operations and tests of a propeller wind tunnel test rig. In Proceedings of the 33rd AIAA Applied Aerodynamics Conference, Dallas, TX, USA, 22–26 June 2015. AIAA 2015-2578. [Google Scholar] [CrossRef]
- McCormick, B.W. The production of trust. In Aerodynamics, Aeronautics, and Flight Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1979. [Google Scholar]
- Kutty, H.A.; Rajendran, P. Review on Numerical and Experimental Research on Conventional and Unconventional Propeller Blade Design. Int. Rev. Aerosp. Eng. 2017, 10, 61. [Google Scholar] [CrossRef]
- Uhlig, D.; Selig, M. Post Stall Propeller Behavior at Low Reynolds Numbers. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008. AIAA-2008-407. [Google Scholar] [CrossRef] [Green Version]
- Xiang, S.; Liu, Y.-Q.; Tong, G.; Zhao, W.-P.; Tong, S.-X.; Li, Y.-D. An improved propeller design method for the electric aircraft. Aerosp. Sci. Technol. 2018, 78, 488–493. [Google Scholar] [CrossRef]
- Jakubowski, A.; Kubacki, A.; Minorowicz, B.; Nowak, A. Analysis thrust for different kind of propellers. In Progress in Automation, Robotics and Measuring Techniques, Control and Automation, Advances in Intelligent Systems and Computing, Proceedings of the International Conference on Automation, Warsaw, Poland, 18–20 March 2015; Szewczyk, R., Zieliński, C., Kaliczyńska, M., Eds.; Springer: Cham, Switzerland, 2015; pp. 85–90. [Google Scholar] [CrossRef]
- Aminaei, H.; Manshadi, M.D.; Mostofizadeh, A.R. Experimental investigation of propeller slipstream effects on the wing aerodynamics and boundary layer treatment at low Reynolds number. Proc. Inst. Mech. Eng. G J. Aerosp. Eng. 2019, 233, 3033–3041. [Google Scholar] [CrossRef]
- Ning, Z.; Hu, H. An Experimental Study on the Aerodynamics and Aeroacoustic Characteristics of Small Propellers. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef] [Green Version]
- Roosenboom, E.W.M.; Heider, A.; Schröder, A. Investigation of the Propeller Slipstream with Particle Image Velocimetry. J. Aircr. 2009, 46, 442–449. [Google Scholar] [CrossRef]
- Zawodny, N.S.; Haskin, H. Small Propeller and Rotor Testing Capabilities of the NASA Langley Low Speed Aeroacoustic Wind Tunnel. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–9 June 2017. AIAA 2017-3709. [Google Scholar] [CrossRef] [Green Version]
- Merchant, M.; Miller, L.S. Propeller Performance Measurement for Low Reynolds Number UAV Applications. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. AIAA 2006-1127. [Google Scholar] [CrossRef]
- Brandt, J.; Selig, M. Propeller Performance Data at Low Reynolds Numbers. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. AIAA 2011-1255. [Google Scholar] [CrossRef] [Green Version]
- Theys, B.; Dimitriadis, G.; Andrianne, T.; Hendrick, P.; De Schutter, J. Wind tunnel testing of a VTOL MAV propeller in tilted operating mode. In Proceedings of the IEEE International Conference on Unmanned Aircraft Systems ICUAS, Orlando, FL, USA, 27–30 May 2014; pp. 1064–1072. [Google Scholar] [CrossRef]
- Yilmaz, S.; Erdem, D.; Kavsaoglu, M. Performance of a ducted propeller designed for UAV applications at zero angle of attack flight: An experimental study. Aerosp. Sci. Technol. 2015, 45, 376–386. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, P.; Tang, Z.; Guo, H. Wind tunnel tests of stratospheric airship counter rotating propellers. Theor. Appl. Mech. Lett. 2015, 5, 58–61. [Google Scholar] [CrossRef] [Green Version]
- Molter, C.; Cheng, P. Propeller performance calculation for multicopter aircraft at forward flight conditions and validation with wind tunnel measurements. In Proceedings of the International Micro Air Vehicle Conference and Flight Competition IMAV, Toulouse, France, 18–21 September 2017; pp. 307–315. [Google Scholar]
- Tan, C.H.; Voo, K.S.; Siauw, W.L.; Alderton, J.; Boudjir, A.; Mendonça, F. CFD Analysis of the Aerodynamics and Aeroacoustics of the NASA SR2 Propeller. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. GT2014-26779. [Google Scholar] [CrossRef]
- Yomchinda, T. Simplified Propeller Model for the Study of UAV Aerodynamics using CFD method. In Proceedings of the 2018 IEEE 5th Asian Conference on Defense Technology ACDT, Hanoi, Vietnam, 25–26 October 2018; pp. 69–74. [Google Scholar] [CrossRef]
- Kuantama, E.; Craciun, D.; Tarca, I.; Tarca, R. Quadcopter Propeller Design and Performance Analysis. In New Advances in Mechanisms, Mechanical Transmissions and Robotics, Proceedings of the Joint International Conference of the XII International Conference on Mechanisms and Mechanical Transmissions (MTM) and the XXIII International Conference on Robotics (Robotics’16); Corves, B., Lovasz, E.C., Hüsing, M., Maniu, I., Gruescu, C., Eds.; Springer: Cham, Switzerland, 2017; pp. 269–277. [Google Scholar] [CrossRef]
- Seeni, A.; Rajendran, P. Numerical Validation of NACA 0009 Airfoil in Ultra-Low Reynolds Number Flows. Int. Rev. Aerosp. Eng. 2019, 12, 83–92. [Google Scholar] [CrossRef]
- Bousquet, J.-M.; Gardarein, P. Improvements on computations of high speed propeller unsteady aerodynamics. Aerosp. Sci. Technol. 2003, 7, 465–472. [Google Scholar] [CrossRef]
- Aziz, M.A.; Elsayed, A.M. CFD Investigations for UAV and MAV Low Speed Airfoils Characteristics. Int. Rev. Aerosp. Eng. 2015, 8, 95–100. [Google Scholar] [CrossRef]
- Czyż, Z.; Karpiński, P.; Stryczniewicz, W. Measurement of the Flow Field Generated by Multicopter Propellers. Sensors 2020, 20, 5537. [Google Scholar] [CrossRef] [PubMed]
- Khan, W.; Nahon, M. A propeller model for general forward flight conditions. Int. J. Intell. Unmanned Syst. 2015, 3, 72–92. [Google Scholar] [CrossRef]
- Theys, B.B.; Dimitriadis, G.G.; Hendrick, P.; De Schutter, J.J. Experimental and Numerical Study of Micro-Aerial-Vehicle Propeller Performance in Oblique Flow. J. Aircr. 2017, 54, 1076–1084. [Google Scholar] [CrossRef]
- Khan, A.M.; Adams, D.O.; Dayal, V.; Vogel, J.M. Effects of bend–twist coupling on composite propeller performance. Mech. Compos. Mater. Struct. 2000, 7, 383–401. [Google Scholar] [CrossRef]
- Gill, R.; D’Andrea, R. Propeller thrust and drag in forward flight. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications CCTA, Kohala Coast, HI, USA, 27–30 August 2017; pp. 73–79. [Google Scholar] [CrossRef]
- MacNeill, R.; Verstraete, D. Blade element momentum theory extended to model low Reynolds number propeller performance. Aeronaut. J. 2017, 121, 835–857. [Google Scholar] [CrossRef] [Green Version]
- Carroll, J.; Marcum, D. Comparison of a Blade Element Momentum Model to 3D CFD Simulations for Small Scale Propellers. SAE Int. J. Aerosp. 2013, 6, 721–726. [Google Scholar] [CrossRef]
- Bristeau, P.-J.; Martin, P.; Salaun, E.; Petit, N. The role of propeller aerodynamics in the model of a quadrotor UAV. In Proceedings of the 2009 IEEE European Control Conference ECC, Budapest, Hungary, 23–26 August 2009; pp. 683–688. [Google Scholar]
- Ol, M.; Zeune, C.; Logan, M. Analytical/experimental comparison for small electric unmanned air vehicle propellers. In Proceedings of the 26th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 18–21 August 2008. AIAA 2008-7345. [Google Scholar] [CrossRef]
- Gur, O.; Rosen, A. Propeller Performance at Low Advance Ratio. J. Aircr. 2005, 42, 435–441. [Google Scholar] [CrossRef]
- Silvestre, M.A.R.; Morgado, J.; Alves, P.; Santos, P.; Gamboa, P.; Páscoa, J.C. Propeller Performance Measurements at Low Reynolds Numbers. Int. J. Mech. 2015, 9, 154–166. [Google Scholar]
- Czyz, Z.; Karpinski, P.; Skiba, K. Wind tunnel investigation of the propellers for unmanned aerial vehicle. In Proceedings of the 2021 IEEE 8th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Naples, Italy, 23–25 June 2021; pp. 672–676. [Google Scholar] [CrossRef]
- Czyz, Z.; Karpinski, P.; Skiba, K. Experimental study of propellers for the electric propulsion system. In Proceedings of the 2021 IEEE 8th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Naples, Italy, 23–25 June 2021; pp. 682–686. [Google Scholar] [CrossRef]
- BrotherHobby Motors Manufacturer Website. Available online: www.brotherhobbystore.com/tornado-t5-3115-pro-motor-p0088-p0088.html (accessed on 31 January 2021).
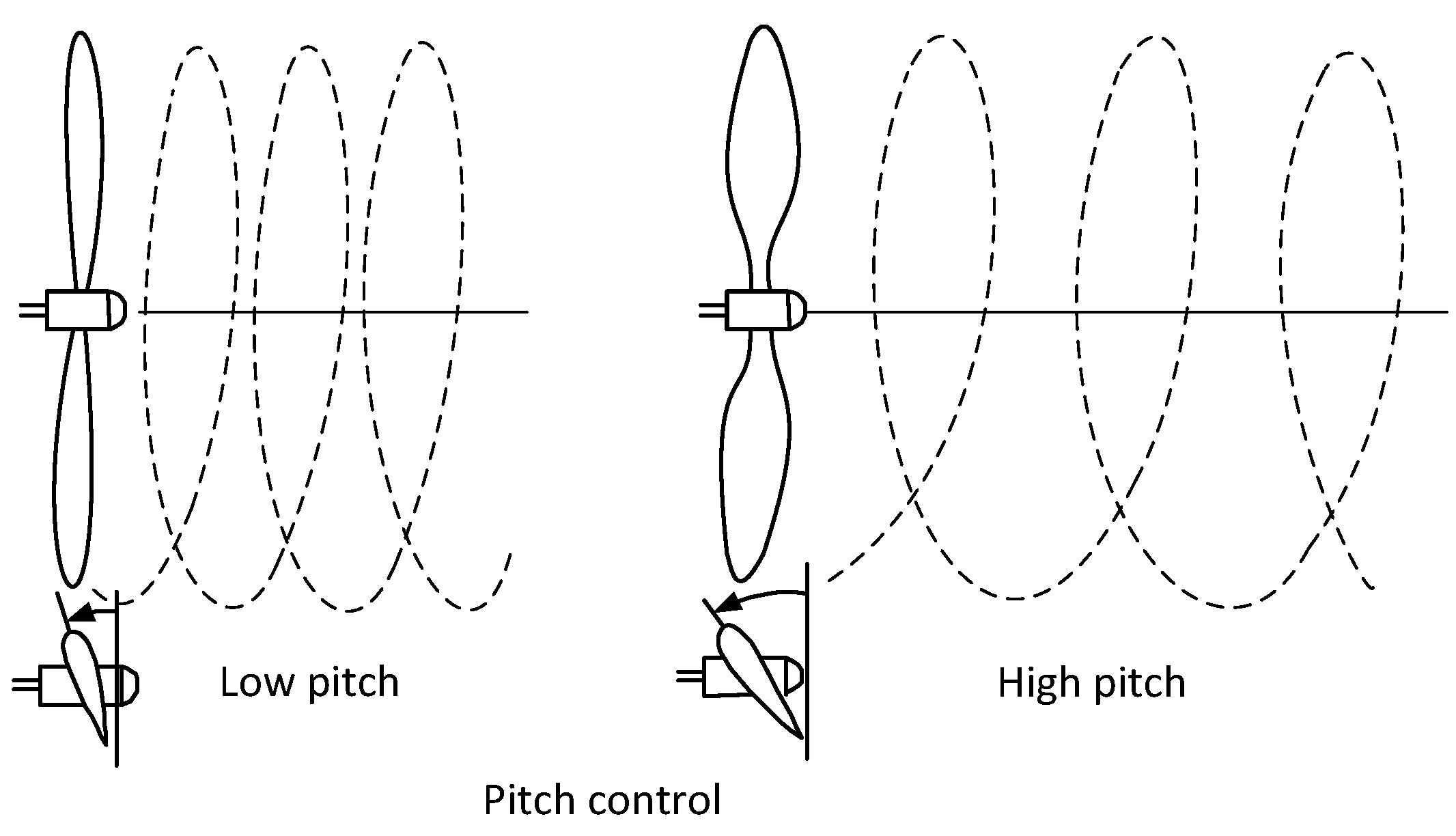


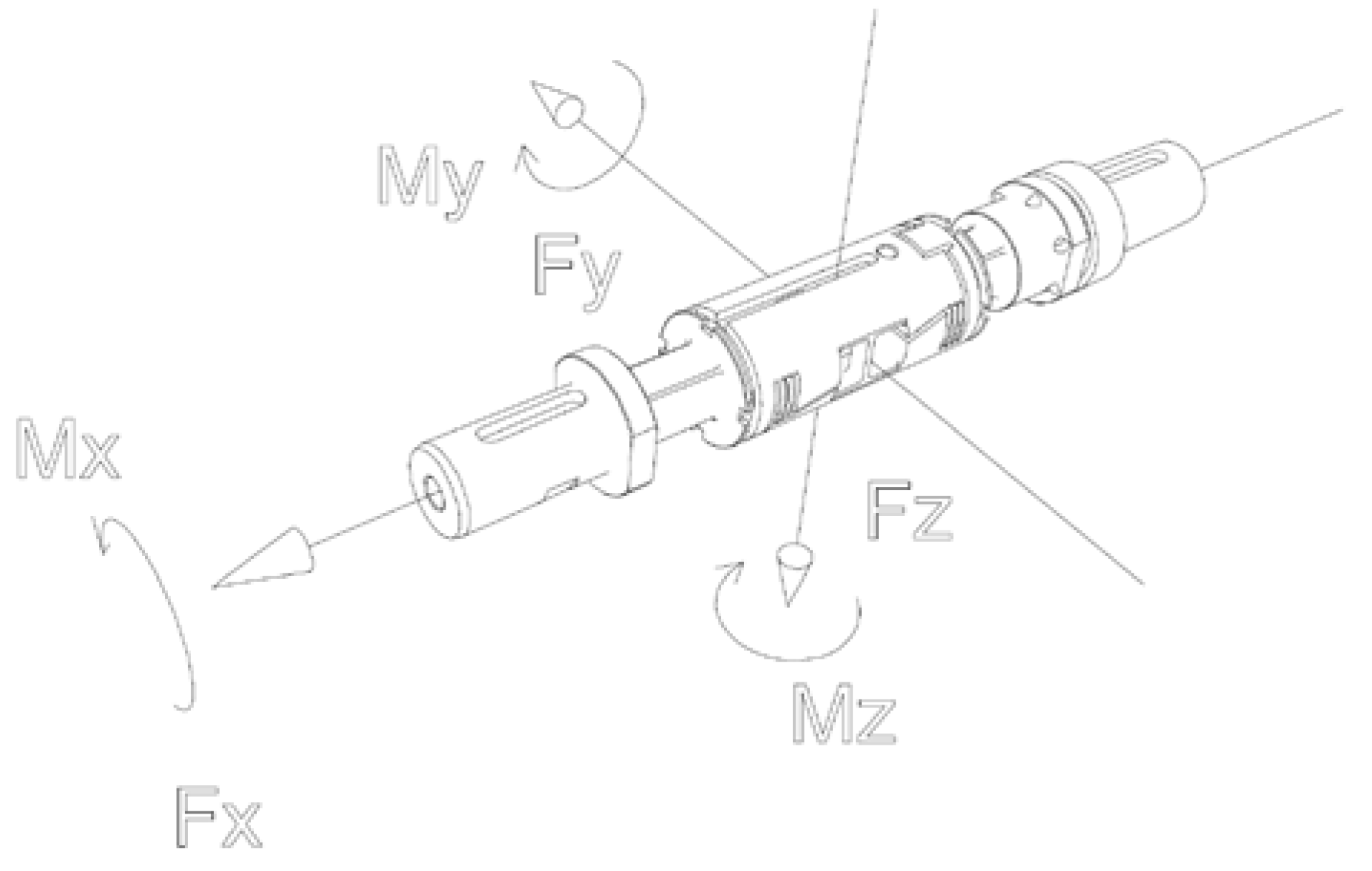
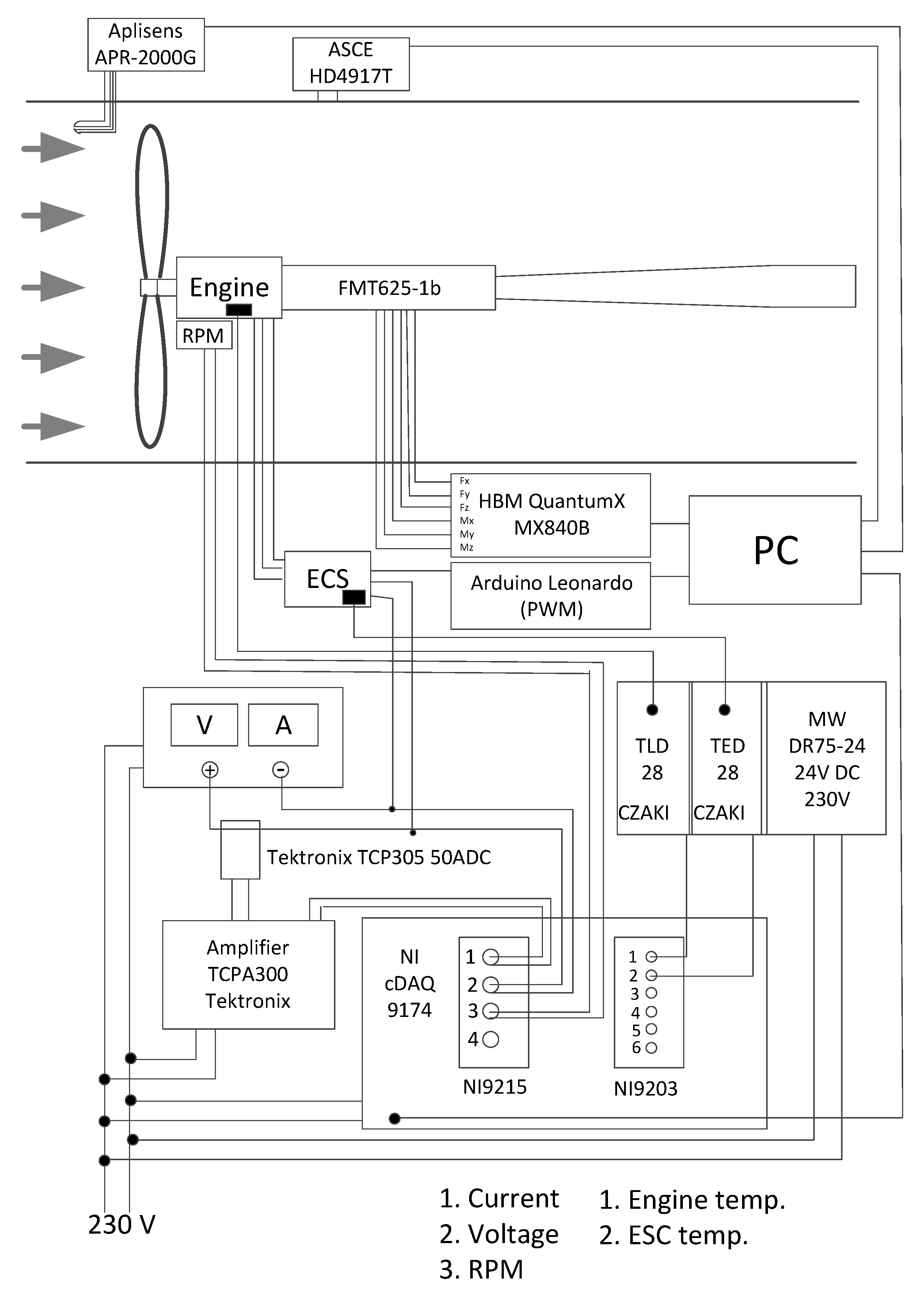



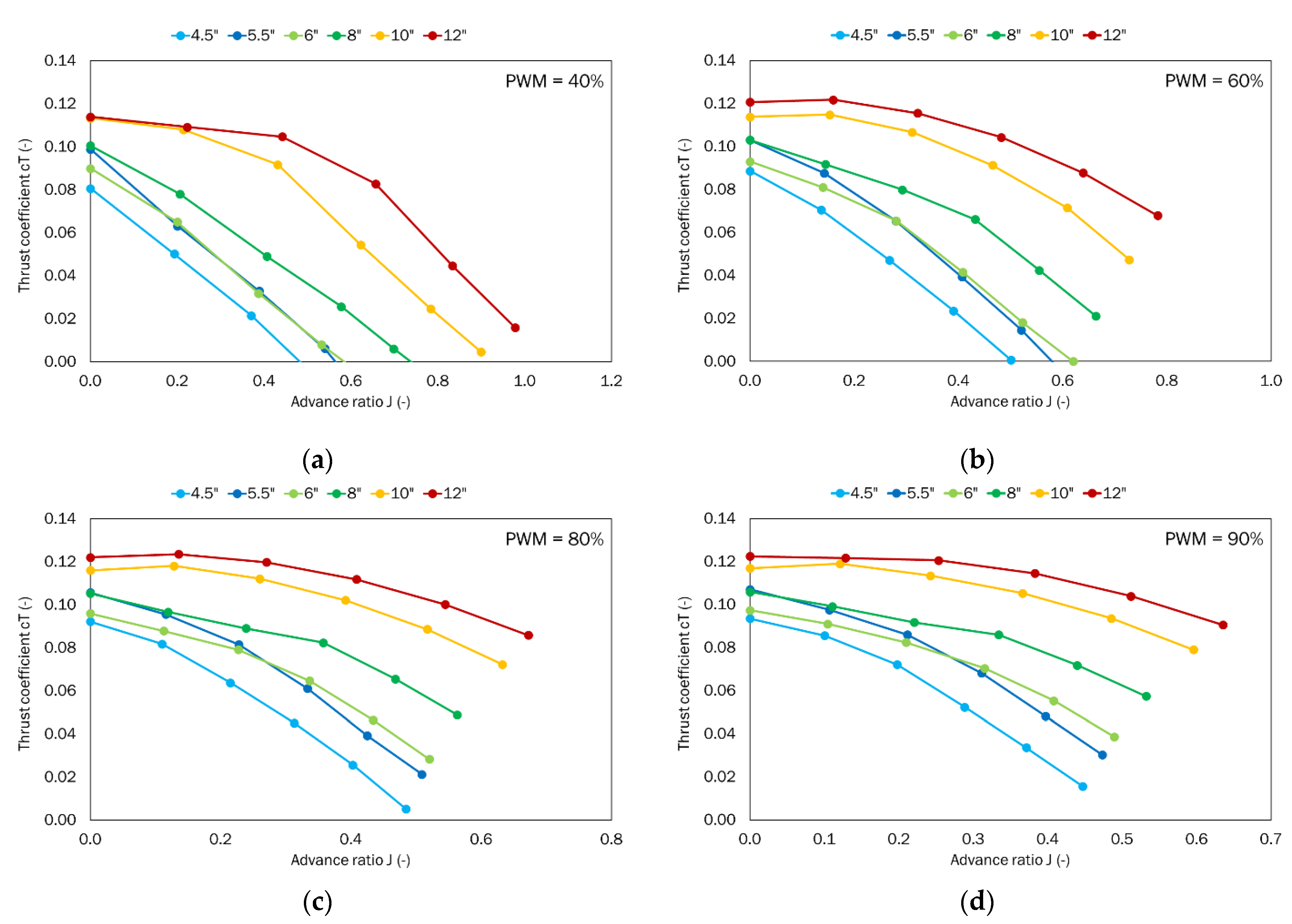


| Parameter | Sensor | Sensor Parameters |
|---|---|---|
| Engine speed | Honeywell SS411P bipolar Hall sensor | Sensor type: bipolar Case: TO92 Operate flux: −30…140 Gs Supply voltage: 2.7…7 V DC Temperature range: 40…150 °C |
| Supply voltage | NI-9215 analog input module with a voltage divider 1:3 | Signal levels: ± 10 V, Channels: 4 (differential), Sample rate: 100 kS/s/ch, Simultaneous: Yes, Resolution: 16-bit, Connectivity: Screw-Terminal, Spring-Terminal, BNC |
| Supply current | Tektronix TCP305 current measurement system with a current probe | AC/DC measurement capabilities, Bandwidth (−3 dB): DC—50 MHz, Risetime: ≤ 7 ns, High-current sensitivity range: 10 A/V, DC (continuous): 50 A, DC Accuracy, Typical (Operating temp. 23 °C ± 5 °C): ±1% of reading |
| ESC and engine temperature | PT 100 RS PRO SONDE PLATE thermocouple with the programmable measuring Czaki TED 28 transducer | RS PRO PT 100: Type: PT 100—A Class, Probe diameter: 2 mm, Probe length: 10 mm, Maximum temperature: 600°C, Reaction time: 1 m/s Czaki TED 28: Measuring range: 100…800 °C, Processing error: 0.15% or ±0.2 °C, Temperature error/10 °C: 0.05% or ±0.1 °C, Current output signal: 4…20 mA, two-wire, Input-output galvanic isolation, Programmable input signal range, Compensation of the cold ends of the thermocouple |
| Air temperature, pressure and humidity | Bosch BME280 sensor | Supply voltage: 3.3 V, Interface: I2C and SPI, Temperature range: 40 °C…85 °C, Temperature accuracy: ±1 °C Humidity range: 10% RH to 100% RH, Humidity accuracy: ± 3% relative humidity Pressure range: 300…1100 hPa Pressure measurement error: ±0.25% |
| Propeller Pitch (Inches) | PWM (%) | Airflow Velocity (m/s) |
|---|---|---|
| 4.5 | 40 | 0 |
| 5.5 | 60 | 5 |
| 6 | 80 | 10 |
| 8 | 90 | 15 |
| 10 | 20 | |
| 12 | 25 |
| Parameter | Sensor Parameters |
|---|---|
| Weight | 110 g with 25 cm SR wires |
| Motor dimensions (length × diameter) | 49.5 mm × 37.5 mm |
| Rotor | N52H arc magnets |
| Stator | 0.2 mm Kawasaki silicon steel |
| Shaft dimensions (length × diameter) | 16 mm × M5 |
| Maximum power | 1150 W |
| KV factor | 640 rpm/V |
| Maximum voltage | 22.2 V |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czyż, Z.; Karpiński, P.; Skiba, K.; Wendeker, M. Wind Tunnel Performance Tests of the Propellers with Different Pitch for the Electric Propulsion System. Sensors 2022, 22, 2. https://doi.org/10.3390/s22010002
Czyż Z, Karpiński P, Skiba K, Wendeker M. Wind Tunnel Performance Tests of the Propellers with Different Pitch for the Electric Propulsion System. Sensors. 2022; 22(1):2. https://doi.org/10.3390/s22010002
Chicago/Turabian StyleCzyż, Zbigniew, Paweł Karpiński, Krzysztof Skiba, and Mirosław Wendeker. 2022. "Wind Tunnel Performance Tests of the Propellers with Different Pitch for the Electric Propulsion System" Sensors 22, no. 1: 2. https://doi.org/10.3390/s22010002
APA StyleCzyż, Z., Karpiński, P., Skiba, K., & Wendeker, M. (2022). Wind Tunnel Performance Tests of the Propellers with Different Pitch for the Electric Propulsion System. Sensors, 22(1), 2. https://doi.org/10.3390/s22010002





