A Hybrid Visual-Based SLAM Architecture: Local Filter-Based SLAM with KeyFrame-Based Global Mapping
Abstract
:1. Introduction
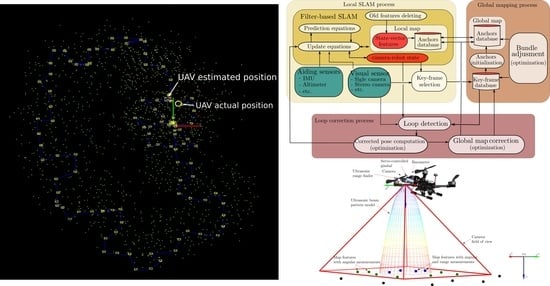
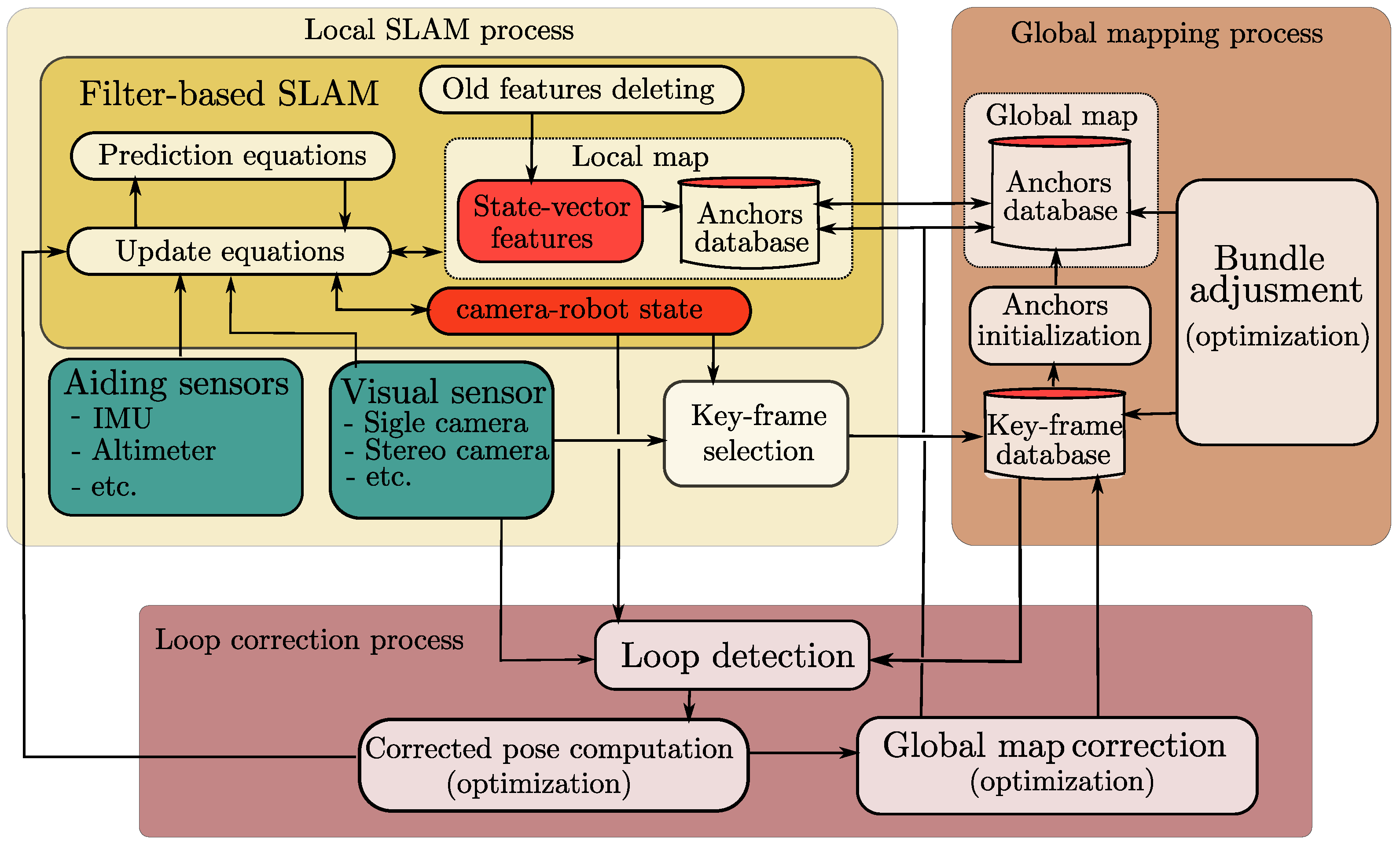
2. Proposed Architecture
2.1. Local SLAM Process
- Deleting of old features. It is well known that the computational cost of filter-based SLAM methods scales poorly as the size of the state vector increases. Therefore, “old” features that are left behind by the movement of the robot-camera must be removed from the vector state and covariance matrix to maintain a stable computational cost (see [32]).
- Observation of anchors. We will call anchors to the map features whose state and uncertainties are not stored respectively in the state vector and the covariance matrix . Similar to a map feature, an anchor can be any 3d static point of the environment that can be visually detected and tracked frame to frame (e.g., a corner of a desktop, or the edge of a rock). The difference to a map feature is that the anchor is considered to be a fixed reference for estimating the camera pose. That is, when an anchor is observed, the state of the camera-robot is affected through the filter update, but the state of the anchor remains the same. Thus, the anchors act like “fixed” visual landmarks for the filter-SLAM estimation process. Anchors can use the same or different parameterization than state vector features , but a new measurement model (see Equation (7)) that depends on the state of the camera-robot and the constant parameter must be defined.The global map is composed only of anchors, so these will act as an interface between the local SLAM and the global mapping process. For instance, if the global mapping process modifies the position of the anchors observed by the camera, then the state of the local SLAM will be affected accordingly.
- Key-frame selection. Key-frames are frames captured by the camera which are selected regularly among the video stream according to some specific criteria (e.g., spatial [18] or visual [19]). Each jth key-frame will store the camera-robot state at the moment that the frame was captured. Hereafter let define as the camera-robot state associated with the jth key-frame. After a Key-frame is selected it is sent to the Global mapping module to be processed.
- Position measurement update. To provide an interface with the loop correction process, a position update stage must be implemented to the local SLAM process. In this case, a position measurement model of the following type must be defined:where is the position of the camera-robot expressed in the world reference frame. The corrected camera-robot positions computed by the loop correction process, are incorporated into the local SLAM by mean of this update stage.
2.2. Global Mapping Process
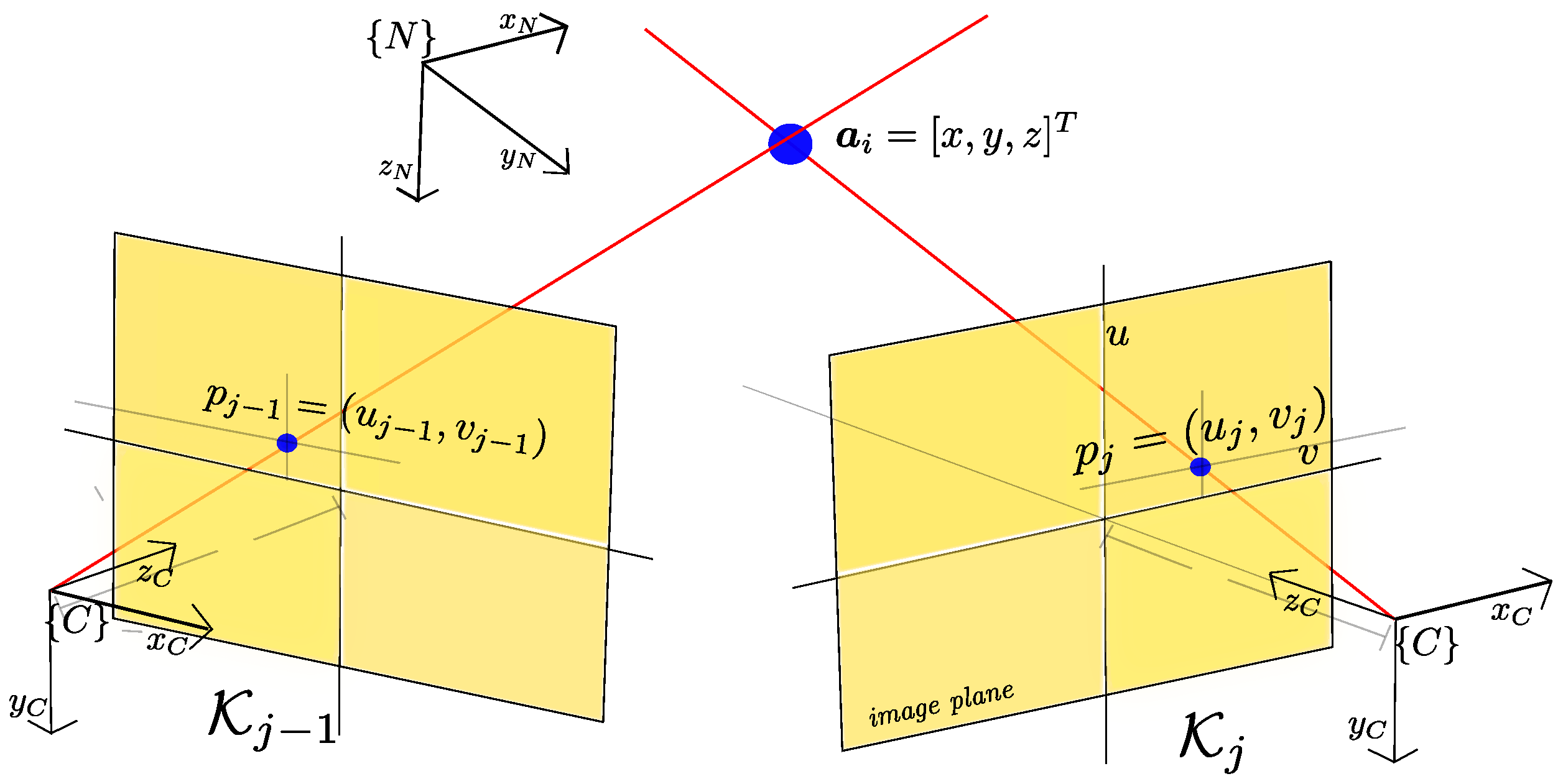
- Anchors initialization. As new key-frames arrive from the local SLAM module, new anchors are computed. Each key-frame can represent a camera view since it has associate visual and spatial information. Therefore, a multiview geometry technique (e.g., [33]) can be used to compute the position of new anchors. For instance, a new subset of anchors can be computed using a stereo-based triangulation technique, where (see Figure 2).
- Bundle adjustment. In order to refine the global map, a local bundle adjustment technique is used (e.g., [34]). Assume that n anchors are seen (projected) in m key-frames, and let be the measured projection of the ith anchor on the jth key-frame. Also let be the predicted projection of the ith anchor on the jth key-frame, where is the camera-robot state associated with the jth key-frame. Then, bundle adjustment minimizes the total reprojection error with respect to n anchors belonging to and the m camera states associated with the m key-frames contained to , orwhere denotes the Euclidean distance between the image points represented by vectors and . If the anchor i is not visible in the key-frame j then .
2.3. Loop Correction Process
- Loop detection. Let define as the current frame captured by the camera, which has the current camera-state associated with it. Then, different heuristic criteria can be established, but in general, a loop is detected if enough number of visual features, belonging to , are visually matched against some previous (old) key-frame . Given the above, let defined the matched key-frame as and its associated camera-robot state as .
- Corrected camera-robot pose computation. If a loop is detected, this functionality is intended to compute the corrected (relatively to the previously mapped area) camera-robot position. Let define the subset of anchors that have a projection on the key-frame as , where . Let define the subset of anchors belonging to that have a measured (matched) projection on the current frame as , where . Moreover, let be the measured projection of the ith anchor on the frame . Then, the minimization of total reprojection error with respect to n anchors belonging to and the camera states associated with the frame , oris called Perspective-n-Point (or PnP) problem (see [38]). Now let define the camera-robot state that minimizes the PnP problem as . We will also refer to as the corrected camera-robot state or corrected pose. The state is composed by the corrected position and the corrected orientation of the camera-robot. When a corrected camera-robot pose is computed, a filter update is executed in the local SLAM process, to update the state of the local SLAM with as position measurement.
- Global map correction. If a corrected camera-robot state is available, then a Graph-based SLAM technique (see [39]) can be used to accordingly correct the camera-robot states associated with the key-frames contained in . Now, let define as the vector of parameters to be optimized by the graph-based SLAM, where describe the pose of node i. Note that in , one parameter correspond to the state of key-frame which was matched during the loop detection. Also in , the last parameter correspond to state of the camera-robot when the current frame was captured. Let and be respectively the mean and the information matrix of a virtual measurement between the node i and the node j. And let be the prediction of a virtual measurement given a configuration of the nodes and . Finally let be an error function that computes the difference between the expected measurement and the actual measurement :
- -
- Visual odometry measurements are defined by the relative transformation between consecutive camera-robot states, so , where . In this case, there will be visual odometry measurements linking all the camera-robot states in . The prediction can be set to zero if not visual odometry model is available (or only by simplicity).
- -
- A single closed-loop measurement, which is defined by the relative transformation between the corrected camera-robot pose and the state of the matched key-frame , or . In this case the prediction is defined by the relative transformation between the current camera-robot pose and the state of the matched key-frame , or . In this case, for and , since it corresponds to the current camera-robot state.
3. Implementation Case
3.1. Local SLAM
- Old features deleting. A map feature is removed from the state vector and the covariance matrix , when the ratio of unmatched-matched times of a map feature is high, or number of times that it is not considered to be matched is high.
- Observation of anchors. Anchors are parameterized in the same manner as state map features:and therefore the measurement model (7) is similar to (18), but in this case are fixed parameters and the jacobians does not depend on them. The local SLAM process owns a structure for storing local anchors. A local anchor is one that can be potentially projected into the current camera image-frame. Let be the set of anchors belonging to the structure owned by the local SLAM process. Anchors are added to in two ways:
- -
- The global mapping process copy anchors from to that are visually linked to the current camera frame. This process will be explained in more detail later.
- -
- The map features contained in the state , whose position exhibits some good degree of convergence, are removed from the EKF state and transformed into anchors contained in . In this case, the following simple condition is proposed:If the above criteria is met, then the transformation is carried out (simply ). Where represent the variances of of the feature along each axis taken from the system covariance matrix, and is a threshold. In our implementation, a value of was used.
On the other hand, anchors are removed from in the following cases:- -
- An anchor is removed from if similar conditions that those for deleting local map features are accomplished.
- -
- If the loop correction process has detected a loop closing condition and a corrected pose is available, all the anchors in are deleted and replaced with visually linked anchors from the corrected global map.
In the same manner as state features, anchors have associated an ORB descriptor. Every time a new camera frame is available the anchors are projected into the image frame, and they are attempted to be matched in the same manner as the local map features to determine visual measurements of anchors . - Key-frame selection. A camera frame is selected as key-frame if two criteria are met:
- -
- The displacement of the camera-robot is bigger than some threshold depending on the average depth of the n local map features, orIn our implementation, a value of was used.
- -
- A minimum number of features (or anchors) were visually matched at that frame. In our implementation, a value of 10 was used for this criteria.
- Position measurement update. If the loop correction process has detected a loop closing condition and therefore a corrected pose is is available, the filter is updated in a standard manner with the measurement model (8) and the measurement .
3.2. Global Mapping
- Computing new anchors. If a new key-frame is available and the number of visual links of the previous key-frame is below a threshold, then new anchors are initialized by triangulation. First, visual matches are searched between the ORB descriptors of key-frames and . Then Outliers are removed using RANSAC. If and are respectively the (undistorted) projection of the anchor over the key-frames and , then the location of the anchor can be computed by triangulation as follows:From model (18) we have that:where , and is the position of the anchor expressed in the navigation frame . Let be the i row of the projection matrix of the key-frame j. We have that , , and . Substituting the last expression, we have that: and . Considering both projections and , of the same anchor , the following linear system can be formed:The above linear system can be solved for . New anchors computed by triangulation are added to the global map
- Adding anchors computed by the local SLAM. The anchors computed by the local SLAM process are added to the global map .
- Visibility graph update. Every time a new key-frame is available, the visibility graph is updated. In this case, the visual links are updated by taking into account the projections of the new initialized anchors over previous key-frames, and also the projections of old anchors over the new key-frame .
- Bundle adjustment. First, let define the subset as the subset of m key-frames that are visually linked to the most recent key-frame . A key-frame is visually linked to another key-frame if . Moreover, let define the subset as the subset of n anchors that have at least three measured projections over three different key-frames . A measured projection is determined by visually matching an anchor , with predicted projection , on the key-frame using ORB descriptors.The global map is optimized by applying local bundle adjustment (Equation (9)) to anchors and setting each camera state of the key-frames as fixed parameters.
- Weak anchors deleting. Anchors that can not be matched in at least three key-frames are removed from the global map to maintain only anchors with a good likelihood to be visually matched when the camera-robot revisits previously mapped areas.
- Local map anchors updating. Every time the global map is optimized by the local bundle adjustment the set of anchors owned by the local SLAM process is updated. In this case, the optimized anchors replaces their counterparts owned by the local SLAM . Moreover, the new anchors computed (and optimized) by the global SLAM process are added to the local SLAM set .
3.3. Loop Correction
- Loop detection. If is the most recent key-frame, and is the oldest key-frame visually linked to , and is the oldest key-frame visually linked to , first lets define as the subset of all key-frames not containing the key-frames visually linked to nor , or: .The ORB descriptors, computed from the current frame , are attempted to be matched against the ORB descriptors of key-frames . RANSAC is applied to remove potential match outliers. Now, let define as the subset of consecutive key-frames with at least n number of matches ( is used by the implementation). A potential loop is detected if contain at least three key-frames. The key-frame is the key-frame with the highest number of matches (see Section 2.3).
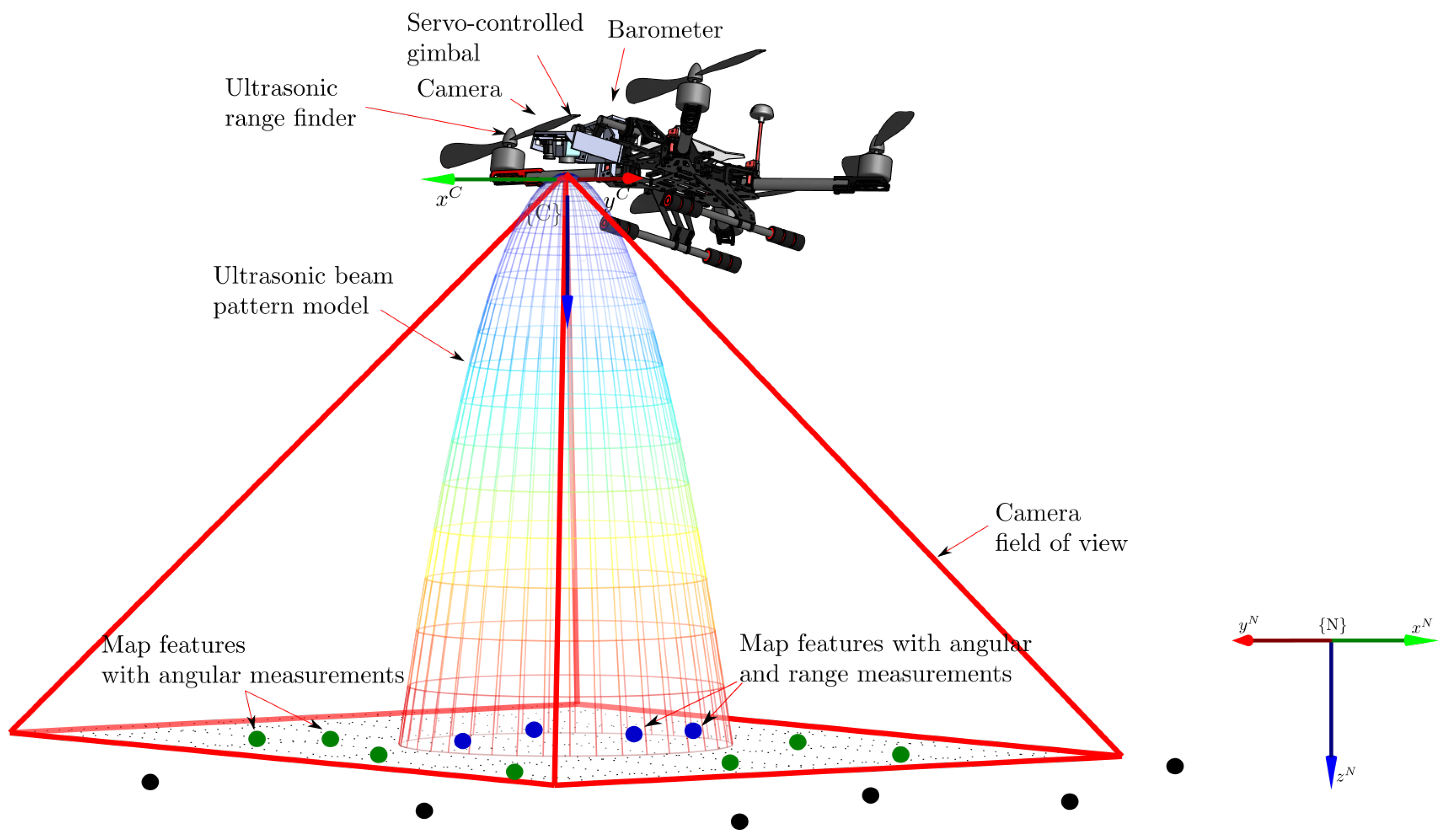
- Camera pose computation. The corrected camera pose is computed through Equation (10), selecting the anchors as it is described in Section 2.3, and with defined by the projection model (18) with . The following considerations are taken into account for the minimization:
- -
- Due to the gimbal assumption, is set as a known fixed parameter in Equation (10).
- -
- Due to the integration of the altimeter, (the z-axis location of the camera-robot) is set as a fixed parameter in Equation (10) equal to the current altitude camera-robot position computed by the local SLAM in .
It is important to note that the subset must contain a minimum number of four anchors to compute , but in practice, to improve robustness, a minimum number of 10 anchors is required in this implementation; otherwise, the loop closure is rejected.Additionally, in this implementation to improve the robustness of the solution of the corrected camera pose an additional test was considered. For this test, the anchors are re-projected to the image plane through (10) using the computed . If the projection of a single anchor lies outside of the image frame then the loop closure is rejected. - Global map correction. If a corrected camera pose is available, then the global map (position of key-frames and anchors ) is corrected through Equations (12) and (13) as it is described in Section 2.3. But in this case, due to that, only the position of the camera-robot must be estimated (gimbal assumption) and that the altitude computed by the local SLAM is taken to be the best estimate (altimeter assumption), the graph SLAM problem is simplified to a 2DOF (x-y) position estimation problem. Therefore, in Equation (12):After a loop closure is carried out, the visibility graph is completely recomputed to reflect the actual visual relationships between key-frames.
- Position update triggering. When a corrected camera pose is available and the global map is rectified, a position update is triggered in the local SLAM process using as the measurement to correct the local map accordingly to the loop close condition.
3.4. Implementation Notes
4. Experimental Results
4.1. Local SLAM
4.2. Global Mapping
4.3. Loop Correction
4.4. Comparison with an Optimization-Based Method
4.5. Other Flight Trajectories
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pan, L.; Cheng, J.; Zhang, Q. UFSM VO: Stereo Odometry Based on Uniformly Feature Selection and Strictly Correspondence Matching. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 4148–4152. [Google Scholar] [CrossRef]
- Kostavelis, I.; Boukas, E.; Nalpantidis, L.; Gasteratos, A. Stereo-Based Visual Odometry for Autonomous Robot Navigation. Int. J. Adv. Robot. Syst. 2016, 13, 21. [Google Scholar] [CrossRef] [Green Version]
- Ullah, I.; Su, X.; Zhang, X.; Choi, D. Simultaneous Localization and Mapping Based on Kalman Filter and Extended Kalman Filter. Wirel. Commun. Mob. Comput. 2020, 2020, 2138643. [Google Scholar] [CrossRef]
- Kim, P.; Coltin, B.; Kim, H.J. Linear RGB-D SLAM for Planar Environments. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Chen, M.; Yang, S.; Yi, X.; Wu, D. Real-time 3D mapping using a 2D laser scanner and IMU-aided visual SLAM. In Proceedings of the 2017 IEEE International Conference on Real-time Computing and Robotics (RCAR), Okinawa, Japan, 14–18 July 2017; pp. 297–302. [Google Scholar] [CrossRef]
- Motlagh, H.D.K.; Lotfi, F.; Taghirad, H.D.; Germi, S.B. Position Estimation for Drones based on Visual SLAM and IMU in GPS-denied Environment. In Proceedings of the 2019 7th International Conference on Robotics and Mechatronics (ICRoM), Tehran, Iran, 20–21 November 2019; pp. 120–124. [Google Scholar] [CrossRef]
- Zhou, H.; Zou, D.; Pei, L.; Ying, R.; Liu, P.; Yu, W. StructSLAM: Visual SLAM With Building Structure Lines. IEEE Trans. Veh. Technol. 2015, 64, 1364–1375. [Google Scholar] [CrossRef]
- Bloesch, M.; Burri, M.; Omari, S.; Hutter, M.; Siegwart, R. Iterated extended Kalman filter based visual-inertial odometry using direct photometric feedback. Int. J. Robot. Res. 2017, 36, 1053–1072. [Google Scholar] [CrossRef] [Green Version]
- Quan, M.; Piao, S.; Tan, M.; Huang, S.S. Accurate Monocular Visual-Inertial SLAM Using a Map-Assisted EKF Approach. IEEE Access 2019, 7, 34289–34300. [Google Scholar] [CrossRef]
- Holmes, S.; Klein, G.; Murray, D.W. A Square Root Unscented Kalman Filter for visual monoSLAM. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 3710–3716. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.H. Real-time camera tracking using a particle filter combined with unscented Kalman filters. J. Electron. Imaging 2014, 23, 013029. [Google Scholar] [CrossRef]
- Tang, M.; Chen, Z.; Yin, F. Robot Tracking in SLAM with Masreliez-Martin Unscented Kalman Filter. Int. J. Control Autom. Syst. 2020, 18, 2315–2325. [Google Scholar] [CrossRef]
- Eustice, R.M.; Singh, H.; Leonard, J.J.; Walter, M.R. Visually Mapping the RMS Titanic: Conservative Covariance Estimates for SLAM Information Filters. Int. J. Robot. Res. 2006, 25, 1223–1242. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Valls MirÓ, J.; Dissanayake, G. Information-Efficient 3-D Visual SLAM for Unstructured Domains. IEEE Trans. Robot. 2008, 24, 1078–1087. [Google Scholar] [CrossRef] [Green Version]
- Celik, K.; Chung, S.J.; Clausman, M.; Somani, A.K. Monocular vision SLAM for indoor aerial vehicles. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 1566–1573. [Google Scholar] [CrossRef] [Green Version]
- Wen, S.; Chen, J.; Lv, X.; Tong, Y. Cooperative simultaneous localization and mapping algorithm based on distributed particle filter. Int. J. Adv. Robot. Syst. 2019, 16, 1729881418819950. [Google Scholar] [CrossRef] [Green Version]
- Liu, W. Slam algorithm for multi-robot communication in unknown environment based on particle filter. J. Ambient. Intell. Human Comput. 2021. [Google Scholar] [CrossRef]
- Klein, G.; Murray, D. Parallel Tracking and Mapping for Small AR Workspaces. In Proceedings of the 2007 6th IEEE and ACM International Symposium on Mixed and Augmented Reality, Nara, Japan, 13–16 November 2007; pp. 225–234. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef] [Green Version]
- Concha, A.; Civera, J. DPPTAM: Dense piecewise planar tracking and mapping from a monocular sequence. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 5686–5693. [Google Scholar] [CrossRef] [Green Version]
- Lin, X.; Wang, F.; Guo, L.; Zhang, W. An Automatic Key-Frame Selection Method for Monocular Visual Odometry of Ground Vehicle. IEEE Access 2019, 7, 70742–70754. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X.; Zhang, N.; Lv, Y. A Semantic SLAM System for Catadioptric Panoramic Cameras in Dynamic Environments. Sensors 2021, 21, 5889. [Google Scholar] [CrossRef] [PubMed]
- Liao, Z.; Wang, W.; Qi, X.; Zhang, X. RGB-D Object SLAM Using Quadrics for Indoor Environments. Sensors 2020, 20, 5150. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Vela, P.A. Good Feature Selection for Least Squares Pose Optimization in VO/VSLAM. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1183–1189. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.P.; Mourikis, A.I.; Roumeliotis, S.I. Observability-based Rules for Designing Consistent EKF SLAM Estimators. Int. J. Robot. Res. 2010, 29, 502–528. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.P.; Mourikis, A.I.; Roumeliotis, S.I. A Quadratic-Complexity Observability-Constrained Unscented Kalman Filter for SLAM. IEEE Trans. Robot. 2013, 29, 1226–1243. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.M.; Jung, J.; Kim, S.; Kim, I.J.; Myung, H. DV-SLAM (Dual-Sensor-Based Vector-Field SLAM) and Observability Analysis. IEEE Trans. Ind. Electron. 2015, 62, 1101–1112. [Google Scholar] [CrossRef]
- Reif, K.; Gunther, S.; Yaz, E.; Unbehauen, R. Stochastic stability of the discrete-time extended Kalman filter. IEEE Trans. Autom. Control 1999, 44, 714–728. [Google Scholar] [CrossRef]
- Kluge, S.; Reif, K.; Brokate, M. Stochastic Stability of the Extended Kalman Filter With Intermittent Observations. IEEE Trans. Autom. Control 2010, 55, 514–518. [Google Scholar] [CrossRef]
- Poulose, A.; Han, D.S. Hybrid Indoor Localization Using IMU Sensors and Smartphone Camera. Sensors 2019, 19, 5084. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Strasdat, H.; Montiel, J.; Davison, A.J. Visual SLAM: Why filter? Image Vis. Comput. 2012, 30, 65–77. [Google Scholar] [CrossRef]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-Time Single Camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hartley, R.I.; Sturm, P. Triangulation. Comput. Vis. Image Underst. 1997, 68, 146–157. [Google Scholar] [CrossRef]
- Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle Adjustment—A Modern Synthesis. In Vision Algorithms: Theory and Practice; Triggs, B., Zisserman, A., Szeliski, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 298–372. [Google Scholar]
- Xia, Y.; Li, J.; Qi, L.; Yu, H.; Dong, J. An Evaluation of Deep Learning in Loop Closure Detection for Visual SLAM. In Proceedings of the 2017 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Exeter, UK, 21–23 June 2017; pp. 85–91. [Google Scholar] [CrossRef]
- Chen, S.; Zhou, B.; Jiang, C.; Xue, W.; Li, Q. A LiDAR/Visual SLAM Backend with Loop Closure Detection and Graph Optimization. Remote Sens. 2021, 13, 2720. [Google Scholar] [CrossRef]
- Konolige, K.; Agrawal, M. FrameSLAM: From Bundle Adjustment to Real-Time Visual Mapping. IEEE Trans. Robot. 2008, 24, 1066–1077. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, Z. PnP Problem Revisited. J. Math. Imaging Vis. 2006, 24, 131–141. [Google Scholar] [CrossRef]
- Grisetti, G.; Kümmerle, R.; Stachniss, C.; Burgard, W. A Tutorial on Graph-Based SLAM. IEEE Intell. Transp. Syst. Mag. 2010, 2, 31–43. [Google Scholar] [CrossRef]
- Urzua, S.; Munguía, R.; Grau, A. Monocular SLAM System for MAVs Aided with Altitude and Range Measurements: A GPS-free Approach. J. Intell. Robot. Syst. 2018, 94, 203–217. [Google Scholar] [CrossRef] [Green Version]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar] [CrossRef]
- Bailo, O.; Rameau, F.; Joo, K.; Park, J.; Bogdan, O.; Kweon, I.S. Efficient adaptive non-maximal suppression algorithms for homogeneous spatial keypoint distribution. Pattern Recognit. Lett. 2018, 106, 53–60. [Google Scholar] [CrossRef]
- Bouguet, J. Camera Calibration Toolbox for Matlab. 2008. Available online: http://www.vision.caltech.edu/bouguetj/calib_doc/ (accessed on 23 December 2021).
- MUJA, M.; Lowe, D. Fast approximate nearest neighbors with automatic algorithm configuration. In Proceedings of the 2009 International Conference on Computer Vision Theory and Applications, Lisboa, Portugal, 5–8 February 2009; pp. 331–340. [Google Scholar]
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef] [Green Version]
- Bailey, T.; Durrant-Whyte, H. Simultaneous localization and mapping (SLAM): Part II. IEEE Robot. Autom. Mag. 2006, 13, 108–117. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, S.; Mierle, K. Ceres Solver. Available online: http://ceres-solver.org (accessed on 23 December 2021).
- Itseez. Open Source Computer Vision Library. 2015. Available online: https://github.com/itseez/opencv (accessed on 23 December 2021).
- Sanderson, C.; Curtin, R. A User-Friendly Hybrid Sparse Matrix Class in C++. In Mathematical Software—ICMS 2018; Davenport, J.H., Kauers, M., Labahn, G., Urban, J., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 422–430. [Google Scholar]
- Parrot Bebop Drone for Developers. Available online: https://developer.parrot.com/docs/SDK3/ (accessed on 23 December 2021).
- Palacin, J.; Rubies, E.; Clotet, E.; Martinez, D. Evaluation of the Path-Tracking Accuracy of a Three-Wheeled Omnidirectional Mobile Robot Designed as a Personal Assistant. Sensors 2021, 7216, 7216. [Google Scholar] [CrossRef] [PubMed]





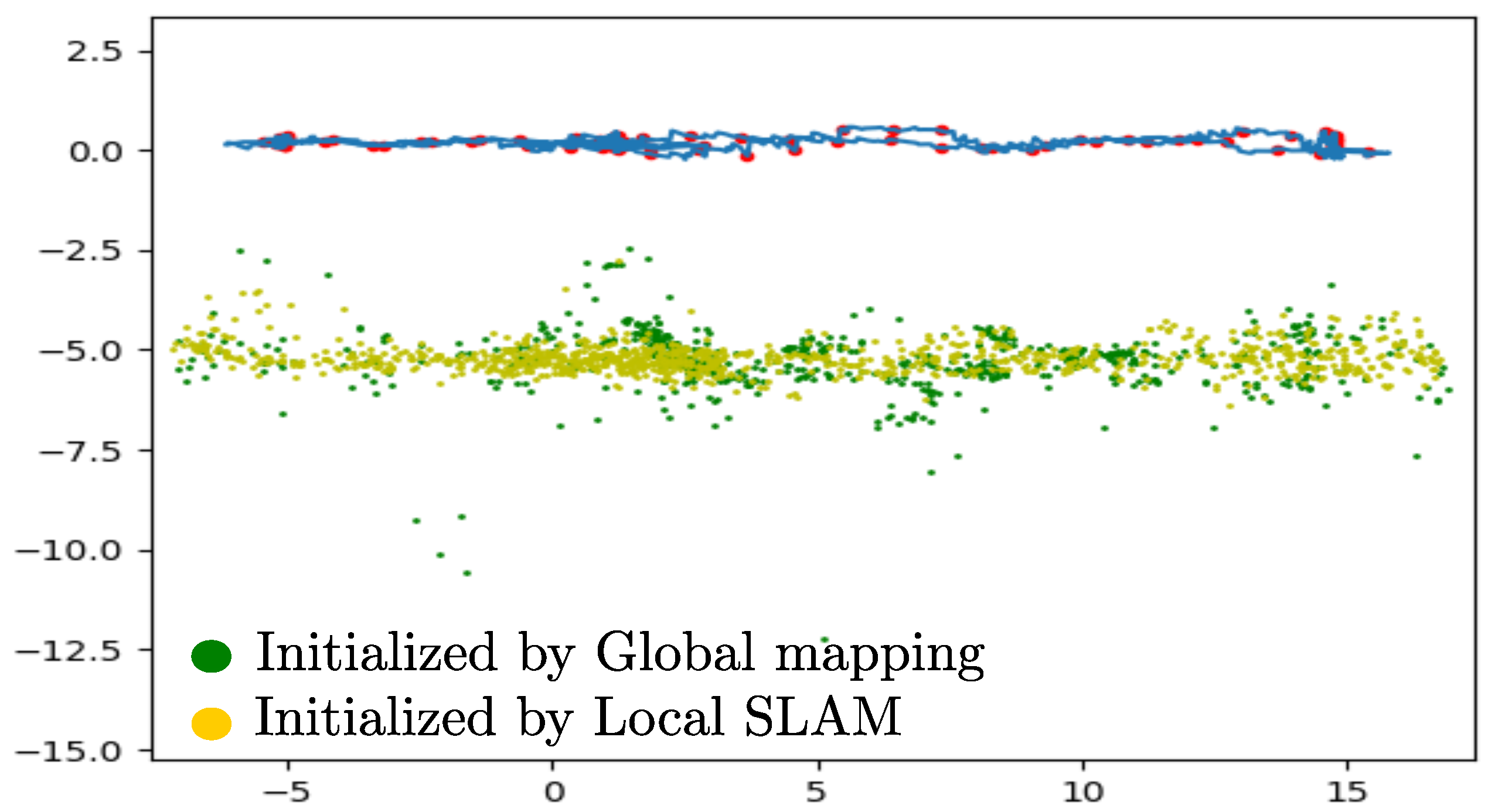

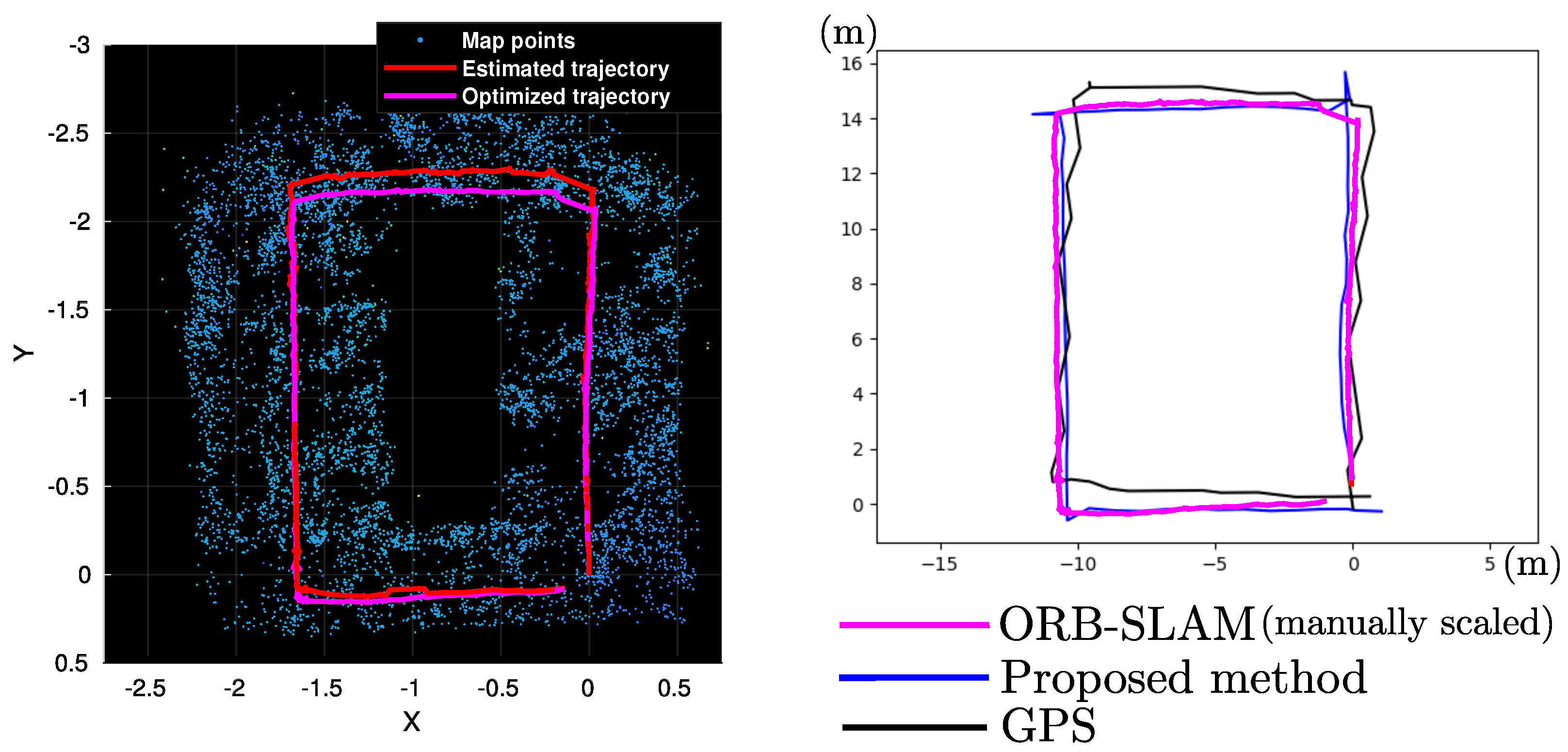
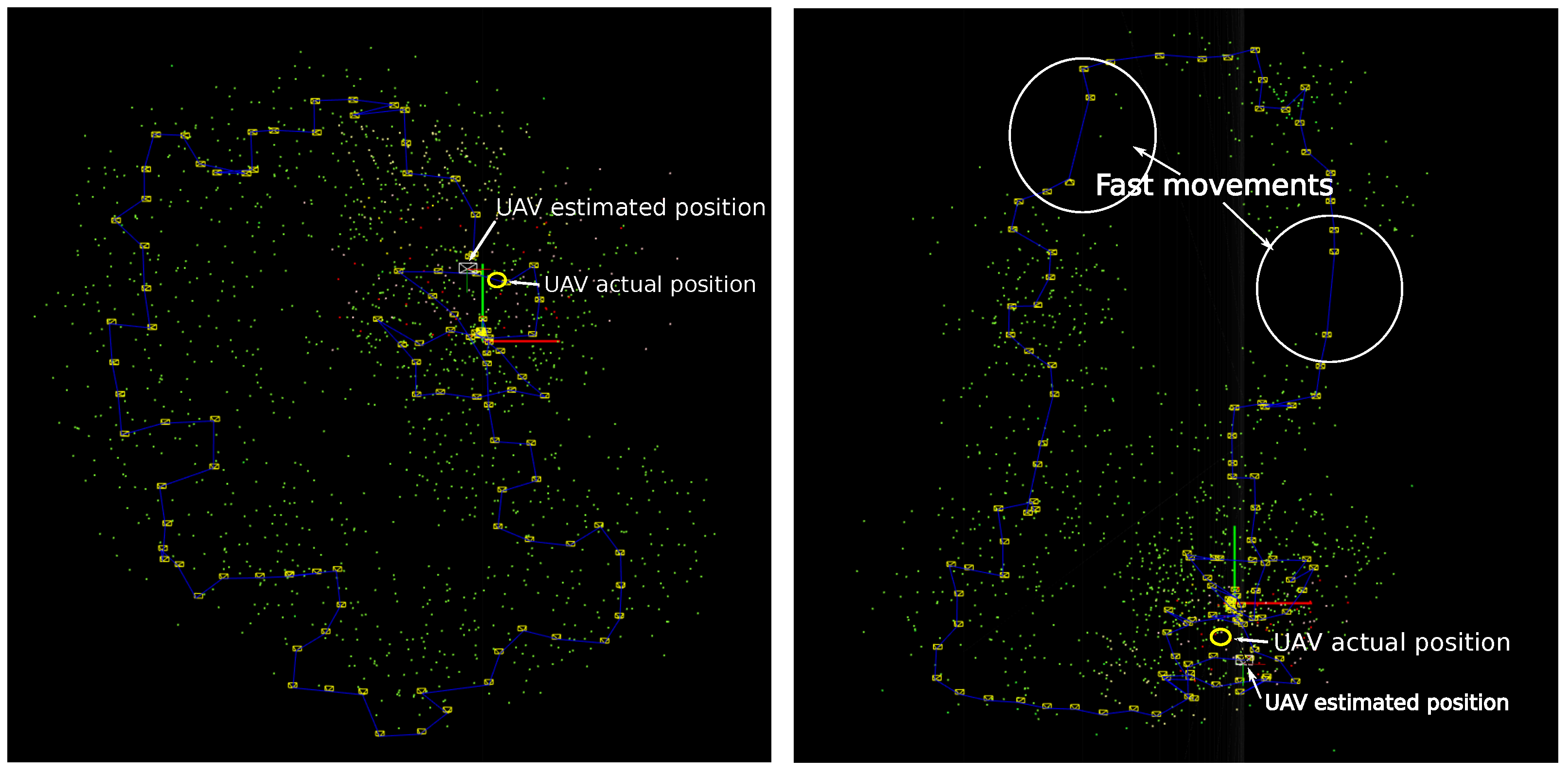
| Feats:I/D | Feat/Frame | Anchors:I/D | Anchors/Frame | Time(s)/Frame | Total Time(s) | |
|---|---|---|---|---|---|---|
| No anchors | 17,226/17,146 | 83.2 ± 7.03 | 0 | 0 | 0.0118 ± 0.0025 | 30.77 |
| With anchors | 11,163/11,134 | 30.49 ± 9.42 | 1496/1436 | 60.4 ± 11.82 | 0.0106 ± 0.0023 | 27.54 |
| Number KF | Anchors:I/D | Anchors:GM | Anchors:LS | Anchors:Total | |
|---|---|---|---|---|---|
| Global Map | 99 | 2299/1624 | 675 | 1008 | 1683 |
| n Updates | KF Optimized per Update | Time per Update (s) | Total Time (s) | |
|---|---|---|---|---|
| Global Map | 97 | 17.4 ± 8.1 | 0.082 ± 0.032 | 8.001 |
| Loop Detection (s) | Camera Pose Comp. (s) | Global Map Correction (s) | |
|---|---|---|---|
| Loop correction | 0.183 ± 0.161 | 0.382 ± 0.021 | 0.379 ± 0.010 |
| n Map Feats | n Key-Frames | Execution Time (s) | |
|---|---|---|---|
| ORB-SLAM (MATLAB) | 8704 | 274 | 331.72 |
| Hybrid SLAM (C++) | 846 | 58 | 20.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munguia, R.; Trujillo, J.-C.; Guerra, E.; Grau, A. A Hybrid Visual-Based SLAM Architecture: Local Filter-Based SLAM with KeyFrame-Based Global Mapping. Sensors 2022, 22, 210. https://doi.org/10.3390/s22010210
Munguia R, Trujillo J-C, Guerra E, Grau A. A Hybrid Visual-Based SLAM Architecture: Local Filter-Based SLAM with KeyFrame-Based Global Mapping. Sensors. 2022; 22(1):210. https://doi.org/10.3390/s22010210
Chicago/Turabian StyleMunguia, Rodrigo, Juan-Carlos Trujillo, Edmundo Guerra, and Antoni Grau. 2022. "A Hybrid Visual-Based SLAM Architecture: Local Filter-Based SLAM with KeyFrame-Based Global Mapping" Sensors 22, no. 1: 210. https://doi.org/10.3390/s22010210
APA StyleMunguia, R., Trujillo, J.-C., Guerra, E., & Grau, A. (2022). A Hybrid Visual-Based SLAM Architecture: Local Filter-Based SLAM with KeyFrame-Based Global Mapping. Sensors, 22(1), 210. https://doi.org/10.3390/s22010210