Fault Identification in Electric Servo Actuators of Robot Manipulators Described by Nonstationary Nonlinear Dynamic Models Using Sliding Mode Observers
Abstract
:1. Introduction
2. Preliminaries
3. Reduced Order Model Design
4. Reduced Order Model Transformation
5. Sliding Mode Observer Design
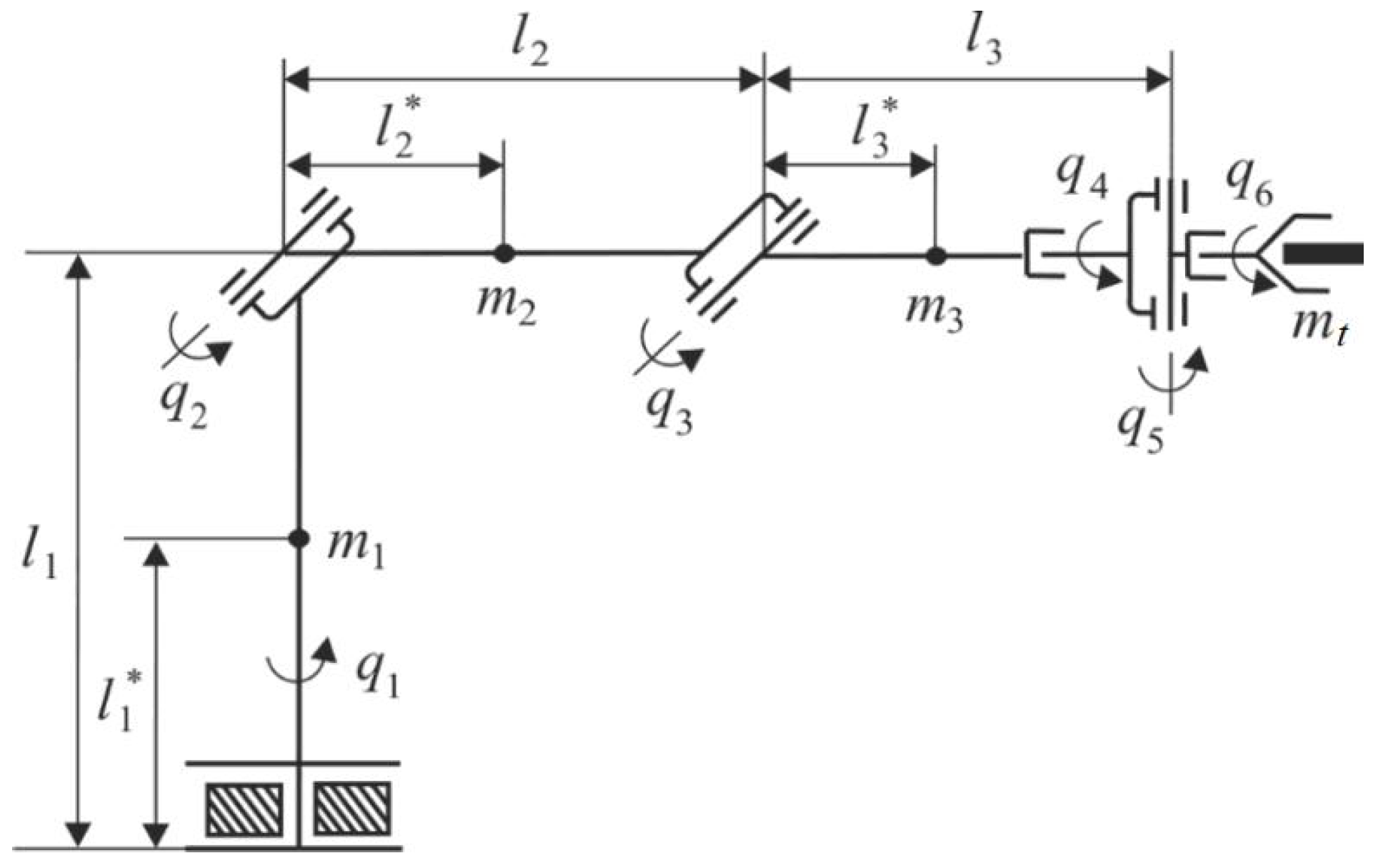
6. Practical Example
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SMO | Sliding mode observer |
| DOF | Degree of freedom |
References
- Capisani, L.; Ferrera, A.; de Loza, A.; Fridman, L. Manipulator fault diagnosis via higher order sliding-mode observers. IEEE Trans. Ind. Electron. 2012, 59, 3979–3986. [Google Scholar] [CrossRef]
- Utkin, V. Sliding Modes in Control Optimiztion; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Aguilar-Ibanez, C.; Moreno-Valenzuela, J.; Garcia-Alarcin, O.; Martinez-Lopez, M.; Acosta, J.; Suarez-Castanon, M. PI-type controllers and Σ-Δ modulation for saturated DC-DC buck power converters. IEEE Access 2021, 9, 20346–20357. [Google Scholar] [CrossRef]
- Rubio, J.; Lughofer, E.; Pieper, J.; Cruz, P.; Martinez, D.; Ochoa, G.; Islas, M.; Garcia, E. Adapting H-infinity controller for the desired reference tracking of the sphere position in the maglev process. Inf. Sci. 2021, 569, 669–686. [Google Scholar] [CrossRef]
- Silva-Ortigoza, R.; Hernandez-Marquez, E.; Roldan-Caballero, A.; Tavera-Mosqueda, S.; Marciano-Melchor, M.; Garcia-Sanchez, J.; Hernandez-Guzman, V.; Silva-Ortigoza, G. Sensorless tracking control for a full-bridge Buck inverter-DC motor system: Passivity and flatness-based design. IEEE Access 2021, 9, 132191–132204. [Google Scholar] [CrossRef]
- Soriano, L.; Zamora, E.; Vazquez-Nicolas, J.; Hernndez, G.; Madrigal, J.; Balderas, D. PD control compensation based on a cascade neural network applied to a robot manipulator. Front. Neurorobot. 2020, 14, 1–9. [Google Scholar] [CrossRef]
- Chan, J.; Tan, C.; Trinh, H. Robust fault reconstruction for a class of infinitely unobservable descriptor systems. Int. J. Syst. Sci. 2017, 48, 1–10. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S.; Patton, R. Sliding mode observers for fault detection and isolation. Automatica 2000, 36, 541–553. [Google Scholar] [CrossRef]
- Fridman, L.; Shtessel, Y.; Edwards, C.; Yan, X. High-order sliding-mode observer for state estimation and input reconstruction in nonlinear systems. Int. J. Robust Nonlinear Control 2008, 18, 399–412. [Google Scholar] [CrossRef]
- Tan, C.; Edwards, E. Sliding mode observers for robust detection and reconstruction of actuator and sensor faults. Int. J. Robust Nonlinear Control 2003, 13, 443–463. [Google Scholar] [CrossRef]
- Tan, C.P.; Edwards, C. Robust fault reconstruction using multiple sliding mode observers in cascade: Development and design. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009. [Google Scholar]
- Yan, X.; Edwards, C. Nonlinear robust fault reconstruction and estimation using a sliding modes observer. Automatica 2007, 43, 1605–1614. [Google Scholar] [CrossRef]
- Zhirabok, A.; Zuev, A.; Shumsky, A. Fault diagnosis in linear systems via sliding mode observers. Int. J. Control 2021, 94, 327–335. [Google Scholar] [CrossRef]
- Alwi, H.; Edwards, C. Fault tolerant control using sliding modes with on-line control allocation. Automatica 2008, 44, 1859–1866. [Google Scholar] [CrossRef] [Green Version]
- Edwards, C.; Alwi, H.; Tan, C. Sliding mode methds for fault detection and fault tolerant control with application to aerospace systems. Int. J. Appl. Math. Comput. Sci. 2012, 22, 109–124. [Google Scholar] [CrossRef] [Green Version]
- Defoort, M.; Veluvolu, K.; Rath, J.; Djemai, M. Adaptive sensor and actuator fault estimation for a class of uncertain Lipschitz nonlinear systems. Int. J. Adapt. Control Signal Process. 2016, 30, 271–283. [Google Scholar] [CrossRef]
- Bejarano, F.; Fridman, L. High-order sliding mode observer for linear systems with unbounded unknown inputs. Int. J. Control 2010, 83, 1920–1929. [Google Scholar] [CrossRef]
- Floquet, T.; Edwards, C.; Spurgeon, S. On sliding mode observers for systems with unknown inputs. Int. J. Adapt. Control Signal Process. 2007, 21, 638–656. [Google Scholar] [CrossRef] [Green Version]
- Fridman, L.; Levant, A.; Davila, J. Observation of linear systems with unknown inputs via high-order sliding-modes. Int. J. Syst. Sci. 2007, 38, 773–791. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, F.; Sun, X. State estimation and simultaneous unknown input and measurement noise reconstruction based on associated observers. Int. J. Adapt. Control Signal Process. 2013, 27, 846–858. [Google Scholar] [CrossRef]
- Alwi, H.; Edwards, C.; Tan, C. Sliding mode estimation schemes for incipient sensor faults. Automatica 2009, 45, 1679–1685. [Google Scholar] [CrossRef] [Green Version]
- Rios, H.; Efimov, D.; Davila, J.; Raissi, T.; Fridman, L.; Zolghadri, A. Nonminimum phase switched systems: HOSM based fault detection and fault identification via Volterra integral equation. Int. J. Adapt. Control Signal Process. 2014, 28, 1372–1397. [Google Scholar] [CrossRef] [Green Version]
- Bejarano, F.; Fridman, L.; Pozhyak, A. Unknown input and state estimation for unobservable systems. SIAM J. Control Opt. 2009, 48, 1155–1178. [Google Scholar] [CrossRef]
- Bejarano, F. Partial unknown input reconstruction for linear systems. Automatica 2011, 47, 1751–1756. [Google Scholar] [CrossRef]
- Hmidi, R.; Brahim, A.; Hmida, F.; Sellami, A. Robust fault tolerant control desing for nonlinear systems not satisfing maching and minimum phase conditions. Int. J. Control Autom. Syst. 2020, 18, 1–14. [Google Scholar] [CrossRef]
- Wang, X.; Tan, C.; Zhou, D. A novel sliding mode observer for state and fault estimation in systems not satisfing maching and minimum phase conditions. Automatica 2017, 79, 290–295. [Google Scholar] [CrossRef]
- Alwi, H.; Edwards, C. Robust fault reconstruction for linear parameter varying systems using sliding mode observers. Int. J. Robust Nonlinear Control 2014, 24, 1947–1968. [Google Scholar] [CrossRef] [Green Version]
- Chandra, K.; Alwi, H.; Edwards, C. Fault detection in uncertain LPV systems with imperfect scheduling parameter using sliding mode observers. Eur. J. Control 2017, 34, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Edwards, C.; Alwi, H. On the synthesis of variable structure observers for LPV systems. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, Australia, 12–15 December 2017; pp. 5420–5425. [Google Scholar]
- Kochetkov, S. A sliding mode algorithm for non-stationary parameters identification. In Proceedings of the 7th IFAC Conf. Manufacturing Modelling, Management, and Control, Saint Petersburg, Russia, 19–21 June 2013; 1182–1187. [Google Scholar]
- Luzar, M.; Witczak, M. Fault-tolerant control and diagnosis for LPV system with H-infinity virtual sensor. In Proceedings of the 3rd Conference Control and Fault-Tolerant Systems, Barcelona, Spain, 7–9 September 2016; pp. 825–830. [Google Scholar]
- Chen, L.; Alwi, H.; Edwards, C. On the synthesis of an integrated active LPV FTC schem using sliding modes. Automatica 2019, 110, 108536. [Google Scholar] [CrossRef]
- Filaretov, V.; Vukobratovich, M. Synthesis of adaptive robot control-systems for simplified forms of driving torques. Mechatronic 1995, 5, 41–59. [Google Scholar] [CrossRef]
- Zuev, A.; Filaretov, V. Features of designing combined force/position manipulator control systems. J. Comput. Syst. Sci. Int. 2009, 48, 146–154. [Google Scholar] [CrossRef]
- Zhirabok, A.; Shumsky, A.; Pavlov, S. Diagnosis of linear dynamic systems by the nonparametric method. Autom. Remote Control 2017, 78, 1173–1188. [Google Scholar] [CrossRef]
- Zhirabok, A.; Shumsky, A.; Solyanik, S.; Suvorov, A. Fault detection in nonlinear systems via linear methods. Int. J. Appl. Math. Comput. Sci. 2017, 27, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Kwakernaak, H.; Sivan, R. Linear Optimal Control Systems; Wiley-Interscience: London, UK, 1972. [Google Scholar]
- Keijezer, T.; Ferrari, R. Threshold design for fault detection with first order sliding mode observers. Automatica, accepted.
- Zhirabok, A.; Zuev, A.; Shumsky, A. Diagnosis of linear dynamic systems: An approach based on sliding mode observers. Autom. Remote Control 2020, 81, 211–225. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuev, A.; Zhirabok, A.N.; Filaretov, V.; Protsenko, A. Fault Identification in Electric Servo Actuators of Robot Manipulators Described by Nonstationary Nonlinear Dynamic Models Using Sliding Mode Observers. Sensors 2022, 22, 317. https://doi.org/10.3390/s22010317
Zuev A, Zhirabok AN, Filaretov V, Protsenko A. Fault Identification in Electric Servo Actuators of Robot Manipulators Described by Nonstationary Nonlinear Dynamic Models Using Sliding Mode Observers. Sensors. 2022; 22(1):317. https://doi.org/10.3390/s22010317
Chicago/Turabian StyleZuev, Alexander, Alexey N. Zhirabok, Vladimir Filaretov, and Alexander Protsenko. 2022. "Fault Identification in Electric Servo Actuators of Robot Manipulators Described by Nonstationary Nonlinear Dynamic Models Using Sliding Mode Observers" Sensors 22, no. 1: 317. https://doi.org/10.3390/s22010317
APA StyleZuev, A., Zhirabok, A. N., Filaretov, V., & Protsenko, A. (2022). Fault Identification in Electric Servo Actuators of Robot Manipulators Described by Nonstationary Nonlinear Dynamic Models Using Sliding Mode Observers. Sensors, 22(1), 317. https://doi.org/10.3390/s22010317





