A Two-Stage STAP Method Based on Fine Doppler Localization and Sparse Bayesian Learning in the Presence of Arbitrary Array Errors
Abstract
:1. Introduction
2. Signal Model
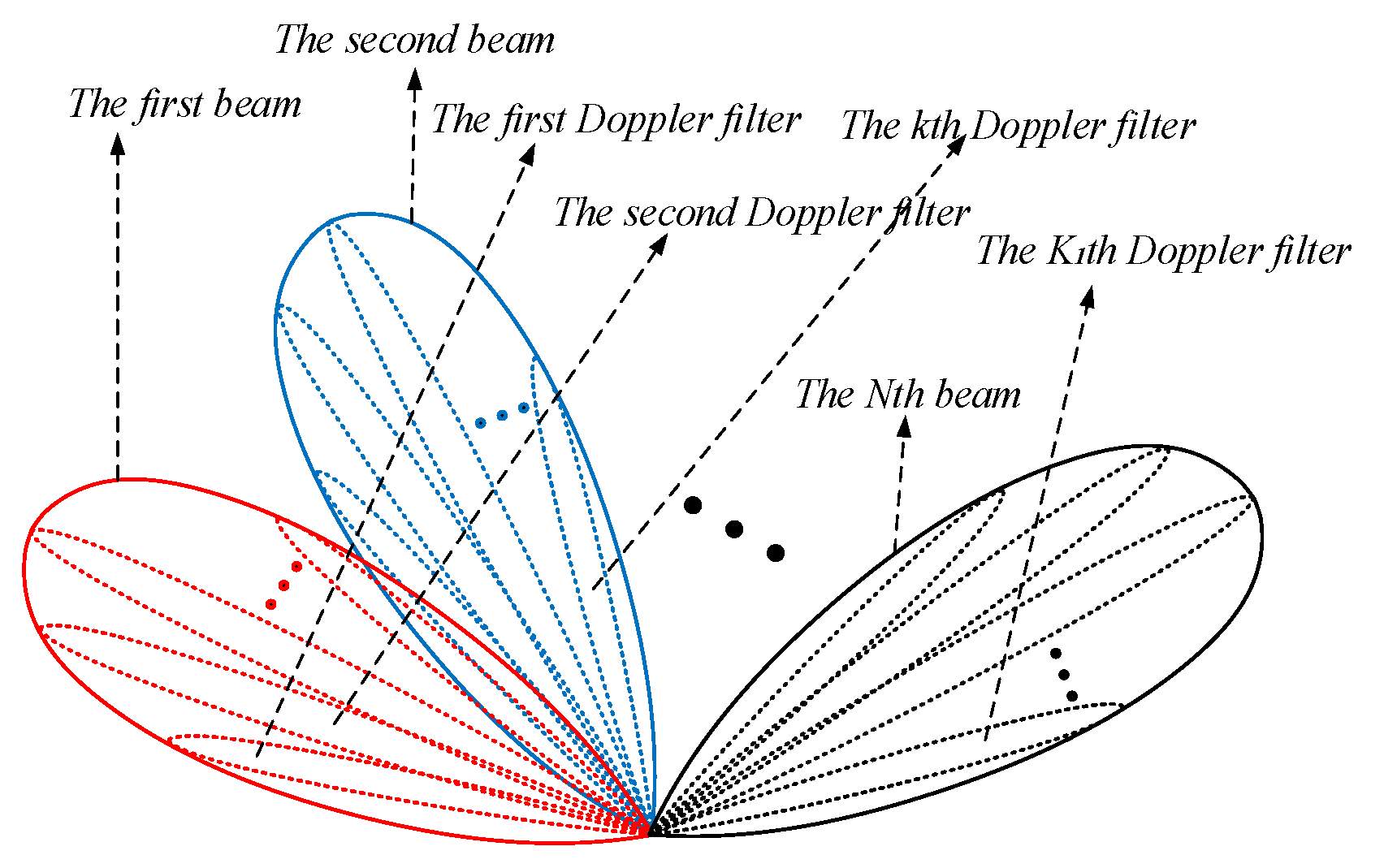
3. Proposed Method
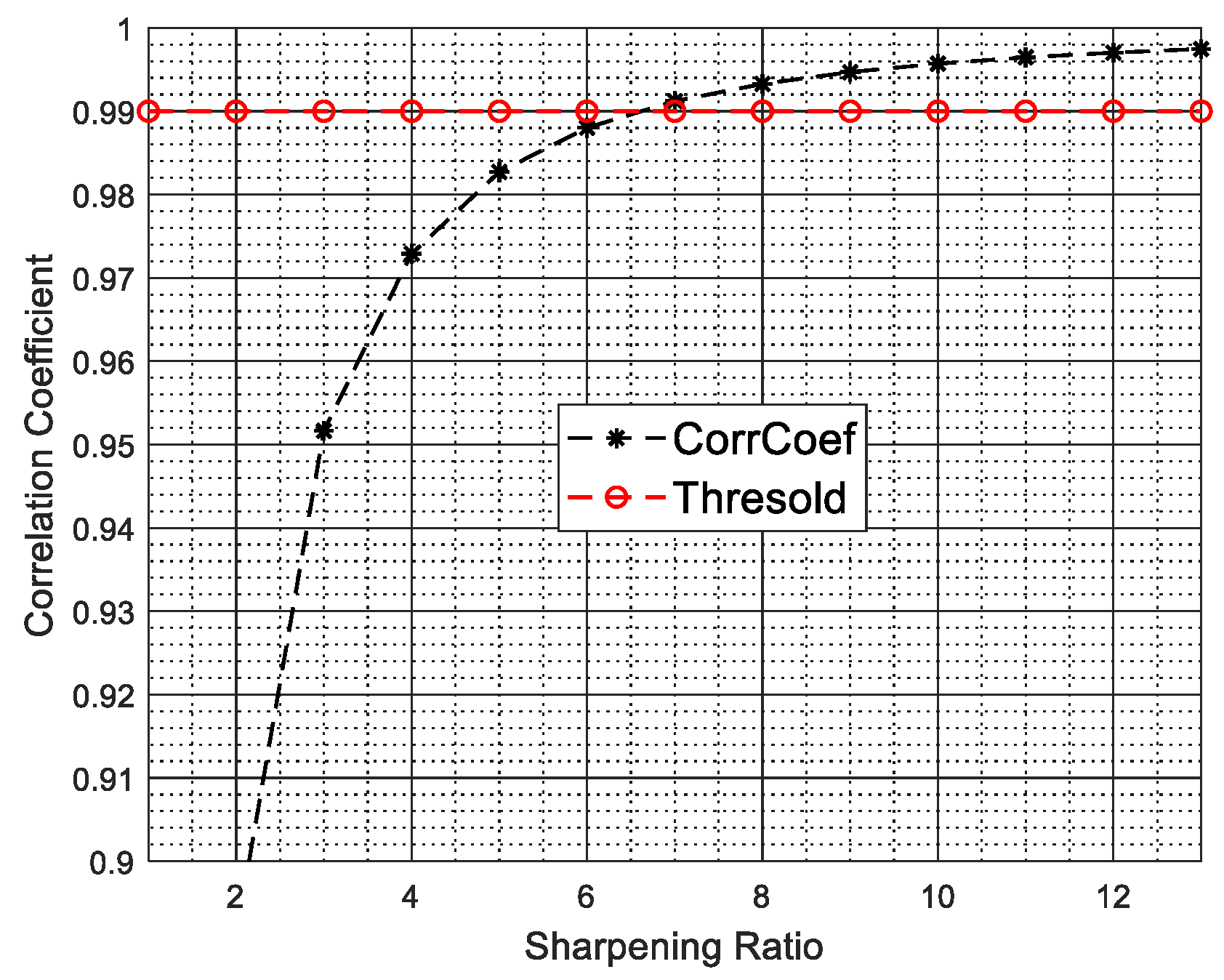
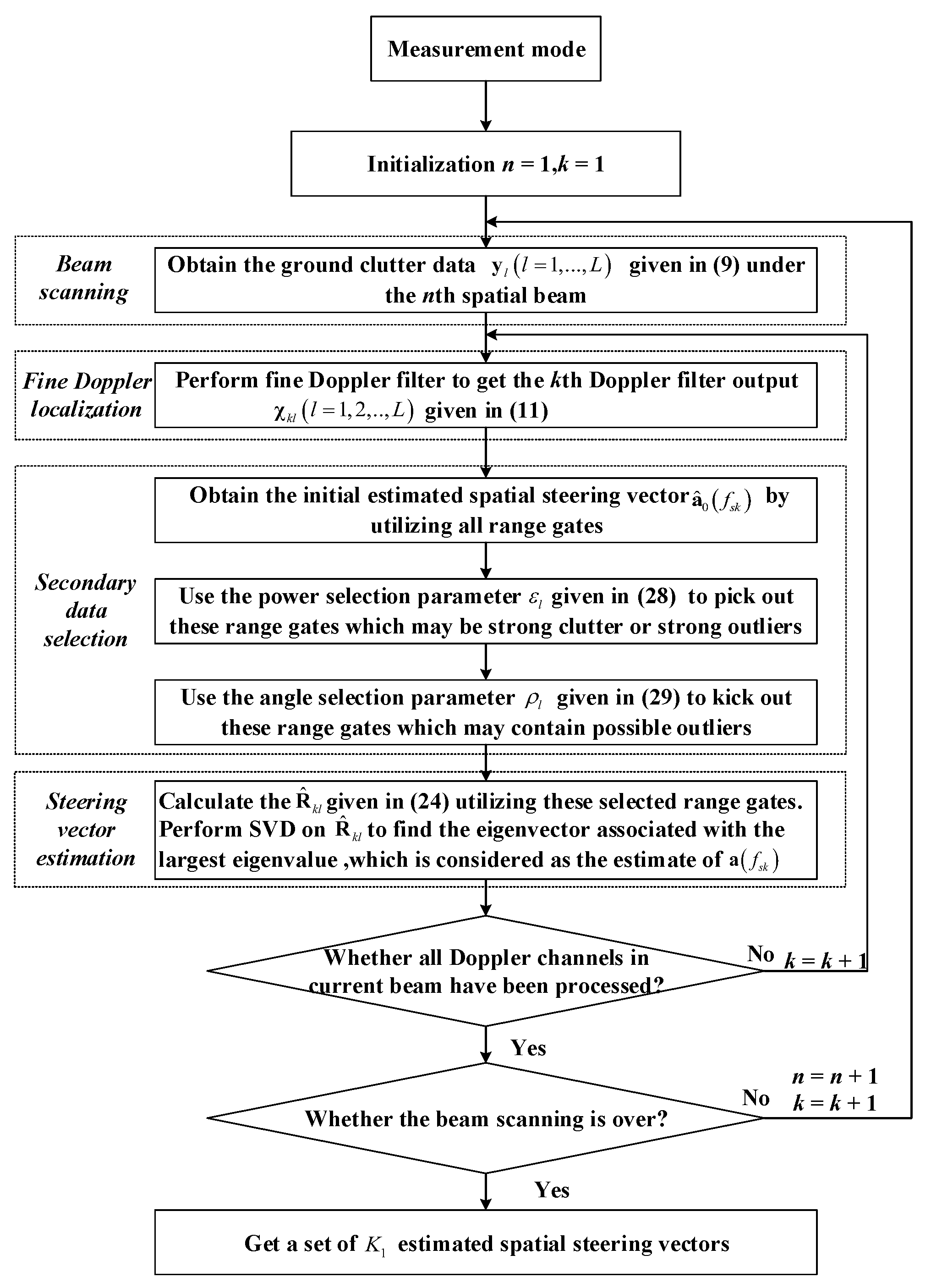
3.1. Steering Vector Estimation
3.2. SR-STAP Method
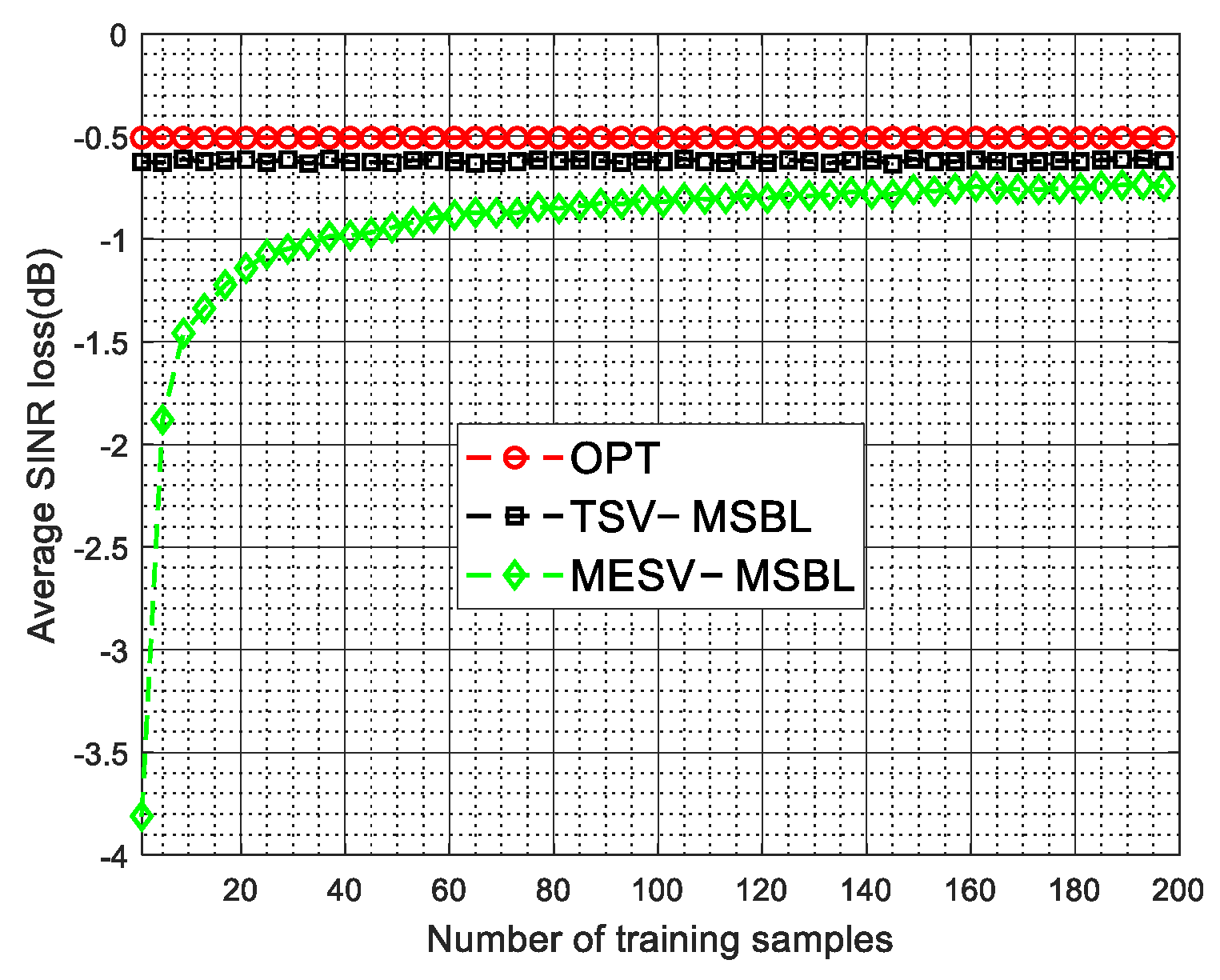
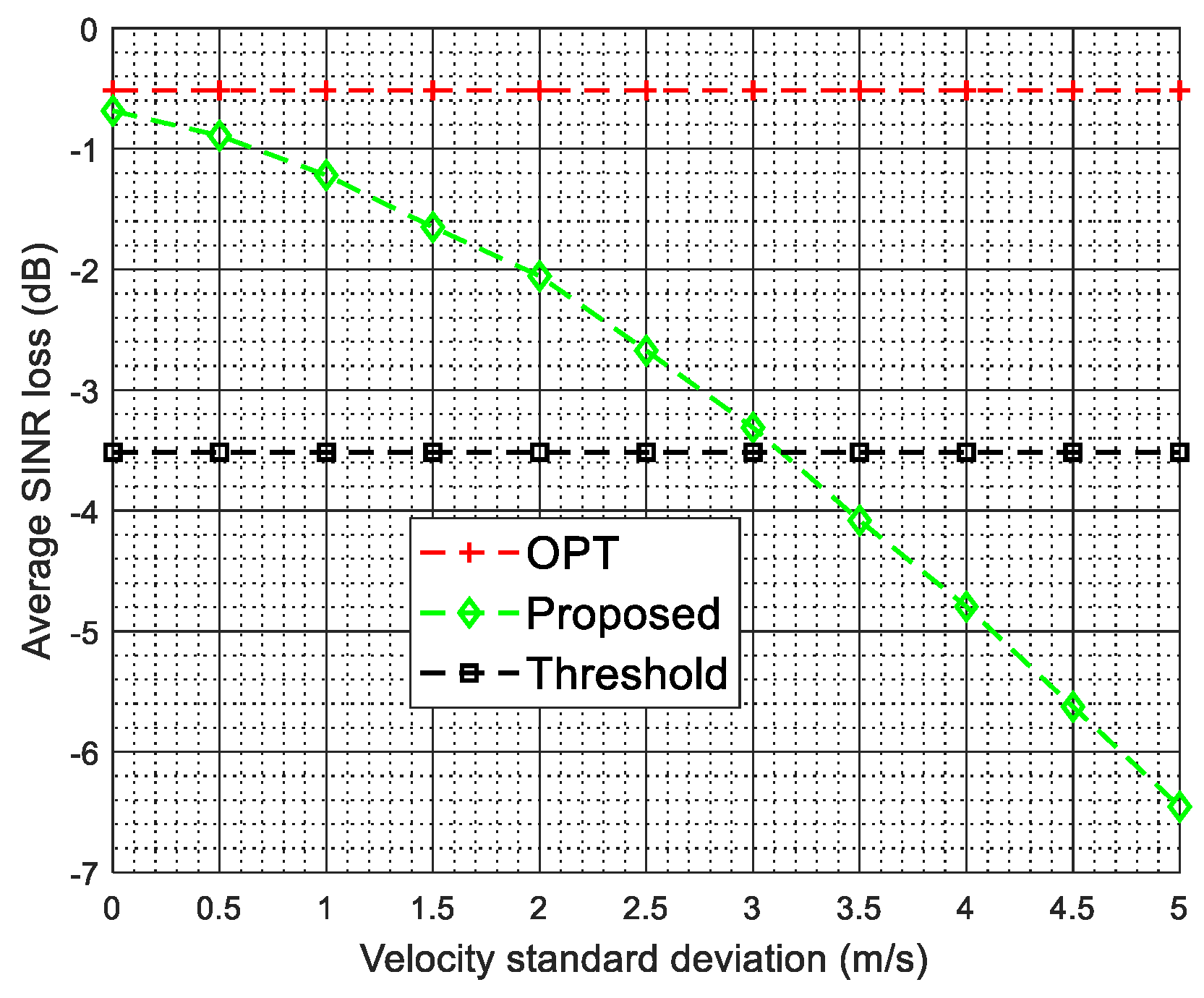
4. Numerical Experiments
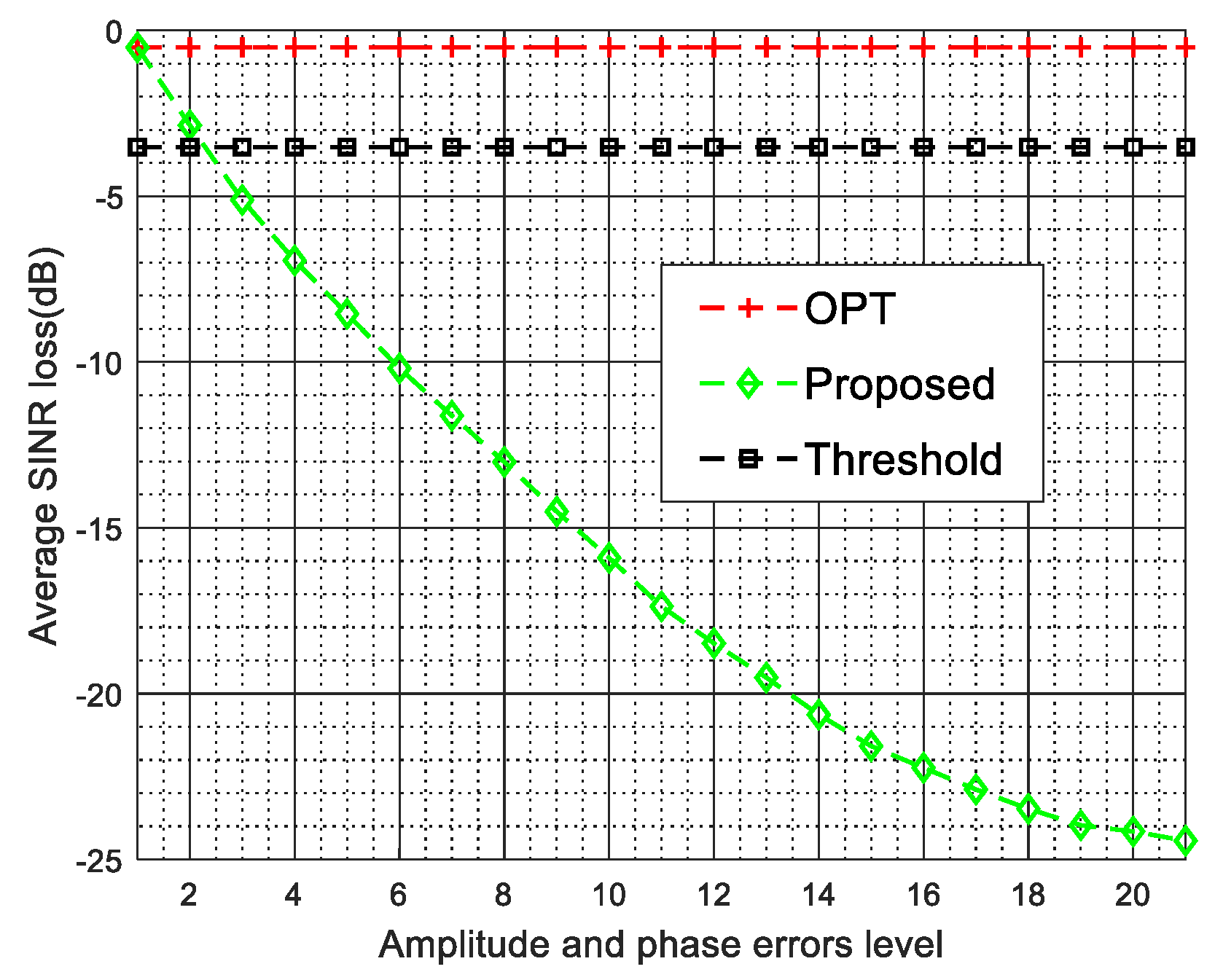
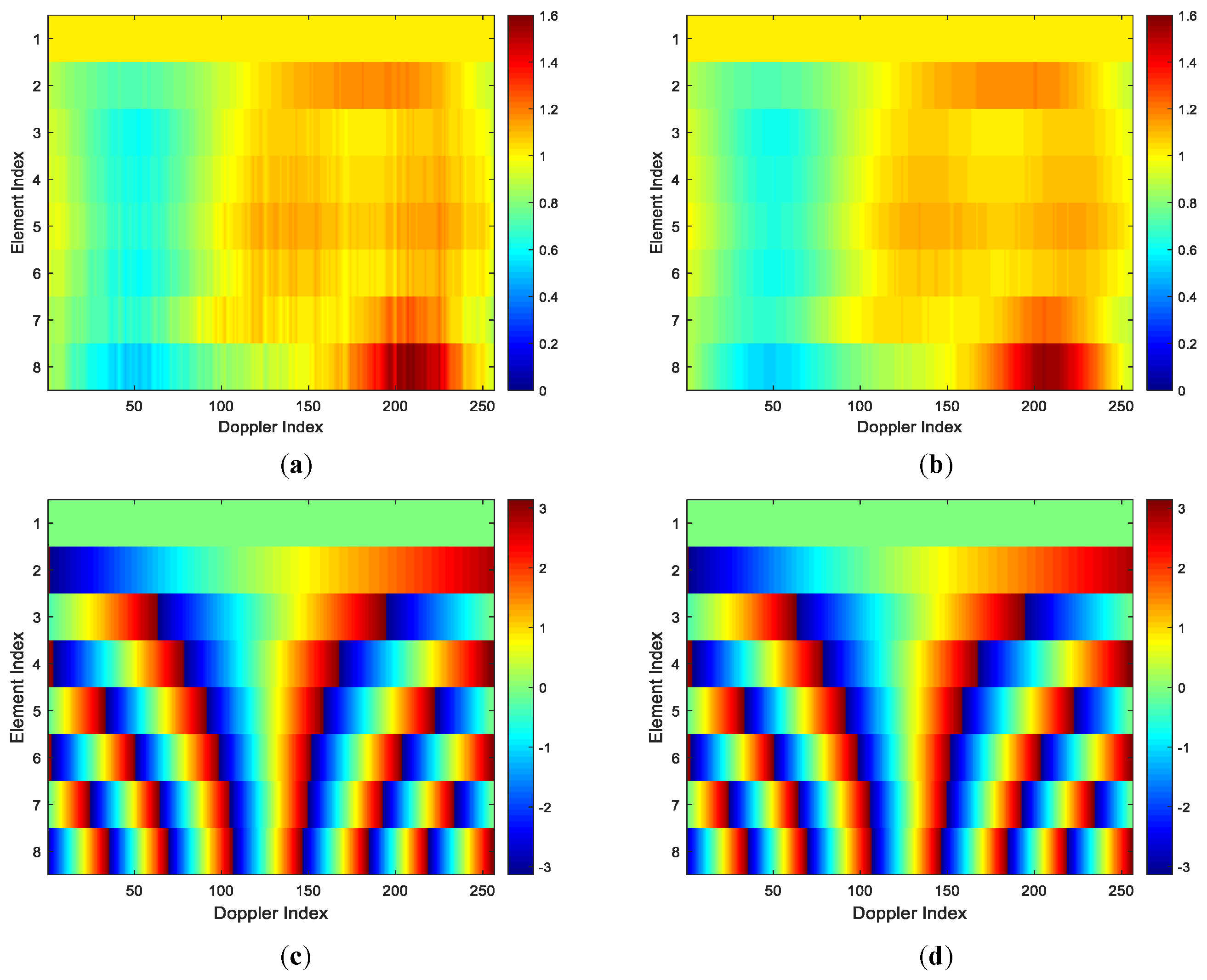
4.1. Gain and Phase Errors
4.2. Mutual Coupling
4.3. Sensor Location Errors
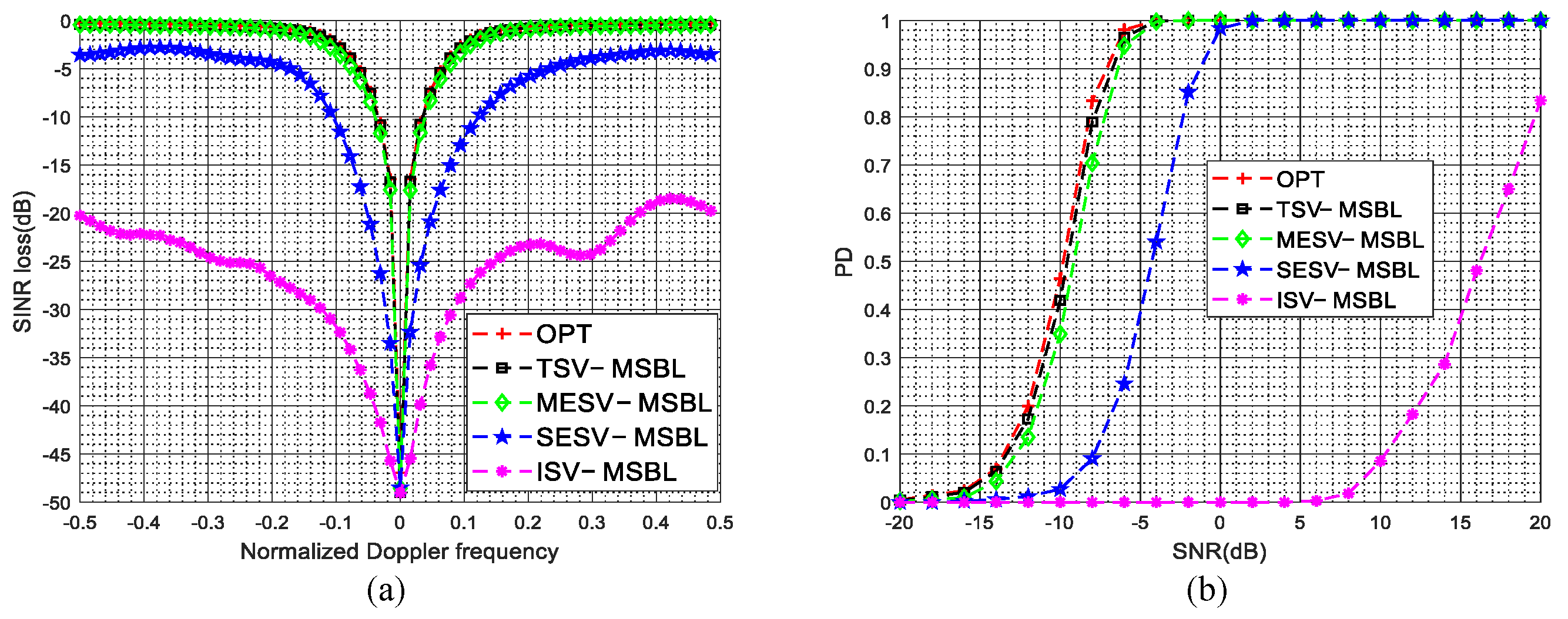
4.4. Arbtrary Array Errors
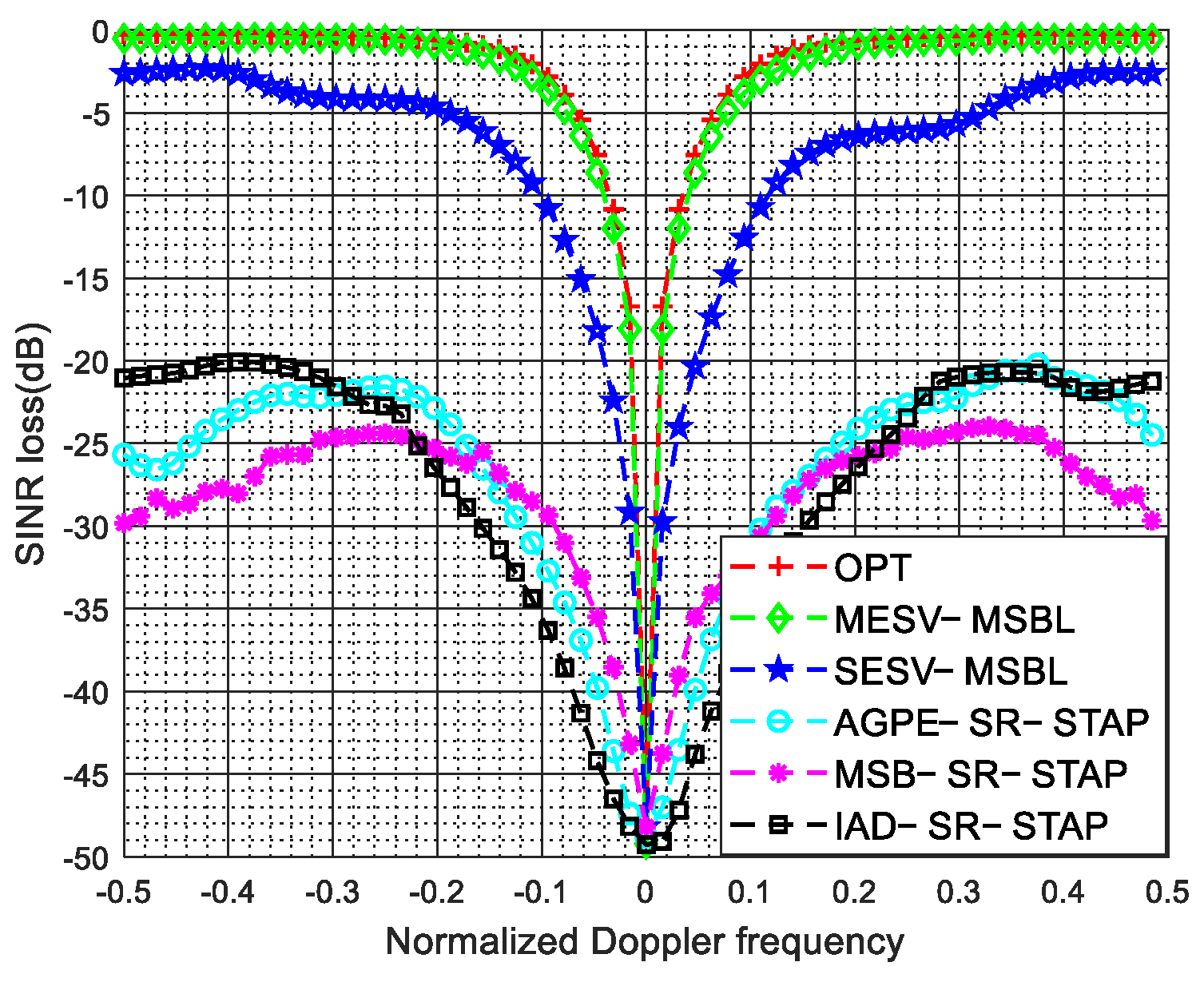
4.5. Arbitrary Array Errors and Intrinsic Clutter Motion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ward, J. Space-Time Adaptive Processing for Airborne Radar; Technical Report; MIT Lincoln Laboratory: Lexington, KY, USA, 1998. [Google Scholar]
- Klemm, R. Principles of Space-Time Adaptive Processing; The Institution of Electrical Engineers: London, UK, 2002. [Google Scholar]
- Brennan, L.E.; Reed, L. Theory of adaptive radar. IEEE Trans. Aerosp. Electron. Syst. 1973, AES-9, 237–252. [Google Scholar] [CrossRef]
- Guerci, J.R. Space-Time Adaptive Processing for Radar; Artech House: Boston, MA, USA, 2014. [Google Scholar]
- Aboutanios, E.; Mulgrew, B. Hybrid detection approach for STAP in heterogeneous clutter. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1021–1033. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, T.; Zhang, S.; Wen, C. A robust refined training sample reweighting space-time adaptive processing method for airborne radar in heterogeneous environment. IET Radar Sonar Navig. 2021, 15, 310–322. [Google Scholar] [CrossRef]
- Zhu, S.; Liao, G.; Xu, J.; Huang, L.; So, H.C. Robust STAP based on magnitude and phase constrained iterative optimization. IEEE Sens. J. 2019, 19, 8650–8656. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, T.; Wen, C.; Ren, B. A generalised eigenvalue reweighting covariance matrix estimation algorithm for airborne STAP radar in complex environment. IET Radar Sonar Navig. 2021, 15, 1309–1324. [Google Scholar] [CrossRef]
- Reed, I.S.; Mallett, J.D.; Brennan, L.E. Rapid convergence rate in adaptive arrays. IEEE Trans. Aerosp. Electron. Syst. 1974, AES-10, 853–863. [Google Scholar] [CrossRef]
- Klemm, R. Adaptive airborne MTI: An auxiliary channel approach. IEE Proc. F Commun. Radar Signal Process. 1987, 134, 269–276. [Google Scholar] [CrossRef]
- DiPietro, R.C. Extended factored space-time processing for airborne radar systems. In Proceedings of the Twenty-Sixth Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 26–28 October 1992; pp. 425–426. [Google Scholar]
- Wang, H.; Cai, L. On adaptive spatial-temporal processing for airborne surveillance radar systems. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 660–670. [Google Scholar] [CrossRef]
- Tong, Y.; Wang, T.; Wu, J. Improving EFA-STAP performance using persymmetric covariance matrix estimation. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 924–936. [Google Scholar] [CrossRef]
- Zhang, W.; He, Z.; Li, J.; Liu, H.; Sun, Y. A method for finding best channels in beam-space post-Doppler reduced-dimension STAP. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 254–264. [Google Scholar] [CrossRef]
- Xie, L.; He, Z.; Tong, J.; Zhang, W. A recursive angle-Doppler channel selection method for reduced-dimension space-time adaptive processing. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3985–4000. [Google Scholar] [CrossRef]
- Shi, J.; Xie, L.; Cheng, Z.; He, Z.; Zhang, W. Angle-Doppler Channel Selection Method for Reduced-Dimension STAP based on Sequential Convex Programming. IEEE Commun. Lett. 2021, 25, 3080–3084. [Google Scholar] [CrossRef]
- Haimovich, A. The eigencanceler: Adaptive radar by eigenanalysis methods. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 532–542. [Google Scholar] [CrossRef]
- Haimovich, A. Asymptotic distribution of the conditional signal-to-noise ratio in an eigenanalysis-based adaptive array. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 988–997. [Google Scholar]
- Goldstein, J.S.; Reed, I.S. Subspace selection for partially adaptive sensor array processing. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 539–544. [Google Scholar] [CrossRef]
- Goldstein, J.S.; Reed, I.S.; Zulch, P.A. Multistage partially adaptive STAP CFAR detection algorithm. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 645–661. [Google Scholar] [CrossRef]
- Wang, X.; Aboutanios, E.; Amin, M.G. Reduced-rank STAP for slow-moving target detection by antenna-pulse selection. IEEE Signal Process. Lett. 2015, 22, 1156–1160. [Google Scholar] [CrossRef]
- Roman, J.R.; Rangaswamy, M.; Davis, D.W.; Zhang, Q.; Himed, B.; Michels, J.H. Parametric adaptive matched filter for airborne radar applications. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 677–692. [Google Scholar] [CrossRef]
- Wang, P.; Li, H.; Himed, B. Parametric Rao tests for multichannel adaptive detection in partially homogeneous environment. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1850–1862. [Google Scholar] [CrossRef]
- Sarkar, T.K.; Wang, H.; Park, S.; Adve, R.; Koh, J.; Kim, K.; Zhang, Y.; Wicks, M.C.; Brown, R.D. A deterministic least-squares approach to space-time adaptive processing (STAP). IEEE Trans. Antennas Propag. 2001, 49, 91–103. [Google Scholar] [CrossRef] [Green Version]
- Cristallini, D.; Burger, W. A robust direct data domain approach for STAP. IEEE Trans. Signal Process. 2011, 60, 1283–1294. [Google Scholar] [CrossRef]
- Stoica, P.; Li, J.; Zhu, X.; Guerci, J.R. On using a priori knowledge in space-time adaptive processing. IEEE Trans. Signal Process. 2008, 56, 2598–2602. [Google Scholar] [CrossRef]
- Zhu, X.; Li, J.; Stoica, P. Knowledge-aided space-time adaptive processing. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1325–1336. [Google Scholar] [CrossRef]
- Riedl, M.; Potter, L.C. Multimodel shrinkage for knowledge-aided space-time adaptive processing. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2601–2610. [Google Scholar] [CrossRef]
- Liu, M.; Zou, L.; Yu, X.; Zhou, Y.; Wang, X.; Tang, B. Knowledge aided covariance matrix estimation via Gaussian kernel function for airborne SR-STAP. IEEE Access 2020, 8, 5970–5978. [Google Scholar] [CrossRef]
- Tao, F.; Wang, T.; Wu, J.; Lin, X. A novel KA-STAP method based on Mahalanobis distance metric learning. Digital Signal Process. 2020, 97, 102613. [Google Scholar] [CrossRef]
- Sun, K.; Meng, H.; Wang, Y.; Wang, X. Direct data domain STAP using sparse representation of clutter spectrum. Signal Process. 2011, 91, 2222–2236. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Li, X.; Wang, H.; Jiang, W. On clutter sparsity analysis in space–time adaptive processing airborne radar. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1214–1218. [Google Scholar] [CrossRef]
- Duan, K.; Yuan, H.; Xu, H.; Liu, W.; Wang, Y. Sparsity-based non-stationary clutter suppression technique for airborne radar. IEEE Access 2018, 6, 56162–56169. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Z.; Liu, W.; de Lamare, R.C. Reduced-dimension space-time adaptive processing with sparse constraints on beam-Doppler selection. Signal Process. 2019, 157, 78–87. [Google Scholar] [CrossRef]
- Zhang, W.; An, R.; He, N.; He, Z.; Li, H. Reduced dimension STAP based on sparse recovery in heterogeneous clutter environments. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 785–795. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Z.; Huang, J.; de Lamare, R.C. Robust two-stage reduced-dimension sparsity-aware STAP for airborne radar with coprime arrays. IEEE Trans. Signal Process. 2019, 68, 81–96. [Google Scholar] [CrossRef]
- Li, Z.; Wang, T. ADMM-Based Low-Complexity Off-Grid Space-Time Adaptive Processing Methods. IEEE Access 2020, 8, 206646–206658. [Google Scholar] [CrossRef]
- Su, Y.; Wang, T.; Tao, F.; Li, Z. A Grid-Less Total Variation Minimization-Based Space-Time Adaptive Processing for Airborne Radar. IEEE Access 2020, 8, 29334–29343. [Google Scholar] [CrossRef]
- Li, Z.; Wang, T.; Su, Y. A fast and gridless STAP algorithm based on mixed-norm minimisation and the alternating direction method of multipliers. IET Radar Sonar Navig. 2021. [Google Scholar] [CrossRef]
- Daubechies, I.; Defrise, M.; De Mol, C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. 2004, 57, 1413–1457. [Google Scholar] [CrossRef] [Green Version]
- Yang, A.Y.; Sastry, S.S.; Ganesh, A.; Ma, Y. Fast Solution of L1-Norm Minimization Problems When the Solution May Be Sparse. IEEE Trans. Inf. Theory 2008, 54, 4789–4812. [Google Scholar]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Wipf, D.P.; Rao, B.D. Sparse Bayesian learning for basis selection. IEEE Trans. Signal Process. 2004, 52, 2153–2164. [Google Scholar] [CrossRef]
- Wipf, D.P.; Rao, B.D. An empirical Bayesian strategy for solving the simultaneous sparse approximation problem. IEEE Trans. Signal Process. 2007, 55, 3704–3716. [Google Scholar] [CrossRef]
- Duan, K.; Wang, Z.; Xie, W.; Chen, H.; Wang, Y. Sparsity-based STAP algorithm with multiple measurement vectors via sparse Bayesian learning strategy for airborne radar. IET Signal Process. 2017, 11, 544–553. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, W.; Duan, K.; Wang, Y. Clutter suppression algorithm based on fast converging sparse Bayesian learning for airborne radar. Signal Process. 2017, 130, 159–168. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, Z.; Huang, J. Sparsity-based space-time adaptive processing considering array gain/phase error. In Proceedings of the CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; pp. 1–4. [Google Scholar]
- Ma, Z.; Liu, Y.; Meng, H.; Wang, X. Sparse recovery-based space-time adaptive processing with array error self-calibration. Electron. Lett. 2014, 50, 952–954. [Google Scholar] [CrossRef]
- Li, Z.; Guo, Y.; Zhang, Y.; Zhou, H.; Zheng, G. Sparse Bayesian learning based space-time adaptive processing against unknown mutual coupling for airborne radar using middle subarray. IEEE Access 2018, 7, 6094–6108. [Google Scholar] [CrossRef]
- Yang, Z.; de Lamare, R.C.; Liu, W. Sparsity-based STAP using alternating direction method with gain/phase errors. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2756–2768. [Google Scholar]
- Robey, F.C.; Fuhrmann, D.R.; Kelly, E.J.; Nitzberg, R. A CFAR adaptive matched filter detector. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 208–216. [Google Scholar] [CrossRef] [Green Version]
- Zhen, J.; Ding, Q. Calibration method of sensor location error in direction of arrival estimation for wideband signals. In Proceedings of the IEEE International Conference on Electronic Information and Communication Technology (ICEICT), Harbin, China, 20–22 August 2016; pp. 298–302. [Google Scholar]
- Guerci, J.R. Theory and application of covariance matrix tapers for robust adaptive beamforming. IEEE Trans. Signal Process. 1999, 47, 977–985. [Google Scholar] [CrossRef]
- Guerci, J.; Bergin, J. Principal components, covariance matrix tapers, and the subspace leakage problem. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 152–162. [Google Scholar] [CrossRef]
- Nathanson, F.E. Radar Design Principles, 2nd ed.; McGrawHill: New York, NY, USA, 1990. [Google Scholar]








| Parameter | Value |
|---|---|
| Bandwidth | 2.5 M |
| Wavelength | 0.3 m |
| Pulse repetition frequency | 2000 Hz |
| Platform velocity | 150 m/s |
| Platform height | 9 km |
| Element number | 8 |
| Pulse number in the first stage | 256 |
| Pulse number in the second stage | 8 |
| CNR | 40 dB |
| True | Estimated | |
|---|---|---|
| g1 | 1 | 1 |
| g2 | 0.9178 + j0.0642 | 0.9183 + j0.0644 |
| g3 | 1.1288 + j0.0461 | 1.1298 + j0.0466 |
| g4 | 0.8951 + j0.0941 | 0.8965 + j0.0944 |
| g5 | 0.9277 + j0.0649 | 0.9291 + j0.0651 |
| g6 | 0.8888 + j0.0466 | 0.8898 + j0.0469 |
| g7 | 1.0946 + j0.0951 | 1.0955 + j0.0956 |
| g8 | 0.8988 + j0.0471 | 0.8985 + j0.0471 |
| True | Estimated | |
|---|---|---|
| c1 | 1 | 1 |
| c2 | 0.1250 + j0.2165 | 0.1253 + j0.2169 |
| c3 | 0.0866 + j0.0500 | 0.0869 + j0.0498 |
| True (m) | Estimated (m) | |
|---|---|---|
| 0 | 0 | |
| −0.0041 | −0.0042 | |
| 0.004 | 0.0041 | |
| 0.0003 | 0.0002 | |
| −0.014 | −0.0139 | |
| 0.0123 | 0.0122 | |
| −0.0021 | −0.0022 | |
| −0.0135 | −0.0135 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Wang, T.; Wu, J.; Chen, J. A Two-Stage STAP Method Based on Fine Doppler Localization and Sparse Bayesian Learning in the Presence of Arbitrary Array Errors. Sensors 2022, 22, 77. https://doi.org/10.3390/s22010077
Liu K, Wang T, Wu J, Chen J. A Two-Stage STAP Method Based on Fine Doppler Localization and Sparse Bayesian Learning in the Presence of Arbitrary Array Errors. Sensors. 2022; 22(1):77. https://doi.org/10.3390/s22010077
Chicago/Turabian StyleLiu, Kun, Tong Wang, Jianxin Wu, and Jinming Chen. 2022. "A Two-Stage STAP Method Based on Fine Doppler Localization and Sparse Bayesian Learning in the Presence of Arbitrary Array Errors" Sensors 22, no. 1: 77. https://doi.org/10.3390/s22010077
APA StyleLiu, K., Wang, T., Wu, J., & Chen, J. (2022). A Two-Stage STAP Method Based on Fine Doppler Localization and Sparse Bayesian Learning in the Presence of Arbitrary Array Errors. Sensors, 22(1), 77. https://doi.org/10.3390/s22010077





