Distributed Bragg Reflectors Employed in Sensors and Filters Based on Cavity-Mode Spectral-Domain Resonances
Abstract
:1. Introduction
2. Material Characterization
3. Theoretical Analysis
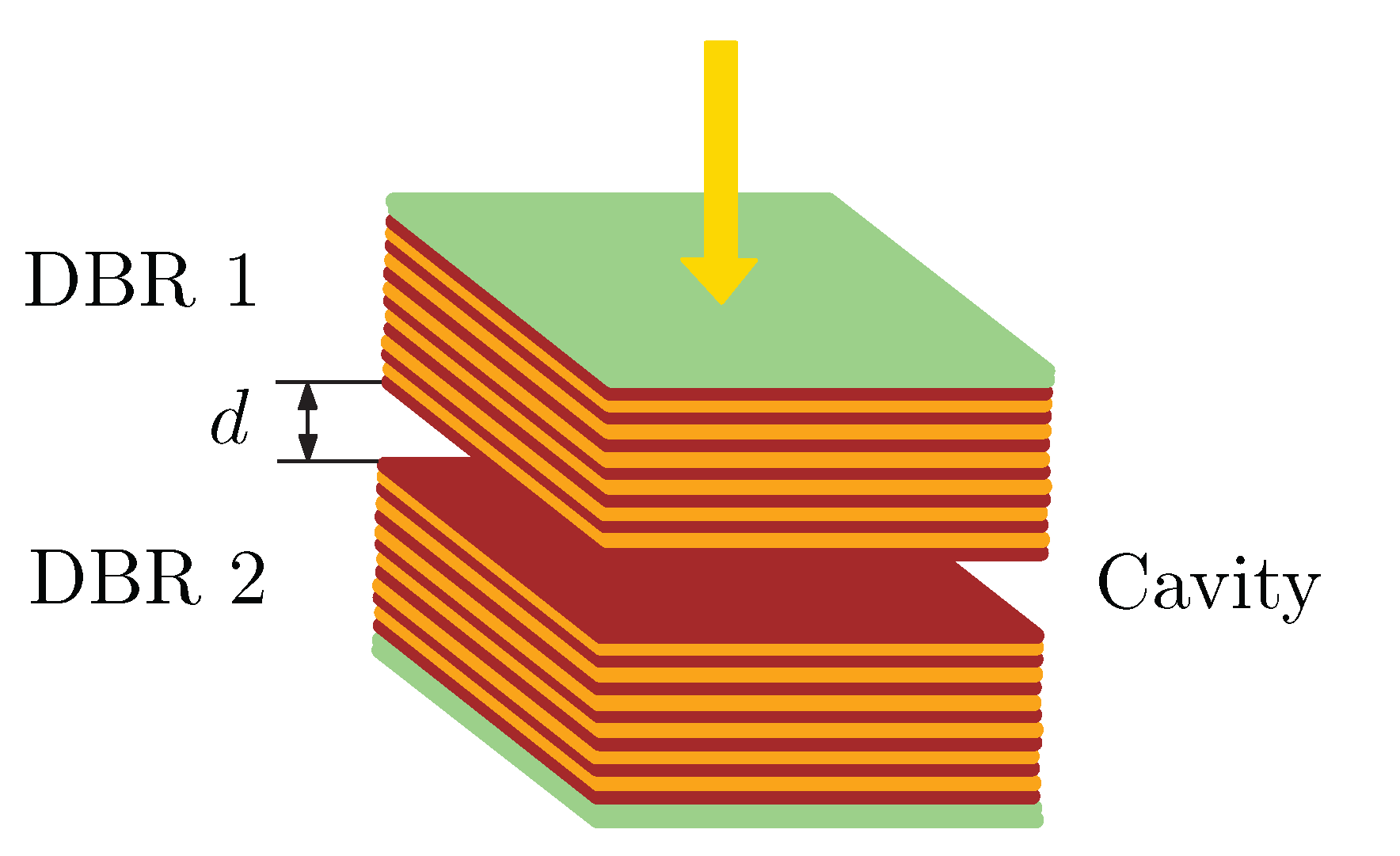
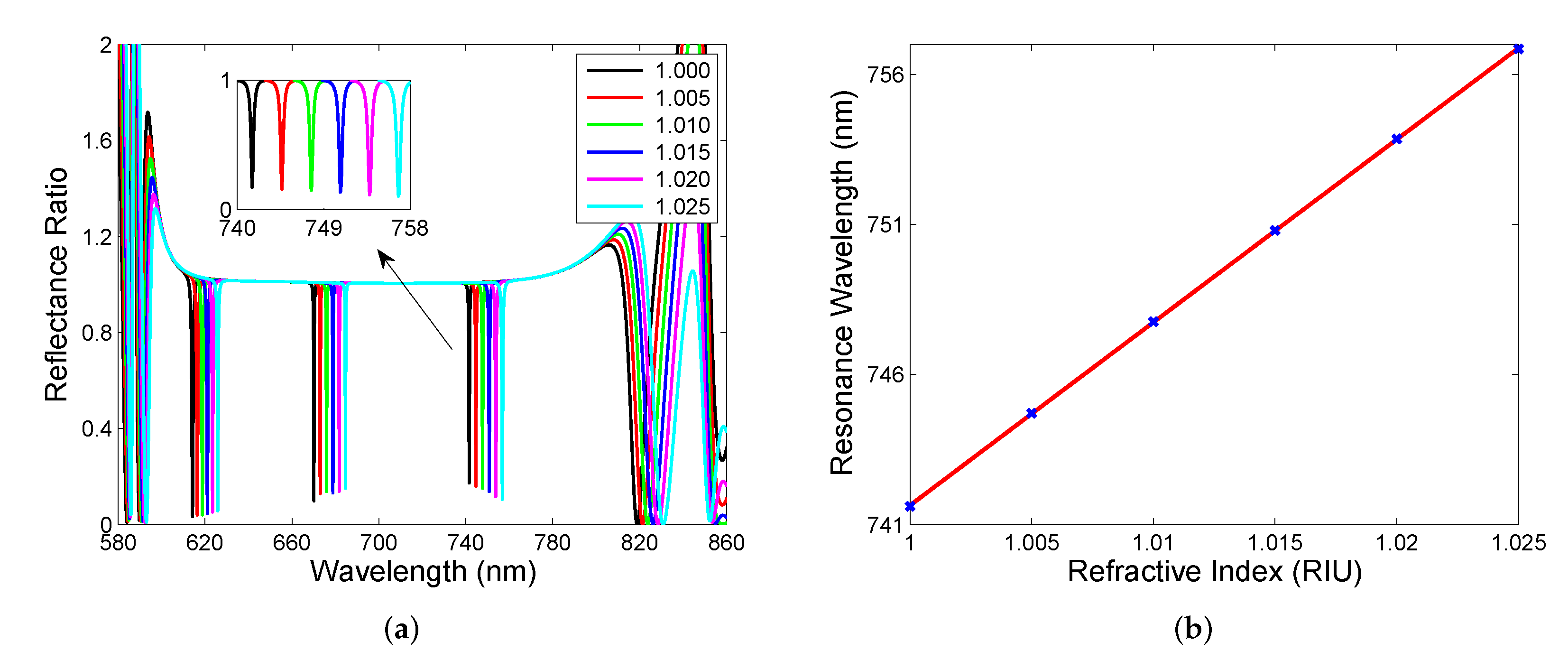
3.1. Spectral Reflectance
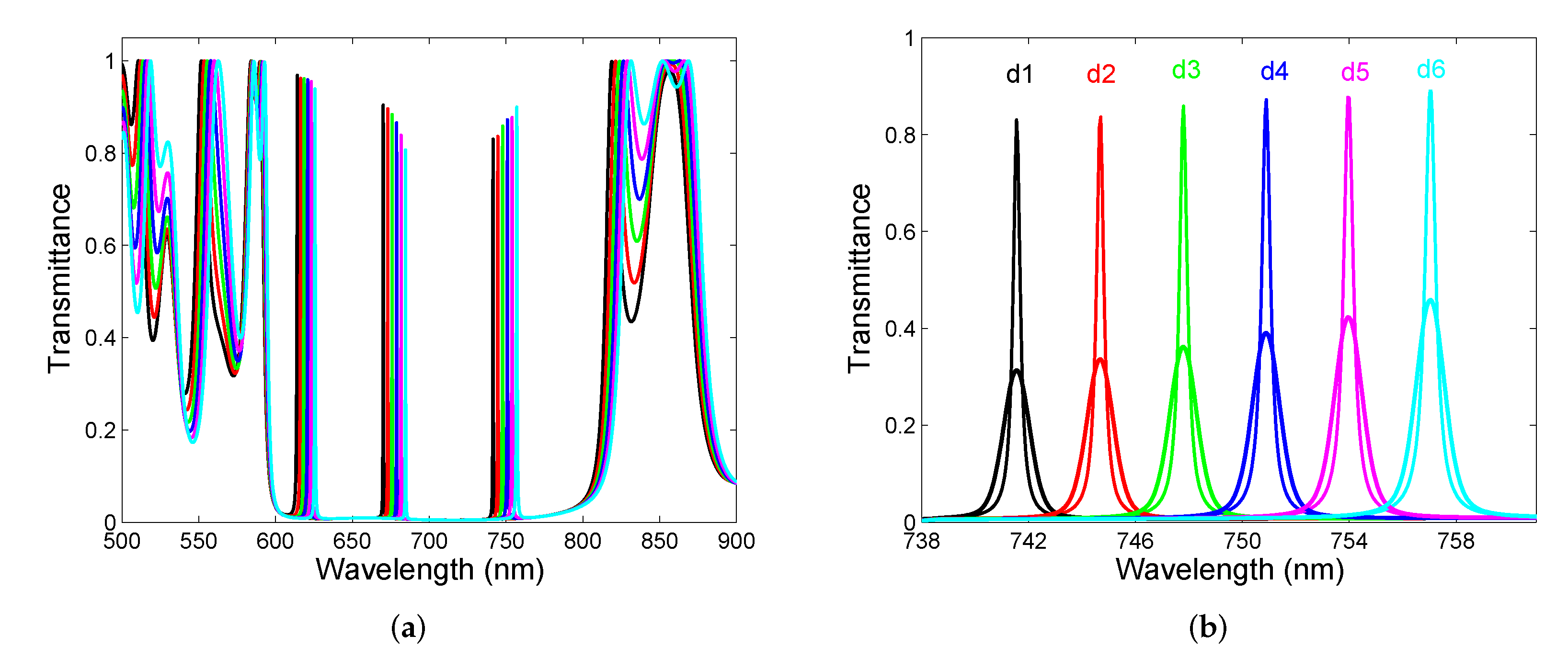
3.2. Spectral Transmittance
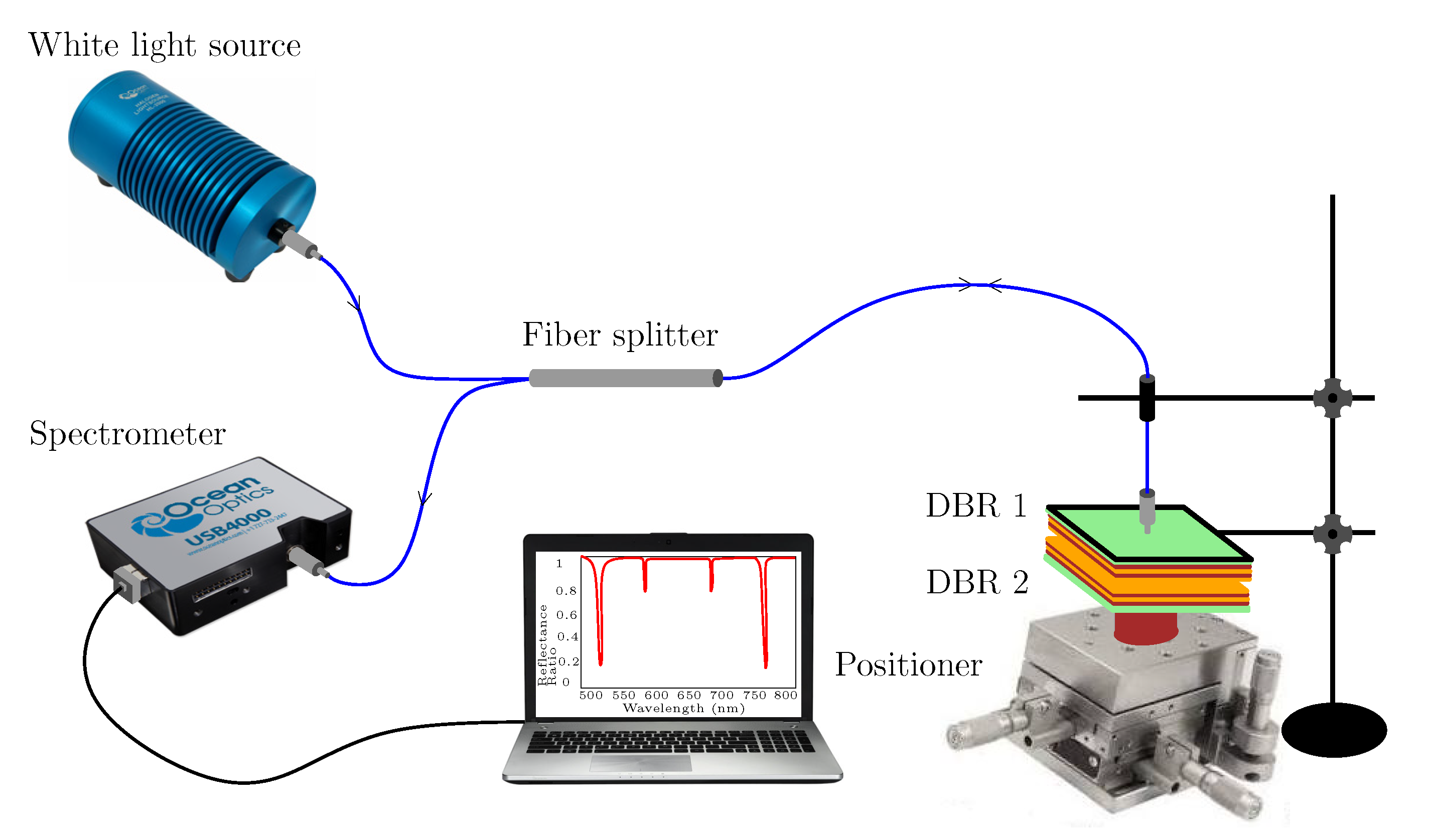
4. Experimental Setups
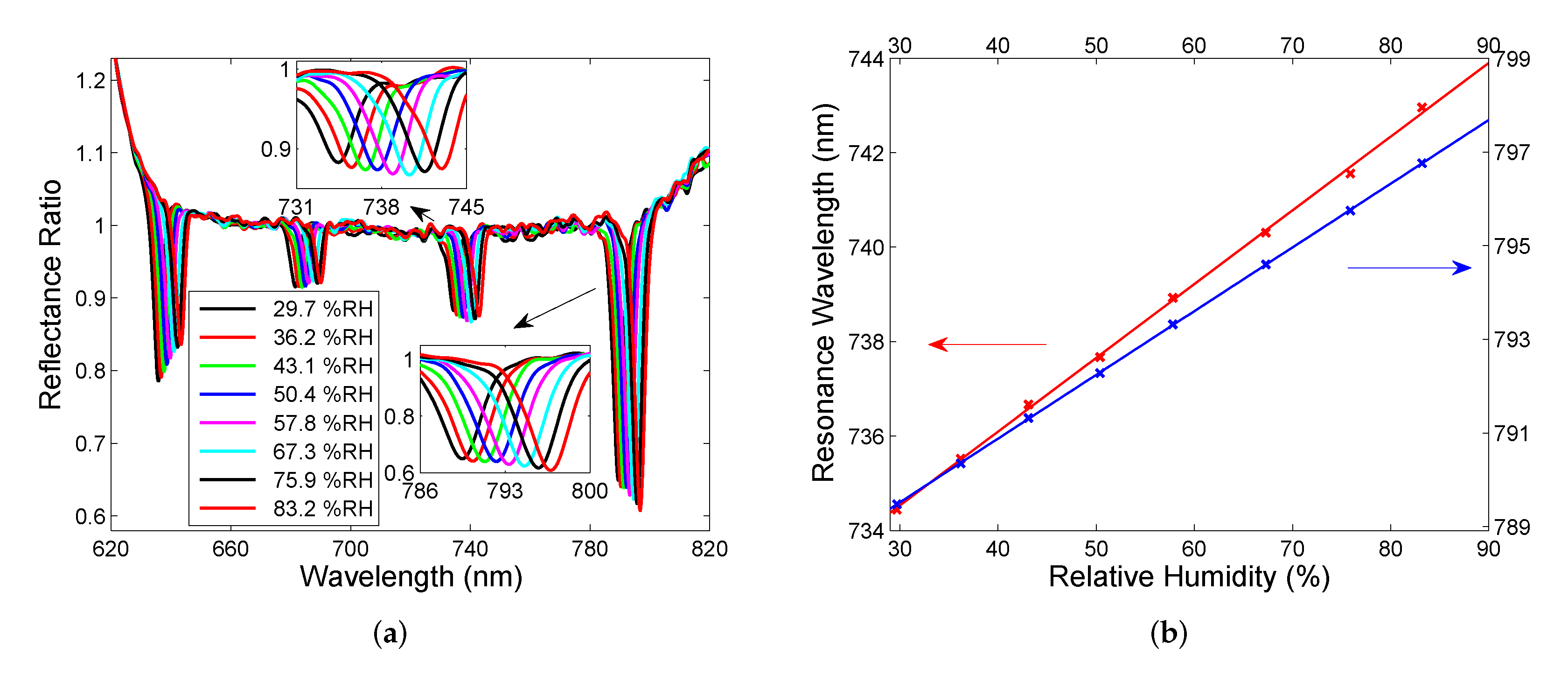
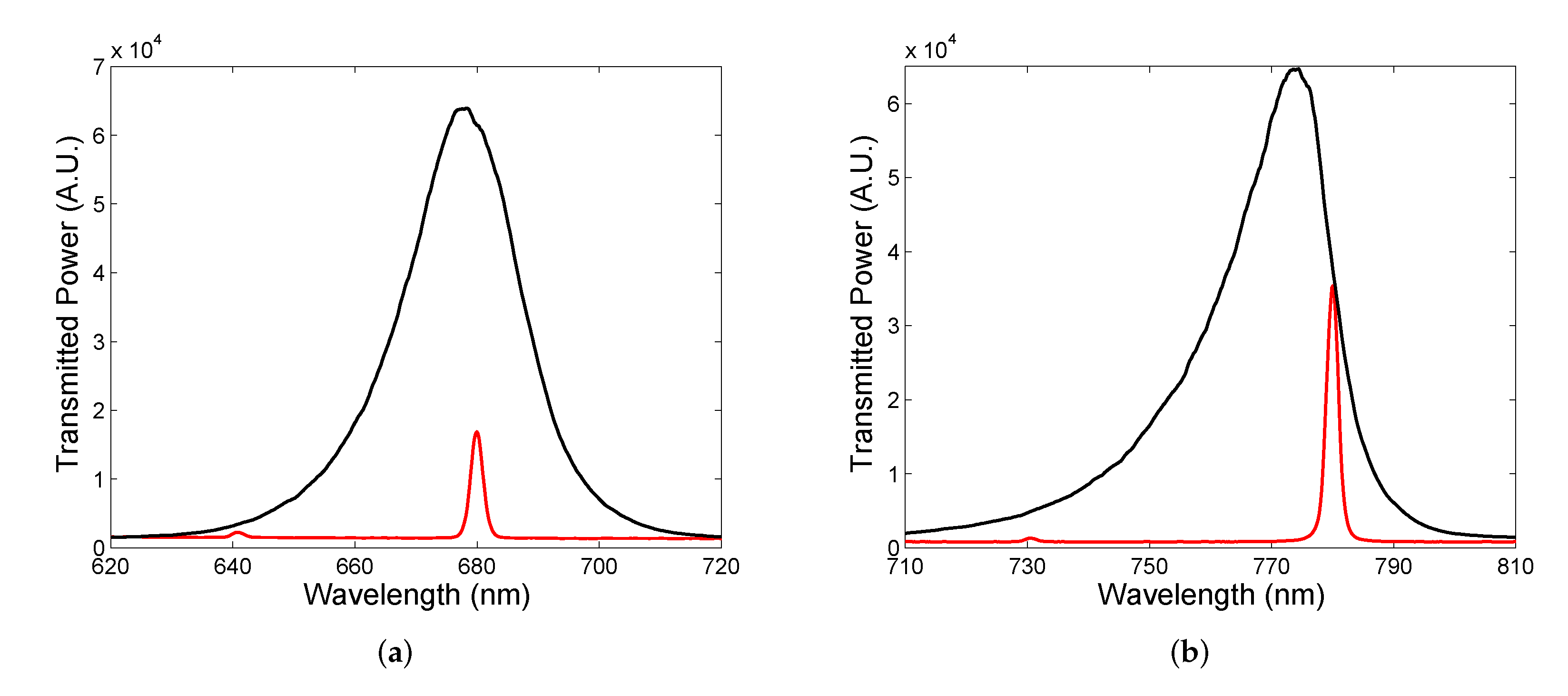
5. Experimental Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Fink, Y.; Winn, J.N.; Fan, S.; Chen, C.; Miche, J.; Joannopoulos, J.D.; Thomas, E.L. A Dielectric Omnidirectional Reflector. Science 1998, 282, 1679–1682. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, F.; Lu, G.; Guo, Z.; Jiang, H.; Xue, C.; Zheng, M.; Chen, C.; Du, G.; Chen, H. Redshift gaps in one-dimensional photonic crystals containing hyperbolic metamaterials. Phys. Rev. Appl. 2018, 10, 064022. [Google Scholar] [CrossRef]
- Villar, I.D.; Matías, I.R.; Arregui, F.J.; Claus, R.O. Analysis of one-dimensional photonic band gap structures with a liquid crystal defect towards development of fiber-optic tunable wavelength filters. Opt. Express 2003, 11, 430–436. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, R.; Ghosh, K.K.; Chakraborty, R. A novel tunable filter featuring defect mode of the TE wave from one-dimensional photonic crystals doped by magnetized plasma. Opt. Commun. 2013, 289, 75–80. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, Y.; Wen, J.; Chen, Z.; Zhang, M.; Fei, H.; Hao, Y. Tunable dual-channel filter based on the photonic crystal with air defects. Appl. Opt. 2017, 56, 5463–5469. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Cheng, Y.Z.; Wang, X.; Zhang, Y.N.; Nie, Y.; Gong, R.Z. Narrow Band Filter at 1550 nm Based on Quasi-One-Dimensional Photonic Crystal with a Mirror-Symmetric Heterostructure. Materials 2018, 11, 1099. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guillermain, E.; Lysenko, V.; Orobtchouk, R.; Benyattou, T.; Roux, S.; Pillonnet, A.; Perriat, P. Bragg surface wave device based on porous silicon and its application for sensing. Appl. Phys. Lett. 2007, 90, 241116. [Google Scholar] [CrossRef]
- Liscidini, M.; Sipe, J.E. Analysis of Bloch-surface-wave assisted diffraction-based biosensors. J. Opt. Soc. Am. B 2009, 26, 279–289. [Google Scholar] [CrossRef]
- Chang, Y.H.; Jhu, Y.Y.; Wu, C.J. Temperature dependence of defect mode in a defective photonic crystal. Opt. Commun. 2012, 285, 1501–1504. [Google Scholar] [CrossRef]
- Farmer, A.; Friedli, A.C.; Wright, S.M.; Robertson, W.M. Biosensing using surface electromagnetic waves in photonic band gap multilayers. Sens. Actuators B Chem. 2012, 173, 79–84. [Google Scholar] [CrossRef]
- Sinibaldi, A.; Rizzo, R.; Figliozzi, G.; Descrovi, E.; Danz, N.; Munzert, P.; Anopchenko, A.; Michelotti, F. A full ellipsometric approach to optical sensing with Bloch surface waves on photonic crystals. Opt. Express 2013, 21, 23331–23344. [Google Scholar] [CrossRef]
- Li, Y.; Yang, T.; Pang, Z.; Du, G.; Song, S. Phase-sensitive Bloch surface wave sensor based on variable angle spectroscopic ellipsometry. Opt. Express 2014, 22, 21403–21410. [Google Scholar] [CrossRef]
- Kong, W.; Zheng, Z.; Wan, Y.; Li, J.; Liu, J. High-sensitivity sensing based on intensity-interrogated Bloch surface wave sensors. Sens. Actuators B Chem. 2014, 193, 467–471. [Google Scholar] [CrossRef]
- Bouzidi, A.; Bria, D.; Akjouj, A.; Pennec, Y.; Djafari-Rouhani, B. A tiny gas-sensor system based on 1D photonic crystal. J. Phys. D Appl. Phys. 2015, 48, 495102. [Google Scholar] [CrossRef]
- Kang, X.B.; Wen, L.; Wang, Z.G. Design of guided Bloch surface wave resonance bio-sensors with high sensitivity. Opt. Commun. 2017, 383, 531–536. [Google Scholar] [CrossRef]
- Gryga, M.; Vala, D.; Kolejak, P.; Gembalova, L.; Ciprian, D.; Hlubina, P. One-dimensional photonic crystal for Bloch surface waves and radiation modes based sensing. Opt. Mater. Express 2019, 9, 4009–4022. [Google Scholar] [CrossRef]
- Goyal, A.K.; Pal, S. Design analysis of Bloch surface wave based sensor for haemoglobin concentration measurement. Appl. Nanosci. 2020, 10, 3639–3647. [Google Scholar] [CrossRef]
- Gryga, M.; Ciprian, D.; Gembalova, L.; Hlubina, P. Sensing based on Bloch surface wave and self-referenced guided mode resonances employing a one-dimensional photonic crystal. Opt. Express 2021, 29, 12996–13010. [Google Scholar] [CrossRef]
- Kaliteevski, M.; Iorsh, I.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Kavokin, A.V.; Shelykh, I.A. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys. Rev. B 2007, 76, 165415. [Google Scholar] [CrossRef] [Green Version]
- Auguié, B.; Fuertes, M.C.; Angelomié, P.C.; Abdala, N.L.; Illia, G.J.A.A.S.; Fainstein, A. Tamm Plasmon Resonance in Mesoporous Multilayers: Toward a Sensing Application. ACS Photonics 2014, 9, 775–780. [Google Scholar] [CrossRef]
- Kumar, S.; Shukla, M.K.; Maji, P.S.; Das, R. Self-referenced refractive index sensing with hybrid-Tamm-plasmon-polariton modes in subwavelength analyte layers. J. Phys. D Appl. Phys. 2017, 50, 375106. [Google Scholar] [CrossRef]
- Maji, P.S.; Shukla, M.K.; Das, R. Blood component detection based on miniaturized self-referenced hybrid Tamm-plasmon-polariton sensor. Sens. Actuators B Chem. 2018, 255, 729–734. [Google Scholar] [CrossRef]
- Zaky, Z.A.; Ahmed, A.M.; Shalaby, A.S.; Aly, A.H. Refractive index gas sensor based on the Tamm state in a onedimensional photonic crystal: Theoretical optimisation. Sci. Rep. 2020, 10, 9736. [Google Scholar] [CrossRef]
- Jena, S.; Tokas, R.B.; Thakur, S.; Udupa, D.V. Rabi-like splitting and refractive index sensing with hybrid Tamm plasmon-cavity modes. J. Phys. D Appl. Phys. 2022, 55, 175104. [Google Scholar] [CrossRef]
- Xu, H.; Wu, P.; Zhu, C.; Elbaza, A.; Gu, Z.Z. Photonic crystal for gas sensing. J. Mater. Chem. C 2013, 1, 6087–6098. [Google Scholar] [CrossRef]
- Chen, Y.H.; Shi, W.H.; Feng, L.; Xu, X.Y.; Shang-Guan, M.Y. Study on simultaneous sensing of gas concentration and temperature in one-dimensional photonic crystal. Superlattices Microstruct. 2019, 131, 53–58. [Google Scholar] [CrossRef]
- Surdo, S.; Barillaro, G. On the performance of label-free biosensors based on vertical one-dimensional photonic crystal resonant cavities. Opt. Express 2015, 23, 9192–9201. [Google Scholar] [CrossRef] [Green Version]
- El-Khozondar, H.J.; Mahalakshmi, P.; El-Khozondar, R.J.; Ramanujam, N.R.; Amiri, I.S.; Yupapin, P. Design of one dimensional refractive index sensor using ternary photonic crystal waveguide for plasma blood samples applications. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 111, 173120. [Google Scholar] [CrossRef]
- Hao, J.J.; Xie, X.; Gu, K.D.; Du, W.C.; Liu, Y.J.; Yang, H.W. Research on Photonic Crystal-Based Biosensor for Detection of Escherichia coli Colony. Plasmonics 2019, 14, 1919–1928. [Google Scholar] [CrossRef]
- Goyal, A.K. Design Analysis of One-Dimensional Photonic Crystal Based Structure for Hemoglobin Concentration Measurement. Prog. Electromagn. Res. M 2020, 97, 77–86. [Google Scholar] [CrossRef]
- Bijalwan, A.; Singh, B.K.; Rastogi, V. Analysis of one-dimensional photonic crystal based sensor for detection of blood plasma and cancer cells. Optik 2021, 226, 165994. [Google Scholar] [CrossRef]
- Ghasemi, F.; Razi, S. Novel Photonic Bio-Chip Sensor Based on Strained Graphene Sheets for Blood Cell Sorting. Molecules 2021, 26, 5585. [Google Scholar] [CrossRef] [PubMed]
- Sinibaldi, A.; Danz, N.; Descrovi, E.; Munzert, P.; Schulz, U.; Sonntag, F.; Dominici, L.; Michelotti, F. Direct comparison of the performance of Bloch surface wave and surface plasmon polariton sensors. Sens. Actuators B Chem. 2012, 174, 292–298. [Google Scholar] [CrossRef]
- Gryga, M.; Ciprian, D.; Hlubina, P. Bloch surface wave resonance based sensors as an alternative to surface plasmon resonance sensors. Sensors 2020, 20, 5119. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, D.; Wang, P.; Ming, H.; Lakowicz, J.R. Strong Polarization Transformation of Bloch Surface Waves. Phys. Rev. Appl. 2018, 9, 024008. [Google Scholar] [CrossRef] [Green Version]
- Lahijani, B.V.; Descharmes, N.; Barbey, R.; Osowiecki, G.D.; Wittwer, V.J.; Razskazovskaya, O.; Südmeyer, T.; Herzig, H.P. Centimeter-Scale Propagation of Optical Surface Waves at Visible Wavelengths. Adv. Opt. Mater. 2022, 10, 2102854. [Google Scholar]
- Mejía-Salazar, J.R.; Oliveira, O.N., Jr. Plasmonic Biosensing: Focus review. Chem. Rev. 2018, 118, 10617–10625. [Google Scholar] [CrossRef]
- Xu, Y.; Bai, P.; Zhou, X.; Akimov, Y.; Png, C.E.; Ang, L.K.; Knoll, W.; Wu, L. Optical Refractive Index Sensors with Plasmonic and Photonic Structures: Promising and Inconvenient Truth. Adv. Opt. Mater. 2019, 7, 1801433. [Google Scholar] [CrossRef]
- Ahmadivand, A.; Gerislioglu, B.; Ahuja, R.; Mishra, Y.K. Terahertz plasmonics: The rise of toroidal metadevices towards immunobiosensings. Mater. Today 2020, 32, 108–130. [Google Scholar] [CrossRef]
- Bahramipanah, M.; Dutta-Gupta, S.; Abasahl, B.; Martin, O.J.F. Cavity-Coupled Plasmonic Device with Enhanced Sensitivity and Figure-of-Merit. ACS Nano 2015, 9, 7621–7633. [Google Scholar] [CrossRef]
- Zhang, X.L.; Song, J.F.; Li, X.B.; Feng, J.; Sun, H.B. Optical Tamm states enhanced broad-band absorption of organic solar cells. Appl. Phys. Lett. 2012, 101, 243901. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Wu, K.; Giannini, V.; Li, X. Planar Hot-Electron Photodetection with Tamm Plasmons. ACS Nano 2017, 11, 1719–1727. [Google Scholar] [CrossRef] [Green Version]
- Mitra, S.; Biswas, T.; Chattopadhyay, R.; Ghosh, J.; Bysakh, S.; Bhadra, S.K. Safe and simple detection of sparse hydrogen by Pd-Au alloy/air based 1D photonic crystal sensor. J. Appl. Phys. Lett. 2016, 120, 173120. [Google Scholar] [CrossRef]
- Domash, L.; Wu, M.; Nemchuk, N.; Ma, E. Tunable and switchable multiple-cavity thin film filters. J. Light. Technol. 2004, 22, 126–135. [Google Scholar] [CrossRef]
- Greuter, L.; Starosielec, S.; Najer, D.; Ludwig, A.; Duempelmann, L.; Rohner, D.; Warburton, R.J. A small mode volume tunable microcavity: Development and characterization. Appl. Phys. Lett. 2014, 105, 121105. [Google Scholar] [CrossRef] [Green Version]
- Dai, J.; Gao, W.; Liu, B.; Cao, X.; Tao, T.; Xie, Z.; Zhao, H.; Chen, D.; Ping, H.; Zhang, R. Design and fabrication of UV band-pass filters based on SiO2/Si3N4 dielectric distributed bragg reflectors. Appl. Surf. Sci. 2016, 364, 866–891. [Google Scholar] [CrossRef]
- Fang, C.; Dai, B.; Xu, Q.; Wang, Q.; Zhang, D. Optofluidic tunable linear narrow-band filter based on Bragg nanocavity. IEEE Photonics J. 2017, 9, 7801608. [Google Scholar] [CrossRef]
- Peng, J.; Wang, W.; Qu, Y.; Sun, T.; Lv, D.; Dai, J.; Yang, M. Thin films based one-dimensional photonic crystal for humidity detection. Sens. Actuators A Phys. 2017, 263, 209–215. [Google Scholar] [CrossRef]
- Sayginer, O.; Chiasera, A.; Zur, L.; Varas, S.; Tran, L.T.N.; Armellini, C.; Ferrari, M.; Bursi, O.S. Fabrication, modelling and assessment of hybrid 1-D elastic Fabry Perot microcavity for mechanical sensing applications. Ceram. Int. 2019, 45, 7785–7788. [Google Scholar] [CrossRef]
- Rho, D.; Breaux, C.; Kim, S. Label-Free Optical Resonator-Based Biosensors. Sensors 2020, 20, 5901. [Google Scholar] [CrossRef]
- Kaňok, R.; Hlubina, P.; Gembalová, L.; Ciprian, D. Efficient optical sensing based on phase shift of waves supported by a one-dimensional photonic crystal. Sensors 2021, 21, 6535. [Google Scholar] [CrossRef]
- Pettersson, L.A.A.; Roman, L.S.; Inganäs, O. Modeling photocurrent action spectra of photovoltaic devices based on organic thin films. J. Appl. Phys. 1999, 86, 487–496. [Google Scholar] [CrossRef]
- Hlubina, P. Dispersive spectral-domain two-beam interference analysed by a fibre-optic spectrometer. J. Mod. Opt. 2004, 51, 537–547. [Google Scholar] [CrossRef]
- Ghulinyan, M.; Oton, C.J.; Bonetti, G.; Gaburro, Z.; Pavesi, L. Free-standing porous silicon single and multiple optical cavities. J. Appl. Phys. 2003, 93, 9724–9729. [Google Scholar] [CrossRef]
- Hlubina, P.; Gryga, M.; Ciprian, D.; Pokorny, P.; Gembalova, L.; Sobota, J. High performance liquid analyte sensing based on Bloch surface wave resonances in the spectral domain. Opt. Laser Technol. 2022, 145, 107492. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gryga, M.; Ciprian, D.; Hlubina, P. Distributed Bragg Reflectors Employed in Sensors and Filters Based on Cavity-Mode Spectral-Domain Resonances. Sensors 2022, 22, 3627. https://doi.org/10.3390/s22103627
Gryga M, Ciprian D, Hlubina P. Distributed Bragg Reflectors Employed in Sensors and Filters Based on Cavity-Mode Spectral-Domain Resonances. Sensors. 2022; 22(10):3627. https://doi.org/10.3390/s22103627
Chicago/Turabian StyleGryga, Michal, Dalibor Ciprian, and Petr Hlubina. 2022. "Distributed Bragg Reflectors Employed in Sensors and Filters Based on Cavity-Mode Spectral-Domain Resonances" Sensors 22, no. 10: 3627. https://doi.org/10.3390/s22103627





