Information Theory Solution Approach to the Air Pollution Sensor Location–Allocation Problem
Abstract
:1. Introduction
2. Materials and Methods
2.1. Simulation Study
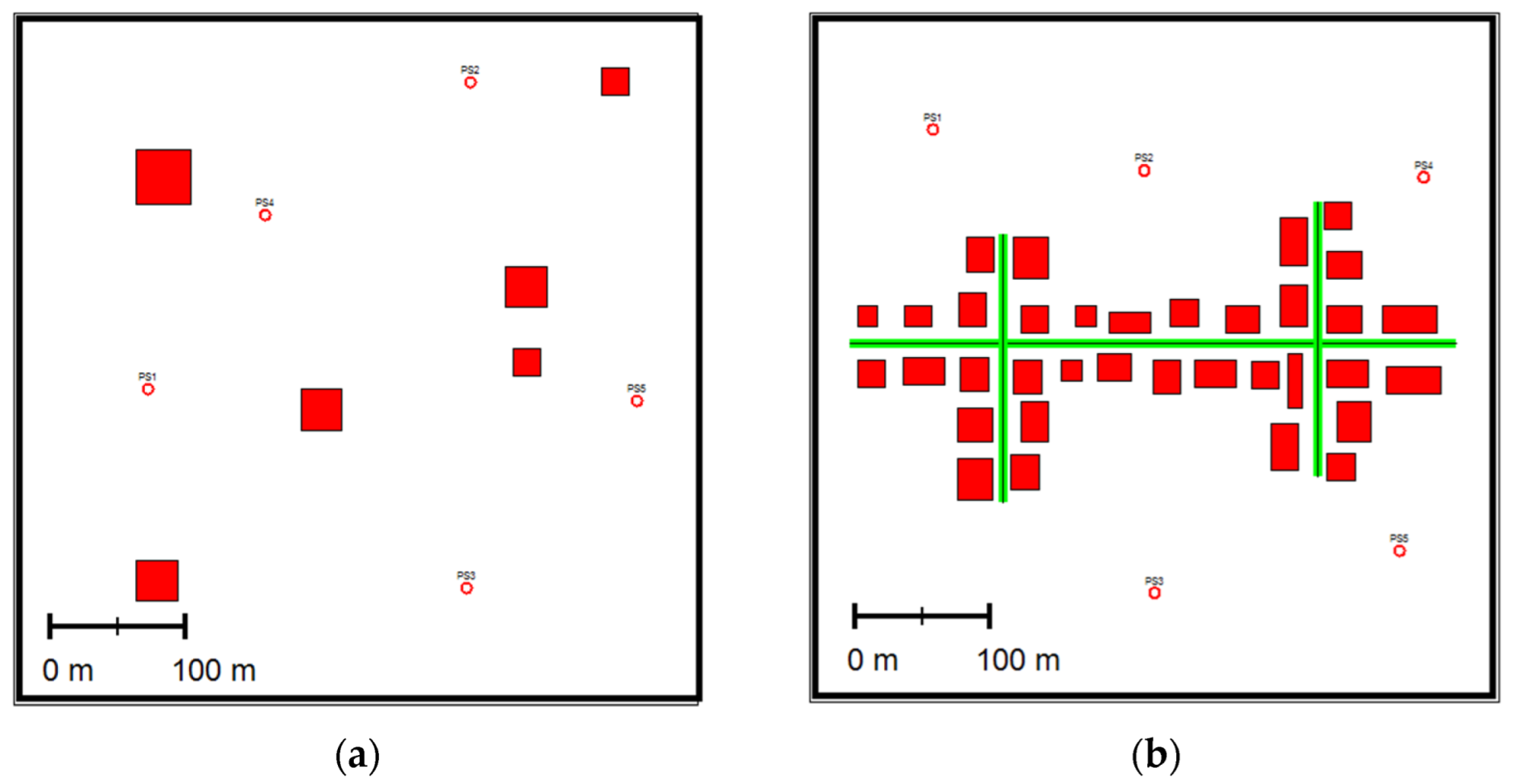
- A Small NeighBorHood, SNBH, consists of six buildings of different sizes and five-point sources emitting at different rates.
- A Central Business District, CBD, consists of 35 buildings, three-line sources (i.e., roads), and five-point sources. was emitted from the point sources and the roads at different rates. Figure 1 depicts the two computer-generated scenarios.
2.2. System Overview
2.3. Algorithmic Approach
| Algorithm 1: Placing sensors with the highest DM score and the lowest correlation |
|
2.4. Deployment Evaluation
2.4.1. Formulation
2.4.2. Source Term Estimation
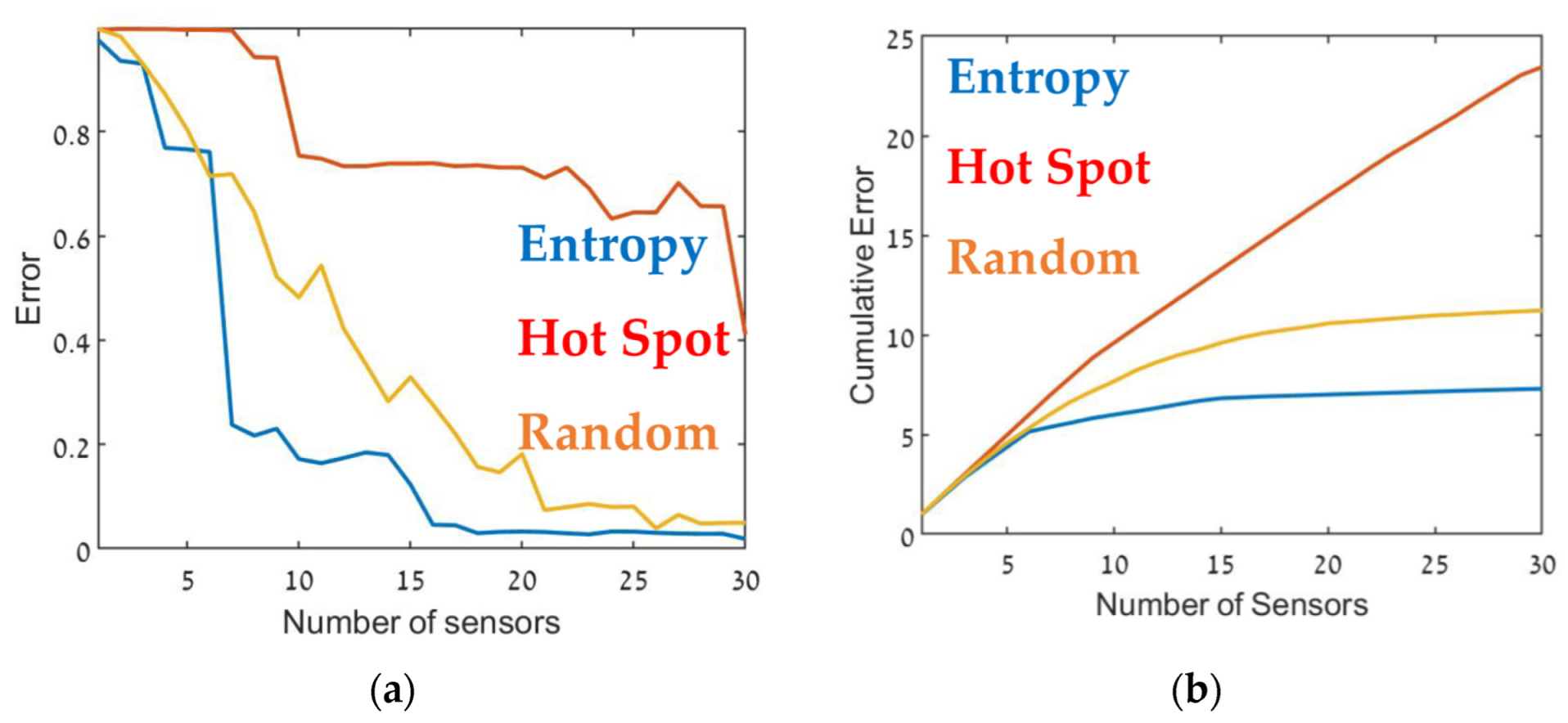
2.4.3. Comparison of Deployment Methods
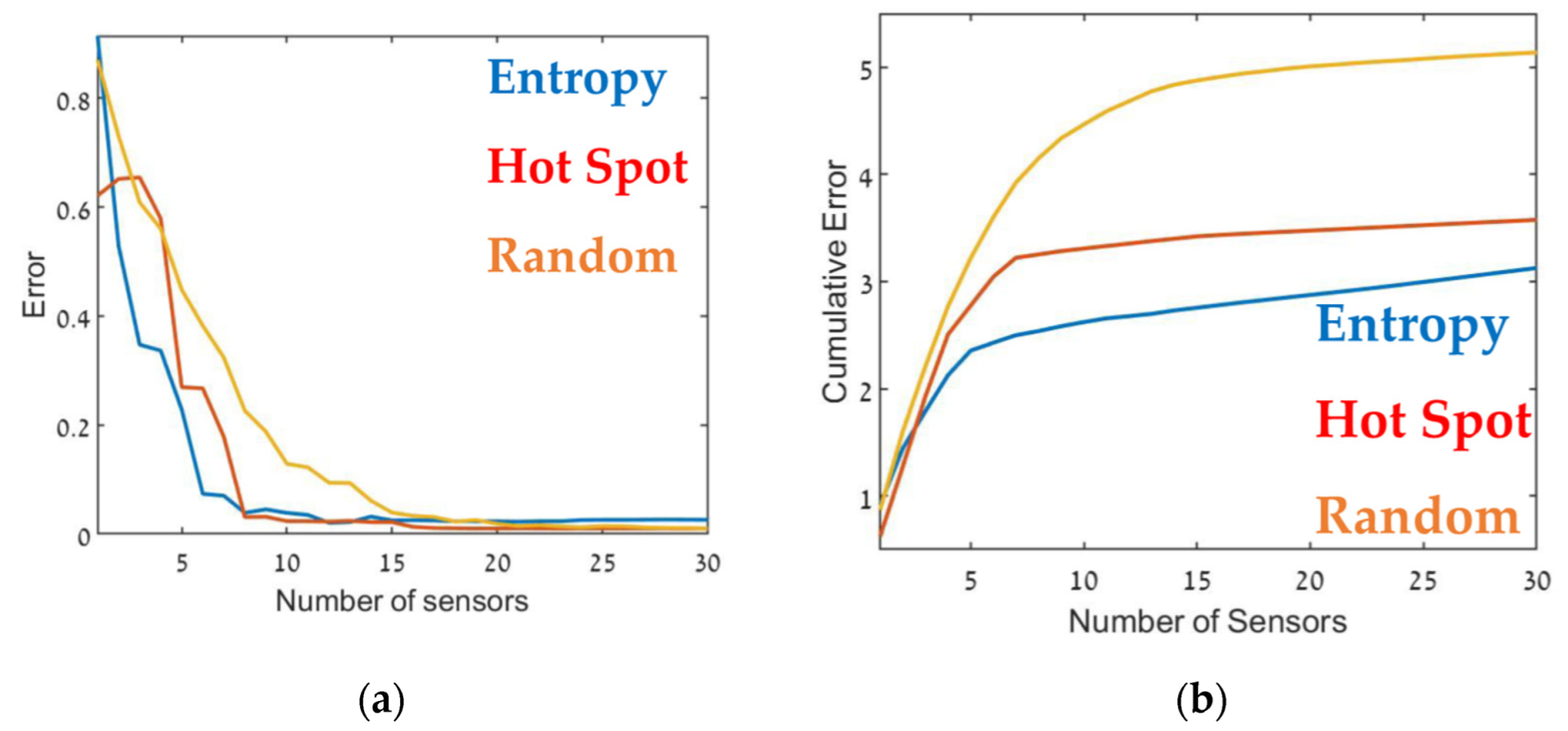
3. Results and Discussion
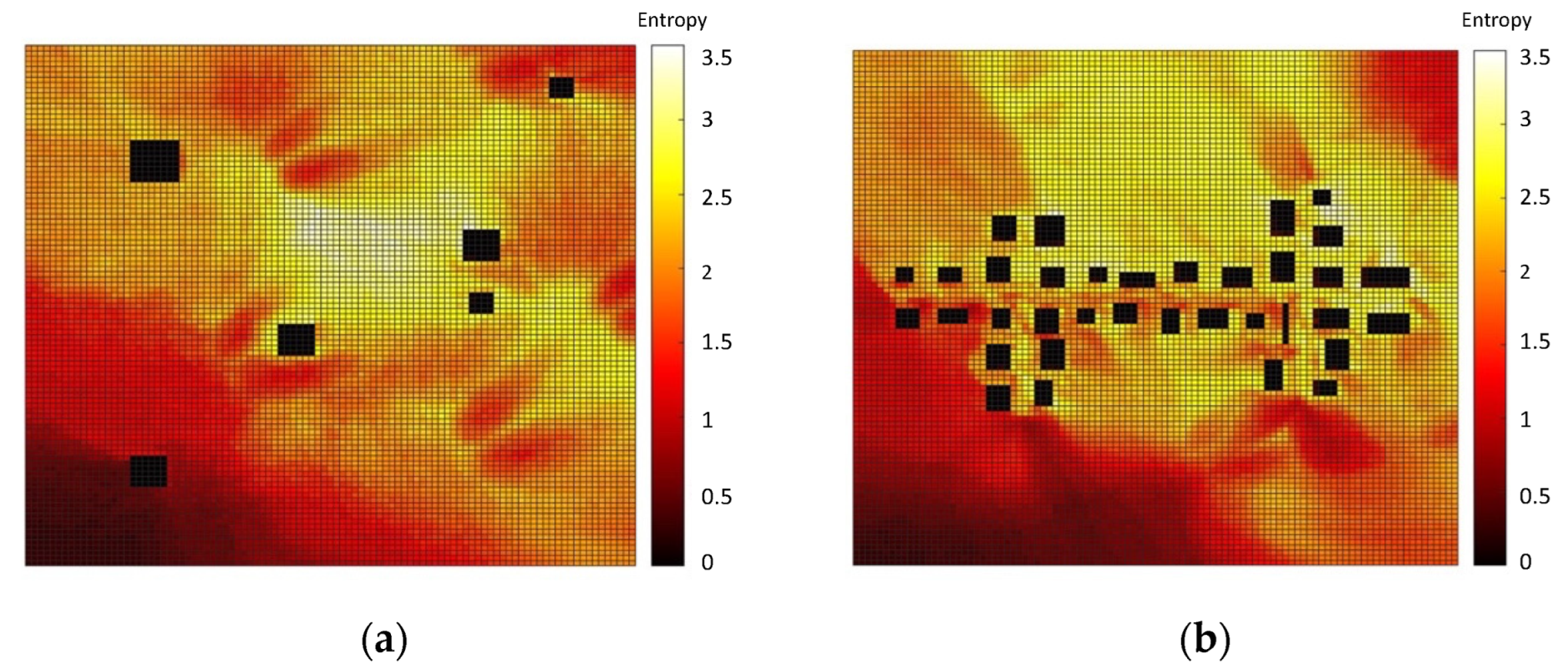
3.1. Dense Pollution Maps
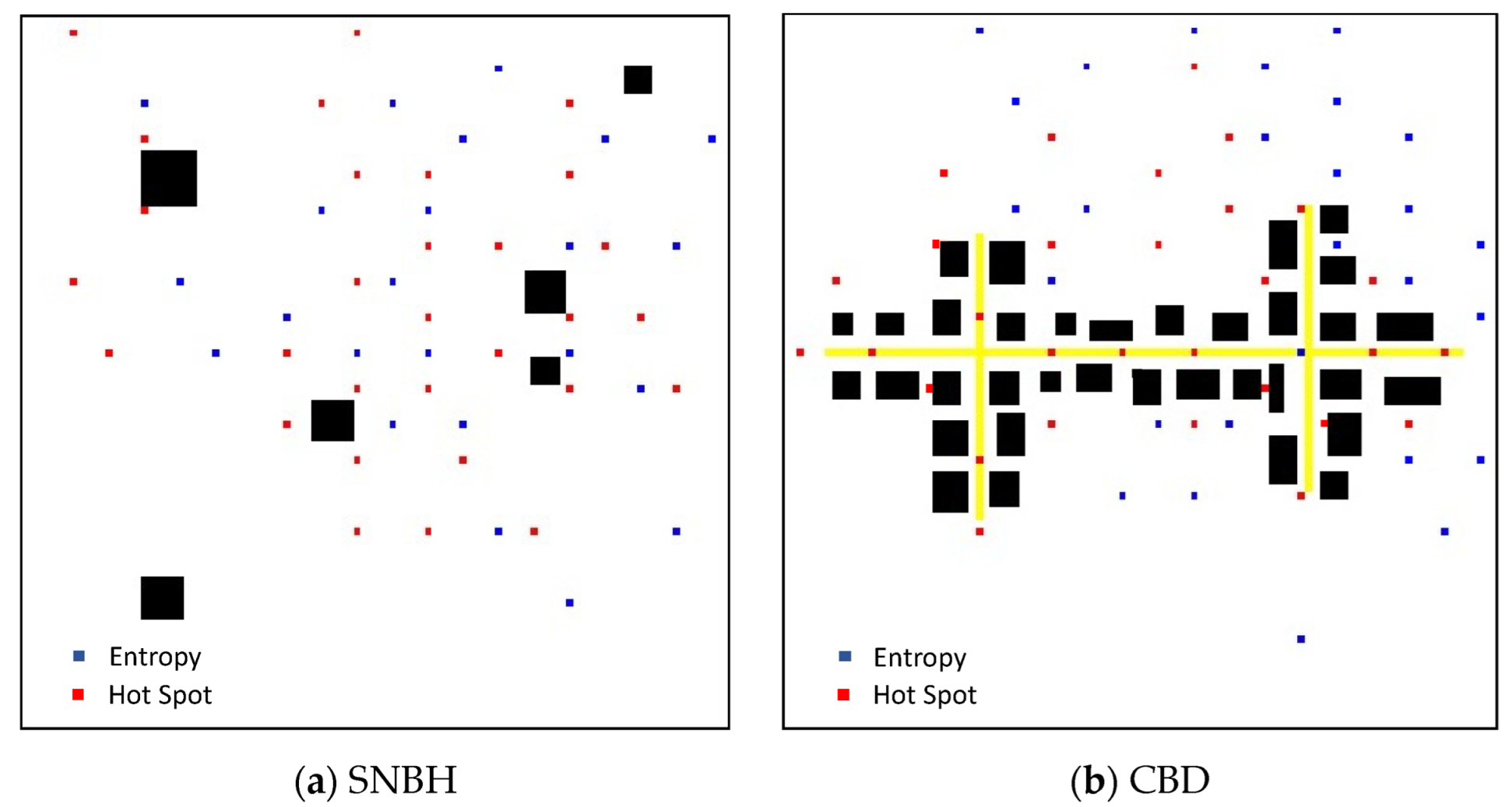
3.2. Decision Matrix
3.3. Sensor Placement
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smith, K.R.; Bruce, N.; Balakrishnan, K.; Adair-Rohani, H.; Balmes, J.; Chafe, Z.; Dherani, M.; Hosgood, H.D.; Mehta, S.; Pope, D.; et al. Millions Dead: How Do We Know and What Does It Mean? Methods Used in the Comparative Risk Assessment of Household Air Pollution. Annu. Rev. Public Health 2014, 35, 185–206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- World Bank. The Cost of Air Pollution; World Bank: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Voegele, J.; Kemper, K.; Bucknall, J.; Bosquet, B.; Blarel, B.; Shuker, I.; Christian, A.P. The Global Health Cost of Ambient PM2.5 Air Pollution; World Bank: Washington, DC, USA, 2020. [Google Scholar]
- Moltchanov, S.; Levy, I.; Etzion, Y.; Lerner, U.; Broday, D.M.D.M.; Fishbain, B. On the feasibility of measuring urban air pollution by wireless distributed sensor networks. Sci. Total Environ. 2015, 502, 537–547. [Google Scholar] [CrossRef] [PubMed]
- Fishbain, B.; Lerner, U.; Castell, N.; Cole-Hunter, T.; Popoola, O.; Broday, D.; Iñiguez, T.M.; Nieuwenhuijsen, M.; Jovasevic-Stojanovic, M.; Topalovic, D.; et al. An evaluation tool kit of air quality micro-sensing units. Sci. Total Environ. 2017, 575, 639–648. [Google Scholar] [CrossRef]
- Woo, J.H.; An, S.M.; Hong, K.; Kim, J.J.; Lim, S.B.; Kim, H.S.; Eum, J.H. Integration of CFD-Based Virtual Sensors to A Ubiquitous Sensor Network to Support Micro-Scale Air Quality Management. J. Environ. Inform. 2016, 27, 85–97. [Google Scholar] [CrossRef] [Green Version]
- Becker, T.; Mühlberger, S.; Braunmühl, C.B.; Müller, G.; Ziemann, T.; Hechtenberg, K.V. Air pollution monitoring using tin-oxide-based microreactor systems. Sens. Actuators B Chem. 2000, 69, 108–119. [Google Scholar] [CrossRef]
- Barrenetxea, G.; Ingelrest, F.; Schaefer, G.; Vetterli, M. The hitchhiker’s guide to successful wireless sensor network deployments. In Proceedings of the 6th ACM Conference on Embedded Network Sensor Systems, Raleigh, NC, USA, 5–7 November 2008; pp. 43–56. [Google Scholar] [CrossRef] [Green Version]
- Cooper, L. Location-Allocation Problems. Oper. Res. 1963, 11, 331–343. [Google Scholar] [CrossRef]
- Kanaroglou, P.S.; Jerrett, M.; Morrison, J.; Beckerman, B.; Arain, M.A.; Gilbert, N.; Brook, J.R. Establishing an air pollution monitoring network for intra-urban population exposure assessment: A location-allocation approach. Atmos. Environ. 2005, 39, 2399–2409. [Google Scholar] [CrossRef]
- Lerner, U.; Hirshfeld, O.; Fishbasin, B. Optimal deployment of a heterogeneous air quality sensor network. J. Environ. Inform. 2019, 34, 99–107. [Google Scholar] [CrossRef] [Green Version]
- Kendler, S.; Nebenzal, A.; Gold, D.; Reed, P.M.; Fishbain, B. The effects of air pollution sources/sensor array configurations on the likelihood of obtaining accurate source term estimations. Atmos. Environ. 2020, 246, 117754. [Google Scholar] [CrossRef]
- Perelman, L.S.; Abbas, W.; Koutsoukos, X.; Amin, S. Sensor placement for fault location identification in water networks: A minimum test cover approach. Automatica 2016, 72, 166–176. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Schwartz, R.; Salomons, E.; Ostfeld, A.; Poor, H.V. New formulation and optimization methods for water sensor placement. Environ. Model. Softw. 2016, 76, 128–136. [Google Scholar] [CrossRef]
- Sankary, N.; Ostfeld, A. Multiobjective Optimization of Inline Mobile and Fixed Wireless Sensor Networks under Conditions of Demand Uncertainty. J. Water Resour. Plan. Manag. 2018, 144, 04018043. Available online: https://ascelibrary.org/doi/abs/10.1061/%28ASCE%29WR.1943-5452.0000930 (accessed on 29 December 2021). [CrossRef]
- Li, D.-S.; Li, H.-N. The state of the art of sensor placement methods in structural health monitoring. Proc. SPIE 2006, 6174, 1217–1227. [Google Scholar]
- Yoshida, I.; Tasaki, Y.; Tomizawa, Y. Optimal Placement of Sampling Locations for Identification of a Two-Dimensional Space; Taylor & Francis: Abingdon, UK, 2021. [Google Scholar]
- Zou, B.; Zheng, Z.; Wan, N.; Qiu, Y.; Wilson, J. An optimized spatial proximity model for fine particulate matter air pollution exposure assessment in areas of sparse monitoring. Int. J. Geogr. Inf. Sci. 2016, 30, 727–747. [Google Scholar] [CrossRef]
- Feng, Q.; Peng, D.; Gu, Y. Research of regularization techniques for SAR target recognition using deep CNN models. In Proceedings of the Tenth International Conference on Graphics and Image Processing (ICGIP 2018), Chengdu, China, 6 May 2019; p. 5. [Google Scholar] [CrossRef]
- Alsahli, M.; Al-Harbi, M. Allocating optimum sites for air quality monitoring stations using GIS suitability analysis. Urban Clim. 2018, 24, 875–886. [Google Scholar] [CrossRef]
- Walsh, S.J.; Lightfoot, D.R.; Butler, D.R. Recognition and assessment of error in geographic information systems. Photogramm. Eng. Remote Sens. 1987, 53, 1423–1430. Available online: https://www.asprs.org/wp-content/uploads/pers/1987journal/oct/1987_oct_1423-1430.pdf (accessed on 25 December 2021).
- Al-Karaki, J.; Gawanmeh, A. The Optimal Deployment, Coverage, and Connectivity Problems in Wireless Sensor Networks: Revisited. IEEE Access 2017, 5, 18051–18065. [Google Scholar] [CrossRef]
- Boubrima, A.; Matigot, F.; Bechkit, W.; Rivano, H.; Ruas, A. Optimal Deployment of Wireless Sensor Networks for Air Pollution Monitoring. In Proceedings of the 2015 24th International Conference on Computer Communication and Networks (ICCCN), Las Vegas, NV, USA, 3–6 August 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Boubrima, A.; Bechkit, W.; Rivano, H. A new WSN deployment approach for air pollution monitoring. In Proceedings of the 2017 14th IEEE Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 8–11 January 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 455–460. [Google Scholar]
- Boubrima, A.; Bechkit, W.; Rivano, H. Optimal WSN Deployment Models for Air Pollution Monitoring. IEEE Trans. Wirel. Commun. 2017, 16, 2723–2735. [Google Scholar] [CrossRef] [Green Version]
- Benis, K.Z.; Fatehifar, E.; Shafiei, S.; Nahr, F.K.; Purfarhadi, Y. Design of a sensitive air quality monitoring network using an integrated optimization approach. Stoch. Environ. Res. Risk Assess. 2016, 30, 779–793. [Google Scholar] [CrossRef]
- Al-Adwani, S.; Elkamel, A.; Duever, T.; Yetilmezsoy, K.; Abdul-Wahab, S. A Surrogate-Based Optimization Methodology for the Optimal Design of an Air Quality Monitoring Network. Can. J. Chem. Eng. 2015, 93, 1176–1187. [Google Scholar] [CrossRef]
- Hassin, R.; Levin, A. A Better-Than-Greedy Approximation Algorithm for the Minimum Set Cover Problem. SIAM J. Comput. 2006, 35, 189–200. Available online: http://www.siam.org/journals/sicomp/35-1/44475.html (accessed on 29 December 2021). [CrossRef] [Green Version]
- Kumar, N.; Nixon, V.; Sinha, K.; Jiang, X.; Ziegenhorn, S.; Peters, T. An Optimal Spatial Configuration of Sample Sites for Air Pollution Monitoring. J. Air Waste Manag. Assoc. 2009, 59, 1308–1316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berchet, A.; Zink, K.; Oettl, D.; Brunner, J.; Emmenegger, L.; Brunner, D. Evaluation of high-resolution GRAMM-GRAL (v15.12/v14.8) NOx simulations over the city of Zürich, Switzerland. Geosci. Model Dev. 2017, 10, 3441–3459. [Google Scholar] [CrossRef] [Green Version]
- Oettl, D.; Sturm, P.; Almbauer, R. Evaluation of GRAL for the pollutant dispersion from a city street tunnel portal at depressed level. Environ. Model. Softw. 2005, 20, 499–504. [Google Scholar] [CrossRef]
- Oettl, D. Evaluation of the Revised Lagrangian Particle Model GRAL against Wind-Tunnel and Field Observations in the Presence of Obstacles. Bound.-Layer Meteorol. 2015, 155, 271–287. [Google Scholar] [CrossRef]
- Graz University of Technology. GRAL-Graz Lagrangian Model. 2020. Available online: http://lampz.tugraz.at/~gral/index.php/2-uncategorised/1-description# (accessed on 24 April 2020).
- Salim, S.M.; Buccolieri, R.; Chan, A.; di Sabatino, S. Numerical simulation of atmospheric pollutant dispersion in an urban street canyon: Comparison between RANS and LES. J. Wind Eng. Ind. Aerodyn. 2011, 99, 103–113. [Google Scholar] [CrossRef]
- Woodward, J. Appendix A: Atmospheric Stability Classification Schemes, Estimating the Flammable Mass of a Vapor Cloud. In Estimating the Flammable Mass of a Vapor Cloud: A CCPS Concept Book; Wiley: Hoboken, NJ, USA, 2010; pp. 209–212. [Google Scholar] [CrossRef]
- Nebenzal, A.; Fishbain, B.; Kendler, S. Model-based dense air pollution maps from sparse sensing in multi-source scenarios. Environ. Model. Softw. 2020, 128, 104701. [Google Scholar] [CrossRef]
- Kendler, S.; Fishbain, B. Optimal Wireless Distributed Sensor Network Design and Ad-Hoc Deployment in a Chemical Emergency Situation. Sensors 2022, 22, 2563. [Google Scholar] [CrossRef]
- Nebenzal, A.; Fishbain, B. Hough-based Interpolation Scheme for Generating Accurate Dense Spatial Maps of Air Pollutants from Sparse Sensing. Int. Fed. Inf. Process. Adv. Inf. Commun. Technol. 2018, 507, 51–60. [Google Scholar] [CrossRef] [Green Version]




| PS1 | PS2 | PS3 | PS4 | PS5 | Line 1 | Line 2 | Line 3 | |||
|---|---|---|---|---|---|---|---|---|---|---|
| SNBH | Emission rate: | 100 | 50 | 200 | 100 | 0 | N/A | N/A | N/A | |
| CBD | CBD.1 | 150 | 100 | 50 | 200 | 0 | 10 | 15 | 20 | |
| CBD.2 | 5 | 3 | 9 | 7 | 10 | 1000 | 1000 | 1000 | ||
| CBD.3 | 50 | 30 | 90 | 70 | 10 | 100 | 200 | 150 |
| Entropy | Hot Spot | Random | Max Random | |
|---|---|---|---|---|
| SNBH | 6.34 | 8.85 | 6.44 | 13.64 |
| CBD.1 | 7.29 | 23.45 | 11.23 | 25.14 |
| CBD.2 | 3.13 | 3.58 | 5.14 | 12.77 |
| CBD.3 | 6.04 | 11.25 | 7.92 | 23.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mano, Z.; Kendler, S.; Fishbain, B. Information Theory Solution Approach to the Air Pollution Sensor Location–Allocation Problem. Sensors 2022, 22, 3808. https://doi.org/10.3390/s22103808
Mano Z, Kendler S, Fishbain B. Information Theory Solution Approach to the Air Pollution Sensor Location–Allocation Problem. Sensors. 2022; 22(10):3808. https://doi.org/10.3390/s22103808
Chicago/Turabian StyleMano, Ziv, Shai Kendler, and Barak Fishbain. 2022. "Information Theory Solution Approach to the Air Pollution Sensor Location–Allocation Problem" Sensors 22, no. 10: 3808. https://doi.org/10.3390/s22103808
APA StyleMano, Z., Kendler, S., & Fishbain, B. (2022). Information Theory Solution Approach to the Air Pollution Sensor Location–Allocation Problem. Sensors, 22(10), 3808. https://doi.org/10.3390/s22103808








