Compression Reconstruction and Fault Diagnosis of Diesel Engine Vibration Signal Based on Optimizing Block Sparse Bayesian Learning
Abstract
:1. Introduction
- In the process of wireless transmission, due to the limitation of network bandwidth and low power consumption, massive vibration signals bring considerable challenges to data storage and wireless network transmission;
- The problem of the reconstruction accuracy of the structured non-sparse signal of the reciprocating mechanical vibration signal cannot be satisfied by the traditional data compression technology;
- Aiming at the compression and reconstruction effects of reciprocating mechanical vibration signals, there is a lack of an effective, comprehensive evaluation index for data compression effects;
- There is a lack of relevant research on compressive sensing technology and fault diagnosis methods and their application in fault diagnosis of reciprocating machinery.
- Using the BSBL-KSVD algorithm and exploiting the intra-block correlation of the vibration signal, we can recover the structured non-sparse signal efficiently. Compared with other traditional compression and reconstruction algorithms. We can effectively improve the reconstruction accuracy and compression effect;
- A comprehensive evaluation index of compression effect suitable for reciprocating mechanical vibration signal is constructed, and it has a good engineering application prospect;
- We apply compressed sensing technology to fault diagnosis. The wireless trans-mission efficiency of the vibration signal can be effectively improved to achieve a better diagnosis effect and has a better reference value.
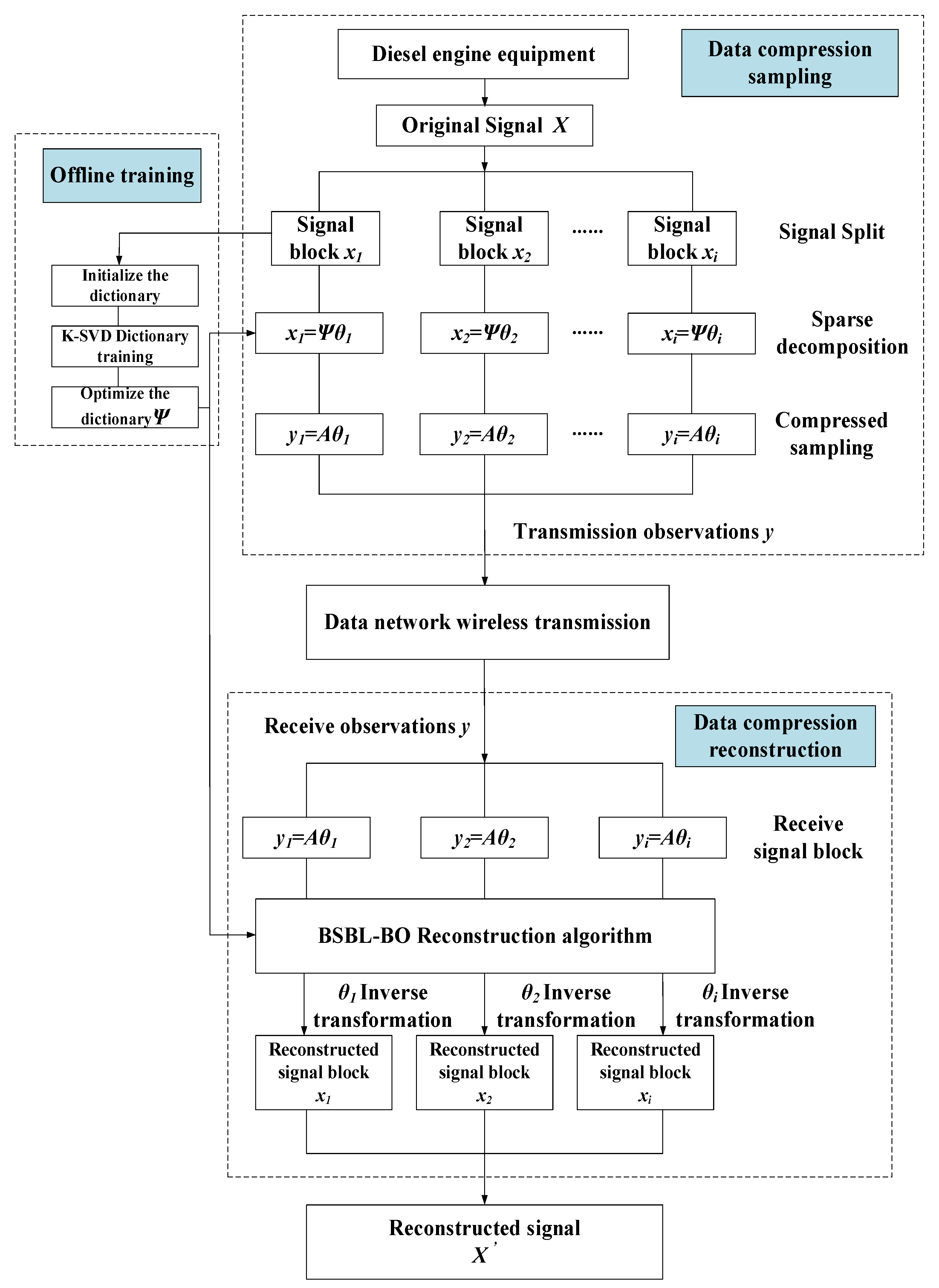
2. Model of Diesel Engine Compression Reconstruction Method Based on BSBL-KSVD
2.1. Compressed Sensing
2.2. Block Sparse Bayesian Learning Reconstruction Algorithm
2.3. K-SVD Adaptive Over-Complete Dictionary
2.4. Basic Flow of BSBL-KSVD Algorithm
| Algorithm 1 BSBL-KSVD algorithm pseudo code |
| 1. Input: x = [ x1, x2, …, xi], blkLen, N, M; |
| 2. Initialize dictionary parameters: param. L = 5, param. K = 70, param. numIteration = 20, param. Initialization Method = ‘Data Elements’; group Start Loc = 1:blkLen:N; |
| 3. K-SVD dictionary training: [Ψ, output] = KSVD(xi, param); the core is to use Equations (6)–(8) to generate a new dictionary Ψ through multiple iterative updates; |
| 4. Sparse transformation: xi = Ψθ; |
| 5. Sensor matrix: Ai = ΦΨ; |
| 6. Using the combination of Equations (1) and (2), the observation value of the data compression signal is obtained yi = Aiθ; |
| 7. Signal transmission: The block-compressed signals y1, …, yi are successively transmitted through the data network; |
| 8. For i = 1: size(xi,2)/N (signal reconstruction); |
| 9. θi = BSBL_BO (Ai, yi, groupStartLoc, 0, ‘prune_gamma’, −1, ‘max_iters’, 20); the core is to use Formula (3)–(5) to solve the reconstructed signal θi; |
| 10. Perform inverse sparse transformation to obtain reconstructed signal blocks: x1, …, xi; |
| 11. Connect the reconstructed signal blocks one by one to finally form a complete reconstructed signal: x′ = x1 + x2, + … + xi; |
| 12. End; |
| 13. Output: x′. |
3. Comprehensive Evaluation Index of Vibration Data Compression Effect
3.1. Data Compression Rate Evaluation Index
3.2. Standard Mean Square Error Evaluation Index
3.3. Peak Signal-to-Noise Ratio Evaluation Index
3.4. Pearson Correlation Coefficient Evaluation Index
3.5. Comprehensive Evaluation Index in Time Domain
4. Experimental Data Verification
4.1. Experiment Preparation
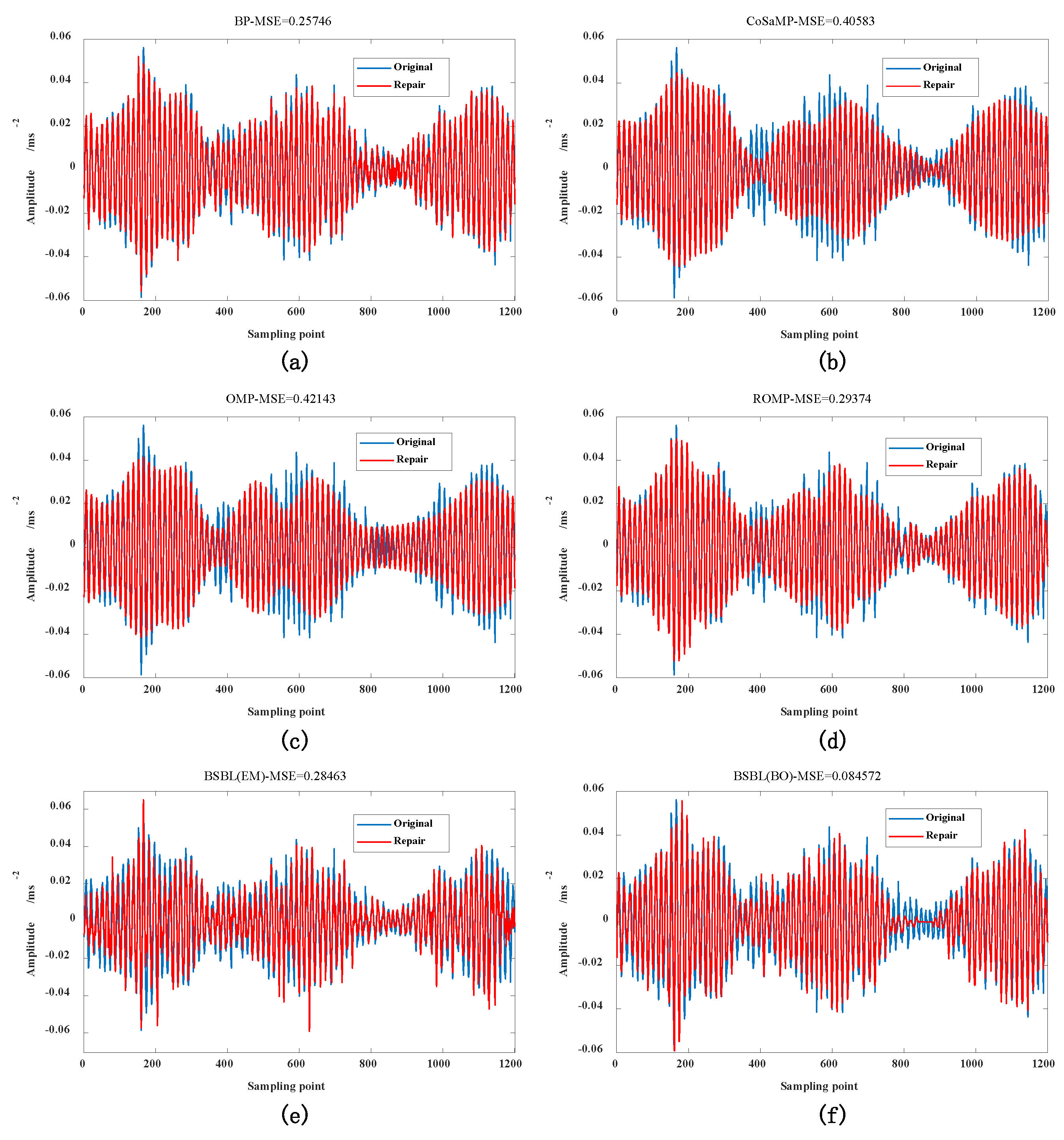
4.2. Comparison of BSBL-BO Algorithm with Other Compression and Reconstruction Algorithms
4.2.1. Evaluation Index of Reconstructed Signal MSE under the Same Compression Ratio
4.2.2. Evaluation Index of Reconstructed Signal MSE under Different Compression Ratios
4.2.3. Peak Signal-to-Noise Ratio Evaluation and Pearson Correlation Coefficient under Different Compression Ratios
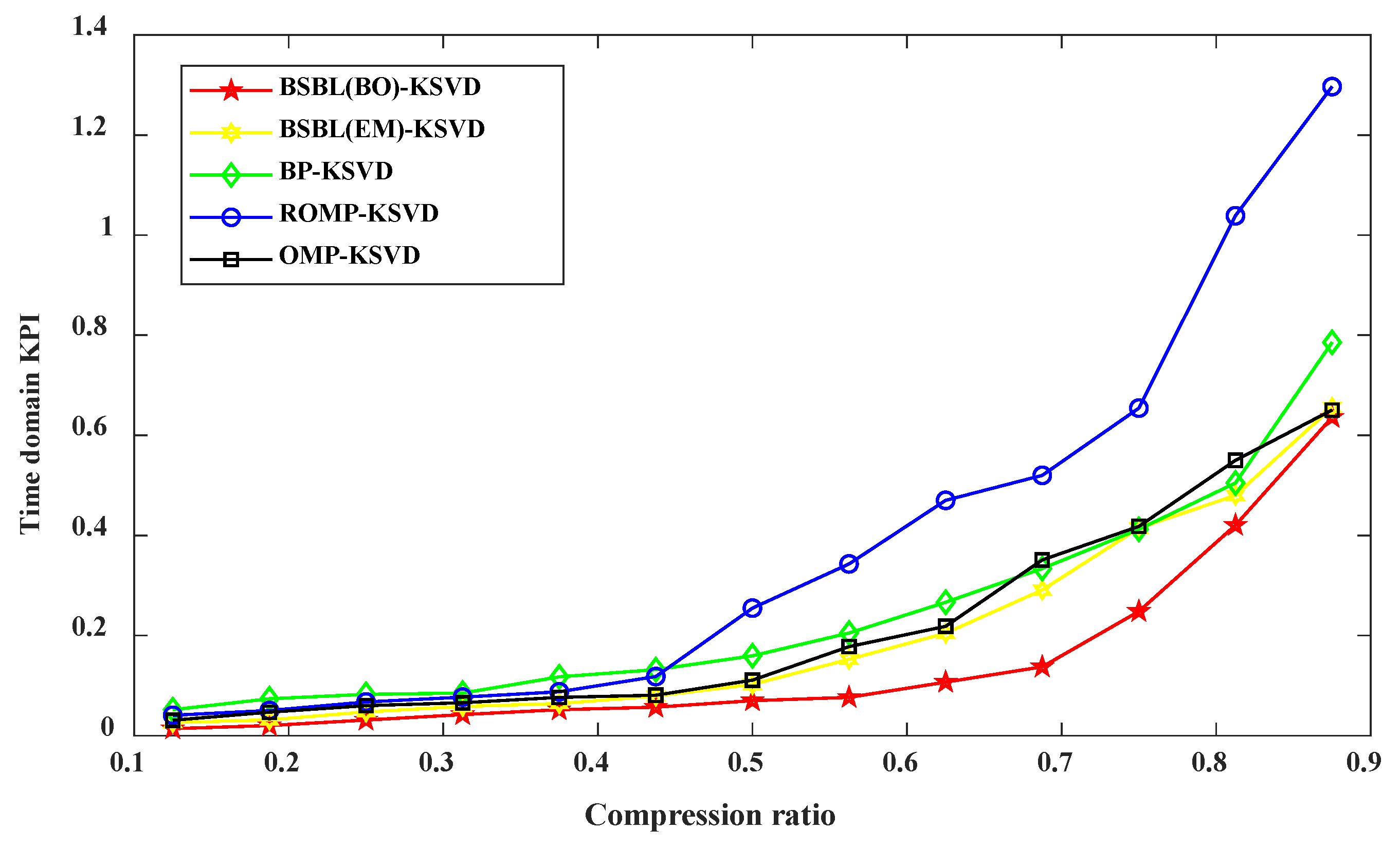
4.2.4. Comprehensive Evaluation Index of Reconstructed Signal in Time Domain under Different Compression Ratios
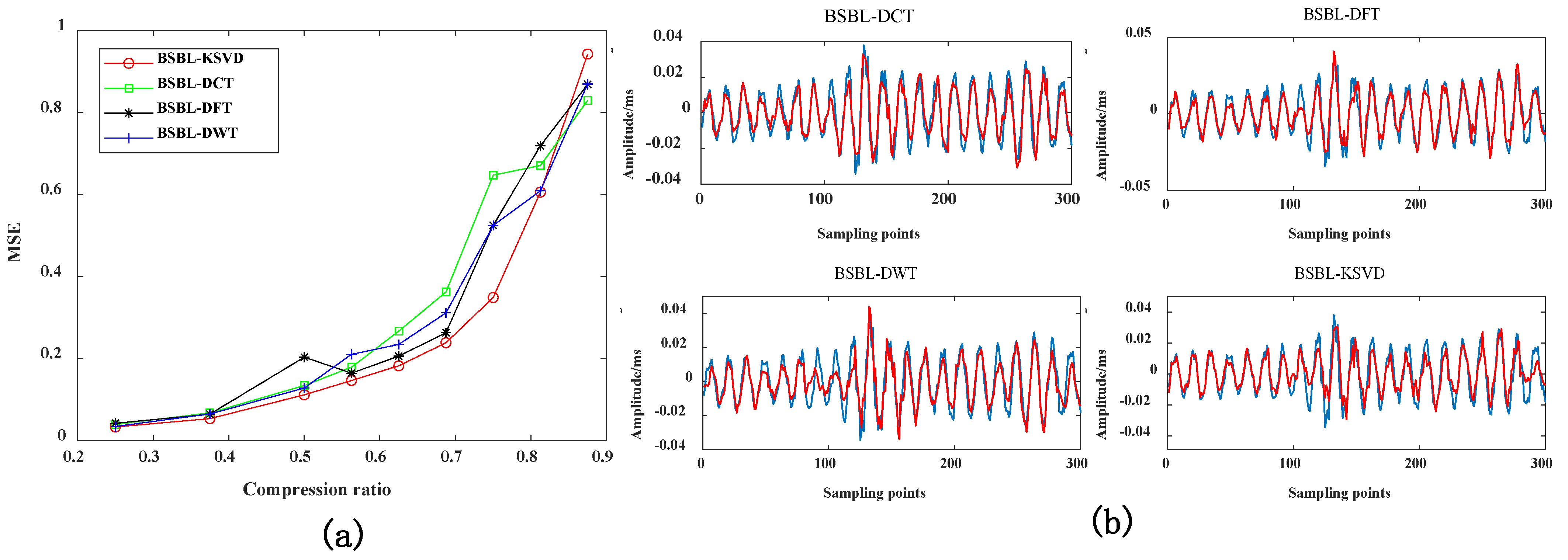
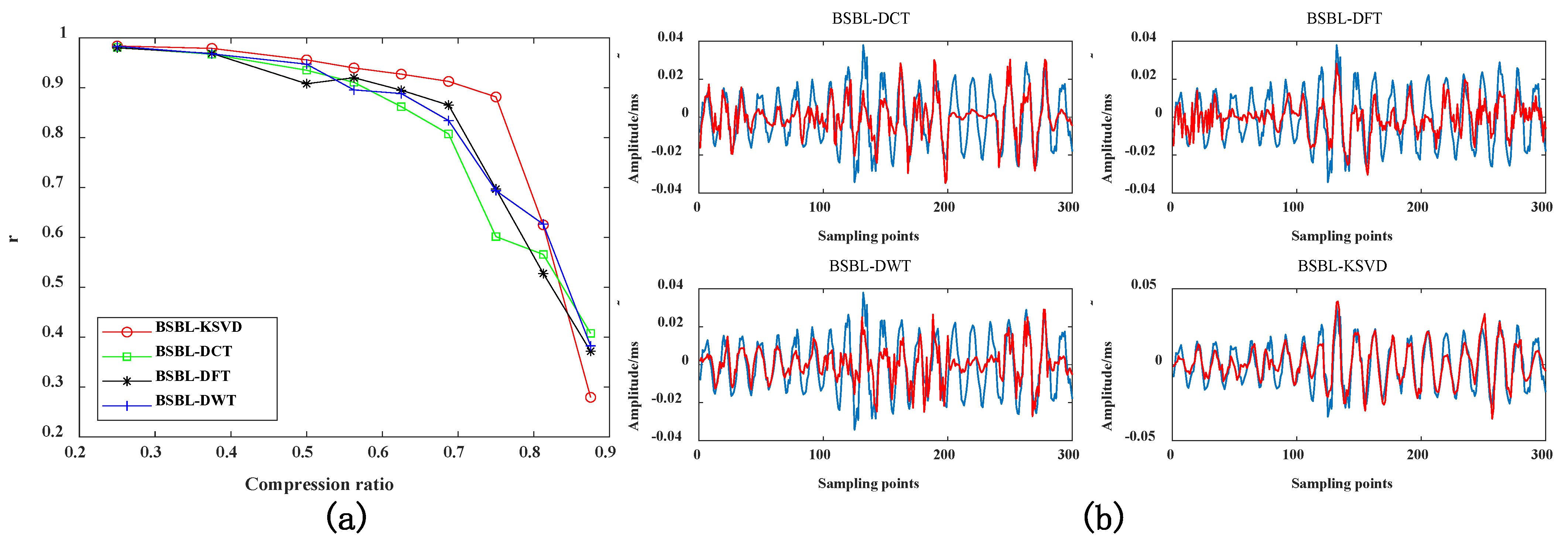
4.3. K-SVD Dictionary and Other Dictionary Effect Verification Comparison
4.3.1. Evaluation Index of Reconstructed Signal MSE under Different Compression Ratios
4.3.2. Peak Signal-to-Noise Ratio of Reconstructed Signal under Different Compression Ratios
4.3.3. Pearson Correlation Coefficient of Reconstructed Signal under Different Compression Ratios
5. Application of Compressed and Reconstructed Signal in Fault Diagnosis
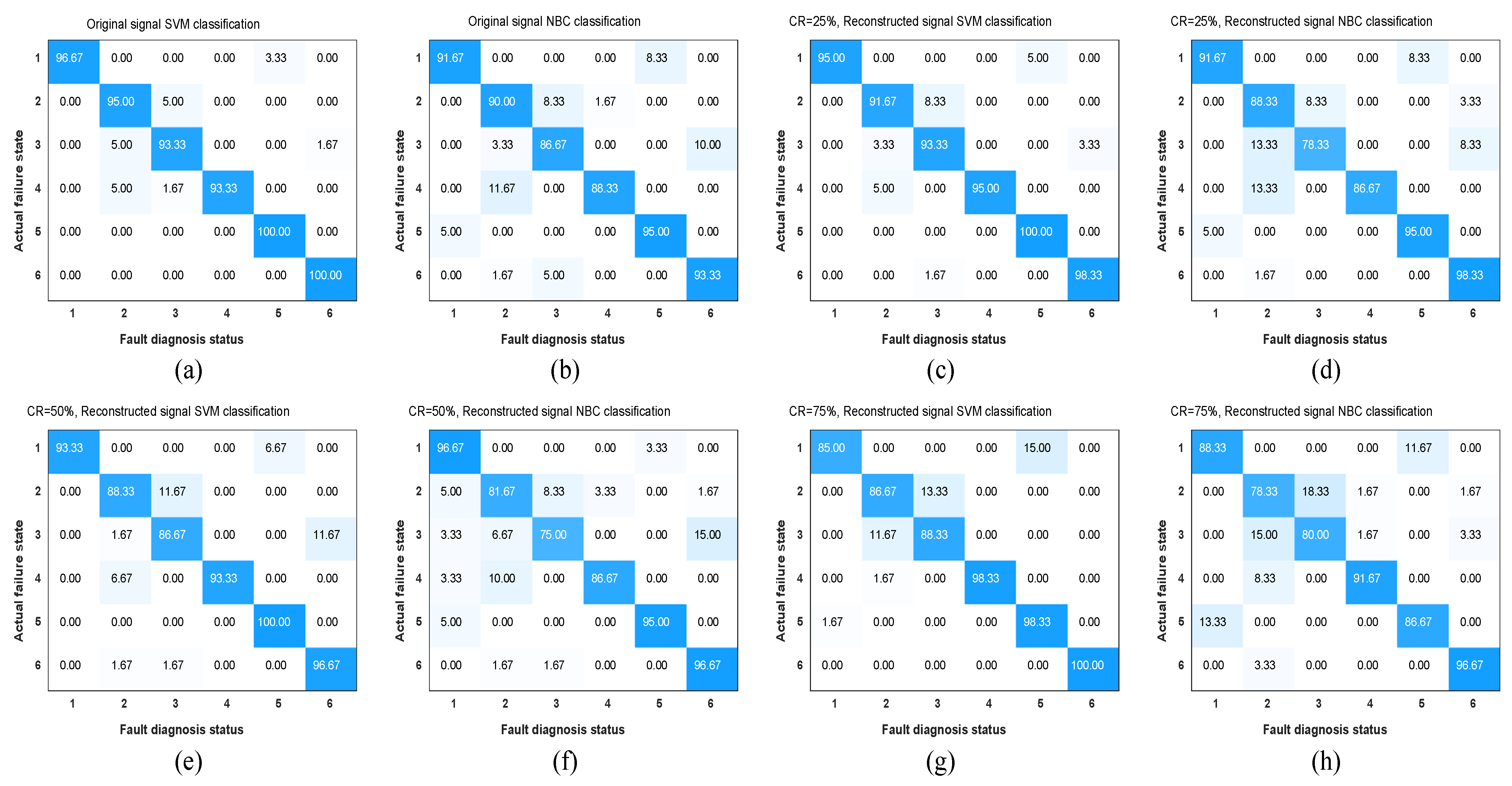
5.1. Comparative Analysis of Fault Classification under Different Compression Ratios
5.2. Comparative Analysis of Fault Diagnosis Results of Different Compression and Reconstruction Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, R.; Chen, H.; Guan, C. Random convolutional neural network structure: An intelligent health monitoring scheme for diesel engines. Measurement 2021, 171, 108786. [Google Scholar] [CrossRef]
- Lan, F.; Jiang, Y.; Wang, H. Performance Prediction Method of Prognostics and Health Management of Marine Diesel Engine. J. Phys. Conf. Ser. 2020, 1670, 12014. [Google Scholar] [CrossRef]
- Jin, C.; Zhao, W.; Liu, Z.; Lee, J.; He, X. A vibration-based approach for diesel engine fault diagnosis. In Proceedings of the 2014 International Conference on Prognostics and Health Management, Cheney, WA, USA, 22–25 June 2014; pp. 1–9. [Google Scholar]
- Wang, X.; Wang, Y.; Shi, X.; Gao, L.; Li, P. A probabilistic multimodal optimization algorithm based on Buffon principle and Nyquist sampling theorem for noisy environment. Appl. Soft Comput. 2021, 104, 107068. [Google Scholar] [CrossRef]
- Antonopoulos, C.P.; Voros, N.S. A data compression hardware accelerator enabling long-term biosignal monitoring based on ultra-low power IoT platforms. Electronics 2017, 6, 54. [Google Scholar] [CrossRef] [Green Version]
- Ma, N. Distributed video coding scheme of multimedia data compression algorithm for wireless sensor networks. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 254. [Google Scholar] [CrossRef]
- Yi, J.M.; Oh, E.J.; Noh, D.K.; Yoon, I. Energy-aware data compression and transmission range control for energy-harvesting wireless sensor networks. Int. J. Distrib. Sens. Netw. 2017, 13, 1550147717705785. [Google Scholar] [CrossRef]
- Hameed, M.E.; Ibrahim, M.M.; Abd Manap, N.; Mohammed, A.A. A lossless compression and encryption mechanism for remote monitoring of ECG data using Huffman coding and CBC-AES. Future Gener. Comput. Syst. 2020, 111, 829–840. [Google Scholar] [CrossRef]
- Khosravy, M.; Cabral, T.W.; Luiz, M.M.; Gupta, N.; Crespo, R.G. Random Acquisition in Compressive Sensing: A Comprehensive Overview. Int. J. Ambient. Comput. Intell. 2021, 12, 140–165. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, F.; Xiong, Q.; Zhang, W. A secondary selection-based orthogonal matching pursuit method for rolling element bearing diagnosis. Measurement 2021, 176, 109199. [Google Scholar] [CrossRef]
- Rahim, T.; Novamizanti, L.; Ramatryana IN, A.; Shin, S.Y. Compressed medical imaging based on average sparsity model and reweighted analysis of multiple basis pursuit. Comput. Med. Imaging Graph. 2021, 90, 101927. [Google Scholar] [CrossRef]
- Dey, M.R.; Shiraz, A.; Sharif, S.; Lota, J.; Demosthenous, A. Dictionary selection for compressed sensing of EEG signals using sparse binary matrix and spatiotemporal sparse Bayesian learning. Biomed. Phys. Eng. Express 2020, 6, 65024. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Shu, M.; Chen, C. ECG signal denoising and reconstruction based on basis pursuit. Appl. Sci. 2021, 11, 1591. [Google Scholar] [CrossRef]
- Cheng, C.; Lin, D. Based on Compressed Sensing of Orthogonal Matching Pursuit Algorithm Image Recovery. J. Internet Things 2020, 2, 37–45. [Google Scholar] [CrossRef]
- Sajjad, M.; Mehmood, I.; Baik, S.W. Sparse coded image super-resolution using K-SVD trained dictionary based on regularized orthogonal matching pursuit. Bio-Med. Mater. Eng. 2015, 26, S1399–S1407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Rao, B.D. Extension of SBL Algorithms for the Recovery of Block Sparse Signals with Intra-Block Correlation. IEEE Trans. Signal Process. 2013, 61, 2009–2015. [Google Scholar] [CrossRef] [Green Version]
- Mahrous, H.; Ward, R. Block sparse compressed sensing of electroencephalogram (EEG) signals by exploiting linear and non-linear dependencies. Sensors 2016, 16, 201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, G.; Ye, W.; Lao, G.; Kong, S.; Yan, D. Narrowband Interference Separation for Synthetic Aperture Radar via Sensing Matrix Op-timization-Based Block Sparse Bayesian Learning. Electronics 2019, 8, 458. [Google Scholar] [CrossRef] [Green Version]
- Almasri, N.; Sadhu, A.; Chaudhuri, S.R. Toward compressed sensing of structural monitoring data using discrete cosine transform. J. Comput. Civ. Eng. 2020, 34, 4019041. [Google Scholar] [CrossRef]
- Borghesani, P.; Pennacchi, P.; Chatterton, S.; Ricci, R. The velocity synchronous discrete Fourier transform for order tracking in the field of rotating machinery. Mech. Syst. Signal Process. 2014, 44, 118–133. [Google Scholar] [CrossRef]
- Belkacemi, B.; Saad, S.; Ghemari, Z.; Zaamouche, F.; Khazzane, A. Detection of induction motor improper bearing lubrication by discrete wavelet transforms (DWT) decomposition. Instrum. Mes. Métrologie 2020, 19, 347–354. [Google Scholar] [CrossRef]
- Liang, K.; Zhao, M.; Lin, J.; Jiao, J. An information-based K-singular-value decomposition method for rolling element bearing diagnosis. ISA Trans. 2020, 96, 444–456. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, M.; Riahi, M.A. Using input-adaptive dictionaries trained by the method of optimal directions to estimate the permeability model of a reservoir. J. Appl. Geophys. 2019, 165, 16–28. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y. Microstructure Images Restoration of Metallic Materials Based upon KSVD and Smoothing Penalty Sparse Representation Approach. Materials 2018, 11, 637. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, J.; Zhang, X.; Peng, W.; Liu, Z. A novel regularized K-SVD dictionary learning based medical image super-resolution algorithm. Multimed. Tools Appl. 2016, 75, 13107–13120. [Google Scholar] [CrossRef]
- Gu, C.; Qiao, X.-Y.; Li, H.; Jin, Y. Misfire fault diagnosis method for diesel engine based on MEMD and dispersion entropy. Shock Vib. 2021, 2021, 9213697. [Google Scholar] [CrossRef]
- Chen, K.; Mao, Z.; Zhao, H.; Jiang, Z.; Zhang, J. A variational stacked autoencoder with harmony search optimizer for valve train fault diagnosis of diesel engine. Sensors 2019, 20, 223. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, B.; Ke, H.; Ma, X.; Yu, B. Fault Diagnosis Method for Engine Control System Based on Probabilistic Neural Network and Support Vector Machine. Appl. Sci. 2019, 9, 4122. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Hu, N.; Hu, L.; Chen, L. A bearing fault detection method with low-dimensional compressed measurements of vibration signal. J. Vibroeng. 2015, 17, 1253–1265. [Google Scholar]
- Tang, G.; Hou, W.; Wang, H.; Luo, G.; Ma, J. Compressive sensing of roller bearing faults via harmonic detection from under-sampled vibration signals. Sensors 2015, 15, 25648–25662. [Google Scholar] [CrossRef] [Green Version]
- Du, Z.; Chen, X.; Zhang, H.; Miao, H.; Guo, Y.; Yang, B. Feature identification with compressive measurements for machine fault diagnosis. IEEE Trans. Instrum. Meas. 2016, 65, 977–987. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, Y.; Gao, Y.; Zhang, W. Autonomous compressive-sensing-augmented spectrum sensing. IEEE Trans. Veh. Technol. 2018, 67, 6970–6980. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Šaliga, J.; Andráš, I.; Dolinský, P.; Michaeli, L.; Kováč, O.; Kromka, J. ECG compressed sensing method with high compression ratio and dynamic model reconstruction. Measurement 2021, 183, 109803. [Google Scholar] [CrossRef]
- Dileep BP, V.; Das, T.; Dutta, P.K. Greedy algorithms for diffuse optical tomography reconstruction. Opt. Commun. 2018, 410, 164–173. [Google Scholar] [CrossRef]
- Zhiyong, L.; Hongdong, Z.; Ruili, Z.; Kewen, X.; Qiang, G.; Yuhai, L. Fault identification method of diesel engine in light of pearson correlation coefficient diagram and orthogonal vibration signals. Math. Probl. Eng. 2019, 2019, 2837580. [Google Scholar] [CrossRef]
- Samuel, P.D.; Pines, D.J. A review of vibration-based techniques for helicopter transmission diagnostics. J. Sound Vib. 2005, 282, 475–508. [Google Scholar] [CrossRef]
- Liu, Z.; Qu, J.; Zuo, M.J.; Xu, H.B. Fault level diagnosis for planetary gearboxes using hybrid kernel feature selection and kernel Fisher discriminant analysis. Int. J. Adv. Manuf. Technol. 2013, 67, 1217–1230. [Google Scholar] [CrossRef]




| No. | Dataset | State | Rotating Speed | Inlet Valve Clearance |
|---|---|---|---|---|
| 1 | Valve_800_3mm | Normal Status | 800 | 0.3 mm |
| 2 | Valve_800_7mm | Fault 1 | 800 | 0.7 mm |
| 3 | Valve_1200_3mm | Fault 2 | 1200 | 0.3 mm |
| 4 | Valve_1200_4mm | Fault 3 | 1200 | 0.4 mm |
| 5 | Valve_1200_5mm | Fault 4 | 1200 | 0.5 mm |
| 6 | Valve_1200_7mm | Fault 5 | 1200 | 0.7 mm |
| State | Original Signal | CR = 0.25 | CR = 0.5 | CR = 0.75 | ||||
|---|---|---|---|---|---|---|---|---|
| SVM | NBC | SVM | NBC | SVM | NBC | SVM | NBC | |
| Normal Status | 96.67% | 91.67% | 95.00% | 91.67% | 93.33% | 96.67% | 85.00% | 88.33% |
| Fault 1 | 95.00% | 90.00% | 91.67% | 88.33% | 88.33% | 81.67% | 86.67% | 78.33% |
| Fault 2 | 93.33% | 86.67% | 93.33% | 78.33% | 86.67% | 75.00% | 88.33% | 80.00% |
| Fault 3 | 93.33% | 88.33% | 95.00% | 86.67% | 93.33% | 86.67% | 98.33% | 91.67% |
| Fault 4 | 100.0% | 95.00% | 100.0% | 95.00% | 100.0% | 95.00% | 98.33% | 86.67% |
| Fault 5 | 100.0% | 93.33% | 98.33% | 98.33% | 96.67% | 96.67% | 100.0% | 96.67% |
| Total Accuracy | 96.39% | 90.83% | 95.56% | 89.72% | 93.06% | 88.61% | 92.78% | 86.95% |
| State | BSBL(BO)-KSVD | BSBL(EM)-KSVD | BP-KSVD | ROMP-KSVD | OMP-KSVD |
|---|---|---|---|---|---|
| Normal Status | 95.00% | 91.33% | 83.33% | 86.67% | 85.33% |
| Fault 1 | 91.67% | 85.00% | 95.00% | 86.67% | 90.00% |
| Fault 2 | 93.33% | 83.33% | 81.67% | 83.33% | 82.67% |
| Fault 3 | 95.00% | 93.33% | 88.33% | 81.67% | 80.67% |
| Fault 4 | 100.0% | 95.67% | 85.00% | 95.00% | 90.33% |
| Fault 5 | 98.33% | 100.0% | 95.00% | 91.33% | 92.00% |
| Total Accuracy | 95.56% | 91.44% | 88.06% | 87.45% | 86.83% |
| State | BSBL(BO)-KSVD | BSBL(EM)-KSVD | BP-KSVD | ROMP-KSVD | OMP-KSVD |
|---|---|---|---|---|---|
| Normal Status | 93.33% | 87.67% | 78.33% | 80.67% | 83.67% |
| Fault 1 | 88.33% | 83.33% | 80.00% | 82.33% | 72.00% |
| Fault 2 | 86.67% | 85.00% | 75.00% | 70.33% | 72.33% |
| Fault 3 | 93.33% | 88.33% | 81.67% | 76.00% | 68.00% |
| Fault 4 | 100.0% | 95.00% | 92.33% | 87.67% | 82.33% |
| Fault 5 | 96.67% | 90.67% | 88.33% | 88.00% | 85.67% |
| Total Accuracy | 93.06% | 88.33% | 82.61% | 80.83% | 77.33% |
| State | BSBL(BO)-KSVD | BSBL(EM)-KSVD | BP-KSVD | ROMP-KSVD | OMP-KSVD |
|---|---|---|---|---|---|
| Normal Status | 85.00% | 81.00% | 72.67% | 76.67% | 65.00% |
| Fault 1 | 86.67% | 77.33% | 75.00% | 65.00% | 74.67% |
| Fault 2 | 88.33% | 77.33% | 71.33% | 73.67% | 67.33% |
| Fault 3 | 98.33% | 89.00% | 83.33% | 67.33% | 67.33% |
| Fault 4 | 98.33% | 82.67% | 75.67% | 70.00% | 72.00% |
| Fault 5 | 100.0% | 85.33% | 80.00% | 75.67% | 63.67% |
| Total Accuracy | 92.78% | 82.11% | 76.33% | 71.39% | 68.33% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, H.; Wen, L.; Ma, Y.; Jia, X. Compression Reconstruction and Fault Diagnosis of Diesel Engine Vibration Signal Based on Optimizing Block Sparse Bayesian Learning. Sensors 2022, 22, 3884. https://doi.org/10.3390/s22103884
Bai H, Wen L, Ma Y, Jia X. Compression Reconstruction and Fault Diagnosis of Diesel Engine Vibration Signal Based on Optimizing Block Sparse Bayesian Learning. Sensors. 2022; 22(10):3884. https://doi.org/10.3390/s22103884
Chicago/Turabian StyleBai, Huajun, Liang Wen, Yunfei Ma, and Xisheng Jia. 2022. "Compression Reconstruction and Fault Diagnosis of Diesel Engine Vibration Signal Based on Optimizing Block Sparse Bayesian Learning" Sensors 22, no. 10: 3884. https://doi.org/10.3390/s22103884
APA StyleBai, H., Wen, L., Ma, Y., & Jia, X. (2022). Compression Reconstruction and Fault Diagnosis of Diesel Engine Vibration Signal Based on Optimizing Block Sparse Bayesian Learning. Sensors, 22(10), 3884. https://doi.org/10.3390/s22103884






