Characteristic Differences of Wind-Blown Sand Flow Field of Expressway Bridge and Subgrade and Their Implications on Expressway Design
Abstract
:1. Introduction
2. Research Methods
2.1. Models and Their Dimensions
2.2. Layout of Wind Tunnel Test
2.2.1. Layout of Wind Speed Test in Wind Tunnel
2.2.2. Test Layout of Sand Transport in Wind Tunnel
3. Test Results
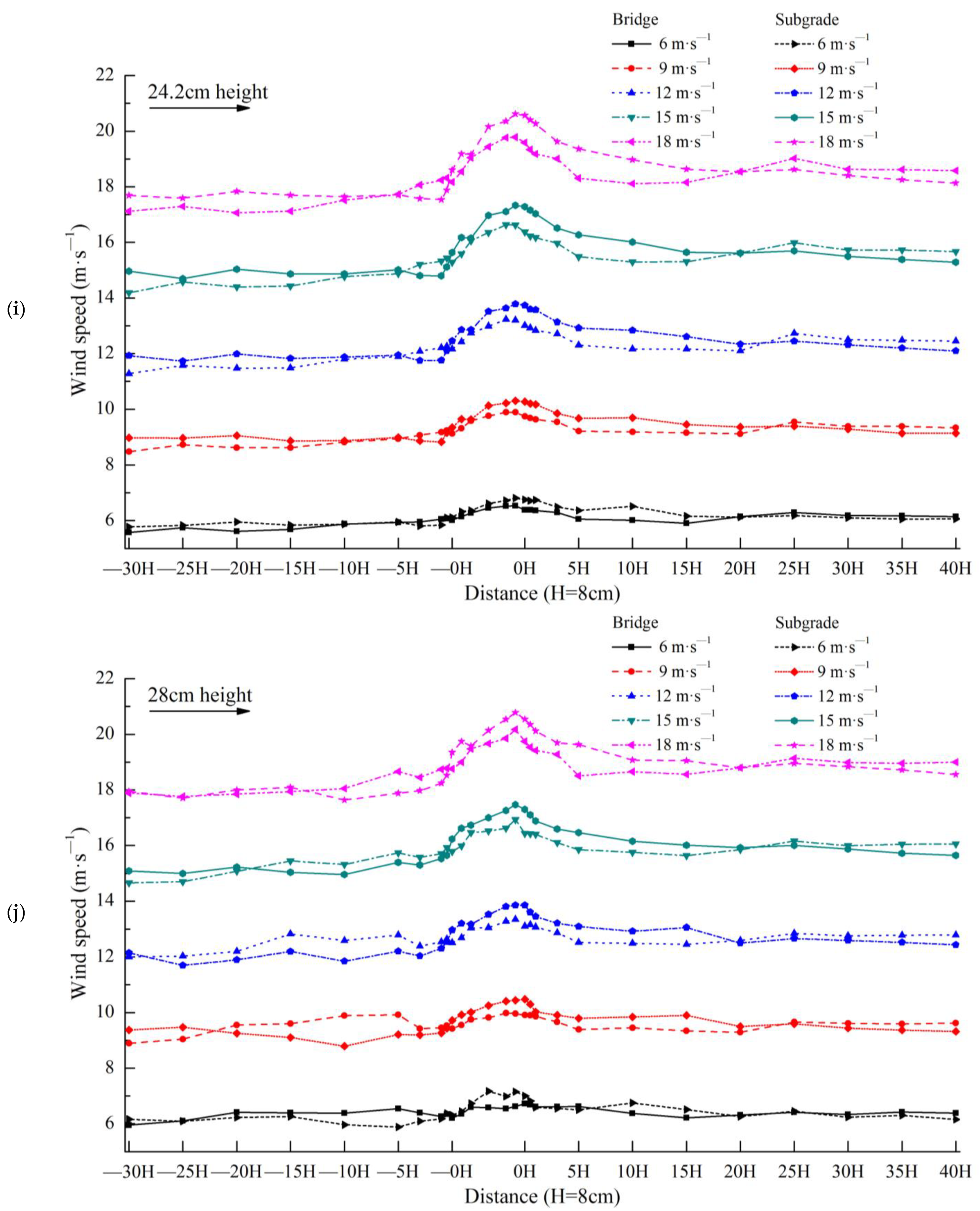
3.1. Wind Speed at Each Observation Point
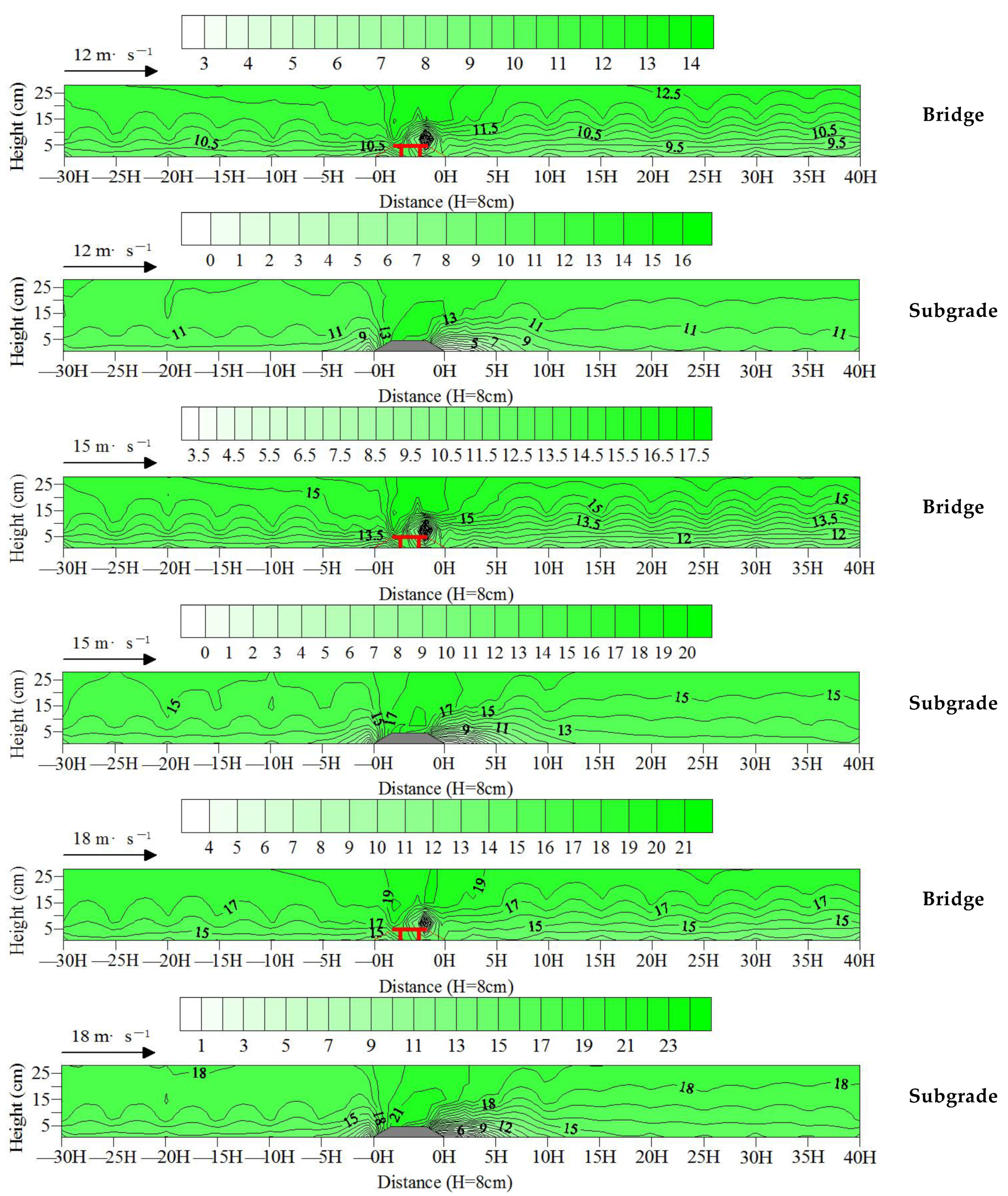
3.2. Wind Flow Field
3.3. Sand Transport
4. Cause Analysis
5. Results Discussion
6. Conclusions and Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bhattachan, A.; Okin, G.S.; Zhang, J.; Vimal, S.; Lettenmaier, D.P. Characterizing the role of wind and dust in traffic accidents in California. GeoHealth 2019, 3, 328–336. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.R.; Kandakji, T.; Lee, J.A.; Tatarko, J.; Blackwell, J.; Gill, T.E.; Collins, J.D. Blowing dust and highway safety in the southwestern United States: Characteristics of dust emission “hotspots” and management implications. Sci. Total Environ. 2018, 621, 1023–1032. [Google Scholar] [CrossRef] [PubMed]
- Horvat, M.; Bruno, L.; Khris, S.; Raffaele, L. Aerodynamic shape optimization of barriers for windblown sand mitigation using CFD analysis. J. Wind Eng. Ind. Aerodyn. 2020, 197, 104058. [Google Scholar] [CrossRef]
- Hu, L.; Shan, Y.T.; Chen, R.H.; Guo, W.; Wang, Q.; Li, Z.B. A study of erosion control on expressway embankment sideslopes with three-dimensional net seeding on the Qinghai-Tibet Plateau. Catena 2016, 147, 463–468. [Google Scholar] [CrossRef]
- Wang, C.; Li, S.Y.; Lei, J.Q.; Li, Z.N.; Chen, J. Effect of the W–beam central guardrails on wind–blown sand deposition on desert expressways in sandy regions. J. Arid Land 2020, 12, 154–165. [Google Scholar] [CrossRef] [Green Version]
- Yan, M.; Wang, H.B.; Zuo, H.J.; Li, G.T. Wind tunnel simulation of an opencut tunnel airflow field along the Linhe–Ceke Railway, China. Aeolian Res. 2019, 39, 66–76. [Google Scholar] [CrossRef]
- Li, S.H.; Li, C.; Yao, D.; Ge, X.D.; Zhang, G.P. Wind tunnel experiments for dynamic modeling and analysis of motion trajectories of wind–blown sands. Eur. Phys. J. E 2020, 43, 22. [Google Scholar] [CrossRef]
- He, W.; Huang, N.; Xu, B.; Wang, W.B. Numerical simulation of wind–sand movement in the reversed flow region of a sand dune with a bridge built downstream. Eur. Phys. J. E 2018, 41, 53. [Google Scholar] [CrossRef]
- Thalla, O.; Stiros, S.C. Wind-induced fatigue and asymmetric damage in a timber bridge. Sensors 2018, 18, 3867. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Jung, H.; Kong, M.J.; Lee, D.K.; An, Y.K. In-situ data-driven buffeting response analysis of a cable-stayed bridge. Sensors 2019, 19, 3048. [Google Scholar] [CrossRef] [Green Version]
- Bruno, L.; Horvat, M.; Raffaele, L. Windblown sand along railway infrastructures: A review of challenges and mitigation measures. J. Wind Eng. Ind. Aerodyn. 2018, 177, 340–365. [Google Scholar] [CrossRef]
- Pozzebon, A.; Cappelli, I.; Mecocci, A.; Bertoni, D.; Sarti, G.; Alquini, F. A wireless sensor network for the real-time remote measurement of aeolian sand transport on sandy beaches and dunes. Sensors 2018, 18, 820. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Albarakat, R.; Lakshmi, V. Monitoring dust storms in Iraq using satellite data. Sensors 2019, 19, 3687. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, N.; Gong, K.; Xu, B.; Zhao, J.; Dun, H.C.; He, W.; Xin, G.W. Investigations into the law of sand particle accumulation over railway subgrade with wind–break wall. Eur. Phys. J. E 2019, 42, 145. [Google Scholar] [CrossRef] [PubMed]
- Udo, K. New method for estimation of aeolian sand transport rate using ceramic sand flux sensor (UD-101). Sensors 2009, 9, 9058–9072. [Google Scholar] [CrossRef] [Green Version]
- Govaerts, Y.M. Sand dune ridge alignment effects on surface BRF over the Libya-4 CEOS calibration site. Sensors 2015, 15, 3453–3470. [Google Scholar] [CrossRef] [Green Version]
- Li, C.J.; Wang, Y.D.; Lei, J.Q.; Xu, X.W.; Wang, S.J.; Fan, J.L.; Li, S.Y. Damage by wind–blown sand and its control measures along the Taklimakan Desert Highway in China. J. Arid Land 2021, 13, 98–106. [Google Scholar] [CrossRef]
- Antonio, C.D.; Jorge, C.; Manuel, V.; Eduardo, R.; Luis, H. A DIY low-cost wireless wind data acquisition system used to study an arid coastal foredune. Sensors 2020, 20, 1064. [Google Scholar]
- Zdravko, K.; Bernard, Ž.; Biljana, M.B. FOCUSED–short-term wind speed forecast correction algorithm based on successive NWP forecasts for use in traffic control decision support systems. Sensors 2021, 21, 3405. [Google Scholar]
- Xie, S.B.; Qu, J.J.; Zhang, K.C.; Han, Q.J.; Pang, Y.J. The mechanism of sand damage at the Fushaliang section of the Liuyuan–Golmud Expressway. Aeolian Res. 2021, 48, 100648. [Google Scholar] [CrossRef]
- Xie, S.B.; Qu, J.J.; Han, Q.J.; Pang, Y.J. Wind dynamic environment and wind tunnel simulation experiment of bridge sand damage in Xierong section of Lhasa–Linzhi Railway. Sustainability 2020, 12, 5689. [Google Scholar] [CrossRef]
- Tetsuya, K.; Yamagishi, Y.; Kimura, S.; Sato, K. Aerodynamic behavior of snowflakes on an uneven road surface during a snowstorm. Open J. Fluid Dyn. 2017, 7, 696–708. [Google Scholar] [CrossRef] [Green Version]
- Dun, H.C.; Xin, G.W.; Huang, N.; Shi, G.T.; Zhang, J. Wind-tunnel studies on sand sedimentation around wind-break walls of Lanxin High-Speed Railway II and its prevention. Appl. Sci. 2021, 11, 5989. [Google Scholar] [CrossRef]
- Raffaele, L.; Bruno, L. Windblown sand mitigation along railway megaprojects: A comparative study. Struct. Eng. Int. 2020, 30, 355–364. [Google Scholar] [CrossRef]
- Lima, I.A.; Parteli, E.J.R.; Shao, Y.P.; Andrade, J.S.; Herrmann, H.J.; Araújo, A.D. CFD simulation of the wind field over a terrain with sand fences: Critical spacing for the wind shear velocity. Aeolian Res. 2020, 43, 100574. [Google Scholar] [CrossRef]
- Liu, J.Q.; Kimura, R.; Miyawaki, M.; Kinugasab, T. Effects of plants with different shapes and coverage on the blown-sand flux and roughness length examined by wind tunnel experiments. Catena 2021, 197, 104976. [Google Scholar] [CrossRef]
- Shen, Y.P.; Zhang, C.L.; Huang, X.Q.; Wang, X.S.; Cen, S.B. The effect of wind speed averaging time on sand transport estimates. Catena 2019, 175, 286–293. [Google Scholar] [CrossRef]
- Jiang, Y.S.; Gao, Y.H.; Dong, Z.B.; Liu, B.L.; Zhao, L. Simulations of wind erosion along the Qinghai–Tibet Railway in north–central Tibet. Aeolian Res. 2018, 32, 192–201. [Google Scholar] [CrossRef]
- Cheng, H.; He, J.J.; Xu, X.R.; Zou, X.Y.; Wu, Y.Q.; Liu, C.C.; Dong, Y.F.; Pan, M.H.; Wang, Y.Z.; Zhang, H.Y. Blown sand motion within the sand–control system in the southern section of the Taklimakan Desert Highway. J. Arid Land 2015, 7, 599–611. [Google Scholar] [CrossRef]
- Xiao, J.H.; Yao, Z.Y.; Qu, J.J. Influence of Golmud–Lhasa section of Qinghai–Tibet Railway on blown sand transport. Chin. Geogr. Sci. 2015, 25, 39–50. [Google Scholar] [CrossRef]
- Zhang, K.C.; Qu, J.J.; Han, Q.J.; Xie, S.B.; Kai, K.; Niu, Q.H.; An, Z.S. Wind tunnel simulation of windblown sand along China’s Qinghai–Tibet Railway. Land Degrad. Dev. 2014, 25, 244–250. [Google Scholar] [CrossRef]
- Draut, A. Effects of river regulation on aeolian landscapes, Colorado River, southwestern USA. J. Geophys. Res. Earth Surf. 2012, 117, 1–22. [Google Scholar] [CrossRef]











| Route Forms | Wind Speed (m·s−1) | Fitting Function Type | Fitting Function Formula | a | b | c | R2 |
|---|---|---|---|---|---|---|---|
| Bridge | 6 | Exponential | y = a × exp(b × x) | 45.30 | −0.51 | 0.99 | |
| Bridge | 9 | Exponential | y = a × exp(b × x) | 10.98 | −0.30 | 0.98 | |
| Bridge | 12 | Exponential | y = a × exp(b × x) | 28.60 | −0.23 | 0.96 | |
| Bridge | 15 | Exponential | y = a × exp(b × x) | 36.87 | −0.15 | 0.96 | |
| Bridge | 18 | Exponential | y = a × exp(b × x) | 37.48 | −0.11 | 0.98 | |
| Subgrade | 6 | Gaussian | y = a × exp(−((x − b)/c)2) | 999.70 | −118.30 | 45.69 | 0.94 |
| Subgrade | 9 | Gaussian | y = a × exp(−((x − b)/c)2) | 2.84 | 14.67 | 13.68 | 0.95 |
| Subgrade | 12 | Gaussian | y = a × exp(−((x − b)/c)2) | 6.34 | 24.88 | 14.65 | 0.95 |
| Subgrade | 15 | Gaussian | y = a × exp(−((x − b)/c)2) | 10.88 | 26.99 | 15.69 | 0.97 |
| Subgrade | 18 | Gaussian | y = a × exp(−((x − b)/c)2) | 15.89 | 27.64 | 15.68 | 0.98 |
| Environmental Indexes of Blown Sand | Contrast | Advantage Item | Disadvantage Item | |
|---|---|---|---|---|
| Wind speed | Variation range | bridge < subgrade | bridge | subgrade |
| Required distance to recover the wind speed | bridge > subgrade | subgrade | bridge | |
| Wind flow field | Variation range | bridge < subgrade | bridge | subgrade |
| Required distance to recover the wind field | bridge > subgrade | subgrade | bridge | |
| Wind-speed-weakening area upwind | Range | bridge < subgrade | bridge | subgrade |
| Intensity | bridge < subgrade | bridge | subgrade | |
| Wind-speed-increasing area on the top | Range | bridge < subgrade | bridge | subgrade |
| Intensity | bridge < subgrade | bridge | subgrade | |
| Wind-speed-weakening area downwind | Range | bridge > subgrade | subgrade | bridge |
| Intensity | bridge < subgrade | bridge | subgrade | |
| Passing rate of wind-blown sand flow (Average under the experimental wind speed of five groups) | Ratio (bridge/subgrade) | 0.8627 | subgrade | bridge |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, S.; Zhang, X.; Pang, Y. Characteristic Differences of Wind-Blown Sand Flow Field of Expressway Bridge and Subgrade and Their Implications on Expressway Design. Sensors 2022, 22, 3988. https://doi.org/10.3390/s22113988
Xie S, Zhang X, Pang Y. Characteristic Differences of Wind-Blown Sand Flow Field of Expressway Bridge and Subgrade and Their Implications on Expressway Design. Sensors. 2022; 22(11):3988. https://doi.org/10.3390/s22113988
Chicago/Turabian StyleXie, Shengbo, Xian Zhang, and Yingjun Pang. 2022. "Characteristic Differences of Wind-Blown Sand Flow Field of Expressway Bridge and Subgrade and Their Implications on Expressway Design" Sensors 22, no. 11: 3988. https://doi.org/10.3390/s22113988
APA StyleXie, S., Zhang, X., & Pang, Y. (2022). Characteristic Differences of Wind-Blown Sand Flow Field of Expressway Bridge and Subgrade and Their Implications on Expressway Design. Sensors, 22(11), 3988. https://doi.org/10.3390/s22113988






