Time-Correction Model Based on Diverter Speed for a pVTt Gas Flow Primary Standard
Abstract
:1. Introduction
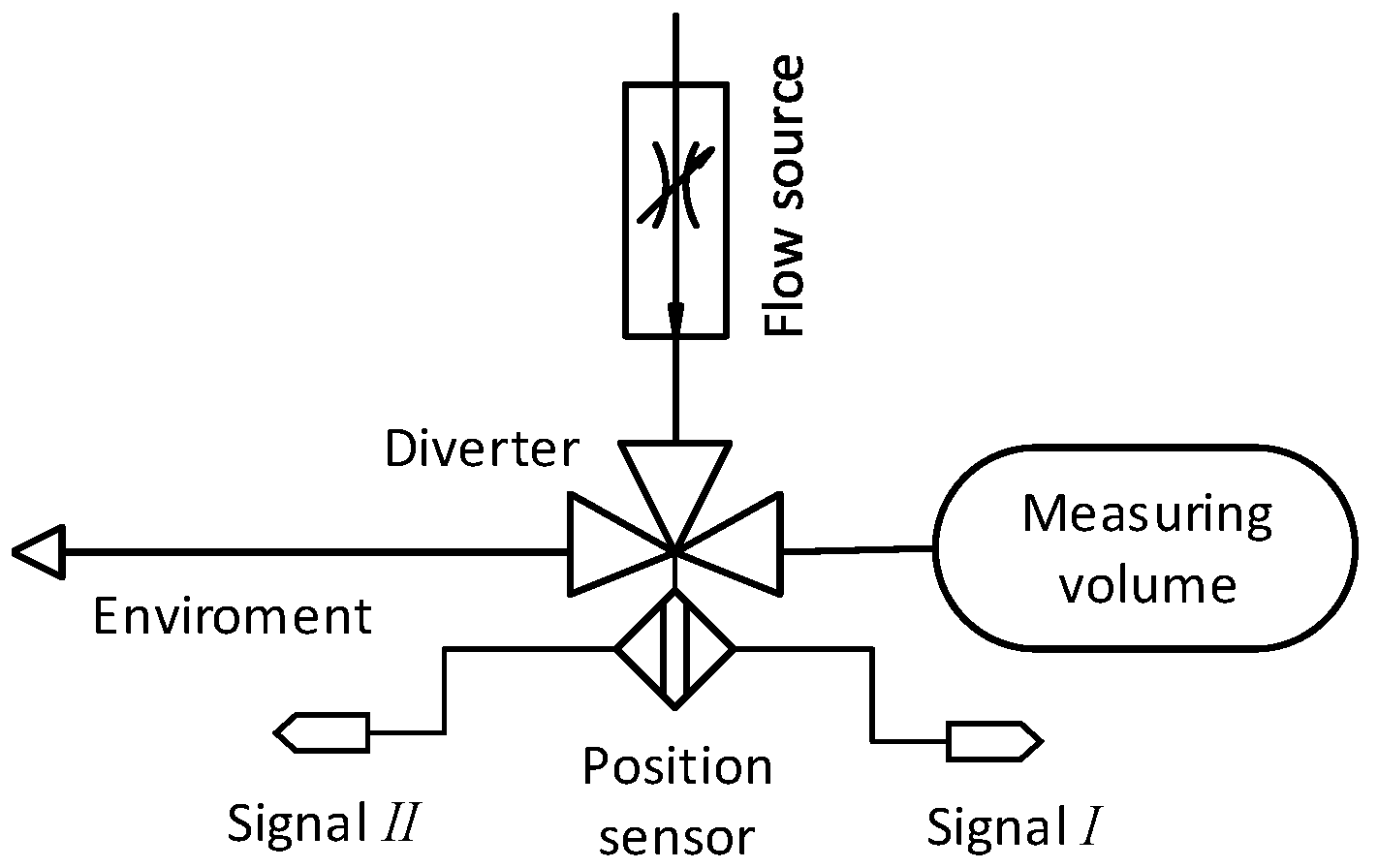
2. Physical Background of the Flow Diversion
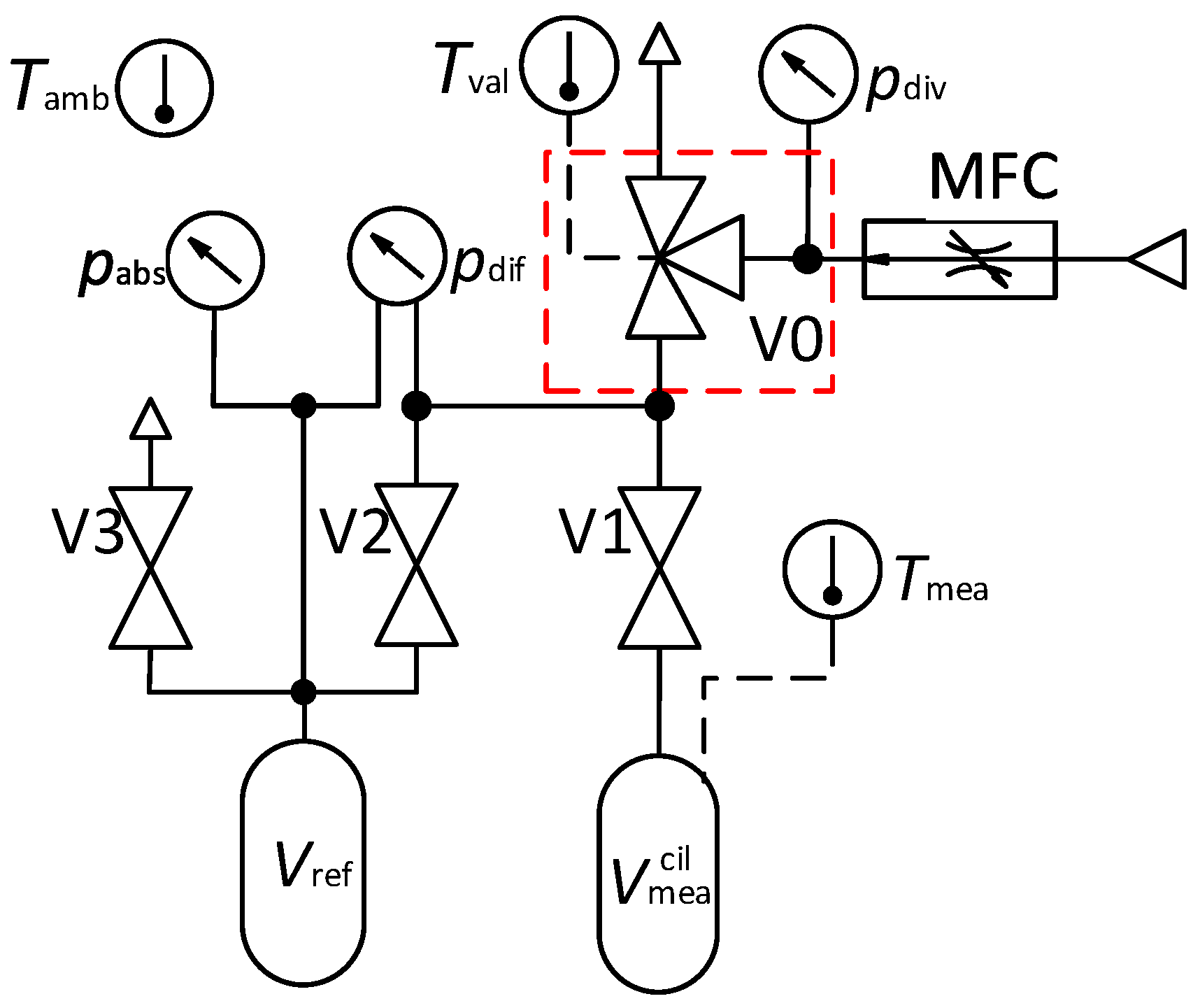
3. Measurement System
4. Measurement Methods for the Correction Time
4.1. Method 1: Varying the Collection Time
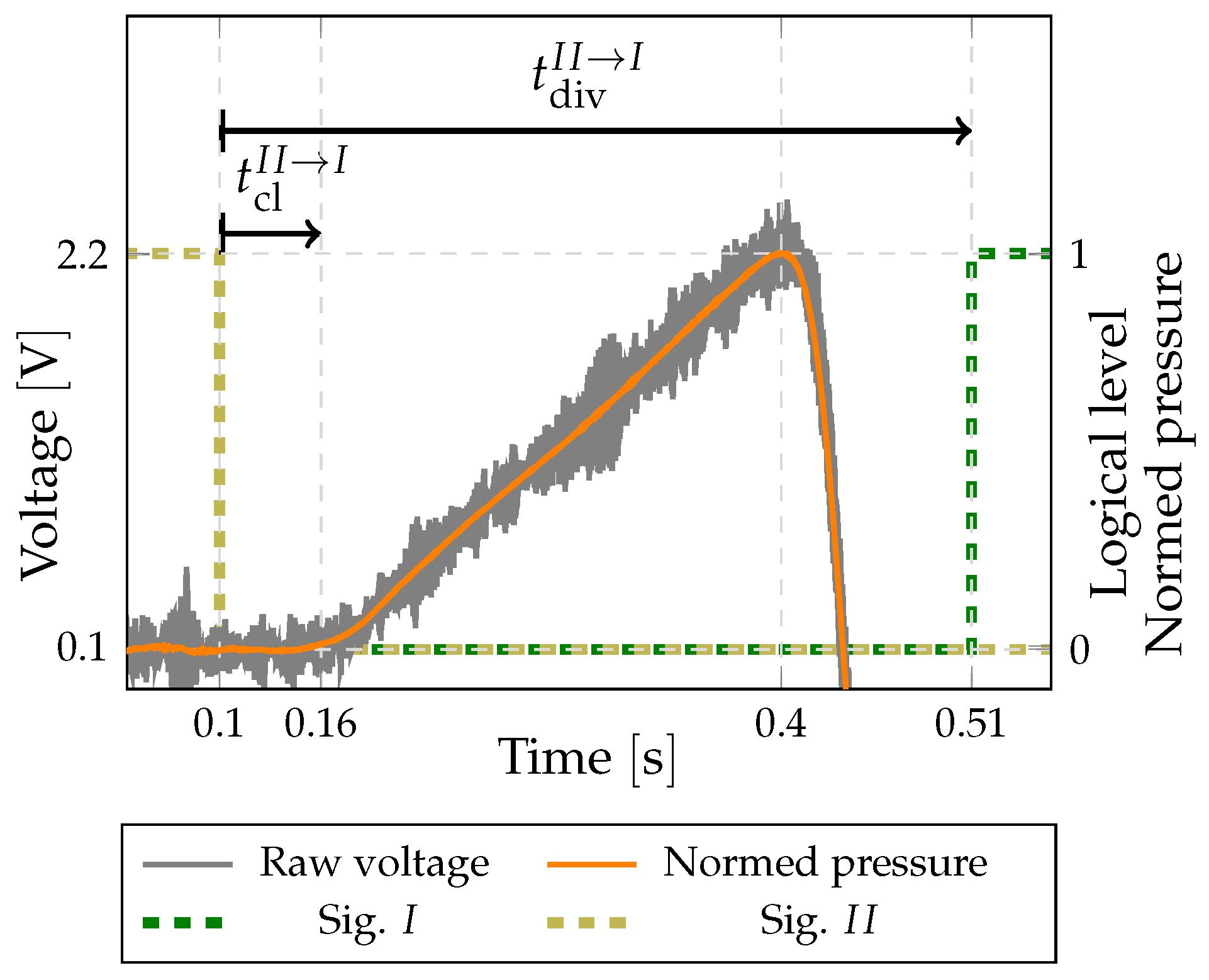
4.2. Method 2: Closing-Time Determination Using a Pressure Sensor
4.3. Effects on Measurement of the Correction Time
5. Model for the Correction Time’s Dependency on the Diverter’s Speed
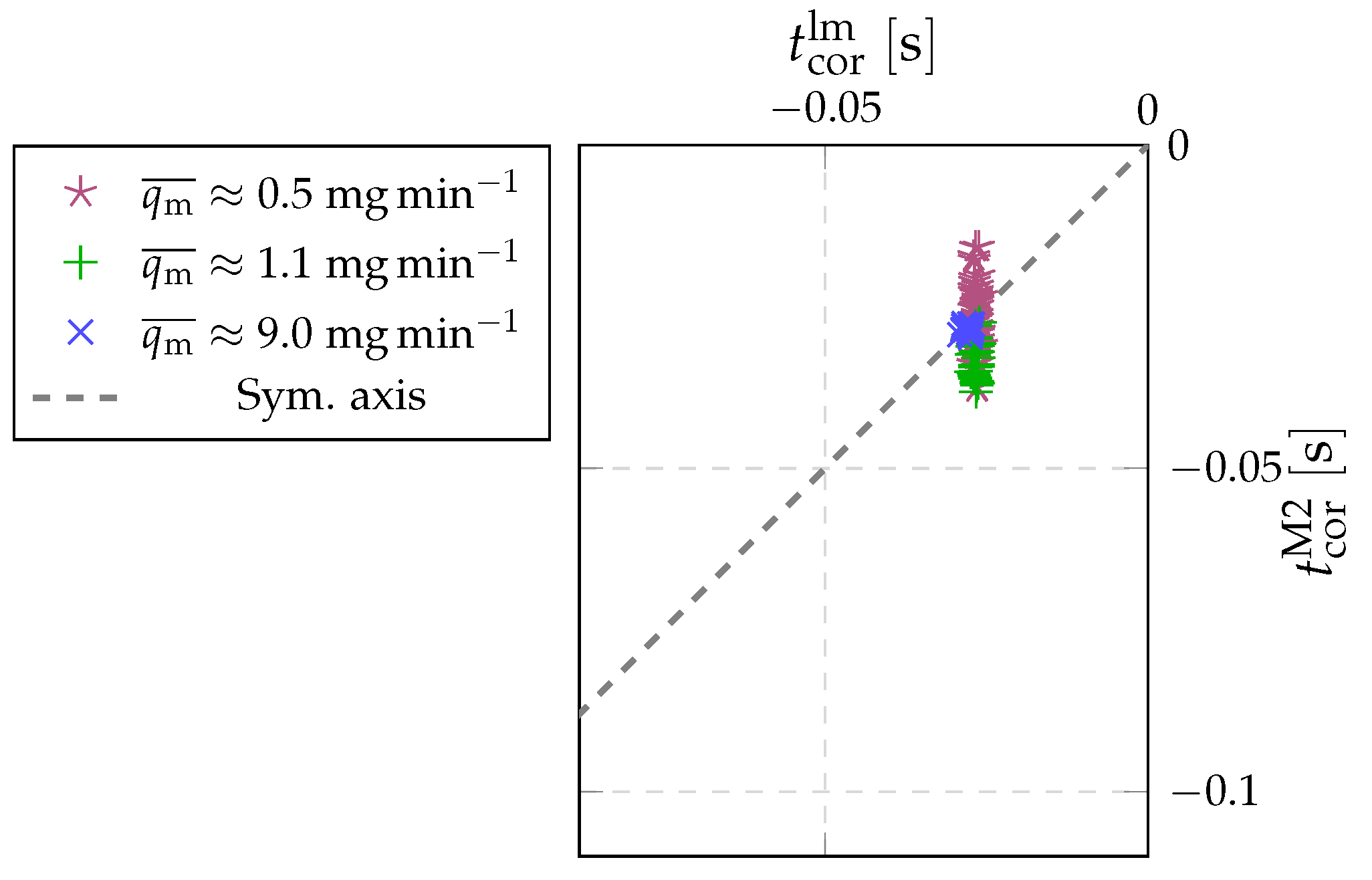
6. Validation of Pressure Based Method for the Time Correction (Method 2)
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bobovnik, G.; Kutin, J.; Bajsić, I. Uncertainty analysis of gas flow measurements using clearance-sealed piston provers in the range from 0.0012 g min−1 to 60 g min−1. Metrologia 2016, 53, 1061–1068. [Google Scholar] [CrossRef]
- Berg, R.; Tison, S. Two Primary Standards for Low Flows of Gases. J. Res. Natl. Inst. Stand. Technol. 2004, 109, 435. [Google Scholar] [CrossRef] [PubMed]
- Vičar, M.; Krajíček, Z.; Pražák, D.; Sedlák, V.; Gronych, T.; Hajduk, T.; Tesař, J. Gravimetric flow standard in the vacuum and hermetic modes. Meas. Sci. Technol. 2018, 29, 095011. [Google Scholar] [CrossRef]
- Ren, J.; Duan, J.; Dong, Y. Application and uncertainty analysis of a balance weighing system used in natural gas primary standard up to 60 bar. Flow Meas. Instrum. 2021, 77, 101836. [Google Scholar] [CrossRef]
- Berg, R.F.; Cignolo, G. NIST–IMGC comparison of gas flows below one litre per minute. Metrologia 2003, 40, 154–158. [Google Scholar] [CrossRef]
- Cignolo, G.; Alasia, F.; Capelli, A.; Goria, R.; La Piana, G. A primary standard piston prover for measurement of very small gas flows: An update. Sens. Rev. 2005, 25, 40–45. [Google Scholar] [CrossRef]
- Berg, R.F.; Gooding, T.; Vest, R.E. Constant pressure primary flow standard for gas flows from 0.01 cm3/min to 100 cm3/min (0.007–74 μmol/s). Flow Meas. Instrum. 2014, 35, 84–91. [Google Scholar] [CrossRef]
- Bobovnik, G.; Kutin, J. Experimental identification and correction of the leakage flow effects in a clearance-sealed piston prover. Metrologia 2018, 56, 015013. [Google Scholar] [CrossRef]
- Bobovnik, G.; Kutin, J. Correlation of the leakage flow rate with pressure changes in a clearance-sealed piston prover. Flow Meas. Instrum. 2020, 74, 101785. [Google Scholar] [CrossRef]
- Kutin, J.; Bobovnik, G.; Bajsić, I. Dynamic effects in a clearance-sealed piston prover for gas flow measurements. Metrologia 2011, 48, 123–132. [Google Scholar] [CrossRef]
- Kutin, J.; Bobovnik, G.; Bajsić, I. Dynamic pressure corrections in a clearance-sealed piston prover for gas flow measurements. Metrologia 2013, 50, 66–72. [Google Scholar] [CrossRef]
- Kramer, R.; Mickan, B.; Dopheide, D. Double piston prover usable as flowrate comparator for various gases. In XVIII IMEKO World Congress; Metrology for a Sustainable Development: Rio de Janeiro, Brazil, 2006. [Google Scholar]
- Jousten, K.; Menzer, H.; Niepraschk, R. A new fully automated gas flowmeter at the PTB for flow rates between 10−13 mol/s and 10−6 mol/s. Metrologia 2002, 39, 519. [Google Scholar] [CrossRef]
- Wright, J.; Mattingly, G. NIST Measurement Services: NIST Calibration Services for Gas Flow Meters. Piston Prover and Bell Prover Gas Flow Facilities; NIST: Gaithersburg, MD, USA, 1998. [Google Scholar]
- Boineau, F. Characterization of the LNE constant pressure flowmeter for the leak flow rates measurements with reference to vacuum and atmospheric pressure. PTB Mitteilungen 2011, 121, 313. [Google Scholar]
- Wright, J.D.; Johnson, A.N.; Moldover, M.R. Design and Uncertainty Analysis for a PVTt Gas Flow Standard. J. Res. Natl. Inst. Stand. Technol. 2003, 108, 21–47. [Google Scholar] [CrossRef]
- Johnson, A.N.; Wright, J.D. Gas Flowmeter Calibrations with the 26 m3 PVTt Standard; NIST Special Publication 250-1046; NIST: Gaithersburg, MD, USA, 2005. [Google Scholar]
- Li, C.; Johnson, A. Bilateral comparison between NIM’s and NIST’s gas flow standards. MAPAN 2011, 26, 211–224. [Google Scholar] [CrossRef]
- Ishibashi, M.; Morioka, T. The renewed airflow standard system in Japan for 5–1000 m3/h. Flow Meas. Instrum. 2006, 17, 153–161. [Google Scholar] [CrossRef]
- Arai, K.; Yoshida, H. Primary flow meter for calibrating a sniffer test leak artefact by a pressure rise method. Metrologia 2014, 51, 522–527. [Google Scholar] [CrossRef]
- ichi Nakao, S. Development of the PVTt system for very low gas flow rates. Flow Meas. Instrum. 2006, 17, 193–200. [Google Scholar] [CrossRef]
- Wright, J.D.; Johnson, A.N. Lower Uncertainty (0.015% to 0.025%) of NIST’s Standards for Gas Flow from 0.01 to 2000 Standard Liters/Minute. In Proceedings of the 2009 Measurement Science Conference, Anaheim, CA, USA, 23 March 2009. [Google Scholar]
- Wright, J.; Johnson, A.; Moldover, M.; Kline, G. Gas Flowmeter Calibrations with the 34 L and 677 L PVTt Standards; NIST: Gaithersburg, MD, USA, 2004. [Google Scholar]
- Chahine, K.; Wang, Z. Establishment of an Ultra-High Accuracy 670 PVTt Gas Flow Primary Standard at NMIA. In Proceedings of the 18th International Flow Measurement Conference, Portugal, Lisbon, 26–28 June 2019. [Google Scholar]
- Cheong, K.H.; Doihara, R.; Shimada, T.; Terao, Y. Gravimetric system using high-speed double switching valves for low liquid flow rates. Meas. Sci. Technol. 2018, 29, 075304. [Google Scholar] [CrossRef]
- ISO 4185; Measurement of Liquid Flow in Closed Conduits—Weighing Method. Standard, International Organization for Standardization: Geneva, Switzerland, 1980.
- Lemmon, E.; Bell, I.H.; Huber, M.; McLinden, M. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 10.0, National Institute of Standards and Technology; Standard Reference Data Program: Gaithersburg, MD, USA, 2018. [Google Scholar]
- JCGM 100:2008; Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. Technical Report; Joint Committee for Guides in Metrology: Paris, France, 2008.







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Žibret, P.; Bobovnik, G.; Kutin, J. Time-Correction Model Based on Diverter Speed for a pVTt Gas Flow Primary Standard. Sensors 2022, 22, 4001. https://doi.org/10.3390/s22114001
Žibret P, Bobovnik G, Kutin J. Time-Correction Model Based on Diverter Speed for a pVTt Gas Flow Primary Standard. Sensors. 2022; 22(11):4001. https://doi.org/10.3390/s22114001
Chicago/Turabian StyleŽibret, Primož, Gregor Bobovnik, and Jože Kutin. 2022. "Time-Correction Model Based on Diverter Speed for a pVTt Gas Flow Primary Standard" Sensors 22, no. 11: 4001. https://doi.org/10.3390/s22114001
APA StyleŽibret, P., Bobovnik, G., & Kutin, J. (2022). Time-Correction Model Based on Diverter Speed for a pVTt Gas Flow Primary Standard. Sensors, 22(11), 4001. https://doi.org/10.3390/s22114001





