JSQE: Joint Surveillance Quality and Energy Conservation for Barrier Coverage in WSNs
Abstract
:1. Introduction
- (1)
- Guaranteeing the predefined surveillance quality of the boundary barrier
- (2)
- Lower number of working sensors
- (3)
- Scalability due to adopting the distributed approaches
- (4)
- Realistic
2. Related Work
2.1. Centralized Approaches for Barrier Coverage
2.2. Distributed Approaches for Barrier Coverage
3. Network Environment and Problem
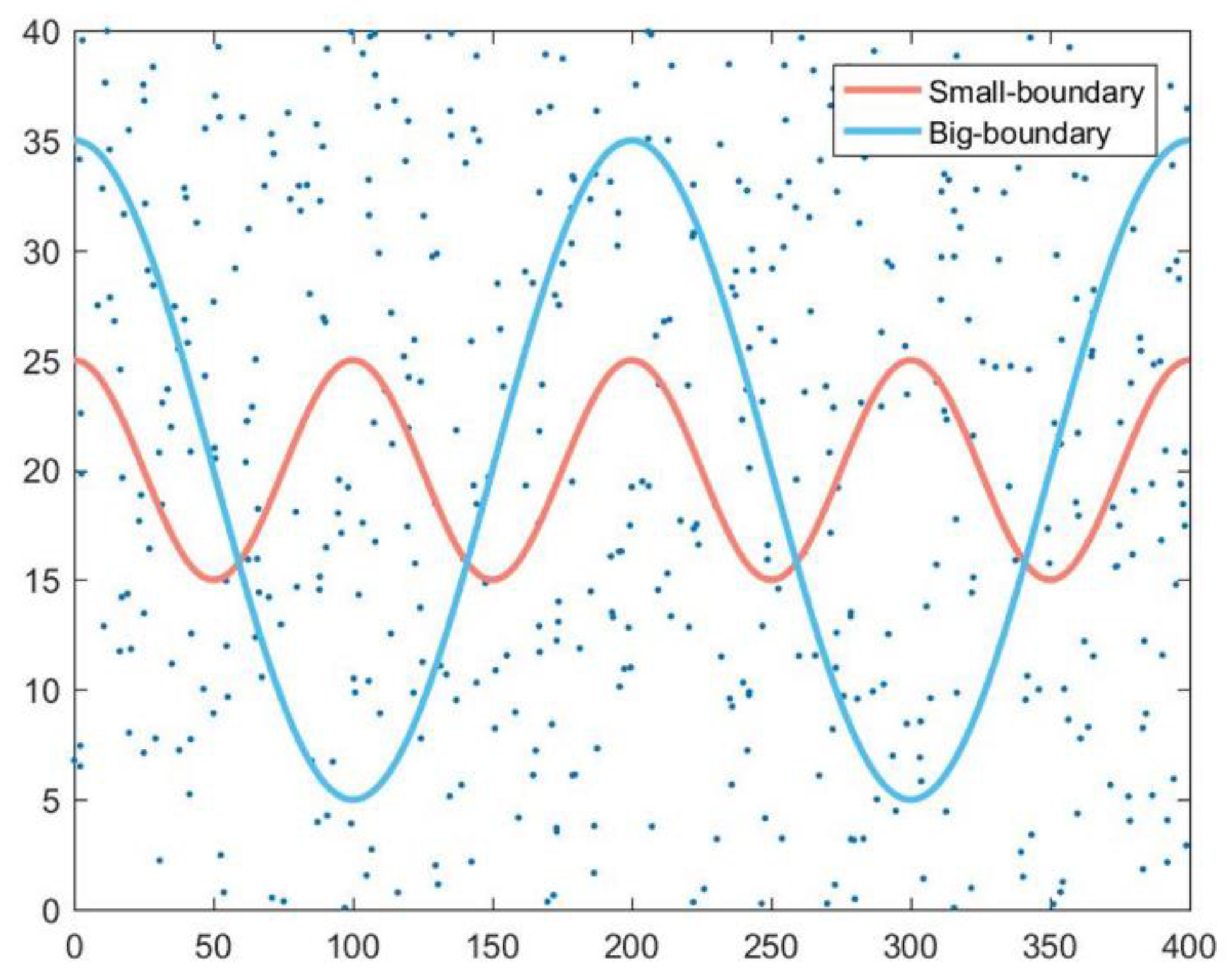
3.1. Network Environment
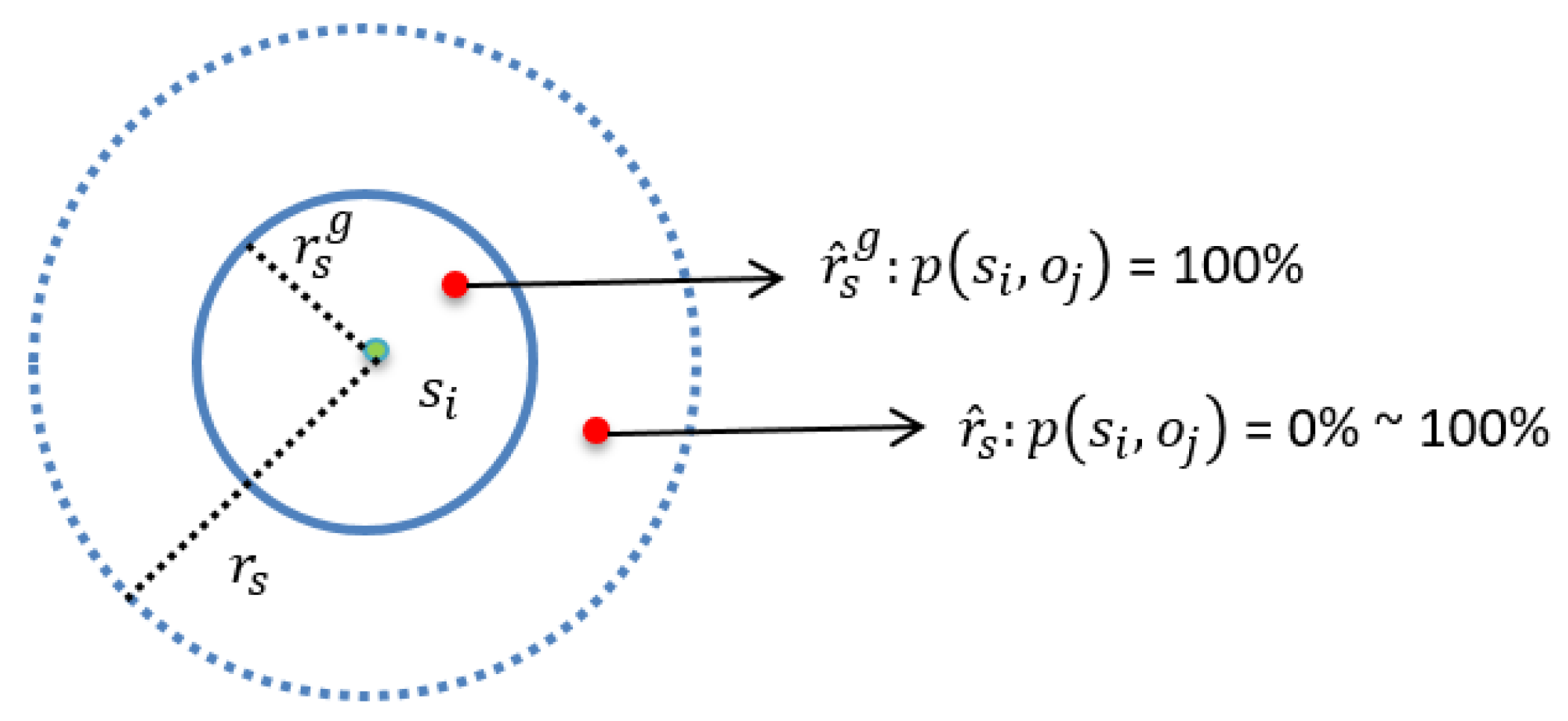
3.2. Sensing Model
3.3. Problem Formulation
- (1)
- Working State constraint:
- (2)
- Sensor energy constraint:
- (3)
- Continuous constraint:
- (4)
- Boundary constraint:
4. Joint Surveillance Quality and Energy Conservation (JSQE) Algorithm
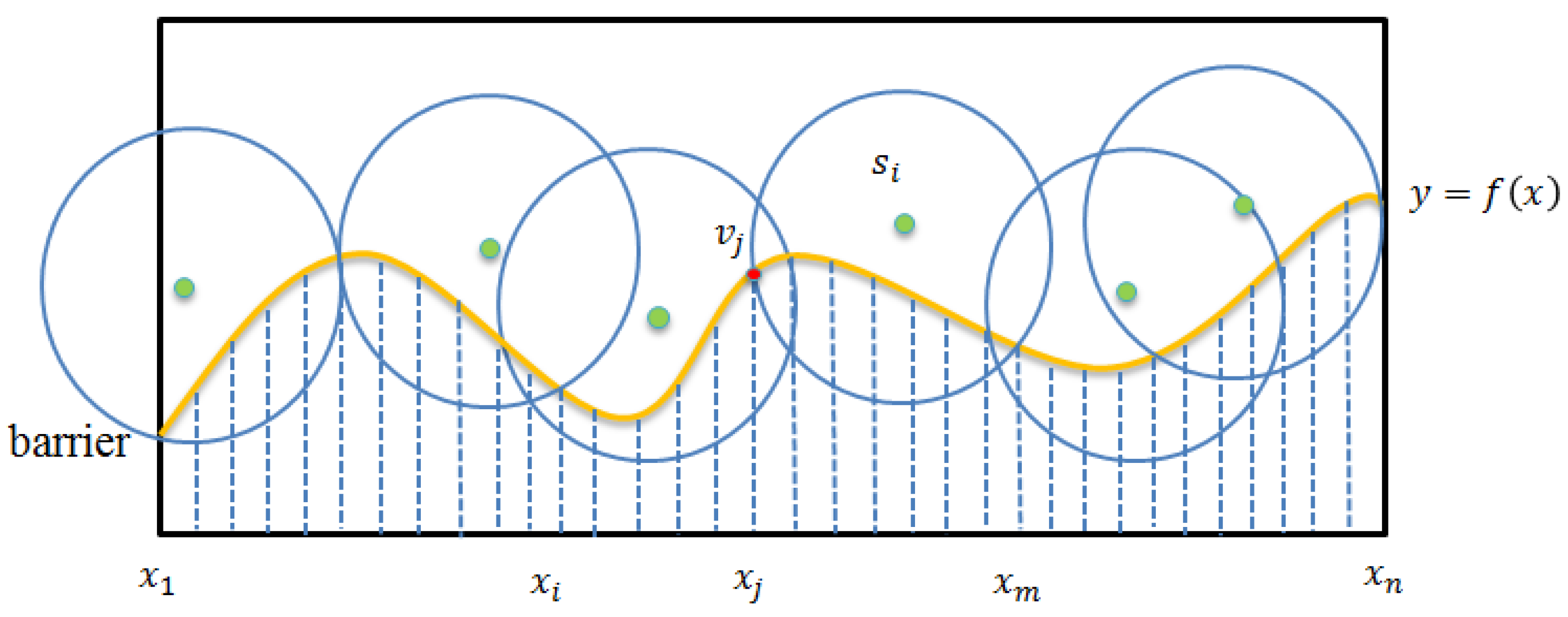
4.1. Boundary Curve Partitioning Phase
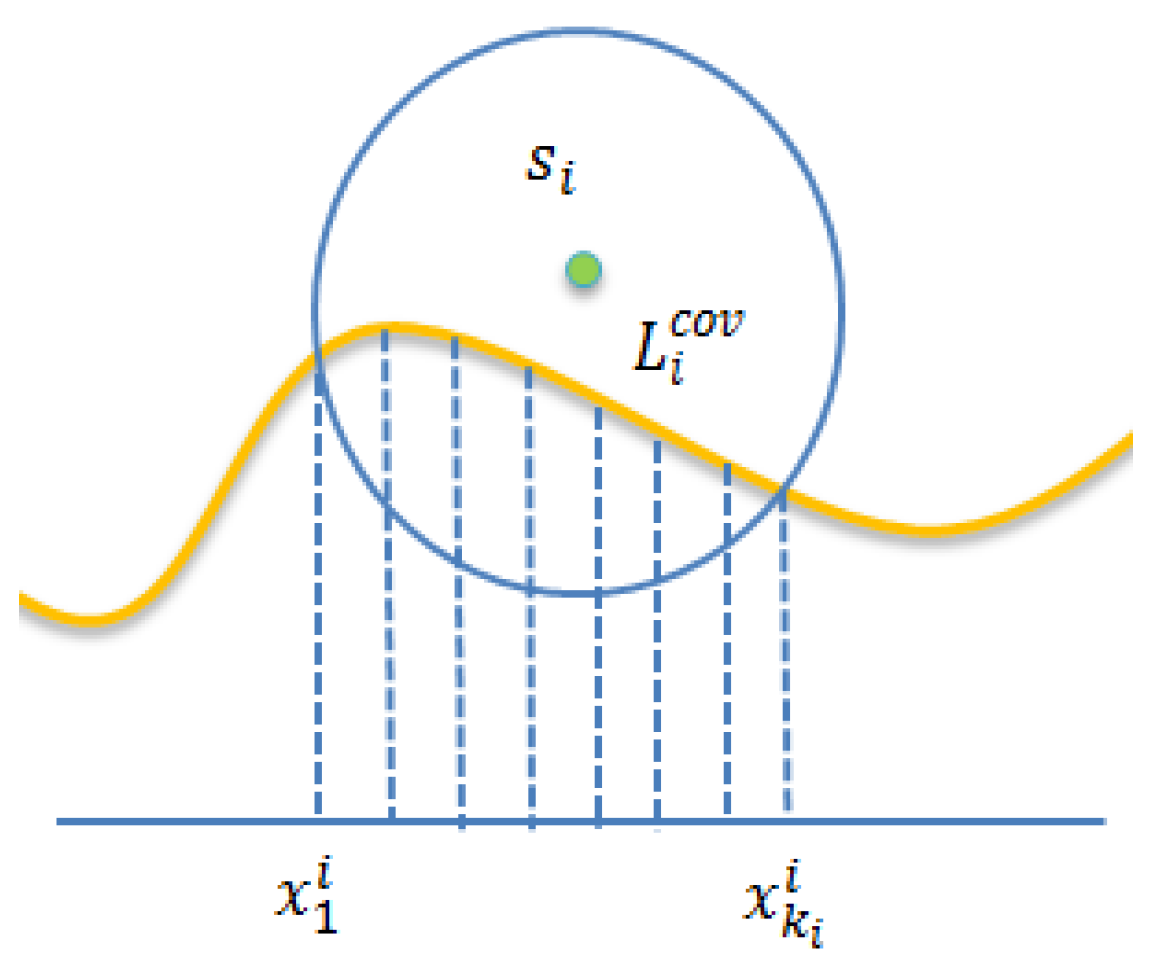
4.2. Basic Contribution Evaluation Phase
- (1)
- Sensor neighbors .
- (2)
- The covered segments of and are overlapped, that is, the following condition holds.
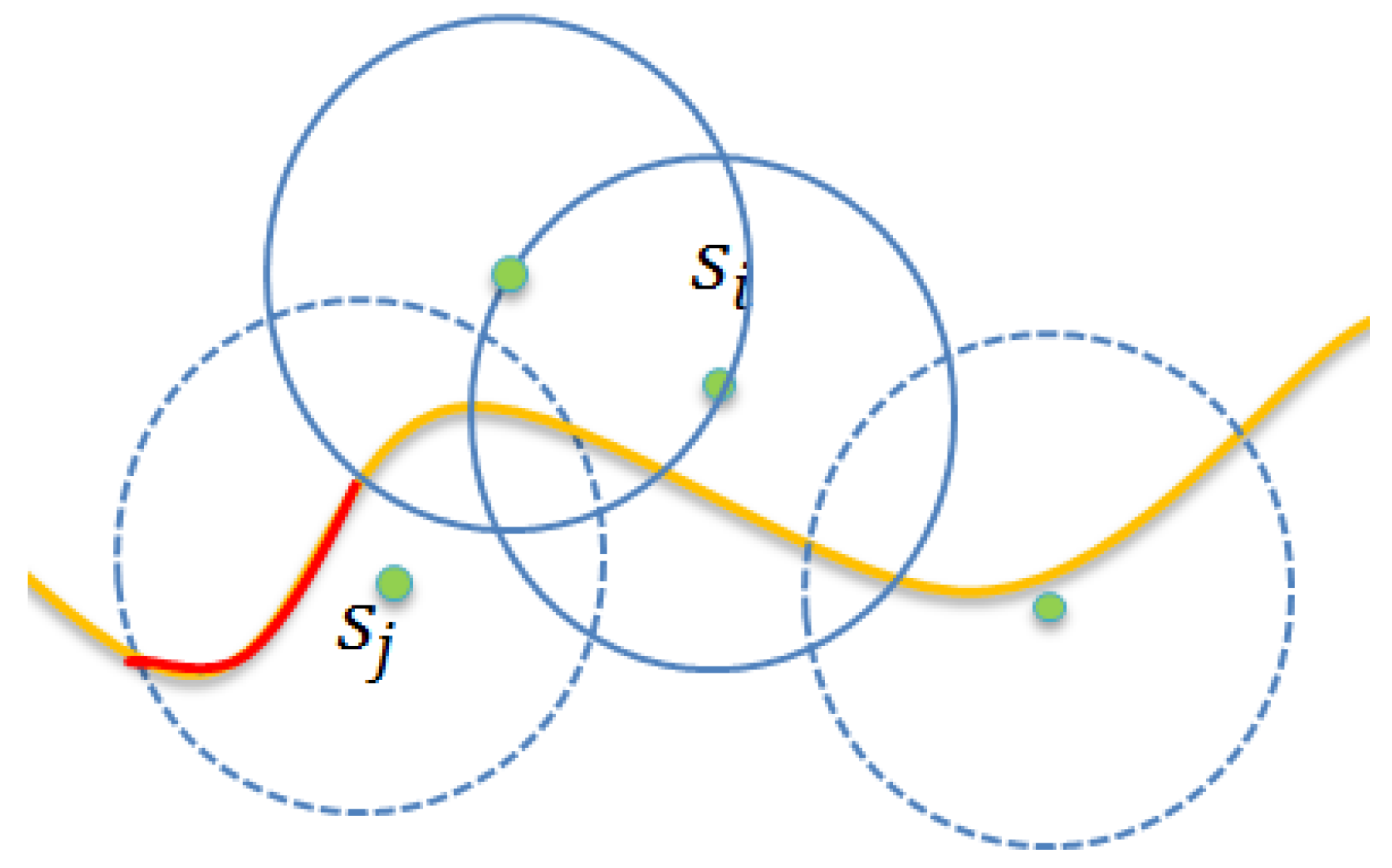
4.3. Collaborative Contribution Evaluation Phase
4.4. Terminating Phase
4.5. The Proposed JSQE Algorithm
| Algorithm 1. Joint Surveillance Quality and Energy Conservation (JSQE) |
| Inputs: A set of sensors, . Notation (xi, yi) denotes the location of sensor . The boundary curve can be modeled by function , where and denote the x coordinates of the leftmost and rightmost points of the boundary curve, respectively. A partitioned boundary curve with n line segments. |
| Output: The set of working sensors . |
| //Phase I. Boundary Curve Partitioning Phase// 1. Sensor evaluates the covered line segments according to Equation (12); 2. Let denote the number of line segments covered by sensor ; //Phase II. Basic Contribution Evaluation Phase// 3. Each sensor executes the following operations. 4. Evaluate its contribution according to Equation (15); 5. Set up its waiting time according to Equation (16); 6. Call ; 7. If (The loser has no overlapped segment with any neighboring working sensor) 8. Go to Step 6; 9. End If //Phase III. Collaborative Contribution Evaluation Phase// 10. For each 11. Evaluate ; 12. ; 13. End for 14. Evaluate according to Equation (21); 15. ; 16. Evaluate ; 17. Let ; 18. Evaluate according to Equation (25); 19. Evaluate according to Equation (26); //set up waiting time 20. Call ; 21. If ()// is the predefined contribution threshold 22. Goto 10; 23. End if //Phase IV. Terminating Phase// 24. Sensor stays in sleeping state; 25. While (listen()! = null) 26. Goto 10;// is a loser again 27. EndWhile 28. Return ;//the set of working sensors //Procedure Wait()// Procedure Wait(Timer ti){ While(listen( )=Null or backoff time ti >0){ Wait for one time slot; backoff time --; } EndWhile If (backoff time = 0) { Wake up and set My_role = winner; End of Scheduling and switch to working state; } End If My_role = loser; } |
5. Simulation
5.1. Simulation Environment
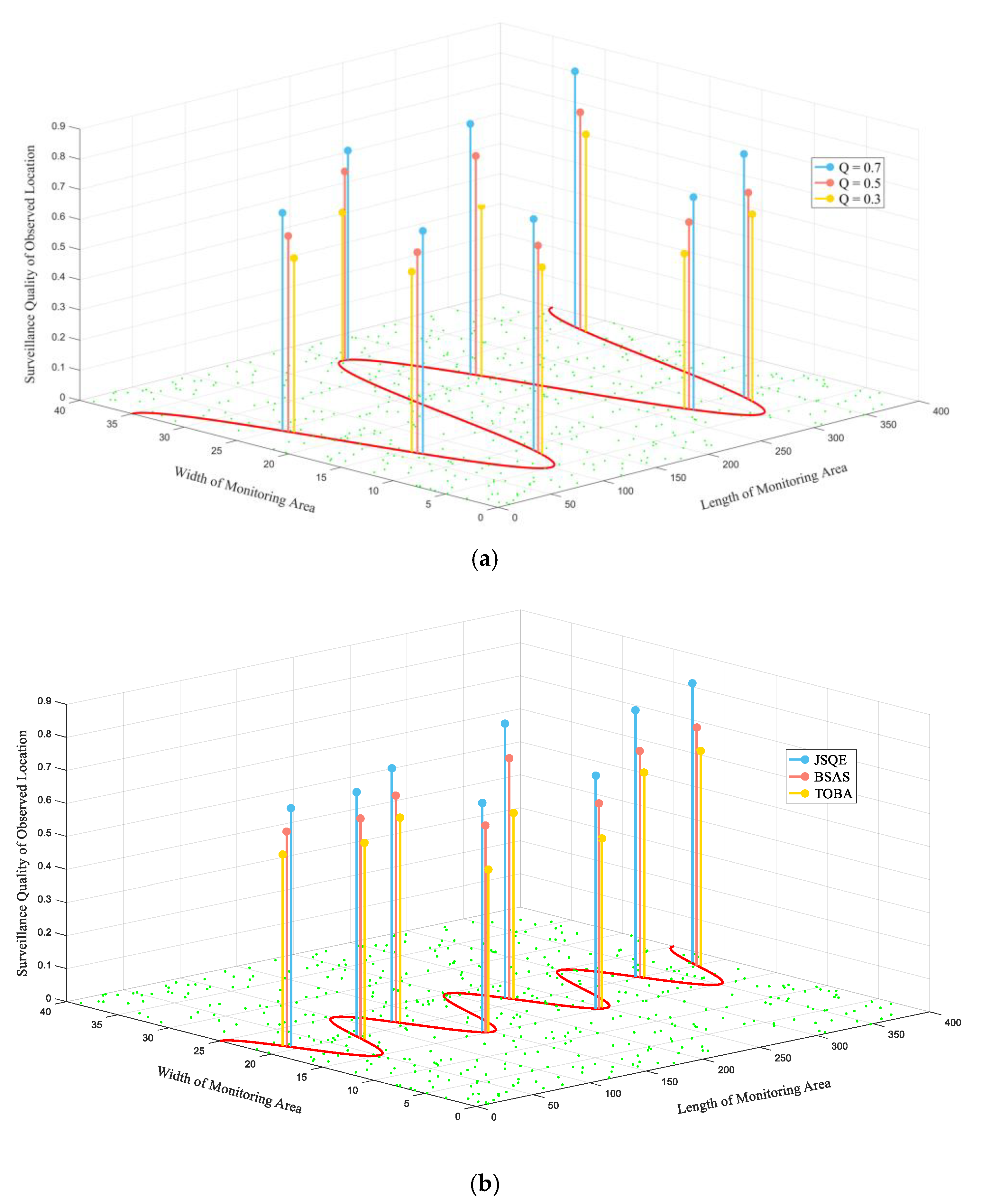
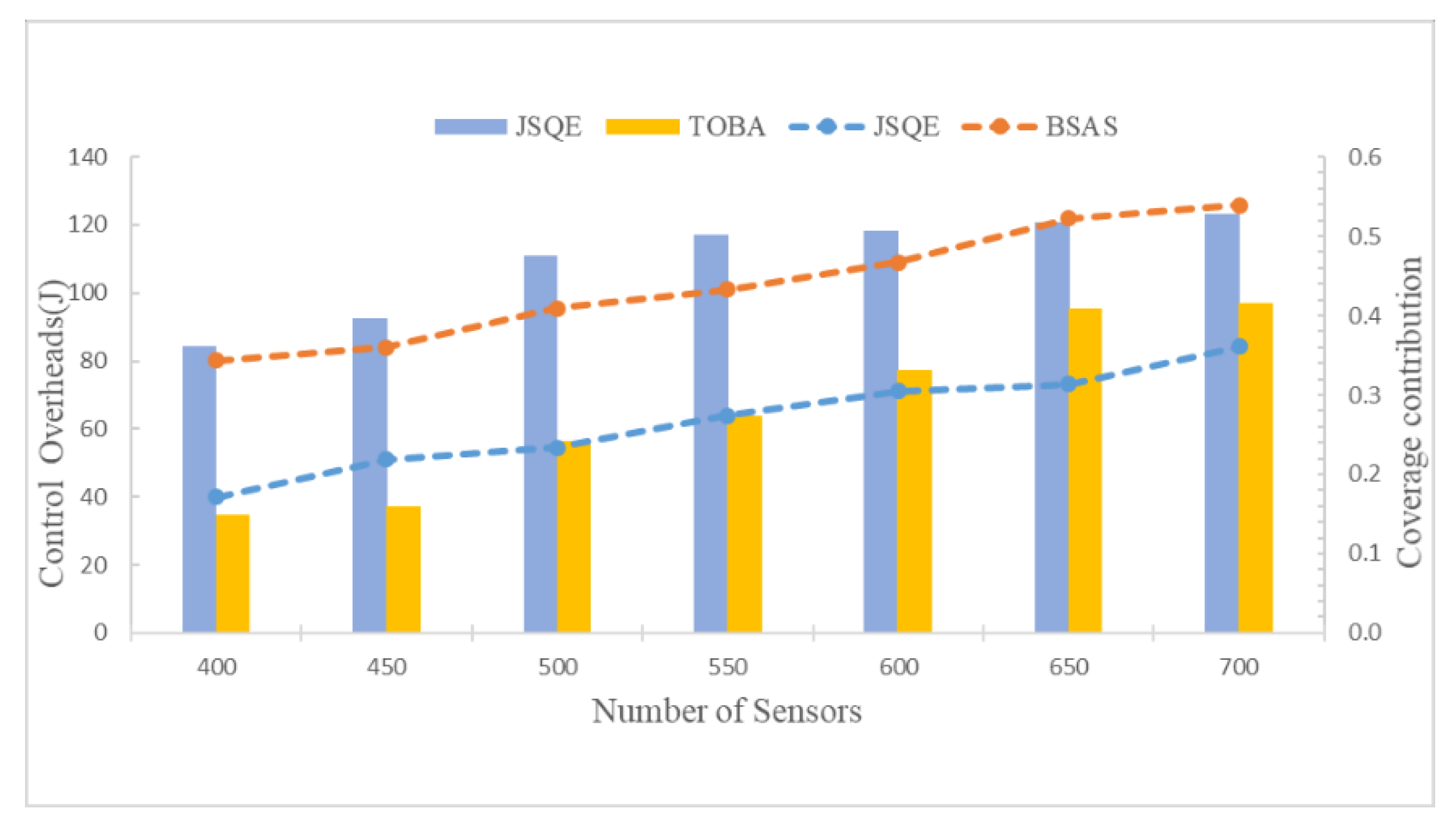
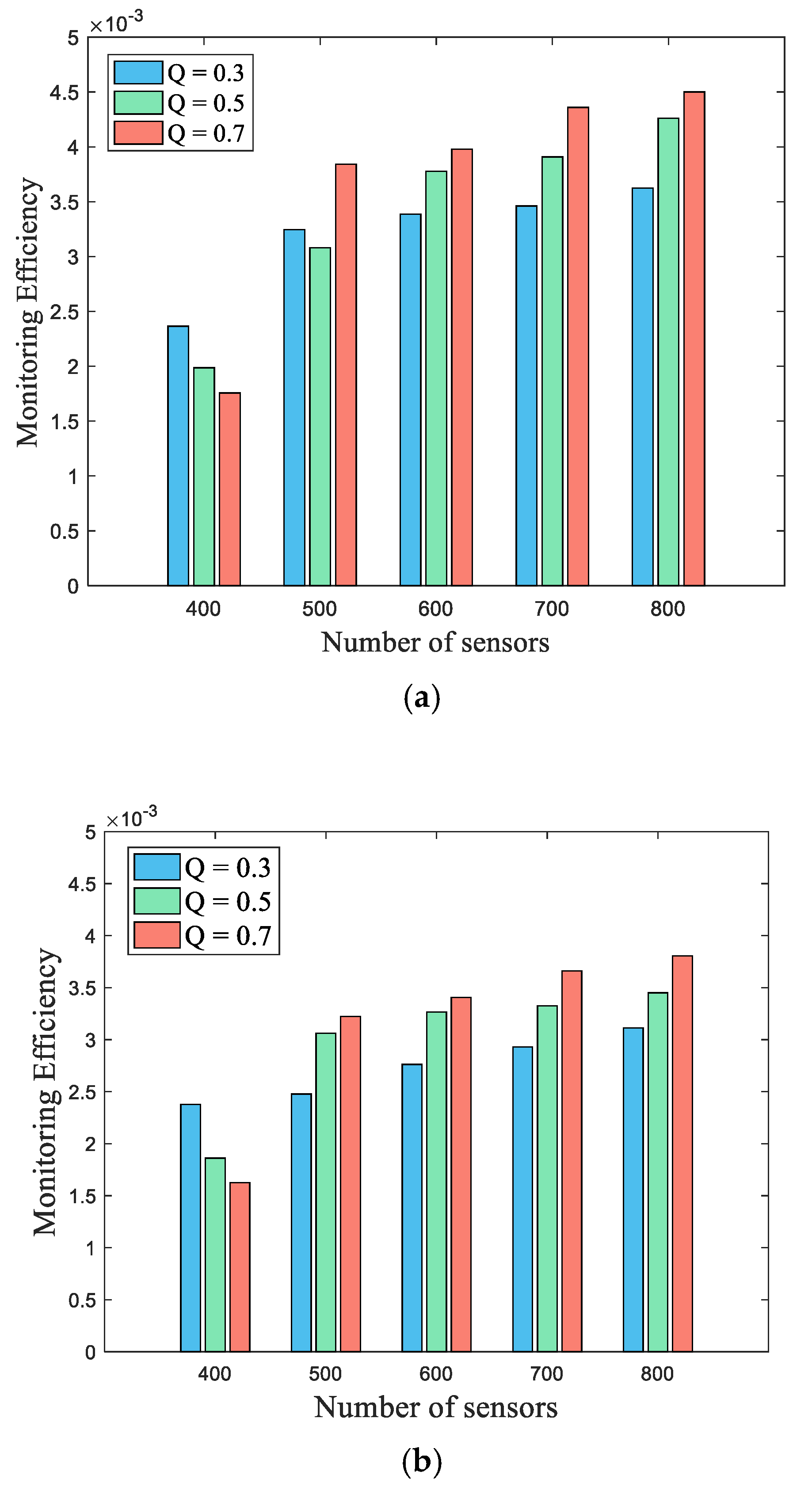
5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hazarika, A.; Poddar, S.; Nasralla, M.M.; Rahaman, H. Area and energy efficient shift and accumulator unit for object detection in IoT applications. AEJ Alex. Eng. J. 2022, 61, 795–809. [Google Scholar] [CrossRef]
- Fascista, A. Toward Integrated Large-Scale Environmental Monitoring Using WSN/UAV/Crowdsensing: A Review of Applications, Signal Processing, and Future Perspectives. Sensors 2022, 22, 1824. [Google Scholar] [CrossRef] [PubMed]
- Brito, T.; Pereira, A.I.; Lima, J.; Valente, A. Wireless Sensor Network for Ignitions Detection: A IoT approach. Electronics 2020, 9, 893. [Google Scholar] [CrossRef]
- Wang, X.; Yang, L.T.; Kuang, L.; Liu, X.; Zhang, Q.; Deen, M.J. A tensor-based big data-driven routing recommendation approach for heterogeneous networks. IEEE Netw. 2019, 33, 64–69. [Google Scholar] [CrossRef]
- Akram, J.; Munawar, H.S.; Kouzani, A.Z.; Mahmud, M.A.P. Using Adaptive Sensors for Optimised Target Coverage in Wireless Sensor Networks. Sensors 2022, 22, 1083. [Google Scholar] [CrossRef] [PubMed]
- Ghazalian, R.; Aghagolzadeh, A.; Andargoli, S.M.H. Energy Optimization of Wireless Visual Sensor Networks with the Consideration of the Desired Target Coverage. IEEE Trans. Mob. Comput. 2021, 20, 2795–2807. [Google Scholar] [CrossRef]
- Chakraborty, S.; Goyal, N.K.; Soh, S. On Area Coverage Reliability of Mobile Wireless Sensor Networks with Multistate Nodes. IEEE Sens. J. 2020, 20, 4992–5003. [Google Scholar] [CrossRef]
- Chang, J.; Shen, X.; Bai, W.; Li, X. Energy-Efficient Barrier Coverage Based on Nodes Alliance for Intrusion Detection in Underwater Sensor Networks. IEEE Sens. J. 2022, 22, 3766–3776. [Google Scholar] [CrossRef]
- Cheng, C.-F.; Hsu, C.-C. The Deterministic Sensor Deployment Problem for Barrier Coverage in WSNs with Irregular Shape Areas. IEEE Sens. J. 2022, 22, 2899–2911. [Google Scholar] [CrossRef]
- Anand, A.S.; Anitha, V.S. Energy efficiency and lifetime enhancement of K-Barrier coverage in Wireless Sensor Networks. In Proceedings of the International Conference on Inventive Communication and Computational Technologies (ICICCT), Coimbatore, India, 20–21 April 2018; pp. 1888–1893. [Google Scholar]
- Han, R.; Yang, W.; Zhang, L. Achieving Crossed Strong Barrier Coverage in Wireless Sensor Network. Sensors 2018, 18, 534. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Silvestri, S.; Goss, K. MobiBar: An autonomous deployment algorithm for barrier coverage with mobile sensors. Ad Hoc Netw. 2017, 54, 111–129. [Google Scholar] [CrossRef]
- Chen, A.; Kumar, S.; Lai, T.H. Local Barrier Coverage in Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2010, 9, 491–504. [Google Scholar] [CrossRef]
- Saipulla, A.; Westphal, C.; Liu, B.; Wang, J. Barrier Coverage with Line-Based Deployed Mobile Sensors. Ad Hoc Netw. 2013, 11, 1381–1391. [Google Scholar] [CrossRef]
- Weng, C.-I.; Chang, C.-Y.; Hsiao, C.-Y.; Chang, C.-T.; Chen, H. On-supporting energy balanced k-barrier coverage in wireless sensor networks. IEEE Access 2018, 6, 13261–13274. [Google Scholar] [CrossRef]
- Xu, P.; Chang, I.; Chang, C.; Dande, B.; Hsiao, C. A Distributed Barrier Coverage Mechanism for Supporting Full View in Wireless Visual Sensor Networks. IEEE Access 2019, 7, 156895–156906. [Google Scholar] [CrossRef]
- Dong, Z.; Shang, C.; Chang, C.-Y.; Roy, D.S. Barrier Coverage Mechanism Using Adaptive Sensing Range for Renewable WSNs. IEEE Access 2020, 8, 86065–86080. [Google Scholar] [CrossRef]
- Si, P.; Ma, J.; Tao, F.; Fu, Z.; Shu, L. Energy-Efficient Barrier Coverage with Probabilistic Sensors in Wireless Sensor Networks. IEEE Sens. J. 2020, 20, 5624–5633. [Google Scholar] [CrossRef]
- Zhang, X.; Wymore, M.L.; Qiao, D. An iterative method for strong Barrier coverage under practical constraints. In Proceedings of the IEEE International Conference on Communication (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 1–7. [Google Scholar]
- Chen, J.; Li, J.; Lai, T.H. Energy-Efficient Intrusion Detection with a Barrier of Probabilistic Sensors: Global and Local. IEEE Trans. Wirel. Commun. 2013, 12, 4742–4755. [Google Scholar] [CrossRef]
- Xu, X.; Dai, Z.; Shan, A.; Gu, T. Connected Target ϵ-probability Coverage in WSNs with Directional Probabilistic Sensors. IEEE Syst. J. 2020, 14, 3399–3409. [Google Scholar] [CrossRef]
- Fan, X.; Hu, F.; Liu, T.; Chi, K.; Xu, J. Cost effective directional barrier construction based on zooming and united probabilistic detection. IEEE Trans. Mob. Comput. 2020, 19, 1555–1569. [Google Scholar] [CrossRef]






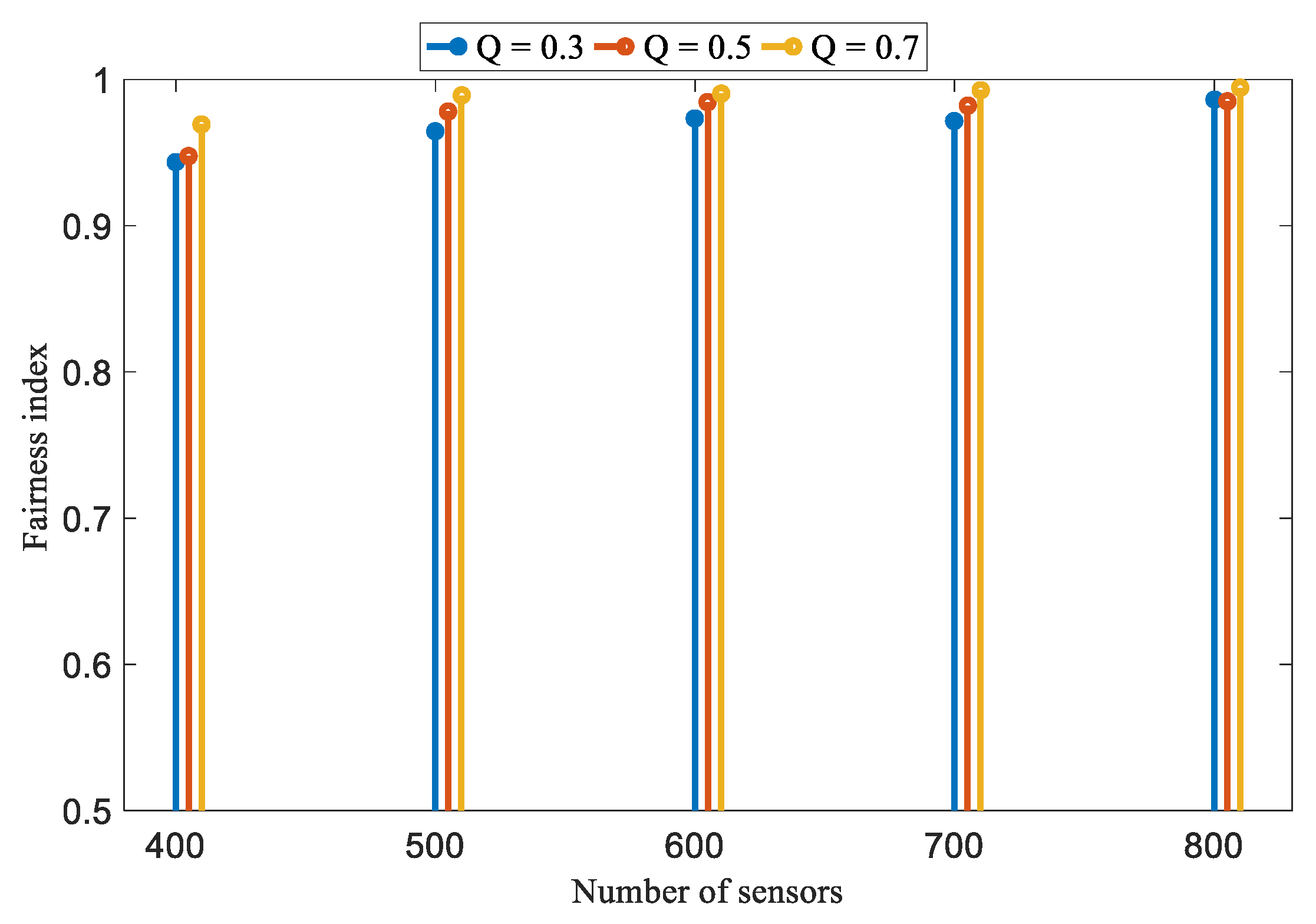
| Studies | Distributed | ESM Model | Monitoring Quality | Goal of Minimum Numbers of Sensors |
|---|---|---|---|---|
| [13] | ✗ | ✗ | ✓ | ✗ |
| [14] | ✗ | ✗ | ✓ | ✗ |
| [15] | ✓ | ✗ | ✗ | ✗ |
| [16] | ✓ | ✗ | ✗ | ✓ |
| [17] | ✗ | ✓ | ✓ | ✗ |
| [22] | ✓ | ✓ | ✗ | ✗ |
| JSQE | ✓ | ✓ | ✓ | ✓ |
| Parameter | Description |
|---|---|
| Monitoring area | 400 m × 40 m |
| Number of sensor nodes | 400–800 |
| Sensing range | 10 m |
| Communication range | 20 m |
| Required monitoring quality | 0.3, 0.5, 0.7 |
| Working energy cost | 0.05 J/s |
| Deployment | Randomly |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, X.; Chang, C.-Y.; Zhao, S.; Kuo, C.-H.; Roy, D.S.; Pi, X.; Yang, S.-J. JSQE: Joint Surveillance Quality and Energy Conservation for Barrier Coverage in WSNs. Sensors 2022, 22, 4120. https://doi.org/10.3390/s22114120
Shao X, Chang C-Y, Zhao S, Kuo C-H, Roy DS, Pi X, Yang S-J. JSQE: Joint Surveillance Quality and Energy Conservation for Barrier Coverage in WSNs. Sensors. 2022; 22(11):4120. https://doi.org/10.3390/s22114120
Chicago/Turabian StyleShao, Xuemei, Chih-Yung Chang, Shenghui Zhao, Chin-Hwa Kuo, Diptendu Sinha Roy, Xinzhe Pi, and Shin-Jer Yang. 2022. "JSQE: Joint Surveillance Quality and Energy Conservation for Barrier Coverage in WSNs" Sensors 22, no. 11: 4120. https://doi.org/10.3390/s22114120
APA StyleShao, X., Chang, C. -Y., Zhao, S., Kuo, C. -H., Roy, D. S., Pi, X., & Yang, S. -J. (2022). JSQE: Joint Surveillance Quality and Energy Conservation for Barrier Coverage in WSNs. Sensors, 22(11), 4120. https://doi.org/10.3390/s22114120






