Solid-Phase Reference Baths for Fiber-Optic Distributed Sensing
Abstract
:1. Introduction
2. Materials and Methods
2.1. SoPhaB Design and Use
2.2. Field and Laboratory Evaluations
3. Results
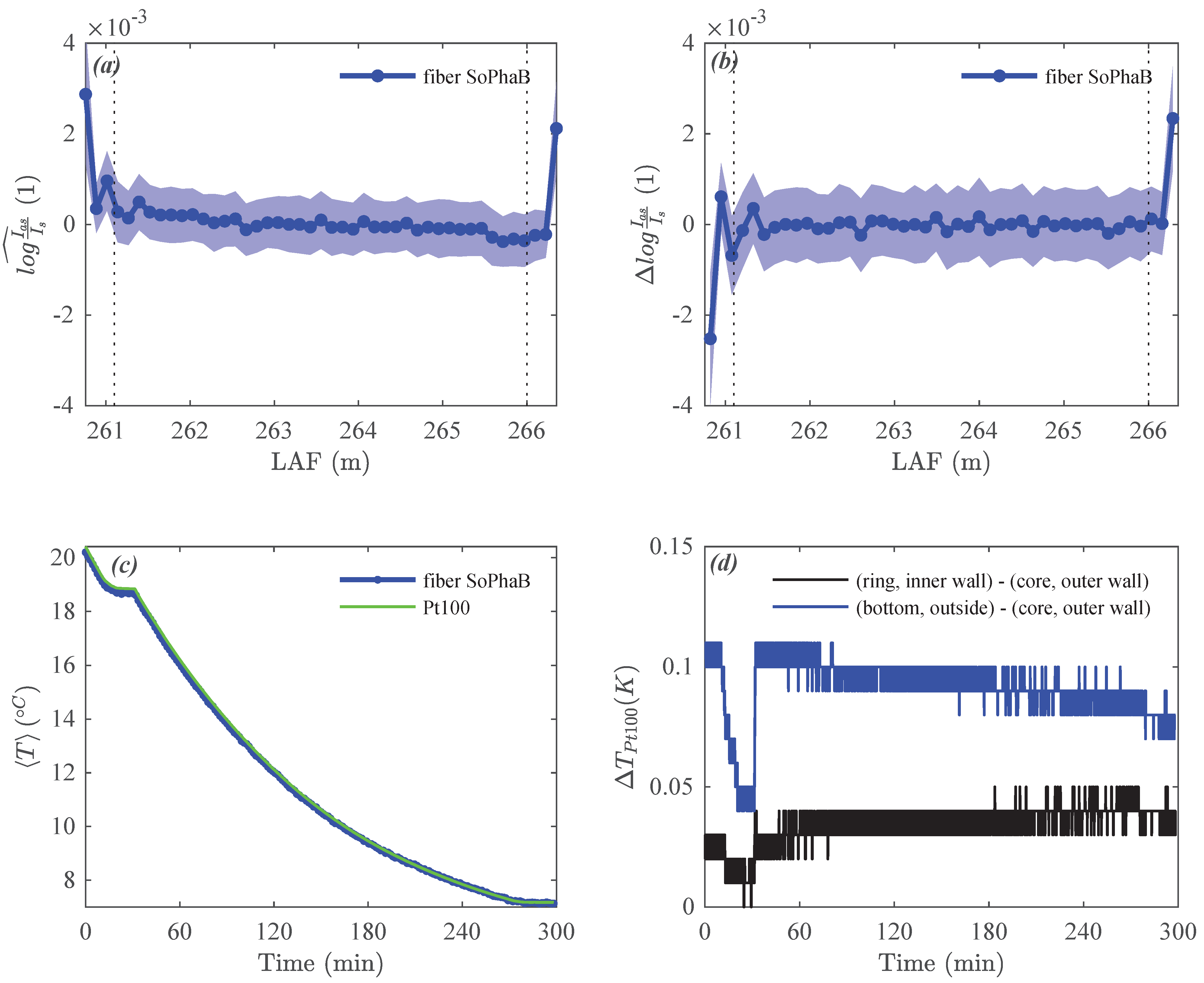
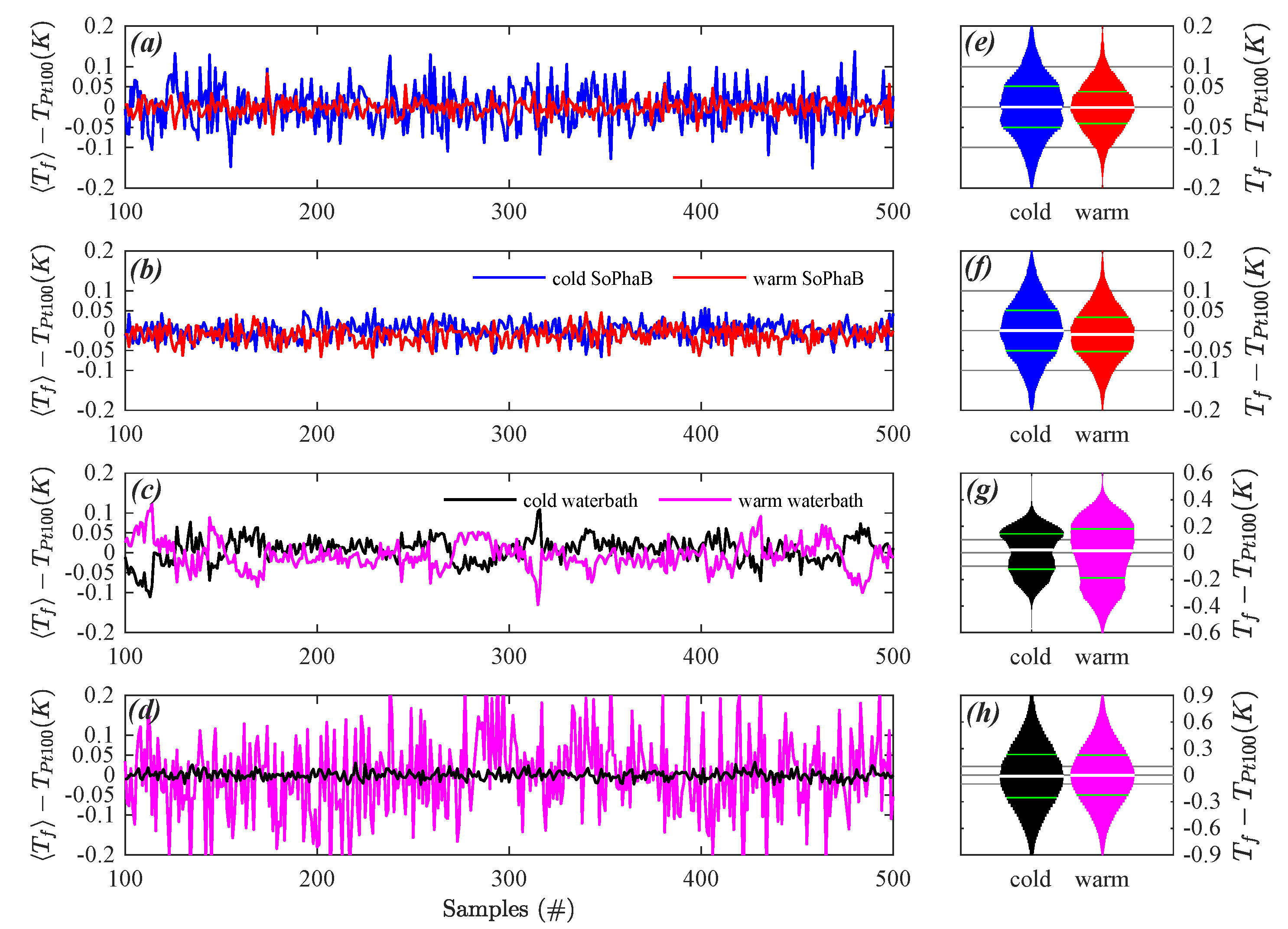
3.1. Windtunnel Evaluation
3.2. Field Deployments
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Constructing a Solid-Phase Bath for Referencing Fiber-Optic Observations
| Component | Quantity | Source, Manufacturer | Article No. |
|---|---|---|---|
| Pelican cases, 371 mm × 258 mm × 152 mm inside | 2 | www.captura-systems.com (accessed on 8 April 2022) Peli, Torrance, CA, USA | 1450-001-190E |
| Peltier element 140 W, 62 mm × 62 mm | 4 | www.peltron.de (accessed on 8 April 2022) | TEC1-12714S |
| Electronics housing, 265 mm × 185 mm × 95 mm | 1 | www.reichelt.de (accessed on 8 April 2022) | RND 455-00166 |
| Display, heating | 1 | www.quick-ohm.de (accessed on 8 April 2022) | QC-PC-D-100 |
| Display, cooling/heating | 1 | www.quick-ohm.de (accessed on 8 April 2022) | QC-PC-D-CH1 |
| Peltier controller, heating | 1 | www.quick-ohm.de (accessed on 8 April 2022) | QC-PC-C01H |
| Peltier controller, cooling/heating | 1 | www.quick-ohm.de (accessed on 8 April 2022) | QC-PC-CO-CH1 |
| Platinum wire thermometer (Pt100) | 4 | www.electrotherm.de (accessed on 8 April 2022) | WTY-00DU |
| CPU cooler | 2 | www.mindfactory.de (accessed on 8 April 2022), Cooler Master Hyper H412R, Taipei City, Taiwan | 8828510 |
| Power supply | 1 | www.reichelt.de (accessed on 8 April 2022) | MW GST280A12 |
| Connector female CA | 5 | www.reichelt.de (accessed on 8 April 2022), Hirschmann, Neckartenzlingen, Germany | CA 3 GD |
| Connector male CA | 5 | www.reichelt.de (accessed on 8 April 2022), Hirschmann, Neckartenzlingen, Germany | CA 3 LS |
| Connector female CA | 4 | www.reichelt.de (accessed on 8 April 2022), Hirschmann, Neckartenzlingen, Germany | CA 6 GD |
| Connector male CA | 4 | www.reichelt.de (accessed on 8 April 2022), Hirschmann, Neckartenzlingen, Germany | CA 6 LS |
| Copper block D200 × 50 mm (for core and ring) | 2 | www.jera-metall.de (accessed on 8 April 2022) | - |
| Copper block D200 × 23 mm (for top and bottom slab) | 4 | www.jera-metall.de (accessed on 8 April 2022) | - |
| Copper pin D15 × 10 mm (connector) | 4 | www.jera-metall.de (accessed on 8 April 2022) | - |
| Copper pin D8 × 10 mm (connector) | 2 | www.jera-metall.de (accessed on 8 April 2022) | - |
| Aluminium block 105 mm × 58 mm × 58 mm | 2 | www.jera-metall.de (accessed on 8 April 2022) | - |
| Production Process | Quantity |
|---|---|
| Final assemblage including electronics and carrying case | 80 h |
| Electrical discharge machining (EDM) | 10 h |
| EDM wire | 6 km |
| Traditional machining | 80 h |
References
- Higgins, C.W.; Wing, M.G.; Kelley, J.; Sayde, C.; Burnett, J.; Holmes, H.A. A high resolution measurement of the morning ABL transition using distributed temperature sensing and an unmanned aircraft system. Environ. Fluid Mech. 2018, 18, 683–693. [Google Scholar] [CrossRef]
- Peltola, O.; Lapo, K.; Martinkauppi, I.; O’Connor, E.; Thomas, C.K.; Vesala, T. Suitability of fibre-optic distributed temperature sensing for revealing mixing processes and higher-order moments at the forest–air interface. Atmos. Meas. Tech. 2021, 14, 2409–2427. [Google Scholar] [CrossRef]
- Fritz, A.M.; Lapo, K.; Freundorfer, A.; Linhardt, T.; Thomas, C.K. Revealing the Morning Transition in the Mountain Boundary Layer Using Fiber-Optic Distributed Temperature Sensing. Geophys. Res. Lett. 2021, 48, e2020GL092238. [Google Scholar] [CrossRef]
- Sayde, C.; Thomas, C.K.; Wagner, J.; Selker, J.S. High-resolution wind speed measurements using actively heated fiber optics. Geophys. Res. Lett. 2015, 42, 10064–10073. [Google Scholar] [CrossRef] [Green Version]
- Pfister, L.; Sigmund, A.; Olesch, J.; Thomas, C.K. Nocturnal Near-Surface Temperature, but not Flow Dynamics, can be Predicted by Microtopography in a Mid-Range Mountain Valley. Bound.-Layer Meteorol. 2017, 165, 333–348. [Google Scholar] [CrossRef]
- Pfister, L.; Lapo, K.; Mahrt, L.; Thomas, C.K. Thermal Submesoscale Motions in the Nocturnal Stable Boundary Layer. Part 1: Detection and Mean Statistics. Bound.-Layer Meteorol. 2021, 180, 180–202. [Google Scholar] [CrossRef]
- Thomas, C.K.; Kennedy, A.M.; Selker, J.S.; Moretti, A.; Schroth, M.H.; Smoot, A.R.; Tufillaro, N.B.; Zeeman, M.J. High-resolution fibre-optic temperature sensing: A new tool to study the two-dimensional structure of atmospheric surface layer flow. Bound.-Layer Meteorol. 2012, 142, 177–192. [Google Scholar] [CrossRef]
- Zeeman, M.; Selker, J.S.; Thomas, C.K. Near-surface motion in the nocturnal, stable boundary layer observed with fibre-optic distributed temperature sensing. Bound.-Layer Meteorol. 2015, 154, 189–205. [Google Scholar] [CrossRef]
- Hilgersom, K.P.; van de Giesen, N.C.; de Louw, P.G.B.; Zijlema, M. Three-dimensional dense distributed temperature sensing for measuring layered thermohaline systems. Water Resour. Res. 2016, 52, 6656–6670. [Google Scholar] [CrossRef] [Green Version]
- Thomas, C.; Selker, J. Optical fiber-based distributed sensing methods. In Springer Handbook of Atmospheric Measurements; Foken, T., Ed.; Springer: Basel, Switzerland, 2021; Chapter 20; pp. 609–631. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.j.; Song, S.; Li, F. Overview of Fibre Optic Sensing Technology in the Field of Physical Ocean Observation. Front. Phys. 2021, 9, 1–9. [Google Scholar] [CrossRef]
- Min, R.; Liu, Z.; Pereira, L.; Yang, C.; Sui, Q.; Marques, C. Optical fiber sensing for marine environment and marine structural health monitoring: A review. Opt. Laser Technol. 2021, 140, 107082. [Google Scholar] [CrossRef]
- Selker, J.; van de Giesen, N.; Westhoff, M.; Luxemburg, W.; Parlange, M.B. Fiber optics opens window on stream dynamics. Geophys. Res. Lett. 2006, 33, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Hausner, M.B.; Suárez, F.; Glander, K.E.; van de Giesen, N.; Selker, J.S.; Tyler, S.W. Calibrating Single-Ended Fiber-Optic Raman Spectra Distributed Temperature Sensing Data. Sensors 2011, 11, 10859–10879. [Google Scholar] [CrossRef]
- van de Giesen, N.; Steele-Dunne, S.C.; Jansen, J.; Hoes, O.; Hausner, M.B.; Tyler, S.; Selker, J. Double-Ended Calibration of Fiber-Optic Raman Spectra Distributed Temperature Sensing Data. Sensors 2012, 12, 5471–5485. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- des Tombe, B.; Schilperoort, B.; Bakker, M. Estimation of Temperature and Associated Uncertainty from Fiber-Optic Raman-Spectrum Distributed Temperature Sensing. Sensors 2020, 20, 2235. [Google Scholar] [CrossRef] [Green Version]
- Lapo, K.; Freundorfer, A.; Fritz, A.; Schneider, J.; Olesch, J.; Babel, W.; Thomas, C.K. The Large eddy Observatory, Voitsumra Experiment 2019 (LOVE19) with high-resolution, spatially distributed observations of air temperature, wind speed, and wind direction from fiber-optic distributed sensing, towers, and ground-based remote sensing. Earth Syst. Sci. Data 2022, 14, 885–906. [Google Scholar] [CrossRef]
- Zeller, M.L.; Huss, J.M.; Pfister, L.; Lapo, K.E.; Littmann, D.; Schneider, J.; Schulz, A.; Thomas, C.K. The NY-Alesund TurbulencE Fiber Optic eXperiment (NYTEFOX): Investigating the Arctic boundary layer, Svalbard. Earth Syst. Sci. Data 2021, 13, 3439–3452. [Google Scholar] [CrossRef]
- Enescu, D.; Virjoghe, E.O. A review on thermoelectric cooling parameters and performance. Renew. Sustain. Energy Rev. 2014, 38, 903–916. [Google Scholar] [CrossRef]
- Lapo, K.; Freundorfer, A. Klapo/Pyfocs v0.5; Zenodo: Genève, Switzerland, 2020. [Google Scholar] [CrossRef]
- Lapo, K.; Freundorfer, A.; Pfister, L.; Schneider, J.; Selker, J.; Thomas, C. Distributed observations of wind direction using microstructures attached to actively heated fiber-optic cables. Atmos. Meas. Tech. 2020, 13, 1563–1573. [Google Scholar] [CrossRef] [Green Version]
- Esders, E.M.; Georgi, C.; Babel, W.; Thomas, C.K. Quantitative detection of aerial suspension of particles with a full-frame visual camera for atmospheric wind tunnel studies. Aerosol Sci. Technol. 2022, 56, 530–544. [Google Scholar] [CrossRef]
- Sigmund, A.; Pfister, L.; Sayde, C.; Thomas, C.K. Quantitative analysis of the radiation error for aerial coiled-fiber-optic distributed temperature sensing deployments using reinforcing fabric as support structure. Atmos. Meas. Tech. 2017, 10, 2149–2162. [Google Scholar] [CrossRef] [Green Version]
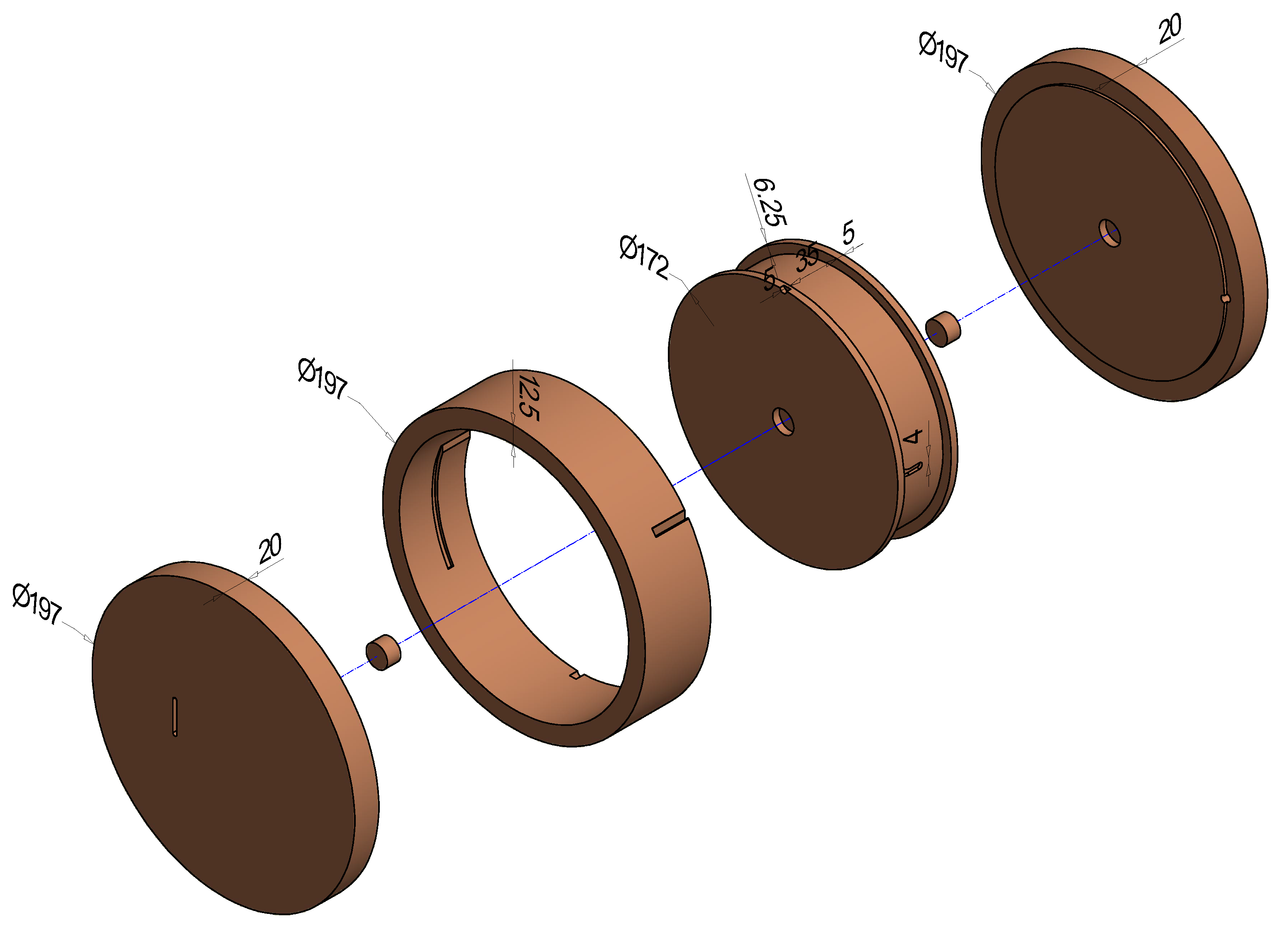


| Reference Label | Fiber-Optic Cable | Fiber-Optic Sampling and Cable Length | DTS Instrument | Calibration Routine | Reference Bath |
|---|---|---|---|---|---|
| Windtunnel | SMM, stainless-steel sheath (0.82 mm OD), loosely buffered, gel-filled, with red PE coating (0.15 mm), OD 1.12 mm | 0.127 m, 30 s avg sampled every 90 s, length 270 m | Silixa Ultima 5 km variant | internal manufacturer calibration with differential attenuation estimated visually; single-ended | SoPhaB, Pt100 read by external data logger |
| Arctic polarnight | SMM, with transparent PE jacket, OD 0.25 mm | 0.254 m, 5 s avg sampled every 15 s, length 250 m | Silixa XT | ordinary least squares; single-ended | SoPhaB, Pt100 read by DTS machine |
| Urban summer | SMM, PVC sheath, tightly buffered, aramid reinforced, white, OD 0.9 mm | 0.254 m, 12 s avg sampled every 12 s, length 610 m | Silixa XT | weighted least squares; double-ended | SoPhaB, Pt100 read by DTS machine |
| Arctic pier | SMM, PVC sheath, tightly buffered, aramid reinforced, white, OD 0.9 mm | 0.254 m, 10 s avg sampled every 10 s, length 320 m | Silixa XT | ordinary least squares; single-ended | liquid-phase filled with antifreeze, crushed ice (cold), Pt100 read by DTS machine |
| Grass summer | SMM, PVC sheath, tightly buffered, aramid reinforced, white, OD 0.9 mm | 0.125 m, 1 s avg sampled every 4 s, length 600 m | Silixa Ultima 2 km variant | ordinary least squares; single-ended | liquid-phase water, crushed ice (cold), Pt100 read by external data logger |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thomas, C.K.; Huss, J.-M.; Abdoli, M.; Huttarsch, T.; Schneider, J. Solid-Phase Reference Baths for Fiber-Optic Distributed Sensing. Sensors 2022, 22, 4244. https://doi.org/10.3390/s22114244
Thomas CK, Huss J-M, Abdoli M, Huttarsch T, Schneider J. Solid-Phase Reference Baths for Fiber-Optic Distributed Sensing. Sensors. 2022; 22(11):4244. https://doi.org/10.3390/s22114244
Chicago/Turabian StyleThomas, Christoph K., Jannis-Michael Huss, Mohammad Abdoli, Tim Huttarsch, and Johann Schneider. 2022. "Solid-Phase Reference Baths for Fiber-Optic Distributed Sensing" Sensors 22, no. 11: 4244. https://doi.org/10.3390/s22114244
APA StyleThomas, C. K., Huss, J.-M., Abdoli, M., Huttarsch, T., & Schneider, J. (2022). Solid-Phase Reference Baths for Fiber-Optic Distributed Sensing. Sensors, 22(11), 4244. https://doi.org/10.3390/s22114244






