Development of Magnetically Levitated Rotary Table for Repetitive Trajectory Tracking
Abstract
:1. Introduction
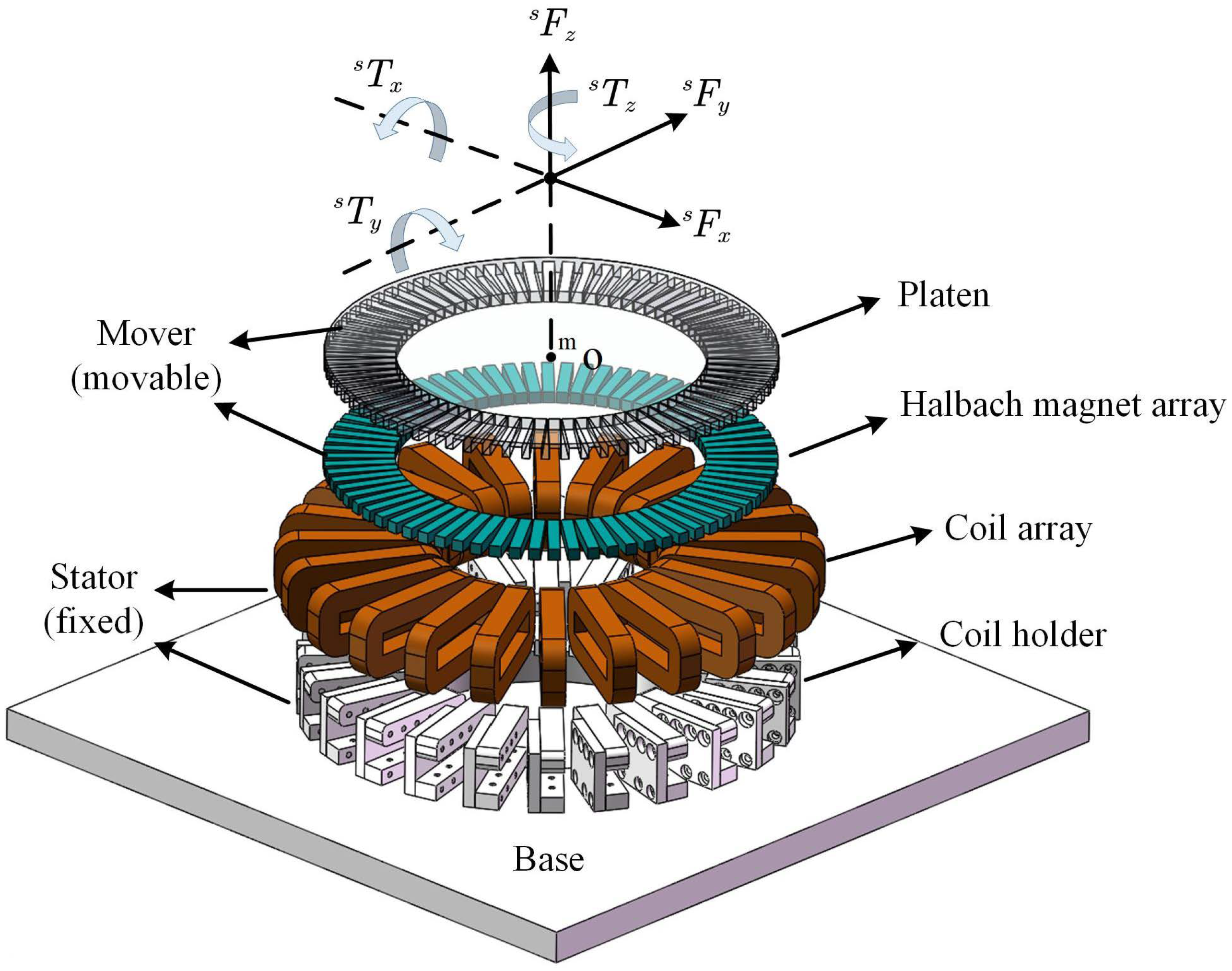
2. Dynamic Model Description of the MLRT
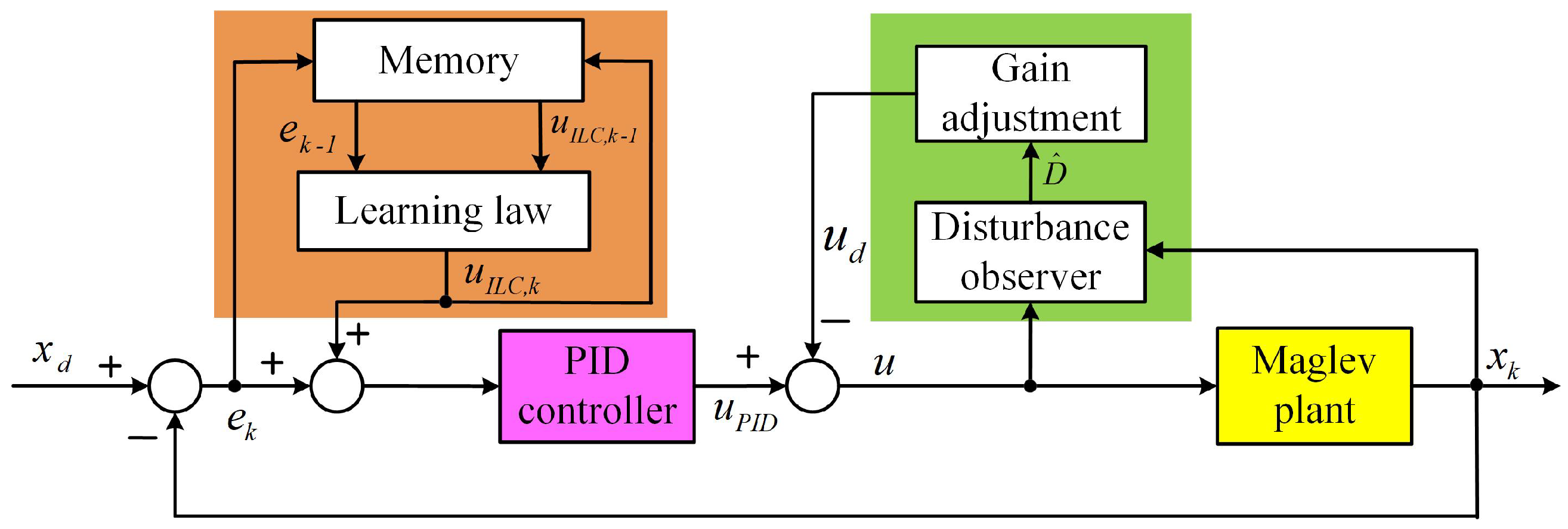
3. LPIDDC Approach
3.1. PID Term
3.2. Disturbance Compensation Term
3.3. Iterative Learning Term
3.4. Summary of LPIDDC Control Strategy
4. Experimental Studies
4.1. Hardware Setup
- (1)
- Track1: the MLRT is controlled to track the sinusoidal trajectory in -axis below with the unit being ,which has an an angular speed of and a velocity of .
- (2)
- Track2: the MLRT is controlled to track the sinusoidal trajectory in -axis below with unit being ,which has an angular speed of and a velocity of .
- (1)
- , the root-mean-square value of the trajectory tracking error, where T is the period of tracking trajectory.
- (2)
- , the maximal absolute value of the trajectory tracking error.
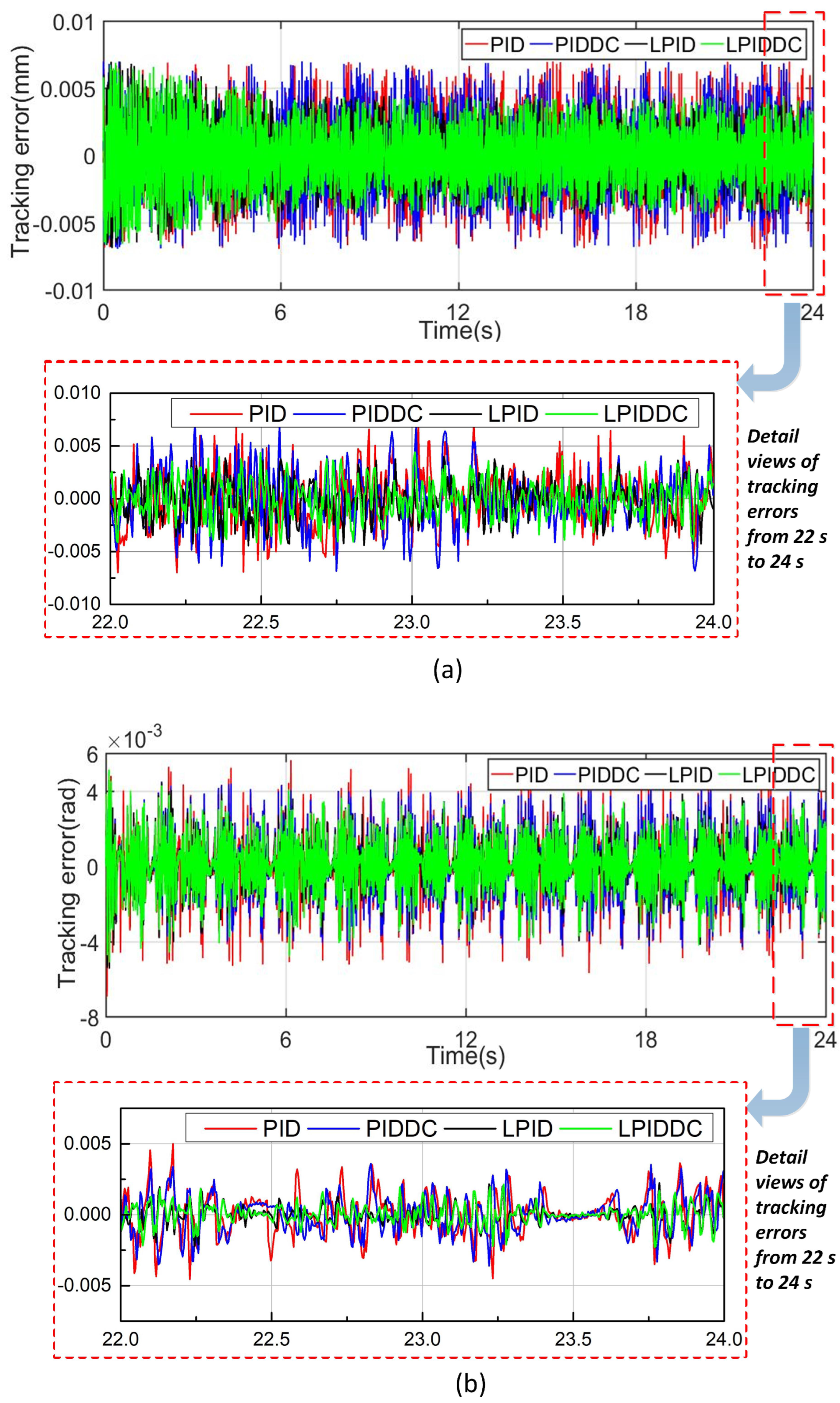
4.2. Trajectory Tracking without External Disturbance
4.3. Trajectory Tracking with External Disturbance
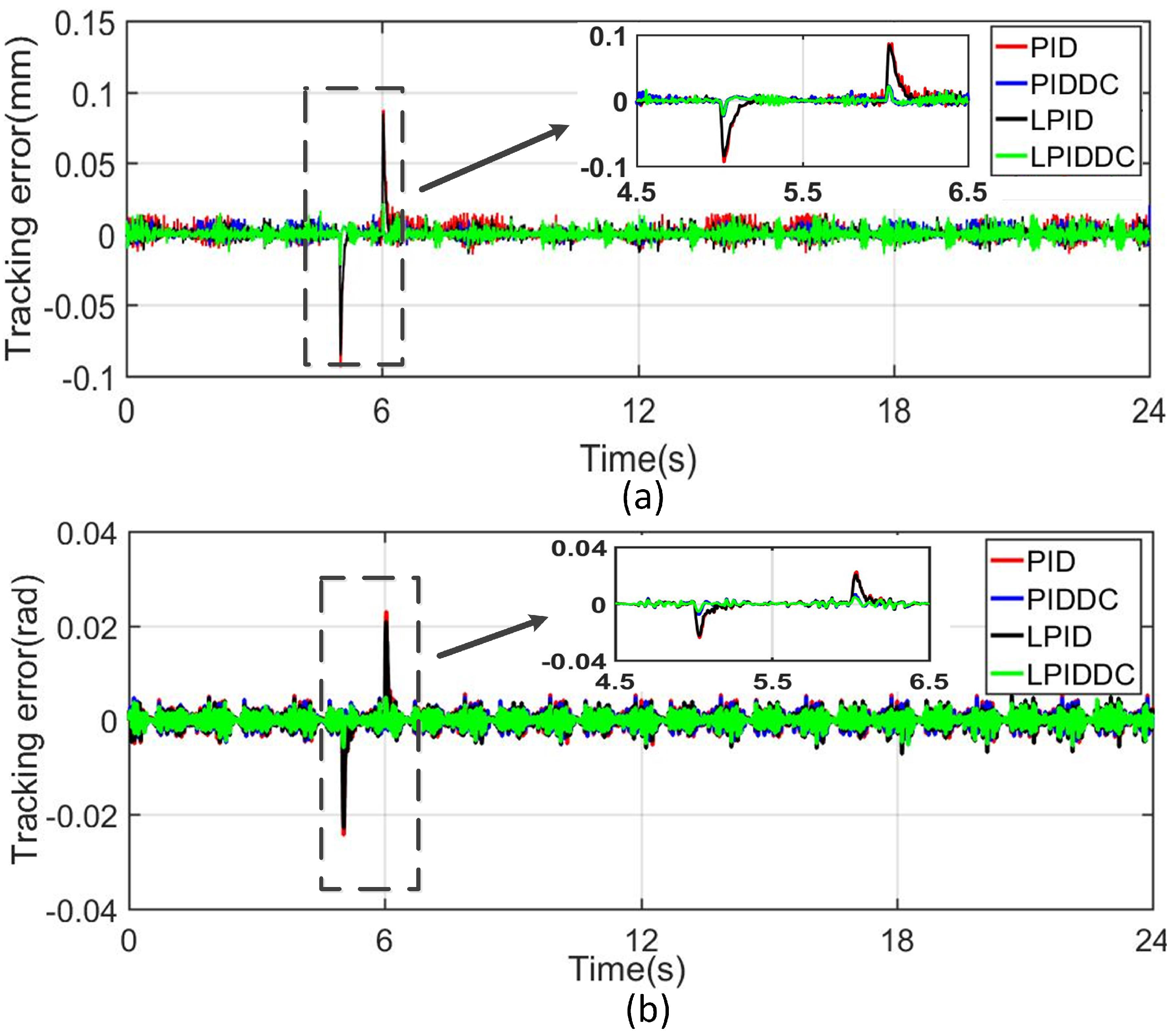
4.3.1. Step Disturbance
4.3.2. Complex Disturbance
4.3.3. Disturbance Caused by Polyfoam
4.3.4. Circle Trajectory Tracking
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MLRT | Magnetically levitated rotary table |
| PID | Proportion-integral-derivative |
| ILC | Iterative learning control |
| DC | Disturbance compensation |
| LPIDDC | Iterative learning PID control strategy with disturbance compensation |
| PM | Permanent magnet |
| PIDDC | PID with Disturbance compensation |
| LPID | Iterative learning feed-forwad PID |
References
- Xu, T.; Yu, J.; Yan, X.; Choi, H.; Zhang, L. Magnetic Actuation Based Motion Control for Microrobots: An Overview. Micromachines 2015, 6, 1346–1364. [Google Scholar] [CrossRef]
- Kumar, P.; Malik, S.; Toyserkani, E.; Khamesee, M.B. Development of an Electromagnetic Micromanipulator Levitation System for Metal Additive Manufacturing Applications. Micromachines 2022, 13, 585. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wu, Q.; Liu, B.; Gong, Z. Optimal Design of Magneto-Force-Thermal Parameters for Electromagnetic Actuators with Halbach Array. Actuators 2021, 10, 231. [Google Scholar] [CrossRef]
- Dyck, M.; Lu, X.; Altintas, Y. Magnetically Levitated Rotary Table with Six Degrees of Freedom. IEEE/ASME Trans. Mechatronics 2016, 22, 530–540. [Google Scholar] [CrossRef]
- Xu, X.; Zheng, C.; Xu, F. A Real-Time Numerical Decoupling Method for Multi-DoF Magnetic Levitation Rotary Table. Appl. Sci. 2019, 9, 3263. [Google Scholar] [CrossRef] [Green Version]
- Kou, B.; Xing, F.; Zhang, L.; Zhang, C.; Zhou, Y. A Real-Time Computation Model of the Electromagnetic Force and Torque for a Maglev Planar Motor with the Concentric Winding. Appl. Sci. 2017, 7, 98. [Google Scholar] [CrossRef] [Green Version]
- Lu, X. 6D Direct-drive Technology for Planar Motion Stages. CIRP Ann. 2012, 61, 359–362. [Google Scholar] [CrossRef]
- Li, J.H.; Chiou, J.S. GSA-Tuning IPD Control of a Field-Sensed Magnetic Suspension System. Sensors 2015, 15, 31781–31793. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, W.J.; Verma, S.; Shakir, H. Design and Precision Construction of Novel Magnetic-levitation-based Multi-axis Nanoscale Positioning Systems. Precis. Eng. 2007, 31, 337–350. [Google Scholar] [CrossRef]
- Silva-Rivas, J.C.; Kim, W.J. Multivariable Control and Optimization of a Compact 6-DOF Precision Positioner With Hybrid and Digital Filtering. IEEE Trans. Control Syst. Technol. 2012, 21, 1641–1651. [Google Scholar] [CrossRef]
- Fallaha, C.; Kanaan, H.; Saad, M. Real Time Implementation of a Sliding Mode Regulator for Current-Controlled Magnetic Levitation System. In Proceedings of the 2005 IEEE International Symposium on, Mediterrean Conference on Control and Automation Intelligent Control, Limassol, Cyprus, 27–29 June 2005; pp. 696–701. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X. Real-Time Adaptive Control of a Magnetic Levitation System with a Large Range of Load Disturbance. Sensors 2018, 18, 1512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, M.Y.; Tsai, C.F.; Fu, L.C. A Novel Design and Control to Improve Positioning Precision and Robustness for a Planar Maglev System. IEEE Trans. Ind. Electron. 2019, 66, 4860–4869. [Google Scholar] [CrossRef]
- Basovich, S.; Arogeti, S.A.; Menaker, Y.; Brand, Z. Magnetically Levitated Six-DOF Precision Positioning Stage with Uncertain Payload. IEEE/ASME Trans. Mechatronics 2016, 21, 660–673. [Google Scholar] [CrossRef]
- de Jesús Rubio, J.; Zhang, L.; Lughofer, E.; Cruz, P.; Alsaedi, A.; Hayat, T. Modeling and Control with Neural Networks for a Magnetic Levitation System. Neurocomputing 2017, 227, 113–121. [Google Scholar] [CrossRef]
- Liang, S.; Xi, R.; Xiao, X.; Yang, Z. Adaptive Sliding Mode Disturbance Observer and Deep Reinforcement Learning Based Motion Control for Micropositioners. Micromachines 2022, 13, 458. [Google Scholar] [CrossRef]
- Kazemzadeh Heris, P.; Khamesee, M.B. Design and Fabrication of a Magnetic Actuator for Torque and Force Control Estimated by the ANN/SA Algorithm. Micromachines 2022, 13, 327. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Huang, Y.; Wang, Y. Research on Compound PID Control Strategy Based on Input Feedforward and Dynamic Compensation Applied in Noncircular Turning. Micromachines 2022, 13, 341. [Google Scholar] [CrossRef] [PubMed]
- Mishra, S.; Tomizuka, M. Projection-based iterative learning control for wafer scanner systems. IEEE/ASME Trans. Mechatronics 2009, 14, 388–393. [Google Scholar] [CrossRef]
- Mao, W.L. Indirect fuzzy contour tracking for X–Y PMSM actuated motion system applications. IET Electr. Power Appl. 2018, 12, 12–24. [Google Scholar] [CrossRef]
- Yu, D.; Zhu, Y.; Yang, K.; Hu, C.; Li, M. A Time-varying Q-filter Design for Iterative Learning Control with Application to an Ultra-precision Dual-stage Actuated Wafer Stage. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2014, 228, 658–667. [Google Scholar] [CrossRef]
- Bai, L.; Feng, Y.W.; Li, N.; Xue, X.F. Robust Model-Free Adaptive Iterative Learning Control for Vibration Suppression Based on Evidential Reasoning. Micromachines 2019, 10, 196. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Huang, J.; Wang, J.; Meng, F.; Gong, H.; Ping, B. The Driving Waveform Design Method of Power-Law Fluid Piezoelectric Printing Based on Iterative Learning Control. Sensors 2022, 22, 935. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Zheng, T.; Xu, F.; Xu, X. Semi-Analytical Solution of Magnetic Force and Torque for a Novel Magnetically Levitated Actuator in Rotary Table. IEEE Trans. Magn. 2019, 55, 1–8. [Google Scholar] [CrossRef]

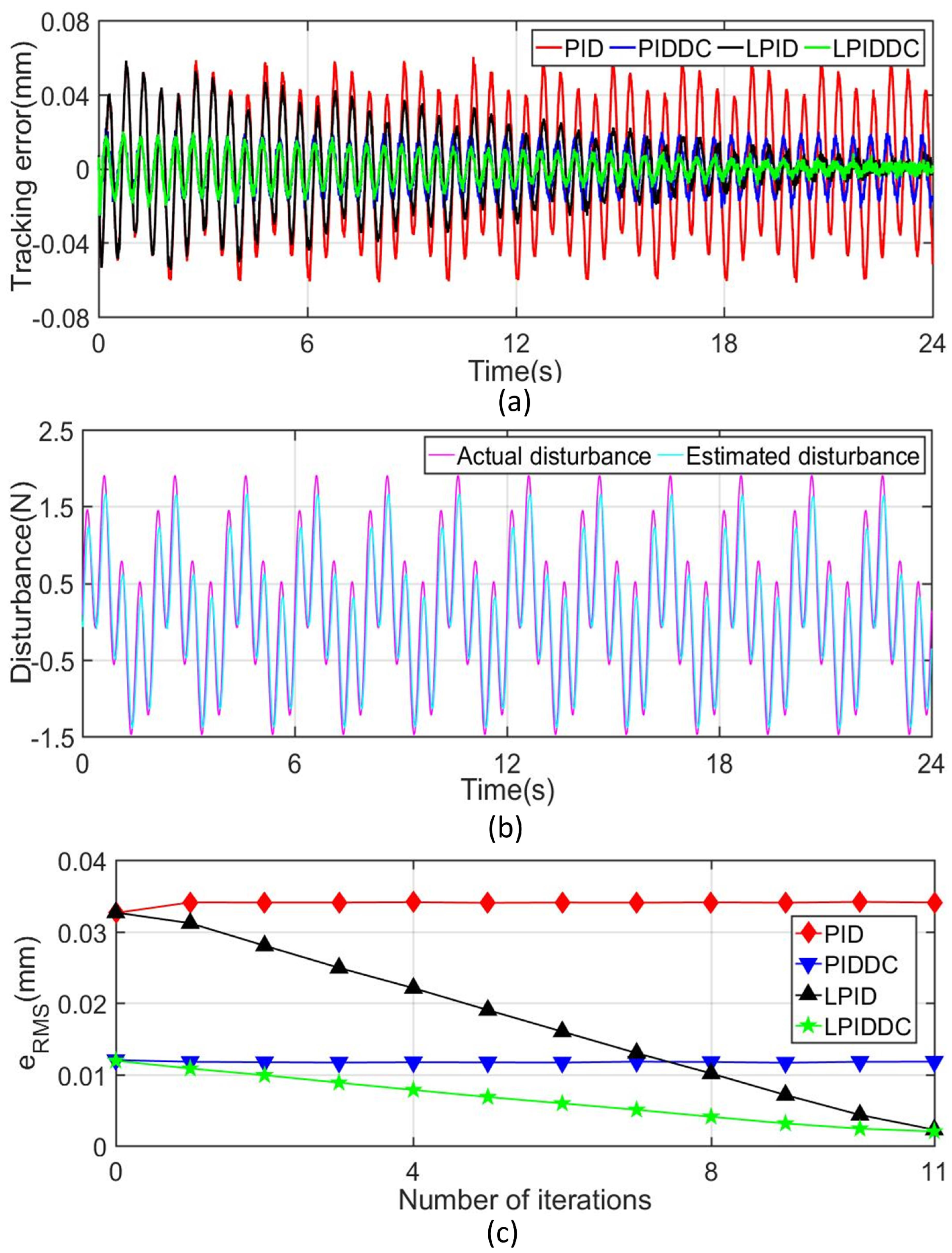
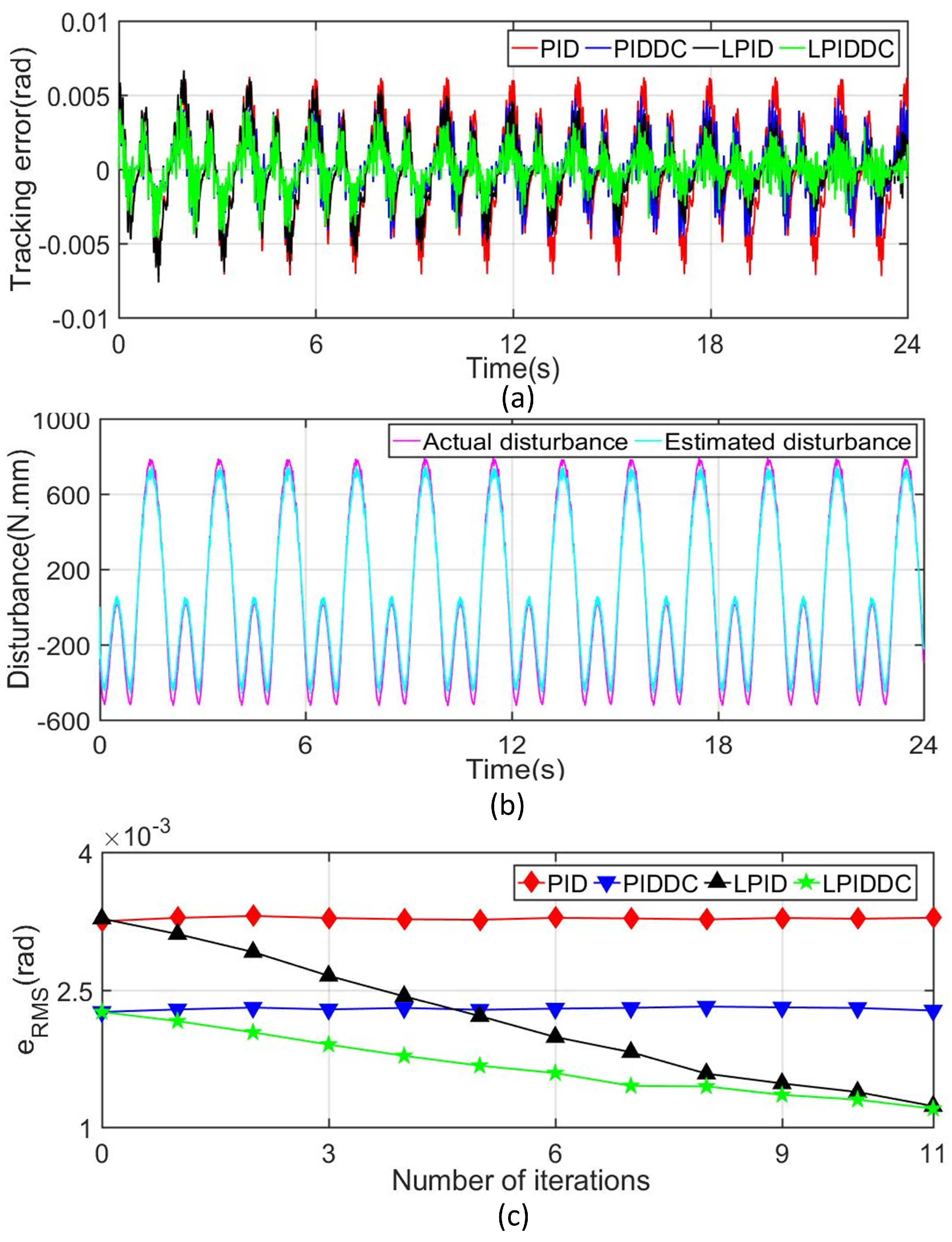

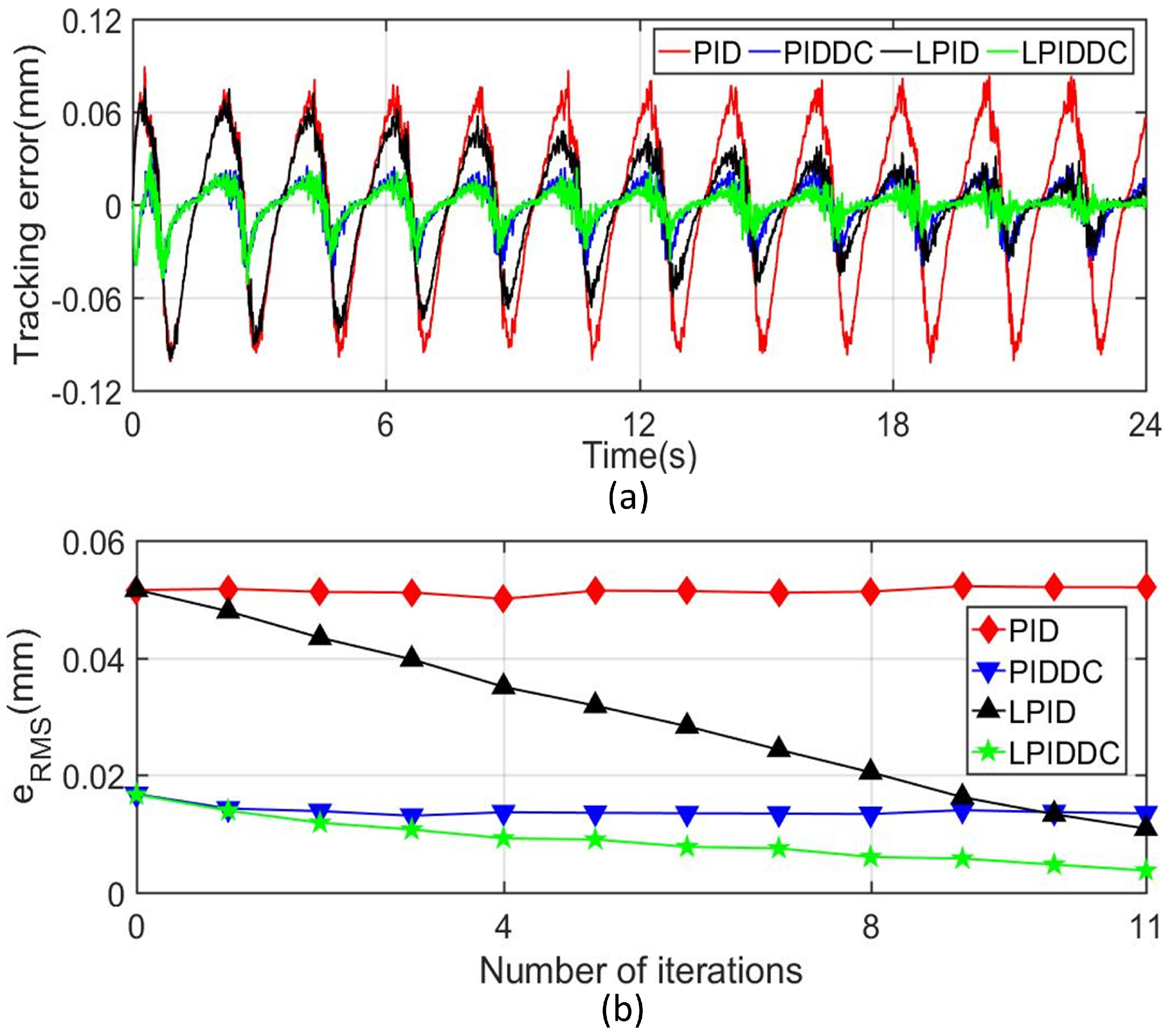

| Trajectory | Track1 | Track1 | Track2 | Track2 |
|---|---|---|---|---|
| Index | ||||
| Trajectory | Track1 | Track1 | Track2 | Track2 |
|---|---|---|---|---|
| Index | ||||
| Index | ||
|---|---|---|
| Index | ||
|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, F.; Zhang, K.; Xu, X. Development of Magnetically Levitated Rotary Table for Repetitive Trajectory Tracking. Sensors 2022, 22, 4270. https://doi.org/10.3390/s22114270
Xu F, Zhang K, Xu X. Development of Magnetically Levitated Rotary Table for Repetitive Trajectory Tracking. Sensors. 2022; 22(11):4270. https://doi.org/10.3390/s22114270
Chicago/Turabian StyleXu, Fengqiu, Kaiyang Zhang, and Xianze Xu. 2022. "Development of Magnetically Levitated Rotary Table for Repetitive Trajectory Tracking" Sensors 22, no. 11: 4270. https://doi.org/10.3390/s22114270
APA StyleXu, F., Zhang, K., & Xu, X. (2022). Development of Magnetically Levitated Rotary Table for Repetitive Trajectory Tracking. Sensors, 22(11), 4270. https://doi.org/10.3390/s22114270






