1. Introduction
Magnetic suspension support technology uses electromagnetic force to realize the contactless suspension of the suspended body. Compared with the traditional mechanical support technology and air suspension support technology, it has many advantages and is widely used in magnetic suspension trains, magnetic suspension bearing and magnetic suspension vibration isolation devices [
1,
2]. However, with the increase in the operation energy consumption of the magnetic suspension support system (MSSS), the temperature of the system rises. The temperature rise mainly has the following effects on the MSSS: (1) It affects the reliability of the system. When the system temperature exceeds its allowable temperature, it leads to the aging of insulating materials and reduce its service life; (2) When the system temperature is too high, the temperature drift of the sensor affects the accuracy of displacement detection, which further affects the dynamic performance of the whole system. It can be seen that the temperature rise is an important factor limiting the development of suspension support technology. At present, there are many methods of temperature measurement. Thermocouple and thermal resistance are common “point” contact temperature measurement technology. Through this method, the temperature values of multiple positions of the measured object can be obtained. When using this temperature measurement technology to measure the temperature of multiple positions, the monitoring system will have too many wires, which is complicated, and the temperature measurement technology is vulnerable to electromagnetic interference and poor stability. The point thermometer also belongs to the contact temperature measurement technology. When measuring the temperature, it must contact the surface of the measured object. Its measurement accuracy is affected by the roughness of the measured surface and the perpendicularity between the probe and the measured surface, and the accuracy is low; an infrared thermal imager is a typical non-contact temperature measurement technology, which has the advantages of non-contact, fast and high-temperature resolution. However, an infrared thermal imager can only measure the surface temperature field that can be photographed; compared with these temperature measurement technologies, fiber Bragg grating (FBG) temperature sensor has the advantages of small volume, good stability, high measurement accuracy, electromagnetic interference immunity and “one-line and multi-point” distributed online monitoring.
At present, FBG sensing technology is widely used in industry, medicine and other fields. Rao [
3] gave a systematic and detailed introduction to FBG sensing technology. Rao, David, Webb et al. [
4] applied FBG sensor technology to the medical field and measured the temperature of the human body through the FBG temperature sensor. The experiment shows that the measurement accuracy of the FBG sensor can reach ±0.2 °C in the range of 30–60 °C [
5]. Scholars applied FBG sensor technology to the baby delivery room, designed an external real-time monitoring system, used multiple FBG sensors for measurement, optimized the way of measuring and processing data and reduced the measurement error caused by multiple sensors [
6]. Scholars presented the detection of flaws in the outer bearing’s raceway from the measurement of motor dynamic strain signals collected from sensors based on fiber Bragg grating (FBG). Aiming to carry out real-time online monitoring of the thermal characteristics and their effect on the machine tool spindle bearing stiffness, a fiber Bragg grating (FBG) sensors network was proposed [
7]. The online measurement of oil-film pressure inside a journal bearing based on an optical fiber Bragg grating (FBG) is proposed and described for the first time [
8]. The FBG temperature sensors had good accuracy, stability and consistency when measuring the temperature distribution of the bearing bush [
9]. Liu et al. [
10] proposed a multi-point quasi-distributed sensing method based on embedded fiber Bragg grating (FBG) sensors to measure the temperature field of the outer ring of the bearing under three different working conditions: idling, uploading axial and radial cutting force. Wang et al. [
11] modified temperature-compensation function with the influence of interfacial action considered is proposed to enhance the measurement accuracy of FBG-based sensors. From the research status of FBG sensor technology at home and abroad, FBG sensor has been applied to the temperature field measurement of machine tool spindle and bearing and has high measurement accuracy.
At present, many scholars at home and abroad have conducted a lot of research on the temperature rise of magnetic bearing. Mizuno, T. [
12] studied the loss of magnetic bearing under the two configurations of magnetic pole NSNS and NNSS. Through experimental verification, it was concluded that the iron loss of magnetic pole of magnetic bearing under NNSS configuration is slightly smaller, and its loss value is also affected by ampere turns, speed, control current and air gap. David C. Meeker et al. [
13], taking the homopolar laminated radial magnetic bearing as the research object, proposed the analytical solution of rotor rotation loss and verified the correctness of the analytical solution by comparing the experimental data. Jiang et al. [
14] proposed a novel analytical calculation method based on distributed magnetic circuit method (DMCM) to solve the problem of coupled magnetic flux and saturation of active magnetic bearing (AMB). Cao, Y. et al. [
15] analyzed the loss and temperature of the hybrid magnetic bearings (HMB), and the results showed that the loss of HMB is mainly distributed in the rotor part, and the temperature of the rotor part is obviously higher than that of the stator part. Li et al. [
16] established the thermal model of the motorized spindle and simulated the steady-state temperature field of the motorized spindle by using ANSYS. Zhai et al. [
17] established the prediction models of iron loss and copper loss for magnetic bearings and BLDCM and determined the loss coefficients of iron core by measured loss curves at different frequencies. Dong et al. [
18] proposed a multi-physical field simulation based on a magneto-thermal-fluid coupled iterative solution. Kondaiah, V.V. et al. [
19] proposed an experimental approach to study the loss factor and efficiency of an active magnetic thrust bearing. Zan et al. [
20] combined thermal network analysis with the temperature field distribution to obtain the key factors affecting the heat dissipation of the flywheel. Kepsu, D. et al. [
21] analyzed the influence of segmentation of the magnets on losses. Zhong Ma et al. [
22] used chitosan as a multifunctional layer to create a dual-modal flexible sensor. The frequency dependency of the capacitive output enabled modulations of the responses and a simple yet effective approach for decoupling the pressure and temperature responses with an average accuracy of ~92.3%. Basov, M. [
23] developed a small silicon chip of Schottky diode (0.8 × 0.8 × 0.4 mm
3) with the planar arrangement of electrodes (chip PSD) as a temperature sensor and proved the application of PSD chip for a wider temperature range from −65 to +115 °C. Nuo Zhang et al. [
24] demonstrated a high-performance temperature sensor based on a 4H-SiC pn diode at a forward current density of 0.44 mA/cm
2; the device achieves a sensitivity of 3.5 mV/°C.
From the current research status, it can be seen that the FBG temperature sensor has not been used to monitor its temperature in the research on the temperature field of magnetic suspension support. Compared with other temperature measuring instruments, the FBG temperature sensor has higher measurement accuracy, strong anti-interference and smaller volume. It is just suitable for the occasion of compact structure and high operation accuracy of MSSS. Therefore, an FBG temperature sensor is introduced into the research of the temperature field of magnetic suspension bearing in this paper.
2. FBG-Based Temperature Sensors
2.1. FBG Sensing Principle for Temperature
As a new type of temperature sensor, the FBG temperature sensor has the characteristics of small and soft optical fiber, electromagnetic interference immunity, strong environmental adaptability, corrosion resistance, long-distance transmission of sensing optical signal, and multiple sensing gratings can be prepared on one optical fiber to realize “one-line and multi-point” signal sensing, breaking through the limitations of few measuring points and single output function of traditional sensors. It has technical advantages and prospects for wide application in the field of multi-parameter distribution dynamic detection.
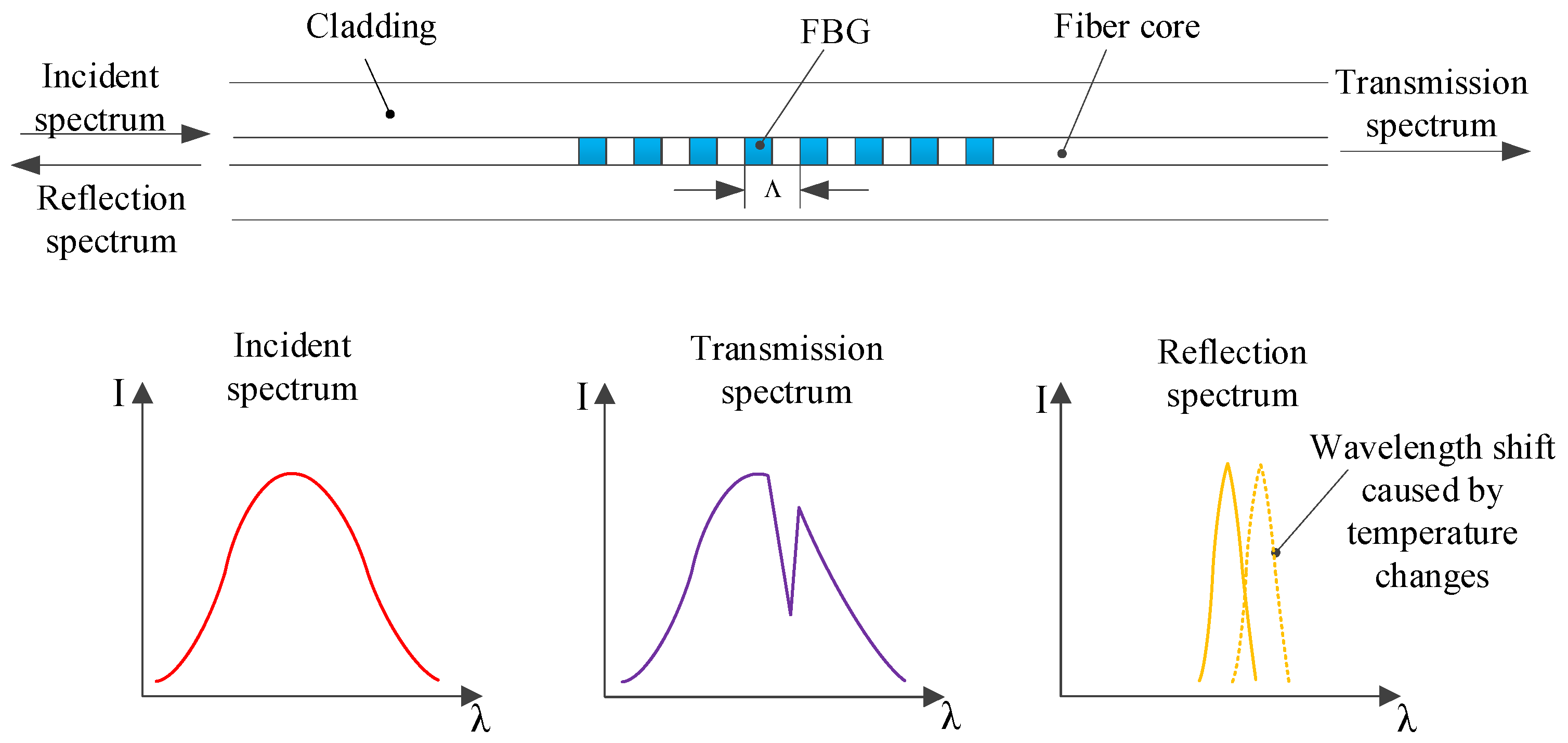
The structure and principle of FBG are shown in
Figure 1. The principle is that when the broadband light source passes through the grating as the incident light, the light wave with the same phase as the grating is reflected, and the other light waves are transmitted from the FBG. The measured physical quantity can be obtained through the light wave reflection theory [
25].
According to the principle of FBG optical detection, the reflection wavelength moves to the right or left depending on the measured physical size. The most important measurement of the FBG detection system is wavelength measurement. Then, the wavelength offset is converted into amplitude, phase, frequency and other amplitude, which can be measured more easily. Amplitude measurement is the most common and direct measurement method in optical fiber sensors. The wavelength shift is converted into amplitude change, which makes the detection system simpler and cheaper.
When a broadband light is an incident on the fiber grating, the grating is used as a narrow-band filter. The periodic structure of the refractive index makes the reflection of a specific wavelength, and the central wavelength of the reflected light signal depends on the Bragg wavelength. FBG reflects light at the
Bragg wavelength:
Here, is the grid period, and the is an effective refractive index. As temperature change with and , the wavelength of the reflected light will also change. Therefore, the temperature measurement can be realized by wavelength offset.
When the temperature changes, the wavelength of the emitted light changes [
26,
27]:
Combining Equations (1) and (2), we obtain:
When Equation (3) is rearranged:
Here, the change in is Bragg wavelength, and and are thermal expansion and thermo-optic coefficients, respectively. In the normal temperature area, °C−1. Compared with the coefficient of thermal expansion, the contribution of the thermo-optic effect to the wavelength change is 95%. For fiber gratings with a central wavelength of 1300 nm, a temperature change of 1 °C leads to a wavelength of 9.13 pm.
When multiple FBGs are used in combination, the above equation also applies to a single FBG. However, the bandwidth of FBG needs to be reasonably selected to avoid interference with each other.
2.2. Sticking and Calibration of FBG Temperature Sensor
The application of FBG for thermal sensors faces the problem of the cross-impact of temperature and stress. Both can make the wavelength of FBG drift, so in one judge, only considering the wavelength drift, the reason is not clear; it is very difficult to attribute the wavelength change to thermal change or strain change. Therefore, in order to implement the practical use of the FBG thermal sensor, we must choose appropriate packaging technology or eliminate the effect of non-temperature.
Packaging structure [
28] pastes the FBG and its both ends in the trough, the pasted points approach both ends, and between the points in one extreme little bend, the pipe is filled with non-solidified thermal paste. When exterior load is imposed on both ends, each pasted point of both ends can bear part of the force; at the same time, the bending part performs a buffer role against the tensile deformation caused by an outside force. In addition, the measured object electromagnet has small stress deformation during operation.
In order to ensure that the measured data of the FBG temperature sensor are more accurate and reliable, the temperature of the FBG sensor must be calibrated in the electrothermal incubator before the experiment, and the relationship between FBG central wavelength and temperature can be obtained through the experiment.
In the experiment, when the data acquisition time is 5 s at a certain temperature, 5000 data can be obtained. The average value of the collected 5000 data is taken as the central wavelength of FBG at that temperature. Each sensor is calibrated twice. The experimental data are processed by the least square method, and the calibration data of each sensor are linearly fitted to obtain the fitted result diagram of each sensor, as shown in
Figure 2. Finally, the sensitivity range of the FBG temperature sensor used in the experiment is 9.5 pm/°C~10.5 pm/°C, and the linear correlation is high.
5. Experiment
5.1. FBG Layout and Experimental Platform Design
Firstly, the quasi-distributed temperature detection system based on FBG is designed. As shown in
Figure 11, the system is divided into three modules: (1) the quasi- distributed temperature sensor network composed of FBG; (2) the transmission module composed of optical fiber jumper; (3) the sensor demodulator and computer. The quasi-distributed temperature sensor network has multiple independent optical signal demodulation channels. Many FBG temperature measurement points can be distributed on each optical fiber channel (the number of FBGs is determined by the temperature measurement range and the number of sites to be measured). Each FBG can independently measure its surrounding temperature.
When the FBG temperature sensor is used to measure the temperature of the MSSS, the number of temperature measurement points is related to the accuracy of the prediction results of the thermal analysis model. If more temperature measurement points are selected, it will increase the difficulty of measurement. If fewer temperature measurement points are selected, some important information points may be omitted, which is not enough to reflect the current temperature field; it is very important to select an appropriate number of temperature measurement points and the location of measurement points in the process of experiment. The following principles shall be followed when arranging the measuring points of the FBG sensor:
- (1)
The measuring point position of the sensor shall be close to the heat source as far as possible and only affected by the heat source.
- (2)
During the experiment, arrange as many temperature measurement points as possible to avoid missing important information when obtaining the best measurement points and numbers.
According to the above principles, select representative location points and reasonably arrange temperature measurement points. The selection of measurement points is shown in
Figure 12. The wiring mode of the FBG sensor at the edges and corners of the iron core is shown in
Figure 13.
The FBG temperature sensor is arranged on the iron core and coil winding of the E-type suspension electromagnet in the magnetic suspension support device. The sensor with multiple grid areas engraved on an optical fiber and combined with the quasi-distributed temperature measurement system can realize the “one-line and multi-point” monitoring of the FBG sensor.
The suspension bearing temperature monitoring experimental platform is mainly composed of a magnetic suspension bearing device, FBG temperature sensor, FBG demodulator, infrared thermal imager, linear DC regulated power supply and computer. The temperature monitoring experimental platform of magnetic bearing is shown in
Figure 14.
In the process of applying different currents to E-type suspended electromagnetic iron, the central wavelength of the FBG temperature sensor changes with the increase in temperature. The changed wavelength is collected by the FBG demodulator, and the collected data are stored and displayed by computer. Since the FBG temperature sensor was calibrated in advance, the obtained wavelength signal can be transformed into a temperature signal to obtain the temperature value at the measuring point.
5.2. Temperature Measurement Experiment of Magnetic Suspension Bearing under Different Current
The temperature of a magnetic suspension bearing system is mainly determined by the temperature of the E-type suspension electromagnet. In order to obtain the temperature distribution of the E-type suspension electromagnet in a suspension bearing system under different currents, the temperature of the E-type suspension electromagnet under five different currents is measured. Apply , , , and currents to the coil winding. When the temperature of the E-type suspension electromagnet basically does not change, use the FBG demodulator to collect data for the central wavelength of each sensor on the iron core and coil winding at this time. Repeat the above operation three times.
During the experiment, several measuring points are arranged on the iron core and coil winding of the suspended electromagnet in the MSSS, and their positions are slightly different from those of the theoretical design, but they are basically on the same plane as those of the theoretical design. In the actual wiring, there are 24 measuring points on the coil winding and 18 measuring points on the iron core. Next, the data collected by the FBG temperature sensor of coil winding and iron core are analyzed. The data in the analysis process are the average value of three repeated experiments.
(1) Data analysis of FBG temperature sensor in coil winding
During the experiment, three FBG temperature sensors are arranged on the coil winding part, and each has eight grid areas, namely eight FBG temperature sensors, which are respectively recorded as FBG1–FBG8 (shown in
Figure 15). In
Figure 16a–c are the variation curves of temperature measured by the three FBG temperature sensors on the coil winding part with the current.
As can be seen from
Figure 16a–c, under the same current, the temperature of FBG at different positions on the same optical fiber, i.e., FBG1–FBG8, is almost the same; Under different currents, the temperature of FBG on the same optical fiber has the same trend with the current; for FBG that is not at the symmetrical position on the same optical fiber, as shown in FBG1 in
Figure 16a and FBG1 in
Figure 16b, the temperature value displayed when the current is the same is almost the same. It can be seen from the analysis that the temperature measured by FBG at different positions on the outer surface of coil winding is almost the same within the allowable error range.
(2) Data analysis of FBG temperature sensor in iron core
During the experiment, a total of 7 FBG temperature sensors were arranged in the iron core, including 17 FBG temperature sensors. For the convenience of narration, the pole posts on both sides of the E-type electromagnet are marked as pole post 1 and pole post 3, the pole post in the middle is marked as pole post 2, and the part with the FBG sensor at the bottom is marked as the bottom of the iron core (shown in
Figure 17).
Figure 18a–d are the variation curves of temperature measured by 7 FBG temperature sensors in the iron core with current.
It can be seen from
Figure 18d that the temperature variation trend of the four FBG temperature sensors on the bottom of the iron core with current is consistent, and the temperature variation curve with current is almost coincident. Compared with the variation curve of FBG temperature with the current in
Figure 18a–c. Under the same current, the temperature value measured by each FBG at the bottom of the iron core is slightly less than that measured by each FBG on the pole column of the iron core. The analysis shows that due to the existence of coil winding on the pole column of the iron core, the heat of the coil winding transfers the heat to the iron core through heat conduction. Therefore, the iron core with the FBG sensor at the bottom of the iron core is directly exposed to the air. The three pole columns of the iron core are wrapped by the coil winding. Therefore, the heat dissipation at the bottom of the iron core is better than that of the three pole columns of the iron core, and the temperature at the bottom of the iron core is slightly lower than that of the three pole columns of the iron core.
The temperature distribution law obtained from the above simulation analysis is consistent with that of the electromagnet.
Figure 19 shows the comparison between the maximum temperature measured in the experiment and the maximum temperature analyzed in the simulation under different currents.
Table 4 shows the relative error between the maximum temperature in the experiment and the maximum temperature in the simulation under different currents.
The overall trend of the model and experimental results is consistent, and the error between them is less than 15%. Due to the insufficient accuracy of eddy current loss and iron loss calculation, there may be errors in applying excitation in finite element simulation, resulting in the above errors. Based on the conclusion that the temperature distribution law of the suspension electromagnet obtained from the above analysis is consistent with the temperature distribution law obtained from the simulation, the accuracy of the equivalent model in the simulation analysis and the reliability of FBG temperature measurement are verified.