Nonlinear Dynamic Measures of Walking in Healthy Older Adults: A Systematic Scoping Review
Abstract
1. Introduction
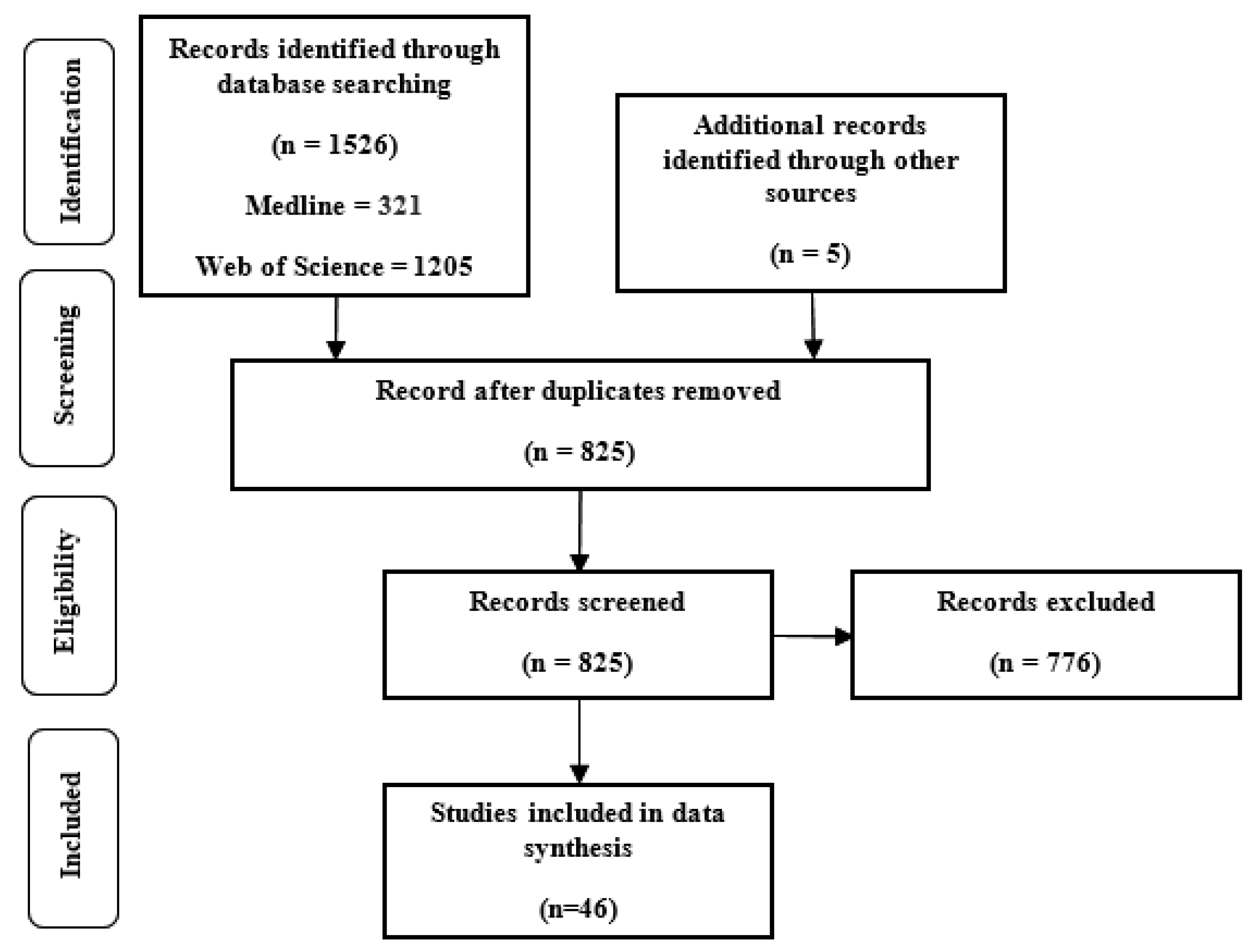
2. Methods
2.1. Search Strategy
- gait.ti,ab.;
- walk*. ti, ab.;
- exp Gait Analysis/ or Gait/;
- 1 or 2 or 3;
- (dynam* adj2 stabil*). ti, ab.;
- Lyapunov.ti, ab.;
- (nonlinear adj2 dynamic*).ti, ab.;
- 5 or 6 or 7;
- old*.ti,ab.;
- elder*.ti, ab.;
- 9 or 10;
- 4 and 8 and 11.
2.2. Inclusion and Exclusion Criteria
2.3. Data Extraction
2.4. Data Visualisation
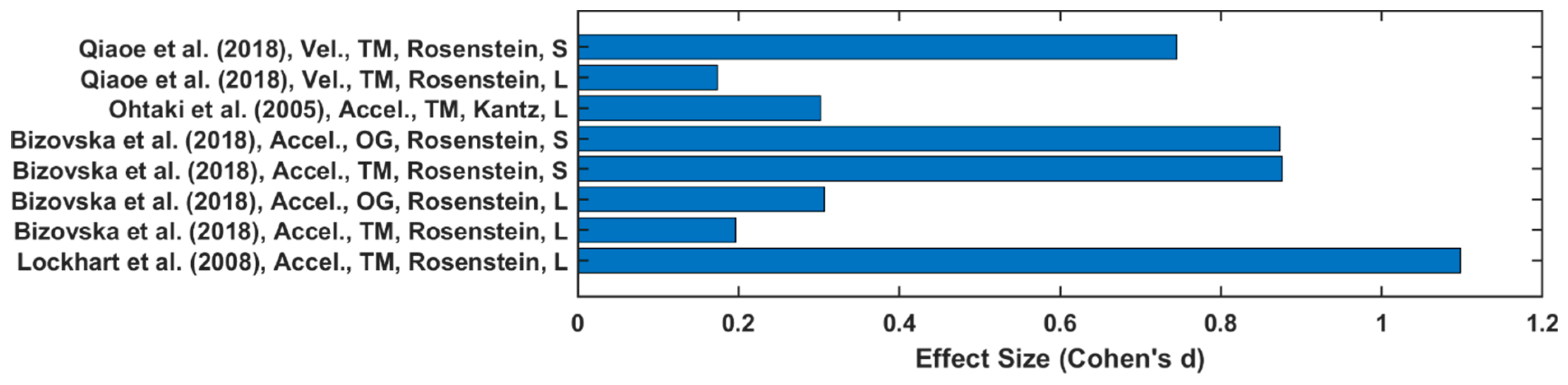
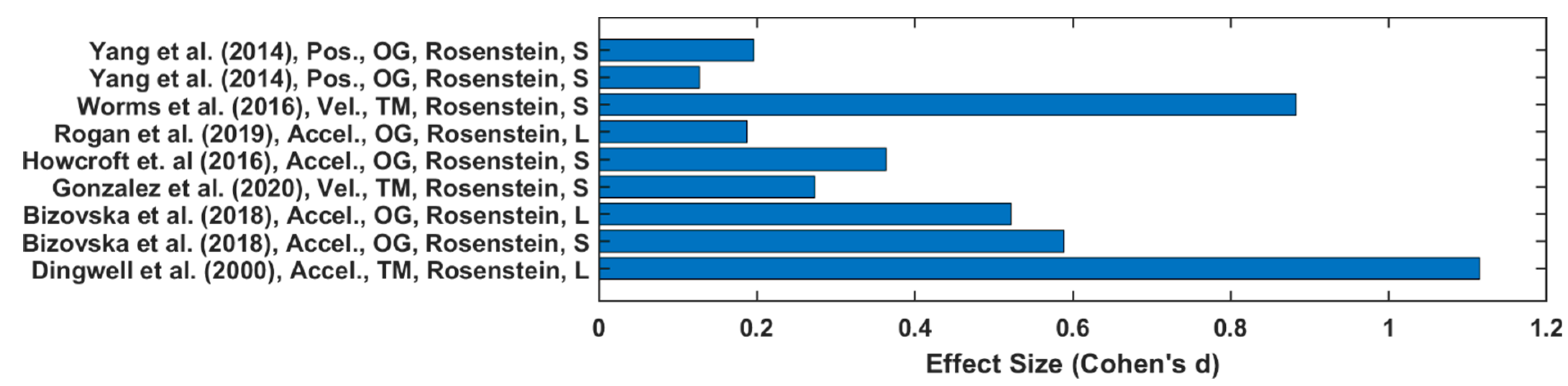
2.5. Effect Sizes
3. Results
3.1. Study Design Characteristics
3.1.1. Population
3.1.2. Sample Size
3.1.3. Fall Risk Assessment Tools
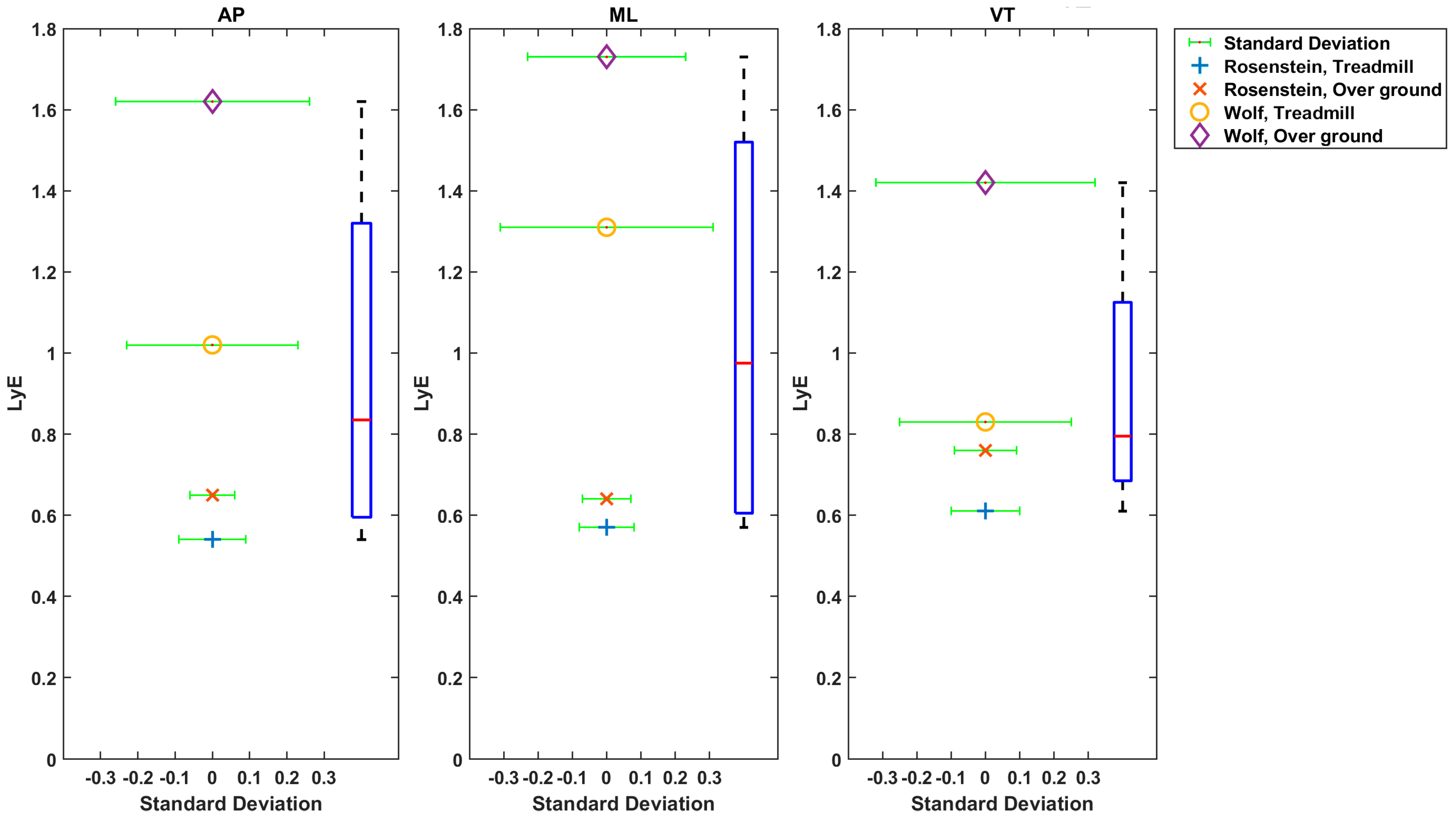
3.1.4. Treadmill (TM) versus Overground (OG) for Estimating Non-Linear Dynamics
3.2. Data Collection Modality and Kinematic Variables Analysed
3.3. Nonlinear Dynamic Analysis
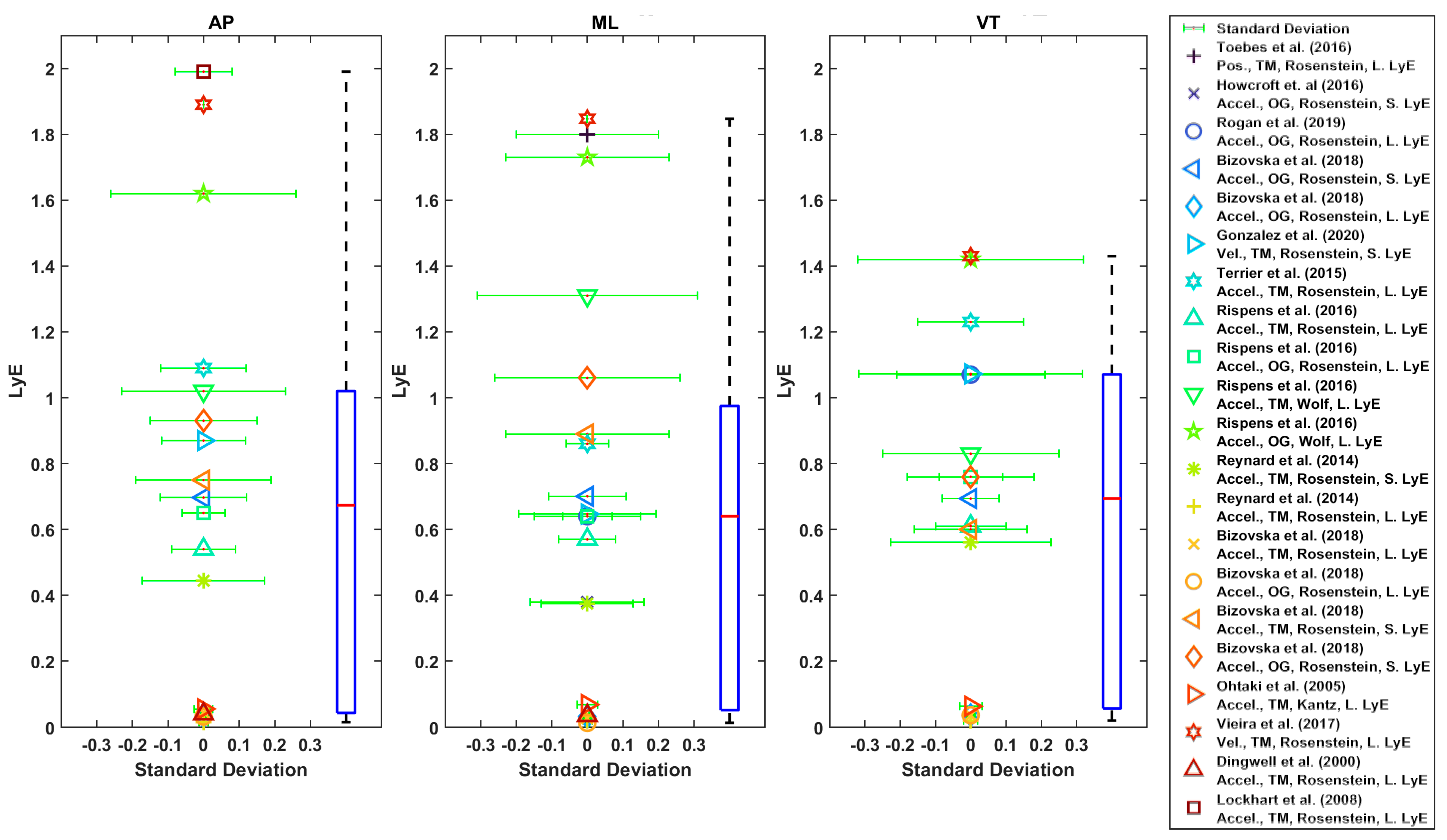
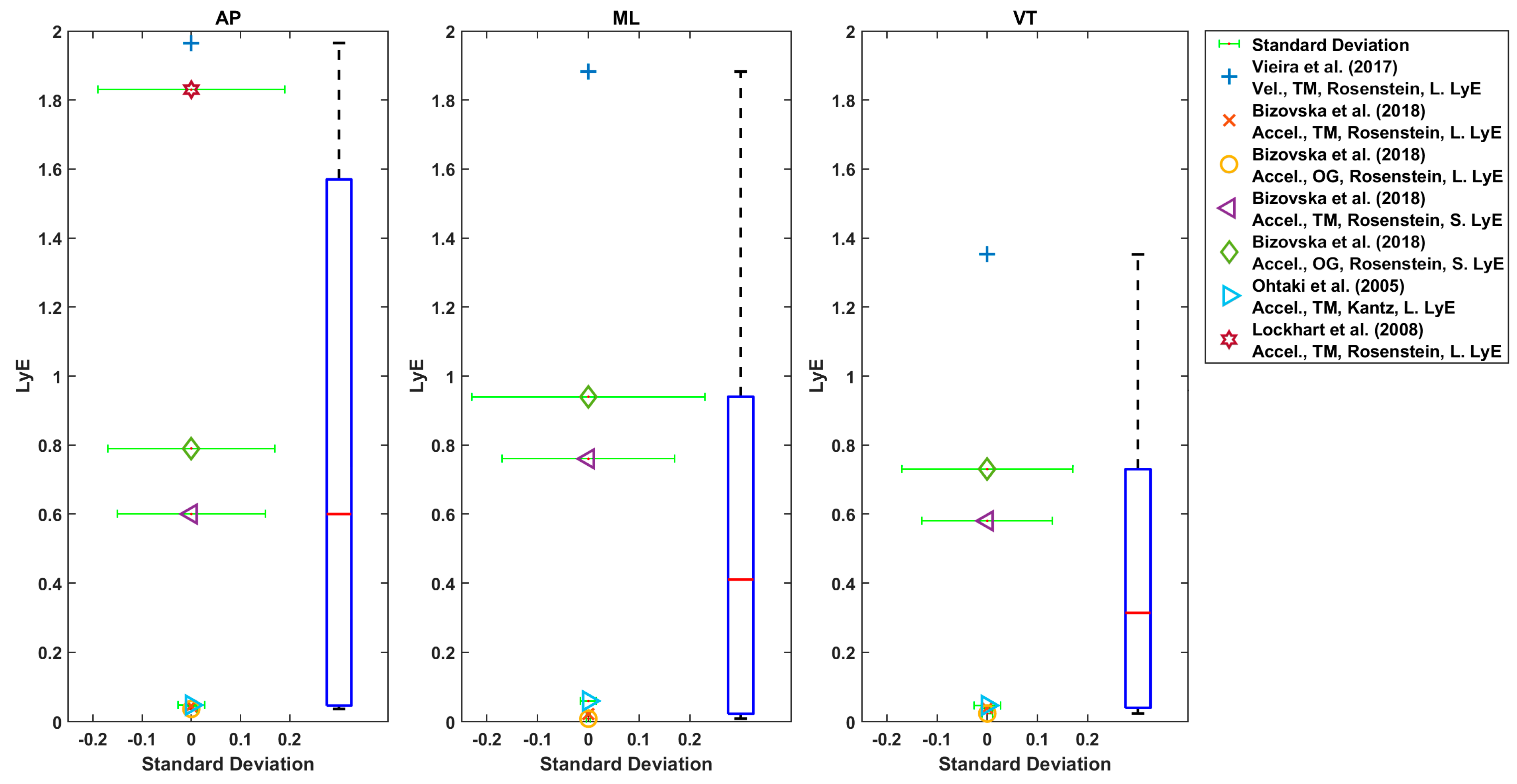
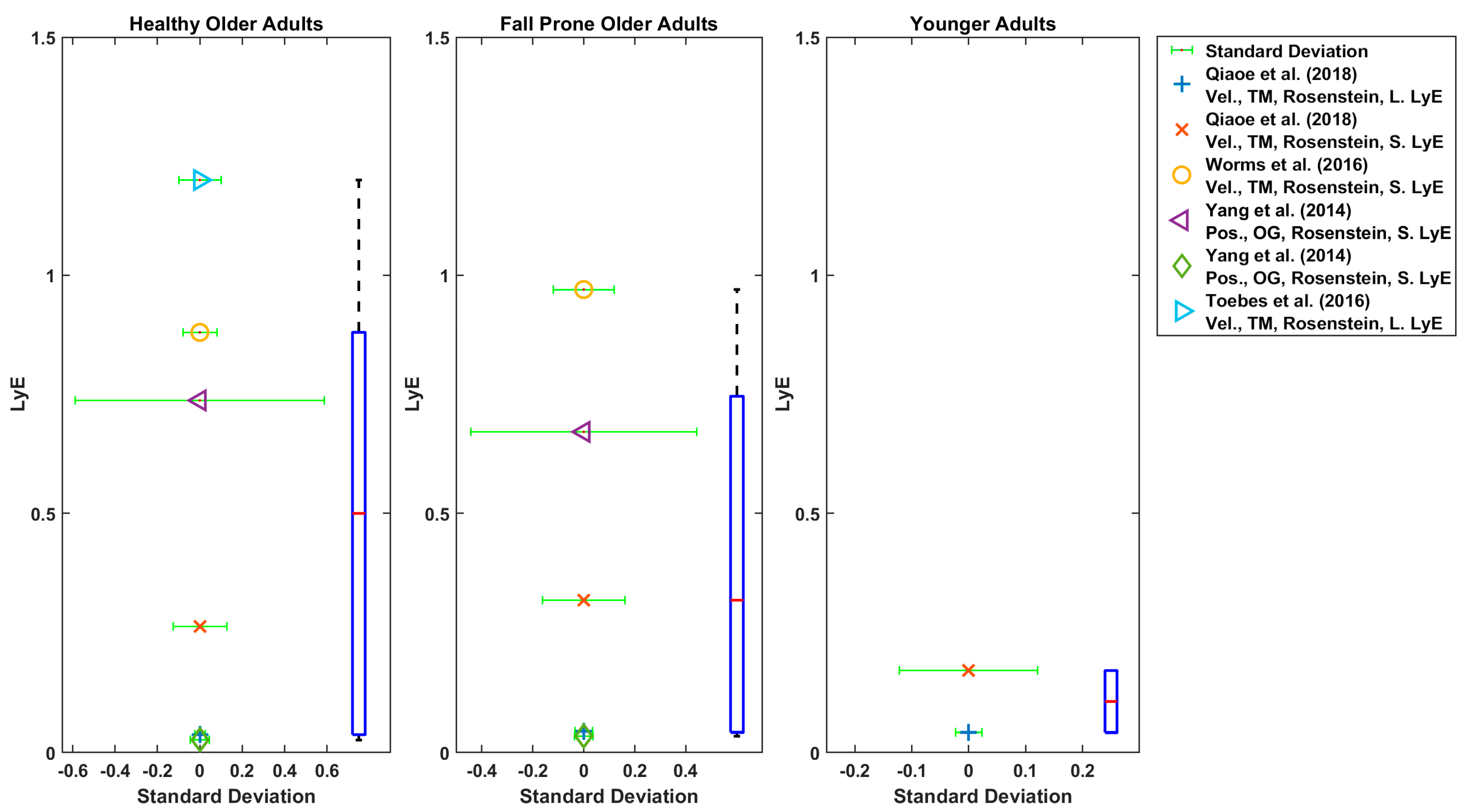
3.4. Nonlinear Dynamic Variable Values
4. Discussion
4.1. Study Design Characteristics
4.1.1. Sample Size and Characteristics
4.1.2. Fall Risk Assessment Tools
4.1.3. Treadmill versus Overground
4.2. Data Collection Modality and Kinematic Variables Analysed
4.3. Nonlinear Dynamic Analysis
4.4. Nonlinear Dynamic Variable Values
4.5. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LyE | Lyapunov Exponent |
| FMs | Fouquet Multipliers |
| MSE | Multiscale Entropy |
| RQA | Recurrence quantification analysis |
| TM | treadmill |
| OG | overground |
| AP | anterior-posterior |
| VT | vertical |
| ML | medio-lateral |
| YO | younger adults and older adults |
| F-NF | Fall-prone older adults and non-faller older adults |
| SAFE | the Survey of Activities and Fear of Falling in the Elderly |
| MSRS | Movement Specific Reinvestment Scale |
| FES-I | The Falls Efficacy Scale International |
| CES-D | depression |
| LAPAQ | The Longitudinal Aging Study Amsterdam Physical Activity Questionnaire |
| MMSE | Mini mental state examination score |
| TBAT | Tinetti Balance Assessment Tool |
| SD | Standard deviation |
| Sen | Sample Entropy |
| CD | Correlation Dimension |
| ShE | Shannon Entropy |
References
- World Health Organization. WHO Global Report on Falls Prevention in Older Age; World Health Organization: Geneva, Switzerland, 2008. [Google Scholar]
- Berg, R.L.; Cassells, J.S. The Second Fifty Years: Promoting Health and Preventing Disability; National Academy Press: Washington, DC, USA, 1990. [Google Scholar]
- Hamacher, D.; Liebl, D.; Hödl, C.; Heßler, V.; Kniewasser, C.K.; Thönnessen, T.; Zech, A. Gait stability and its influencing factors in older adults. Front. Physiol. 2019, 9, 1955. [Google Scholar] [CrossRef]
- Ambrose, A.F.; Paul, G.; Hausdorff, J.M. Risk factors for falls among older adults: A review of the literature. Maturitas 2013, 75, 51–61. [Google Scholar] [CrossRef]
- Tinetti, M.E.; Williams, T.F.; Mayewski, R. Fall risk index for elderly patients based on number of chronic disabilities. Am. J. Med. 1986, 80, 429–434. [Google Scholar] [CrossRef]
- Bisi, M.C.; Riva, F.; Stagni, R. Measures of gait stability: Performance on adults and toddlers at the beginning of independent walking. J. Neuroeng. Rehabil. 2014, 11, 131. [Google Scholar] [CrossRef]
- Buzzi, U.H.; Stergiou, N.; Kurz, M.J.; Hageman, P.A.; Heidel, J. Nonlinear dynamics indicates aging affects variability during gait. Clin. Biomech. 2003, 18, 435–443. [Google Scholar] [CrossRef]
- Terrier, P.; Dériaz, O. Kinematic variability, fractal dynamics and local dynamic stability of treadmill walking. J. Neuroeng. Rehabil. 2011, 8, 12. [Google Scholar] [CrossRef]
- Bizovska, L.; Svoboda, Z.; Kubonova, E.; Vuillerme, N.; Hirjakova, Z.; Janura, M. The differences between overground and treadmill walking in nonlinear, entropy-based and frequency variables derived from accelerometers in young and older women: Preliminary report. Acta Bioeng. Biomech. 2018, 20, 93–100. [Google Scholar]
- Brauer, S.G.; Burns, Y.R.; Galley, P. A prospective study of laboratory and clinical measures of postural stability to predict community-dwelling fallers. J. Gerontol. Ser. A Biol. Sci. Med. Sci. 2000, 55, M469–M476. [Google Scholar] [CrossRef]
- Buatois, S.; Gueguen, R.; Gauchard, G.C.; Benetos, A.; Perrin, P.P. Posturography and risk of recurrent falls in healthy non-institutionalized persons aged over 65. Gerontology 2006, 52, 345–352. [Google Scholar] [CrossRef]
- Bruijn, S.; Meijer, O.; Beek, P.; Van Dieën, J. Assessing the stability of human locomotion: A review of current measures. J. R. Soc. Interface 2013, 10, 20120999. [Google Scholar] [CrossRef]
- Johansson, J.; Nordström, A.; Nordström, P. Greater fall risk in elderly women than in men is associated with increased gait variability during multitasking. J. Am. Med. Dir. Assoc. 2016, 17, 535–540. [Google Scholar] [CrossRef] [PubMed]
- Wong, D.W.-C.; Lam, W.-K.; Lee, W.C.-C. Gait asymmetry and variability in older adults during long-distance walking: Implications for gait instability. Clin. Biomech. 2020, 72, 37–43. [Google Scholar] [CrossRef] [PubMed]
- Stergiou, N. Innovative Analyses of Human Movement; Human Kinetics Publishers: Champaign, IL, USA, 2004. [Google Scholar]
- Lipsitz, L.A.; Goldberger, A.L. Loss of ‘complexity’ and aging: Potential applications of fractals and chaos theory to senescence. JAMA 1992, 267, 1806–1809. [Google Scholar] [CrossRef] [PubMed]
- Hamacher, D.; Singh, N.; Van Dieen, J.; Heller, M.; Taylor, W. Kinematic measures for assessing gait stability in elderly individuals: A systematic review. J. R. Soc. Interface 2011, 8, 1682–1698. [Google Scholar] [CrossRef]
- Mehdizadeh, S. The largest Lyapunov exponent of gait in young and elderly individuals: A systematic review. Gait Posture 2018, 60, 241–250. [Google Scholar] [CrossRef]
- Riva, F.; Bisi, M.; Stagni, R. Orbital stability analysis in biomechanics: A systematic review of a nonlinear technique to detect instability of motor tasks. Gait Posture 2013, 37, 1–11. [Google Scholar] [CrossRef]
- Yentes, J.M.; Raffalt, P.C. Entropy Analysis in Gait Research: Methodological Considerations and Recommendations. Ann. Biomed. Eng. 2021, 49, 979–990. [Google Scholar] [CrossRef]
- Liberati, A.; Altman, D.G.; Tetzlaff, J.; Mulrow, C.; Gøtzsche, P.C.; Ioannidis, J.P.; Clarke, M.; Devereaux, P.J.; Kleijnen, J.; Moher, D. The PRISMA statement for reporting systematic reviews and meta-analyses of studies that evaluate health care interventions: Explanation and elaboration. J. Clin. Epidemiol. 2009, 62, e1–e34. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; de Luca, C.J. A practical method for calculating largest Lyapunov exponents from small data sets. Phys. D Nonlinear Phenom. 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Ihlen, E.A.; Goihl, T.; Wik, P.B.; Sletvold, O.; Helbostad, J.; Vereijken, B. Phase-dependent changes in local dynamic stability of human gait. J. Biomech. 2012, 45, 2208–2214. [Google Scholar] [CrossRef] [PubMed]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2004; Volume 7. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Erbaum Press: Hillsdale, NJ, USA, 1988. [Google Scholar]
- Dingwell, J.B.; Cusumano, J.P. Nonlinear time series analysis of normal and pathological human walking. Chaos Interdiscip. J. Nonlinear Sci. 2000, 10, 848–863. [Google Scholar] [CrossRef] [PubMed]
- Bizovska, L.; Svoboda, Z.; Janura, M.; Bisi, M.C.; Vuillerme, N. Local dynamic stability during gait for predicting falls in elderly people: A one-year prospective study. PLoS ONE 2018, 13, e0197091. [Google Scholar] [CrossRef] [PubMed]
- Ihlen, E.A.; Weiss, A.; Beck, Y.; Helbostad, J.L.; Hausdorff, J.M. A comparison study of local dynamic stability measures of daily life walking in older adult community-dwelling fallers and non-fallers. J. Biomech. 2016, 49, 1498–1503. [Google Scholar] [CrossRef] [PubMed]
- Riva, F.; Toebes, M.; Pijnappels, M.; Stagni, R.; Van Dieën, J. Estimating fall risk with inertial sensors using gait stability measures that do not require step detection. Gait Posture 2013, 38, 170–174. [Google Scholar] [CrossRef]
- Toebes, M.J.; Hoozemans, M.J.; Furrer, R.; Dekker, J.; van Dieën, J.H. Associations between measures of gait stability, leg strength and fear of falling. Gait Posture 2015, 41, 76–80. [Google Scholar] [CrossRef]
- Bizovska, L.; Svoboda, Z.; Vuillerme, N.; Janura, M. Multiscale and Shannon entropies during gait as fall risk predictors—A prospective study. Gait Posture 2017, 52, 5–10. [Google Scholar] [CrossRef]
- Lockhart, T.E.; Liu, J. Differentiating fall-prone and healthy adults using local dynamic stability. Ergonomics 2008, 51, 1860–1872. [Google Scholar] [CrossRef]
- Howcroft, J.; Kofman, J.; Lemaire, E.D.; McIlroy, W.E. Analysis of dual-task elderly gait in fallers and non-fallers using wearable sensors. J. Biomech. 2016, 49, 992–1001. [Google Scholar] [CrossRef]
- Ihlen, E.A.; Van Schooten, K.S.; Bruijn, S.M.; Van Dieen, J.H.; Vereijken, B.; Helbostad, J.L.; Pijnappels, M. Improved prediction of falls in community-dwelling older adults through phase-dependent entropy of daily-life walking. Front. Aging Neurosci. 2018, 10, 44. [Google Scholar] [CrossRef]
- Ihlen, E.A.; Weiss, A.; Helbostad, J.L.; Hausdorff, J.M. The discriminant value of phase-dependent local dynamic stability of daily life walking in older adult community-dwelling fallers and nonfallers. BioMed Res. Int. 2015, 2015, 402596. [Google Scholar] [CrossRef] [PubMed]
- Rogan, S.; Taeymans, J.; Bangerter, C.; Simon, S.; Terrier, P.; Hilfiker, R. Influence of single and dual tasks on gait stability and gait speed in the elderly. Z. Für Gerontol. Und Geriatr. 2019, 52, 23–27. [Google Scholar] [CrossRef] [PubMed]
- De Melker Worms, J.L.; Stins, J.F.; van Wegen, E.E.; Loram, I.D.; Beek, P.J. Influence of focus of attention, reinvestment and fall history on elderly gait stability. Physiol. Rep. 2017, 5, e13061. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Pai, Y.-C. Can stability really predict an impending slip-related fall among older adults? J. Biomech. 2014, 47, 3876–3881. [Google Scholar] [CrossRef] [PubMed]
- Ihlen, E.A.; Sletvold, O.; Goihl, T.; Wik, P.B.; Vereijken, B.; Helbostad, J. Older adults have unstable gait kinematics during weight transfer. J. Biomech. 2012, 45, 1559–1565. [Google Scholar] [CrossRef]
- Kang, H.G.; Dingwell, J.B. Dynamic stability of superior vs. inferior segments during walking in young and older adults. Gait Posture 2009, 30, 260–263. [Google Scholar] [CrossRef]
- Vieira, M.F.; Rodrigues, F.B.; e Souza, G.S.d.S.; Magnani, R.M.; Lehnen, G.C.; Andrade, A.O. Linear and nonlinear gait features in older adults walking on inclined surfaces at different speeds. Ann. Biomed. Eng. 2017, 45, 1560–1571. [Google Scholar] [CrossRef]
- Terrier, P.; Reynard, F. Effect of age on the variability and stability of gait: A cross-sectional treadmill study in healthy individuals between 20 and 69 years of age. Gait Posture 2015, 41, 170–174. [Google Scholar] [CrossRef]
- Cignetti, F.; Decker, L.M.; Stergiou, N. Sensitivity of the Wolf’s and Rosenstein’s algorithms to evaluate local dynamic stability from small gait data sets. Ann. Biomed. Eng. 2012, 40, 1122–1130. [Google Scholar] [CrossRef]
- Hamacher, D.; Hamacher, D.; Singh, N.B.; Taylor, W.R.; Schega, L. Towards the assessment of local dynamic stability of level-grounded walking in an older population. Med. Eng. Phys. 2015, 37, 1152–1155. [Google Scholar] [CrossRef]
- Kang, H.G.; Dingwell, J.B. A direct comparison of local dynamic stability during unperturbed standing and walking. Exp. Brain Res. 2006, 172, 35. [Google Scholar] [CrossRef]
- Kyvelidou, A.; Kurz, M.J.; Ehlers, J.L.; Stergiou, N. Aging and partial body weight support affects gait variability. J. Neuroeng. Rehabil. 2008, 5, 22. [Google Scholar] [CrossRef]
- Ohtaki, Y.; Arif, M.; Suzuki, A.; Fujita, K.; Inooka, H.; Nagatomi, R.; Tsuji, I. Assessment of walking stability of elderly by means of nonlinear time-series analysis and simple accelerometry. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2005, 48, 607–612. [Google Scholar] [CrossRef][Green Version]
- Segal, A.D.; Orendurff, M.S.; Czerniecki, J.M.; Shofer, J.B.; Klute, G.K. Local dynamic stability in turning and straight-line gait. J. Biomech. 2008, 41, 1486–1493. [Google Scholar] [CrossRef]
- Granata, K.P.; Lockhart, T.E. Dynamic stability differences in fall-prone and healthy adults. J. Electromyogr. Kinesiol. 2008, 18, 172–178. [Google Scholar] [CrossRef]
- Craig, J.J.; Bruetsch, A.P.; Huisinga, J.M. Coordination of trunk and foot acceleration during gait is affected by walking velocity and fall history in elderly adults. Aging Clin. Exp. Res. 2019, 31, 943–950. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, X.; Lockhart, T.E. Fall risk assessments based on postural and dynamic stability using inertial measurement unit. Saf. Health Work. 2012, 3, 192–198. [Google Scholar] [CrossRef]
- Qiao, M.; Truong, K.N.; Franz, J.R. Does local dynamic stability during unperturbed walking predict the response to balance perturbations? An examination across age and falls history. Gait Posture 2018, 62, 80–85. [Google Scholar] [CrossRef]
- Reynard, F.; Terrier, P. Local dynamic stability of treadmill walking: Intrasession and week-to-week repeatability. J. Biomech. 2014, 47, 74–80. [Google Scholar] [CrossRef]
- Toebes, M.J.; Hoozemans, M.J.; Furrer, R.; Dekker, J.; van Dieën, J.H. Local dynamic stability and variability of gait are associated with fall history in elderly subjects. Gait Posture 2012, 36, 527–531. [Google Scholar] [CrossRef]
- Rispens, S.M.; van Schooten, K.S.; Pijnappels, M.; Daffertshofer, A.; Beek, P.J.; van Dieen, J.H. Identification of fall risk predictors in daily life measurements: Gait characteristics’ reliability and association with self-reported fall history. Neurorehabilit. Neural Repair 2015, 29, 54–61. [Google Scholar] [CrossRef] [PubMed]
- Rispens, S.M.; Van Dieën, J.H.; Van Schooten, K.S.; Lizama, L.E.C.; Daffertshofer, A.; Beek, P.J.; Pijnappels, M. Fall-related gait characteristics on the treadmill and in daily life. J. Neuroeng. Rehabil. 2016, 13, 12. [Google Scholar] [CrossRef] [PubMed]
- Lizama, L.E.C.; Pijnappels, M.; Rispens, S.M.; Reeves, N.P.; Verschueren, S.M.; van Dieën, J.H. Mediolateral balance and gait stability in older adults. Gait Posture 2015, 42, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Hamacher, D.; Hamacher, D.; Rehfeld, K.; Schega, L. Motor-cognitive dual-task training improves local dynamic stability of normal walking in older individuals. Clin. Biomech. 2016, 32, 138–141. [Google Scholar] [CrossRef]
- Kang, H.G.; Dingwell, J.B. Effects of walking speed, strength and range of motion on gait stability in healthy older adults. J. Biomech. 2008, 41, 2899–2905. [Google Scholar] [CrossRef]
- Toebes, M.J.; Hoozemans, M.J.; Mathiassen, S.E.; Dekker, J.; van Dieën, J.H. Measurement strategy and statistical power in studies assessing gait stability and variability in older adults. Aging Clin. Exp. Res. 2016, 28, 257–265. [Google Scholar] [CrossRef]
- Aboutorabi, A.; Arazpour, M.; Bahramizadeh, M.; Hutchins, S.W.; Fadayevatan, R. The effect of aging on gait parameters in able-bodied older subjects: A literature review. Aging Clin. Exp. Res. 2016, 28, 393–405. [Google Scholar] [CrossRef]
- Gonzalez, M.; Gates, D.H.; Rosenblatt, N.J. The impact of obesity on gait stability in older adults. J. Biomech. 2020, 100, 109585. [Google Scholar] [CrossRef]
- Lizama, L.E.C.; Pijnappels, M.; Faber, G.H.; Reeves, P.N.; Verschueren, S.M.; van Dieen, J.H. Age effects on mediolateral balance control. PLoS ONE 2014, 9, e110757. [Google Scholar]
- Folstein, M.F.; Folstein, S.E.; McHugh, P.R. “Mini-mental state”: A practical method for grading the cognitive state of patients for the clinician. J. Psychiatr. Res. 1975, 12, 189–198. [Google Scholar] [CrossRef]
- Dingwell, J.B.; Cusumano, J.P.; Sternad, D.; Cavanagh, P. Slower speeds in patients with diabetic neuropathy lead to improved local dynamic stability of continuous overground walking. J. Biomech. 2000, 33, 1269–1277. [Google Scholar] [CrossRef]
- Hurmuzlu, Y.; Basdogan, C. On the measurement of dynamic stability of human locomotion. J. Biomech. Eng. 1994, 116, 30–36. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. -Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Bernsteĭn, N. The Co-Ordination and Regulation of Movements; Pergamon Press: New York, NY, USA, 1967. [Google Scholar]
- England, S.A.; Granata, K.P. The influence of gait speed on local dynamic stability of walking. Gait Posture 2007, 25, 172–178. [Google Scholar] [CrossRef]
- Bruijn, S.M.; van Dieën, J.H.; Meijer, O.G.; Beek, P.J. Is slow walking more stable? J. Biomech. 2009, 42, 1506–1512. [Google Scholar] [CrossRef]
- Lamb, S.E.; Jørstad-Stein, E.C.; Hauer, K.; Becker, C.; Prevention of Falls Network Europe and Outcomes Consensus Group. Development of a common outcome data set for fall injury prevention trials: The Prevention of Falls Network Europe consensus. J. Am. Geriatr. Soc. 2005, 53, 1618–1622. [Google Scholar] [CrossRef]
- Senn, S. Sample size considerations for n-of-1 trials. Stat. Methods Med. Res. 2019, 28, 372–383. [Google Scholar] [CrossRef]
- Wearing, S.C.; Reed, L.F.; Urry, S.R. Agreement between temporal and spatial gait parameters from an instrumented walkway and treadmill system at matched walking speed. Gait Posture 2013, 38, 380–384. [Google Scholar] [CrossRef]
- Usmani, S.; Saboor, A.; Haris, M.; Khan, M.A.; Park, H. Latest Research Trends in Fall Detection and Prevention Using Machine Learning: A Systematic Review. Sensors 2021, 21, 5134. [Google Scholar] [CrossRef]
- Delahoz, Y.S.; Labrador, M.A. Survey on fall detection and fall prevention using wearable and external sensors. Sensors 2014, 14, 19806–19842. [Google Scholar] [CrossRef]
- Preatoni, E.; Bergamini, E.; Fantozzi, S.; Giraud, L.I.; Orejel Bustos, A.S.; Vannozzi, G.; Camomilla, V. The Use of Wearable Sensors for Preventing, Assessing, and Informing Recovery from Sport-Related Musculoskeletal Injuries: A Systematic Scoping Review. Sensors 2022, 22, 3225. [Google Scholar] [CrossRef] [PubMed]
- Huffaker, R.; Bittelli, M.; Rosa, R. Nonlinear Time Series Analysis with R; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
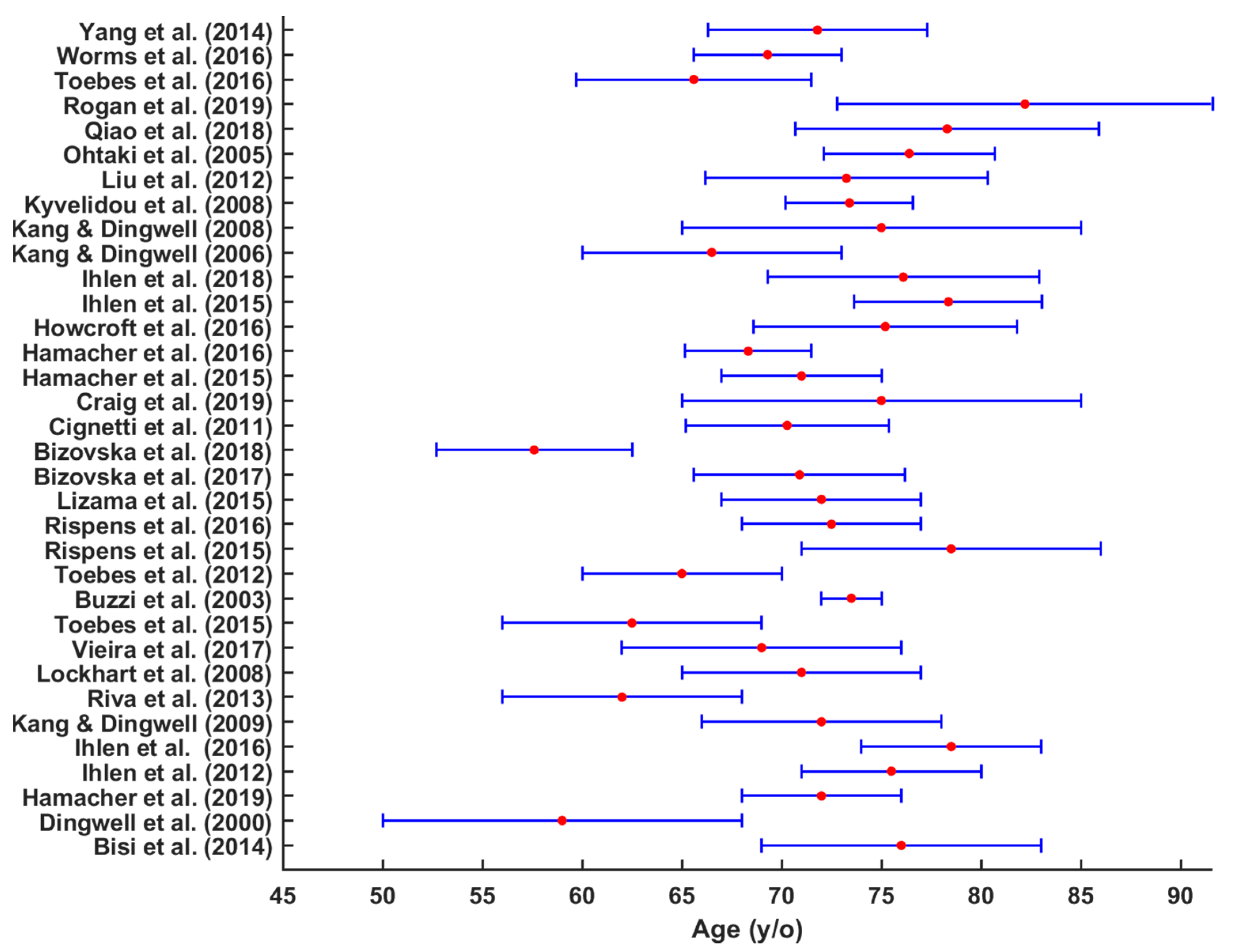

| Author (Year) [Reference] | F-NF | YO | Equal Gender/Sex Ratio | Sample Size | Female/Male | TM/OG/Both |
|---|---|---|---|---|---|---|
| Bisi et al. (2014) [6] | no | yes | no | 30 | nm | TM |
| Dingwell et al. (2000) [27] | yes | no | no | 24 | 7/17 | Both |
| Bizovska et al. (2018) [28] | yes | no | no | 139 | nm | OG |
| Gonzalez et al. (2020) [63] | no | no | no | 34 | nm | TM |
| Granata et al. (2008) [50] | yes | yes | no | 12 | nm | TM |
| Hamacher et al. (2019) [3] | no | yes | no | 102 | 52/50 | OG |
| Ihlen et al. (2012) [40] | no | yes | no | 20 | 8/12 | TM |
| Ihlen et al. (2016) [29] | yes | no | no | 71 | nm | OG |
| Kang & Dingwell (2009) [41] | no | yes | no | 25 | 11/14 | TM |
| Lockhart et al. (2008) [33] | yes | yes | no | 13 | nm | TM |
| Riva et al. (2013) [19] | yes | no | no | 131 | nm | TM |
| Vieira et al. (2017) [42] | no | yes | no | 87 | 46/41 | TM |
| Toebes et al. (2015) [31] | no | no | no | 134 | 85/49 | TM |
| Buzzi et al. (2003) [7] | no | yes | no | 20 | 20/0 | TM |
| Terrier et al. (2015) [43] | no | yes | yes | 100 | 50/50 | TM |
| Toebes et al. (2012) [55] | no | no | no | 134 | 85/49 | TM |
| Rispens et al. (2015) [56] | no | no | no | 110 | 77/33 | OG |
| Rispens et al. (2016) [57] | no | no | no | 18 | 7/11 | Both |
| Lizama et al. (2015) [58] | no | no | no | 19 | 7/12 | TM |
| Bizovska et al. (2017) [32] | yes | no | no | 139 | nm | OG |
| Bizovska et al. (2018) [9] | no | yes | yes | 139 | nm | Both |
| Cignetti et al. (2011) [44] | no | yes | no | 14 | 5/9 | TM |
| Craig et al. (2019) [51] | yes | yes | no | 65 | 48/17 | TM |
| Hamacher et al. (2015) [45] | no | yes | no | 39 | 26/13 | OG |
| Hamacher et al. (2016) [59] | no | no | no | 32 | 21/11 | OG |
| Howcroft et al. (2016) [34] | yes | no | no | 100 | 56/44 | OG |
| Ihlen et al. (2015) [36] | yes | no | no | 71 | nm | OG |
| Ihlen et al. (2018) [35] | yes | no | no | 319 | 162/157 | OG |
| Kang & Dingwell (2006) [46] | no | yes | no | 20 | nm | TM |
| Kang & Dingwell (2008) [60] | no | no | no | 36 | 12/24 | TM |
| Kyvelidou et al. (2008) [47] | no | yes | yes | 20 | 20/0 | TM |
| Liu et al. (2012) [52] | yes | yes | no | 12 | 7/5 | TM |
| Ohtaki et al. (2005) [48] | no | yes | no | 59 | 26/33 | OG |
| Qiao et al. (2018) [53] | yes | yes | no | 33 | 19/14 | TM |
| Reynard et al. (2014) [54] | yes | yes | yes | 100 | 50/50 | TM |
| Rogan et al. (2019) [37] | yes | no | no | 26 | nm | OG |
| Segal et al. (2008) [49] | no | yes | no | 19 | 5/14 | TM |
| Toebes et al. (2016) [61] | no | no | no | 16 | 9/7 | TM |
| Worms et al. (2016) [38] | yes | no | no | 28 | 20/8 | TM |
| Yang et al. (2014) [39] | yes | no | no | 187 | 187/0 | TM |
| Questionnaire | Description | Clinical Assessment | Description |
|---|---|---|---|
| Anamnestic questionnaire [28] | Focusing on participants’ physical condition and fall history in the 3 months prior the measurement. | Tinetti Balance Assessment Tool (TBAT) [28,32] | Assesses the gait and balance in older adults and perception of balance and stability during activities of daily living and fear of falling. |
| Fall history questionnaire [3,28,29,30,31,33,38,40,42,50] | Self-reported medical questionnaires also indicated participants had recent histories of falling (at least one fall within 6 months, 3 months or one year). | Single leg stance test [63] | Assesses static postural and balance control |
| Survey of Activities and Fear of Falling in the Elderly (SAFE) [63] | Includes one scale and one subscale: the scale asks participants whether they perform a series of 11 activities of daily living and, if so, their level of fear of falling during the activity (Fear of Falling subscale). A separate subscale (Activity Restriction subscale) asks participants to rate the extent to which they currently engage in each activity relative to five years ago. | Timed Up and Go [63] | Determines fall risk and measures the progress of balance, sitting to standing and walking |
| The Movement Specific Reinvestment Scale (MSRS) [38] | It is a measure of the propensity for movement-related self-consciousness and for conscious processing of movement and was used to try to discriminate elder fallers from non-fallers. | 10 m Walk Test [63] | It is a performance measure used to assess walking speed in meters per second over a short distance. It can be employed to determine functional mobility, gait and vestibular function. |
| The Falls Efficacy Scale International (FES-I) [38] | A measure quantifying an individual’s concern about falling during various tasks, yielding a score between 16 (low concern about falling) and 64 (high concern about falling). | “Figure 8” Walk [63] | Measures the everyday walking ability of older adults with mobility disabilities. It tests a participant’s gait in both straight and curved paths. |
| The Longitudinal Aging Study Amsterdam Physical Activity Questionnaire (LAPAQ) [30] | A 31-point questionnaire that covers the frequency and duration of walking outside, bicycling, gardening, light household activities, heavy household activities, and a maximum of two sport activities during the previous two weeks. | Four Square Step [63] | Assesses dynamic stability and the ability of the subject to step over low objects forward, sideways, and backward. |
| Mini mental estate examination score (MMSE) [37,38,56,57,58] | A 30-point questionnaire that is used extensively in clinical and research settings to measure cognitive impairment. | Clinical balance assessment (static balance on force plate) [3] | Determine a patient’s ability (or inability) to safely balance during a series of predetermined tasks. It does not include the assessment of gait. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amirpourabasi, A.; Lamb, S.E.; Chow, J.Y.; Williams, G.K.R. Nonlinear Dynamic Measures of Walking in Healthy Older Adults: A Systematic Scoping Review. Sensors 2022, 22, 4408. https://doi.org/10.3390/s22124408
Amirpourabasi A, Lamb SE, Chow JY, Williams GKR. Nonlinear Dynamic Measures of Walking in Healthy Older Adults: A Systematic Scoping Review. Sensors. 2022; 22(12):4408. https://doi.org/10.3390/s22124408
Chicago/Turabian StyleAmirpourabasi, Arezoo, Sallie E. Lamb, Jia Yi Chow, and Geneviève K. R. Williams. 2022. "Nonlinear Dynamic Measures of Walking in Healthy Older Adults: A Systematic Scoping Review" Sensors 22, no. 12: 4408. https://doi.org/10.3390/s22124408
APA StyleAmirpourabasi, A., Lamb, S. E., Chow, J. Y., & Williams, G. K. R. (2022). Nonlinear Dynamic Measures of Walking in Healthy Older Adults: A Systematic Scoping Review. Sensors, 22(12), 4408. https://doi.org/10.3390/s22124408








