Hyperparameter Optimization of Bayesian Neural Network Using Bayesian Optimization and Intelligent Feature Engineering for Load Forecasting
Abstract
:1. Introduction
1.1. Contributions
- An ingenious and robust framework, FE-BNN-BO has been proposed that integrates the FE and BO algorithm with BNN. The FE module solves the concern associated with redundancy and irrelevance (dimension reduction). In the meantime, the BO algorithm optimizes the hyper-parameters of the BNN predictor to enhance accuracy while securing fast convergence. The combination of the FE module and the BO algorithm significantly improves the performance and effectiveness of the BNN model.
- BNN models are complex in estimating computational efficiency and cannot handle uncertainty. Therefore, the iterative and irrelevant features may enhance the complexity, slow down the BNN training process and affect the prediction accuracy. The proposed FE addresses this problem by combining the Random Forest and Relief-F-based feature selector and radial-based kernel principal component analysis (RBKPCA)-based feature extractor. The feature selector converges the Random Forest with Relief-F, calculates the importance of the feature, selects the relevant feature, and discards the irrelevant feature. This further enhances the computational performance and efficacy of the BNN model.
- Moreover, the BO algorithm is automatically applied to search for the best ensemble configuration. The devised BO algorithm is more controllable and efficient in time and complexity than the widely used grid search methods.
- The proposed model is validated against the latest hourly load data obtained from the USA electricity grid. The proposed frameworks outperformed the benchmark frameworks, such as LSTM, ANN-MI, ANN-AFC, and Bi-Level, when considering the accuracy and convergence speed.
1.2. Paper Organization
2. Literature Survey
2.1. Individual ELF Models
2.2. Hybrid ELF Models
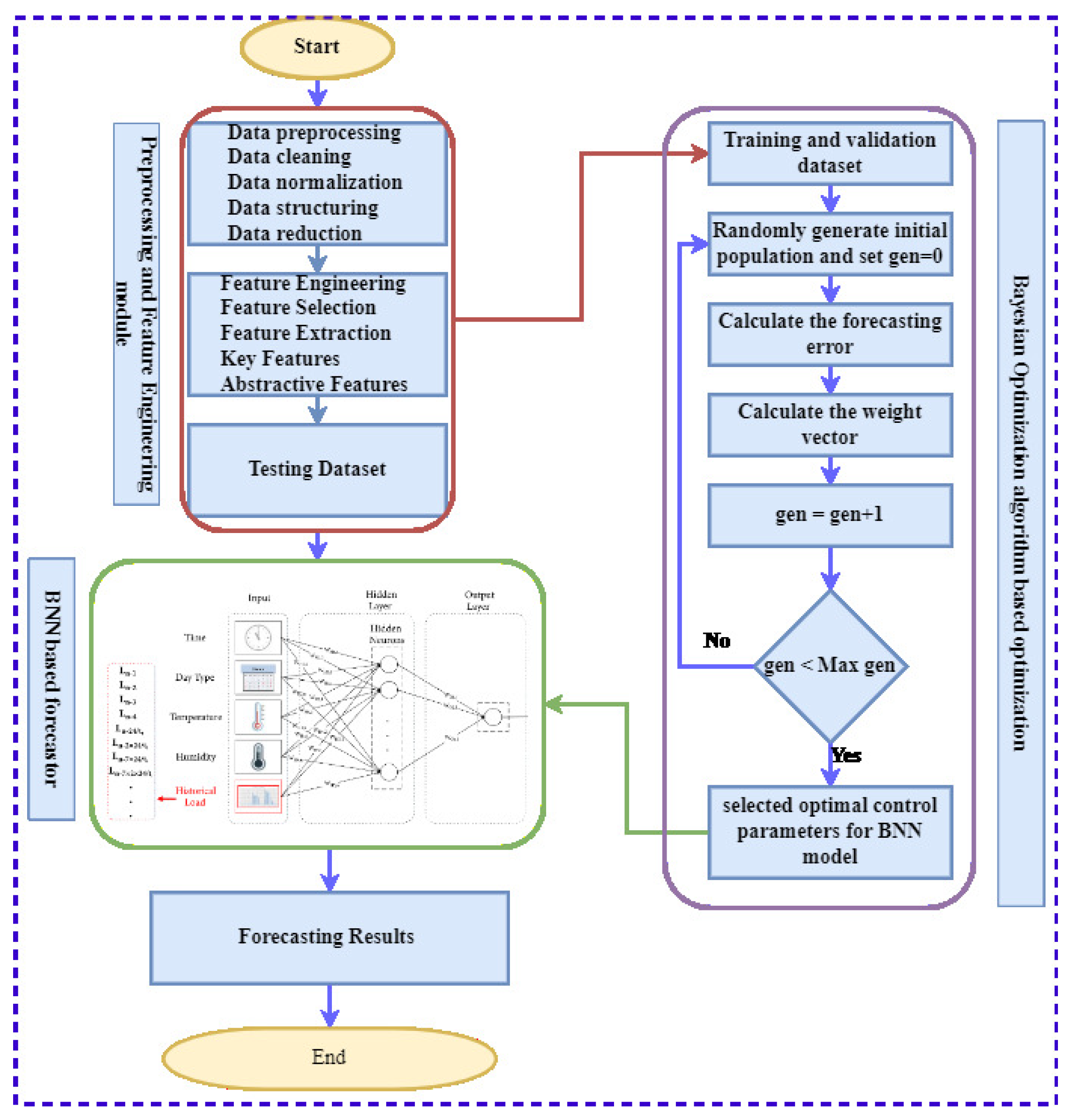
3. Proposed Model
3.1. FE Module
3.1.1. FS
3.1.2. FX
- Linear kernel function: the linear kernel is used when the data is linearly separable. It can be separated by one line. This is one of the most commonly used kernels. This is primarily used when a particular dataset contains a large number of features. Mathematically, it may be formulated in Equation (32):
- Kernel function based on logistic sigmoidal: this function is equivalent to a two-layer, perceptron model of the neural network, which is used as an activation function for artificial neurons. Equation (33) show the mathematical representation of kernel-based sigmoid function:
- Kernel function based on radial basis: radial basis function kernels or RBF kernels are common kernel functions used in various kernel-learning algorithms. In particular, they are often used to classify SVMs. Mathematically, an RBF kernel is represented in Equation (34):
3.2. BNN-Based Forecasting Module
3.3. Optimization Module Based on BO
BO-Based Optimizer
3.4. BO Algorithm for Hyperparameters Tuning
| Algorithm 1 TPE-based BOA for HP tuning. |
|
4. Simulation Results and Discussion
4.1. Simulation Setup
4.2. Compared Models
- Time consumed during execution by the forecasting approach is called convergence rate, and the execution time is calculated in seconds (s).
- While Accuracy () is defined as:and is measured in .
4.3. Description of Dataset
4.4. Learning Curve Evaluation
4.5. Day-Ahead Analysis
4.6. Convergence Rate Evaluation
- Abstractive features are fed into the training and forecasting module, reducing network training time.
- The BO algorithm is used due to its significantly faster convergence rate.
4.7. Scalability Analysis
4.8. Computational Time Analysis
4.9. Robustness Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Masa-Bote, D.; Castillo-Cagigal, M.; Matallanas, E.; Caamaño-Martín, E.; Gutiérrez, A.; Monasterio-Huelín, F.; Jiménez-Leube, J. Improving photovoltaics grid integration through short time forecasting and self-consumption. Appl. Energy 2014, 125, 103–113. [Google Scholar] [CrossRef]
- Feinberg, E.A.; Genethliou, D. Load forecasting. In Applied Mathematics for Restructured Electric Power Systems; Springer: Boston, MA, USA, 2005; pp. 269–285. [Google Scholar]
- Xiao, L.; Wang, J.; Yang, X.; Xiao, L. A hybrid model based on data preprocessing for electrical power forecasting. Int. J. Electr. Power Energy Syst. 2015, 64, 311–327. [Google Scholar] [CrossRef]
- Notton, G.; Voyant, C. Forecasting of intermittent solar energy resource. In Advances in Renewable Energies and Power Technologies; Elsevier: Amsterdam, The Netherlands, 2018; pp. 77–114. [Google Scholar]
- Xiao, L.; Wang, J.; Hou, R.; Wu, J. A combined model based on data pre-analysis and weight coefficients optimization for electrical load forecasting. Energy 2015, 82, 524–549. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Zhang, K. Short-term electric load forecasting based on singular spectrum analysis and support vector machine optimized by Cuckoo search algorithm. Electr. Power Syst. Res. 2017, 146, 270–285. [Google Scholar] [CrossRef]
- Lin, C.T.; Chou, L.D. A novel economy reflecting short-term load forecasting approach. Energy Conv. Manag. 2013, 65, 331–342. [Google Scholar] [CrossRef]
- Zhang, M.; Bao, H.; Yan, L.; Cao, J.P.; Du, J.G. Research on processing of short-term historical data of daily load based on Kalman filter. Power Syst. Technol. 2003, 10, 200. [Google Scholar]
- Irisarri, G.; Widergren, S.; Yehsakul, P. On-line load forecasting for energy control center application. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 71–78. [Google Scholar] [CrossRef]
- Dordonnat, V.; Pichavant, A.; Pierrot, A. GEFCom2014 probabilistic electric load forecasting using time series and semi-parametric regression models. In. J. Forecast. 2016, 32, 1005–1011. [Google Scholar] [CrossRef]
- Christiaanse, W. Short-term load forecasting using general exponential smoothing. IEEE Trans. Power Appar. Syst. 1971, 2, 900–911. [Google Scholar] [CrossRef]
- Amral, N.; Ozveren, C.; King, D. Short term load forecasting using multiple linear regression. In Proceedings of the 2007 42nd International Universities Power Engineering Conference, Brighton, UK, 4–6 September 2007; pp. 1192–1198. [Google Scholar]
- Wang, Y.; Wang, J.; Zhao, G.; Dong, Y. Application of residual modification approach in seasonal ARIMA for electricity demand forecasting: A case study of China. Energy Policy 2012, 48, 284–294. [Google Scholar] [CrossRef]
- Lin, W.M.; Gow, H.J.; Tsai, M.T. An enhanced radial basis function network for short-term electricity price forecasting. Appl. Energy 2010, 87, 3226–3234. [Google Scholar] [CrossRef]
- Xiao, L.; Shao, W.; Liang, T.; Wang, C. A combined model based on multiple seasonal patterns and modified firefly algorithm for electrical load forecasting. Appl. Energy 2016, 167, 135–153. [Google Scholar] [CrossRef]
- Uyar, M.; Yildirim, S.; Gencoglu, M.T. An expert system based on S-transform and neural network for automatic classification of power quality disturbances. Expert Syst. Appl. 2009, 36, 5962–5975. [Google Scholar] [CrossRef]
- Yang, J. Power System Short-Term Load Forecasting. Ph.D. Thesis, Technical University, Darmstadt, Germany, 2006. [Google Scholar]
- Yildiz, B.; Bilbao, J.I.; Sproul, A.B. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- Tong, C.; Li, J.; Lang, C.; Kong, F.; Niu, J.; Rodrigues, J.J. An efficient deep model for day-ahead electricity load forecasting with stacked denoising auto-encoders. J. Parallel Distrib. Comput. 2018, 117, 267–273. [Google Scholar] [CrossRef]
- Metaxiotis, K.; Kagiannas, A.; Askounis, D.; Psarras, J. Artificial intelligence in short term electric load forecasting: A state-of-the-art survey for the researcher. Energy Conv. Manag. 2003, 44, 1525–1534. [Google Scholar] [CrossRef]
- Kim, H.C.; Pang, S.; Je, H.M.; Kim, D.; Bang, S.Y. Constructing support vector machine ensemble. Pattern Recogn. 2003, 36, 2757–2767. [Google Scholar] [CrossRef]
- Buntine, W.L. Bayesian backpropagation. Complex Syst. 1991, 5, 603–643. [Google Scholar]
- MacKay, D.J.; Mac Kay, D.J. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Neal, R.M. Bayesian Training of Backpropagation Networks by the Hybrid Monte Carlo Method; Technical Report; University of Toronto: Toronto, ON, Canada, 1992. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar]
- Alizadeh, B.; Bafti, A.G.; Kamangir, H.; Zhang, Y.; Wright, D.B.; Franz, K.J. A novel attention-based LSTM cell post-processor coupled with bayesian optimization for streamflow prediction. J. Hydrol. 2021, 601, 126526. [Google Scholar] [CrossRef]
- Ma, J.; Ding, Y.; Cheng, J.C.; Jiang, F.; Gan, V.J.; Xu, Z. A Lag-FLSTM deep learning network based on Bayesian Optimization for multi-sequential-variant PM2. 5 prediction. Sustain. Cities Soc. 2020, 60, 102237. [Google Scholar] [CrossRef]
- Abbasimehr, H.; Paki, R. Prediction of COVID-19 confirmed cases combining deep learning methods and Bayesian optimization. Chaos Solitons Fractals 2021, 142, 110511. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Chen, Q.; Yan, J.; Zhang, S.; Xu, J. A novel asynchronous deep reinforcement learning model with adaptive early forecasting method and reward incentive mechanism for short-term load forecasting. Energy 2021, 236, 121492. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Qu, H.; Liu, S. Optimal forecast combination based on neural networks for time series forecasting. Appl. Soft Comput. 2018, 66, 1–17. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M4 Competition: 100,000 time series and 61 forecasting methods. Int. J. Forecast. 2020, 36, 54–74. [Google Scholar] [CrossRef]
- Pelikan, M. Hierarchical Bayesian optimization algorithm. In Hierarchical Bayesian Optimization Algorithm; Springer: Berlin/Heidelberg, Germany, 2005; pp. 105–129. [Google Scholar]
- Khan, N.; Goldberg, D.E.; Pelikan, M. Multi-objective Bayesian optimization algorithm. In Proceedings of the 4th Annual Conference on Genetic and Evolutionary Computation, New York, NY, USA, 9–13 July 2002; p. 684. [Google Scholar]
- Schwarz, J.; Ocenasek, J. A problem knowledge-based evolutionary algorithm KBOA for hypergraph bisectioning. In Proceedings of the 4th Joint Conference on Knowledge-Based Software Engineering, Brno, Czech Republic, 16–21 June 2000; IOS Press: Amsterdam, The Netherlands, 2000; pp. 51–58. [Google Scholar]
- Liu, D.; Zeng, L.; Li, C.; Ma, K.; Chen, Y.; Cao, Y. A distributed short-term load forecasting method based on local weather information. IEEE Syst. J. 2016, 12, 208–215. [Google Scholar] [CrossRef]
- Shi, H.; Xu, M.; Li, R. Deep learning for household load forecasting—A novel pooling deep RNN. IEEE Trans. Smart Grid 2017, 9, 5271–5280. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Hill, D.J.; Luo, F.; Xu, Y. Short-term residential load forecasting based on resident behaviour learning. IEEE Trans. Power Syst. 2017, 33, 1087–1088. [Google Scholar] [CrossRef]
- Huang, X.; Hong, S.H.; Li, Y. Hour-ahead price based energy management scheme for industrial facilities. IEEE Trans. Ind. Inf. 2017, 13, 2886–2898. [Google Scholar] [CrossRef]
- Van der Meer, D.W.; Munkhammar, J.; Widén, J. Probabilistic forecasting of solar power, electricity consumption and net load: Investigating the effect of seasons, aggregation and penetration on prediction intervals. Solar Energy 2018, 171, 397–413. [Google Scholar] [CrossRef]
- Carvallo, J.P.; Larsen, P.H.; Sanstad, A.H.; Goldman, C.A. Long term load forecasting accuracy in electric utility integrated resource planning. Energy Policy 2018, 119, 410–422. [Google Scholar] [CrossRef]
- Wang, P.; Liu, B.; Hong, T. Electric load forecasting with recency effect: A big data approach. Int. J. Forecast. 2016, 32, 585–597. [Google Scholar] [CrossRef]
- Gavrilas, M. Heuristic and Metaheuristic Optimization Techniques with Application to Power Systems; Technical University of Iasi: Iasi, Romania, 2010. [Google Scholar]
- Binitha, S.; Sathya, S.S. A survey of bio inspired optimization algorithms. Int. J. Soft Comput. Eng. 2012, 2, 137–151. [Google Scholar]
- Akbaripour, H.; Masehian, E. Efficient and robust parameter tuning for heuristic algorithms. Int. J. Ind. Eng. Prod. Res. 2013, 24, 143–150. [Google Scholar]
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Yu, F.; Xu, X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network. Appl. Energy 2014, 134, 102–113. [Google Scholar] [CrossRef]
- Liao, G.C. Hybrid improved differential evolution and wavelet neural network with load forecasting problem of air conditioning. Int. J. Electr. Power Energy Syst. 2014, 61, 673–682. [Google Scholar]
- Jawad, M.; Ali, S.M.; Khan, B.; Mehmood, C.A.; Farid, U.; Ullah, Z.; Usman, S.; Fayyaz, A.; Jadoon, J.; Tareen, N.; et al. Genetic algorithm-based non-linear auto-regressive with exogenous inputs neural network short-term and medium-term uncertainty modelling and prediction for electrical load and wind speed. J. Eng. 2018, 2018, 721–729. [Google Scholar] [CrossRef]
- Huyghues-Beaufond, N.; Tindemans, S.; Falugi, P.; Sun, M.; Strbac, G. Robust and automatic data cleansing method for short-term load forecasting of distribution feeders. Appl. Energy 2020, 261, 114405. [Google Scholar] [CrossRef]
- Cai, M.; Pipattanasomporn, M.; Rahman, S. Day-ahead building-level load forecasts using deep learning vs. traditional time-series techniques. Appl. Energy 2019, 236, 1078–1088. [Google Scholar] [CrossRef]
- He, F.; Zhou, J.; Feng, Z.k.; Liu, G.; Yang, Y. A hybrid short-term load forecasting model based on variational mode decomposition and long short-term memory networks considering relevant factors with Bayesian optimization algorithm. Appl. Energy 2019, 237, 103–116. [Google Scholar] [CrossRef]
- Wu, Z.; Zhao, X.; Ma, Y.; Zhao, X. A hybrid model based on modified multi-objective cuckoo search algorithm for short-term load forecasting. Appl. Energy 2019, 237, 896–909. [Google Scholar] [CrossRef]
- Vrablecová, P.; Ezzeddine, A.B.; Rozinajová, V.; Šárik, S.; Sangaiah, A.K. Smart grid load forecasting using online support vector regression. Comput. Electr. Eng. 2018, 65, 102–117. [Google Scholar]
- Li, Y.; Che, J.; Yang, Y. Subsampled support vector regression ensemble for short term electric load forecasting. Energy 2018, 164, 160–170. [Google Scholar] [CrossRef]
- Zhang, F.; Deb, C.; Lee, S.E.; Yang, J.; Shah, K.W. Time series forecasting for building energy consumption using weighted Support Vector Regression with differential evolution optimization technique. Energy Build. 2016, 126, 94–103. [Google Scholar] [CrossRef]
- Cao, G.; Wu, L. Support vector regression with fruit fly optimization algorithm for seasonal electricity consumption forecasting. Energy 2016, 115, 734–745. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Samet, H.; Marzbani, F. A new hybrid modified firefly algorithm and support vector regression model for accurate short term load forecasting. Exp. Syst. Appl. 2014, 41, 6047–6056. [Google Scholar] [CrossRef]
- Xiao, L.; Shao, W.; Wang, C.; Zhang, K.; Lu, H. Research and application of a hybrid model based on multi-objective optimization for electrical load forecasting. Appl. Energy 2016, 180, 213–233. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F.; Zareipour, H. Short-term load forecast of microgrids by a new bilevel prediction strategy. IEEE Trans. Smart Grid 2010, 1, 286–294. [Google Scholar] [CrossRef]
- Hafeez, G.; Alimgeer, K.S.; Wadud, Z.; Shafiq, Z.; Ali Khan, M.U.; Khan, I.; Khan, F.A.; Derhab, A. A novel accurate and fast converging deep learning-based model for electrical energy consumption forecasting in a smart grid. Energies 2020, 13, 2244. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, S.; Sun, Y. A support vector regression model hybridized with chaotic krill herd algorithm and empirical mode decomposition for regression task. Neurocomputing 2020, 410, 185–201. [Google Scholar] [CrossRef]
- Zeng, N.; Zhang, H.; Liu, W.; Liang, J.; Alsaadi, F.E. A switching delayed PSO optimized extreme learning machine for short-term load forecasting. Neurocomputing 2017, 240, 175–182. [Google Scholar] [CrossRef]
- Ghadimi, N.; Akbarimajd, A.; Shayeghi, H.; Abedinia, O. Two stage forecast engine with feature selection technique and improved meta-heuristic algorithm for electricity load forecasting. Energy 2018, 161, 130–142. [Google Scholar] [CrossRef]
- Shiri, A.; Afshar, M.; Rahimi-Kian, A.; Maham, B. Electricity price forecasting using Support Vector Machines by considering oil and natural gas price impacts. In Proceedings of the 2015 IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 17–19 August 2015; pp. 1–5. [Google Scholar]
- Jiang, H.; Zhang, Y.; Muljadi, E.; Zhang, J.J.; Gao, D.W. A short-term and high-resolution distribution system load forecasting approach using support vector regression with hybrid parameters optimization. IEEE Trans. Smart Grid 2016, 9, 3341–3350. [Google Scholar] [CrossRef]
- Fung, C.P. Manufacturing process optimization for wear property of fiber-reinforced polybutylene terephthalate composites with grey relational analysis. Wear 2003, 254, 298–306. [Google Scholar] [CrossRef]
- Julong, D. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Deng, J.L. A Course on Grey System Theory; Huazhong University of Science and Technology Press: Wuhan, China, 1990. [Google Scholar]
- Deng, J. The Essential Methods of Grey Systems; Huazhong University of Science and Technology Press: Wuhan, China, 1992. [Google Scholar]
- Nabavi Karizi, S.; Kabir, E. A Two-Stage Method for Classifiers Combination. Nashriyyah-i Muhandisi-i Barq va Muhandisi-i Kampyutar-i Iran 2008, 1, 63. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Du, Z.; Wang, X.; Zheng, L.; Zheng, Z. Nonlinear system modeling based on KPCA and MKSVM. In Proceedings of the 2009 ISECS International Colloquium on Computing, Communication, Control, and Management, Sanya, China, 8–9 August 2009; IEEE: New York, NY, USA, 2009; Volume 3, pp. 61–64. [Google Scholar]
- Ghofrani, M.; Ghayekhloo, M.; Arabali, A.; Ghayekhloo, A. A hybrid short-term load forecasting with a new input selection framework. Energy 2015, 81, 777–786. [Google Scholar] [CrossRef]
- Neill, S.P.; Hashemi, M.R. Fundamentals of Ocean Renewable Energy: Generating Electricity from the Sea; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Woolf, B.P. Building Intelligent Interactive Tutors: Student-Centered Strategies for Revolutionizing e-Learning; Morgan Kaufmann: Burlington, MA, USA, 2010. [Google Scholar]
- Fox, E.P. Data Analysis: A Bayesian Tutorial; OUP Oxford: Oxford, UK, 1998. [Google Scholar]
- MacKay, D.J. A practical Bayesian framework for backpropagation networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
- Ford, W. Numerical Linear Algebra with Applications: Using MATLAB; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- MacKay, D.J. Probable networks and plausible predictions—A review of practical Bayesian methods for supervised neural networks. Netw. Comput. Neural Syst. 1995, 6, 469–505. [Google Scholar] [CrossRef]
- Hafeez, G.; Islam, N.; Ali, A.; Ahmad, S.; Usman, M.; Saleem Alimgeer, K. A modular framework for optimal load scheduling under price-based demand response scheme in smart grid. Processes 2019, 7, 499. [Google Scholar] [CrossRef]
- Ahmad, A.; Javaid, N.; Guizani, M.; Alrajeh, N.; Khan, Z.A. An accurate and fast converging short-term load forecasting model for industrial applications in a smart grid. IEEE Trans. Ind. Inform. 2016, 13, 2587–2596. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]








| Hyperparameters | Notation | Hyperparameter Space |
|---|---|---|
| Cold-start model index | ||
| Maximum number of chosen models | ||
| Size of past observations to evaluate | ||
| Weight-calculation function | Choice of | |
| Discount factor of past observations | ||
| Updated parameter |
| Control Parameters | Value |
|---|---|
| Hidden layer | 3 |
| Neurons in hidden | 15 |
| Output layer | 1 |
| Number of output neurons | 1 |
| Number of epochs | 200 |
| Number of iterations | 200 |
| Learning rate | 0.0017 |
| Momentum | 0.55 |
| Initial weight | 0.1 |
| Initial bias | 0 |
| Max | 0.8 |
| Min | 0.2 |
| Decision variables | 3 |
| Population size | 23 |
| Delay of weight | 0.0003 |
| Historical load data | 4 yrs |
| Exogenous parameters | 4 yrs |
| Proposed and Benchmark ELF Frameworks | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Hours | Targeted (kW) | Proposed | Bi-Level | ANN-AFC | ANN-MI | ||||
| F.load | MAPE | F.load | MAPE | F.load | MAPE | F.load | MAPE | ||
| (kW) | (%) | (kW) | (%) | (kW) | (%) | (kW) | (%) | ||
| 00.00 | 670.3223 | 667.1829 | 0.4525 | 673.4829 | 1.5400 | 645.5829 | 3.9157 | 650.8923 | 3.1255 |
| 01.00 | 677.7923 | 674.4538 | 0.4926 | 660.4538 | 2.5581 | 665.4538 | 1.8204 | 630.7923 | 6.9343 |
| 02.00 | 700.3192 | 703.7687 | 0.4926 | 715.7687 | 4.6806 | 635.7687 | 9.2173 | 725.3192 | 3.5698 |
| 03.00 | 734.5654 | 738.1835 | 0.4926 | 725.1835 | 2.0696 | 745.1835 | 1.4455 | 759.5654 | 3.4034 |
| 04.00 | 760.9115 | 757.1637 | 0.4924 | 743.1637 | 1.5923 | 777.1637 | 2.1359 | 740.9115 | 2.6284 |
| 05.00 | 767.4346 | 771.2146 | 0.4925 | 755.2146 | 4.4182 | 795.2146 | 3.6199 | 797.4346 | 3.9091 |
| 06.00 | 754.7077 | 758.4250 | 0.4915 | 730.4250 | 4.0749 | 745.4250 | 0.8851 | 750.7077 | 2.3554 |
| 07.00 | 744.3962 | 748.0627 | 0.4923 | 714.0627 | 4.3205 | 755.0627 | 1.2300 | 740.3962 | 0.5300 |
| 08.00 | 731.4692 | 727.8664 | 0.4925 | 699.8664 | 1.7461 | 718.8664 | 1.4329 | 735.4692 | 0.5373 |
| 09.00 | 717.9577 | 714.4214 | 0.4926 | 705.4214 | 0.7822 | 700.4214 | 1.7229 | 720.9577 | 0.5468 |
| 10.00 | 706.0231 | 709.5006 | 0.4926 | 700.5006 | 1.4930 | 730.5006 | 2.4425 | 760.0231 | 6.4179 |
| 11.00 | 699.6500 | 703.0961 | 0.4925 | 710.0961 | 3.9058 | 699.0961 | 0.0792 | 685.6500 | 2.0010 |
| 12.00 | 703.1462 | 706.6095 | 0.4925 | 730.6095 | 2.8131 | 725.6095 | 3.1947 | 707.6213 | 0.9955 |
| 13.00 | 726.0346 | 729.6107 | 0.4926 | 705.6107 | 2.2272 | 750.6107 | 3.3850 | 710.1462 | 1.9283 |
| 14.00 | 753.6077 | 757.3196 | 0.4925 | 755.3196 | 1.1835 | 700.3196 | 7.0711 | 740.0346 | 1.5923 |
| 15.00 | 768.8000 | 772.5867 | 0.4925 | 785.5867 | 3.6695 | 785.5867 | 2.1835 | 765.6077 | 1.2435 |
| 16.00 | 768.8538 | 772.6408 | 0.4925 | 740.6408 | 4.5999 | 778.6408 | 1.9500 | 720.8000 | 6.6503 |
| 17.00 | 754.7423 | 751.0248 | 0.4925 | 720.0248 | 1.1768 | 740.0248 | 0.1325 | 763.8538 | 2.1325 |
| 18.00 | 730.7462 | 734.3454 | 0.4926 | 739.3454 | 1.5246 | 690.9239 | 1.3136 | 755.7423 | 3.7790 |
| 19.00 | 703.3885 | 699.9239 | 0.4926 | 715.9239 | 2.1544 | 670.9967 | 1.7721 | 743.7462 | 8.8145 |
| 20.00 | 682.3577 | 678.9967 | 0.4925 | 760.9967 | 1.2358 | 655.1795 | 1.6650 | 765.3885 | 0.1153 |
| 21.00 | 661.9192 | 665.1795 | 0.4926 | 676.1795 | 2.1540 | 630.0057 | 1.0182 | 682.3577 | 2.1151 |
| 22.00 | 672.6923 | 676.0057 | 0.4926 | 681.0057 | 1.2822 | 630.1417 | 6.3456 | 675.9192 | 0.4797 |
| 23.00 | 676.6923 | 680.1750 | 0.4926 | 686.5057 | 1.4502 | 633.1530 | 5.8778 | 680.6923 | 1.1893 |
| Avg. | 0.4920 | 2.4741 | 2.9186 | 4.3371 | |||||
| Models without FE and Optimization Modules | Models with FE and Optimization Modules | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| LSTM | Bi-Level | BNN | ANN-AFC | ANN-MI | Proposed | ||||||
(s) | MAPE (%) | (s) | MAPE (%) | (s) | MAPE (%) | (s) | MAPE (%) | (s) | MAPE (%) | (s) | MAPE (%) |
| 172 | 2.31 | 182 | 2.1 | 112 | 2.3 | 510 | 1.45 | 348 | 0.95 | 217 | 0.39 |
| 240 | 2.31 | 276 | 2.1 | 187 | 2.3 | 579 | 1.45 | 408 | 0.95 | 265 | 0.39 |
| 308 | 2.31 | 321 | 2.1 | 245 | 2.3 | 456 | 1.45 | 456 | 0.95 | 412 | 0.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zulfiqar, M.; Gamage, K.A.A.; Kamran, M.; Rasheed, M.B. Hyperparameter Optimization of Bayesian Neural Network Using Bayesian Optimization and Intelligent Feature Engineering for Load Forecasting. Sensors 2022, 22, 4446. https://doi.org/10.3390/s22124446
Zulfiqar M, Gamage KAA, Kamran M, Rasheed MB. Hyperparameter Optimization of Bayesian Neural Network Using Bayesian Optimization and Intelligent Feature Engineering for Load Forecasting. Sensors. 2022; 22(12):4446. https://doi.org/10.3390/s22124446
Chicago/Turabian StyleZulfiqar, M., Kelum A. A. Gamage, M. Kamran, and M. B. Rasheed. 2022. "Hyperparameter Optimization of Bayesian Neural Network Using Bayesian Optimization and Intelligent Feature Engineering for Load Forecasting" Sensors 22, no. 12: 4446. https://doi.org/10.3390/s22124446
APA StyleZulfiqar, M., Gamage, K. A. A., Kamran, M., & Rasheed, M. B. (2022). Hyperparameter Optimization of Bayesian Neural Network Using Bayesian Optimization and Intelligent Feature Engineering for Load Forecasting. Sensors, 22(12), 4446. https://doi.org/10.3390/s22124446







