A Global Fundamental Matrix Estimation Method of Planar Motion Based on Inlier Updating
Abstract
:1. Introduction
2. Related Work in Robotic Applications
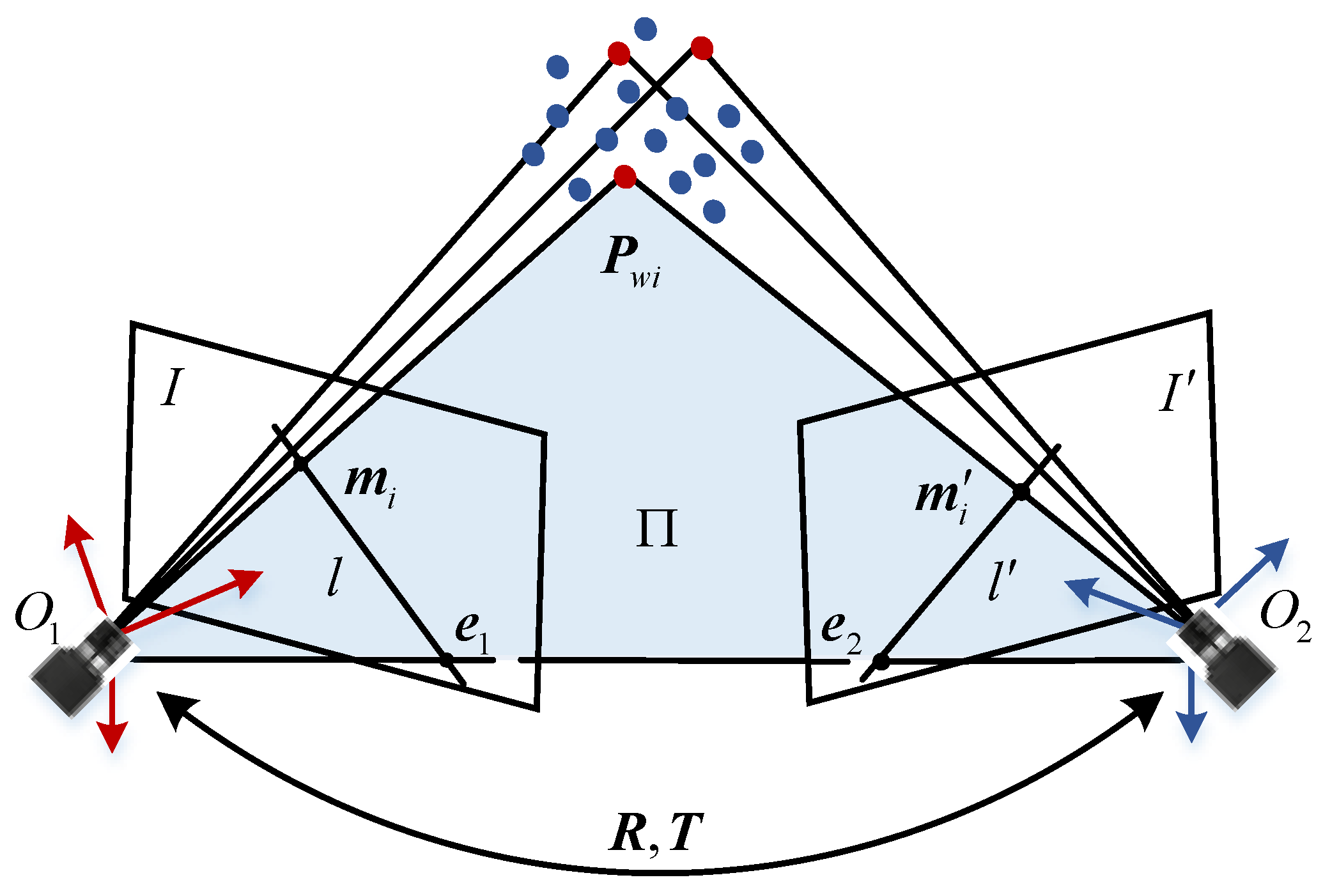
3. Fundamental Matrix Estimation Method Based on RANSAC Method
4. The Improved Fundamental Matrix Estimation Method of Planar Motion
4.1. Robust Null Space Estimation Method Based on Inlier Updating
4.2. Four-Point Iterative Method for Global Fundamental Matrix Estimation
5. Experimental Results and Analysis
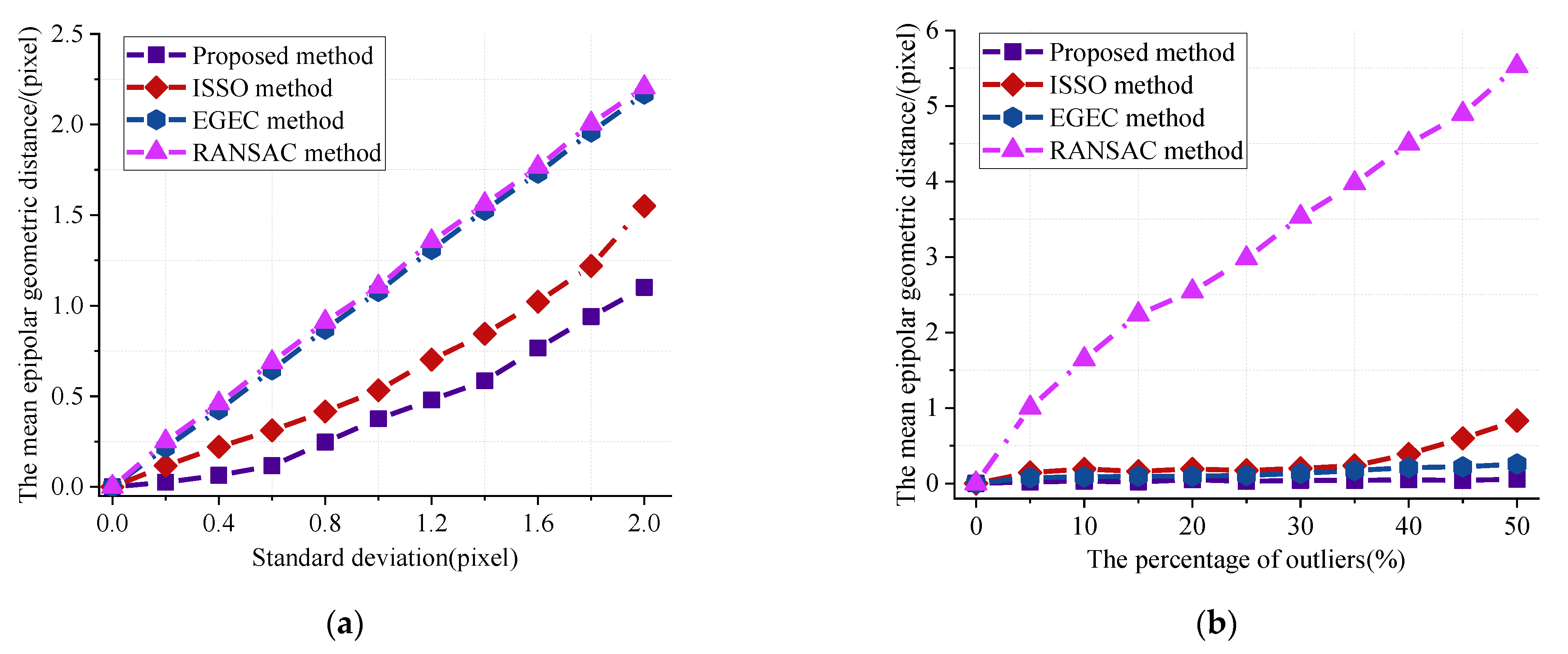
5.1. Experiments on the Simulated Dataset
5.2. Experiments on Real Dataset
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khattar, F.; Franck, L.; Larroque, B.; Dornaika, F. Visual localization and servoing for drone use in indoor remote laboratory environment. Mach. Vis. Appl. 2021, 32, 32. [Google Scholar] [CrossRef]
- Yu, H.Y.; Zhu, H.J.; Huang, F.R. Visual simultaneous localization and mapping (SLAM) based on blurred image detection. J. Intell. Robot. Syst. 2021, 103, 12. [Google Scholar] [CrossRef]
- Zia, M.Z.; Stark, M.; Schiele, B.; Schindler, K. Detailed 3d representations for object recognition and modelling. IEEE. Trans. Pattern Anal. Mach. Intell. 2013, 35, 2608–2623. [Google Scholar] [CrossRef] [PubMed]
- Pizarro, D.; Bartoli, A. Feature-based deformable surface detection with self-occlusion reasoning. Int. J. Comput. Vis. 2012, 97, 54–70. [Google Scholar] [CrossRef]
- Wang, J.H.; Zhou, Z.H. The 3D reconstruction method of a line-structured light vision sensor based on composite depth images. Meas. Sci. Technol. 2021, 32, 075101. [Google Scholar] [CrossRef]
- Ingale, K.; Udayan, D.J. Real-time 3D reconstruction techniques applied in dynamic scenes: A systematic literature review. Comput. Sci. Rev. 2021, 39, 100338. [Google Scholar] [CrossRef]
- Park, S.M.; Kim, Y.G. A metaverse: Taxonomy, components, applications, and open challenges. IEEE Access 2022, 10, 4209–4251. [Google Scholar] [CrossRef]
- Li, W.; Zhu, D.L.; Wang, Q. A single view leaf reconstruction method based on the fusion of ResNet and differentiable render in plant growth digital twin system. Comput. Electron. Agric. 2022, 193, 106712. [Google Scholar] [CrossRef]
- Matuzevicius, D.; Serackis, A. Three-dimensional human head reconstruction using smartphone-based close-range video photogrammetry. Appl. Sci. 2022, 12, 229. [Google Scholar] [CrossRef]
- Wang, F.Y.; Ma, X.D.; Liu, M.; Wei, B.X. Three-dimensional reconstruction of soybean canopy based on multivision technology for calculation of phenotypic traits. Agronomy 2022, 12, 692. [Google Scholar] [CrossRef]
- Ortín, D.; Montiel, J.M.M. Indoor robot motion based on monocular images. Robotica 2001, 19, 331–342. [Google Scholar] [CrossRef]
- Li, X.S.; Yuan, X.D. Fundamental matrix computing based on 3D metrical distance. Algorithms 2021, 14, 89. [Google Scholar] [CrossRef]
- Schonberger, J.L.; Frahm, J.M. Structure-from-motion revisited. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- He, Z.X.; Shen, C.T.; Wang, Q.Y.; Zhao, X.Y.; Jiang, H.L. Mismatching removal for feature-point matching based on triangular topology probability sampling consensus. Remote Sens. 2022, 14, 706. [Google Scholar] [CrossRef]
- Chen, H.Y.; Lin, Y.Y.; Chen, B.Y. Robust feature matching with alternate hough and inverted hough transforms. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Valgaerts, L.; Bruhn, A.; Mainberger, M.; Weickert, J. Dense versus sparse approaches for estimating the fundamental matrix. Int. J. Comput. Vis. 2012, 96, 212–234. [Google Scholar] [CrossRef] [Green Version]
- Nistér, D. An efficient solution to the five-point relative pose problem. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 756–770. [Google Scholar] [CrossRef] [PubMed]
- Torr, P.H.S.; Murray, D.W. The development and comparison of robust methods for estimating the fundamental matrix. Int. J. Comput. Vis. 1997, 24, 271–300. [Google Scholar] [CrossRef]
- Armangué, X.; Salvi, J. Overall view regarding fundamental matrix estimation. Image Vis. Comput. 2003, 21, 205–220. [Google Scholar] [CrossRef]
- Zou, Y.X.; Chan, S.C.; Ng, T.S. Least mean M-estimate algorithms for robust adaptive filtering in impulse noise. IEEE Trans. Circuits Syst. II-Analog Digit. Signal Process. 2002, 47, 1564–1569. [Google Scholar]
- Zhen, Y.; Liu, X.J.; Wang, M.Z. Precise fundamental matrix estimation based on inlier distribution constraint. In Proceedings of the 2012 International Conference on Information Technology and Software Engineering, Beijing, China, 8–10 December 2012. [Google Scholar]
- Jian, B.; Vemuri, B.C. Robust point set registration using gaussian mixture models. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1633–1645. [Google Scholar] [CrossRef]
- Zhang, Z.Y. Determining the epipolar geometry and its uncertainty: A review. Int. J. Comput. Vis. 1998, 27, 161–195. [Google Scholar] [CrossRef]
- Xu, M.; Lu, J. Distributed RANSAC for the robust estimation of three-dimensional reconstruction. IET Comput. Vis. 2012, 6, 324–333. [Google Scholar] [CrossRef]
- Andrew, A.M. Multiple view geometry in computer vision. Kybernetes 2001, 30, 1333–1341. [Google Scholar] [CrossRef]
- Chum, O.; Matas, J. Optimal randomized RANSAC. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1472–1482. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghergherehchi, M.; Kim, S.Y.; Afarideh, H.; Kim, Y.S. Random sample consensus algorithm for enhancing overlapped etched track counting. IET Image Process. 2015, 9, 97–106. [Google Scholar] [CrossRef]
- Fu, Q.; Mu, X.X.; Wang, Y. Minimal solution for estimating fundamental matrix under planar motion. Sci. China-Inf. Sci. 2021, 64, 209203. [Google Scholar] [CrossRef]
- Xiao, C.B.; Feng, D.Z.; Yuan, M.D. An efficient fundamental matrix estimation method for wide baseline images. Pattern Anal. Appl. 2018, 21, 35–44. [Google Scholar] [CrossRef]
- Yan, K.; Zhao, R.J.; Liu, E.H.; Ma, Y.B. A robust fundamental matrix estimation method based on epipolar geometric error criterion. IEEE Access 2019, 7, 147523–147533. [Google Scholar] [CrossRef]
- Fraundorfer, F.; Tanskanen, P.; Pollefeys, M. A minimal case solution to the calibrated relative pose problem for the case of two known orientation angles. In Proceedings of the 11th European Conference on Computer Vision, Heraklion, Greece, 5–11 September 2010. [Google Scholar]
- Chou, C.C.; Wang, C.C. 2-point RANSAC for scene image matching under large viewpoint changes. In Proceedings of the IEEE International Conference on Robotics and Automation, Seattle, WA, USA, 26–30 May 2015. [Google Scholar]
- He, W.; Li, Z.J.; Chen, C.L.P. A survey of human-centered intelligent robots: Issues and challenges. IEEE-CAA J. Autom. Sin. 2017, 4, 602–609. [Google Scholar] [CrossRef]
- Jiao, Y.M.; Liu, L.L.; Fu, B.; Ding, X.Q.; Wang, M.H.; Wang, Y.; Xiong, R. Robust localization for planar moving robot in changing environment: A perspective on density of correspondence and depth. In Proceedings of the IEEE International Conference on Robotics and Automation, Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Choi, S.; Kim, J.H. Fast and reliable minimal relative pose estimation under planar motion. Image Vis. Comput. 2018, 69, 103–112. [Google Scholar] [CrossRef]
- Choi, S.I.; Park, S.Y. A new 2-point absolute pose estimation algorithm under planar motion. Adv. Robot. 2015, 29, 1005–1013. [Google Scholar] [CrossRef]
- Wang, C.G.; Li, G.; Wang, X.; Zhang, Y.Y. Research on visual odometer of wheeled robot with motion constraints. J. Phys. Conf. Ser. 2022, 2171, 012064. [Google Scholar]
- Dong, S.Y.; Xu, K.; Zhou, Q.; Tagliasacchi, A.; Xin, S.Q.; Niessner, M.; Chen, B.Q. Multi-robot collaborative dense scene reconstruction. ACM Trans. Graph. 2019, 38, 1–16. [Google Scholar] [CrossRef]
- Ferraz, L.; Binefa, X.; Moreno-Noguer, F. Very fast solution to the pnp problem with algebraic outlier rejection. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Kukelova, Z.; Bujnak, M.; Pajdla, T. Automatic generator of minimal problem solvers. In Proceedings of the 10th European Conference on Computer Vision, Marseille, France, 12–18 October 2008. [Google Scholar]
- Scharstein, D.; Pal, C. Learning conditional random fields for stereo. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007. [Google Scholar]








| Noise Level | Proposed Method | ISSO Method | EGEC Method | RANSAC Method |
|---|---|---|---|---|
| 0 | 0.031 | 0.191 | 0.086 | 1.645 |
| 0.2 | 0.056 | 0.308 | 0.303 | 1.896 |
| 0.4 | 0.094 | 0.412 | 0.511 | 2.105 |
| 0.6 | 0.147 | 0.503 | 0.731 | 2.333 |
| 0.8 | 0.277 | 0.607 | 0.955 | 2.556 |
| 1 | 0.406 | 0.724 | 1.164 | 2.75 |
| 1.2 | 0.51 | 0.893 | 1.396 | 3.001 |
| 1.4 | 0.616 | 1.036 | 1.612 | 3.206 |
| 1.6 | 0.797 | 1.213 | 1.817 | 3.411 |
| 1.8 | 0.971 | 1.411 | 2.045 | 3.65 |
| 2 | 1.132 | 1.741 | 2.254 | 3.851 |
| Noise Level | Proposed Method | ISSO Method | EGEC Method | RANSAC Method |
|---|---|---|---|---|
| 0 | 0.191 | 0.534 | 0.354 | 2.812 |
| 0.2 | 0.345 | 0.983 | 0.934 | 3.524 |
| 0.4 | 0.498 | 1.135 | 1.502 | 4.013 |
| 0.6 | 0.641 | 1.432 | 1.752 | 4.292 |
| 0.8 | 0.875 | 1.652 | 2.141 | 4.733 |
| 1 | 1.19 | 1.836 | 2.352 | 4.95 |
| 1.2 | 1.43 | 2.047 | 2.553 | 5.163 |
| 1.4 | 1.574 | 2.207 | 2.851 | 5.514 |
| 1.6 | 1.723 | 2.491 | 3.207 | 5.87 |
| 1.8 | 2.13 | 2.713 | 3.524 | 6.183 |
| 2 | 2.231 | 3.135 | 3.857 | 6.488 |
| Data | Proposed Method | ISSO Method | EGEC Method |
|---|---|---|---|
| Image1 | 0.618 | 0.992 | 1.615 |
| Image2 | 0.815 | 1.241 | 1.826 |
| Image3 | 1.038 | 1.41 | 2.346 |
| Image4 | 0.509 | 0.976 | 1.587 |
| Image5 | 1.161 | 1.817 | 2.455 |
| Image6 | 1.291 | 2.019 | 2.532 |
| Data | Proposed Method | ISSO Method | EGEC Method |
|---|---|---|---|
| Image1 | 1.513 | 2.162 | 2.893 |
| Image2 | 1.775 | 2.685 | 3.381 |
| Image3 | 2.309 | 2.787 | 3.502 |
| Image4 | 1.402 | 2.054 | 2.586 |
| Image5 | 2.271 | 3.017 | 3.883 |
| Image6 | 2.406 | 3.137 | 4.038 |
| Data | Measured Angle | Standard Angel | Absolute Error | ||
|---|---|---|---|---|---|
| Proposed Method | ISSO Method | Proposed Method | ISSO Method | ||
| 1 | 0.013 | 0.023 | 0 | 0.013 | 0.023 |
| 2 | 2.034 | 1.942 | 2 | 0.034 | 0.058 |
| 3 | 3.949 | 3.923 | 4 | 0.051 | 0.077 |
| 4 | 6.075 | 6.086 | 6 | 0.075 | 0.086 |
| 5 | 8.091 | 7.887 | 8 | 0.091 | 0.113 |
| 6 | 9.896 | 10.138 | 10 | 0.104 | 0.138 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, L.; Huo, J. A Global Fundamental Matrix Estimation Method of Planar Motion Based on Inlier Updating. Sensors 2022, 22, 4624. https://doi.org/10.3390/s22124624
Wei L, Huo J. A Global Fundamental Matrix Estimation Method of Planar Motion Based on Inlier Updating. Sensors. 2022; 22(12):4624. https://doi.org/10.3390/s22124624
Chicago/Turabian StyleWei, Liang, and Ju Huo. 2022. "A Global Fundamental Matrix Estimation Method of Planar Motion Based on Inlier Updating" Sensors 22, no. 12: 4624. https://doi.org/10.3390/s22124624
APA StyleWei, L., & Huo, J. (2022). A Global Fundamental Matrix Estimation Method of Planar Motion Based on Inlier Updating. Sensors, 22(12), 4624. https://doi.org/10.3390/s22124624





