Thermo-Optical Sensitivity of Whispering Gallery Modes in As2S3 Chalcogenide Glass Microresonators
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Materials and Methods
2.2. Theoretical Model and Methods
3. Results
3.1. Theoretical Study of Temperature Distributions
3.2. Theoretical Study of Steady-State Wavelength Shifts of the WGMs
3.3. Experimental and Theoretical Study of Temporal Dynamics of the Wavelength Shifts of the WGMs
3.4. Experimental and Theoretical Study of Δλ/P
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Matsko, A.B. (Ed.) Practical Applications of Microresonators in Optics and Photonics; CRC Press: London, UK, 2018. [Google Scholar]
- Yu, D.; Humar, M.; Meserve, K.; Bailey, R.C.; Nic Chormaic, S.; Vollmer, F. Whispering-gallery-mode sensors for biological and physical sensing. Nat. Rev. Methods Primers 2021, 1, 83. [Google Scholar] [CrossRef]
- Jiang, X.; Qavi, A.J.; Huang, S.H.; Yang, L. Whispering-Gallery Sensors. Matter 2020, 3, 371–392. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Lewis, E.; Brambilla, G.; Wang, P. Temperature Sensing Performance of Microsphere Resonators. Sensors 2018, 18, 2515. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Silver, J.M.; Del Bino, L.; Woodley, M.T.M.; Ghalanos, G.N.; Svela, A.Ø.; Moroney, N.; Zhang, S.; Grattan, K.T.V.; Del’Haye, P. Nonlinear Enhanced Microresonator Gyroscope. Optica 2021, 8, 1219–1226. [Google Scholar] [CrossRef]
- Tan, T.; Yuan, Z.; Zhang, H.; Yan, G.; Zhou, S.; An, N.; Peng, B.; Soavi, G.; Rao, Y.; Yao, B. Multispecies and Individual Gas Molecule Detection Using Stokes Solitons in a Graphene Over-Modal Microresonator. Nat. Commun. 2021, 12, 6716. [Google Scholar] [CrossRef]
- Brice, I.; Grundsteins, K.; Draguns, K.; Atvars, A.; Alnis, J. Whispering Gallery Mode Resonator Temperature Compensation and Refractive Index Sensing in Glucose Droplets. Sensors 2021, 21, 7184. [Google Scholar] [CrossRef]
- Geints, Y.E.; Minin, O.V.; Minin, I.V. Proof-of-Concept of a Miniature Pressure Sensor Based on Coupled Optical WGMs Excited in a Dielectric Microsphere. Opt. Laser. Technol. 2022, 151, 108015. [Google Scholar] [CrossRef]
- Zhivotkov, D.; Ristić, D.; Romanova, E.; Ivanda, M. Refractometric Gas Sensing Using a Whispering Gallery Mode Microresonator Coated with a Supra-Micron Sol-Gel Layer. Opt. Mater. 2021, 118, 111286. [Google Scholar] [CrossRef]
- Ma, Q.; Rossmann, T.; Guo, Z. Whispering-Gallery Mode Silica Microsensors for Cryogenic to Room Temperature Measurement. Meas. Sci. Technol. 2010, 21, 025310. [Google Scholar] [CrossRef]
- Yang, Z.; Wu, Y.; Zhang, X.; Zhang, W.; Xu, P.; Dai, S. Low Temperature Fabrication of Chalcogenide Microsphere Resonators for Thermal Sensing. IEEE Photon. Technol. Lett. 2017, 29, 66–69. [Google Scholar] [CrossRef]
- Lin, G.; Coillet, A.; Chembo, Y.K. Nonlinear Photonics with High-Q Whispering-Gallery-Mode Resonators. Adv. Opt. Photon. 2017, 9, 828–890. [Google Scholar] [CrossRef]
- Chiasera, A.; Dumeige, Y.; Féron, P.; Ferrari, M.; Jestin, Y.; Nunzi Conti, G.; Pelli, S.; Soria, S.; Righini, G.C. Spherical Whispering-Gallery-Mode Microresonators. Laser Photon. Rev. 2009, 4, 457–482. [Google Scholar] [CrossRef]
- Webb, K.E.; Erkintalo, M.; Coen, S.; Murdoch, S.G. Experimental Observation of Coherent Cavity Soliton Frequency Combs in Silica Microspheres. Opt. Lett. 2016, 41, 4613–4616. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bochek, D.; Toropov, N.; Vatnik, I.; Churkin, D.; Sumetsky, M. SNAP Microresonators Introduced by Strong Bending of Optical Fibers. Opt. Lett. 2019, 44, 3218–3221. [Google Scholar] [CrossRef]
- Spolitis, S.; Murnieks, R.; Skladova, L.; Salgals, T.; Andrianov, A.V.; Marisova, M.P.; Leuchs, G. IM/DD WDM-PON Communication System Based on Optical Frequency Comb Generated in Silica Whispering Gallery Mode Resonator. IEEE Access 2021, 9, 66335–66345. [Google Scholar] [CrossRef]
- Salgals, T.; Alnis, J.; Murnieks, R.; Brice, I.; Porins, J.; Andrianov, A.V.; Anashkina, E.A.; Spolitis, S.; Bobrovs, V. Demonstration of a Fiber Optical Communication System Employing a Silica Microsphere-Based OFC Source. Opt. Express 2021, 29, 10903–10913. [Google Scholar] [CrossRef]
- Salgals, T.; Alnis, J.; Ozolins, O.; Andrianov, A.V.; Anashkina, E.A.; Brice, I.; Berkis, I.; Pang, X.; Udalcovs, A.; Porins, J.; et al. Silica Microsphere WGMR-Based Kerr-OFC Light Source and Its Application for High-Speed IM/DD Short-Reach Optical Interconnects. Appl. Sci. 2022, 12, 4722. [Google Scholar] [CrossRef]
- Vanier, F.; Rochette, M.; Godbout, N.; Peter, Y.-A. Raman Lasing in As2S3 High-Q Whispering Gallery Mode Resonators. Opt. Lett. 2013, 38, 4966–4969. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Anashkina, E.A. Tunable Raman Lasing in an As2S3 Chalcogenide Glass Microsphere. Opt. Express 2021, 29, 5580. [Google Scholar] [CrossRef]
- Zhang, B.; Zeng, P.; Yang, Z.; Xia, D.; Zhao, J.; Sun, Y.; Huang, Y.; Song, J.; Pan, J.; Cheng, H.; et al. On-Chip Chalcogenide Microresonators with Low-Threshold Parametric Oscillation. Photon. Res. 2021, 9, 1272–1279. [Google Scholar] [CrossRef]
- Xia, D.; Huang, Y.; Zhang, B.; Zeng, P.; Zhao, J.; Yang, Z.; Sun, S.; Luo, L.; Hu, G.; Liu, D.; et al. Engineered Raman Lasing in Photonic Integrated Chalcogenide Microresonators. Laser Photonics Rev. 2022, 16, 2100443. [Google Scholar] [CrossRef]
- Yu, J.; Shen, Z.; Yang, Z.; Qi, S.; Jiang, Y.; Brambilla, G.; Dong, C.-H.; Wang, P. The Investigation of Forward and Backward Brillouin Scattering in High-Q Chalcogenide Microspheres. IEEE Photonics J. 2022, 14, 3011505. [Google Scholar] [CrossRef]
- Jiang, X.; Yang, L. Optothermal Dynamics in Whispering-Gallery Microresonators. Light Sci. Appl. 2020, 9, 24. [Google Scholar] [CrossRef] [Green Version]
- Elliott, G.R.; Murugan, G.S.; Wilkinson, J.S.; Zervas, M.N.; Hewak, D.W. Chalcogenide Glass Microsphere Laser. Opt. Express 2010, 18, 26720. [Google Scholar] [CrossRef] [Green Version]
- Andrianov, A.V.; Anashkina, E.A. L-Band Raman Lasing in Chalcogenide Glass Microresonator Started by Thermal Mode Pulling with Auxiliary Red Diode Laser. Results Phys. 2021, 24, 104170. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Marisova, M.P.; Salgals, T.; Alnis, J.; Lyashuk, I.; Leuchs, G.; Spolitis, S.; Bobrovs, V.; Andrianov, A.V. Optical Frequency Combs Generated in Silica Microspheres in the Telecommunication C-, U-, and E-Bands. Photonics 2021, 8, 345. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Marisova, M.P.; Dorofeev, V.V.; Anashkina, E.A. Thermal Shift of Whispering Gallery Modes in Tellurite Glass Microspheres. Results Phys. 2020, 17, 103128. [Google Scholar] [CrossRef]
- Oraevsky, A.N. Whispering-Gallery Waves. Quantum Electron. 2002, 32, 377–400. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Antipov, O.L.; Anashkina, E.A.; Fedorova, K.A. Electronic and Thermal Lensing in Diode End-Pumped Yb:YAG Laser Rods and Discs. Quantum Electron. 2009, 39, 1131–1136. [Google Scholar] [CrossRef]
- Masselin, P.; Coq, D.L.; Bychkov, E. Refractive index variations induced by femtosecond laser direct writing in the bulk of As2S3 glass at high repetition rate. Opt. Mater. 2011, 33, 872–876. [Google Scholar] [CrossRef]
- Rodney, W.S.; Malitson, I.H.; King, T.A. Refractive Index of Arsenic Trisulfide. J. Opt. Soc. Am. 1958, 48, 633–636. [Google Scholar] [CrossRef]
- Kumta, P.N.; Risbud, S.H. Rare-earth chalcogenides—An emerging class of optical materials. J. Mat. Sci. 1994, 29, 1135–1158. [Google Scholar] [CrossRef]
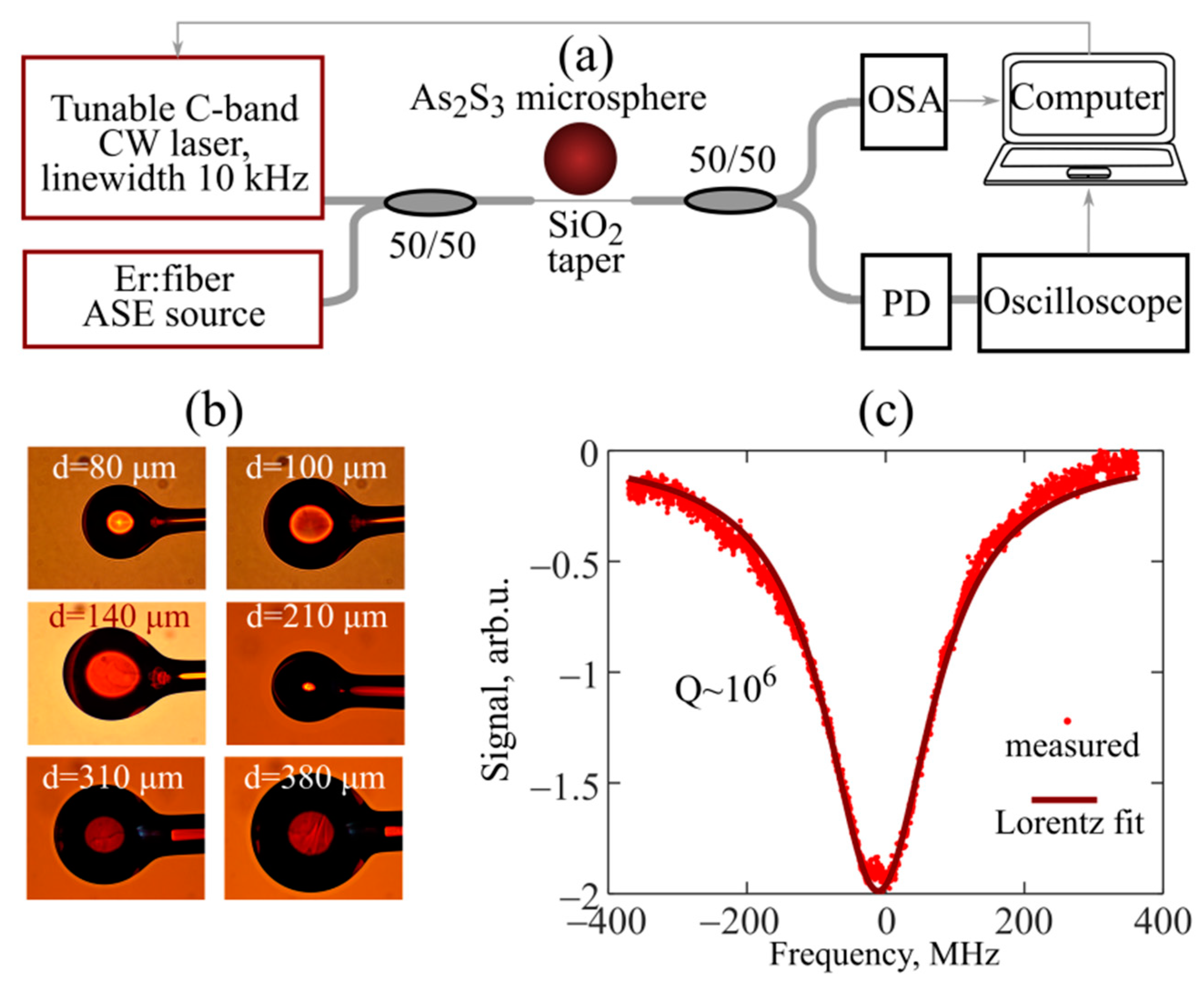


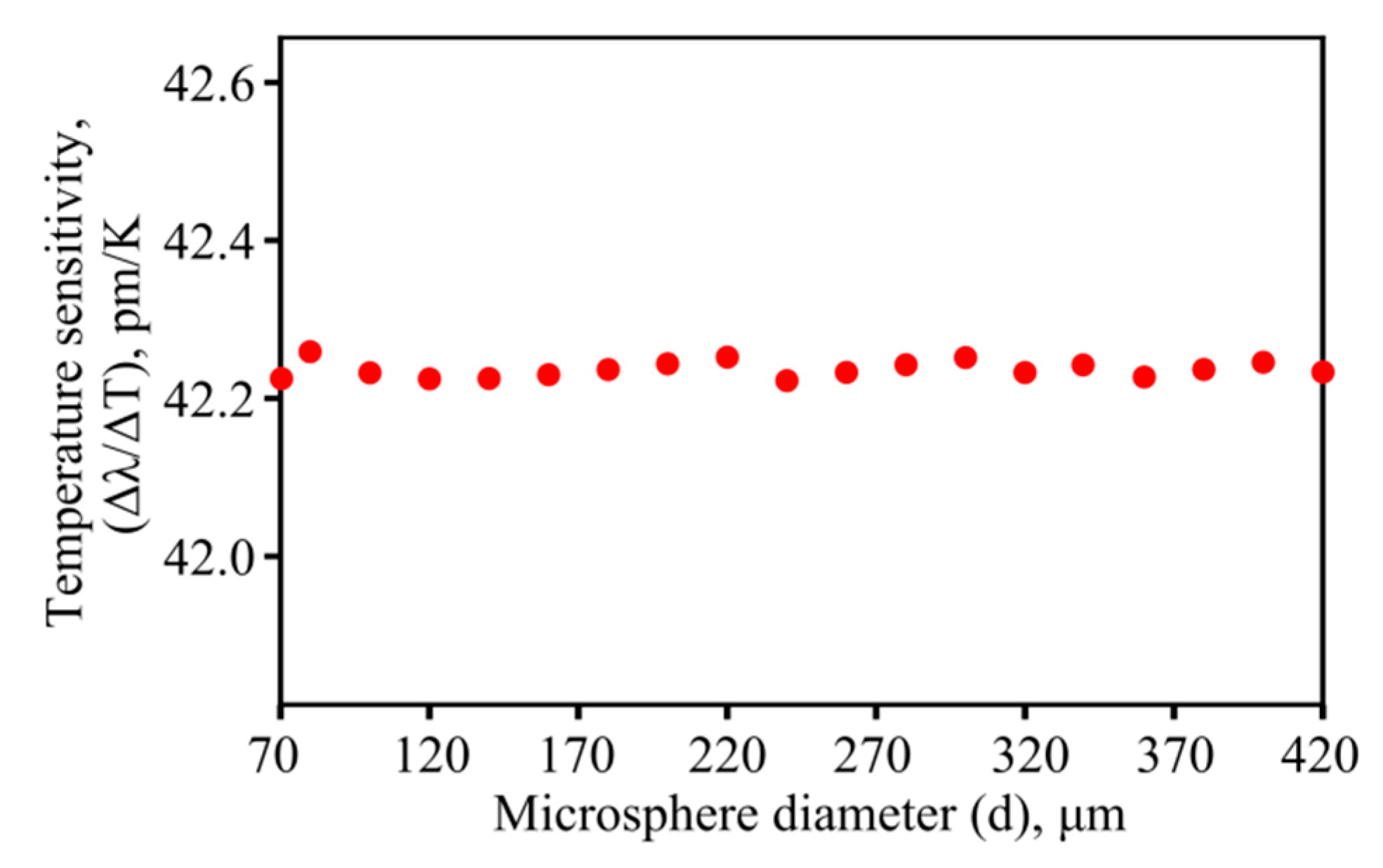

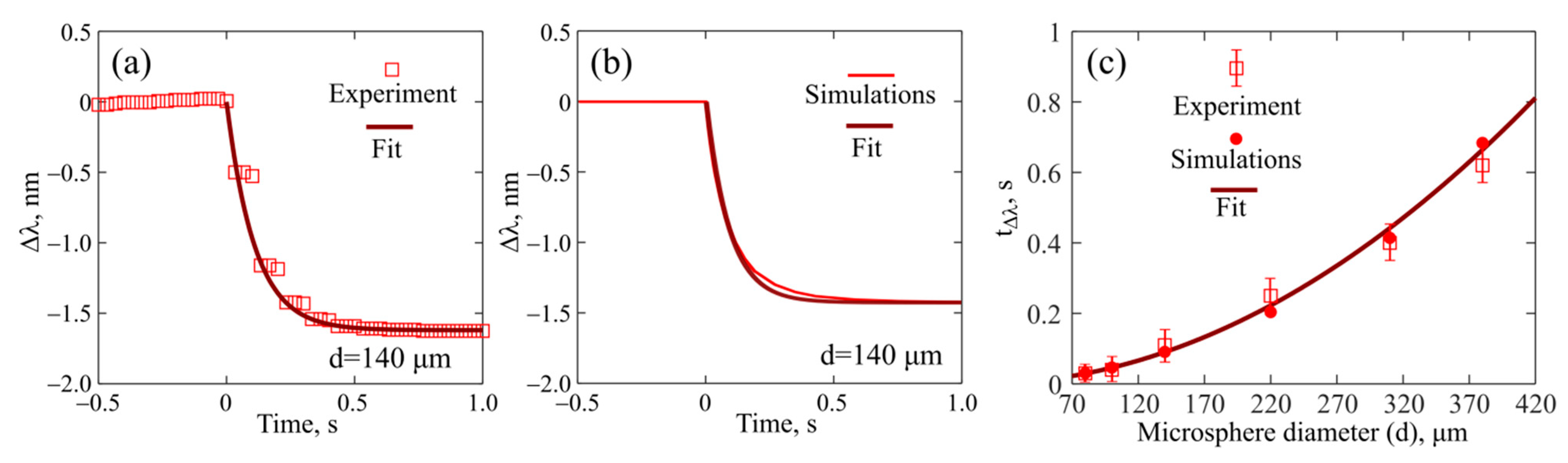
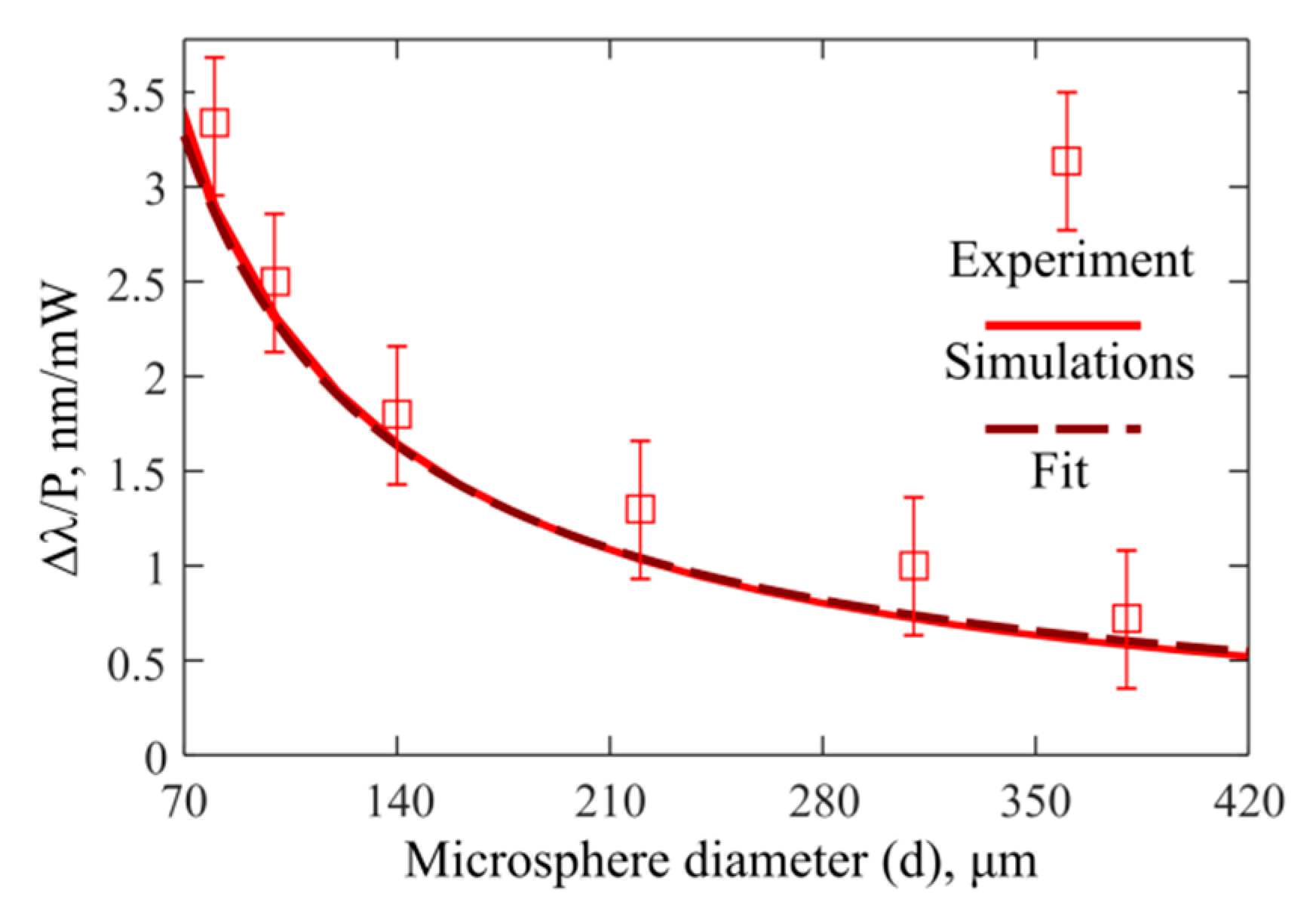
| Parameter | Value | |||
|---|---|---|---|---|
| As2S3 glass thermal conductivity (k) | 0.17 W/(m·K) [32] | |||
| As2S3 glass density (ρ) | 3.20 gm/cm³ [32] | |||
| As2S3 glass heat capacity at constant pressure (cp) | 460 J/(kg·K) [32] | |||
| As2S3 glass thermo-optical coefficient (dn/dT) | 9·10−6 K−1 [33] | |||
| As2S3 glass thermal expansion coefficient (ε) | 25·10−6 K−1 [34] | |||
| Air thermal conductivity (kair) | 0.025 W/(m·K) | |||
| Refractive index (n0). [33] (Ai and Bi are Sellmeier constants) | ||||
| A1 | A2 | A3 | A4 | A5 |
| 1.8983678 | 1.9222979 | 0.8765134 | 0.1188704 | 0.9569903 |
| B1, μm2 | B2, μm2 | B3, μm2 | B4, μm2 | B5, μm2 |
| 0.0225 | 0.0625 | 0.1225 | 0.2025 | 750 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrianov, A.V.; Marisova, M.P.; Anashkina, E.A. Thermo-Optical Sensitivity of Whispering Gallery Modes in As2S3 Chalcogenide Glass Microresonators. Sensors 2022, 22, 4636. https://doi.org/10.3390/s22124636
Andrianov AV, Marisova MP, Anashkina EA. Thermo-Optical Sensitivity of Whispering Gallery Modes in As2S3 Chalcogenide Glass Microresonators. Sensors. 2022; 22(12):4636. https://doi.org/10.3390/s22124636
Chicago/Turabian StyleAndrianov, Alexey V., Maria P. Marisova, and Elena A. Anashkina. 2022. "Thermo-Optical Sensitivity of Whispering Gallery Modes in As2S3 Chalcogenide Glass Microresonators" Sensors 22, no. 12: 4636. https://doi.org/10.3390/s22124636
APA StyleAndrianov, A. V., Marisova, M. P., & Anashkina, E. A. (2022). Thermo-Optical Sensitivity of Whispering Gallery Modes in As2S3 Chalcogenide Glass Microresonators. Sensors, 22(12), 4636. https://doi.org/10.3390/s22124636








