Parallel Sensor-Space Lattice Planner for Real-Time Obstacle Avoidance
Abstract
:1. Introduction
2. Related Work
3. Sensor-Space Lattice Motion Planner
3.1. Offline Step
3.1.1. Computing the Lattice
3.1.2. Obtaining Sensor-to-Graph Mappings
3.1.3. Defining a Global Task
3.2. Online Step
3.2.1. Tree Pruning
3.2.2. Assigning Costs
3.2.3. Searching for the Optimal Path
4. Parallelization
5. Experiments
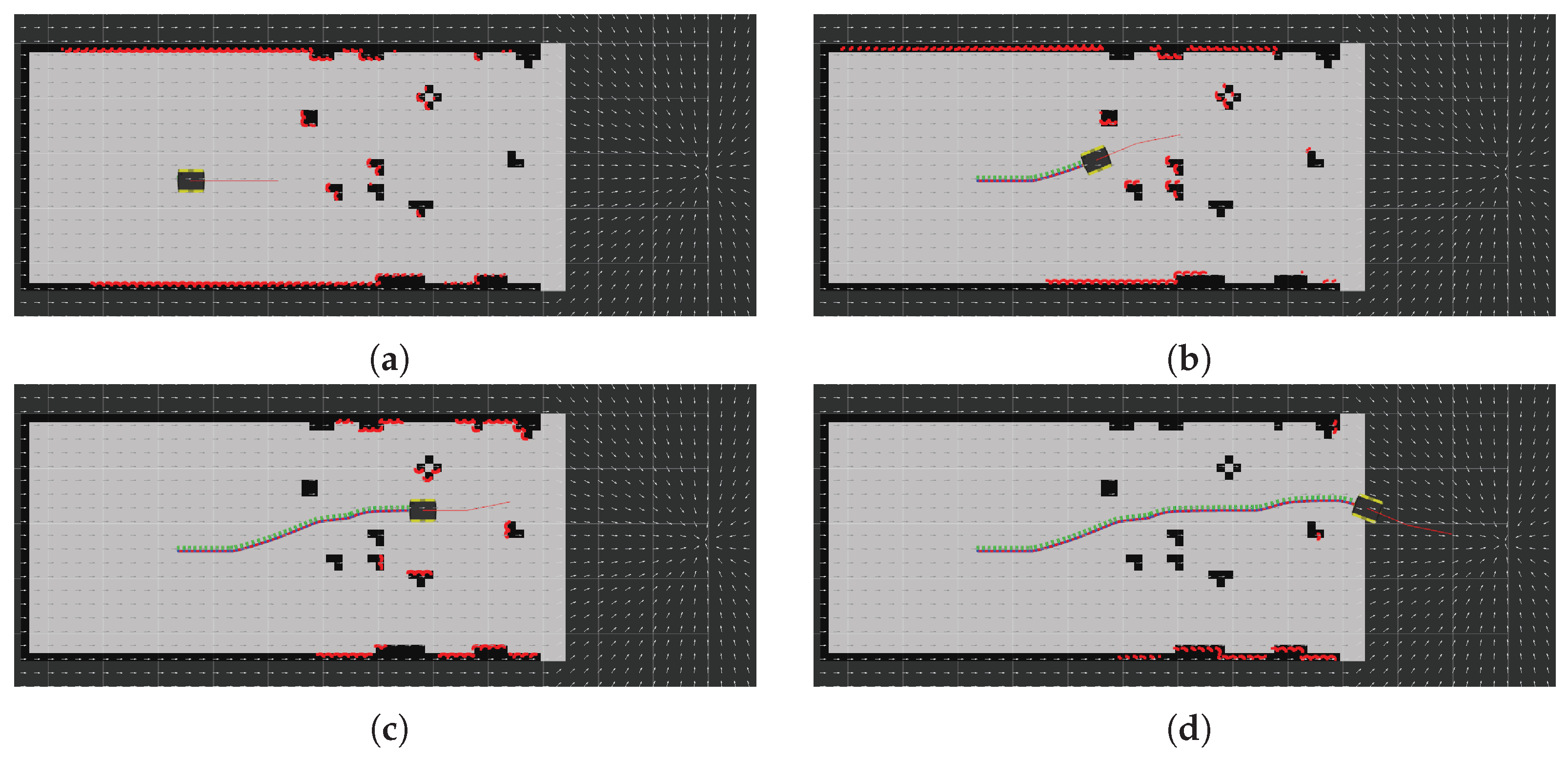
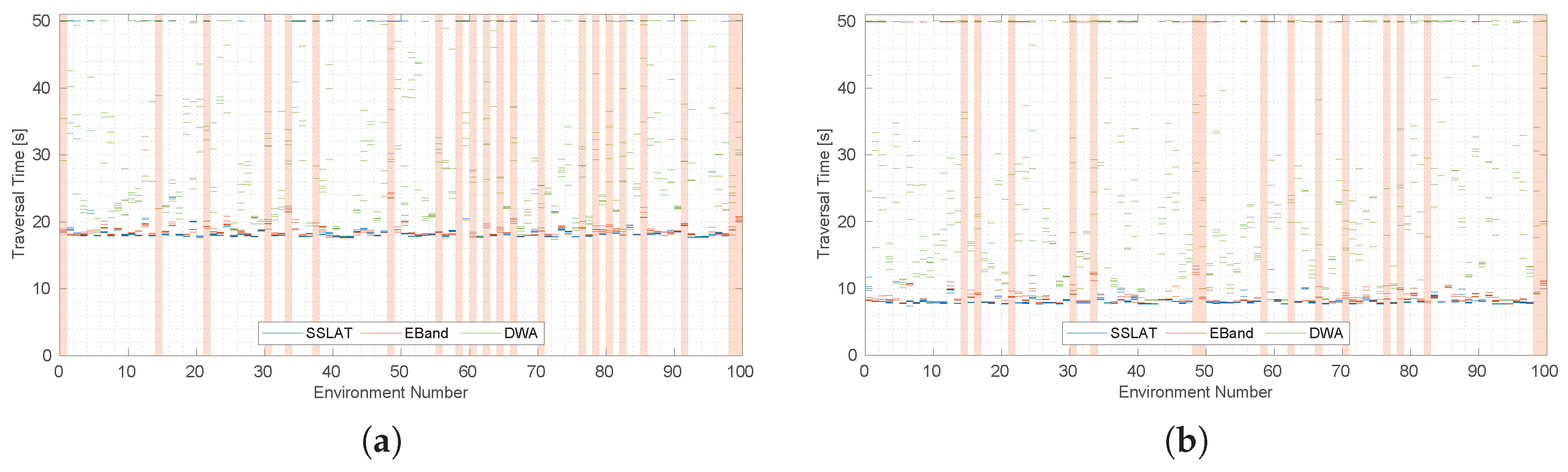
5.1. Simulations with a Ground Robot in Static Environments
5.1.1. Experimental Setup
5.1.2. Results
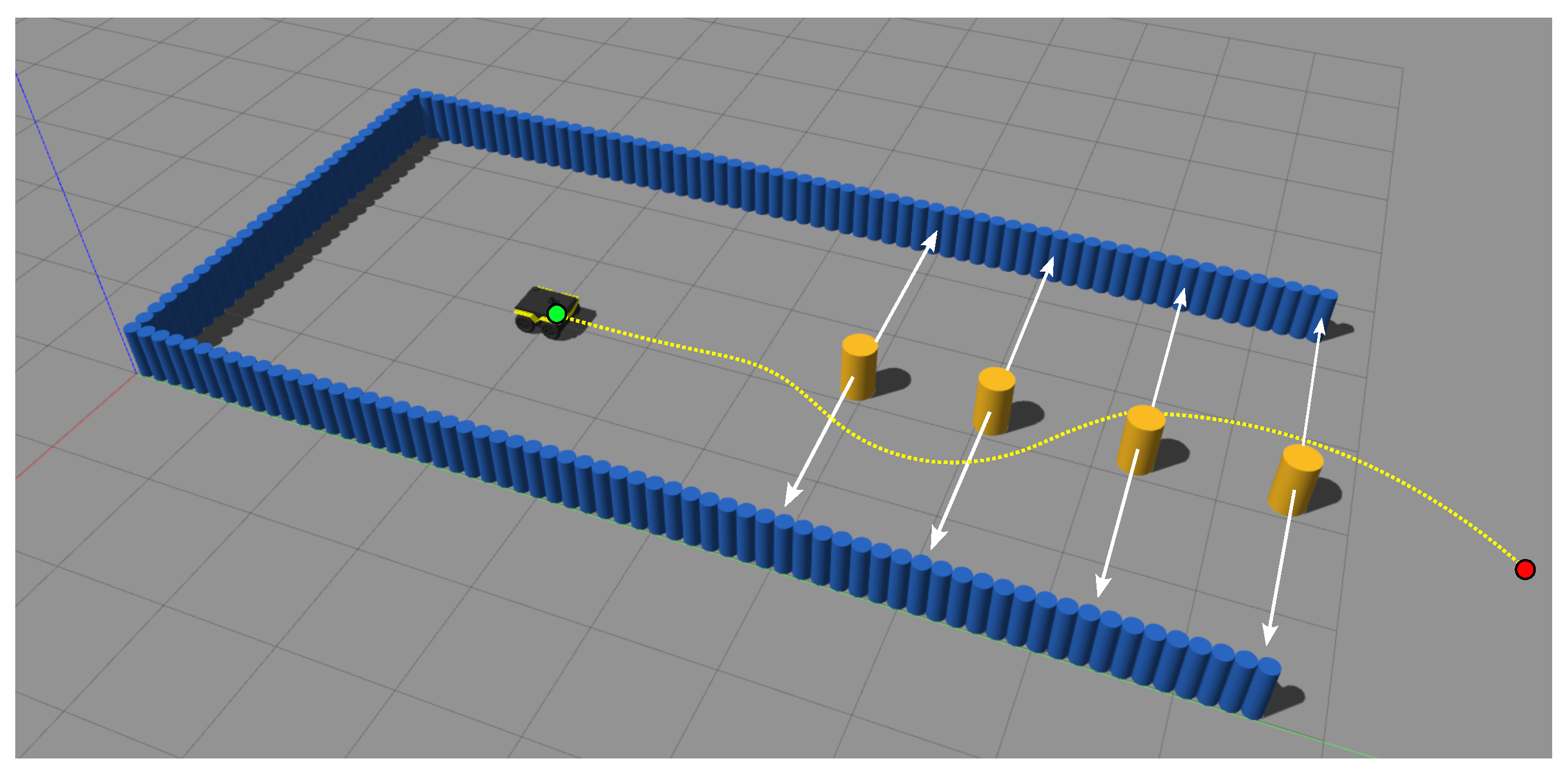
5.2. Simulations with a Ground Robot in a Dynamic Environment
5.2.1. Experimental Setup
5.2.2. Results
5.3. Validation and Evaluation of the Parallel Implementation
5.3.1. Experimental Setup
5.3.2. Results
5.4. Experiments with a Real-World UAV
5.4.1. Experimental Setup
5.4.2. Results
6. Discussion
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SSLAT | Sensor Space Lattice | |
| RRT | Rapidly Exploring Random Tree | |
| PRM | Probabilistic Roadmap | |
| GMT | Group Marching Tree | |
| LIDAR | Light Detection and Ranging | |
| CTG | Cost-to-go | |
| GPU | Graphics Processing Unit | |
| SLAM | Simultaneous Localization and Mapping | |
| CPU | Central Processing Unit | |
| CUDA | Compute Unified Device Architecture | |
| ROS | Robot Operating System | |
| BARN | Benchmark for Autonomous Robot Navigation | |
| APF | Artificial Potential Function | |
| VFF | Virtual Force Field | |
| EBand | Elastic Bands | |
| VFH | Vector Field Histogram | |
| GPS | Global Positioning System | |
| DWA | Dynamic Window Approach | |
| IMU | Inertial Measurement Unit | |
| CDC | Collision Detection Circuit | |
| 2D/3D | Two/Three-Dimensional |
References
- Lemardelé, C.; Estrada, M.; Pagès, L.; Bachofner, M. Potentialities of drones and ground autonomous delivery devices for last-mile logistics. Transp. Res. Part E Logist. Transp. Rev. 2021, 149, 102325. [Google Scholar] [CrossRef]
- Baniasadi, P.; Foumani, M.; Smith-Miles, K.; Ejov, V. A transformation technique for the clustered generalized traveling salesman problem with applications to logistics. Eur. J. Oper. Res. 2020, 285, 444–457. [Google Scholar] [CrossRef]
- Oliveira, L.F.; Moreira, A.P.; Silva, M.F. Advances in forest robotics: A state-of-the-art survey. Robotics 2021, 10, 53. [Google Scholar] [CrossRef]
- Kocer, B.B.; Ho, B.; Zhu, X.; Zheng, P.; Farinha, A.; Xiao, F.; Stephens, B.; Wiesemüller, F.; Orr, L.; Kovac, M. Forest Drones for Environmental Sensing and Nature Conservation. In Proceedings of the 2021 Aerial Robotic Systems Physically Interacting with the Environment (AIRPHARO), Biograd na Moru, Croatia, 4–5 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–8. [Google Scholar]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Ichter, B.; Schmerling, E.; Pavone, M. Group Marching Tree: Sampling-based approximately optimal motion planning on GPUs. In Proceedings of the 2017 First IEEE International Conference on Robotic Computing (IRC), Taichung, Taiwan, 10–12 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 219–226. [Google Scholar]
- Bialkowski, J.; Karaman, S.; Frazzoli, E. Massively parallelizing the RRT and the RRT*. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 3513–3518. [Google Scholar]
- Amato, N.M.; Dale, L.K. Probabilistic roadmap methods are embarrassingly parallel. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), Detroit, MI, USA, 10–15 May 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 1, pp. 688–694. [Google Scholar]
- Martinez, R.B., Jr.; Pereira, G.A.S. Fast path computation using lattices in the sensor-space for forest navigation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 1117–1123. [Google Scholar] [CrossRef]
- Rezende, A.M.C.; Goncalves, V.M.; Pimenta, L.C.A. Constructive Time-Varying Vector Fields for Robot Navigation. IEEE Trans. Robot. 2022, 38, 852–867. [Google Scholar] [CrossRef]
- Yao, W.; de Marina, H.G.; Lin, B.; Cao, M. Singularity-free guiding vector field for robot navigation. IEEE Trans. Robot. 2021, 37, 1206–1221. [Google Scholar] [CrossRef]
- Wu, C.; Chen, J.; Jeltsema, D.; Dai, C. Guidance vector field encoding based on contraction analysis. In Proceedings of the 2018 European Control Conference (ECC), Limassol, Cyprus, 12–15 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 282–287. [Google Scholar]
- Frew, E.W.; Lawrence, D. Tracking dynamic star curves using guidance vector fields. J. Guid. Control Dyn. 2017, 40, 1488–1495. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. IEEE Int. Conf. Robot. Autom. 1985, 2, 500–505. [Google Scholar]
- Rimon, E.; Koditschek, D. Exact robot navigation using artificial potential functions. IEEE Trans. Robot. Autom. 1992, 8, 501–518. [Google Scholar] [CrossRef] [Green Version]
- Pereira, G.A.S.; Choudhury, S.; Scherer, S. A framework for optimal repairing of vector field-based motion plans. In Proceedings of the International Conference on Unmanned Aircraft Systems, Arlington, VA, USA, 7–10 June 2016; pp. 261–266. [Google Scholar]
- Chiella, A.C.; Machado, H.N.; Teixeira, B.O.; Pereira, G.A.S. GNSS/LiDAR-Based Navigation of an Aerial Robot in Sparse Forests. Sensors 2019, 19, 4061. [Google Scholar] [CrossRef] [Green Version]
- Pereira, G.A.S.; Freitas, E.J. Navigation of Semi-autonomous Service Robots Using Local Information and Anytime Motion Planners. Robotica 2020, 38, 2080–2098. [Google Scholar] [CrossRef]
- Gonçalves, V.M.; Pimenta, L.C.; Maia, C.A.; Dutra, B.C.; Pereira, G.A.S. Vector fields for robot navigation along time-varying curves in n-dimensions. IEEE Trans. Robot. 2010, 26, 647–659. [Google Scholar] [CrossRef]
- Clem, G.S. An Optimized Circulating Vector Field Obstacle Avoidance Guidance for Unmanned Aerial Vehicles. Ph.D. Thesis, Ohio University, Athens, OH, USA, 2018. [Google Scholar]
- Quinlan, S.; Khatib, O. Elastic bands: Connecting path planning and control. In Proceedings of the IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; IEEE: Piscataway, NJ, USA, 1993; pp. 802–807. [Google Scholar]
- Borenstein, J.; Koren, Y. Real-time obstacle avoidance for fast mobile robots. IEEE Trans. Syst. Man, Cybern. 1989, 19, 1179–1187. [Google Scholar] [CrossRef] [Green Version]
- Borenstein, J.; Koren, Y. The vector field histogram-fast obstacle avoidance for mobile robots. IEEE Trans. Robot. Autom. 1991, 7, 278–288. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Wang, N.; Liu, X.; Yang, C. VFH* based local path planning for mobile robot. In Proceedings of the 2019 2nd China Symposium on Cognitive Computing and Hybrid Intelligence (CCHI), Xi’an, China, 21–22 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 18–23. [Google Scholar]
- Babinec, A.; Duchoň, F.; Dekan, M.; Mikulová, Z.; Jurišica, L. Vector Field Histogram* with look-ahead tree extension dependent on time variable environment. Trans. Inst. Meas. Control 2018, 40, 1250–1264. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef] [Green Version]
- Hossain, T.; Habibullah, H.; Islam, R.; Padilla, R.V. Local path planning for autonomous mobile robots by integrating modified dynamic-window approach and improved follow the gap method. J. Field Robot. 2022, 39, 371–386. [Google Scholar] [CrossRef]
- De Lima, D.A.; Pereira, G.A.S. Navigation of an autonomous car using vector fields and the dynamic window approach. J. Control Autom. Electr. Syst. 2013, 24, 106–116. [Google Scholar] [CrossRef]
- Murray, S.; Floyd-Jones, W.; Qi, Y.; Sorin, D.J.; Konidaris, G. Robot motion planning on a chip. In Proceedings of the Robotics: Science and Systems, Ann Arbor, MI, USA, 12–16 July 2016. [Google Scholar]
- Zhang, J.; Chadha, R.G.; Velivela, V.; Singh, S. P-CAP: Pre-computed alternative paths to enable aggressive aerial maneuvers in cluttered environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018; pp. 8456–8463. [Google Scholar]
- Ostilli, M. Cayley Trees and Bethe Lattices: A concise analysis for mathematicians and physicists. Phys. A Stat. Mech. Its Appl. 2012, 391, 3417–3423. [Google Scholar] [CrossRef] [Green Version]
- Lacaze, A.; Moscovitz, Y.; DeClaris, N.; Murphy, K. Path planning for autonomous vehicles driving over rough terrain. In Proceedings of the IEEE International Symposium on Intelligent Control, Gaithersburg, MD, USA, 17 September 1998; pp. 50–55. [Google Scholar]
- Pivtoraiko, M.; Knepper, R.A.; Kelly, A. Differentially constrained mobile robot motion planning in state lattices. J. Field Robot. 2009, 26, 308–333. [Google Scholar] [CrossRef]
- Tordesillas, J.; Lopez, B.T.; Everett, M.; How, J.P. Faster: Fast and safe trajectory planner for flights in unknown environments. arXiv 2020, arXiv:2001.04420. [Google Scholar]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Herlihy, M.; Shavit, N.; Luchangco, V.; Spear, M. The Art of Multiprocessor Programming; Morgan Kaufmann: Burlington, MA, USA, 2020. [Google Scholar]
- Carpin, S.; Pagello, E. On parallel RRTs for multi-robot systems. In Proceedings of the 8th Conference Italian Association for Artificial Intelligence, Siena, Italy, 10–13 September 2002; pp. 834–841. [Google Scholar]
- Plaku, E.; Bekris, K.E.; Chen, B.Y.; Ladd, A.M.; Kavraki, L.E. Sampling-based roadmap of trees for parallel motion planning. IEEE Trans. Robot. 2005, 21, 597–608. [Google Scholar] [CrossRef]
- Hidalgo-Paniagua, A.; Bandera, J.P.; Ruiz-de Quintanilla, M.; Bandera, A. Quad-RRT: A real-time GPU-based global path planner in large-scale real environments. Expert Syst. Appl. 2018, 99, 141–154. [Google Scholar] [CrossRef]
- Lawson, R.C.; Wills, L.; Tsiotras, P. GPU Parallelization of Policy Iteration RRT. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 4369–4374. [Google Scholar]
- Bleiweiss, A. GPU accelerated pathfinding. In Proceedings of the 23rd ACM SIGGRAPH/EUROGRAPHICS Symposium on Graphics Hardware, Sarajevo, Bosnia and Herzegovina, 20–21 June 2008; pp. 65–74. [Google Scholar]
- Pan, J.; Lauterbach, C.; Manocha, D. g-Planner: Real-time Motion Planning and Global Navigation using GPUs. In Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; pp. 2243–2248. [Google Scholar]
- Pan, J.; Lauterbach, C.; Manocha, D. Efficient nearest-neighbor computation for GPU-based motion planning. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2243–2248. [Google Scholar]
- Pan, J.; Manocha, D. GPU-based parallel collision detection for fast motion planning. Int. J. Robot. Res. 2012, 31, 187–200. [Google Scholar] [CrossRef]
- Gonçalves, V.M.; Maia, C.A.; Pereira, G.A.S.; Pimenta, L.C.A. Navegação de robôs utilizando curvas implícitas. Sba Controle Automaç Ao Soc. Bras. Autom. 2010, 21, 43–57. [Google Scholar] [CrossRef]
- Ko, I.; Kim, B.; Park, F.C. Randomized path planning on vector fields. Int. J. Robot. Res. 2014, 33, 1664–1682. [Google Scholar] [CrossRef]
- Nvidia CUDA Home Page. Available online: https://developer.nvidia.com/cuda-toolkit (accessed on 21 June 2022).
- CUDA C Pogramming Guide. Available online: https://docs.nvidia.com/cuda/cuda-c-programming-guide/ (accessed on 21 June 2022).
- Perille, D.; Truong, A.; Xiao, X.; Stone, P. Benchmarking metric ground navigation. In Proceedings of the 2020 IEEE International Symposium on Safety, Security and Rescue Robotics (SSRR), Abu Dhabi, United Arab Emirates, 4–6 November 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Koenig, N.; Howard, A. Design and use paradigms for gazebo, an open-source multi-robot simulator. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No. 04CH37566), Sendai, Japan, 28 September–2 October 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 3, pp. 2149–2154. [Google Scholar]
- Robot Operating System. Available online: https://www.ros.org (accessed on 21 June 2022).
- Mohler, B.J.; Thompson, W.B.; Creem-Regehr, S.H.; Pick, H.L.; Warren, W.H. Visual flow influences gait transition speed and preferred walking speed. Exp. Brain Res. 2007, 181, 221–228. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. High-speed flight in an ergodic forest. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 14–18 May 2012; pp. 2899–2906. [Google Scholar]
- Merrill, D.; Garland, M.; Grimshaw, A. Scalable GPU graph traversal. ACM Sigplan Not. 2012, 47, 117–128. [Google Scholar] [CrossRef] [Green Version]
- Pimenta, L.C.; Pereira, G.A.; Gonçalves, M.M.; Michael, N.; Turpin, M.; Kumar, V. Decentralized controllers for perimeter surveillance with teams of aerial robots. Adv. Robot. 2013, 27, 697–709. [Google Scholar] [CrossRef]
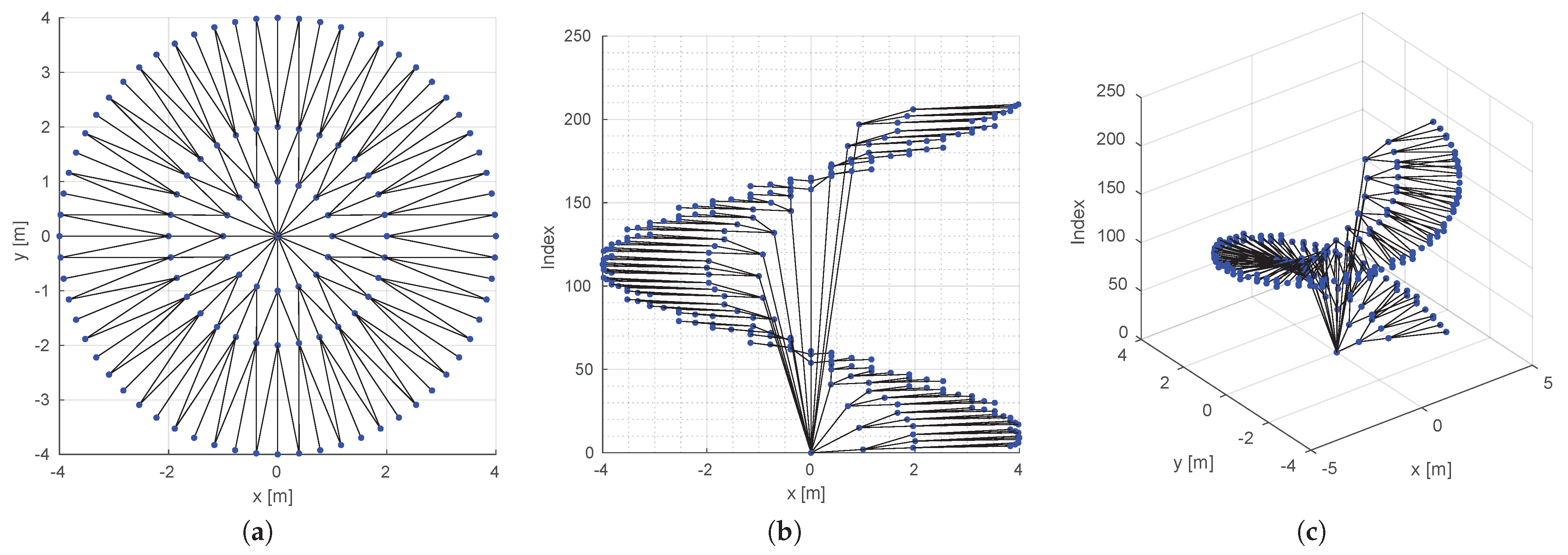
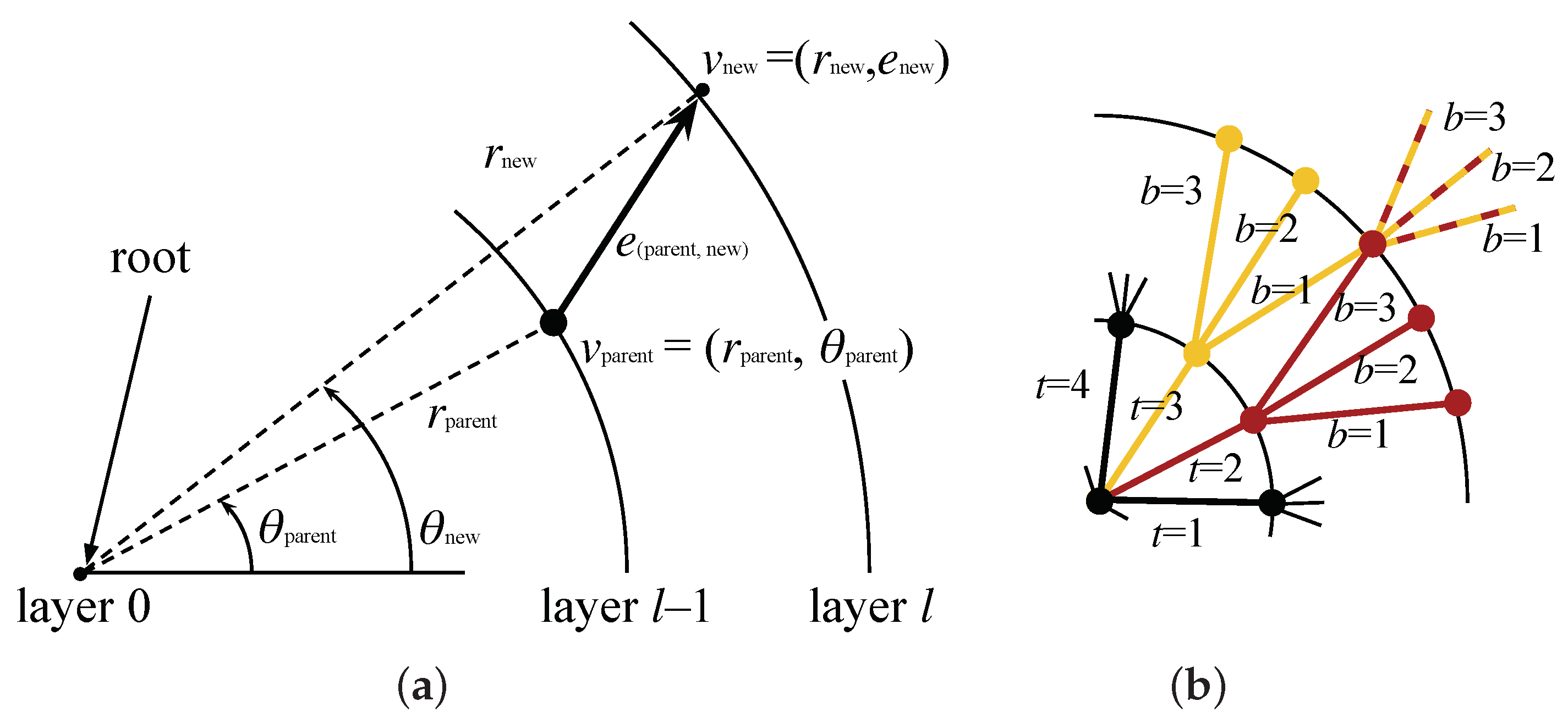


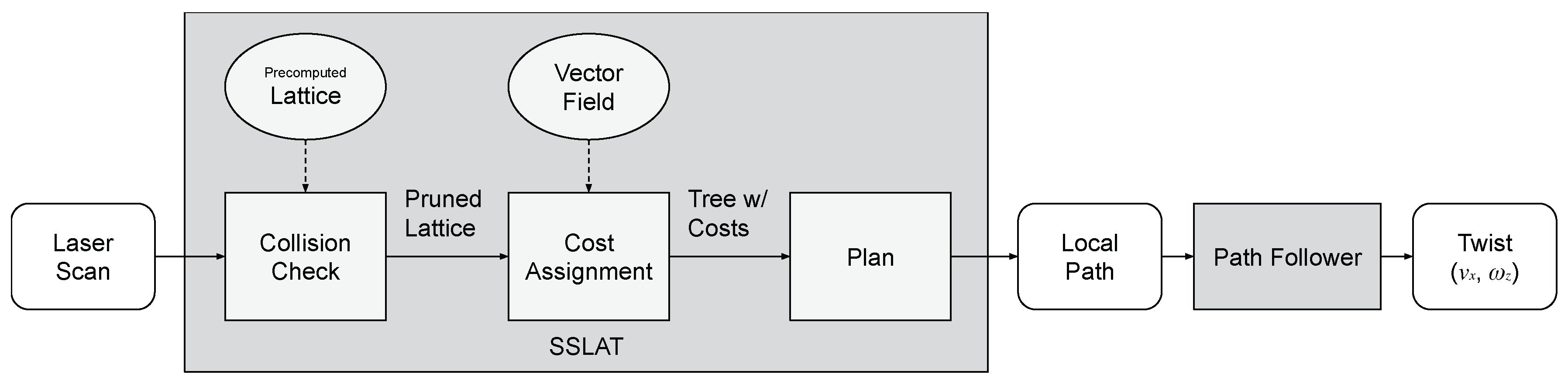







| Method | Robot Speed [m s−1] | Success Rate [%] | Environments with Success in All Five Trials [%] | Environments with Failure in All Five Trials [%] | Traversal Time [s] | |
|---|---|---|---|---|---|---|
| Mean | Std. Dev. | |||||
| SSLAT | 1.15 | 71.8 | 10.6 | 4.4 | 8.540 | 2.000 |
| 0.50 | 69.4 | 12.0 | 28.2 | 18.722 | 2.495 | |
| EBand | 1.15 | 93.4 | 16.4 | 0.4 | 8.540 | 0.931 |
| 0.50 | 97.2 | 18.4 | 0.0 | 18.604 | 0.945 | |
| DWA | 1.15 | 93.6 | 15.6 | 0.0 | 19.787 | 8.478 |
| 0.50 | 97.4 | 18.2 | 0.0 | 27.604 | 7.493 | |
| Method | Robot Speed [m s−1] | Obstacle Speed [m s−1] | Success Rate [%] | Traversal Time [s] | |
|---|---|---|---|---|---|
| Mean | Std. Dev. | ||||
| SSLAT | 0.50 | Slow | 72 | 19.428 | 1.146 |
| Mid | 38 | 19.661 | 0.899 | ||
| Fast | 44 | 19.951 | 0.797 | ||
| 1.15 | Slow | 72 | 8.960 | 1.140 | |
| Mid | 60 | 9.090 | 1.060 | ||
| Fast | 58 | 8.970 | 0.890 | ||
| EBand | 0.50 | Slow | 58 | 19.041 | 0.918 |
| Mid | 32 | 19.860 | 1.128 | ||
| Fast | 24 | 19.931 | 0.910 | ||
| 1.15 | Slow | 58 | 8.800 | 0.710 | |
| Mid | 66 | 8.910 | 0.640 | ||
| Fast | 46 | 9.230 | 0.870 | ||
| DWA | 0.50 | Slow | 82 | 21.625 | 3.785 |
| Mid | 62 | 20.833 | 2.230 | ||
| Fast | 58 | 20.845 | 1.724 | ||
| 1.15 | Slow | 92 | 11.730 | 4.330 | |
| Mid | 82 | 10.310 | 1.870 | ||
| Fast | 80 | 10.660 | 1.450 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinez Rocamora, B., Jr.; Pereira, G.A.S. Parallel Sensor-Space Lattice Planner for Real-Time Obstacle Avoidance. Sensors 2022, 22, 4770. https://doi.org/10.3390/s22134770
Martinez Rocamora B Jr., Pereira GAS. Parallel Sensor-Space Lattice Planner for Real-Time Obstacle Avoidance. Sensors. 2022; 22(13):4770. https://doi.org/10.3390/s22134770
Chicago/Turabian StyleMartinez Rocamora, Bernardo, Jr., and Guilherme A. S. Pereira. 2022. "Parallel Sensor-Space Lattice Planner for Real-Time Obstacle Avoidance" Sensors 22, no. 13: 4770. https://doi.org/10.3390/s22134770






