Raspberry Shake-Based Rapid Structural Identification of Existing Buildings Subject to Earthquake Ground Motion: The Case Study of Bucharest
Abstract
:1. Introduction
2. Instrumentation and Specification
2.1. RS4D Sensors
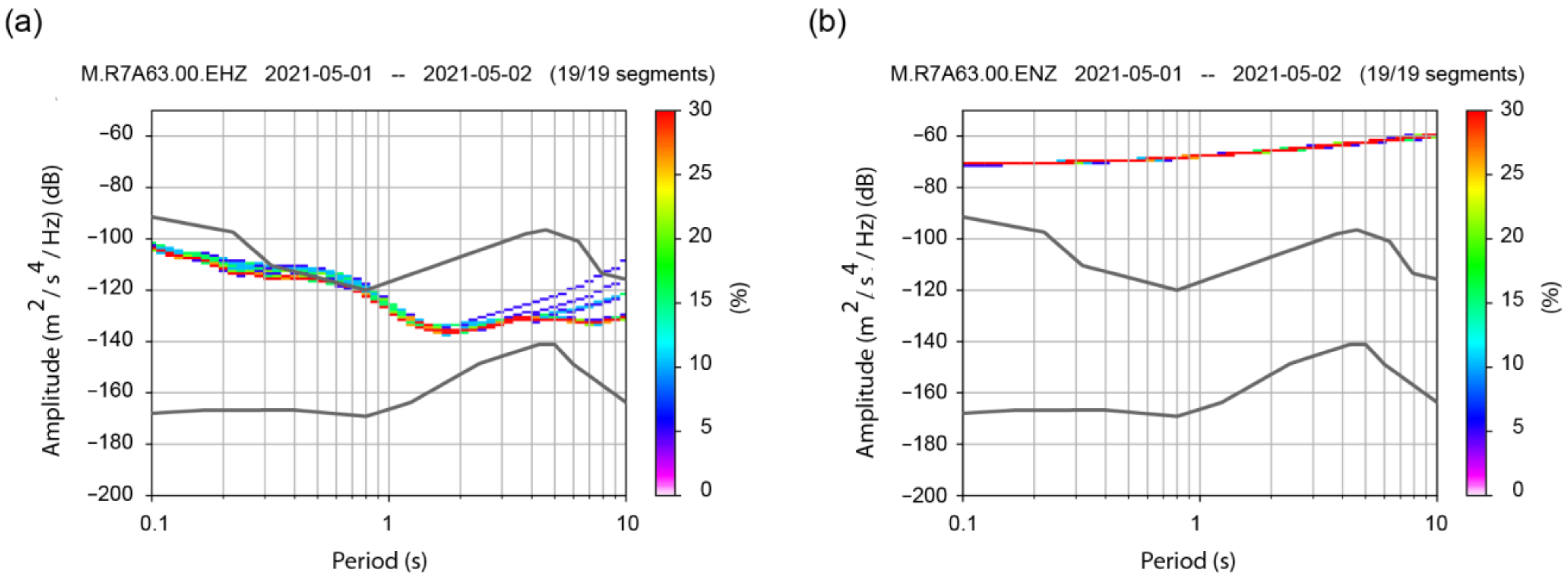
2.2. Broadband Sensors
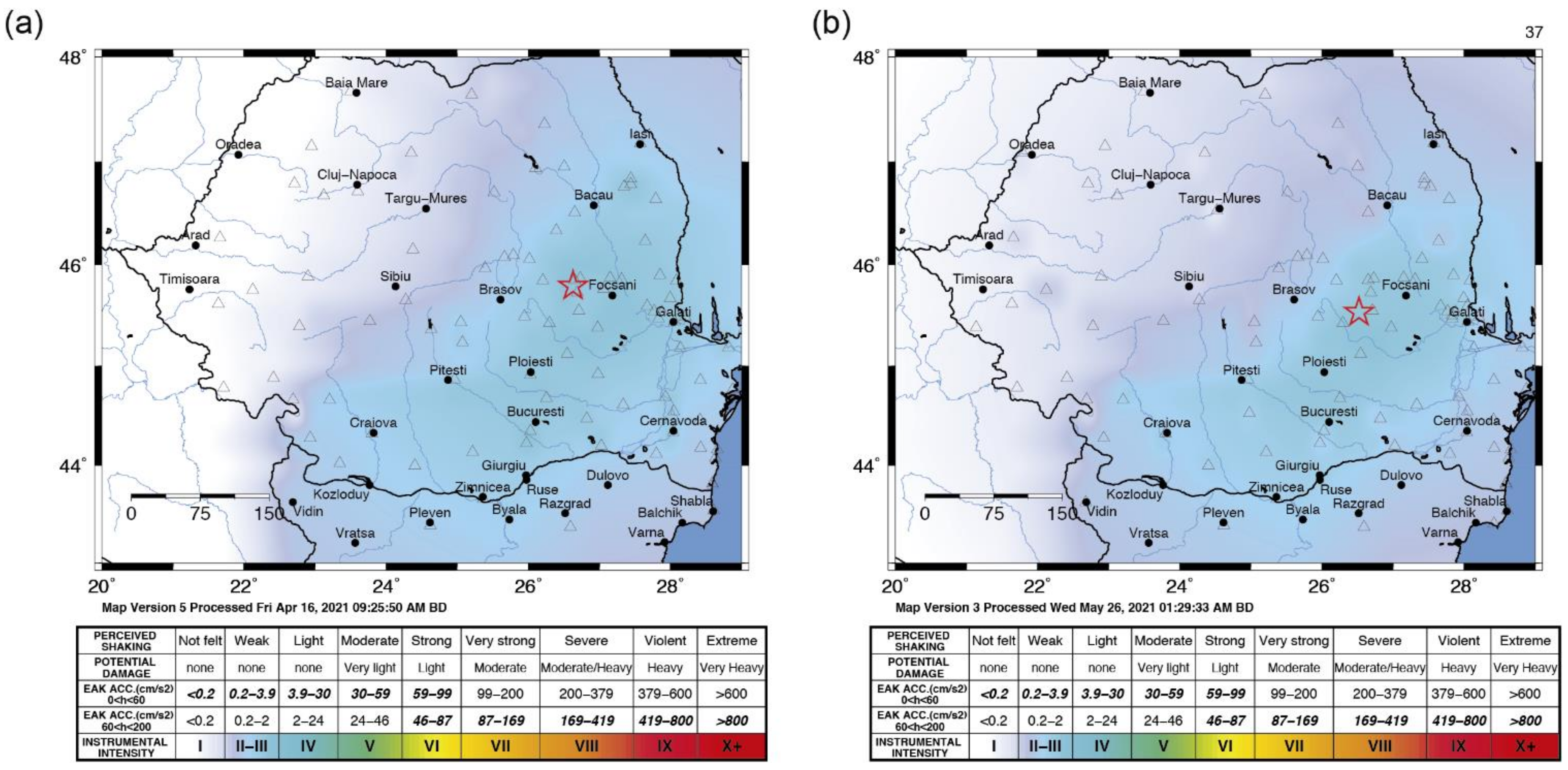
3. Seismicity and Dataset
4. SHM Methodologies
4.1. Output-Only Methods
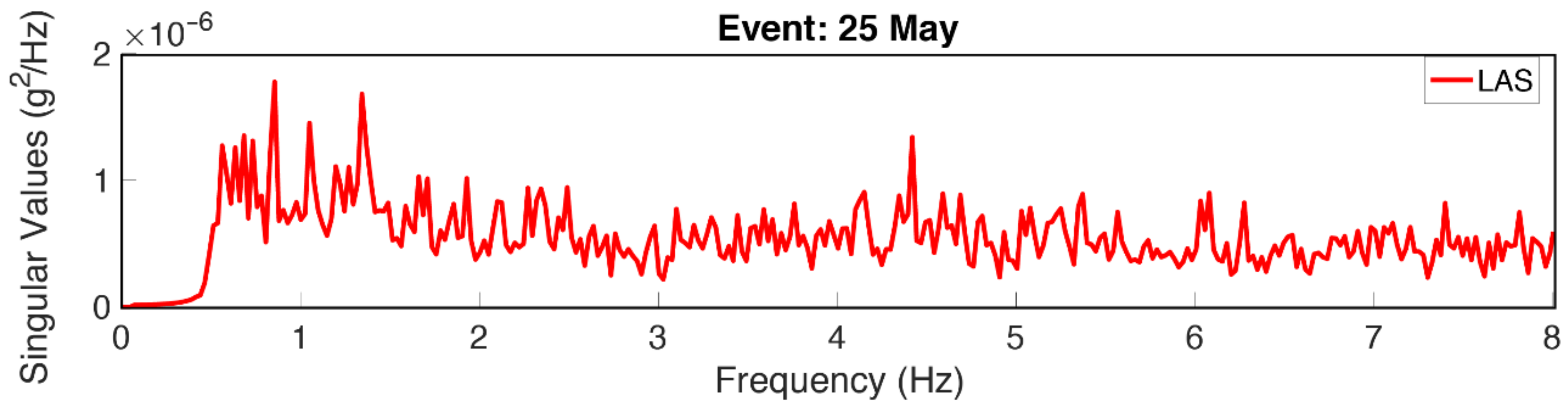
4.1.1. Frequency Domain Decomposition (FDD)
4.1.2. Short-Time Fourier Transform with Wavelet Pre-Filtering (STFT-WF)
4.1.3. Continuous Wavelet Transform (CWT)
4.2. Input–Output Methods
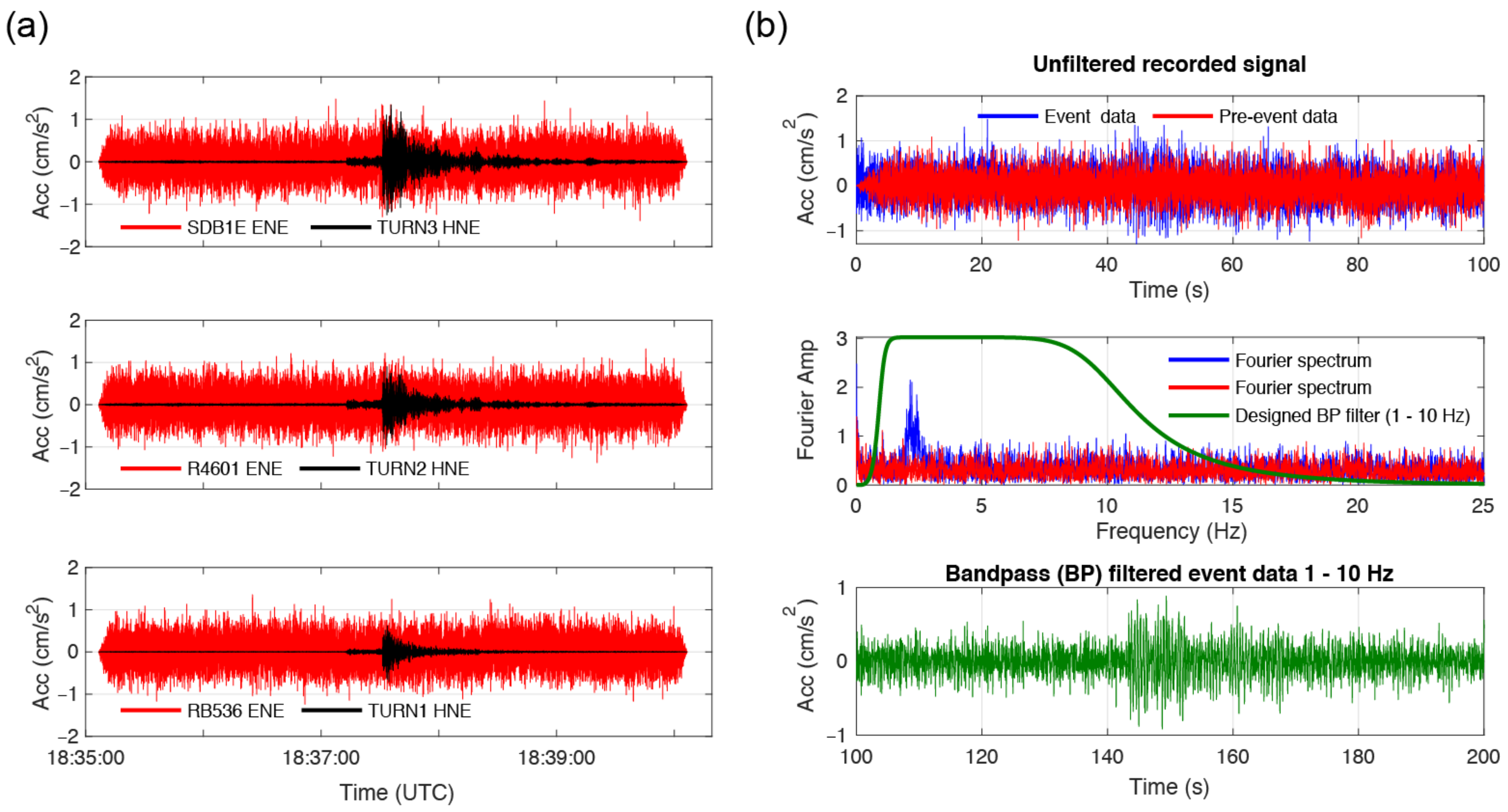
5. Analyses
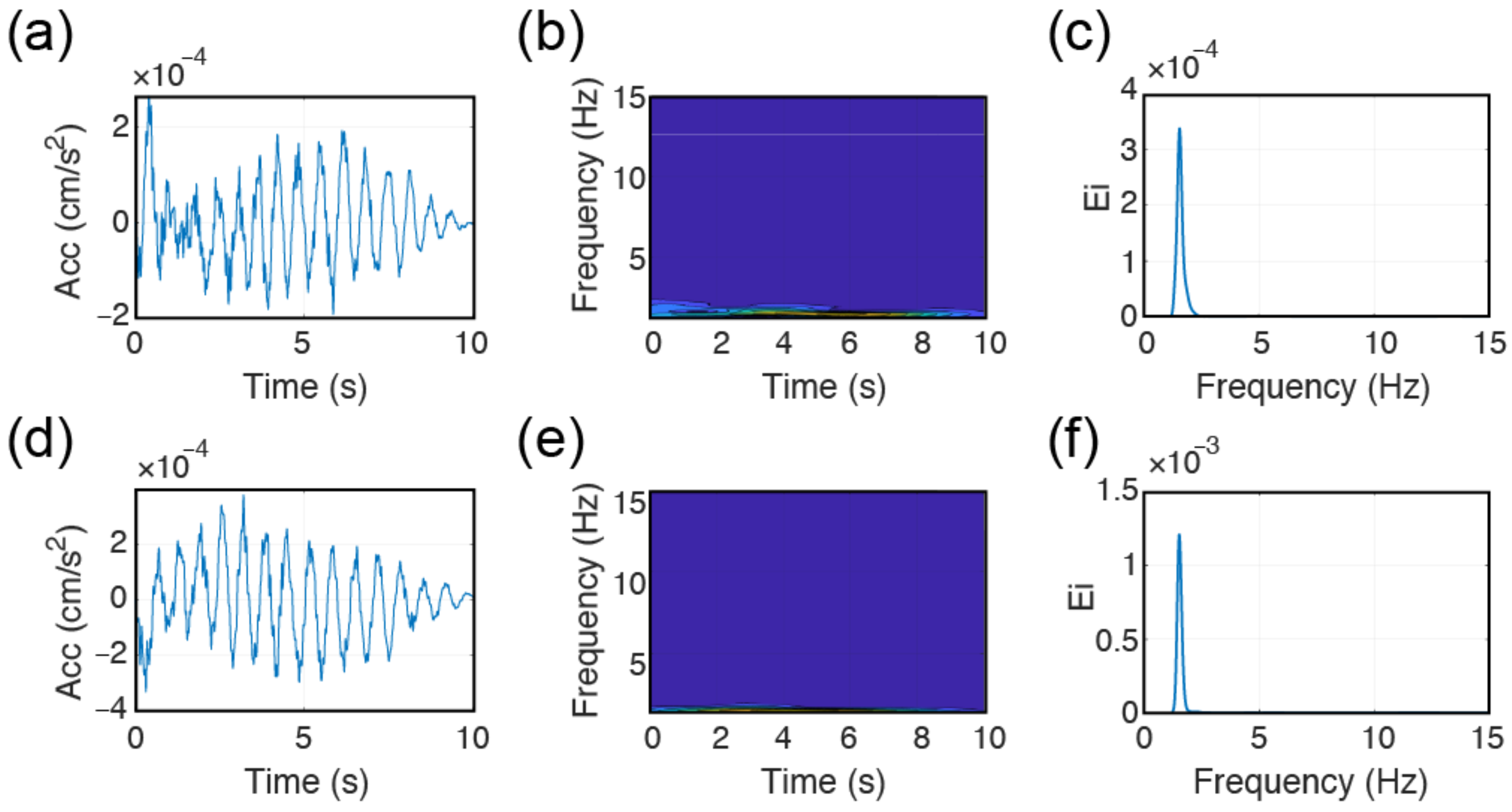
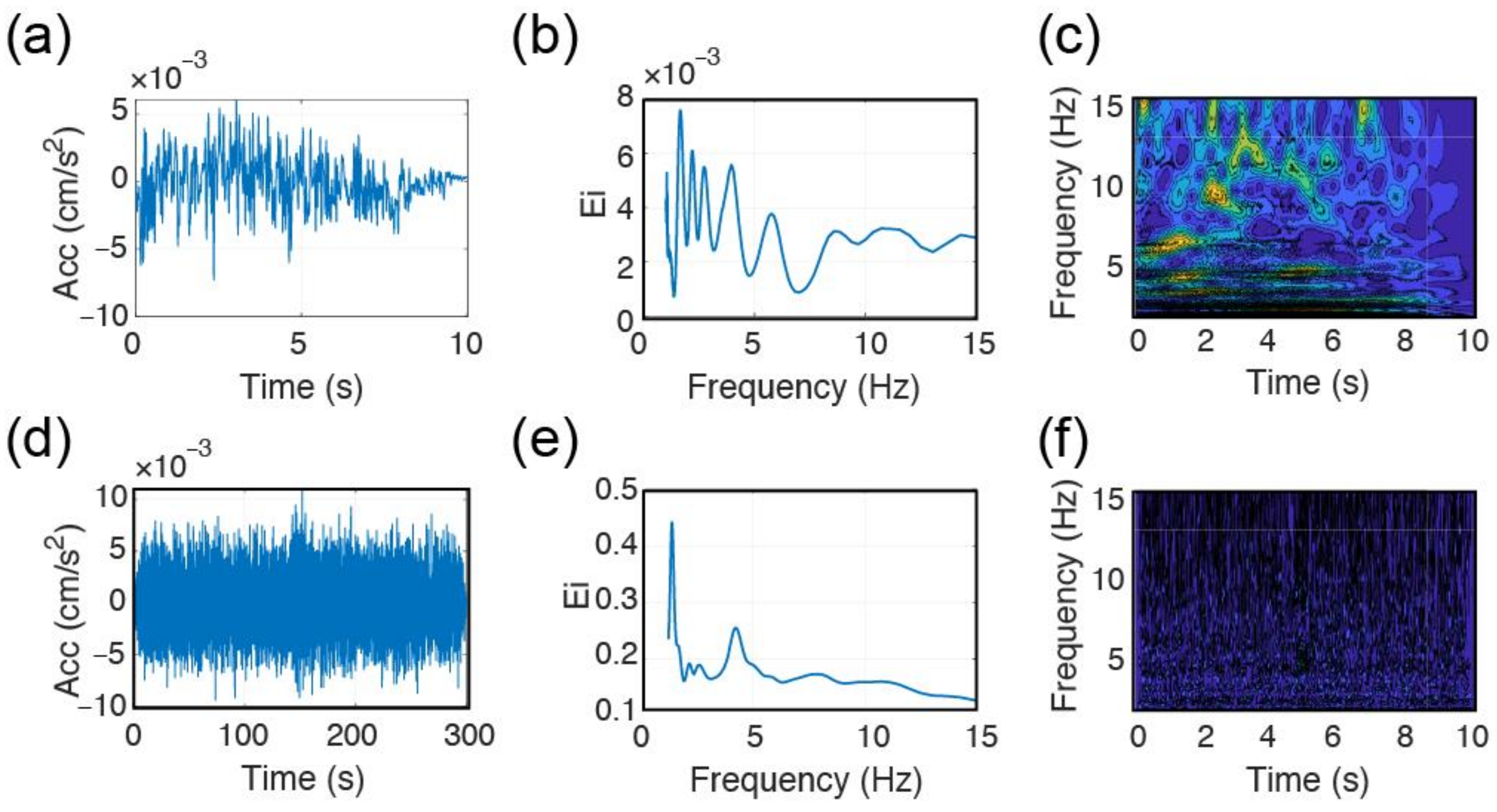
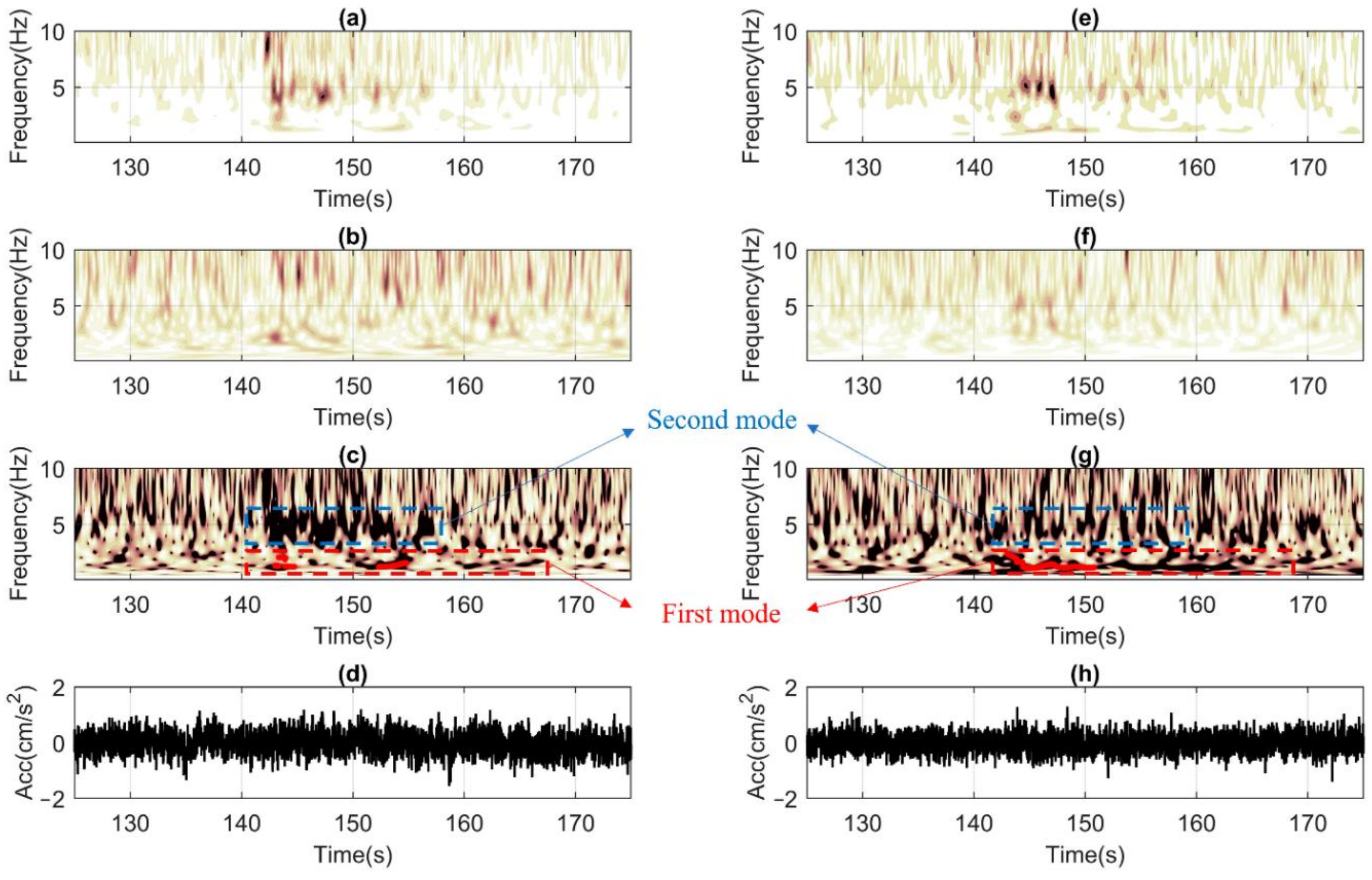
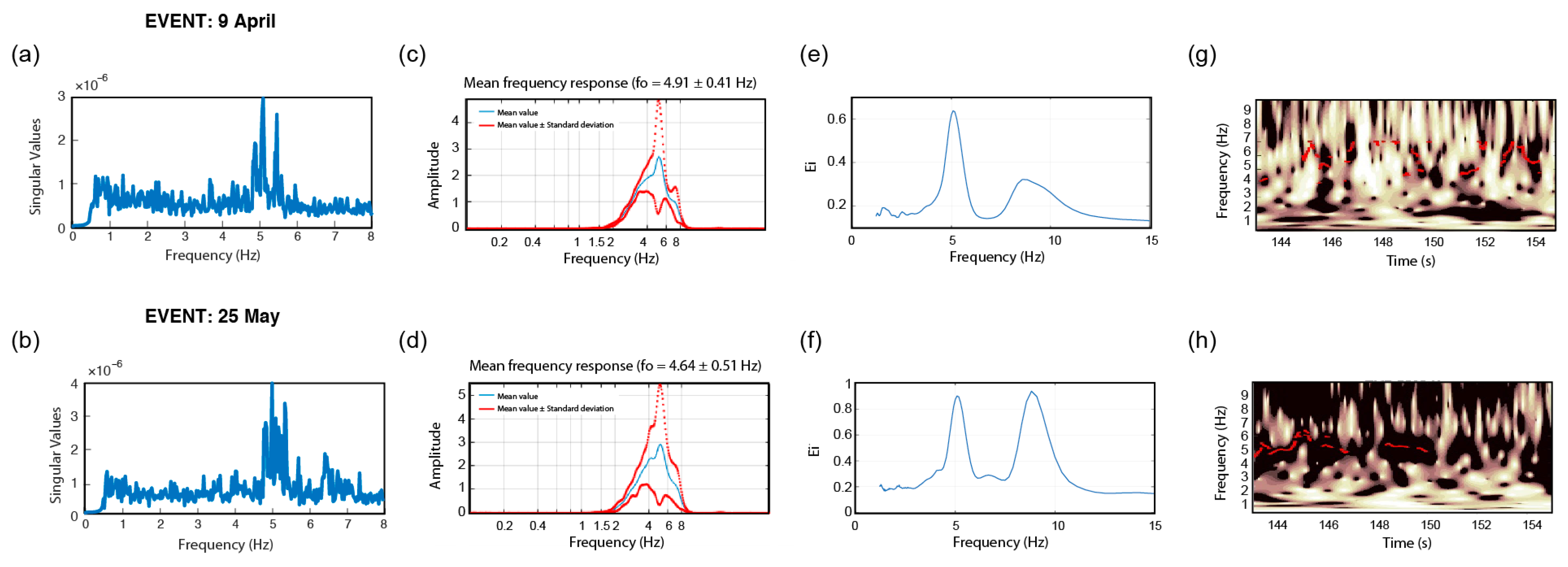
5.1. Comparison of the Methods Considering the Recordings from the High-Fidelity Sensors Installed in the TURN Building
5.2. Comparison of the Methods Considering the Recordings from the RS4D Sensors Installed in the LAS Building
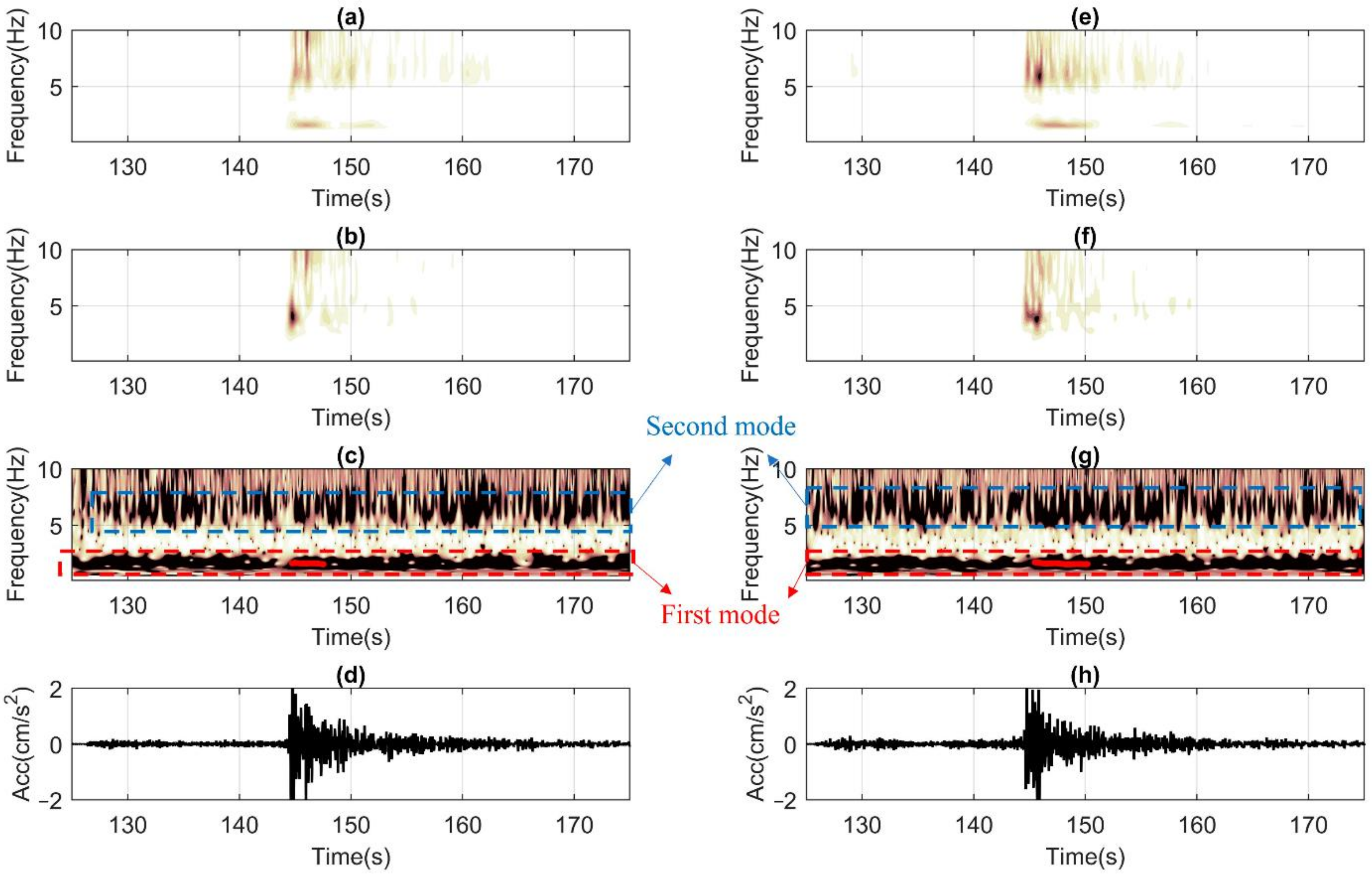
5.3. Method Repeatability in Terms of Frequency Inversions Considering DRG and BAL
5.4. Comments on the Future Usability of the RS4D Sensors for Rapid Response to Earthquakes (RRE) Purposes
6. Concluding Remarks
- Self-noise of RS4D sensors is too high to rely on noise-based SHM methods. For this reason, the domain of FDD is set as EGM and during structural identification, continuous verifications of deformed shape and mode repeatability are consistently confirmed.
- Low S/N ratios present in RS4D sensors adversely affect the precision in terms of frequency identification, the noisier the signal becomes the less becomes the precision of the inversions.
- Unlike standard SHM configurations accessing ambient vibration data, useful measurement lengths with RS4D are short due to the earthquake durations limiting the quality of identification results. This limitation becomes even more prominent when subsets of the measurements are of concern (e.g., tail data).
- Following up from the above, utilization of output-only techniques possesses risks due to the dominance of input signal content with particular spectral characteristics. With low S/N ratios and short-duration measurement issues expressed above, this concern becomes more influential.
- Among the methods, the most precise SHM approach in terms of deviations from the mean is found to be CWT. Besides, executing multiple identification techniques in parallel can increase the confidence level in terms of identification accuracy.
- All SHM techniques provided precise identification for the control building monitored with TSA-100S sensors. This conclusion proves that with high S/N ratios, all methods work reliably.
- It is expected that for a damaging event in Bucharest, RS4D sensors will operate sufficiently well to record the changes in the oscillation periods, which will be correlated with structural damage defined in [16].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Doebling, S.W.; Farrar, C.R.; Prime, M.B.; Shevitz, D.W. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review (No. LA-13070-MS); Los Alamos National Laboratory: Los Alamos, NM, USA, 1996.
- Sohn, H.; Farrar, C.R.; Hemez, F.M.; Shunk, D.D.; Stinemates, D.W.; Nadler, B.R.; Czarnecki, J.J. A Review of Structural Health Monitoring Literature: 1996–2001; Los Alamos National Laboratory: Los Alamos, NM, USA, 2003; Volume 1.
- Lynch, J.P. An overview of wireless structural health monitoring for civil structures. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 345–372. [Google Scholar] [CrossRef] [PubMed]
- Spencer, B.F., Jr.; Ruiz-Sandoval, M.E.; Kurata, N. Smart sensing technology: Opportunities and challenges. Struct. Control. Health Monit. 2004, 11, 349–368. [Google Scholar] [CrossRef]
- Sabato, A.; Niezrecki, C.; Fortino, G. Wireless MEMS-based accelerometer sensor boards for structural vibration monitoring: A review. IEEE Sens. J. 2016, 17, 226–235. [Google Scholar] [CrossRef]
- Malekloo, A.; Ozer, E.; AlHamaydeh, M.; Girolami, M. Machine learning and structural health monitoring overview with emerging technology and high-dimensional data source highlights. Struct. Health Monit. 2021, 21, 14759217211036880. [Google Scholar] [CrossRef]
- Ozer, E.; Feng, M.Q. Structural health monitoring. In Start-Up Creation; Woodhead Publishing: Sawston, UK, 2020; pp. 345–367. [Google Scholar]
- Tokognon, C.A.; Gao, B.; Tian, G.Y.; Yan, Y. Structural health monitoring framework based on Internet of Things: A survey. IEEE Internet Things J. 2017, 4, 619–635. [Google Scholar] [CrossRef]
- Mishra, M.; Lourenço, P.B.; Ramana, G.V. Structural health monitoring of civil engineering structures by using the internet of things: A review. J. Build. Eng. 2022, 48, 103954. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Scudero, S.; Vitale, G. A review of the capacitive MEMS for seismology. Sensors 2019, 19, 3093. [Google Scholar] [CrossRef] [Green Version]
- Contreras, D.; Wilkinson, S.; James, P. Earthquake reconnaissance data sources, a literature review. Earth 2021, 2, 1006–1037. [Google Scholar] [CrossRef]
- Tiganescu, A.; Grecu, B.; Neagoe, C.; Toma-Danila, D.; Tataru, D.; Ionescu, C.; Balan, S.F. PREVENT—An integrated multi-sensor system for seismic monitoring of civil structures. Rom. Rep. Phys. 2022, 74, 706. [Google Scholar]
- Ozer, E.; Purasinghe, R.; Feng, M.Q. Multi-output modal identification of landmark suspension bridges with distributed smartphone data: Golden gate bridge. Struct. Control Health Monit. 2020, 27, e2576. [Google Scholar] [CrossRef]
- European Commission. TURNkey Project—Towards More Earthquake-Resilient Urban Societies through a Multi-Sensor-Based Information System Enabling Earthquake Forecasting, Early Warning and Rapid Response Actions; European Commission: Brussels, Belgium, 2022. [Google Scholar]
- Grünthal, G. European Macroseismic Scale 1998; European Seismological Commission (ESC): Bucharest, Romania, 1998. [Google Scholar]
- Ozer, E.; Özcebe, A.G.; Negulescu, C.; Kharazian, A.; Borzi, B.; Bozzoni, F.; Tubaldi, E. Vibration-based and near real-time seismic damage assessment adaptive to building knowledge level. Buildings 2022, 12, 416. [Google Scholar] [CrossRef]
- Goulet, J.A.; Michel, C.; Kiureghian, A.D. Data-driven post-earthquake rapid structural safety assessment. Earthq. Eng. Struct. Dyn. 2015, 44, 549–562. [Google Scholar] [CrossRef] [Green Version]
- Priestley, M.N.; Seible, F.; Calvi, G.M. Seismic Design and Retrofit of Bridges; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Lagomarsino, S.; Giovinazzi, S. Macroseismic and mechanical models for the vulnerability and damage assessment of current buildings. Bull. Earthq. Eng. 2006, 4, 415–443. [Google Scholar] [CrossRef]
- Rytter, A. Vibrational Based Inspection of Civil Engineering Structures. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 1993. [Google Scholar]
- Tubaldi, E.; Ozer, E.; Douglas, J.; Gehl, P. Examining the contribution of near real-time data for rapid seismic loss assessment of structures. Struct. Health Monit. 2022, 21, 118–137. [Google Scholar] [CrossRef]
- Luş, H.; Betti, R.; Longman, R.W. Identification of linear structural systems using earthquake-induced vibration data. Earthq. Eng. Struct. Dyn. 1999, 28, 1449–1467. [Google Scholar] [CrossRef]
- Sun, Z.; Zou, Z.; Zhang, Y. Utilization of structural health monitoring in long-span bridges: Case studies. Struct. Control. Health Monit. 2017, 24, e1979. [Google Scholar] [CrossRef]
- Şafak, E.; Celebi, M. Seismic response of Transamerica building. II: System identification. J. Struct. Eng. 1991, 117, 2405–2425. [Google Scholar] [CrossRef]
- Zhang, F.L.; Yang, Y.P.; Xiong, H.B.; Yang, J.H.; Yu, Z. Structural health monitoring of a 250-m super-tall building and operational modal analysis using the fast Bayesian FFT method. Struct. Control Health Monit. 2019, 26, e2383. [Google Scholar] [CrossRef]
- Nof, R.N.; Chung, A.I.; Rademacher, H.; Dengler, L.; Allen, R.M. MEMS Accelerometer Mini-Array (MAMA): A Low-Cost Implementation for Earthquake Early Warning Enhancement. Earthq. Spectra 2019, 35, 21–38. [Google Scholar] [CrossRef]
- Halldorsson, B.; Balan, S.; Gehl, P.; Melis, N.S.; Borzi, B.; Ruigrok, E.; Martinelli, M.; Weber, B.; Curone, D.; Schweitzer, J. The TURNkey European Testbeds for Consistent Real-time Monitoring of Seismic Ground Motion and Other Geophysical Markers (Paper No. 0464). In Proceedings of the 3rd European Conference on Earthquake Engineering and Seismology (3ECEES), Bucharest, Romania, 4–9 September 2022; p. 10. [Google Scholar]
- Balan, S.F.; Apostol, B.F.; Tiganescu, A.; Danet, A. Monitoring buildings at INFP for seismic vulnerability mitigation. In Proceedings of the 3rd European Conference on Earthquake Engineering and Seismology (3ECEES), Bucharest, Romania, 4–9 September 2022. [Google Scholar]
- Fayaz, J.; Galasso, C. A deep neural network framework for real-time on-site estimation of acceleration response spectra of seismic ground motions. Comput. Aided Civ. Infrastruct. Eng. 2022, 1–17. [Google Scholar] [CrossRef]
- Sun, L.; D’Ayala, D.; Fayjaloun, R.; Gehl, P. Agent-based model on resilience-oriented rapid responses of road networks under seismic hazard. Reliab. Eng. Syst. Saf. 2021, 216, 108030. [Google Scholar] [CrossRef]
- Cascone, V.; Boaga, J.; Cassiani, G. Small Local Earthquake Detection Using Low-Cost MEMS Accelerometers: Examples in Northern and Central Italy. Seism. Rec. 2021, 1, 20–26. [Google Scholar] [CrossRef]
- Holmgren, J.M.; Werner, M.J. Raspberry Shake Instruments Provide Initial Ground-Motion Assessment of the Induced Seismicity at the United Downs Deep Geothermal Power Project in Cornwall, United Kingdom. Seism. Rec. 2021, 1, 27–34. [Google Scholar] [CrossRef]
- Radulian, M.; Vaccari, F.; Mandrescu, N.; Panza, G.F.; Moldoveanu, C.L. Seismic Hazard of Romania: Deterministic Approach. Pure Appl. Geophys. 2000, 157, 221–247. [Google Scholar] [CrossRef]
- Pavel, F.; Vacareanu, R.; Douglas, J.; Radulian, M.; Cioflan, C.; Barbat, A. An updated probabilistic seismic hazard assessment for Romania and comparison with the approach and outcomes of the SHARE project. Pure Appl. Geophys. 2016, 173, 1881–1905. [Google Scholar] [CrossRef] [Green Version]
- Toma-Danila, D.; Zulfikar, C.; Manea, E.F.; Cioflan, C.O. Improved seismic risk estimation for Bucharest, based on multiple hazard scenarios and analytical methods. Soil Dyn. Earthq. Eng. 2015, 73, 1–16. [Google Scholar] [CrossRef]
- Manea, E.F.; Cioflan, C.O.; Danciu, L. Ground-motion models for Vrancea intermediate-depth earthquakes. Earthq. Spectra 2021, 38, 407–431. [Google Scholar] [CrossRef]
- Georgescu, E.S.; Borcia, I.S.; Praun, I.C.; Dragomir, C.S. State of the Art of Structural Health Monitoring in Seismic Zones of Romania. In Proceedings of the of the MEMSCON Workshop, Bucharest, Romania, 7 October 2010; pp. 89–93. [Google Scholar]
- Craifaleanu, I.G.; Borcia, I.S.; Praun, I.C. Strong-motion Networks in Romania and Their Efficient Use in the Structural Engineering Applications. In Earthquake Data in Engineering Seismology: Predictive Models, Data Management and Networks; Akkar, S., Gülkan, P., van Eck, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 247–259. [Google Scholar] [CrossRef]
- Tiganescu, A.; Craifaleanu, I.G.; Aldea, A.; Grecu, B.; Vacareanu, R.; Toma-Danila, D.; Dragomir, C.S. Evolution, Recent Progress and Perspectives of the Seismic Monitoring of Building Structures in Romania. Front. Earth Sci. 2022, 10, 819153. [Google Scholar] [CrossRef]
- P13-63; Code for the Design of Civil and Industrial Buildings in Seismic Zones. State Committee for Constructions, Architecture and Systematization: Bucharest, Romania, 1963.
- EN1998-1; Eurocode 8: Design Provisions for Earthquake Resistance of Structures—Part 1.1: General Rules, Seismic Actions and Rules for Buildings. European Committee of Standardization: Brussels, Belgium, 2004.
- P100-1/2006; Ministry of Transport, Construction and Tourism, Seismic Design Code—Part I: Design Prescriptions for Buildings. Ministry of Transport, Construction and Tourism: Bucharest, Romania, 2006.
- P100-1/2013; Ministry of Regional Development and Public Administration, Seismic Design Code—Part I: Design Prescriptions for Buildings. Ministry of Regional Development and Public Administration: Bucharest, Romania, 2013.
- Lecocq, T.; Hicks, S.P.; Van Noten, K.; Van Wijk, K.; Koelemeijer, P.; De Plaen, R.S.; Xiao, H. Global quieting of high-frequency seismic noise due to COVID-19 pandemic lockdown measures. Science 2020, 369, 1338–1343. [Google Scholar] [CrossRef]
- Grecu, B.; Borleanu, F.; Tiganescu, A.; Poiata, N.; Dinescu, R.; Tataru, D. The effect of 2020 COVID-19 lockdown measures on seismic noise recorded in Romania. Solid Earth 2021, 12, 2351–2368. [Google Scholar] [CrossRef]
- Anthony, R.E.; Ringler, A.T.; Wilson, D.C.; Wolin, E. Do low-cost seismographs perform well enough for your network? An overview of laboratory tests and field observations of the OSOP Raspberry Shake 4D. Seismol. Res. Lett. 2019, 90, 219–228. [Google Scholar] [CrossRef] [Green Version]
- McNamara, D.E.; Buland, R.P. Ambient noise levels in the continental United States. Bull. Seismol. Soc. Am. 2004, 94, 1517–1527. [Google Scholar] [CrossRef]
- Peterson, J.R. Observations and Modeling of Seismic Background Noise; US Geological Survey: Reston, VA, USA, 1993.
- ObsPy Documentation. Available online: https://docs.obspy.org/master/tutorial/code_snippets/probabilistic_power_spectral_density.html (accessed on 30 May 2022).
- RS4D Technical Specification Document. Available online: https://manual.raspberryshake.org/_downloads/SpecificationsforRaspberryShake4DMEMSV4.pdf (accessed on 30 May 2022).
- Danciu, L.; Nandan, S.; Reyes, C.; Basili, R.; Weatherill, G.; Beauval, C.; Rovida, A.; Vilanova, S.; Sesetyan, K.; Bard, P.-Y.; et al. The 2020 Update of the European Seismic Hazard Model: Model Overview; EFEHR Technical Report 001, v1.0.0; EFEHR: Zurich, Switzerland, 2021. [Google Scholar] [CrossRef]
- Crowley, H.; Dabbeek, J.; Despotaki, V.; Rodrigues, D.; Martins, L.; Silva, V.; Romão, X.; Pereira, N.; Weatherill, G.; Danciu, L. European Seismic Risk Model (ESRM20); EFEHR Technical Report 002, V1.0.0; EFEHR: Zurich, Switzerland, 2021; p. 84. [Google Scholar] [CrossRef]
- Ferrand, T.P.; Manea, E.F. Dehydration-induced earthquakes identified in a subducted oceanic slab beneath Vrancea, Romania. Sci. Rep. 2021, 11, 10315. [Google Scholar] [CrossRef] [PubMed]
- Balan, S.; Capatina, D.; Cornea, I.; Cristescu, V.; Dumitrescu, D.; Enescu, D.; Enescu, S.; Facaoaru, I.; Georgescu, D.; Lazarescu, V.; et al. The 4 March 1977 Earthquake in Romania; The Publishing House of the Romanian Academy: Bucharest, Romania, 1982. (In Romanian) [Google Scholar]
- Berg, G.V.; Bolt, B.A.; Sozen, M.A.; Rojahn, C. Earthquake in Romania, March 4, 1977—An Engineering Report; The National Academies Press: Washington, DC, USA, 1980. [Google Scholar] [CrossRef]
- Georgescu, E.S.; Pomonis, A. Building damage vs. territorial casualty patterns during the Vrancea (Romania) earthquakes of 1940 and 1977. In Proceedings of the 15th World Conference on Earthquake Engineering, Portugal, Lisbon, 24–28 September 2012; pp. 24–28. [Google Scholar]
- Lungu, D.; Aldea, A.; Moldoveanu, T.; Ciugudean, V.; Stefanica, M. Near-surface geology and dynamic properties of soil layers in Bucharest. In Vrancea Earthquakes: Tectonics, Hazard and Risk Mitigation; Springer: Dordrecht, The Netherlands, 1999; pp. 137–148. [Google Scholar]
- Mandrescu, N.; Radulian, M.; Mărmureanu, G. Geological, geophysical and seismological criteria for local response evaluation in Bucharest urban area. Soil Dyn. Earthq. Eng. 2007, 27, 367–393. [Google Scholar] [CrossRef]
- Bala, A.; Grecu, B.; Ciugudean, V.; Raileanu, V. Dynamic properties of the Quaternary sedimentary rocks and their influence on seismic site effects. Case study in Bucharest City, Romania. Soil Dyn. Earthq. Eng. 2009, 29, 144–154. [Google Scholar] [CrossRef]
- Bala, A. Quantitative modelling of seismic site amplification in an earthquake-endangered capital city: Bucharest, Romania. Nat. Hazards 2014, 72, 1429–1445. [Google Scholar] [CrossRef]
- Manea, E.F.; Michel, C.; Poggi, V.; Fäh, D.; Radulian, M.; Balan, S.F. Improving the shear wave velocity structure beneath Bucharest (Romania) using ambient vibrations. Geophys. J. Int. 2016, 207, 848–861. [Google Scholar] [CrossRef] [Green Version]
- Liteanu, G. Geology of the City of Bucharest; Technical Studies, Series E; Hydrology: Bucharest, Romania, 1951; Volume 1. (In Romanian) [Google Scholar]
- Zaharia, B.; Radulian, M.; Popa, M.; Grecu, B.; Bala, A.; Tataru, D. Estimation of the local response using Nakamura method for Bucharest area. Rom. Rep. Phys. 2008, 60, 125–134. [Google Scholar]
- Bonjer, K.-P.; Oncescu, M.C.; Driad, L.; Rizescu, M. A note on empirical site responses in Bucharest, Romania. In Vrancea Earthquakes: Tectonics, Hazard and Risk Mitigation; Wenzel, F., Lungu, D., Novak, O., Eds.; Kluwer Academic Publishers: Norwell, MA, USA, 1999; pp. 149–162. [Google Scholar]
- Grecu, B.; Radulian, M.; Mandrescu, N.; Panza, G.F. H/V spectral ratios technique application in the city of Bucharest: Can we get rid of source effect? J. Seismol. Earthq. Eng. 2007, 9, 1–4. [Google Scholar]
- Popa, M.; Chircea, A.; Dinescu, R.; Neagoe, C.; Grecu, B. Romanian Earthquake Catalogue (ROMPLUS); National Institute for Earth Physics: Magurele, Romania, 2022. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441. [Google Scholar] [CrossRef] [Green Version]
- Tran, T.T.; Ozer, E. Synergistic bridge modal analysis using frequency domain decomposition, observer Kalman filter identification, stochastic subspace identification, system realization using information matrix, and autoregressive exogenous model. Mech. Syst. Signal Process. 2021, 160, 107818. [Google Scholar] [CrossRef]
- Tran, T.T.; Ozer, E. Automated and model-free bridge damage indicators with simultaneous multiparameter modal anomaly detection. Sensors 2020, 20, 4752. [Google Scholar] [CrossRef] [PubMed]
- Mallat, S. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef] [Green Version]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Wickerhauser, M.V. Adapted Wavelet Analysis from Theory to Software; A.K. Peters, Ltd.: Wellesley, MA, USA, 1994. [Google Scholar]
- Strang, G.; Nguyen, T. Wavelets and Filter Banks; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
- Galiana-Merino, J.J.; Rosa-Herranz, J.L.; Rosa-Cintas, S.; Martinez-Espla, J.J. SeismicWaveTool: Continuous and discrete wavelet analysis and filtering for multichannel seismic data. Comput. Phys. Commun. 2013, 184, 162–171. [Google Scholar] [CrossRef]
- Galiana-Merino, J.J.; Pla, C.; Fernandez-Cortes, A.; Cuezva, S.; Ortiz, J.; Benavente, D. EnvironmentalWaveletTool: Continuous and discrete wavelet analysis and filtering for environmental time series. Comput. Phys. Commun. 2014, 185, 2758–2770. [Google Scholar] [CrossRef]
- Percival, D.B.; Walden, A.T. Spectral Analysis for Physical Application; Cambridge University Press: London, UK, 1993; pp. 187–330. [Google Scholar]
- Konno, K.; Ohmachi, T. Ground-Motion Characteristics Estimated from Spectral Ratio between Horizontal and Vertical Components of Microtremor. Bull. Seismol. Soc. Am. 1998, 88, 228–241. [Google Scholar] [CrossRef]
- Mitra, P.P.; Pesaran, B. Analysis of dynamic brain imaging data. Biophys. J. 1999, 76, 691–708. [Google Scholar] [CrossRef] [Green Version]
- Kleinfeld, D.; Mitra, P.P. Spectral methods for functional brain imaging. Cold Spring Harb. Protoc. 2014, 2014, 248–262. [Google Scholar] [CrossRef] [Green Version]
- SESAME. Guidelines for the Implementation of the H/V Spectral Ratio Technique on Ambient Vibrations: Measurements Processing and Interpretation; European Commission-Research General Directorate: Brussels, Belgium, 2004. [Google Scholar]
- Morlet, J.; Arens, G.; Fourgeau, E.; Giard, D. Wave Propagation and Sampling Theory. Geophysics 1982, 47, 203–236. [Google Scholar] [CrossRef] [Green Version]
- Mallat, S. A Wavelet Tour of Signal Processing, 2nd ed.; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Shensa, M. The discrete wavelet transform: Wedding the a trous and Mallat algorithms. IEEE Trans. Signal Process. 1992, 40, 2464–2482. [Google Scholar] [CrossRef] [Green Version]
- Coifman, R.R.; Wickerhauser, M.L. Entropy based algorithms for best-basis selection. IEEE Trans. Inf. Theory 1992, 32, 712–718. [Google Scholar] [CrossRef] [Green Version]
- Wijesundara, K.K.; Negulescu, C.; Foerster, E. Estimation of Modal Properties of Low-Rise Buildings Using Ambient Excitation Measurements. Shock. Vib. 2015, 2015, 173450. [Google Scholar] [CrossRef] [Green Version]
- Wijesundara, K.K.; Negulescu, C.; Monfort, D.; Foerster, E. Identification of Modal Parameters of Ambient Excitation Structures Using Continuous Wavelet Transform; CCSD: Villeurbanne, France, 2022. [Google Scholar]
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: The S transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Stockwell, R.G. Why use the S transform? In Pseudo-Differential Operators: Partial Differential Equations and Time-Frequency Analysis; Rodino, L., Schulze, B.-W., Wong, M.W., Eds.; American Mathematical Society: Providence, RI, USA, 2007; pp. 279–309. [Google Scholar]
- Gusev, A.; Radulian, M.; Rizescu, M.; Panza, G.F. Source scaling of intermediate-depth Vrancea earthquakes. Geophys. J. Int. 2002, 151, 879–889. [Google Scholar] [CrossRef] [Green Version]
- Popescu, E.; Grecu, B.; Popa, M.; Rizescu, M.; Radulian, M. Seismic source properties: Indications of lithosphere irregular structure on depth beneath the Vrancea region. Rom. Rep. Phys. 2003, 55, 485–510. [Google Scholar]
- Vacareanu, R.; Radulian, M.; Iancovici, M.; Pavel, F.; Neagu, C. Fore-arc and back-arc ground motion prediction model for Vrancea intermediate depth seismic source. J. Earthq. Eng. 2015, 19, 535–562. [Google Scholar] [CrossRef]
- Pavel, F.; Calotescu, I.; Stanescu, D.; Badiu, A. Life-cycle and seismic fragility assessment of code-conforming reinforced concrete and steel structures in Bucharest, Romania. Int. J. Disaster Risk Sci. 2018, 9, 263–274. [Google Scholar] [CrossRef]
- Ambraseys, N.N. Long-period effects in the Romanian earthquake of March 1977. Nature 1977, 268, 324–325. [Google Scholar] [CrossRef]
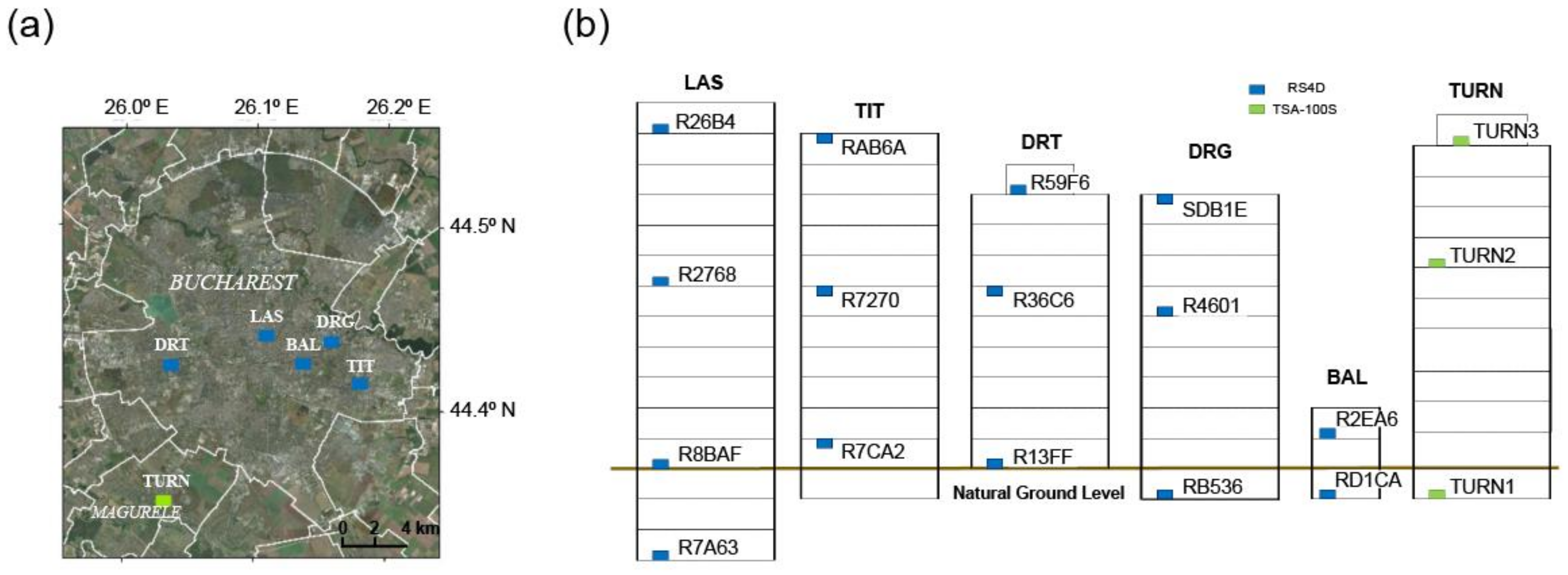







| Building Code | Construction Year | Structure Type | Building Configuration | Sensors Installed | Location of the Sensors |
|---|---|---|---|---|---|
| DRG | 1982 | Large panel structure (precast shear walls structure) | B + GF + 8S | 3 RS4D | B, 5th S, 8th S |
| BAL | before 1963 (<1940) | Unreinforced Masonry | B + GF + A | 2 RS4D | B, A |
| DRT | before 1963 | Large panel structure (precast shear walls structure) | GF + 8S | 3 RS4D | GF, 5th S, 9th S |
| TIT | 1963–1977 | Large panel structure (precast shear walls structure) | B + GF + 10S | 3 RS4D | GF, 5th S, 10th S |
| LAS | 2008 | Reinforced Concrete frame | 3B + GF + 11S | 4 RS4D | 3rd B, GF, 5th S, 11th S |
| TURN | 1973 (retrofitted in the 1990s) | Reinforced Concrete shear walls | B + GF + 9S | 3TSA-100S | B, 6th S, 10th S |
| EQ NO | DATE | TIME (UTC) | DEPTH (km) | ML |
|---|---|---|---|---|
| 1 | 2 June 2020 | 11:12:58 | 101.3 | 4.5 |
| 2 | 21 June 2020 | 03:47:27 | 119.4 | 4 |
| 3 | 25 June 2020 | 17:30:16 | 12.4 | 4.5 |
| 4 | 15 August 2020 | 02:28:54 | 125.1 | 3.9 |
| 5 | 10 October 2020 | 06:29:47 | 65.8 | 4 |
| 6 | 22 October 2020 | 20:21:44 | 122.1 | 4 |
| 7 | 29 October 2020 | 22:39:37 | 9.1 | 4.2 |
| 8 | 3 November 2020 | 09:14:41 | 117.7 | 3.9 |
| 9 | 27 November 2020 | 12:30:16 | 124.9 | 3.8 |
| 10 | 23 December 2020 | 14:27:17 | 126.2 | 3.8 |
| 11 | 5 January 2021 | 23:50:34 | 9.6 | 4 |
| 12 | 14 February 2021 | 17:24:52 | 126.2 | 3.8 |
| 13 | 24 February 2021 | 02:35:09 | 133.9 | 4 |
| 14 | 27 February 2021 | 21:13:11 | 124.8 | 4.2 |
| 15 | 7 March 2021 | 09:52:28 | 144.5 | 4.1 |
| 16 | 7 March 2021 | 22:34:28 | 144.9 | 3.9 |
| 17 | 23 March 2021 | 06:26:54 | 121.3 | 3.8 |
| 18 | 9 April 2021 | 18:36:47 | 79 | 4.6 |
| 19 | 18 April 2021 | 10:03:16 | 134.7 | 3.8 |
| 20 | 25 May 2021 | 21:30:37 | 131.2 | 4.7 |
| SHM Technique Utilized | Acronym | Approach | Intermediary Output |
|---|---|---|---|
| Frequency domain decomposition | FDD | Output only | Singular Value Diagram (SVD) |
| Short-time Fourier transform with wavelet pre–filtering | STFT-WF | Output only | Fourier Amplitude Diagram (FAD) |
| Continuous wavelet transform | CWT | Output only | Energy-Frequency Diagram (EFD) |
| Stockwell transformation-amplification function | ST-AF | Input-output | Stockwell Amplification Diagram (SAD) |
| Building Sensor | f0 (Hz) Dir. | FDD 09/04|25/05 | STFT-WF 09/04|25/05 | CWT 09/04|25/05 | ST-AF 09/04|25/05 | Mean 09/04|25/05 | CoV 09/04|25/05 |
|---|---|---|---|---|---|---|---|
| BAL | x | 5.10|5.03 | 4.91|4.64 | 4.92|5.00 | 5.7 ?|5.2 | 5.16|4.97 | 0.06|0.04 |
| RS4D | y | 3.71|6.59 | 4.59|5.18 | 5.56|6.25 | 5.5 ?|5.8 | 4.84|5.96 | 0.16|0.09 |
| DRG | x | 2.42|2.32 | 2.45|2.07 | 2.21|2.17 | 2.4|2.5 | 2.37|2.27 | 0.04|0.07 |
| RS4D | y | 3.05|3.25 | 2.40|2.19 | 3.00|3.48 | 2.9|3.1 | 2.84|3.01 | 0.09|0.16 |
| DRT | x | 2.91|2.69 | 2.23|2.04 | 2.77 ?| 2.77 ? | 2.7|2.7 | 2.65|2.55 | 0.10|0.12 |
| RS4D | y | 1.88|1.91 | 2.10|2.28 | 1.94|1.85 | 2.3 ?|1.9 | 2.05|1.99 | 0.08|0.09 |
| LAS | x | 1.37|1.34 | 1.30|1.23 | 1.36|1.33 | 1.4|1.4 | 1.36|1.33 | 0.03|0.05 |
| RS4D | y | 1.20|1.20 | 1.21|1.20 | 1.20|1.23 | 2.1 ?|1.4 | 1.42|1.25 | 0.27|0.07 |
| TIT | x | 1.88|1.98 | 1.96|2.04 | 1.86|1.96 | 2.1|2.1 | 1.95|2.02 | 0.05|0.05 |
| RS4D | y | 2.42|2.37 | 2.10|2.28 | 2.38|2.36 | 2.4|2.4 | 2.33|2.35 | 0.06|0.02 |
| TURN | x | 1.56|1.59 | 1.55|1.58 | 1.54|1.54 | 1.6|1.6 | 1.56|1.58 | 0.01|0.01 |
| TSA-100S | y | 1.56|1.56 | 1.54|1.58 | 1.46|1.52 | 1.6|1.6 | 1.54|1.57 | 0.03|0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Özcebe, A.G.; Tiganescu, A.; Ozer, E.; Negulescu, C.; Galiana-Merino, J.J.; Tubaldi, E.; Toma-Danila, D.; Molina, S.; Kharazian, A.; Bozzoni, F.; et al. Raspberry Shake-Based Rapid Structural Identification of Existing Buildings Subject to Earthquake Ground Motion: The Case Study of Bucharest. Sensors 2022, 22, 4787. https://doi.org/10.3390/s22134787
Özcebe AG, Tiganescu A, Ozer E, Negulescu C, Galiana-Merino JJ, Tubaldi E, Toma-Danila D, Molina S, Kharazian A, Bozzoni F, et al. Raspberry Shake-Based Rapid Structural Identification of Existing Buildings Subject to Earthquake Ground Motion: The Case Study of Bucharest. Sensors. 2022; 22(13):4787. https://doi.org/10.3390/s22134787
Chicago/Turabian StyleÖzcebe, Ali Güney, Alexandru Tiganescu, Ekin Ozer, Caterina Negulescu, Juan Jose Galiana-Merino, Enrico Tubaldi, Dragos Toma-Danila, Sergio Molina, Alireza Kharazian, Francesca Bozzoni, and et al. 2022. "Raspberry Shake-Based Rapid Structural Identification of Existing Buildings Subject to Earthquake Ground Motion: The Case Study of Bucharest" Sensors 22, no. 13: 4787. https://doi.org/10.3390/s22134787
APA StyleÖzcebe, A. G., Tiganescu, A., Ozer, E., Negulescu, C., Galiana-Merino, J. J., Tubaldi, E., Toma-Danila, D., Molina, S., Kharazian, A., Bozzoni, F., Borzi, B., & Balan, S. F. (2022). Raspberry Shake-Based Rapid Structural Identification of Existing Buildings Subject to Earthquake Ground Motion: The Case Study of Bucharest. Sensors, 22(13), 4787. https://doi.org/10.3390/s22134787












