A Ka-Band Integrated Six-Port Chip for Analog Complex Correlator
Abstract
:1. Introduction
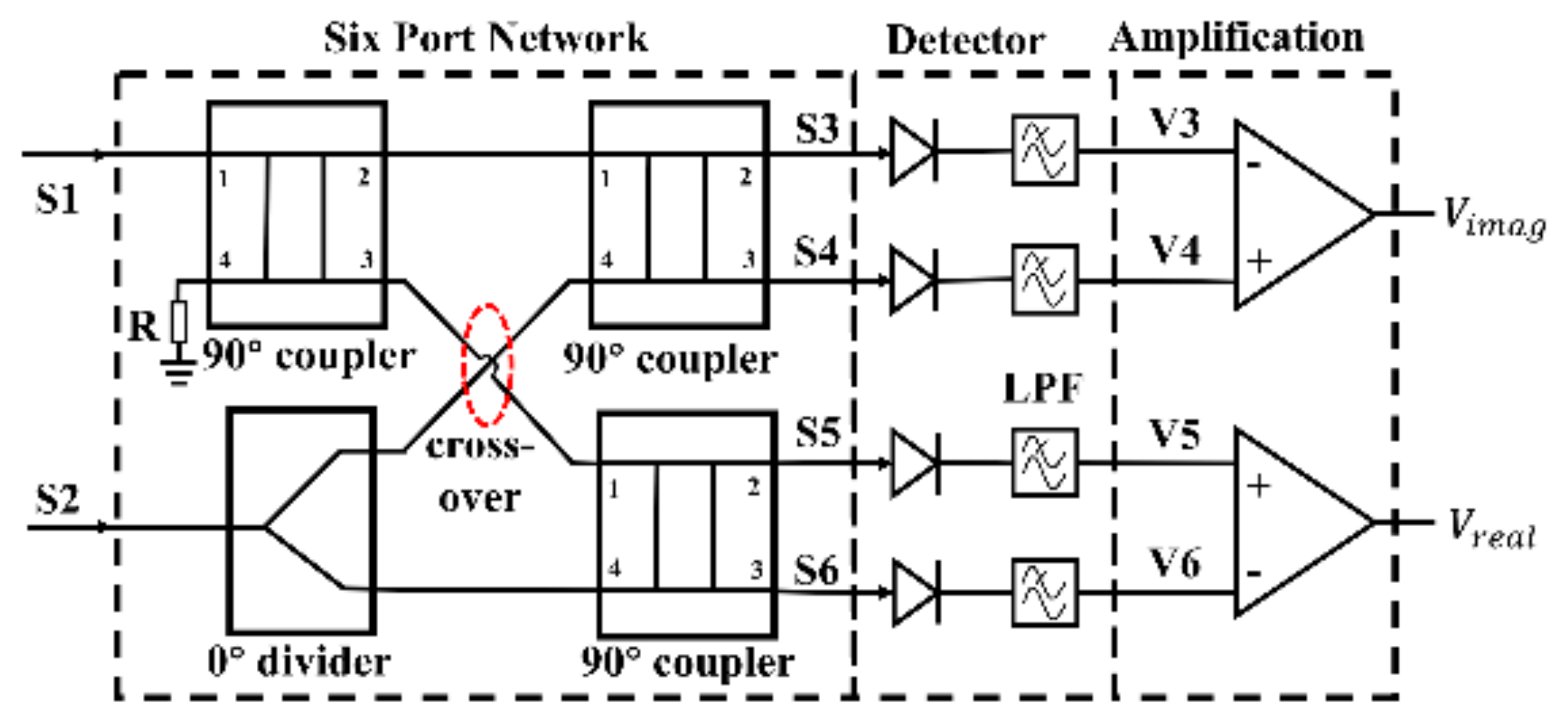
2. Analysis of the Analog Complex Correlator Based on the Integrated Six-Port Chip
2.1. Theory of the Analog Complex Correlator
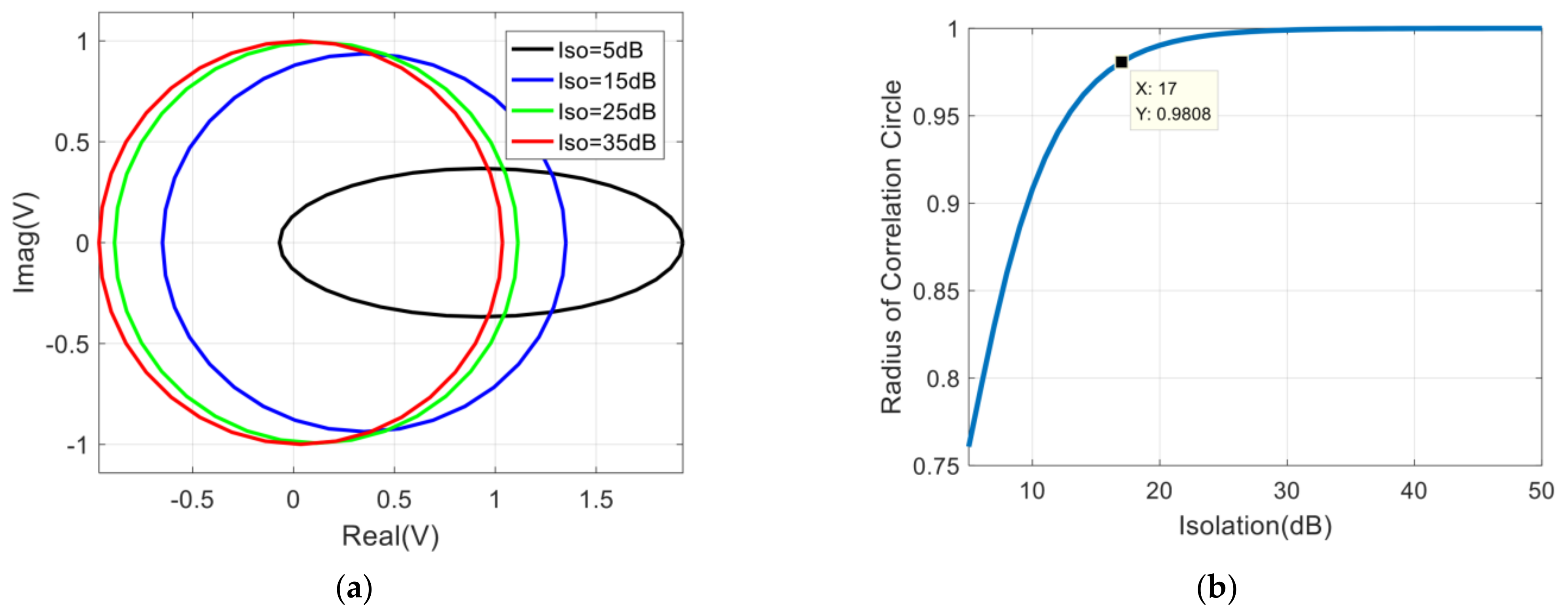
2.2. Influence of Isolation between Two Amplifiers on Correlation Results
2.3. Influence of Phase Shift Range Error on Correlation Results
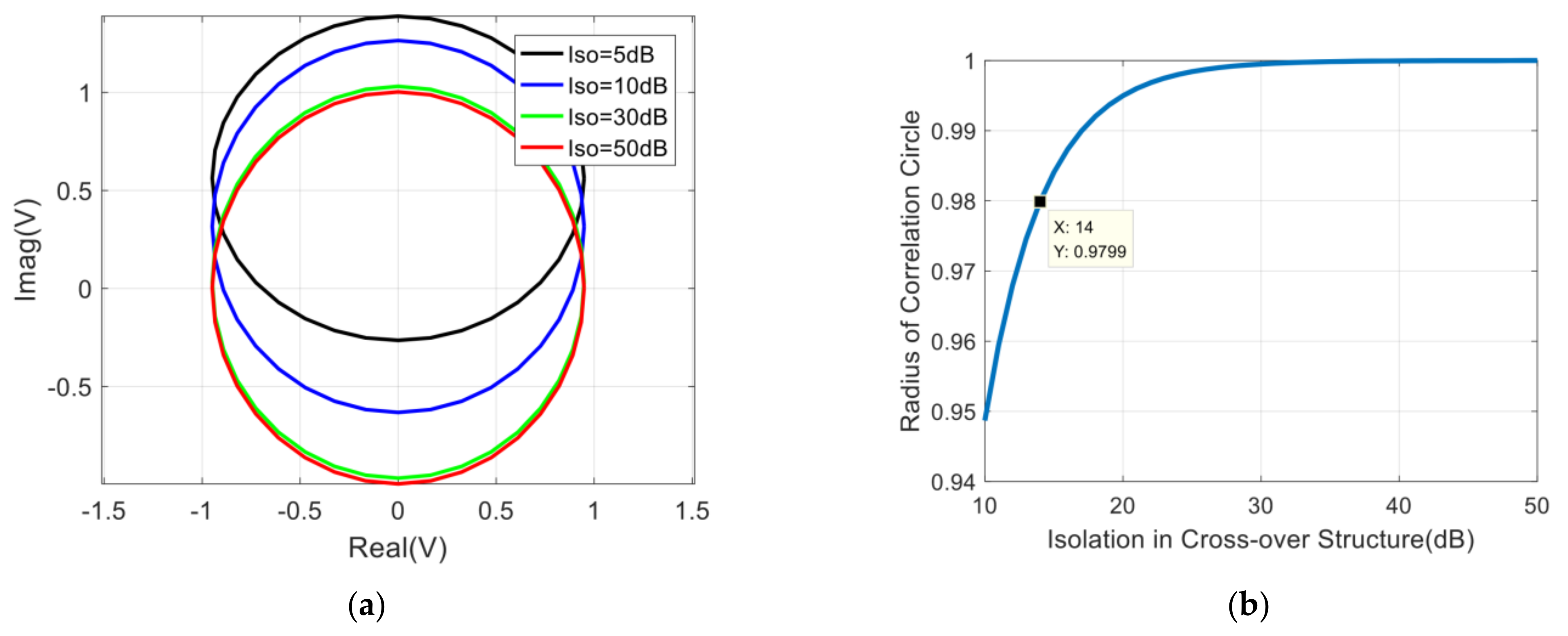
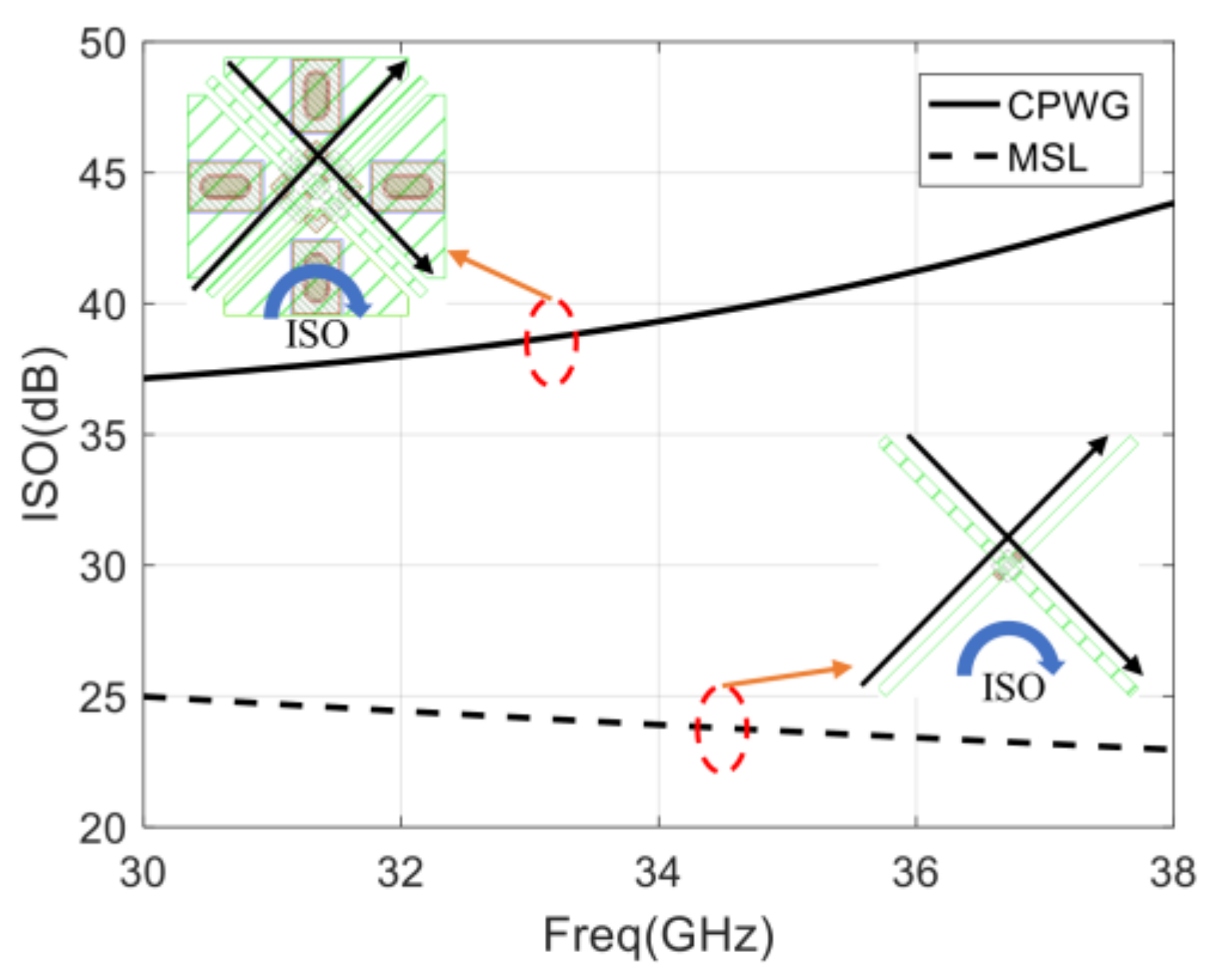
2.4. Influence of Isolation in Cross-Over Structure on Correlation Results
3. Design of the Integrated Six-Port Chip
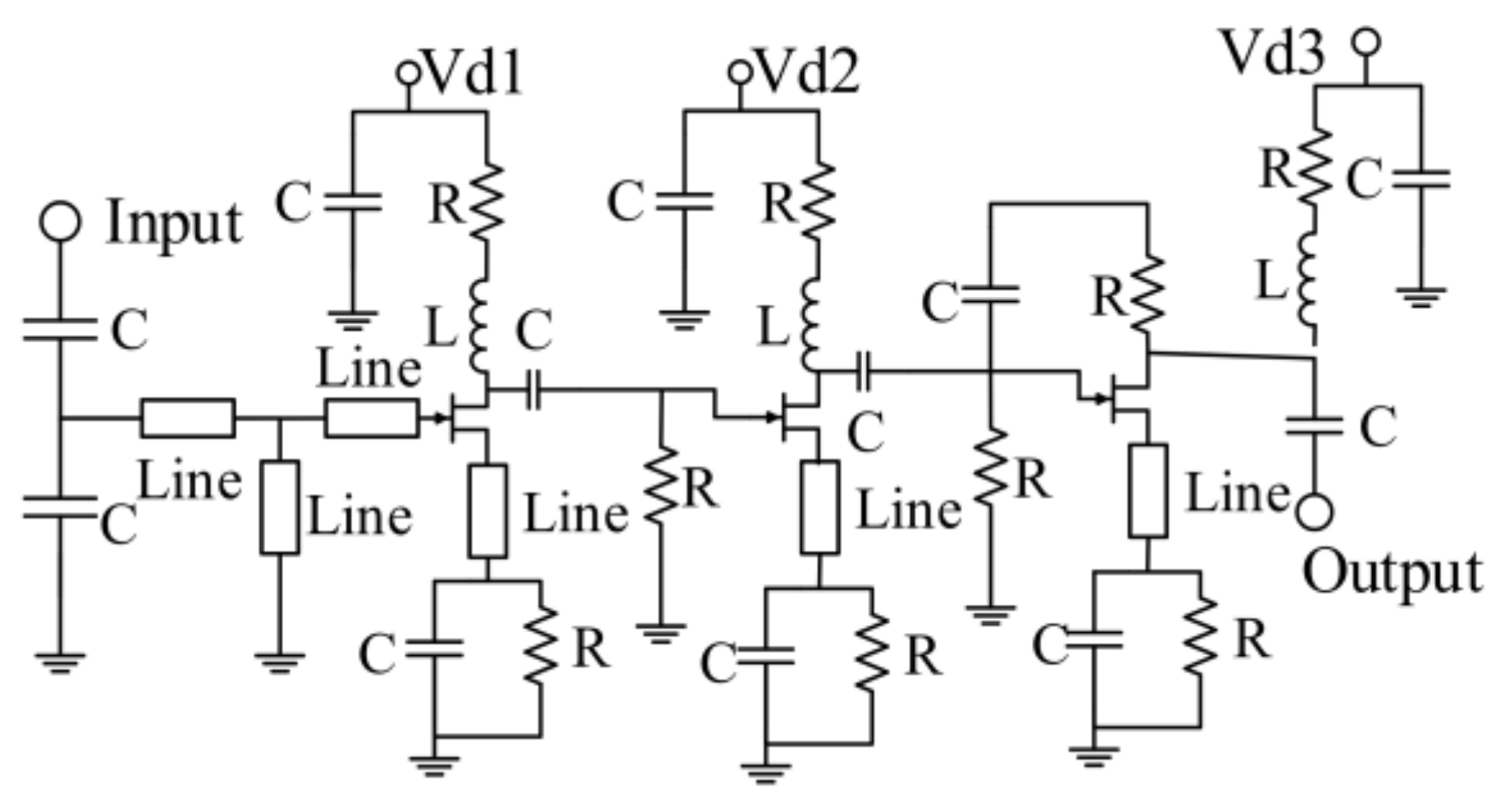
3.1. Design of the Amplifier
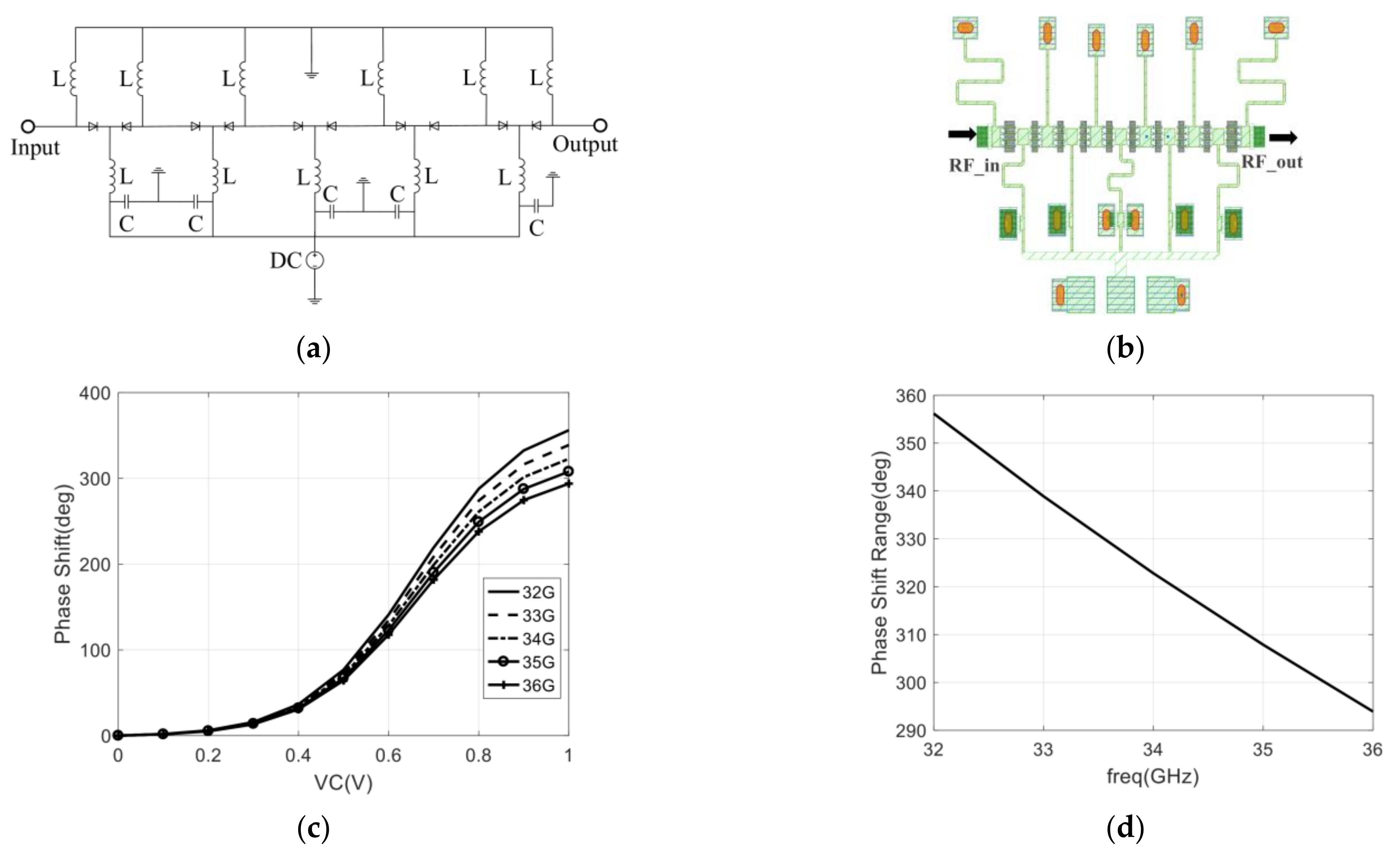
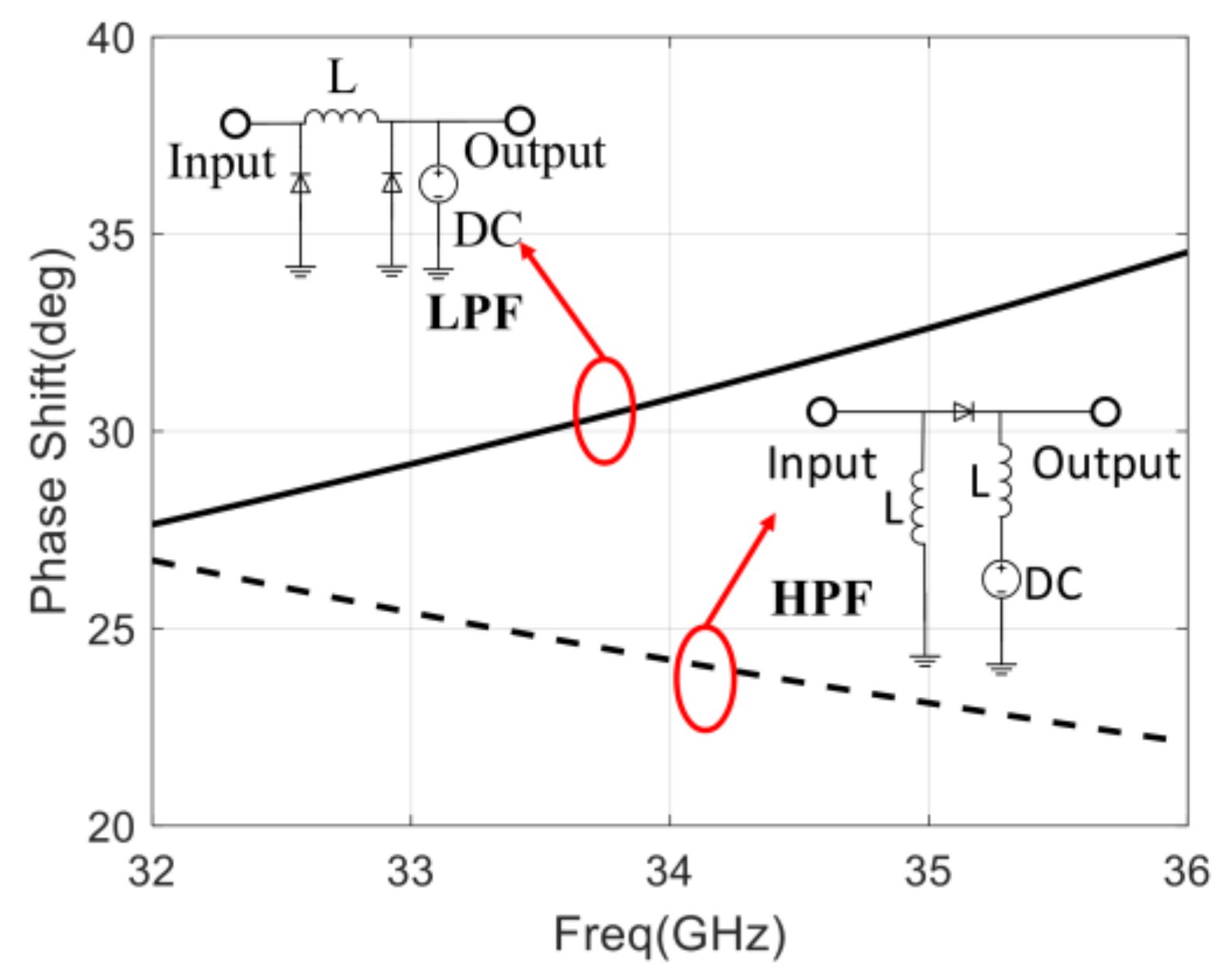
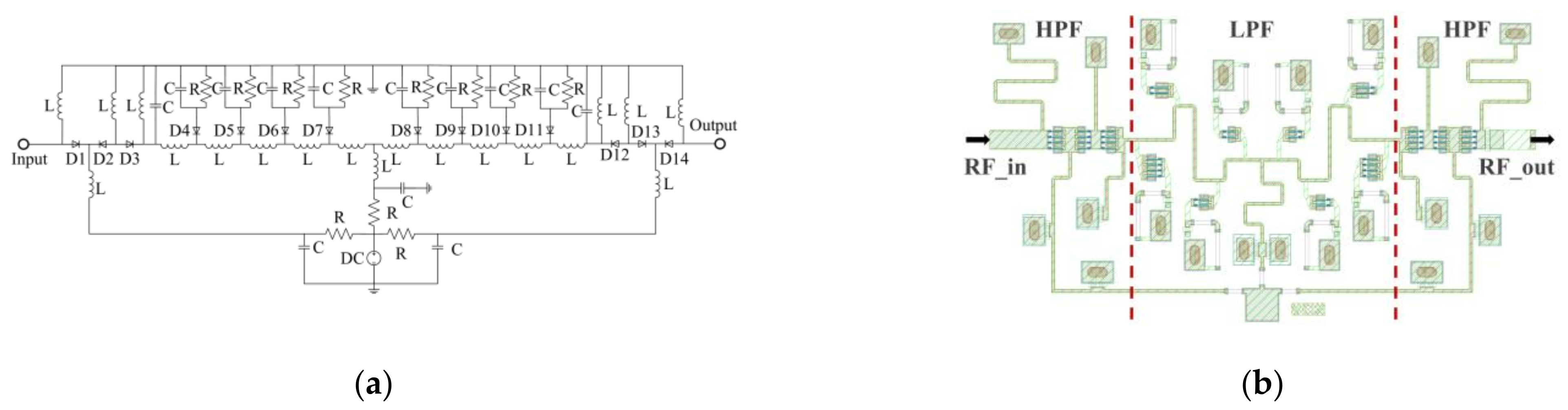
3.2. Design of the Phase Shifter
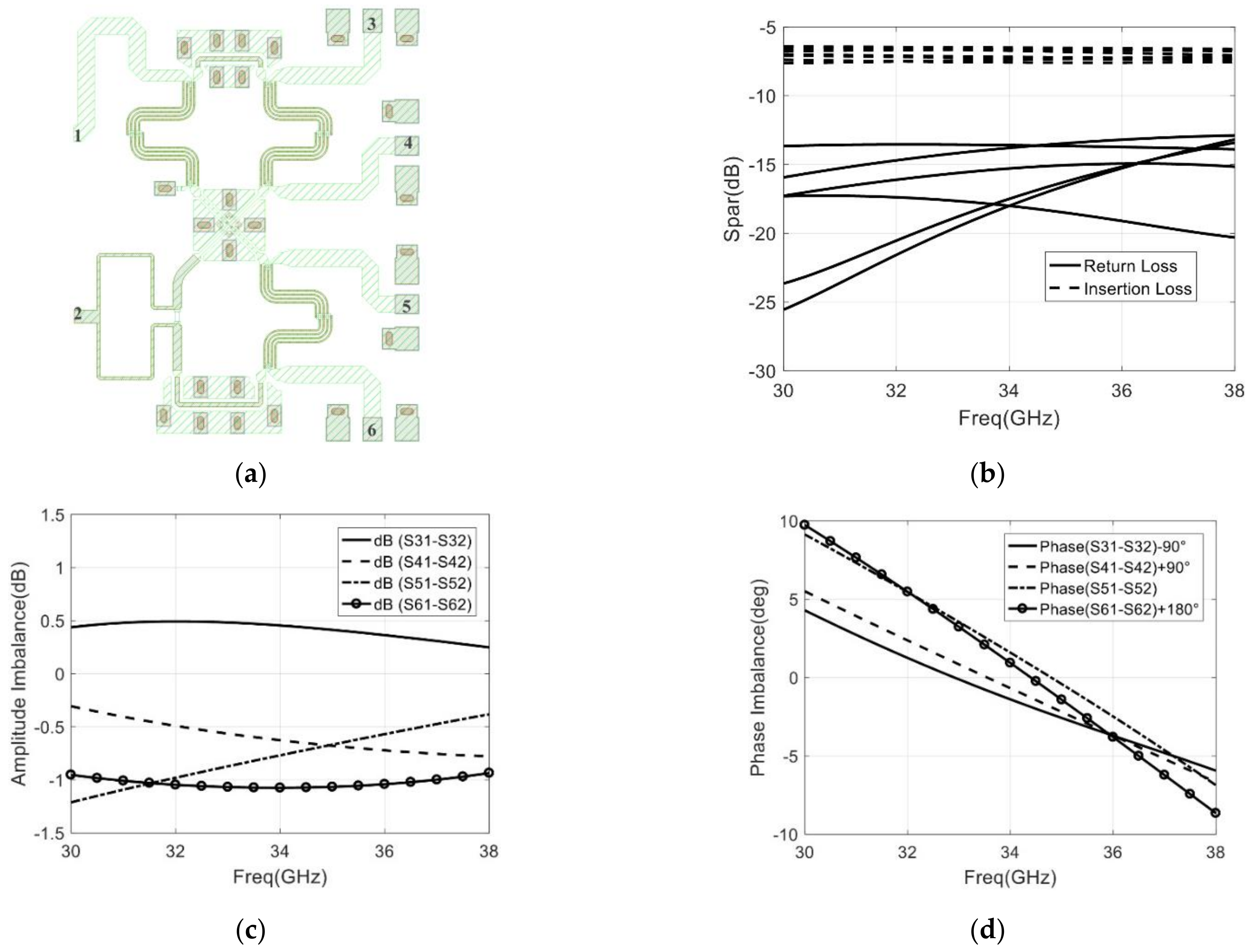
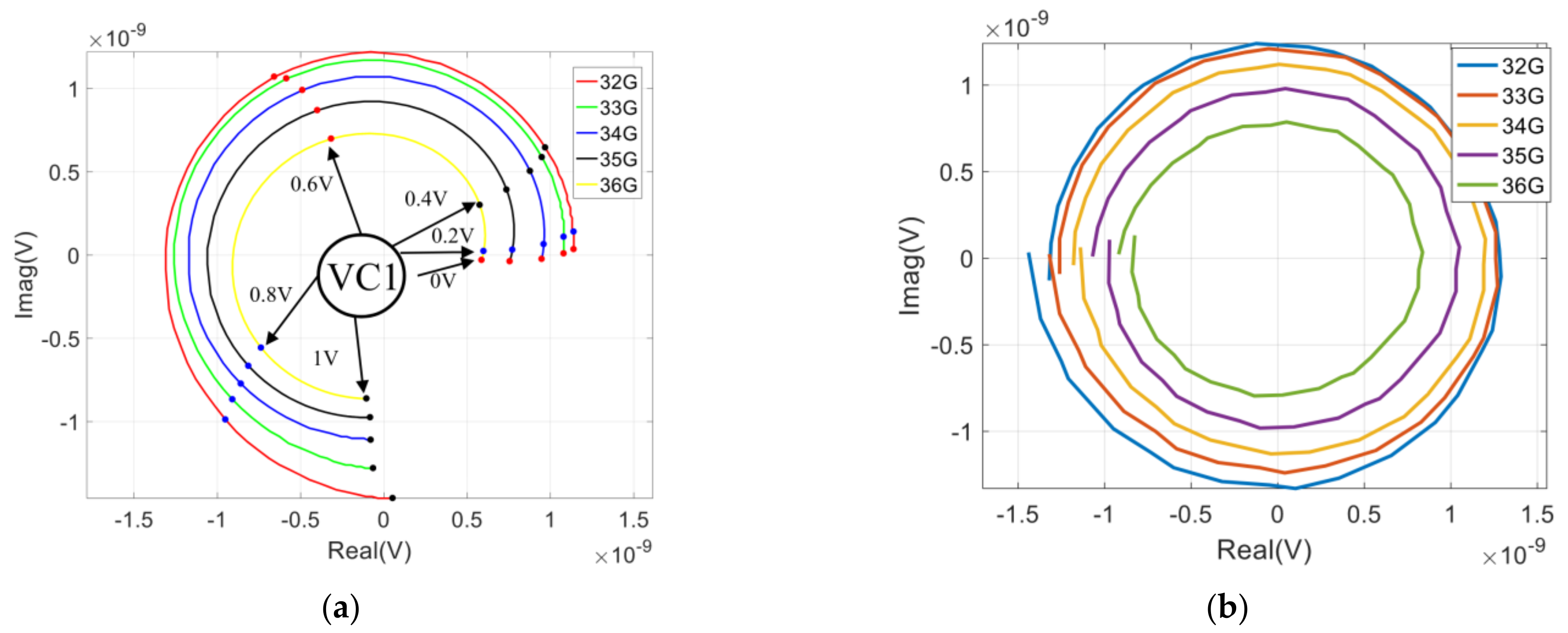
3.3. Design of the Six-Port Network
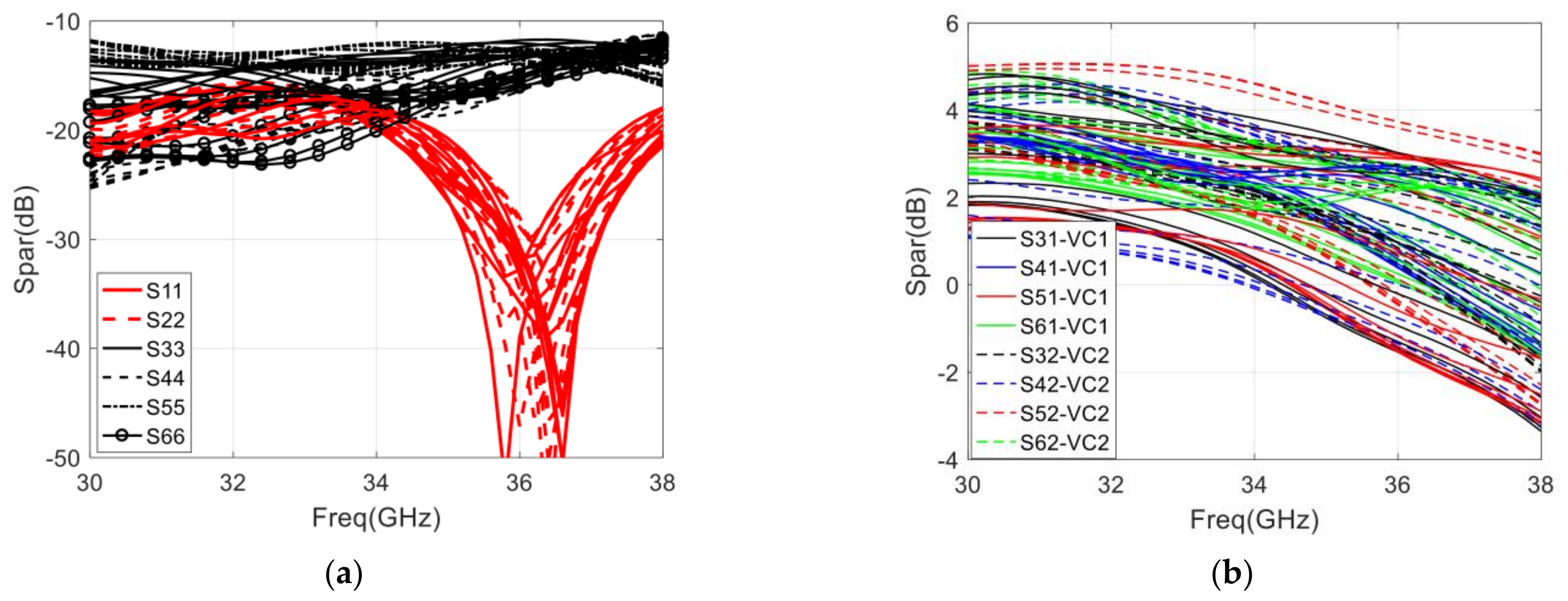
3.4. Simulation of the Integrated Six-Port Chip
4. Measurement of the Integrated Six-Port Chip
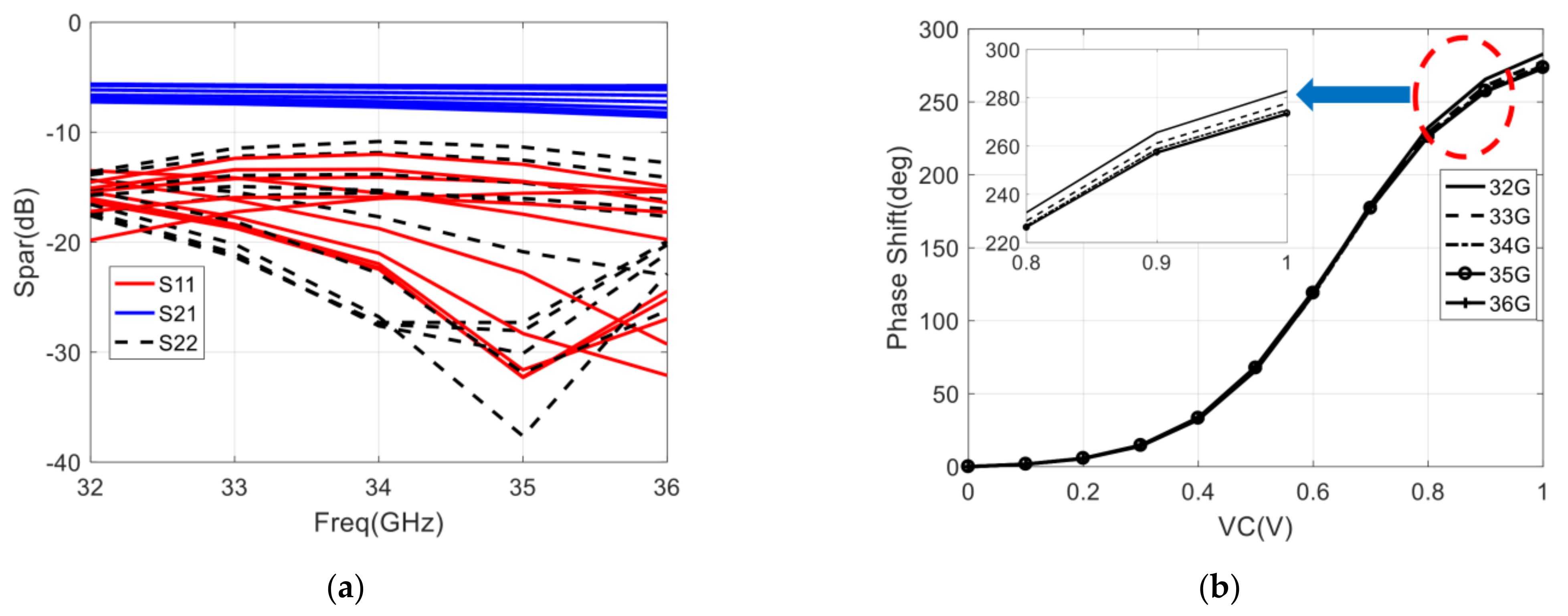
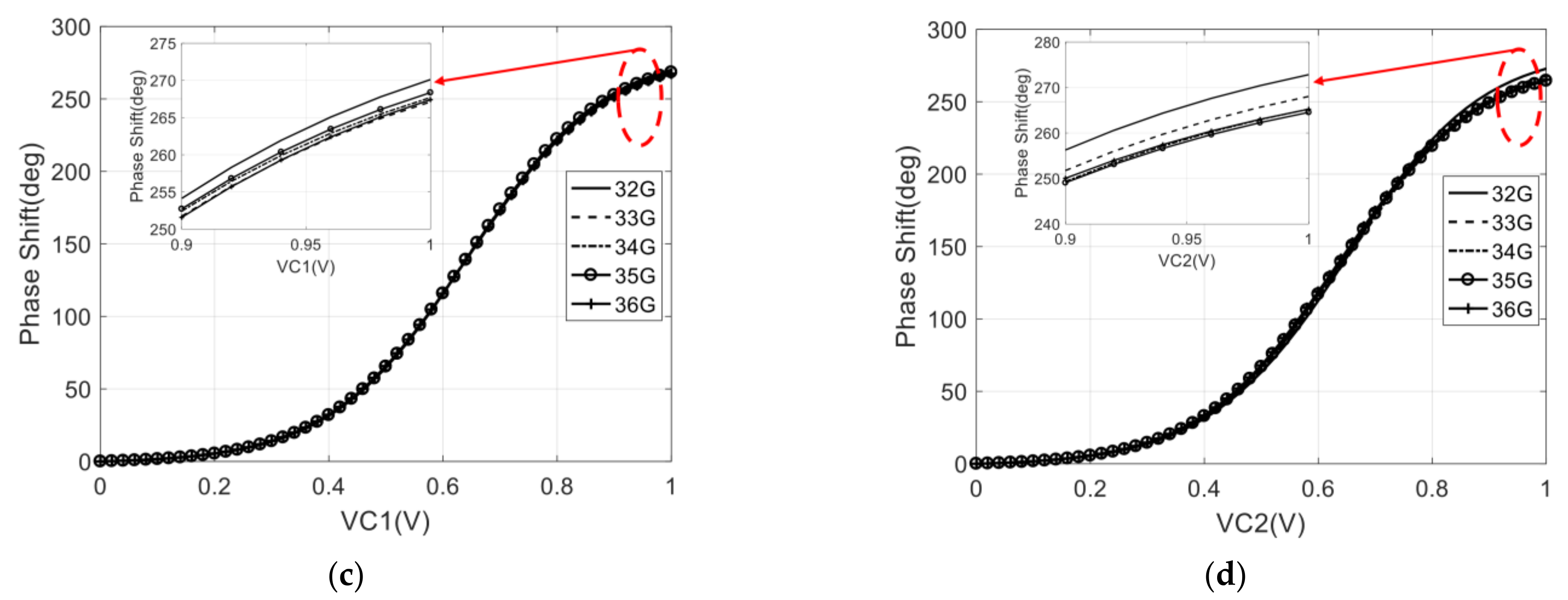
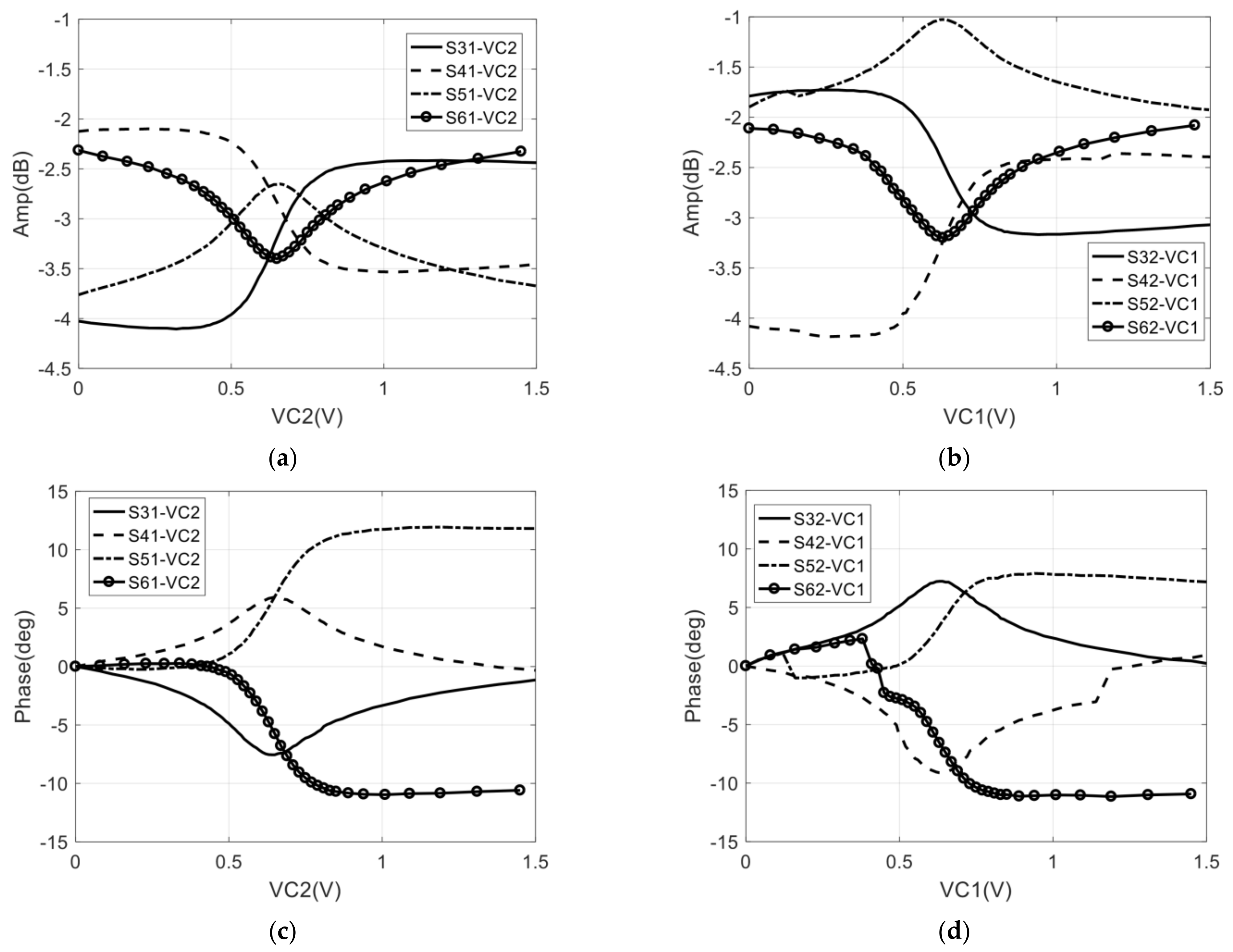
4.1. Measurement of the Return Loss, Gain, and Phase Shift Range
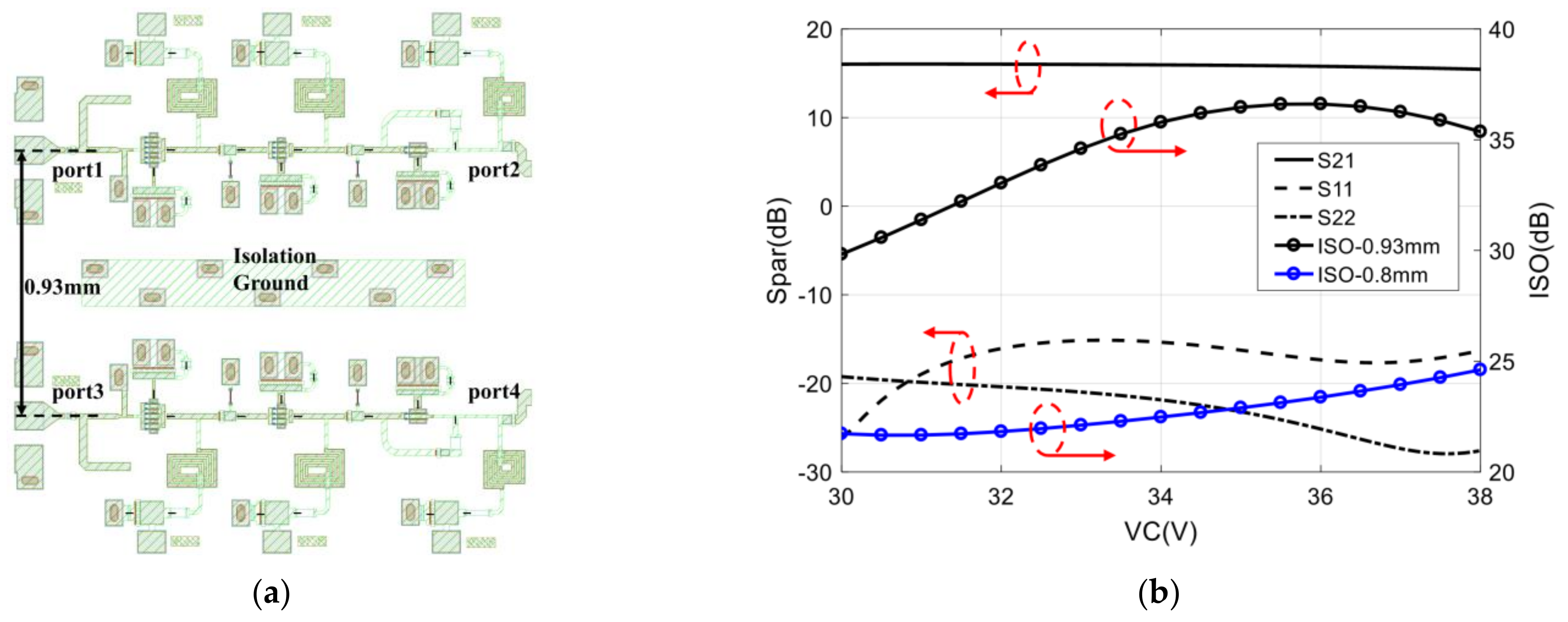
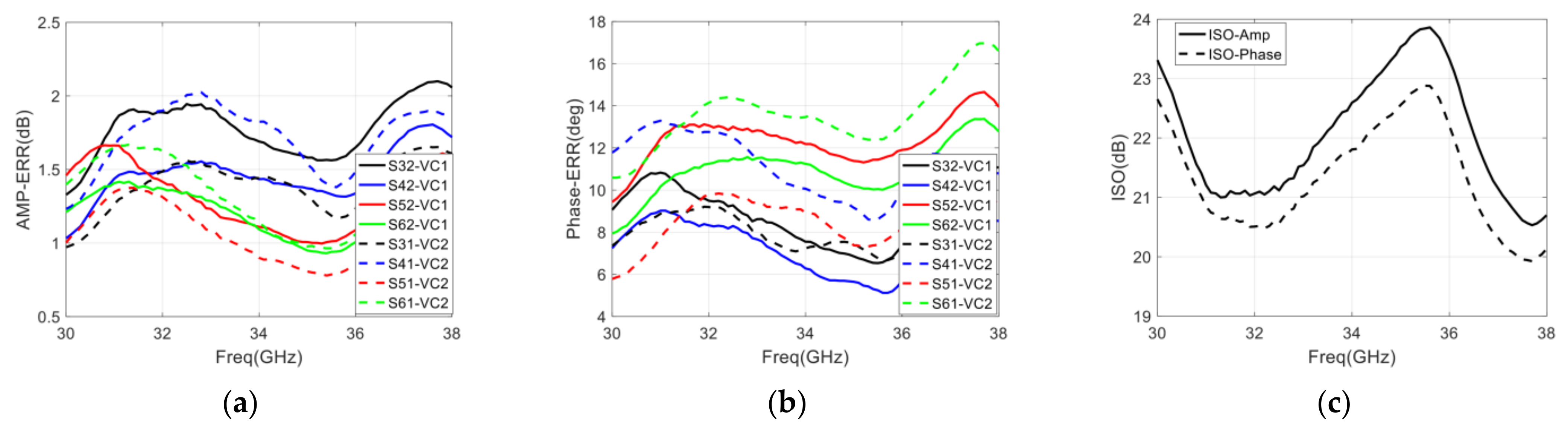
4.2. Measurement of the Isolation between Two Amplifiers
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Engen, G.F. The Six-Port Reflectometer: An Alternative Network Analyzer. IEEE Trans. Microw. Theory Tech. 1977, 25, 1075–1080. [Google Scholar] [CrossRef]
- Engen, G.F. An Overview of the Six-Port Measurement Technique. In Proceedings of the IEEE-MTT-S International Microwave Symposium Digest, Ottawa, ON, Canada, 27–29 June 1978; pp. 174–175. [Google Scholar]
- Hoer, C.A. The Six-Port Coupler: A New Approach to Measuring Voltage, Current, Power, Impedance, and Phase. IEEE Trans. Instrum. Meas. 1972, 21, 466–470. [Google Scholar] [CrossRef]
- Fadhel, G.; Abbas, M. The Six-Port Technique with Microwave and Wireless Applications; Artech: London, UK, 2009. [Google Scholar]
- Julrat, S.; Trabelsi, S. Portable Six-Port Reflectometer for Determining Moisture Content of Biomass Material. IEEE Sensors J. 2017, 17, 4814–4819. [Google Scholar] [CrossRef]
- Staszek, K.; Gruszczynski, S.; Wincza, K. Six-Port Reflectometer Providing Enhanced Power Distribution. IEEE Trans. Microw. Theory Tech. 2016, 64, 939–951. [Google Scholar] [CrossRef]
- Gutierrez Miguelez, C.; Huyart, B.; Bergeault, E.; Jallet, L.P. A new automobile radar based on the six-port phase/frequency discriminator. IEEE Trans. Veh. Technol. 2000, 49, 1416–1423. [Google Scholar] [CrossRef]
- Tatu, S.O.; Wu, K.; Denidni, T.A. Direction-of-arrival estimation method based on six-port technology. IEE Proc.-Microwaves, Antennas Propag. 2006, 153, 263–269. [Google Scholar] [CrossRef]
- Vinci, G.; Koelpin, A. Progress of Six-Port technology for industrial radar applications. In Proceedings of the 2016 IEEE Topical Conference on Wireless Sensors and Sensor Networks (WiSNet), Austin, TX, USA, 24–27 January 2016; pp. 48–51. [Google Scholar]
- Vinci, G.; Lindner, S.; Barbon, F.; Mann, S.; Hofmann, M.; Duda, A.; Weigel, R.; Koelpin, A. Six-Port Radar Sensor for Remote Respiration Rate and Heartbeat Vital-Sign Monitoring. IEEE Trans. Microw. Theory Tech. 2013, 61, 2093–2100. [Google Scholar] [CrossRef]
- Joy, E.; Leach, W.; Rodrigue, G. Applications of probe-compensated near-field measurements. IRE Trans. Antennas Propag. 1978, 26, 379–389. [Google Scholar] [CrossRef]
- Pereira, J.F.R.; Anderson, A.P.; Bennett, J.C. New procedure for near-field measurements of microwave antennas without anechoic environments. Microw. Opt. Antennas Iee Proc. H. 1984, 131, 351–358. [Google Scholar] [CrossRef]
- Yujiri, L.; Shoucri, M.; Moffa, P. Passive millimeter-wave imaging. IEEE Micro. 2003, 4, 39–50. [Google Scholar] [CrossRef] [Green Version]
- Ryman, E.; Emrich, A.; Andersson, S.B.; Svensson, L.; LarssonEdefors, P. 1.6 GHz Low-Power Cross-Correlator System Ena-bling Geostationary Earth Orbit Aperture Synthesis. IEEE J. Solid-State Circuits 2014, 49, 2720–2729. [Google Scholar] [CrossRef] [Green Version]
- Bell, J.; Knag, P.; Sun, S.; Lim, Y.; Chen, T.; Fredenburg, J.; Chen, C.-H.; Zhai, C.; Rocca, A.; Collins, N.; et al. A 1.5-GHz 6.144T Correlations/s 64 $\times $ 64 Cross-Correlator with 128 Integrated ADCs for Real-Time Synthetic Aperture Imaging. IEEE J. Solid-state Circuits 2017, 52, 1450–1457. [Google Scholar] [CrossRef]
- Li, C.-T.; Kubo, D.; Han, C.-C.; Chen, C.-C.; Chen, M.-T.; Lien, C.-H.; Wang, H.; Wei, R.-M.; Yang, C.-H.; Chiueh, T.-D.; et al. A wideband analog correlator system for AMiBA. Proc. SPIE. 2004, 5498, 455–464. [Google Scholar] [CrossRef]
- Padin, S. A wideband analog continuum correlator for radio astronomy. IEEE Trans. Instrum. Meas. 1994, 43, 782–785. [Google Scholar] [CrossRef]
- Li, C.-T.; Kubo, D.Y.; Wilson, W.; Lin, K.-Y.; Chen, M.-T.; Ho, P.; Chen, C.-C.; Han, C.-C.; Oshiro, P.; Martin-Cocher, P.; et al. AMIBA wideband analog correlator. Astrophys. J. Lett. 2010, 716, 746–757. [Google Scholar] [CrossRef] [Green Version]
- Shenoy, V.; Jung, S.; Yoon, Y.; Park, Y.; Kim, H.; Chung, H.-J. A CMOS Analog Correlator-Based Painless Nonenzymatic Glucose Sensor Readout Circuit. IEEE Sens. J. 2014, 14, 1591–1599. [Google Scholar] [CrossRef]
- Koistinen, O.; Lahtinen, J.; Hallikainen, M.T. Comparison of analog continuum correlators for remote sensing and radio as-tronomy. IEEE Trans. Instrum. Meas. 2002, 51, 227–234. [Google Scholar] [CrossRef]
- Javed, A.R.; Scheytt, J.C.; Ahe, U.V.D. Linear ultra-broadband NPN-only analog correlator at 33 Gbps in 130 nm SiGe BiCMOS technology. In Proceedings of the IEEE Bipolar/BiCMOS Circuits and Technology Meeting (BCTM), New Brunswick, NJ, USA, 25–27 September 2016; pp. 78–81. [Google Scholar]
- Wang, C.; Xin, X.; Kashif, M.; Miao, J. A Compact Analog Complex Cross-Correlator for Passive Millimeter-Wave Imager. IEEE Trans. Instrum. Meas. 2017, 66, 2997–3006. [Google Scholar] [CrossRef]
- Seong, J.-T.; Kim, S.-H.; Kim, Y.-H. Error analysis of an analog correlator for polarimetry. IEICE Electron. Express 2018, 15, 20171207. [Google Scholar] [CrossRef] [Green Version]
- Gilbert, B. A precise four-quadrant multiplier with subnanosecond response. IEEE J. Solid-State Circuits 1968, 3, 365–373. [Google Scholar] [CrossRef]
- Kashif, M.; Hu, A.; Miao, J. Design and Implementation of an Analog Complex Correlator for Passive Millimeter Wave Imaging System. In Proceedings of the 13th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 12–16 January 2016; pp. 611–616. [Google Scholar]
- Holler, C.M.; Kaneko, T.; Jones, M.E.; Grainge, K.; Scott, P. A 6–12 GHz analogue lag-correlator for radio interferometry. Astron. Astrophys. 2007, 464, 795–806. [Google Scholar] [CrossRef] [Green Version]
- Ryle, M. A New Radio Interferometer and Its Application to the Observation of Weak Radio Stars. Proc. R. Soc. London A Math. Phys. Eng. Sci. 1952, 211, 351–375. [Google Scholar] [CrossRef]
- Chen, C.; Mehdi, G.; Wang, C.; Dilshad, U.; Hu, A.; Miao, J. A GaAs Power Detector Design for $C$ -Band Wideband Complex Cross Correlation Measurement. IEEE Trans. Instrum. Meas. 2020, 69, 5673–5683. [Google Scholar] [CrossRef]
- Sakr, A.A.; Dyab, W.M.; Wu, K. A Dually Polarized Six-Port Junction Based on Polarization-Selective Coupling for Polarization-Inclusive Remote Sensing. IEEE Trans. Microw. Theory Tech. 2018, 66, 3817–3827. [Google Scholar] [CrossRef]
- Ardakani, M.D.; Tatu, S.O. V-Band Six-Port Interferometer Receiver: High Data-Rate Wireless Applications, BER and EVM Analysis, and CFO Compensation. IEEE Access 2021, 9, 160847–160854. [Google Scholar] [CrossRef]
- Moghaddasi, J.; Wu, K. Multifunction, Multiband, and Multimode Wireless Receivers: A Path toward the Future. IEEE Microw. Mag. 2020, 21, 104–125. [Google Scholar] [CrossRef]
- Hannachi, C.; Tatu, S.O. A new compact V-band six-port receiver for high data-rate wireless applications. In Proceedings of the IEEE Topical Conference on Wireless Sensors and Sensor Networks (WiSNet), San Diego, CA, USA, 25–28 January 2015; pp. 26–28. [Google Scholar]
- Zhang, H.; Li, L.; Wu, K. Software-Defined Six-Port Radar Technique for Precision Range Measurements. IEEE Sensors J. 2008, 8, 1745–1751. [Google Scholar] [CrossRef]
- Vinci, G.; Barbon, F.; Lindner, S.; Weigel, R.; Koelpin, A. Six-port based high-resolution smart antenna alignment sensor. In Proceedings of the IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications (APWC), Cape Town, South Africa, 2–7 September 2012; pp. 280–283. [Google Scholar]
- Arshad, N.S.A.; Ibrahim, S.Z.; Razalli, M.S. Six-port demodulator in homodyne direct conversion receiver. In Proceedings of the 2nd International Conference on Electronic Design (ICED), Penang, Malaysia, 19–21 August 2014; pp. 499–504. [Google Scholar]
- Talebzadeh, A.; Abdipour, A. Miniaturized six-port receiver for 60 GHz communication. In Proceedings of the 22nd Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 20–22 May 2014; pp. 1406–1410. [Google Scholar]
- Lan, M.; Wu, Y.; Huang, Z.; Liu, H.; Zhao, C.; Yu, Y.; Kang, K. An Improved Six-Port Equivalent-Circuit Model for Millimeter-Wave On-Chip Transformers with Accurate Coupling Factor Modeling. IEEE Trans. Microw. Theory Tech. 2021, 69, 3989–4000. [Google Scholar] [CrossRef]
- Wang, C.-H.; Chang, H.-Y.; Wu, P.S.; Lin, K.-Y.; Huang, T.-W.; Wang, H.; Chen, C.H. A 60 GHz Low-Power Six-Port Transceiver for Gigabit Software-Defined Transceiver Applications. In Proceedings of the IEEE International Solid-State Circuits Conference. Digest of Technical Papers, San Francisco, CA, USA, 11–15 February 2007; pp. 192–596. [Google Scholar]
- Laemmle, B.; Schmalz, K.; Borngraeber, J.; Scheytt, J.C.; Weigel, R.; Koelpin, A.; Kissinger, D. A fully integrated 120-GHz six-port receiver frontend in a 130-nm SiGe BiCMOS technology. In Proceedings of the IEEE 13th Topical Meeting on Silicon Monolithic Integrated Circuits in RF Systems, Austin, TX, USA, 21–23 January 2013; pp. 129–131. [Google Scholar]
- Voelkel, M.; Hirsch, H.; Dietz, M.; Weigel, R.; Hagelauer, A.; Kissinger, D. A Low-Power 120-GHz integrated six-port receiver front-end with digital adjustable gain in a 130-nm bicmos technology. In Proceedings of the IEEE Bipolar/BiCMOS Circuits and Technology Meeting (BCTM), Nuremberg, Germany, 8–10 October 2017; pp. 82–85. [Google Scholar]
- Vakalis, S.; Nanzer, J.A. Towards Three-Dimensional Active Incoherent Millimeter-Wave Imaging. In Proceedings of the IEEE International Conference on Autonomous Systems (ICAS), Montreal, QC, Canada, 11–13 August 2021; pp. 1–5. [Google Scholar]
- Vakalis, S.; Gong, L.; He, Y.; Papapolymerou, J.; Nanzer, J.A. Experimental Demonstration and Calibration of a 16-Element Active Incoherent Millimeter-Wave Imaging Array. IEEE Trans. Microw. Theory Tech. 2020, 68, 3804–3813. [Google Scholar] [CrossRef]
- Skou, N. Microwave Radiometer Systems: Design and Analysis; Artech House: Norwood, MA, USA, 1989. [Google Scholar]
- Guo, X.; Asif, M.; Hu, A.; Li, Z.; Miao, J. A 1-GHz 64-Channel Cross-Correlation System for Real-Time Interferometric Aperture Synthesis Imaging. Sensors 2019, 19, 1739. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Ye, X.; Chen, X.; Xin, X.; Liang, B.; Li, Z.; Hu, A.; Miao, J. A 3.5-8 GHz Analog Complex Cross-Correlator for Interferometric Passive Millimeter-Wave Security Imaging Systems. In Proceedings of the 2018 Progress in Electromagnetics Research Symposium (PIERS-Toyama), Toyama, Japan, 1–4 August 2018; pp. 692–699. [Google Scholar]
- Wang, C.; Xin, X.; Liang, B.; Li, Z.; Miao, J. Quadrature Errors and DC Offsets Calibration of Analog Complex Cross-Correlator for Interferometric Passive Millimeter-Wave Imaging Applications. Sensors 2018, 24, 677. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Hu, A.; Si, W.; Guo, X.; Miao, J. Calibration of Visibility Samples for Real-Time Passive Millimeter Wave Imaging. IEEE Access 2021, 9, 106441–106450. [Google Scholar] [CrossRef]
- Thompson, A.R.; D’Addario, L.R. Frequency response of a synthesis array: Performance limitations and design tolerances. Radio Sci. 1982, 17, 357–369. [Google Scholar] [CrossRef]
- Dilshad, U.; Chen, C.; Altaf, A.; Miao, J. An Ultra-Broadband K/Ka-Band (17-40 GHz) LNA MMIC in 0.15µm GaAs pHEMT. In Proceedings of the International Conference on Microwave and Millimeter Wave Technology (ICMMT), Guangzhou, China, 19–22 May 2019; pp. 1–3. [Google Scholar]
- Carneiro, M.L.; Le Roy, M.; PÃl’rennec, A.; Lababidi, R.; Ferrari, P.; Puyal, V. Compact Analog All-Pass Phase-Shifter in 65-nm CMOS for 24/28 GHz on-Chip- and in-Package Phased-Array Antenna. In Proceedings of the IEEE 23rd Workshop on Signal and Power Integrity (SPI), Chambéry, France, 18–21 June 2019; pp. 1–4. [Google Scholar]
- Medina-Rull, A.; Pasadas, F.; Marin, E.G.; Toral-Lopez, A.; Cuesta, J.; Godoy, A.; Jimenez, D.; Ruiz, F.G. A Graphene Field-Effect Transistor Based Analogue Phase Shifter for High-Frequency Applications. IEEE Access 2020, 8, 209055–209063. [Google Scholar] [CrossRef]
- Wu, P.-S.; Chang, H.-Y.; Tsai, M.-D.; Huang, T.-W.; Wang, H. New miniature 15–20-GHz continuous-phase/amplitude control MMICs using 0.18-μm CMOS technology. IEEE Trans. Microw. Theory Tech. 2006, 54, 10–19. [Google Scholar]
- Ellinger, F.; Jackel, H.; Bachtold, W. Varactor-loaded transmission-line phase shifter at C -band using lumped elements. IEEE Trans. Microw. Theory Tech. 2003, 51, 1135–1140. [Google Scholar] [CrossRef]
- Wu, J.-C.; Kao, J.-C.; Kuo, J.-J.; Kao, K.-Y.; Lin, K.-Y. A 60-GHz single-ended-to-differential vector sum phase shifter in CMOS for phased-array receiver. In Proceedings of the 2011 IEEE MTT-S International Microwave Symposium, Baltimore, MD, USA, 5–10 June 2011; pp. 1–4. [Google Scholar]
- Akbar, F.; Mortazawi, A. A New Integrated K-Band Analog Vector Sum Phase Shifter. In Proceedings of the IEEE/MTT-S International Microwave Symposium—IMS, Philadelphia, PA, USA, 10–15 June 2018; pp. 1441–1444. [Google Scholar]






| Parameter | Simulation | Measurement |
|---|---|---|
| Control voltage (V) | 0–1 | 0–1.5 |
| Phase shift range (deg) | ≥265 | ≥222 |
| Phase shift range error (deg) | ≤10 | ≤10 |
| Isolation between two amplifiers (dB) | ≥30 | ≥20 |
| Reference | This Work | [29] | [32] |
|---|---|---|---|
| Process | 0.15-µm GaAs | Waveguide | 130 nm COMS |
| Freq (GHz) | 32–36 | 15–20 | 60–65 |
| Amplitude Imbalance (dB) | −2 ± 2.5 * | −6 ± 2.2 | −6 ± 1 |
| Phase Imbalance (deg) | ±5 * | ±15 | ±5 |
| Return Loss (dB) | <−11 # | <−12 | <−12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, W.; Chen, X.; Gong, J.; Hu, A.; Miao, J. A Ka-Band Integrated Six-Port Chip for Analog Complex Correlator. Sensors 2022, 22, 4877. https://doi.org/10.3390/s22134877
He W, Chen X, Gong J, Hu A, Miao J. A Ka-Band Integrated Six-Port Chip for Analog Complex Correlator. Sensors. 2022; 22(13):4877. https://doi.org/10.3390/s22134877
Chicago/Turabian StyleHe, Wangdong, Xi Chen, Jianhao Gong, Anyong Hu, and Jungang Miao. 2022. "A Ka-Band Integrated Six-Port Chip for Analog Complex Correlator" Sensors 22, no. 13: 4877. https://doi.org/10.3390/s22134877
APA StyleHe, W., Chen, X., Gong, J., Hu, A., & Miao, J. (2022). A Ka-Band Integrated Six-Port Chip for Analog Complex Correlator. Sensors, 22(13), 4877. https://doi.org/10.3390/s22134877






