An Improved Mixture Density Network for 3D Human Pose Estimation with Ordinal Ranking
Abstract
:1. Introduction
- (1)
- We propose an LCN-based human pose estimation network that learns a Gaussian mixture model matching the distribution of human joints to output multiple hypotheses.
- (2)
- LCN is applied to a 3D human pose estimation task with multiple pose outputs, which improves the accuracy of the estimation task by learning the structural relationships of human joints.
- (3)
- A 3D pose selector is design to select the best predicted 3D human pose. In the selector, an ordinal matrix containing joints relationship is learned from the input RGB images via an hourglass network.
- (4)
- Our network achieves comparable or better results than the state-of-the-art in terms of accuracy and visualization with better robustness, and experimental results on the MPII human dataset validate the generalization ability of our method.
2. Related Work
2.1. Graph Convolutional Networks
2.2. 3D Pose Estimation
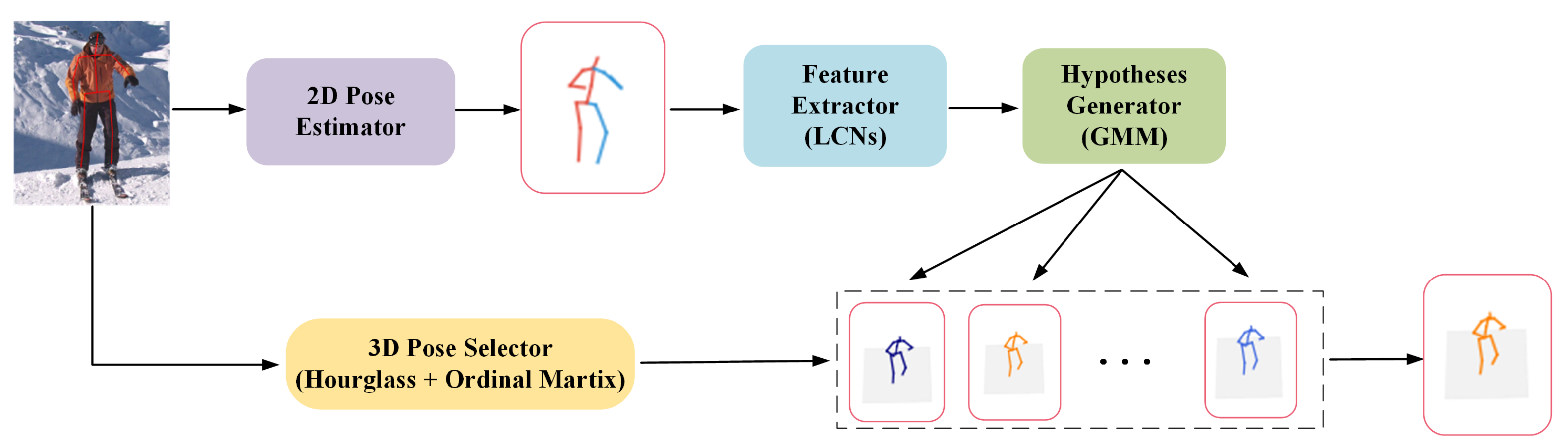
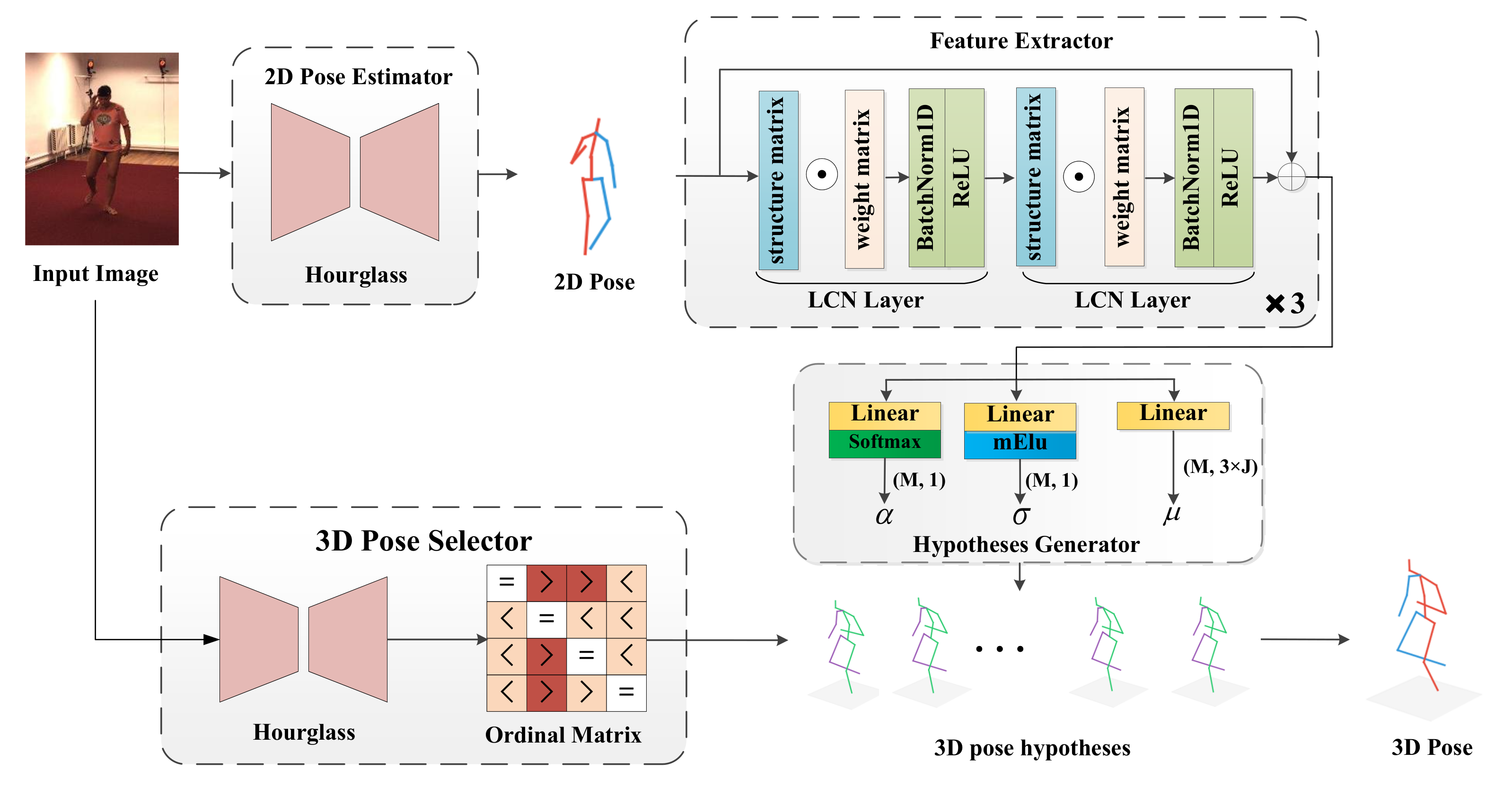
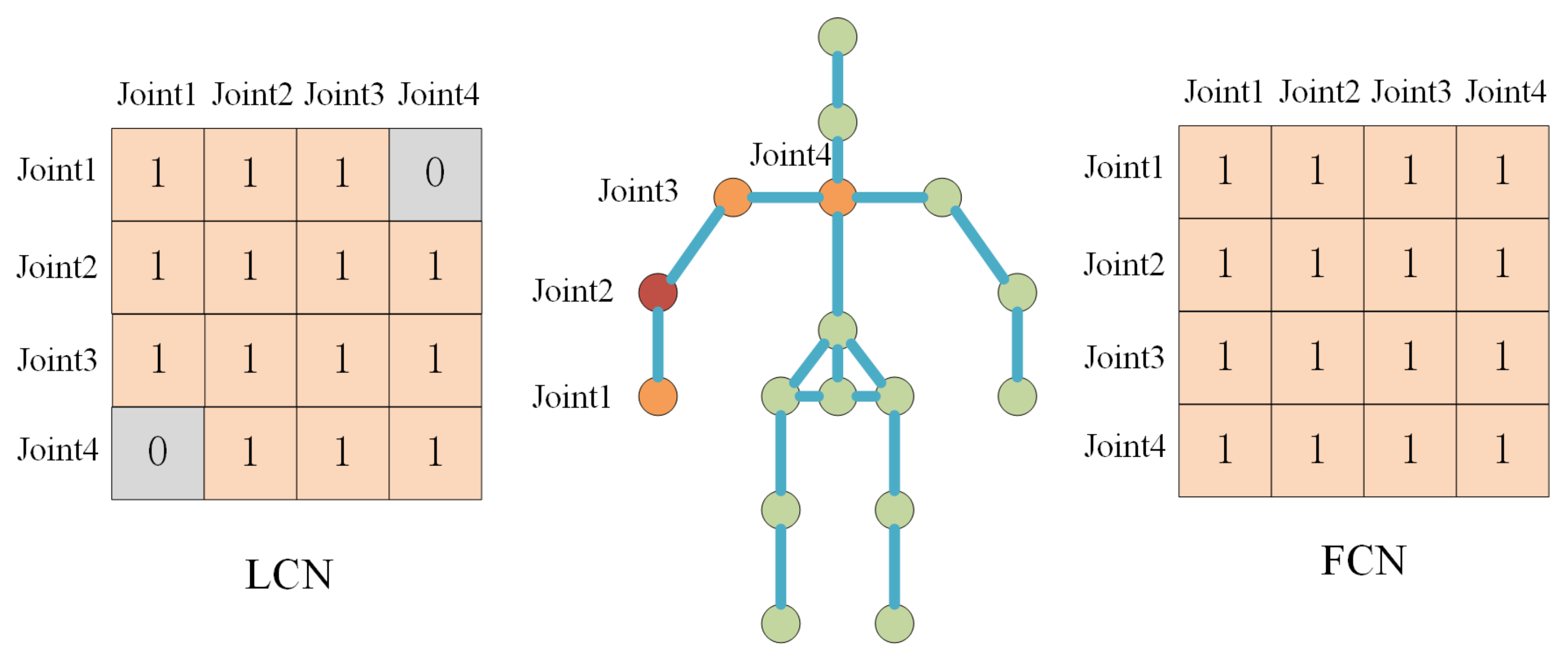
3. Locally Connected Mixture Density Network
3.1. Model Representation
3.2. Two-Dimensional (2D) Pose Estimator and Feature Extractor
3.3. Hypotheses Generator
3.4. 3D Pose Selector
4. Experiments
4.1. Training Details and Developing Environment
4.2. Dataset and Metric
4.3. Results on Human3.6M Dataset
4.4. Ablation Study
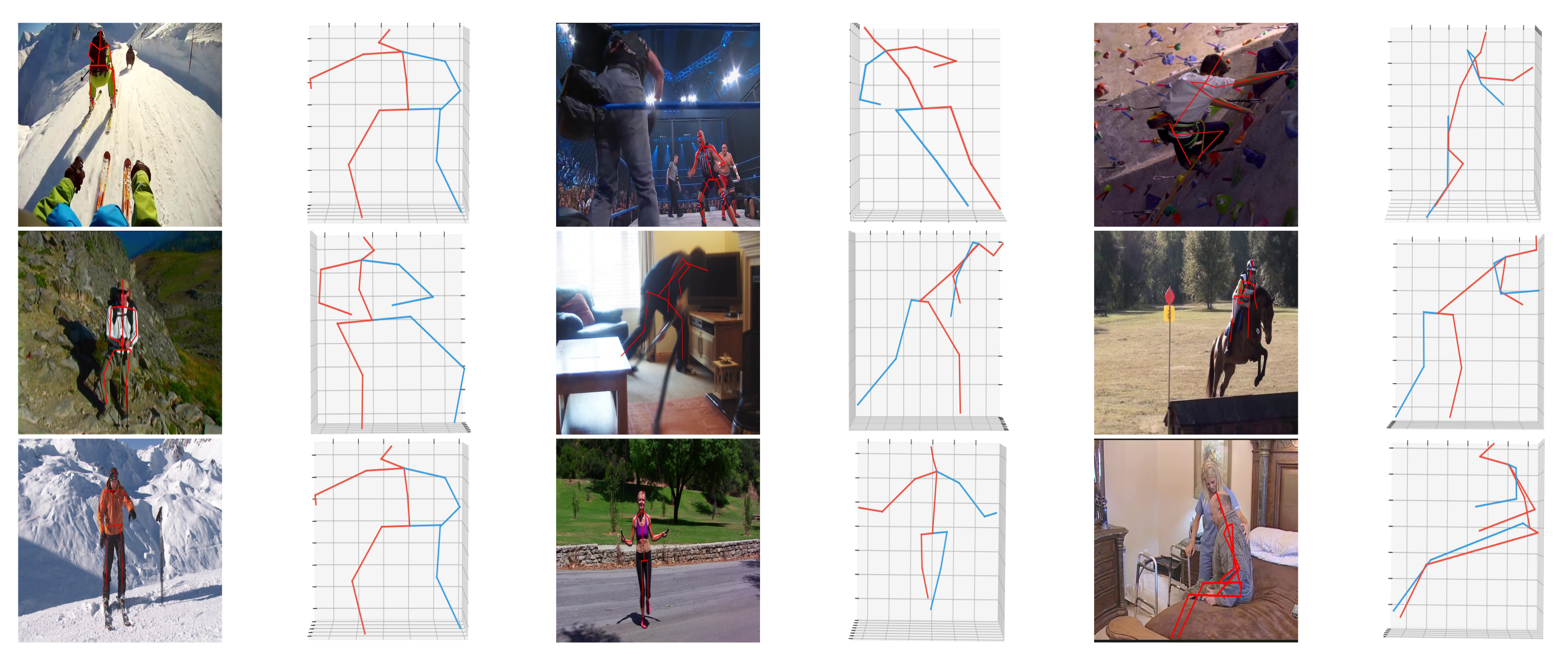
4.5. Three-Dimensional (3D) Human Pose Estimation on MPII Dataset
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Newell, A.; Yang, K.; Deng, J. Stacked hourglass networks for human pose estimation. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 483–499. [Google Scholar]
- Akhter, I.; Black, M.J. Pose-conditioned joint angle limits for 3D human pose reconstruction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1446–1455. [Google Scholar]
- Zhou, X.; Zhu, M.; Leonardos, S.; Derpanis, K.G.; Daniilidis, K. Sparseness meets deepness: 3D human pose estimation from monocular video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4966–4975. [Google Scholar]
- Bogo, F.; Kanazawa, A.; Lassner, C.; Gehler, P.; Romero, J.; Black, M.J. Keep it SMPL: Automatic estimation of 3D human pose and shape from a single image. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 561–578. [Google Scholar]
- Martinez, J.; Hossain, R.; Romero, J.; Little, J.J. A simple yet effective baseline for 3D human pose estimation. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2640–2649. [Google Scholar]
- Rayat Imtiaz Hossain, M.; Little, J.J. Exploiting temporal information for 3D human pose estimation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 4–8 September 2018; pp. 68–84. [Google Scholar]
- Chen, W.; Wang, H.; Li, Y.; Su, H.; Wang, Z.; Tu, C.; Lischinski, D.; Cohen-Or, D.; Chen, B. Synthesizing training images for boosting human 3D pose estimation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 479–488. [Google Scholar]
- Yasin, H.; Iqbal, U.; Kruger, B.; Weber, A.; Gall, J. A dual-source approach for 3D pose estimation from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4948–4956. [Google Scholar]
- Moreno-Noguer, F. 3D human pose estimation from a single image via distance matrix regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2823–2832. [Google Scholar]
- Zhou, X.; Huang, Q.; Sun, X.; Xue, X.; Wei, Y. Towards 3D human pose estimation in the wild: A weakly-supervised approach. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 398–407. [Google Scholar]
- Jahangiri, E.; Yuille, A.L. Generating multiple diverse hypotheses for human 3D pose consistent with 2d joint detections. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 805–814. [Google Scholar]
- Li, C.; Lee, G.H. Generating multiple hypotheses for 3D human pose estimation with mixture density network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9887–9895. [Google Scholar]
- Bishop, C.M. Mixture Density Networks; Aston University: Birmingham, UK, 1994. [Google Scholar]
- Ci, H.; Wang, C.; Ma, X.; Wang, Y. Optimizing Network Structure for 3D Human Pose Estimation. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 2262–2271. [Google Scholar]
- Ci, H.; Ma, X.; Wang, C.; Wang, Y. Locally connected network for monocular 3D human pose estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 1429–1442. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Gupta, A. Videos as space-time region graphs. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 399–417. [Google Scholar]
- Yan, S.; Xiong, Y.; Lin, D. Spatial temporal graph convolutional networks for skeleton-based action recognition. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LO, USA, 2–7 February 2018. [Google Scholar]
- Yang, J.; Lu, J.; Lee, S.; Batra, D.; Parikh, D. Graph r-cnn for scene graph generation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 670–685. [Google Scholar]
- Yao, T.; Pan, Y.; Li, Y.; Mei, T. Exploring visual relationship for image captioning. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 684–699. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Niepert, M.; Ahmed, M.; Kutzkov, K. Learning convolutional neural networks for graphs. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 2014–2023. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Zhao, L.; Peng, X.; Tian, Y.; Kapadia, M.; Metaxas, D.N. Semantic graph convolutional networks for 3D human pose regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3425–3435. [Google Scholar]
- Hammond, D.K.; Vandergheynst, P.; Gribonval, R. Wavelets on graphs via spectral graph theory. Appl. Comput. Harmon. Anal. 2011, 30, 129–150. [Google Scholar] [CrossRef] [Green Version]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 3844–3852. [Google Scholar]
- Pavlakos, G.; Zhou, X.; Derpanis, K.G.; Daniilidis, K. Coarse-to-fine volumetric prediction for single-image 3D human pose. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7025–7034. [Google Scholar]
- Mehta, D.; Rhodin, H.; Casas, D.; Fua, P.; Sotnychenko, O.; Xu, W.; Theobalt, C. Monocular 3D human pose estimation in the wild using improved cnn supervision. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 506–516. [Google Scholar]
- Zhou, X.; Sun, X.; Zhang, W.; Liang, S.; Wei, Y. Deep kinematic pose regression. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 186–201. [Google Scholar]
- Park, S.; Hwang, J.; Kwak, N. 3D human pose estimation using convolutional neural networks with 2d pose information. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 156–169. [Google Scholar]
- Yang, W.; Ouyang, W.; Wang, X.; Ren, J.; Li, H.; Wang, X. 3D human pose estimation in the wild by adversarial learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5255–5264. [Google Scholar]
- Lee, K.; Lee, I.; Lee, S. Propagating lstm: 3D pose estimation based on joint interdependency. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 119–135. [Google Scholar]
- Sun, X.; Xiao, B.; Wei, F.; Liang, S.; Wei, Y. Integral human pose regression. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 529–545. [Google Scholar]
- Wei, S.E.; Ramakrishna, V.; Kanade, T.; Sheikh, Y. Convolutional pose machines. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4724–4732. [Google Scholar]
- Zou, L.; Huang, Z.; Gu, N.; Wang, F.; Yang, Z.; Wang, G. GMDN: A lightweight graph-based mixture density network for 3D human pose regression. Comput. Graph. 2021, 95, 115–122. [Google Scholar] [CrossRef]
- Guillaumes, A.B. Mixture Density Networks for Distribution and Uncertainty Estimation. Ph.D. Thesis, Universitat Politècnica de Catalunya, Facultat d’Informàtica de Barcelona, Barcelona, Spain, 2017. [Google Scholar]
- Sharma, S.; Varigonda, P.T.; Bindal, P.; Sharma, A.; Jain, A. Monocular 3D human pose estimation by generation and ordinal ranking. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 2325–2334. [Google Scholar]
- Ronchi, M.R.; Mac Aodha, O.; Eng, R.; Perona, P. It’s all relative: Monocular 3D human pose estimation from weakly supervised data. arXiv 2018, arXiv:1805.06880. [Google Scholar]
- Pons-Moll, G.; Fleet, D.J.; Rosenhahn, B. Posebits for monocular human pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2337–2344. [Google Scholar]
- Pavlakos, G.; Zhou, X.; Daniilidis, K. Ordinal depth supervision for 3D human pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7307–7316. [Google Scholar]
- Ionescu, C.; Papava, D.; Olaru, V.; Sminchisescu, C. Human3. 6m: Large scale datasets and predictive methods for 3D human sensing in natural environments. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 1325–1339. [Google Scholar] [CrossRef] [PubMed]
- Andriluka, M.; Pishchulin, L.; Gehler, P.; Schiele, B. 2d human pose estimation: New benchmark and state of the art analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3686–3693. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Du, Y.; Wong, Y.; Liu, Y.; Han, F.; Gui, Y.; Wang, Z.; Kankanhalli, M.; Geng, W. Marker-less 3D human motion capture with monocular image sequence and height-maps. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 20–36. [Google Scholar]
- Zhang, D.; He, L.; Luo, M.; Xu, Z.; He, F. Weight asynchronous update: Improving the diversity of filters in a deep convolutional network. Comput. Vis. Media 2020, 6, 455–466. [Google Scholar] [CrossRef]
- Cao, Z.; Simon, T.; Wei, S.E.; Sheikh, Y. Realtime multi-person 2d pose estimation using part affinity fields. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7291–7299. [Google Scholar]
- Zhang, D.; Zhang, Z.; Zou, L.; Xie, Z.; He, F.; Wu, Y.; Tu, Z. Part-based visual tracking with spatially regularized correlation filters. Vis. Comput. 2020, 36, 509–527. [Google Scholar] [CrossRef]
- Zhang, D.; Wu, Y.; Guo, M.; Chen, Y. Deep Learning Methods for 3D Human Pose Estimation under Different Supervision Paradigms: A Survey. Electronics 2021, 10, 2267. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, S.; Zhang, D.; Sun, J. 3D Capsule Hand Pose Estimation Network Based on Structural Relationship Information. Symmetry 2020, 12, 1636. [Google Scholar] [CrossRef]

| Method | Direct. | Discuss. | Eating | Greet | Phone | Photo | Pose | Purch. | Sitting | SittingD. | Smoke | Wait | WalkD. | Walk | WalkT. | Avg. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lin et al. [40] | 132.7 | 183.6 | 132.3 | 164.4 | 162.1 | 205.9 | 150.6 | 171.3 | 151.6 | 243.0 | 162.1 | 170.7 | 177.1 | 96.6 | 127.9 | 162.1 |
| Du et al. [44] | 85.1 | 112.7 | 104.9 | 122.1 | 139.1 | 135.9 | 105.9 | 166.2 | 117.5 | 226.9 | 120.0 | 117.7 | 137.4 | 99.3 | 106.5 | 126.5 |
| Zhou et al. [28] | 87.4 | 109.3 | 87.1 | 103.2 | 116.2 | 143.3 | 106.9 | 99.8 | 124.5 | 199.2 | 107.4 | 118.1 | 114.2 | 79.4 | 97.7 | 113.0 |
| Pavlakos et al. [26] | 67.4 | 71.9 | 66.7 | 69.1 | 72.0 | 77.0 | 65.0 | 68.3 | 83.7 | 96.5 | 71.7 | 65.8 | 74.9 | 59.1 | 63.2 | 71.9 |
| Jahangiri et al. [11] | 63.1 | 55.9 | 58.1 | 64.5 | 68.7 | 61.3 | 55.6 | 86.1 | 117.6 | 71.0 | 71.2 | 66.3 | 57.1 | 62.5 | 61.0 | 68.0 |
| Zhou et al. [10] | 54.8 | 60.7 | 58.2 | 71.4 | 62.0 | 65.5 | 53.8 | 55.6 | 75.2 | 111.6 | 64.1 | 66.0 | 51.4 | 63.2 | 55.3 | 64.9 |
| Martinez et al. [5] | 51.8 | 56.2 | 58.1 | 59.0 | 69.5 | 78.4 | 55.2 | 58.1 | 74.0 | 94.6 | 62.3 | 59.1 | 65.1 | 49.5 | 52.4 | 62.9 |
| Lee et al. [31] | 43.8 | 51.7 | 48.8 | 53.1 | 52.2 | 74.9 | 52.7 | 44.6 | 56.9 | 74.3 | 56.7 | 66.4 | 47.5 | 68.4 | 45.6 | 55.8 |
| Li et al. [12] | 43.8 | 48.6 | 49.1 | 49.8 | 57.6 | 61.5 | 45.9 | 48.3 | 62.0 | 73.4 | 54.8 | 50.6 | 56.0 | 43.4 | 45.5 | 52.7 |
| Ci et al. [14] | 46.8 | 52.3 | 44.7 | 50.4 | 52.9 | 68.9 | 49.6 | 46.4 | 60.2 | 78.9 | 51.2 | 50.0 | 54.8 | 40.4 | 43.3 | 52.7 |
| LCMDN | 42.0 | 47.1 | 44.5 | 48.2 | 54.5 | 58.1 | 44.0 | 45.8 | 57.9 | 71.4 | 52.0 | 48.7 | 52.7 | 41.3 | 42.3 | 50.0 |
| Method | Direct. | Discuss. | Eating | Greet | Phone | Photo | Pose | Purch. | Sitting | SittingD. | Smoke | Wait | WalkD. | Walk | WalkT. | Avg. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jahangiri et al. [11] | 108.6 | 105.9 | 105.6 | 109.0 | 105.5 | 109.9 | 102.0 | 111.3 | 119.6 | 107.8 | 107.1 | 111.3 | 108.4 | 107.0 | 110.3 | 108.6 |
| Martinez et al. [5] | 57.4 | 64.6 | 64.3 | 65.6 | 73.3 | 85.5 | 61.0 | 62.1 | 84.0 | 101.1 | 68.2 | 66.7 | 70.8 | 55.6 | 59.6 | 69.1 |
| Li et al. [12] | 48.9 | 53.9 | 54.5 | 55.5 | 62.6 | 70.4 | 51.3 | 52.0 | 69.7 | 83.9 | 60.7 | 57.2 | 62.4 | 48.3 | 50.8 | 58.8 |
| LCMDN | 46.4 | 50.9 | 50.8 | 51.9 | 58.2 | 64.6 | 47.7 | 48.7 | 64.2 | 77.6 | 56.8 | 53.6 | 57.7 | 45.0 | 46.4 | 54.7 |
| Jahangiri et al. [11] | 125.0 | 121.8 | 115.1 | 124.1 | 116.9 | 123.8 | 116.4 | 119.6 | 130.8 | 120.6 | 118.4 | 127.1 | 125.9 | 121.6 | 127.6 | 122.3 |
| Martinez et al. [5] | 62.9 | 66.9 | 69.9 | 71.4 | 80.2 | 93.8 | 66.3 | 65.9 | 90.6 | 109.7 | 74.2 | 72.1 | 75.5 | 61.7 | 65.7 | 75.1 |
| Li et al. [12] | 54.0 | 58.5 | 60.6 | 61.4 | 68.6 | 77.9 | 56.6 | 57.0 | 77.8 | 92.4 | 66.2 | 62.6 | 67.5 | 52.5 | 55.0 | 64.6 |
| LCMDN | 50.3 | 54.8 | 55.3 | 56.8 | 62.9 | 71.4 | 52.5 | 52.4 | 69.6 | 83.6 | 60.7 | 58.2 | 61.9 | 48.8 | 51.6 | 59.4 |
| Method | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| LCN [14] | 58.77 | 57.73 | 57.56 | 58.37 |
| LCMDN | 51.28 | 50.02 | 50.42 | 50.45 |
| Method | 1 | 3 | 5 | 8 |
|---|---|---|---|---|
| Li et al. [12] | 62.9 | 55.2 | 52.7 | 52.6 |
| LCMDN | 58.8 | 52.4 | 50.0 | 49.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Ma, S.; Zhang, D.; Huang, W.; Chen, Y. An Improved Mixture Density Network for 3D Human Pose Estimation with Ordinal Ranking. Sensors 2022, 22, 4987. https://doi.org/10.3390/s22134987
Wu Y, Ma S, Zhang D, Huang W, Chen Y. An Improved Mixture Density Network for 3D Human Pose Estimation with Ordinal Ranking. Sensors. 2022; 22(13):4987. https://doi.org/10.3390/s22134987
Chicago/Turabian StyleWu, Yiqi, Shichao Ma, Dejun Zhang, Weilun Huang, and Yilin Chen. 2022. "An Improved Mixture Density Network for 3D Human Pose Estimation with Ordinal Ranking" Sensors 22, no. 13: 4987. https://doi.org/10.3390/s22134987
APA StyleWu, Y., Ma, S., Zhang, D., Huang, W., & Chen, Y. (2022). An Improved Mixture Density Network for 3D Human Pose Estimation with Ordinal Ranking. Sensors, 22(13), 4987. https://doi.org/10.3390/s22134987









