Dual-Band Branch-Line Coupler Based on Crossed Lines for Arbitrary Power-Split Ratios
Abstract
:1. Introduction
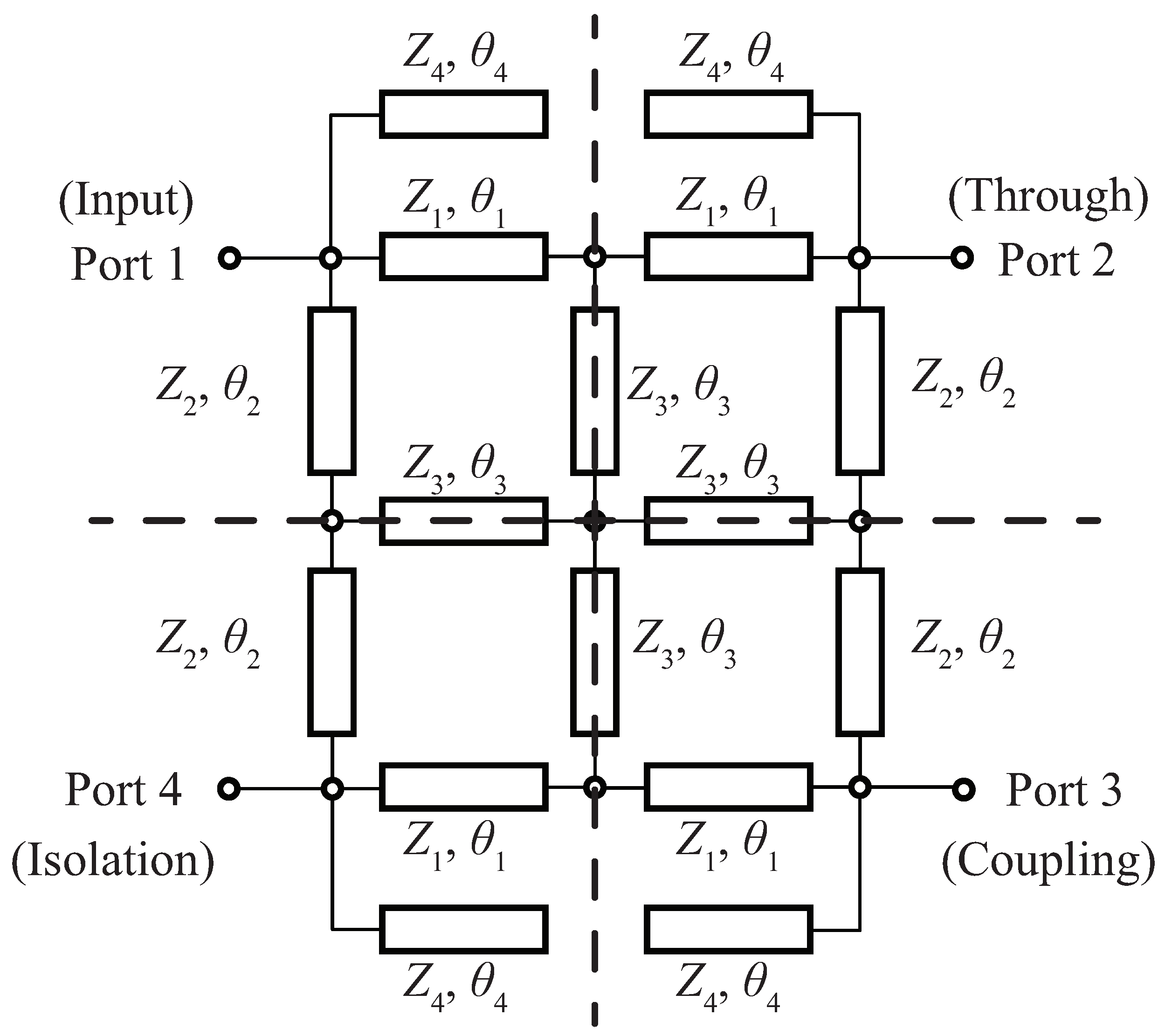
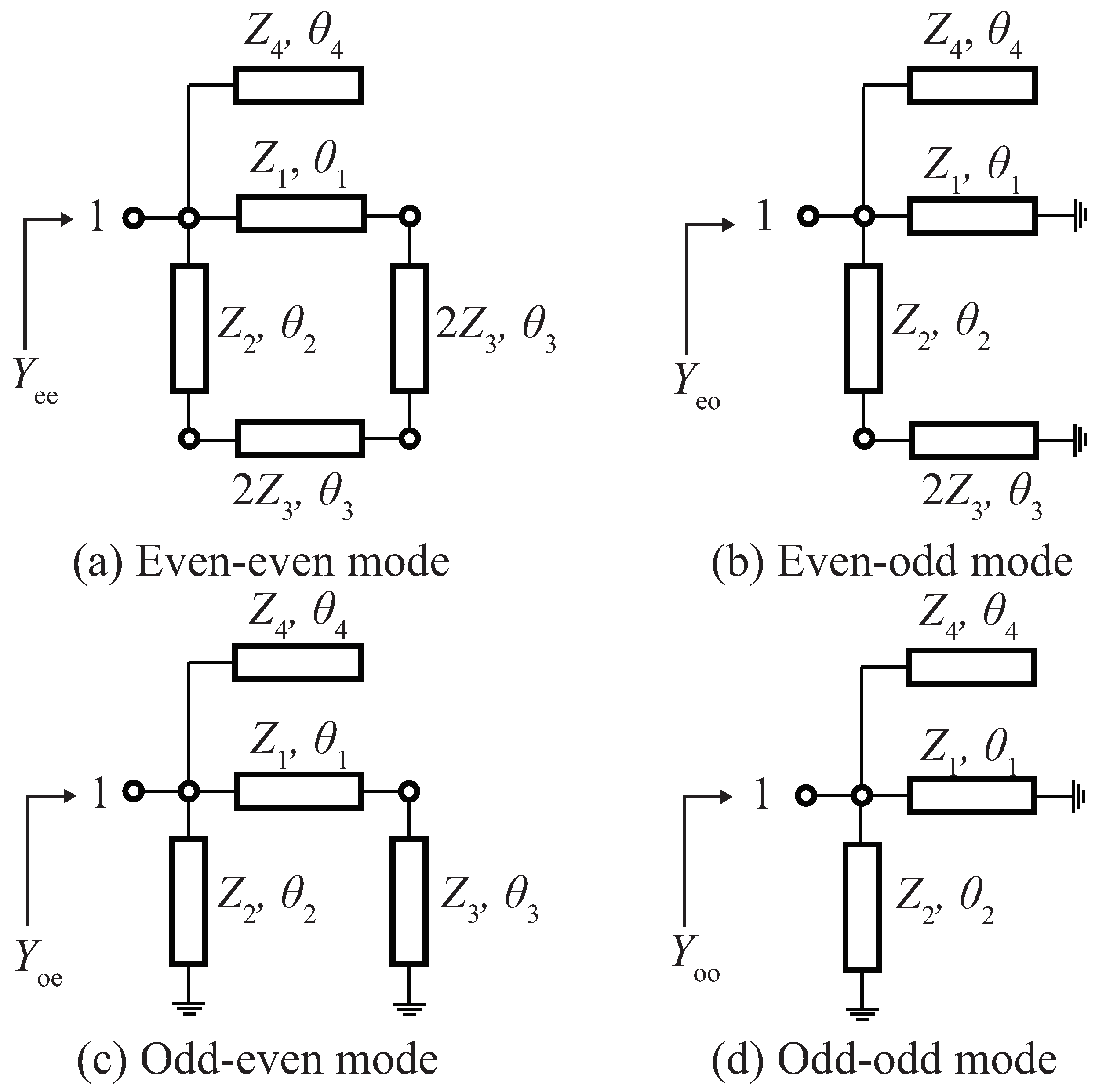
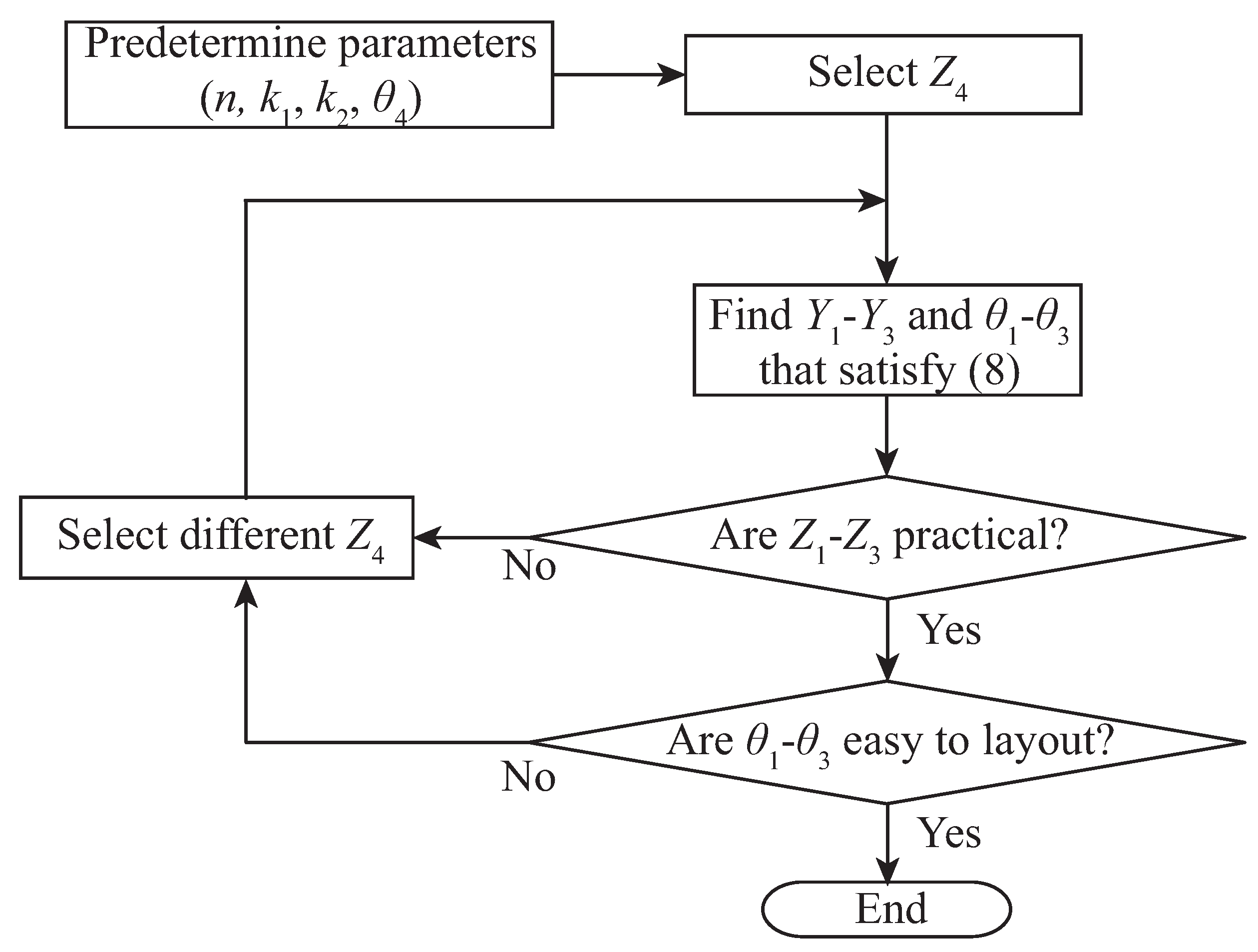
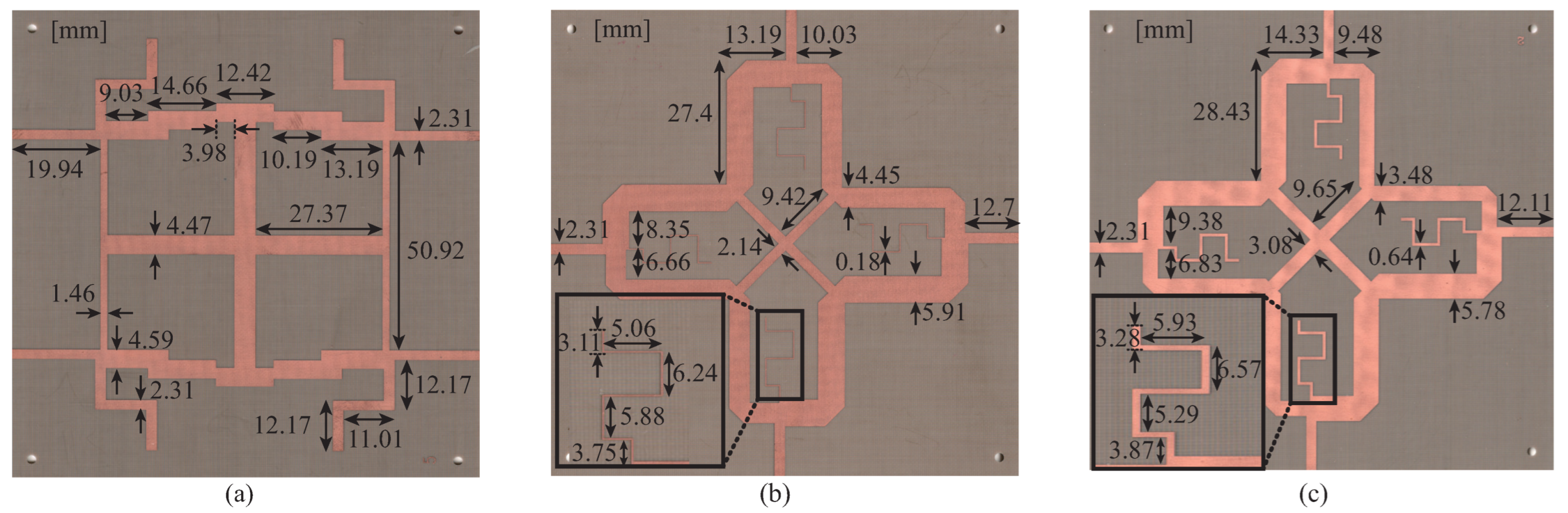
2. Design Procedure
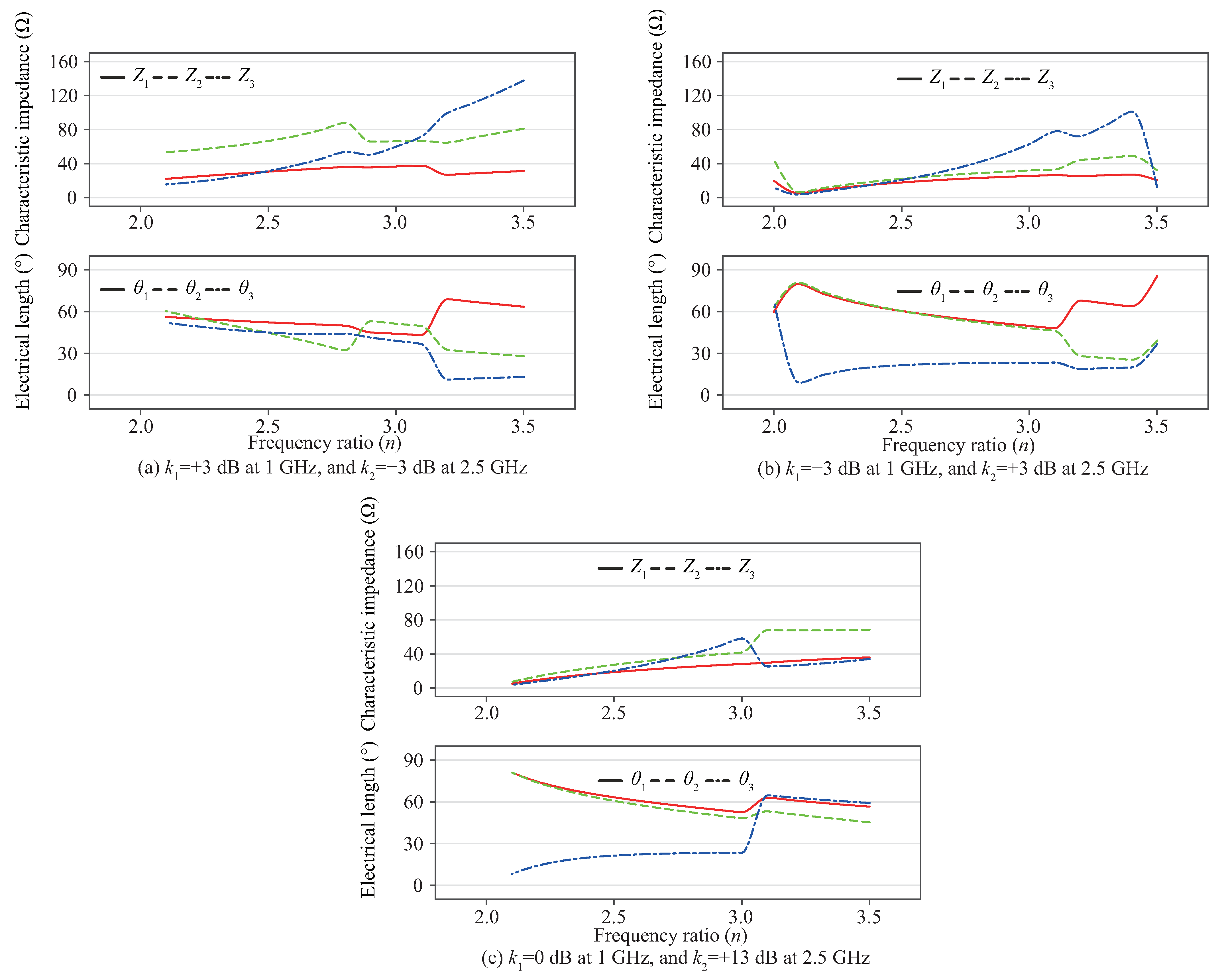
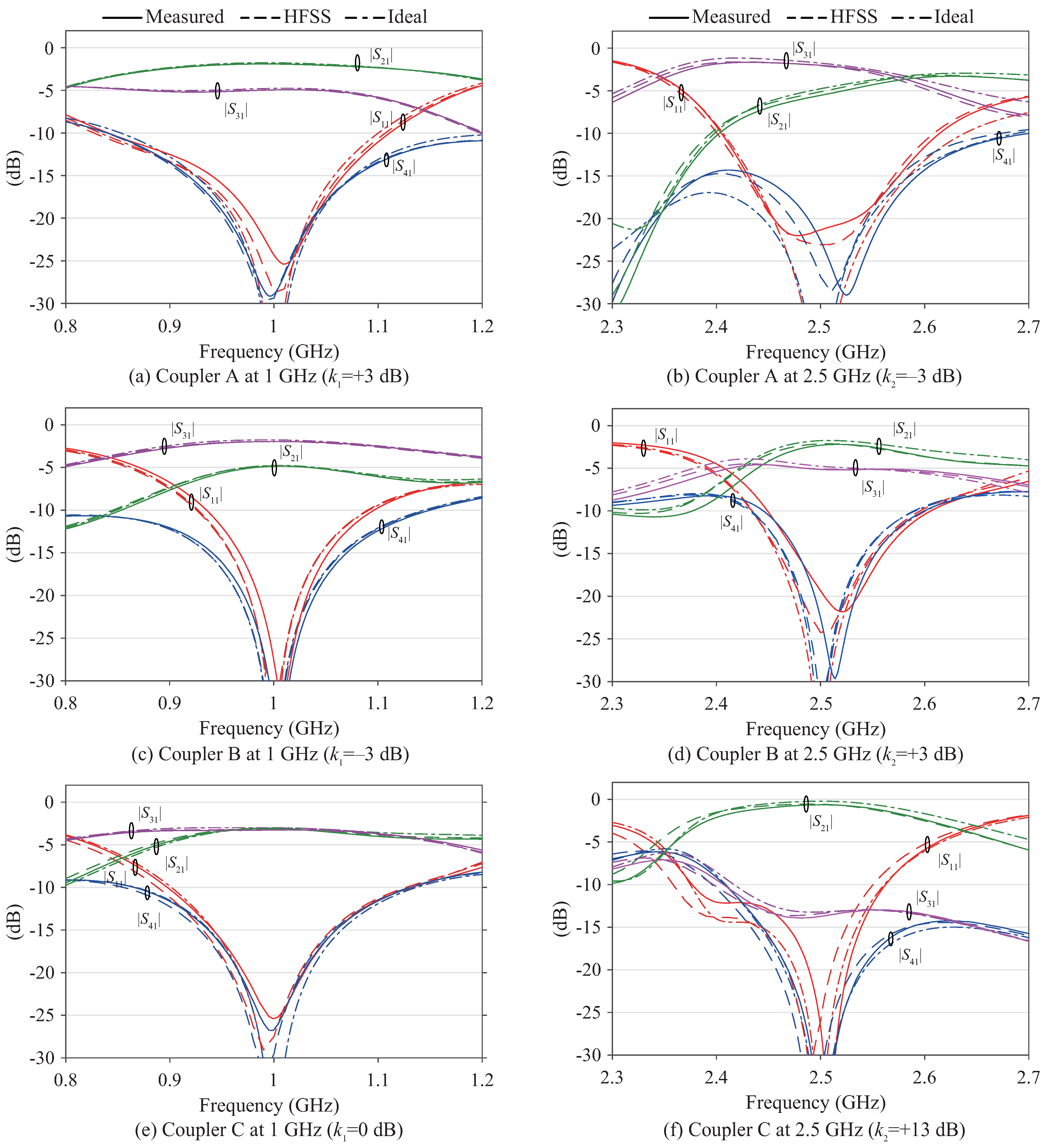
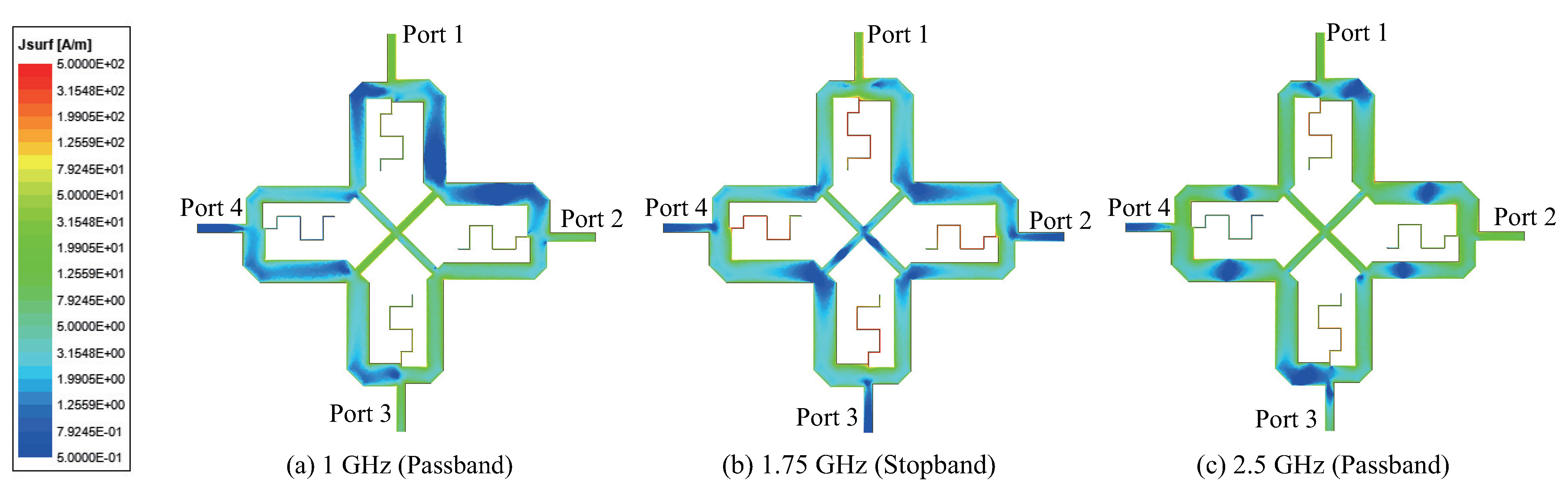
3. Simulation and Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, M.J.; Lee, B. Dual-band, cross coupled branch line coupler. IEEE Microw. Wirel. Compon. Lett. 2005, 15, 655–657. [Google Scholar] [CrossRef]
- Xia, L.; Li, J.L.; Twumasi, B.A.; Liu, P.; Gao, S.S. Planar dual-band branch-line coupler with large frequency ratio. IEEE Access 2020, 8, 33188–33195. [Google Scholar] [CrossRef]
- Chi, P.L. Miniaturized ring coupler with arbitrary power divisions based on the composite right/left-handed transmission lines. IEEE Microw. Wirel. Compon. Lett. 2012, 22, 170–172. [Google Scholar] [CrossRef]
- Gao, L.; Zheng, S.Y.; Hong, W.; Li, Y. Tight coupling dual-band coupler with large frequency ratio and arbitrary power division ratios over two bands. IEEE Access 2019, 7, 184489–184499. [Google Scholar] [CrossRef]
- Ha, J.; Lee, S.; Park, J.H.; Lee, Y. Dual-band branch-line couplers with three parallel lines for arbitrary power-split ratios. J. Electromagn. Waves Appl. 2013, 27, 1220–1229. [Google Scholar] [CrossRef]
- Lin, Y.S.; Lin, C.Y. Miniature dual-band quadrature coupler with arbitrary power division ratios over the two bands. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 27, 634–646. [Google Scholar] [CrossRef]
- Hsu, C.L.; Kuo, J.T.; Chang, C.W. Miniaturized dual-band hybrid couplers with arbitrary power division ratios. IEEE Trans. Microw. Theory Tech. 2008, 57, 149–156. [Google Scholar]
- Zheng, S.Y.; Wu, Y.; Li, Y.; Liu, Y.; Long, Y. Dual-band hybrid coupler with arbitrary power division ratios over the two bands. IEEE Trans. Compon. Packag. Manuf. Technol. 2014, 4, 1347–1358. [Google Scholar] [CrossRef]
- Maktoomi, M.A.; Hashmi, M.S.; Ghannouchi, F.M. A dual-band port-extended branch-line coupler and mitigation of the band-ratio and power division limitations. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 7, 1313–1323. [Google Scholar] [CrossRef]
- Chi, P.L.; Ho, K.L. Design of dual-band coupler with arbitrary power division ratios and phase differences. IEEE Trans. Microw. Theory Tech. 2014, 62, 2965–2974. [Google Scholar] [CrossRef]
- Huang, G.C.; Iskander, M.F.; Hoque, M.; Goodall, S.R.; Bocskor, T. Antenna array design and system for directional networking. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1141–1144. [Google Scholar] [CrossRef]
- Kumar, C.; Kumar, V.S.; Venkataramana, D. A Large Microstrip Patch Array With a Simplified Feed Network: A low cross-polarized design. IEEE Antennas Propag. Mag. 2019, 61, 105–111. [Google Scholar] [CrossRef]
- Abdulkhaleq, A.M.; Yahya, M.A.; McEwan, N.; Rayit, A.; Abd-Alhameed, R.A.; Ojaroudi Parchin, N.; Noras, J. Recent developments of dual-band Doherty power amplifiers for upcoming mobile communications systems. Electronics 2019, 8, 638. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.Y.; Zhai, C.; Cheng, K.K.M. Novel dual-band equal-cell Doherty amplifier design with extended power back-off range. IEEE Trans. Microw. Theory Tech. 2019, 68, 1012–1021. [Google Scholar] [CrossRef]
- Djerafi, T.; Gauthier, J.; Wu, K. Variable coupler for Butler beam-forming matrix with low sidelobe level. IET Microw. Antennas Propag. 2012, 6, 1034–1039. [Google Scholar] [CrossRef]
- Yu, M.X. A Novel microstrip-to-microstrip vertical via transition in X-band multilayer packages. Int. J. Antennas Propag. 2016, 2016, 9562854. [Google Scholar] [CrossRef]
- Chung, Y.; Jeon, S.S.; Kim, S.; Ahn, D.; Choi, J.I.; Itoh, T. Multifunctional microstrip transmission lines integrated with defected ground structure for RF front-end application. IEEE Trans. Microw. Theory Tech. 2004, 52, 1425–1432. [Google Scholar] [CrossRef]
- Grine, F.; Djerafi, T.; Benhabiles, M.T.; Wu, K.; Riabi, M.L. High-Q substrate integrated waveguide resonator filter with dielectric loading. IEEE Access 2017, 5, 12526–12532. [Google Scholar] [CrossRef]
- Vicent, G.; Coves, A.; Bronchalo, E.; Torregrosa, G. Synthesis of an artificial high effective permittivity medium in a SIW periodically loaded with metallic cylinders. In Proceedings of the 2017 Electromagnetics Research Symposium-Spring (PIERS), St. Petersburg, Russia, 22–25 May 2017. [Google Scholar]
- High Frequency Structure Simulator v15.0; Ansys, Inc.: Canonsburg, PA, USA, 2013.
- Zhang, G.; Jiao, F.; Liu, S.; Zhu, L.; Wang, S.; Zhang, Q.; Yang, J. Compact single-and dual-band filtering 180 hybrid couplers on circular patch resonator. IEEE Trans. Microw. Theory Tech. 2020, 68, 3675–3685. [Google Scholar] [CrossRef]
- Gómez-García, R.; Rosario-De Jesus, J.; Psychogiou, D. Multi-band bandpass and bandstop RF filtering couplers with dynamically-controlled bands. IEEE Access 2018, 6, 32321–32327. [Google Scholar] [CrossRef]


| Characteristic Impedance | Electrical Length @ | |||||||
|---|---|---|---|---|---|---|---|---|
| Type | ||||||||
| () | () | () | () | () | () | () | () | |
| Coupler A | 30.6 | 66.6 | 31.3 | 50 | 52.3 | 44.7 | 45.0 | 51.4 |
| Coupler B | 25.1 | 31.3 | 52.7 | 155 | 59.6 | 55.3 | 24.3 | 51.4 |
| Coupler C | 25.6 | 37.7 | 41.1 | 100 | 63.2 | 56.7 | 24.1 | 51.4 |
| Ref. | , (GHz) | R. BW † (%) | I. BW ‡ (%) | Directivity (dB) | , (dB) | / (dB) | () | Max. * (dB) | Substrate /h (mm) | Size () |
|---|---|---|---|---|---|---|---|---|---|---|
| [4] | 1, 6 | >84, >18 | >100, >100 | 21.5, 14.5 | 0.4, 0.1 | 0.3 | −90.9, −88.0 | 2.1 | 3.38/1.524 | 0.14 × 0.05 |
| 2, 4 | >23, >16.8 | >23, >11.5 | 15.8, 13.1 | 0.5, 2.6 | −2.1 | −90.7, −93.0 | 0.64 × 0.11 | |||
| [5] | 1, 2.5 | N.A | N.A | N.A | 3.3, 2.9 | 0.4 | 87.6, −92.7 | 0.5 | 2.2/0.79 | 0.22 × 0.23 |
| 1, 2.5 | N.A | N.A | N.A | −2.5, −3.0 | 0.5 | 86.2, −98.4 | 0.23 × 0.21 | |||
| [6] | 2.45, 5.5 | 10.9, 9.4 | 12.8, 15.8 | −0.4, 2.7 | −3.1, | 88.0, −94.1 | 3.1 | 12.88/N.A | 0.18 × 0.11 | |
| 2.45, 5.5 | 13.2, 9.2 | 18.4, 16.5 | 2.8, 2.8 | 0 | 87.2, −95.0 | 0.14 × 0.01 | ||||
| [7] | 2.45, 5.2 | 15.5, 23.5 | 14.1, 15.5 | 20.4, 19.5 | 3.2, 6.8 | −3.6 | 87.8, 86.9 | 3.6 | 2.2/0.508 | 0.11 × 0.09 |
| [8] | 3, 5.5 | N.A | N.A | N.A | −0.4, −9.7 | 9.3 | −97.9, −92.4 | 10.2 | 2.33/1.57 | 0.14 × 0.19 |
| 3, 4.5 | N.A | N.A | N.A | 10.3, 0.1 | 10.2 | −97.3, −90.9 | 0.16 × 0.16 | |||
| [9] | 1.2, 2.52 | 24.8, 15.1 | 21.8, 11.9 | >13.2 | 5.4, 4.8 | 0.4 | 88.9, −88.9 | 0.4 | 3.55/0.813 | 0.3 × 0.15 |
| 1.0, 2.0 | 11.5, 9 | 11, 8.3 | >15.5 | 1.5, 1.7 | 0.2 | 91.7, −92.8 | 0.37 × 0.18 | |||
| [10] | 2.4, 5.2 | 10.8, 28.6 | 75.6, 13.4 | N.A | 9.2, 5.7 | 3.5 | 61.9, 79.2 | 3.5 | 3.38/1.5 | 0.32 × 0.1 |
| This work | 1, 2.5 | 14.4, 6.3 | >65.1, 6.2 | 24.0, 20.6 | 3.0, −3.5 | 6.5 | 90.2, −90.4 | 13.3 | 2.2/0.76 | 0.27 × 0.27 |
| 1, 2.5 | 27.2, 8.4 | 48.9, 31.1 | 32.1, 17.4 | −2.9, 2.8 | −5.7 | 89.6, −91.3 | 0.28 × 0.3 | |||
| 1, 2.5 | 23.5, 7.5 | 26.7, >23.7 | 23.4, 28.6 | −0.2, 13.1 | −13.3 | 89.5, −91.6 | 0.28 × 0.28 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, H.; Lim, T.; Dimitrov, K.C.; Lee, Y. Dual-Band Branch-Line Coupler Based on Crossed Lines for Arbitrary Power-Split Ratios. Sensors 2022, 22, 5527. https://doi.org/10.3390/s22155527
Chang H, Lim T, Dimitrov KC, Lee Y. Dual-Band Branch-Line Coupler Based on Crossed Lines for Arbitrary Power-Split Ratios. Sensors. 2022; 22(15):5527. https://doi.org/10.3390/s22155527
Chicago/Turabian StyleChang, Hyungjun, Taejun Lim, Kristian Chavdarov Dimitrov, and Yongshik Lee. 2022. "Dual-Band Branch-Line Coupler Based on Crossed Lines for Arbitrary Power-Split Ratios" Sensors 22, no. 15: 5527. https://doi.org/10.3390/s22155527
APA StyleChang, H., Lim, T., Dimitrov, K. C., & Lee, Y. (2022). Dual-Band Branch-Line Coupler Based on Crossed Lines for Arbitrary Power-Split Ratios. Sensors, 22(15), 5527. https://doi.org/10.3390/s22155527







