Design of Under-Actuated Soft Adhesion Actuators for Climbing Robots
Abstract
:1. Introduction
2. Under-Actuated Adhesion Actuator Design
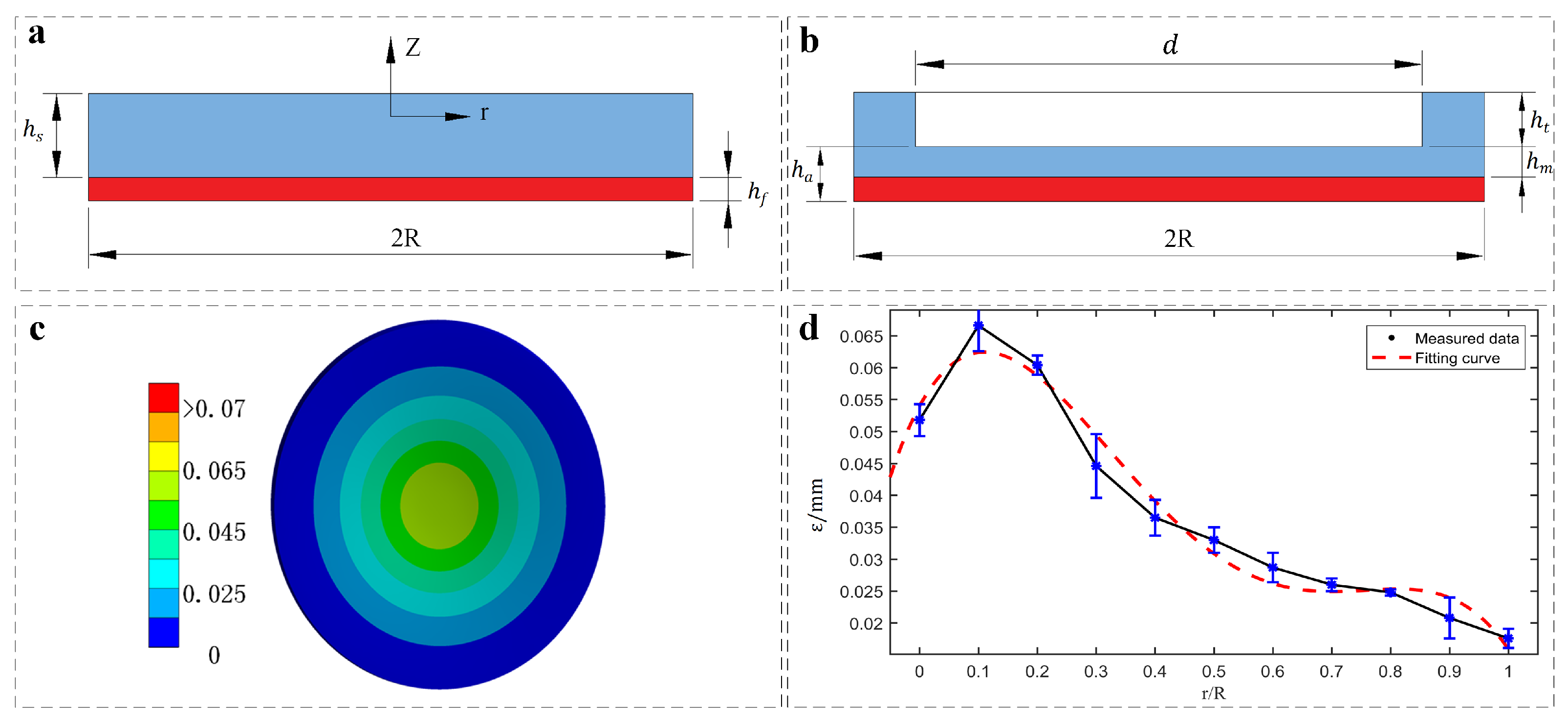
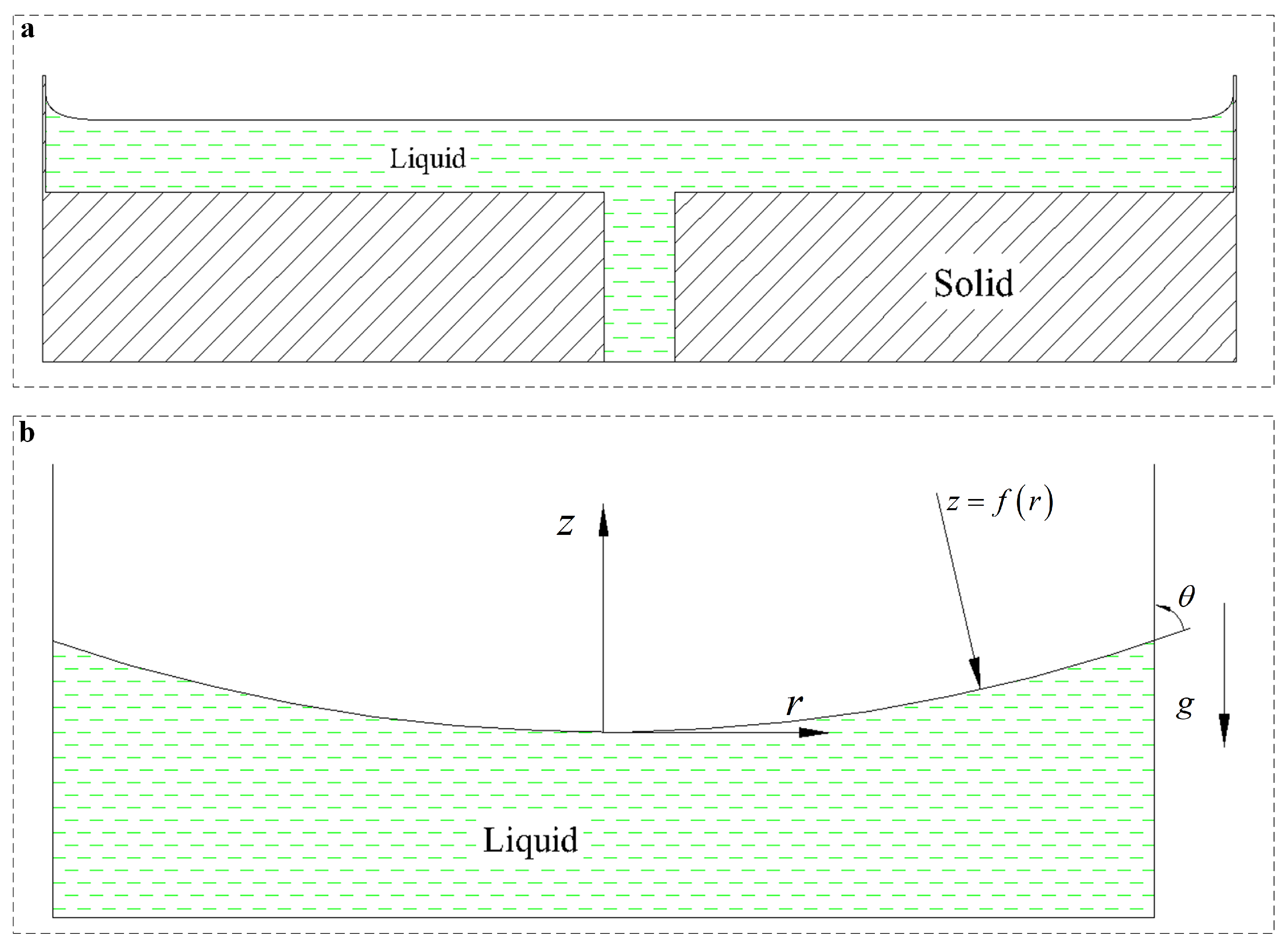
2.1. Modeling Adhesion Actuator as Double-Layer Doming System
2.2. Essential Geometric Parameters in the Adhesion Actuator
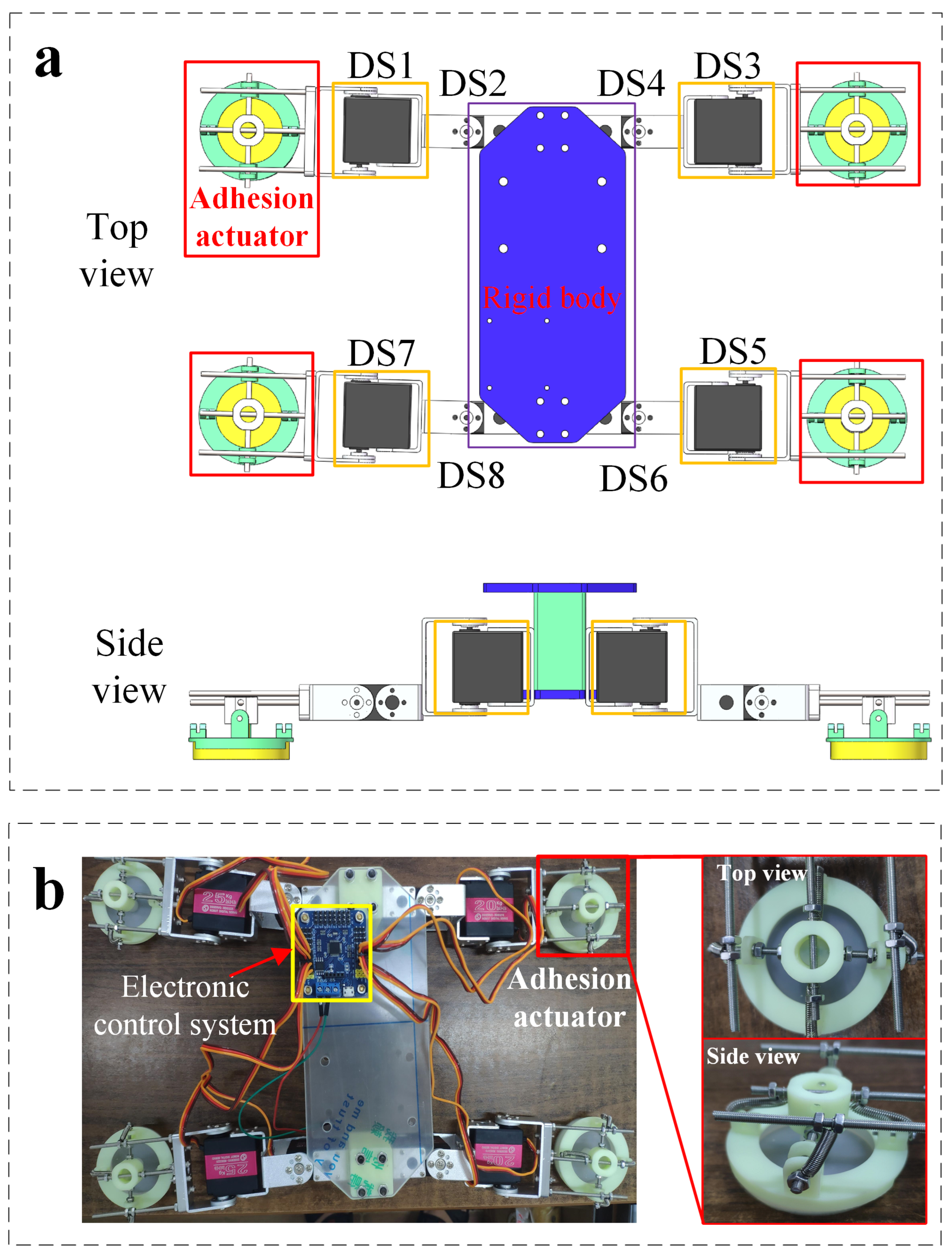
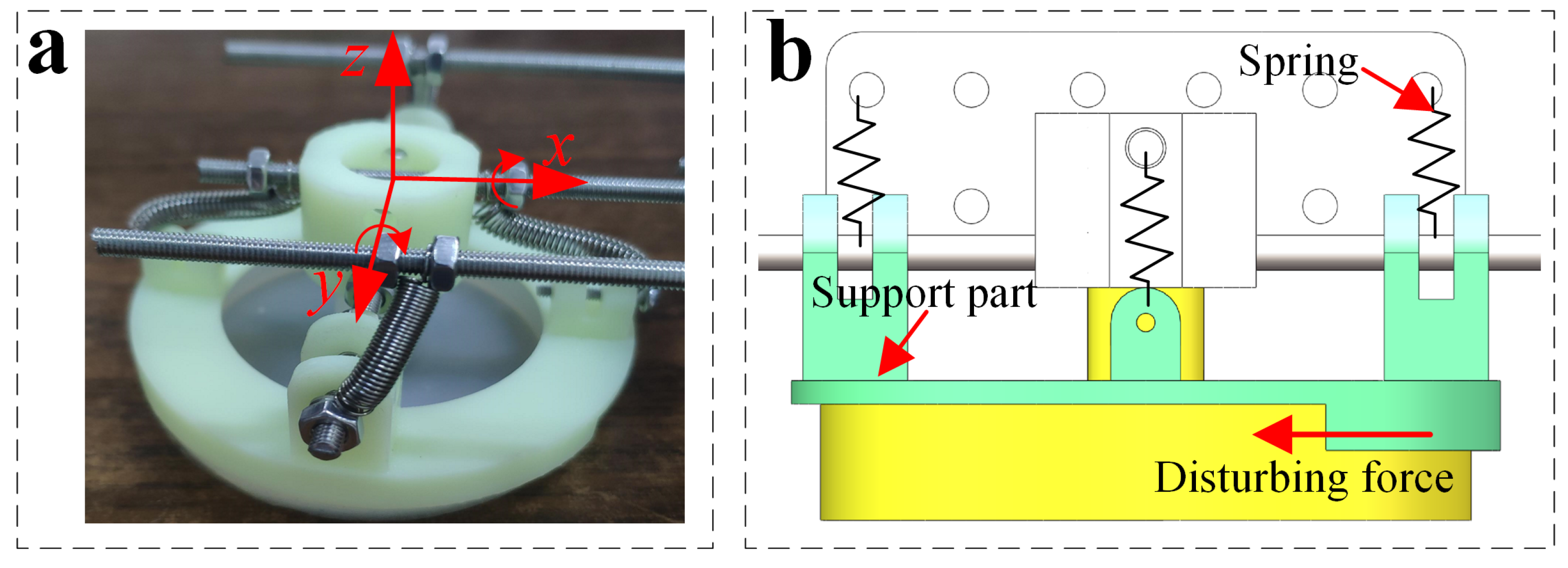
3. Climbing Robot with Soft Adhesion Actuators
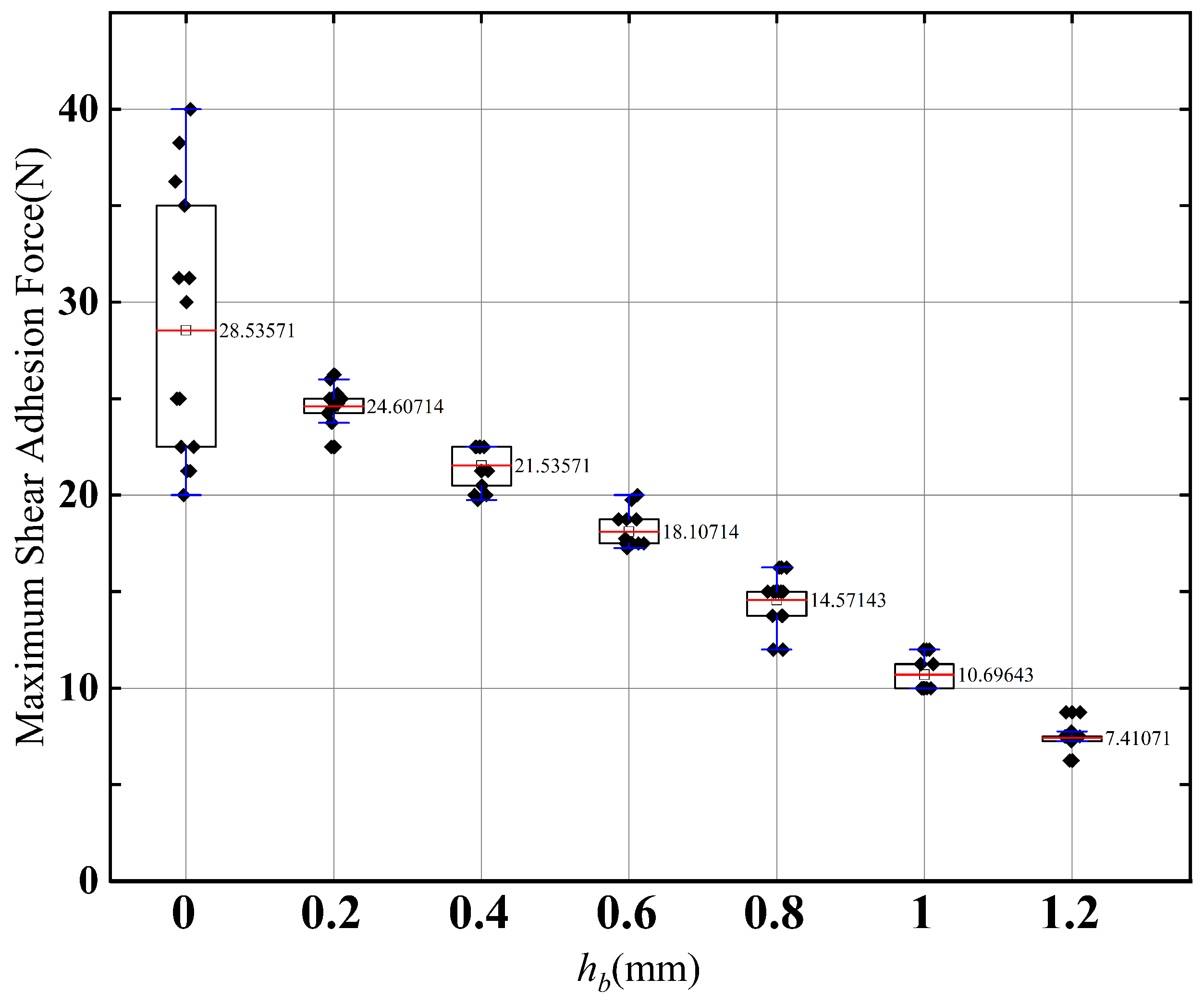
Experiments on Various Types of Target Surfaces
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| USAA | Under-actuated soft adhesion actuator |
References
- Schmidt, D.; Berns, K. Climbing robots for maintenance and inspections of vertical structures—A survey of design aspects and technologies. Robot. Auton. Syst. 2013, 61, 1288–1305. [Google Scholar] [CrossRef]
- Fujita, M.; Ikeda, S.; Fujimoto, T.; Shimizu, T.; Ikemoto, S.; Miyamoto, T. Development of universal vacuum gripper for wall-climbing robot. Adv. Robot. 2018, 32, 283–296. [Google Scholar] [CrossRef]
- Wu, X.; Wang, X.; Mei, T.; Sun, S. Mechanical analyses on the digital behaviour of the Tokay gecko (Gekko gecko) based on a multi-level directional adhesion model. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150085. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Pesika, N.; Zeng, H.; Rosenberg, K.; Zhao, B.; McGuiggan, P.; Autumn, K.; Israelachvili, J. Adhesion and friction in gecko toe attachment and detachment. Proc. Natl. Acad. Sci. USA 2006, 103, 19320–19325. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Xu, L.; Xu, J.; Li, T.; Chen, S.; Xu, H.; Cheng, G.; Ceccarelli, M. Design, modeling and experimentation of a biomimetic wall-climbing robot for multiple surfaces. J. Bionic Eng. 2020, 17, 523–538. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, Q.; Lin, G.; Yin, J. Switchable adhesion actuator for amphibious climbing soft robot. Soft Robot. 2018, 5, 592–600. [Google Scholar] [CrossRef]
- Xie, Z.; Domel, A.G.; An, N.; Green, C.; Gong, Z.; Wang, T.; Knubben, E.M.; Weaver, J.C.; Bertoldi, K.; Wen, L. Octopus arm-inspired tapered soft actuators with suckers for improved grasping. Soft Robot. 2020, 7, 639–648. [Google Scholar] [CrossRef]
- Sholl, N.; Moss, A.; Kier, W.M.; Mohseni, K. A soft end effector inspired by cephalopod suckers and augmented by a dielectric elastomer actuator. Soft Robot. 2019, 6, 356–367. [Google Scholar] [CrossRef]
- Sandoval, J.A.; Jadhav, S.; Quan, H.; Deheyn, D.D.; Tolley, M.T. Reversible adhesion to rough surfaces both in and out of water, inspired by the clingfish suction disc. Bioinspir. Biomim. 2019, 14, 066016. [Google Scholar] [CrossRef]
- Muthugala, M.V.J.; Vega-Heredia, M.; Vengadesh, A.; Sriharsha, G.; Elara, M.R. Design of an adhesion-aware façade cleaning robot. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 1441–1447. [Google Scholar]
- Muthugala, M.V.J.; Vega-Heredia, M.; Mohan, R.E.; Vishaal, S.R. Design and control of a wall cleaning robot with adhesion-awareness. Symmetry 2020, 12, 122. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, D.; Berns, K. Safe navigation of a wall-climbing robot by methods of risk prediction and suitable counteractive measures. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 2309–2314. [Google Scholar]
- De Rivaz, S.D.; Goldberg, B.; Doshi, N.; Jayaram, K.; Zhou, J.; Wood, R.J. Inverted and vertical climbing of a quadrupedal microrobot using electroadhesion. Sci. Robot. 2018, 3, eaau3038. [Google Scholar] [CrossRef] [Green Version]
- Gu, G.; Zou, J.; Zhao, R.; Zhao, X.; Zhu, X. Soft wall-climbing robots. Sci. Robot. 2018, 3, eaat2874. [Google Scholar] [CrossRef] [Green Version]
- Geissmann, L.; Denuder, M.; Keusch, D.; Pfirter, L.; Röthlisberger, D.; Ritter, M.; Thoma, P.; Siegwart, R.Y.; Fischer, W.; Caprari, G.; et al. Paraswift—A Hybrid Climbing and Base Jumping Robot for Entertainment. Field Robot. 2011, 397–406. [Google Scholar]
- Gao, F.; Fan, J.; Zhang, L.; Jiang, J.; He, S. Magnetic crawler climbing detection robot basing on metal magnetic memory testing technology. Robot. Auton. Syst. 2020, 125, 103439. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, S.; Wu, X.; Mei, T. A wheeled wall-climbing robot with bio-inspired spine mechanisms. J. Bionic Eng. 2015, 12, 17–28. [Google Scholar] [CrossRef]
- Huang, J.; Liu, Y.; Yang, Y.; Zhou, Z.; Mao, J.; Wu, T.; Liu, J.; Cai, Q.; Peng, C.; Xu, Y.; et al. Electrically programmable adhesive hydrogels for climbing robots. Sci. Robot. 2021, 6, eabe1858. [Google Scholar] [CrossRef]
- Andrikopoulos, G.; Papadimitriou, A.; Brusell, A.; Nikolakopoulos, G. On Model-based adhesion control of a vortex climbing robot. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 1460–1465. [Google Scholar]
- Laschi, C.; Mazzolai, B.; Cianchetti, M. Soft robotics: Technologies and systems pushing the boundaries of robot abilities. Sci. Robot. 2016, 1, eaah3690. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Um, D.S.; Lee, Y.; Lim, S.; Kim, H.j.; Ko, H. Octopus-inspired smart adhesive pads for transfer printing of semiconducting nanomembranes. Adv. Mater. 2016, 28, 7457–7465. [Google Scholar] [CrossRef]
- Wang, S.; Luo, H.; Linghu, C.; Song, J. Elastic Energy Storage Enabled Magnetically Actuated, Octopus-Inspired Smart Adhesive. Adv. Funct. Mater. 2021, 31, 2009217. [Google Scholar] [CrossRef]
- Sandoval, J.A. Getting a Grip Underwater: The Suction Disc of the Northern Clingfish Inspires a Reversible Underwater Adhesion Mechanism; University of California: San Diego, CA, USA, 2018. [Google Scholar]
- Miyake, T.; Ishihara, H.; Yoshimura, M. Basic studies on wet adhesion system for wall climbing robots. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1920–1925. [Google Scholar]
- Yang, D.; Verma, M.; So, J.; Mosadegh, B.; Keplinger, C.; Lee, B.; Khashai, F.; Lossner, E.; Suo, Z.; Whitesides, G. Buckling Pneumatic Linear Actuators Inspired by Muscle. Adv. Mater. Technol. 2016, 1, 1600055. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Mosadegh, B.; Ainla, A.; Lee, B.; Whitesides, G.M. Buckling of Elastomeric Beams Enables Actuation of Soft Machines. Adv. Mater. 2015, 27, 6323–6327. [Google Scholar] [CrossRef] [PubMed]
- Ge, D.; Ren, C.; Matsuno, T.; Ma, S. Guide rail design for a passive suction cup based wall-climbing robot. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 5776–5781. [Google Scholar]
- Gladman, A.S.; Matsumoto, E.A.; Nuzzo, R.G.; Mahadevan, L.; Lewis, J.A. Biomimetic 4D printing. Nat. Mater. 2016, 15, 413–418. [Google Scholar] [CrossRef] [PubMed]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mosadegh, B.; Polygerinos, P.; Keplinger, C.; Wennstedt, S.; Shepherd, R.F.; Gupta, U.; Shim, J.; Bertoldi, K.; Walsh, C.J.; Whitesides, G.M. Pneumatic networks for soft robotics that actuate rapidly. Adv. Funct. Mater. 2014, 24, 2163–2170. [Google Scholar] [CrossRef]
- Huang, Y.; Rosakis, A. Extension of Stoney’s formula to non-uniform temperature distributions in thin film/substrate systems. The case of radial symmetry. J. Mech. Phys. Solids 2005, 53, 2483–2500. [Google Scholar] [CrossRef]
- Gent, A.N. Engineering with Rubber: How to Design Rubber Components; Carl Hanser: Munich, Germany, 2012. [Google Scholar]
- Göbel, E.; Brichta, A.M. Rubber Springs Design; Spring: Berlin/Heidelberg, Germany, 1974. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Concus, P. Static menisci in a vertical right circular cylinder. J. Fluid Mech. 1968, 34, 481–495. [Google Scholar] [CrossRef] [Green Version]
- Zisman, W.A. Relation of the Equilibrium Contact Angle to Liquid and Solid Constitution; ACS Publications: Washington, DC, USA, 1964. [Google Scholar]
- Dussan, E. On the spreading of liquids on solid surfaces: Static and dynamic contact lines. Annu. Rev. Fluid Mech. 1979, 11, 371–400. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Modjarrad, K.; Ebnesajjad, S. Handbook of Polymer Applications in Medicine and Medical Devices; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Xu, L.; Liang, X.; Liu, J. Design of Under-Actuated Soft Adhesion Actuators for Climbing Robots. Sensors 2022, 22, 5639. https://doi.org/10.3390/s22155639
Liu Z, Xu L, Liang X, Liu J. Design of Under-Actuated Soft Adhesion Actuators for Climbing Robots. Sensors. 2022; 22(15):5639. https://doi.org/10.3390/s22155639
Chicago/Turabian StyleLiu, Zhipeng, Linsen Xu, Xingcan Liang, and Jinfu Liu. 2022. "Design of Under-Actuated Soft Adhesion Actuators for Climbing Robots" Sensors 22, no. 15: 5639. https://doi.org/10.3390/s22155639
APA StyleLiu, Z., Xu, L., Liang, X., & Liu, J. (2022). Design of Under-Actuated Soft Adhesion Actuators for Climbing Robots. Sensors, 22(15), 5639. https://doi.org/10.3390/s22155639





