Resolution Enhancement for Millimeter-Wave Radar ROI Image with Bayesian Compressive Sensing
Abstract
:1. Introduction
2. Holographic Imaging and Wave Number Spatial Spectrum
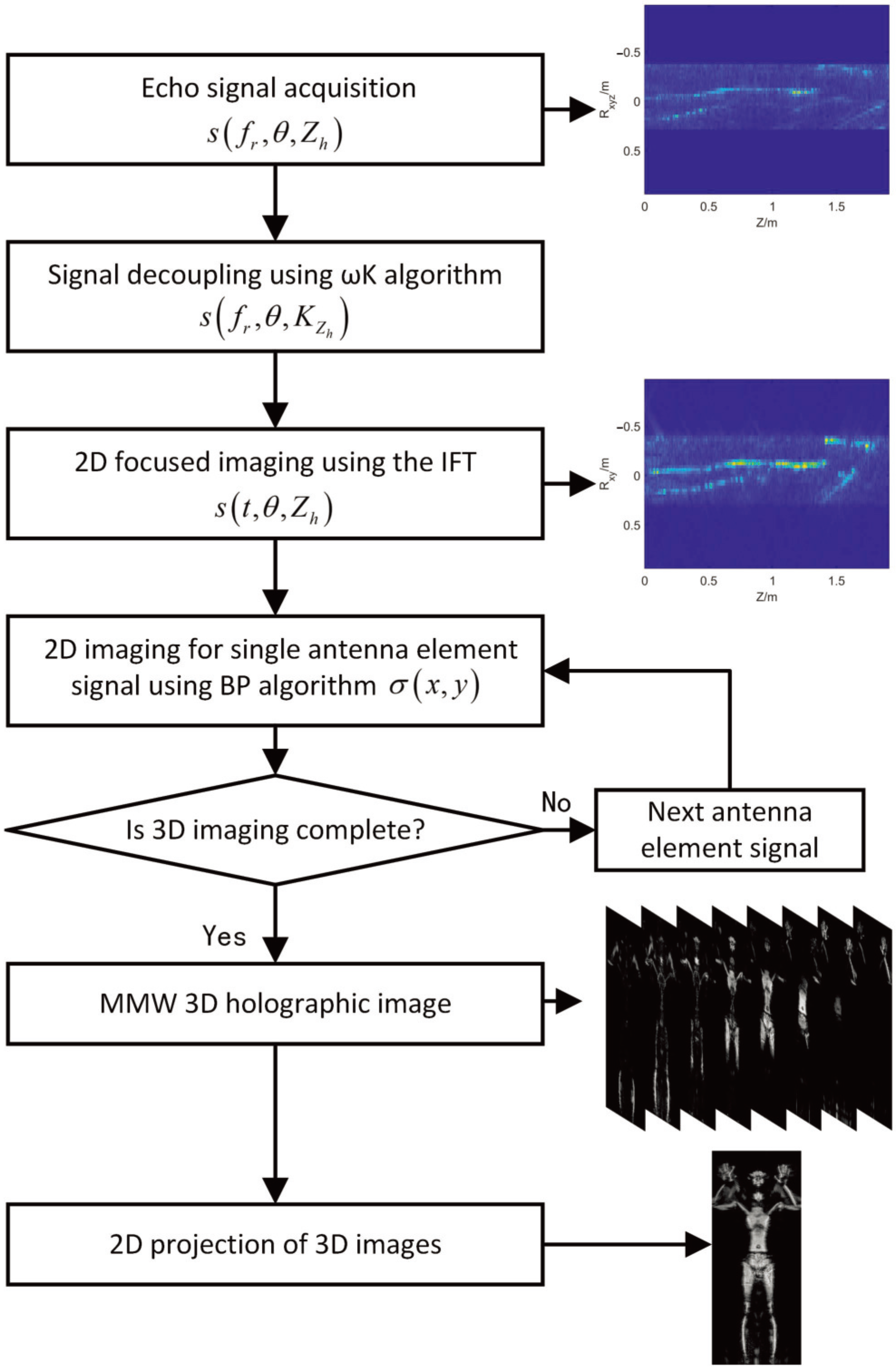
2.1. System Model and Holographic Imaging
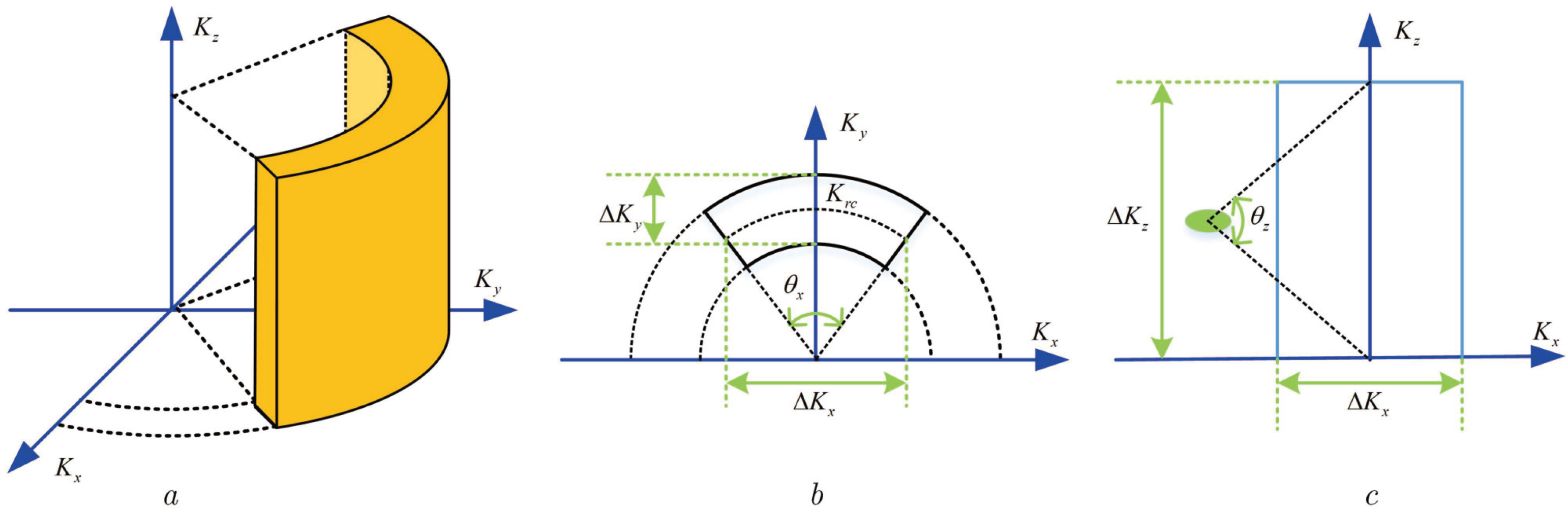
2.2. Spatial Wave Number Spectrum and Resolution
3. Resolution Enhancement with Bayesian Compressive Sensing
3.1. MMW 3D Image Sparsity and ROI
3.2. Bayesian Compressive Sensing
3.3. Target Region Image Resolution Enhancement
4. Experimental Results and Analysis
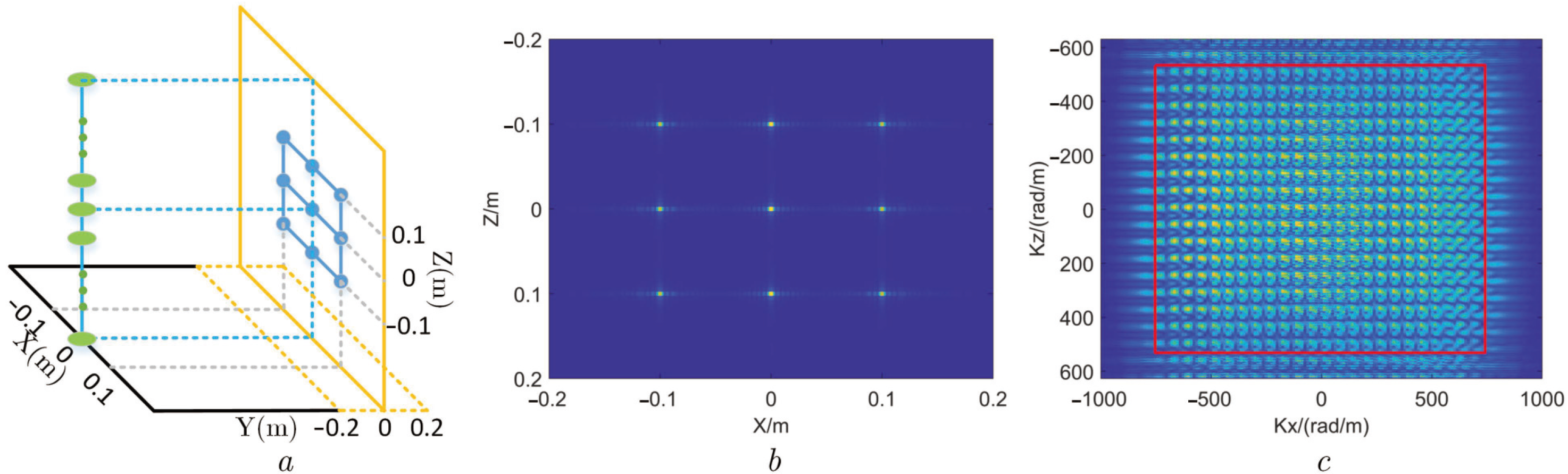
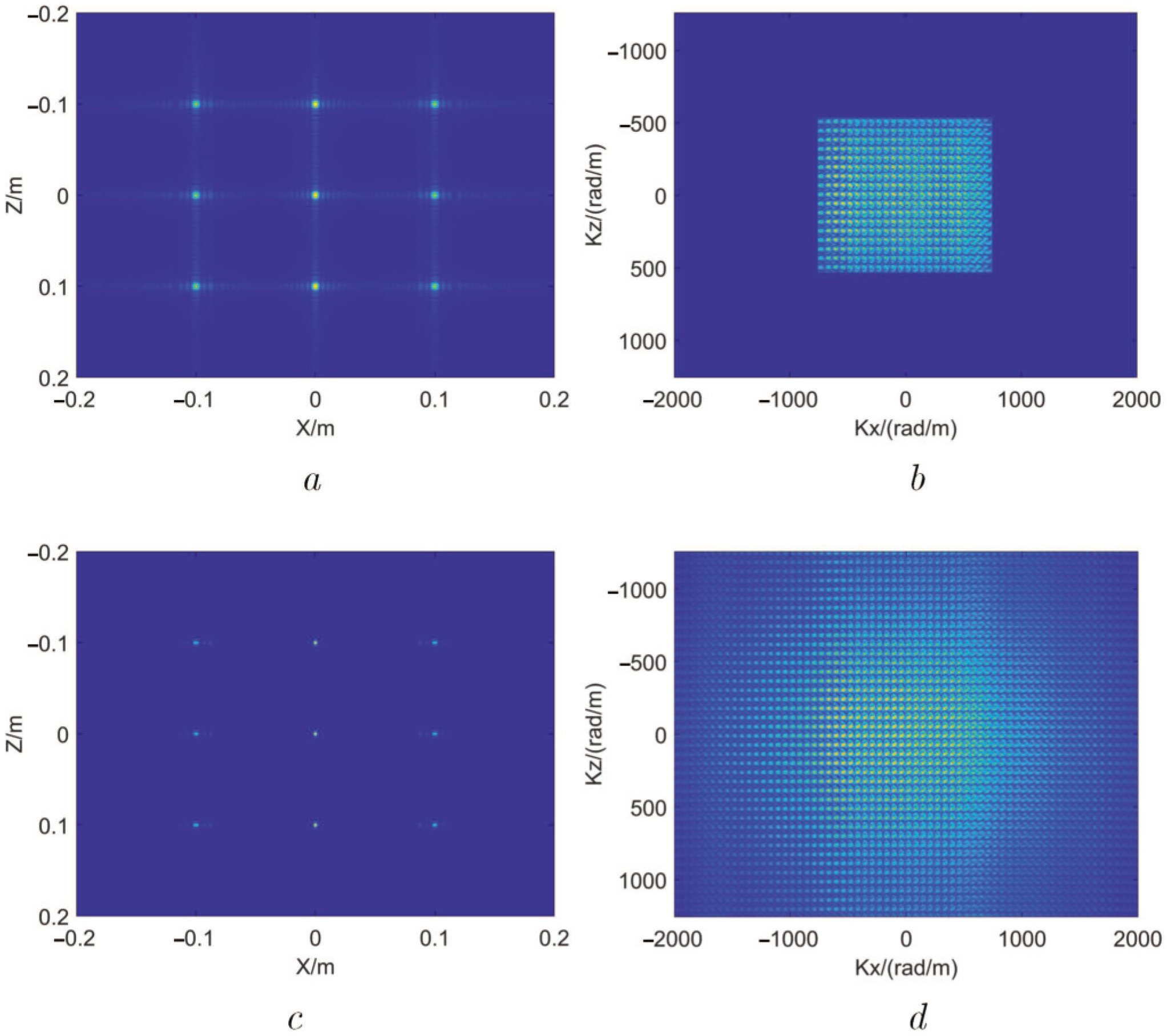
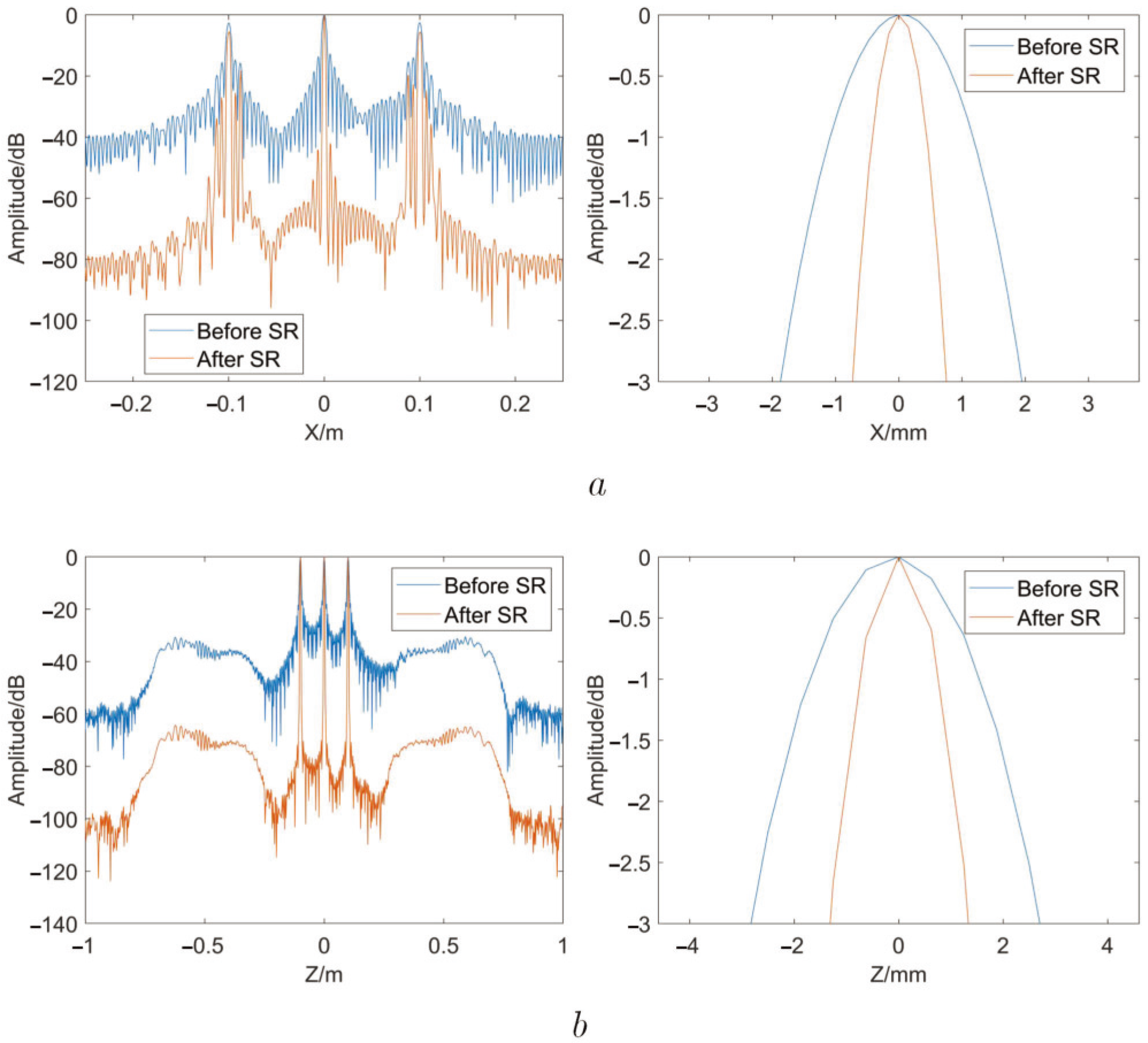
4.1. Lattice Point Targets Simulation Experiment
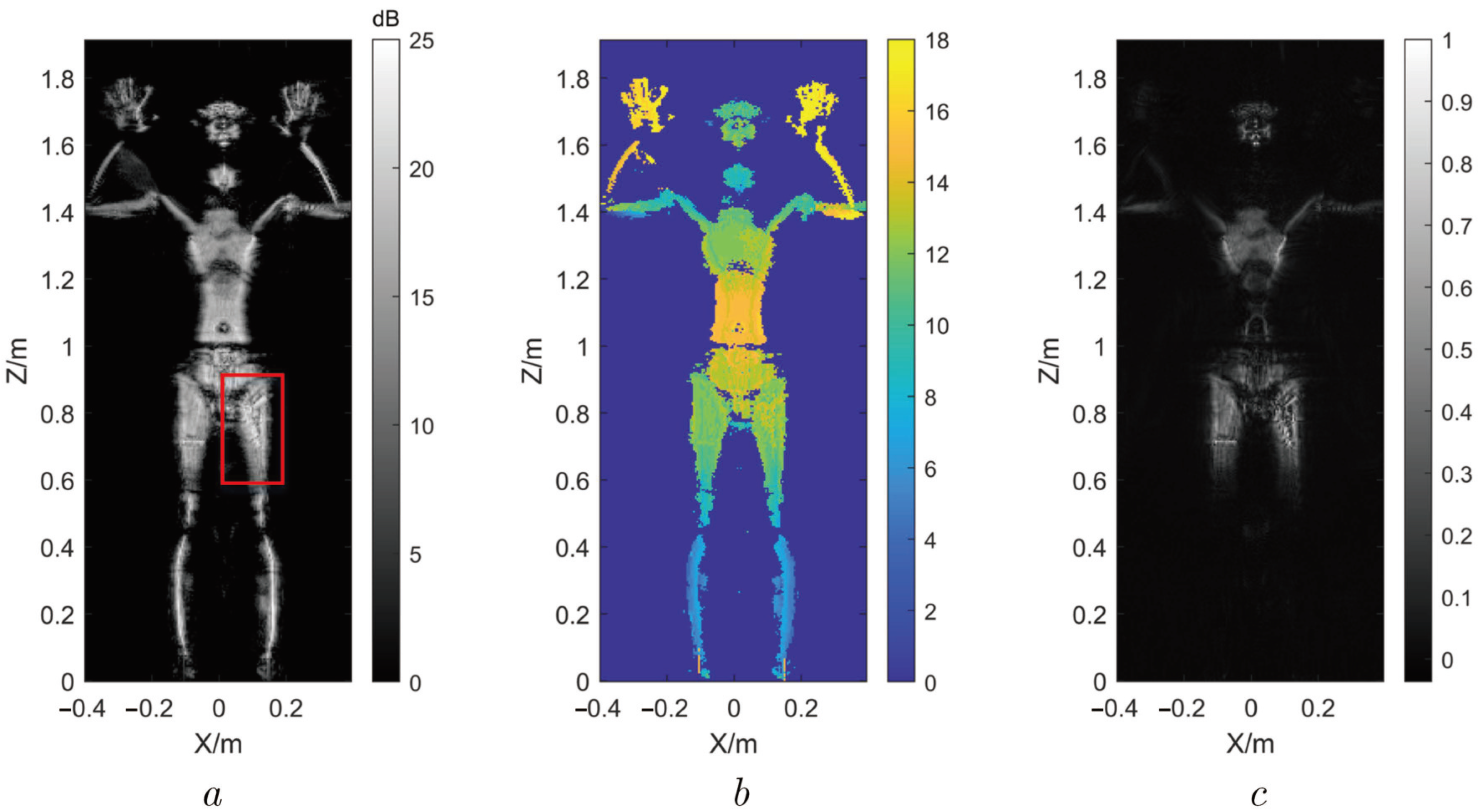
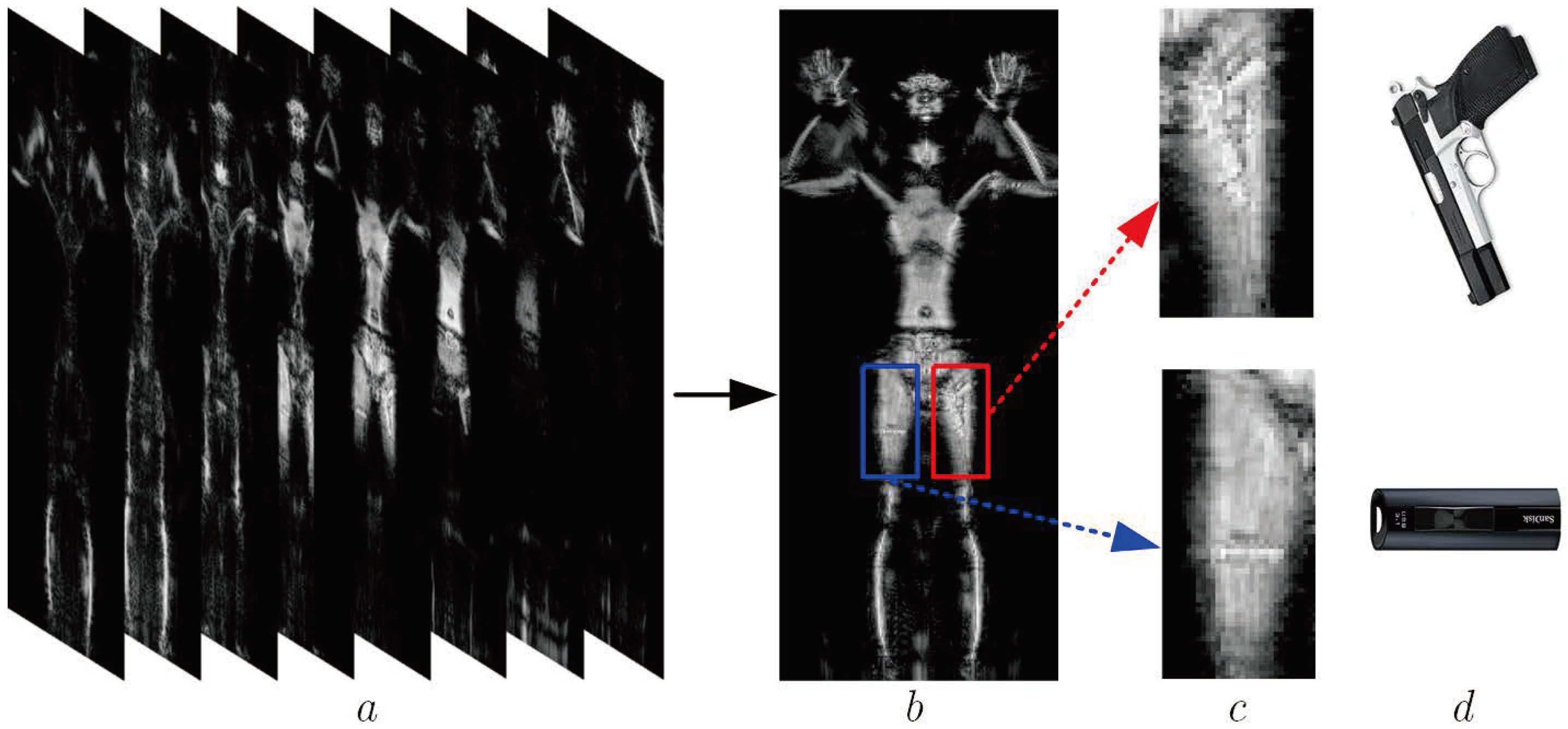
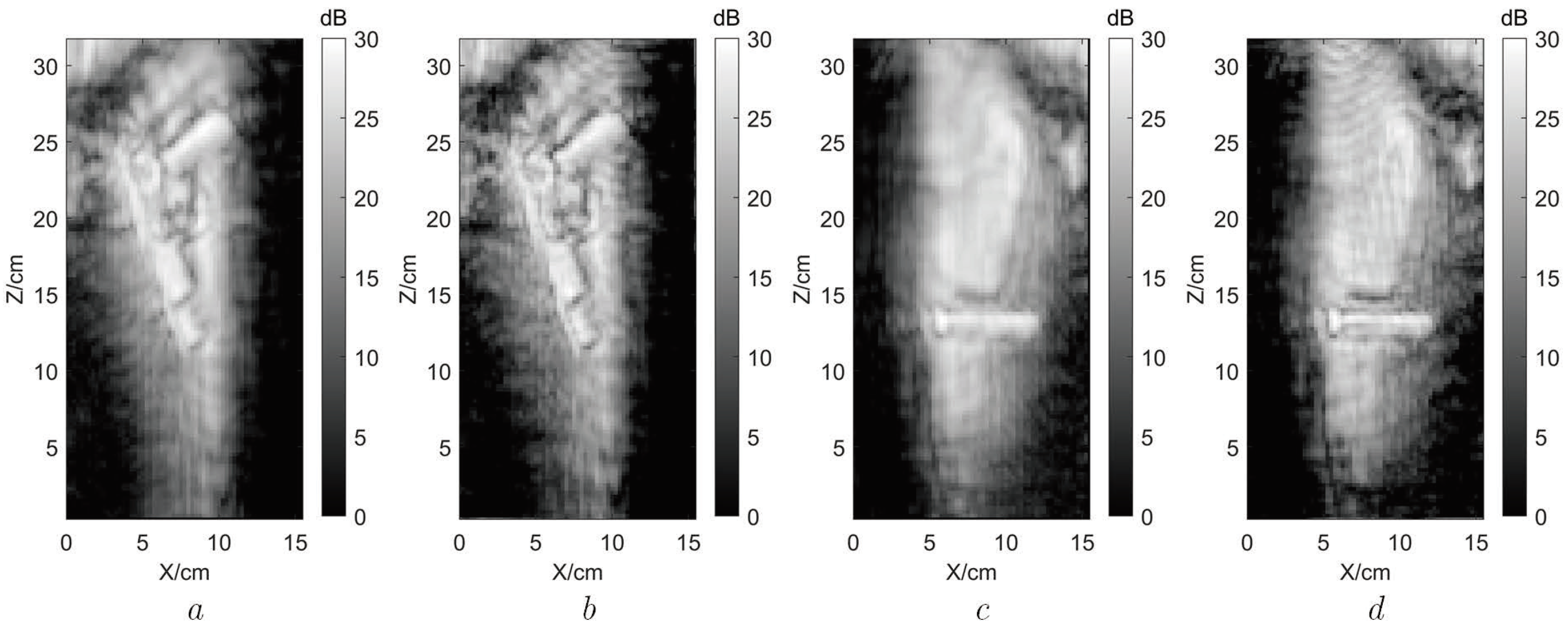
4.2. Measured Super-Resolution Experiment of Human Body Image
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MMW | Millimeter-wave |
| SAR | Synthetic aperture radar |
| ROI | Region of interest |
| CS | Compressive sensing |
| BCS | Bayesian compressive sensing |
| FFT | Fourier transform |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| SR | Super-resolution |
| PSNR | Peak signal-to-noise ratio |
| POSP | Principle of stationary phase |
| SM | Stolt Mapping |
| BP | Back projection |
| MAP | Maximum a posterior |
| CGA | Conjugate gradient algorithm |
References
- Sheen, D.M.; Mcmakin, D.L.; Hall, T.E. Three-dimensional millimeter-wave imaging for concealed weapon detection. IEEE Trans. Microw. Theory Tech. 2001, 49, 1581–1592. [Google Scholar] [CrossRef]
- Xiao, Z.; Hu, T.; Xu, J.; Wu, L. Millimetre-wave radiometric imaging for concealed contraband detection on personnel. IET Image Process. 2011, 5, 375–381. [Google Scholar] [CrossRef]
- Cui, G.; Zhao, C.; Wu, H.; Xiang, W.; Li, Z. Millimeter wave passive imaging system using reflector antenna. In Proceedings of the IET International Radar Conference 2015, Hangzhou, China, 14–16 October 2015. [Google Scholar]
- Liu, T.; Zhao, Y.; Wei, Y.; Zhao, Y.; Wei, S. Concealed Object Detection for Activate Millimeter Wave Image. IEEE Trans. Ind. Electron. 2019, 66, 9909–9917. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, J. Super-resolution processing of passive millimeter-wave images based on adaptive projected landweber algorithm. J. Syst. Eng. Electron. 2008, 19, 709–716. [Google Scholar]
- Yurish, S.Y. Super-resolution algorithm for passive millimeter wave imaging based on maximum likelihood and neighbor wavelet transform. Sens. Transducers J. 2013, 157, 229–233. [Google Scholar]
- Meng, Y.; Qing, A.; Lin, C.; Zang, J. Passive millimeter wave imaging system for public security check. In Proceedings of the 2017 International Applied Computational Electromagnetics Society Symposium (ACES), Suzhou, China, 1–4 August 2017. [Google Scholar]
- Alkuş, Ü.; Ermeydan, E.Ş.; Şahin, A.B.; Çankaya, İ.; Altan, H. Super-resolution image reconstruction applied to an active millimeter wave imaging system based on compressive sensing. In Proceedings of the SPIE Security + Defence, Warsaw, Poland, 6 October 2017. [Google Scholar]
- Ali, S.; Zahra, K.; Mahdi, S. Improved-resolution millimeter-wave imaging through structured illumination. Appl. Opt. 2017, 56, 4454–4465. [Google Scholar]
- Sanam, P.M.; Talebi, M.J.S.; Kazemi, M.; Kavehvash, Z.; Shabany, M. A Thorough Approach toward Cylindrical Millimeter-Wave Image Reconstruction using Sparse Antenna-Array. IET Image Process. 2018, 12, 1458–1466. [Google Scholar] [CrossRef]
- Zamani, H.; Fakharzadeh, M. 1.5-D Sparse Array for Millimeter-Wave Imaging Based on Compressive Sensing Techniques. IEEE Trans. Antennas Propag. 2018, 66, 2008–2015. [Google Scholar] [CrossRef]
- Cheng, Q.; Alomainy, A.; Hao, Y. On the performance of compressed sensing-based methods for millimeter-wave holographic imaging. Appl. Opt. 2016, 55, 728–738. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Zhao, G.; Li, S.; Ren, B.; Qiu, Q.; Sun, H. Cylindrical three-dimensional millimeter-wave imaging via compressive sensing. Int. J. Antennas Propag. 2015, 2015, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Ji, S.; Xue, Y.; Carin, L. Bayesian Compressive Sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Babacan, S.D.; Molina, R.; Katsaggelos, A.K. Bayesian Compressive Sensing Using Laplace Priors. IEEE Trans. Image Process. 2010, 19, 53–63. [Google Scholar] [CrossRef]
- Cetin, M.; Karl, W.C.; Castanon, D.A. Analysis of the impact of feature-enhanced SAR imaging on ATR performance. In Proceedings of the SPIE 4727, Algorithms for Synthetic Aperture Radar Imagery IX, Orlando, FL, USA, 1 August 2002. [Google Scholar]
- Liao, Y.; Wang, W.; Liu, Q. Two-Dimensional Spectrum for Circular Trace Scanning SAR Based on an Implicit Function. IEEE Geosci. Remote Sens. Lett. 2016, 13, 887–891. [Google Scholar] [CrossRef]
- Cumming, I.G.; Neo, Y.L.; Wong, F.H. Interpretations of the omega-K algorithm and comparisons with other algorithms. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003. [Google Scholar]
- Li, S.; Zhao, G.; Sun, H.; Amin, M. Compressive Sensing Imaging of 3-D Object by a Holographic Algorithms. IEEE Trans. Antennas Propag. 2018, 66, 7295–7304. [Google Scholar] [CrossRef]
- Ribalta, A. High resolution SAR image reconstruction: The generalized backprojection algorithm. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011. [Google Scholar]
- Chen, L.; An, D.; Huang, X. Extended Autofocus Backprojection Algorithm for Low-Frequency SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1323–1327. [Google Scholar] [CrossRef]
- Massa, A.; Rocca, P.; Oliveri, G. Compressive Sensing in Electromagnetics—A Review. IEEE Antennas Propag. Mag. 2015, 57, 224–238. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, Y. A MAP Approach for 1-Bit Compressive Sensing in Synthetic Aperture Radar Imaging. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1237–1241. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T. Adaptive sparseness for supervised learning. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 1150–1159. [Google Scholar] [CrossRef] [Green Version]
- Cetins, M.; Karl, W.C. Feature-enhanced synthetic aperture radar image formation based on nonquadratic regularization. IEEE Trans. Image Process. 2001, 10, 623–631. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Wang, H.; Qiao, Z. Resolution enhancement for ISAR imaging via improved statistical compressive sensing. EURASIP J. Appl. Signal Process. 2016, 80, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Beauwens, R. Iterative solution methods. Appl. Numer. Math. 2004, 51, 437–450. [Google Scholar] [CrossRef]


| Item | Value |
|---|---|
| Operation frequency () | 32–38 GHz |
| Beam width of pitch | |
| Number of sensors | 400 |
| Interval of sensors | 5 mm |
| Beam width of azimuth | |
| Radius of gyration | 0.7 m |
| Azimuth sampling interval |
| Item | Value |
|---|---|
| Operation waveband | Ka |
| System bandwidth | 5 GHz |
| Radius of gyration | 0.7 m |
| Azimuth sampling interval | |
| Azimuth resolution () | 5 mm |
| Range resolution () | 30 mm |
| Vertical resolution () | 5 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, P.; Wu, J.; Zhang, L.; Wang, G.; Jin, X. Resolution Enhancement for Millimeter-Wave Radar ROI Image with Bayesian Compressive Sensing. Sensors 2022, 22, 5757. https://doi.org/10.3390/s22155757
Xie P, Wu J, Zhang L, Wang G, Jin X. Resolution Enhancement for Millimeter-Wave Radar ROI Image with Bayesian Compressive Sensing. Sensors. 2022; 22(15):5757. https://doi.org/10.3390/s22155757
Chicago/Turabian StyleXie, Pengfei, Jianxin Wu, Lei Zhang, Guanyong Wang, and Xue Jin. 2022. "Resolution Enhancement for Millimeter-Wave Radar ROI Image with Bayesian Compressive Sensing" Sensors 22, no. 15: 5757. https://doi.org/10.3390/s22155757
APA StyleXie, P., Wu, J., Zhang, L., Wang, G., & Jin, X. (2022). Resolution Enhancement for Millimeter-Wave Radar ROI Image with Bayesian Compressive Sensing. Sensors, 22(15), 5757. https://doi.org/10.3390/s22155757






