A Comparative Study of Parameter Identification Methods for Asymmetric Nonlinear Systems with Quadratic and Cubic Stiffness
Abstract
:1. Introduction
2. Asymmetric Model: A Helmholtz–Duffing Oscillator
3. Identification Methods for the Characteristic Curves
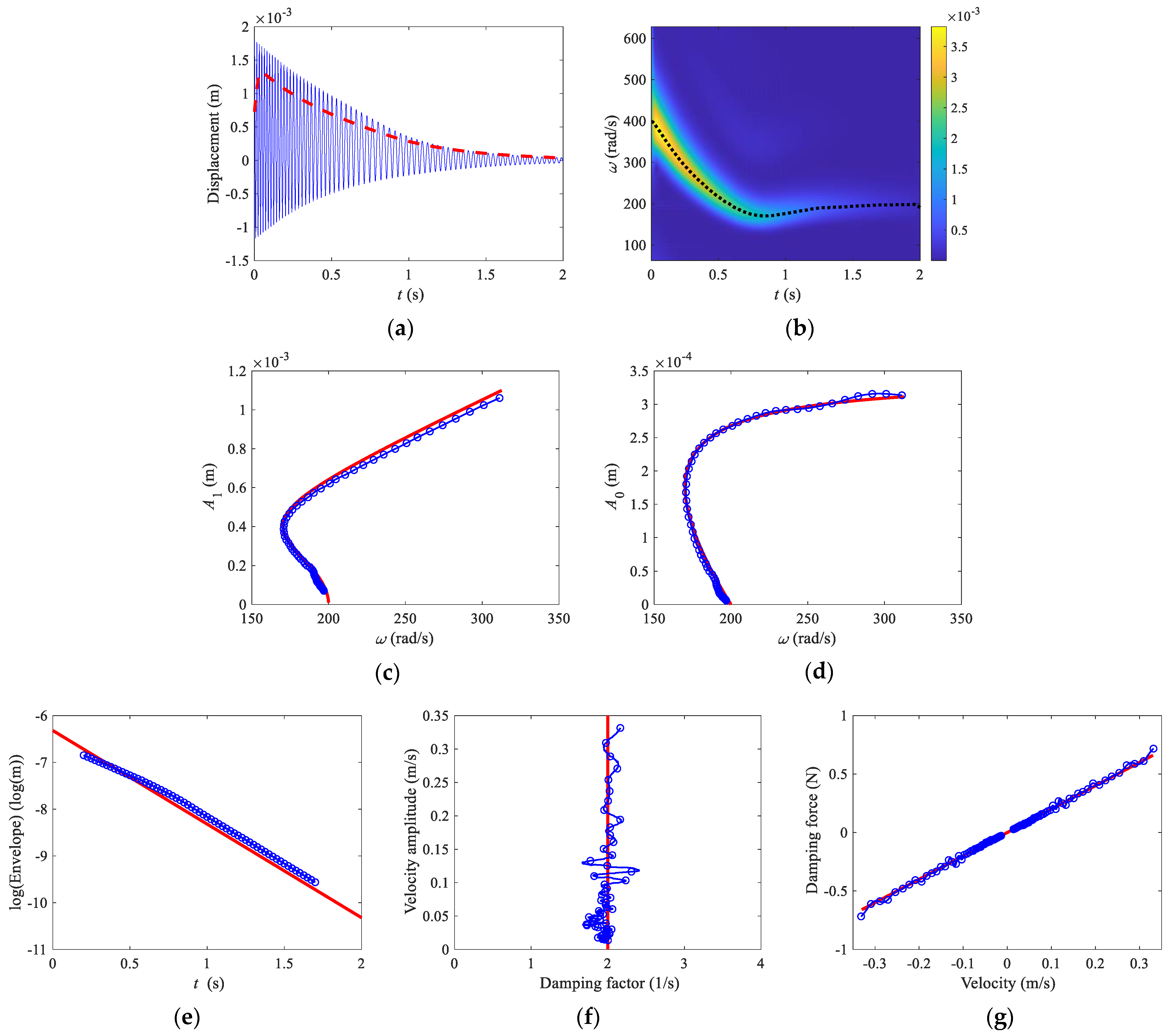
3.1. Hilbert Transform
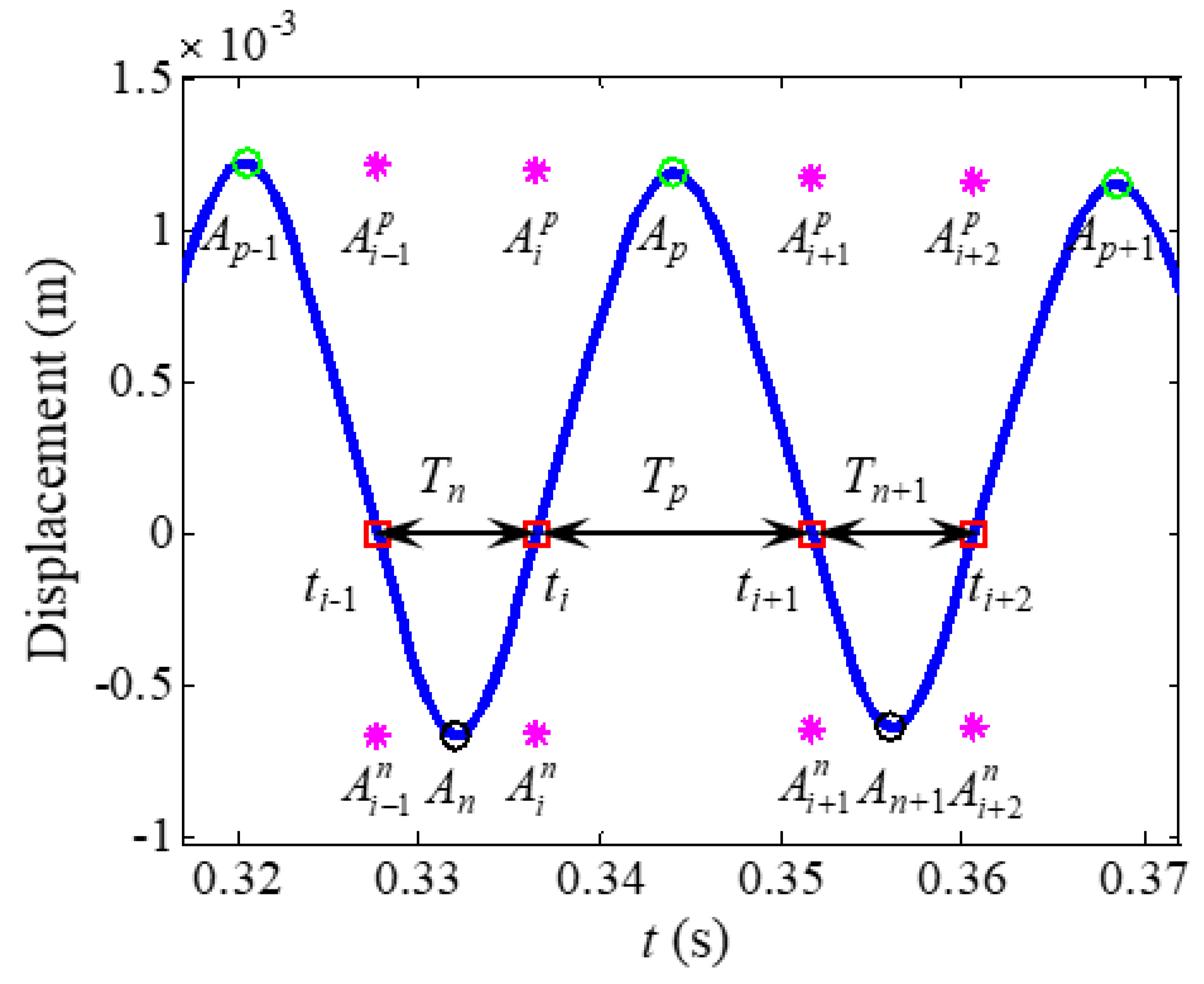
3.2. Zero-Crossing
3.3. Direct Quadrature
3.4. Wavelet Transform
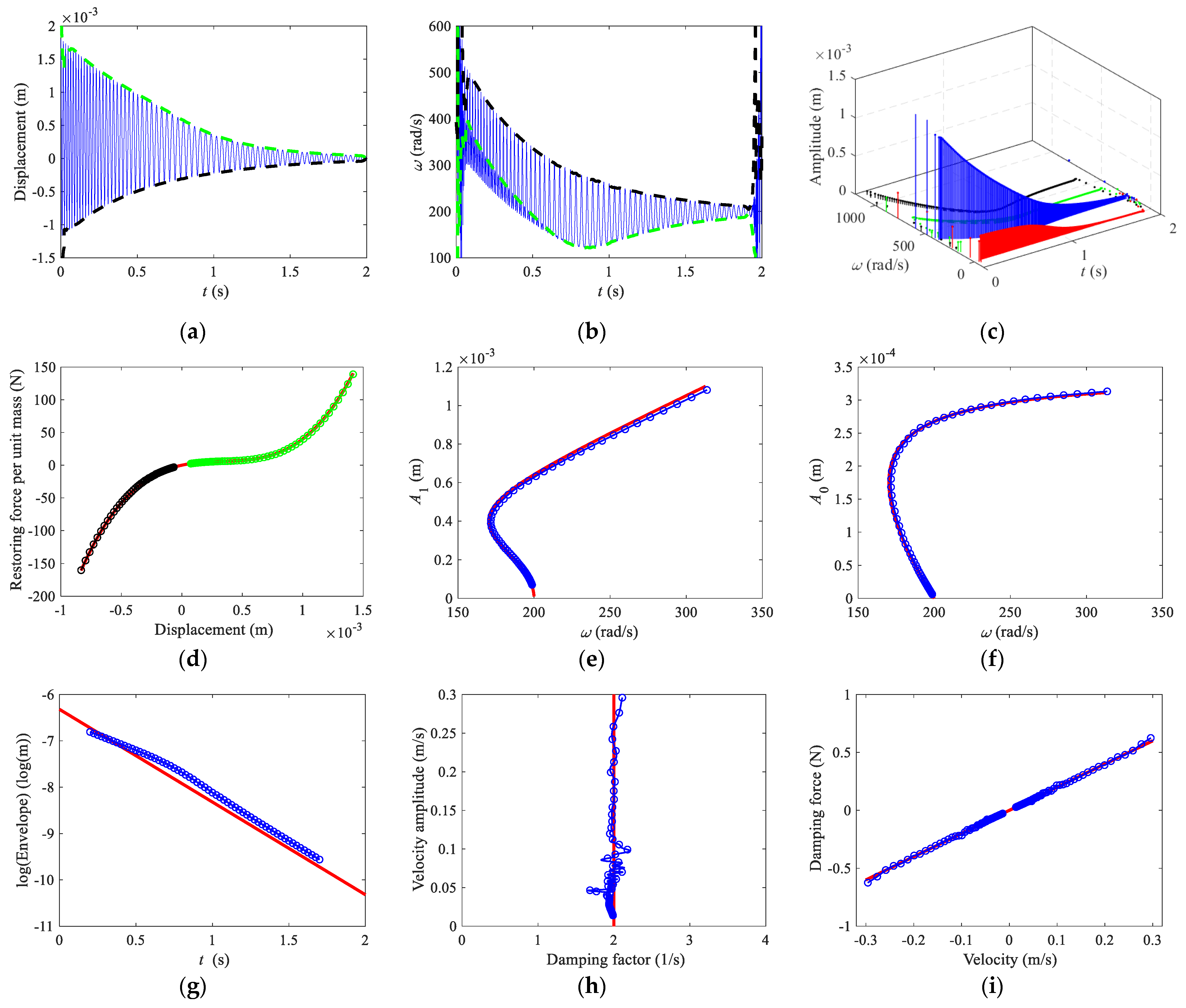
4. Parameter Estimation and Discussion
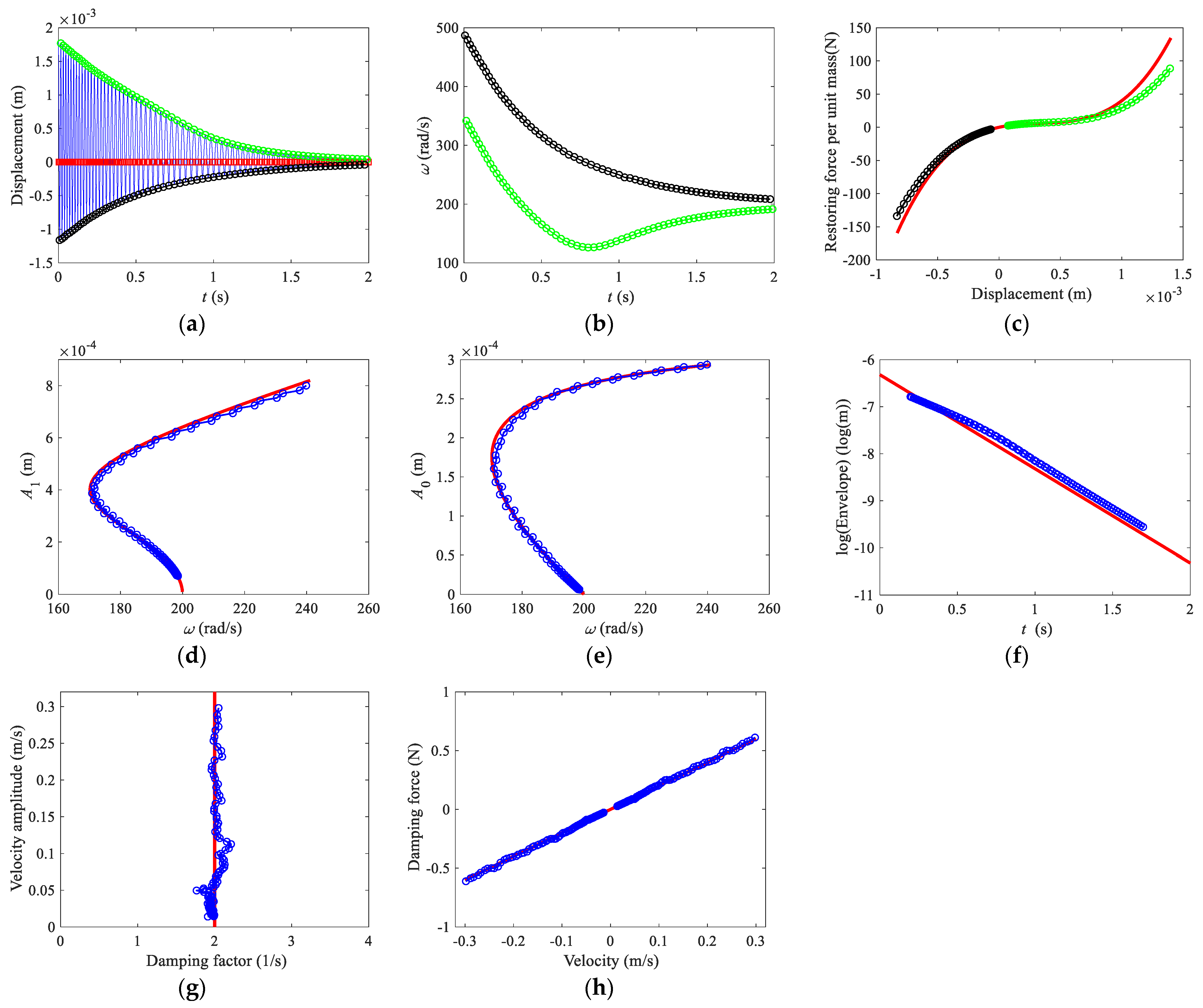
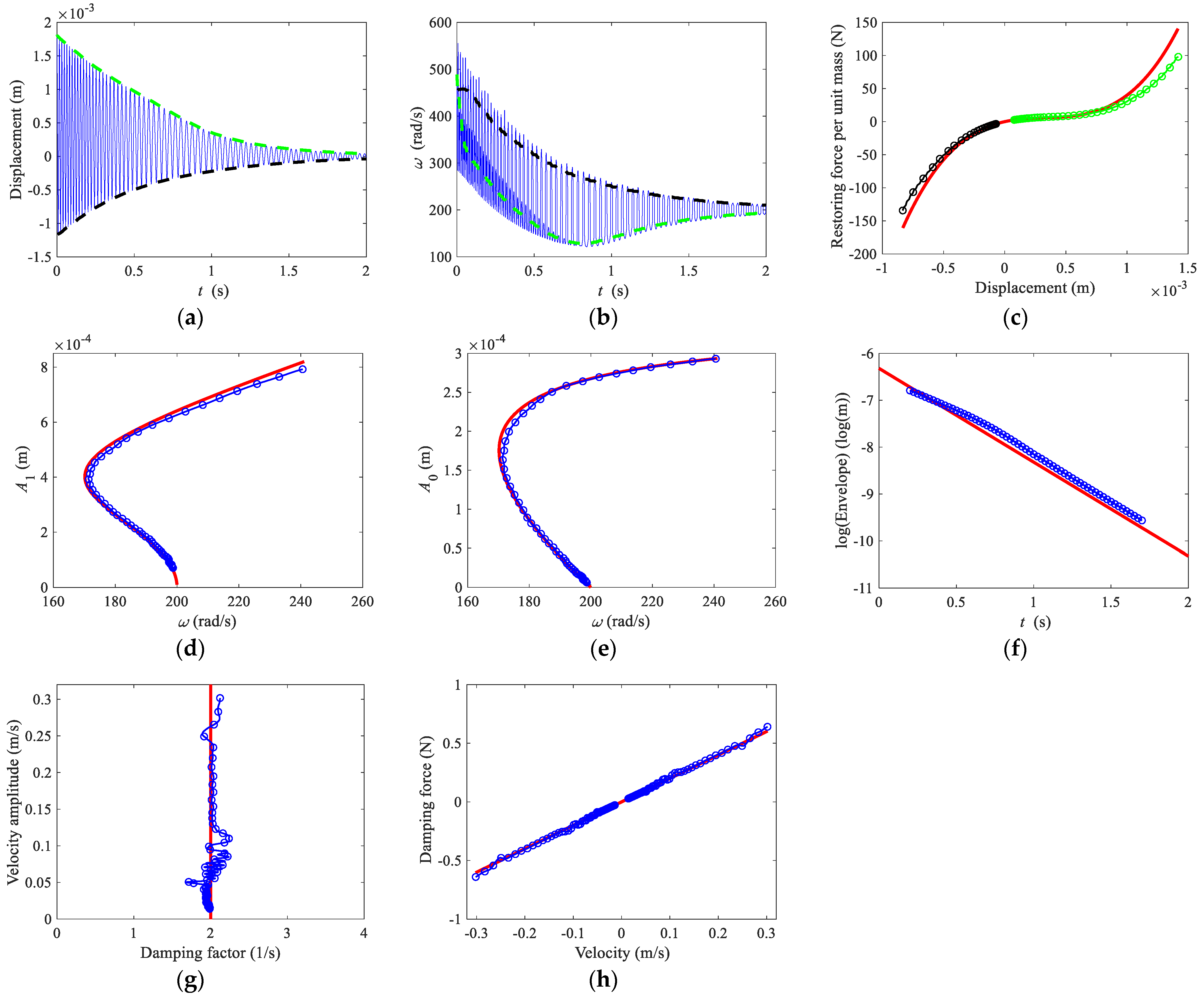
5. Experiment
5.1. Experimental Description
5.2. Estimation and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Abolfathi, A.; Brennan, M.J.; Waters, T.P.; Tang, B. On the effects of mistuning a force excited system containing a quasi-zero-stiffness vibration isolator. J. Vib. Acoust. 2015, 13, 44502. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, M.J.; Lineton, B. Effect of a static force on the dynamic behaviour of a harmonically excited quasi-zero stiffness system. J. Sound Vib. 2009, 325, 870–883. [Google Scholar] [CrossRef]
- Benedettini, F.; Rega, G. Nonlinear dynamics of an elastic cable under planar excitation. Int. J. Non-Linear Mech. 1987, 22, 497–509. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Amabili, M.; Carra, S. Thermal effects on geometrically nonlinear vibrations of rectangular plates with fixed edges. J. Sound Vib. 2009, 321, 936–954. [Google Scholar] [CrossRef]
- Chia, C.Y. Nonlinear Analysis of Plates; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Chia, C.Y. Geometrically nonlinear behavior of composite plates: A review. Appl. Mech. Rev. 1988, 41, 439–451. [Google Scholar] [CrossRef]
- Kerschen, G.; Worden, K.; Vakakis, A.F.; Golinval, J.C. Past, present and future of nonlinear system identification in structural dynamics. Mech. Syst. Signal Process. 2006, 20, 505–592. [Google Scholar] [CrossRef] [Green Version]
- Noël, J.P.; Kerschen, G. Nonlinear system identification in structural dynamics: 10 more years of progress. Mech. Syst. Signal Process. 2017, 83, 2–35. [Google Scholar] [CrossRef]
- Al-hababi, T.; Cao, M.S.; Saleh, B.; Alkayem, N.F.; Xu, H. A critical review of nonlinear damping identification in structural dynamics: Methods, applications, and challenges. Sensors 2020, 20, 7303. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Willey: New York, NY, USA, 1995. [Google Scholar] [CrossRef]
- Neild, S.A.; Wagg, D.J. Applying the method of normal forms to second-order nonlinear vibration problems. Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 467, 1141–1163. [Google Scholar] [CrossRef] [Green Version]
- Neild, S.A.; Champneys, A.R.; Wagg, D.J.; Hill, T.L.; Cammarano, A. The use of normal forms for analysing nonlinear mechanical vibrations. Philos. Trans. R. Soc. A 2015, 373, 20140404. [Google Scholar] [CrossRef]
- Elliott, A.J.; Cammarano, A.; Neild, S.A. Comparing analytical approximation methods with numerical results for nonlinear systems. In Proceedings of the Conference and Exposition on Structural Dynamics, Garden Grove, CA, USA, 30 January–2 February 2017; Volume 1, pp. 37–49. [Google Scholar] [CrossRef] [Green Version]
- Kerschen, G.; Peeters, M.; Golinval, J.C.; Vakakis, A.F. Nonlinear normal modes, Part I: A useful framework for the structural dynamicist. Mech. Syst. Signal Process. 2009, 23, 170–194. [Google Scholar] [CrossRef] [Green Version]
- Peeters, M.; Viguié, R.; Sérandour, G.; Kerschen, G.; Golinval, J.C. Nonlinear normal modes, Part II: Toward a practical computation using numerical continuation techniques. Mech. Syst. Signal Process. 2009, 23, 195–216. [Google Scholar] [CrossRef] [Green Version]
- Renson, L.; Kerschen, G.; Cochelin, B. Numerical computation of nonlinear normal modes in mechanical engineering. J. Sound Vib. 2016, 364, 177–206. [Google Scholar] [CrossRef] [Green Version]
- Naylor, S.; Platten, M.F.; Wright, J.R.; Cooper, J.E. Identification of multi-degree of freedom systems with nonproportional damping using the resonant decay method. J. Vib. Acoust. 2004, 126, 298–306. [Google Scholar] [CrossRef]
- Renson, L.; Gonzalez-Buelga, A.; Barton, D.A.W.; Neild, S.A. Robust identification of backbone curves using control-based continuation. J. Sound Vib. 2016, 367, 145–158. [Google Scholar] [CrossRef] [Green Version]
- Renson, L.; Shaw, A.D.; Barton, D.A.W.; Neild, S.A. Application of control-based continuation to a nonlinear structure with harmonically coupled modes. Mech. Syst. Signal Process. 2019, 120, 449–464. [Google Scholar] [CrossRef] [Green Version]
- Denis, V.; Jossic, M.; Giraud-Audin, C.; Chomette, B.; Renault, A.; Thomas, O. Identification of nonlinear modes using phase-locked-loop experimental continuation and normal form. Mech. Syst. Signal Process. 2018, 106, 430–452. [Google Scholar] [CrossRef] [Green Version]
- Peeters, M.; Kerschen, G.; Golinval, J.C. Dynamic testing of nonlinear vibrating structures using nonlinear normal modes. J. Sound Vib. 2011, 330, 486–509. [Google Scholar] [CrossRef] [Green Version]
- Peeters, M.; Kerschen, G.; Golinval, J.C. Modal testing of nonlinear vibrating structures based on nonlinear normal modes: Experimental demonstration. Mech. Syst. Signal Process. 2011, 25, 1227–1247. [Google Scholar] [CrossRef] [Green Version]
- Ehrhardt, D.A.; Allen, M.S. Measurement of nonlinear normal modes using multi-harmonic stepped force appropriation and free decay. Mech. Syst. Signal Process. 2016, 76–77, 612–633. [Google Scholar] [CrossRef]
- Breunung, T.; Haller, G. Explicit backbone curves from spectral submanifolds of forced-damped nonlinear mechanical systems. Proc. R. Soc. A 2018, 474, 20180083. [Google Scholar] [CrossRef] [Green Version]
- Cenedese, M.; Haller, G. Constructing backbone curves from free-decay vibrations data in multi-degrees of freedom oscillatory systems. In Proceedings of the Conference and Exposition on Structural Dynamics, Houston, TX, USA, 10–13 February 2020; Volume 1, pp. 221–223. [Google Scholar] [CrossRef]
- Londoño, J.M.; Neild, S.A.; Cooper, J.E. Identification of backbone curves of nonlinear systems from resonance decay responses. J. Sound Vib. 2015, 348, 224–238. [Google Scholar] [CrossRef] [Green Version]
- Tang, B.; Brennan, M.J.; Gatti, G.; Ferguson, N.S. Experimental characterization of a nonlinear vibration absorber using free vibration. J. Sound Vib. 2016, 367, 159–169. [Google Scholar] [CrossRef] [Green Version]
- Tang, B.; Wang, S.B.; Brennan, M.J.; Feng, L.Y.; Chen, W.C. Identifying the stiffness and damping of a nonlinear system using its free response perturbed with Gaussian white noise. J. Vib. Control. 2020, 26, 830–839. [Google Scholar] [CrossRef]
- Tang, B.; Brennan, M.J.; Lopes, V., Jr.; da Silva, S.; Ramlan, R. Using nonlinear jumps to estimate cubic stiffness nonlinearity: An experimental study. Proc. Inst. Mech. Eng. Part C 2016, 230, 3575–3581. [Google Scholar] [CrossRef] [Green Version]
- Londoño, J.M.; Cooper, J.E.; Neild, S.A. Identification of systems containing nonlinear stiffnesses using backbone curves. Mech. Syst. Signal Process. 2017, 84, 116–135. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.H.; Zhang, C.; Wang, L.; Chen, L.Y.; Xu, D.M.; Fan, H.W.; Zhu, F.L. A method for parameter identification of composite beam piezoelectric energy harvester. Sensors 2021, 21, 7213. [Google Scholar] [CrossRef]
- Civera, M.; Fragonara, L.Z.; Surace, C. Using Video processing for the full-field identification of backbone curves in case of large vibrations. Sensors 2019, 19, 2345. [Google Scholar] [CrossRef] [Green Version]
- Masri, S.F.; Caughey, T.K. A nonparametric identification technique for nonlinear dynamic problems. J. Appl. Mech. Trans. ASME 1979, 46, 433–447. [Google Scholar] [CrossRef]
- Feldman, M. Nonparametric identification of asymmetric nonlinear vibration systems with the Hilbert transform. J. Sound Vib. 2012, 331, 3386–3396. [Google Scholar] [CrossRef]
- Ondra, V.; Sever, I.A.; Schwingshackl, C.W. A method for non-parametric identification of non-linear vibration systems with asymmetric restoring forces from a resonant decay response. Mech. Syst. Signal Process. 2019, 114, 239–258. [Google Scholar] [CrossRef] [Green Version]
- Feldman, M. Hilbert transform in vibration analysis. Mech. Syst. Signal Process. 2011, 25, 735–802. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z.H.; Long, S.R.; Arnold, K.C.; Chen, X.Y.; Blank, K. On instantaneous frequency. Adv. Adapt. Data Anal. 2009, 1, 177–229. [Google Scholar] [CrossRef]
- Staszewski, W.J. Identification of non-linear systems using multi-scale ridges and skeletons of the wavelet transform. J. Sound Vib. 1998, 214, 639–658. [Google Scholar] [CrossRef]
- Ondra, V.; Riethmueller, R.; Brake, M.R.W.; Schwingshackl, C.W.; Polunin, P.M.; Shaw, S.W. Comparison of nonlinear system identification methods for free decay measurements with application to MEMS devices. In Proceedings of the Conference and Exposition on Structural Dynamics, Garden Grove, CA, USA, 30 January–2 February 2017; Volume 5, pp. 29–46. [Google Scholar] [CrossRef]
- Jin, M.S.; Brake, M.R.W.; Song, H.W. Comparison of nonlinear system identification methods for free decay measurements with application to jointed structures. J. Sound Vib. 2019, 453, 268–293. [Google Scholar] [CrossRef]
- Wang, S.B.; Tang, B. Estimating quadratic and cubic stiffness nonlinearity of a nonlinear vibration absorber with geometric imperfections. Measurement 2021, 185, 110005. [Google Scholar] [CrossRef]
- Feldman, M. Non-linear system vibration analysis using Hilbert transform-I. Free vibration analysis method ‘Freevib’. Mech. Syst. Signal Process. 1994, 8, 119–127. [Google Scholar] [CrossRef]
- Feldman, M. Non-linear system vibration analysis using Hilbert transform-II. Forced vibration analysis method ‘Forcevib’. Mech. Syst. Signal Process. 1994, 8, 309–318. [Google Scholar] [CrossRef]
- Feldman, M. Time-varying vibration decomposition and analysis based on the Hilbert transform. J. Sound Vib. 2006, 295, 518–530. [Google Scholar] [CrossRef]
- Feldman, M. Hilbert Transform. Applications in Mechanical Vibration; Wiley: Chichester, UK, 2011. [Google Scholar] [CrossRef]
- Bedrosian, E. A product theorem for Hilbert transforms. Proc. IEEE 1963, 51, 868–869. [Google Scholar] [CrossRef]
- Nuttall, A.H.; Bedrosian, E. On the quadrature approximation to the Hilbert transform of modulated signals. Proc. IEEE 1966, 54, 1458–1459. [Google Scholar] [CrossRef]
- Staszewski, W.J. Analysis of non-linear systems using wavelets. Proc. Inst. Mech. Eng. Part C 2000, 214, 1339–1353. [Google Scholar] [CrossRef]
- Le, T.P.; Argoul, P. Continuous wavelet transform for modal identification using free decay response. J. Sound Vib. 2004, 277, 73–100. [Google Scholar] [CrossRef]
- Ta, M.N.; Lardis, J. Identification of weak nonlinearities on damping and stiffness by the continuous wavelet transform. J. Sound Vib. 2006, 293, 16–37. [Google Scholar] [CrossRef]



| k1 (N/m) | k2 (N/m2) | k3 (N/m3) | ||||
|---|---|---|---|---|---|---|
| RFCM | BCM | RFCM | BCM | RFCM | BCM | |
| HT | 3940.7 (1.48%) | 4082.0 (2.05%) | −1.002 × 107 (0.20%) | −1.007 × 107 (0.73%) | 9.998 × 109 (0.02%) | 1.023 × 1010 (2.31%) |
| ZC | 4051.5 (1.29%) | 4050.6 (1.27%) | −8.381 × 106 (16.19%) | −9.873 × 106 (1.27%) | 7.213 × 1010 (27.87%) | 1.003 × 1010 (0.31%) |
| DQ | 4052.5 (1.31%) | 4066.5 (1.66%) | −8.273 × 106 (17.27%) | −9.923 × 106 (0.77%) | 7.262 × 109 (27.38%) | 1.008 × 1010 (0.76%) |
| WT | 3989.1 (0.27%) | −9.977 × 106 (0.23%) | 1.043 × 1010 (4.28%) | |||
| True value | 4000 | −107 | 1010 | |||
| c (Ns/m) | LEM | DFCM |
|---|---|---|
| HT | 0.381 (4.80%) | 0.402 (0.37%) |
| ZC | 0.377 (5.76%) | 0.406 (1.58%) |
| DQ | 0.381 (4.82%) | 0.408 (2.02%) |
| WT | 0.370 (7.60%) | 0.405 (1.30%) |
| True value | 0.4 | |
| k1 (N/m) | k2 (N/m2) | k3 (N/m3) | ||||
|---|---|---|---|---|---|---|
| RFCM | BCM | RFCM | BCM | RFCM | BCM | |
| HT | 4837.7 | 4272.9 | −2.252 × 107 | −2.155 × 107 | 5.705 × 1010 | 6.346 × 1010 |
| ZC | 5452.3 | 4265.7 | −2.461 × 107 | −2.109 × 107 | 4.822 × 1010 | 6.302 × 1010 |
| DQ | 5597.5 | 4949.9 | −2.193 × 107 | −2.776 × 107 | 5.123 × 1010 | 8.614 × 1010 |
| WT | 4137.9 | −2.152 × 107 | 7.096 × 1010 | |||
| c (Ns/m) | LEM | DFCM |
|---|---|---|
| HT | 0.234 | 0.320 |
| ZC | 0.232 | 0.317 |
| DQ | 0.232 | 0.325 |
| WT | 0.230 | 0.311 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Tang, B. A Comparative Study of Parameter Identification Methods for Asymmetric Nonlinear Systems with Quadratic and Cubic Stiffness. Sensors 2022, 22, 5854. https://doi.org/10.3390/s22155854
Wang S, Tang B. A Comparative Study of Parameter Identification Methods for Asymmetric Nonlinear Systems with Quadratic and Cubic Stiffness. Sensors. 2022; 22(15):5854. https://doi.org/10.3390/s22155854
Chicago/Turabian StyleWang, Shibo, and Bin Tang. 2022. "A Comparative Study of Parameter Identification Methods for Asymmetric Nonlinear Systems with Quadratic and Cubic Stiffness" Sensors 22, no. 15: 5854. https://doi.org/10.3390/s22155854






