A New De-Noising Method Based on Enhanced Time-Frequency Manifold and Kurtosis-Wavelet Dictionary for Rolling Bearing Fault Vibration Signal
Abstract
:1. Introduction
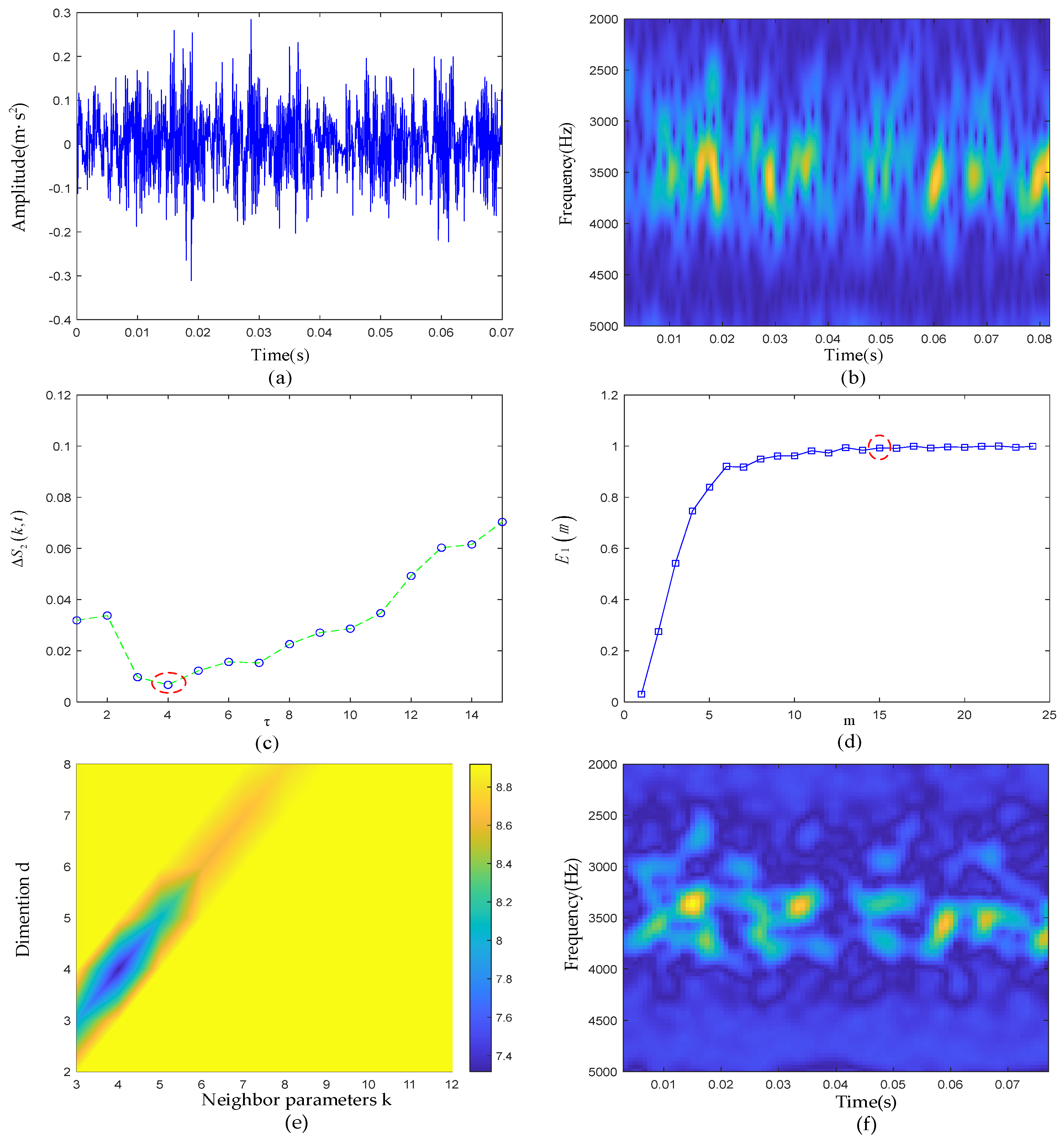
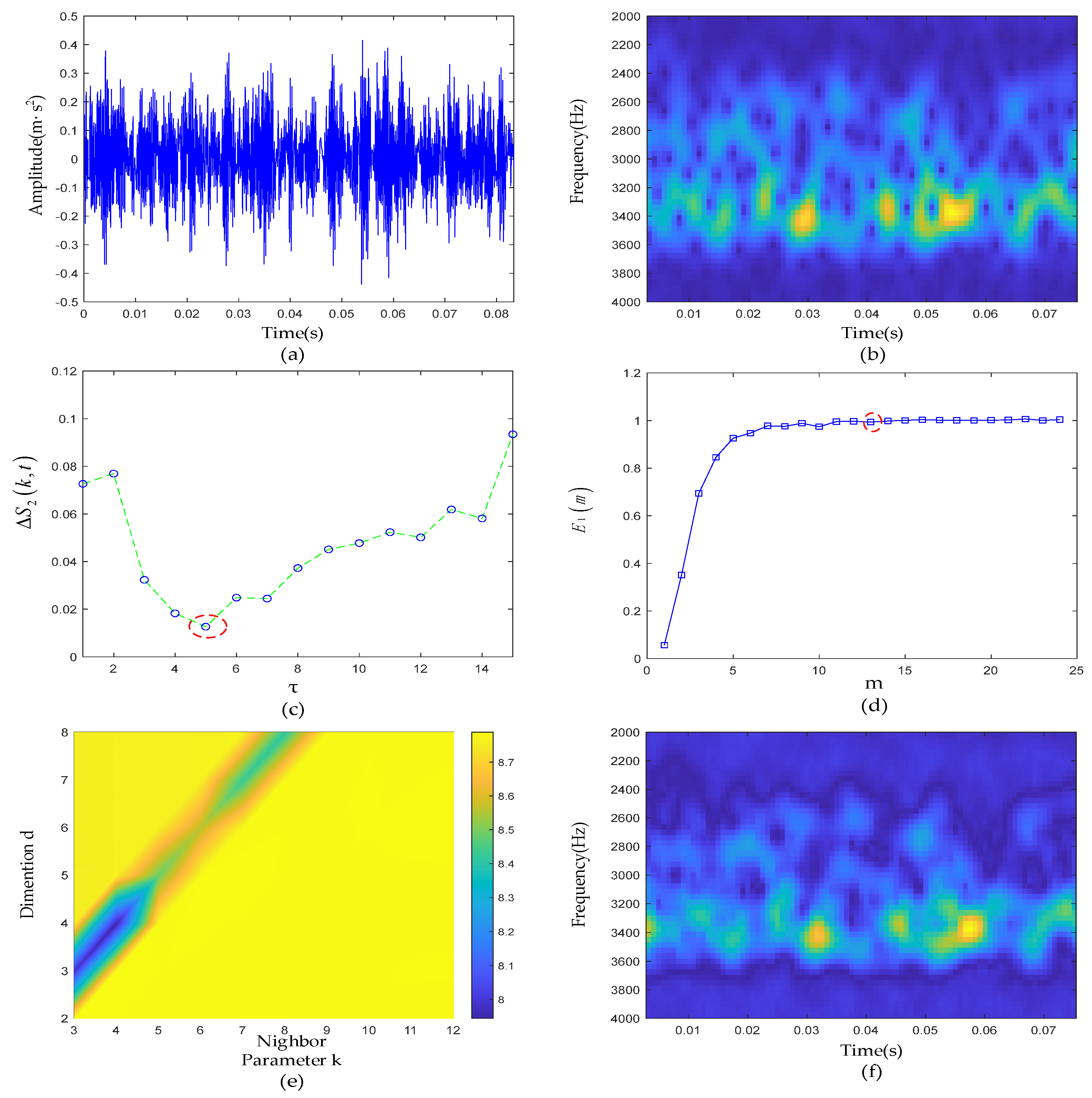
- We propose a method of using C-C method and Cao’s method jointly to determine the time delay and embedding dimension of phase space reconstruction, which reduces the distortion degree of reconstruction space and highlights the fault characteristics.
- LLTSA is optimized by a gridded parameter search method based on Renyi entropy to obtain ETFM with high time-frequency resolution.
- The proposed kurtosis-wavelet dictionary can adaptively select the optimal atomic position with the change of kurtosis, which improves the noise suppression effect and feature extraction ability of sparse representation.
2. Methodology
2.1. Parameter Optimization Phase Space Reconstruction
- Determine the optimal time delay by the C-C method [13]
- 2.
- Determine the optimal embedding dimension [11]
2.2. Enhanced Time-Frequency Manifold
- The time delay τ and the embedding dimension m are obtained by the C-C and Cao’s methods, and the phase space matrix is obtained by the PSR.
- The time-frequency analysis is performed on each time series of the phase space matrix by the STFT, and then the amplitude matrix is obtained.
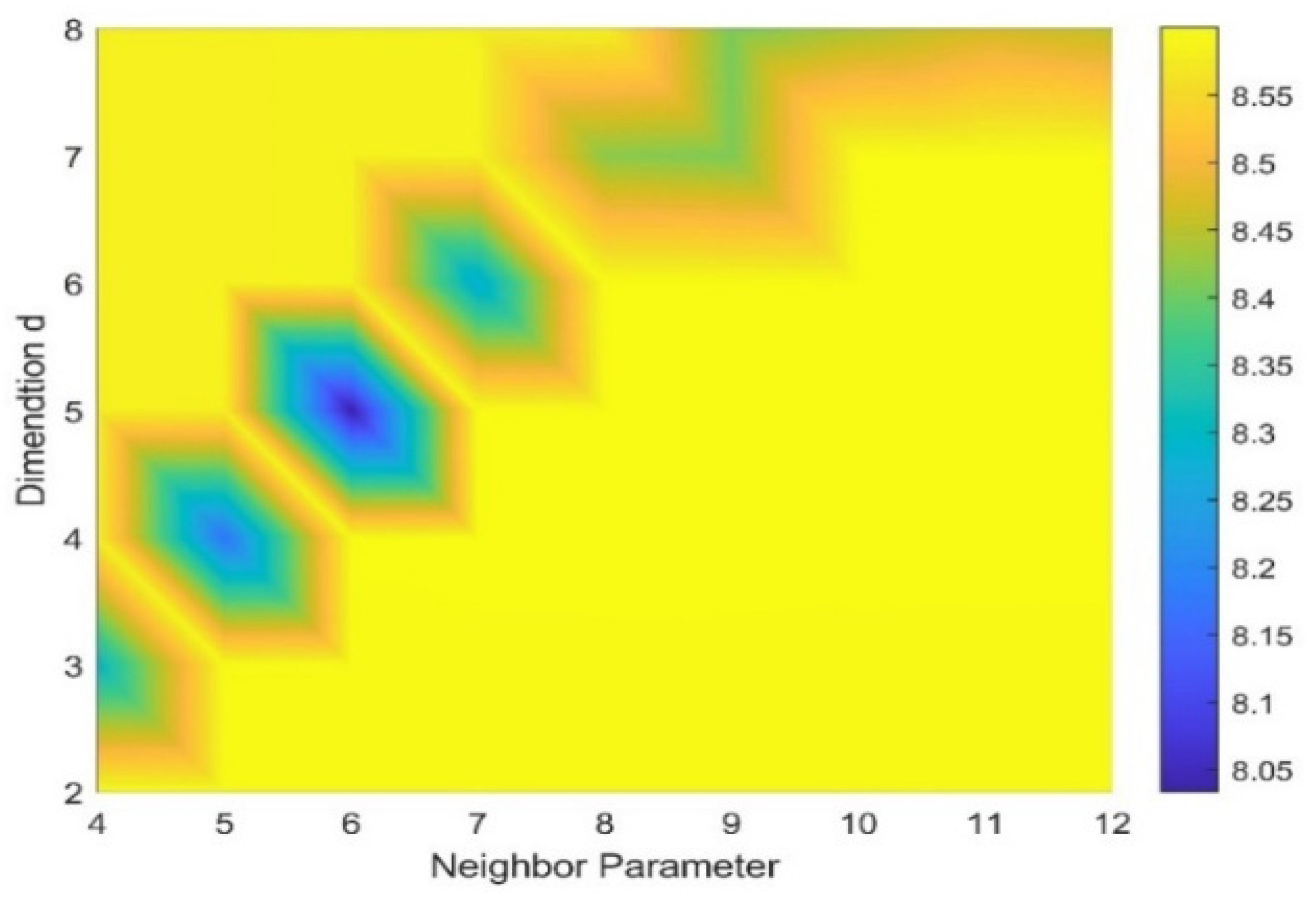
- Set the grid search initialization parameters of LLTSA, the search step size is 1
- Using the grid search method, the Renyi entropy value of TFM in each search is calculated, and the corresponding to the smallest Renyi entropy value is taken as the optimal input parameters of LLTSA.
2.3. Sparse Representation Based on Kurtosis-Wavelet Dictionary
2.3.1. Sparse Representation Principle
2.3.2. ETFM Reconstruction Using Kurtosis-Wavelet Dictionary
3. Complete Framework of the Proposed Method
- PSR: the C-C method and Cao’s method jointly determine the best time delay and the best embedding dimension m, and the PSR technology maps the raw signal to the high-dimensional space. High-dimensional spatial time-frequency features are mined by STFT and divided into amplitude matrix and phase matrix.
- Enhance time-frequency manifold learning: LLTSA is optimized by the gridding search method, and the important features in the high-dimensional space are mined to obtain ETFM, which completes the preliminary noise reduction of the signal.
- Kurtosis-wavelet dictionary generation: divide the raw signal into several segments and calculate the kurtosis of each segment. Set time-frequency wavelet atoms in the signal segment with large kurtosis to complete the construction of kurtosis-wavelet dictionary
- Sparse representation: use the OMP algorithm to solve the sparse representation problem of ETFM and update the kurtosis-wavelet dictionary at the same time. The reconstruction result of the amplitude matrix is obtained by Equations (19) and (20). Then, the reconstructed amplitude matrix is combined with the phase matrix and restored to a one-dimensional signal by the inverse STFT and phase space reconstruction technology.
4. Experimental Results
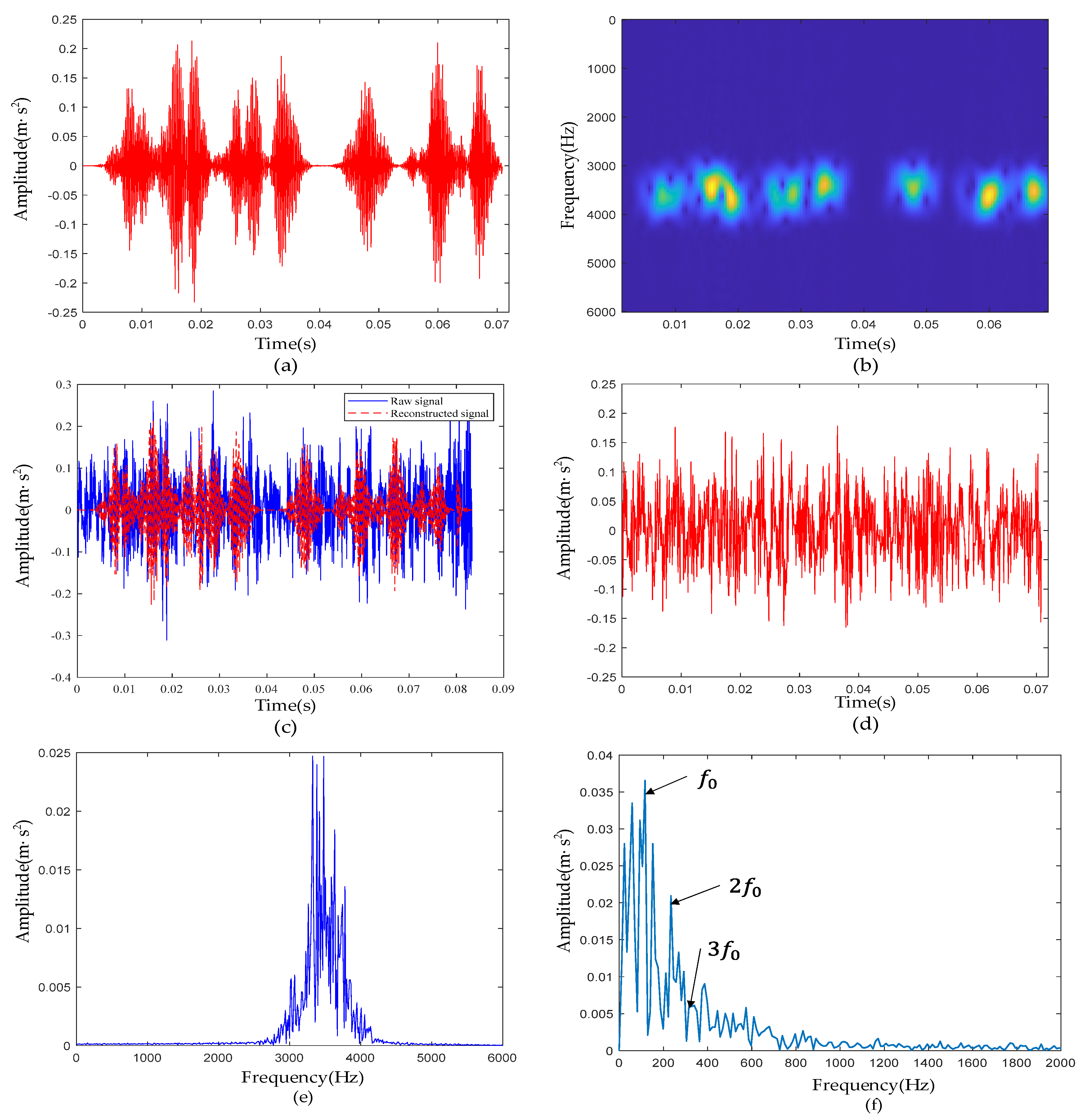
4.1. Experimental Results of Inner-Race Defective Signal
4.1.1. Experimental Results of PSR
4.1.2. Experimental Results of ETFM
4.1.3. Experimental Results of Signal De-Noising
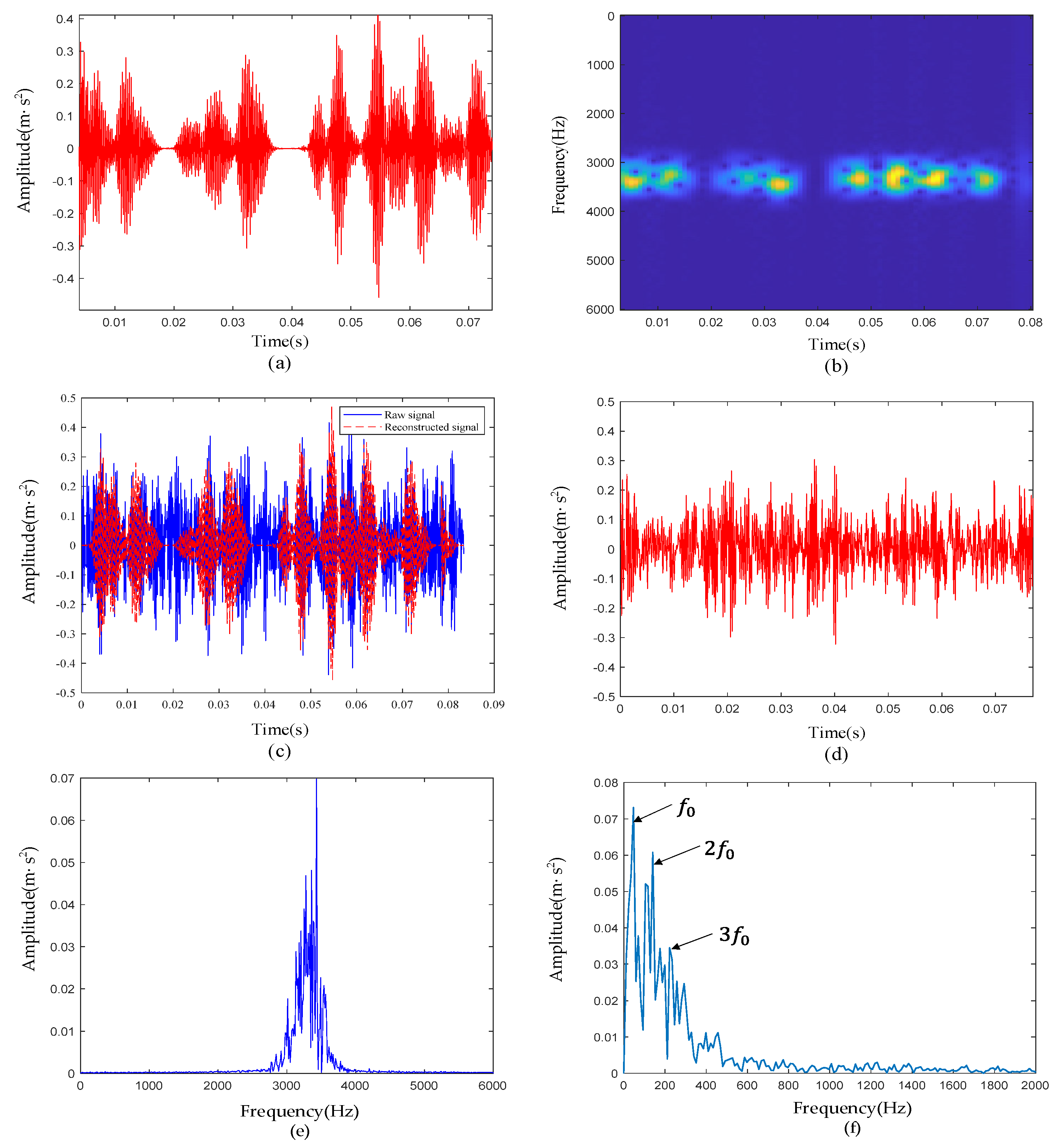
4.2. Experimental Results of Outer-Race Defective Signal
4.3. Experimental Results of Rolling-Element Defective Signal
5. Discussion
5.1. Ablation Experiment
5.2. Comparison with Other Methods
- Discrete wavelet transform (DWT): the specific reconstruction effect is shown in Figure 16a,b. It can be clearly seen from the time-frequency diagram that the high-frequency noise above 4000 Hz was basically filtered out, but the noise suppression effect in other frequency bands was poor. Compared with the time-frequency diagram of the raw signal, the transient pulses at approximately 0.07 s were not reconstructed, resulting in a certain degree of loss of defective features.
- Continuous wavelet transform (CWT): the specific reconstruction effect is shown in Figure 16c,d. Compared with the reconstruction result in Figure 16a,b, it had a good noise suppression effect in both the low-frequency band and high-frequency band, and completely reconstructed all transient pulses. However, the signal de-noising effect was poor at the resonance frequency of 3000 Hz.
- Wavelet packet transform (WPT): the specific reconstruction effect is shown in Figure 16e,f. The number of decomposition layers of WPT was 3. Since the sampling frequency of the signal was 12 kHz, according to Nyquist’s law, the frequency difference of the nodes in the third-level wavelet tree was 6000/8 = 750 Hz. Here, we chose the fourth and fifth wavelet nodes whose frequencies ranged from 2250 to 3750 Hz. From the time-frequency analysis results of the reconstructed signal, it can be clearly seen that compared with the filtering algorithm of CWT, the frequency band at the center frequency of 3000 Hz was narrower. However, the noise in the resonance band was still not filtered out, and it can be seen from Figure 16e that the transient pulses were submerged in a large amount of noise.
- The filtering effect based on the EMD algorithm is shown in Figure 16g,h, and the IMF whose center frequency was approximately 3000 Hz was selected as the reconstructed signal. It can be seen from its time-frequency diagram that the reconstructed signal contained considerable noise because the EMD algorithm had bandpass filtering characteristics for white noise.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Antoni, J. Cyclic spectral analysis of rolling-element bearing signals: Facts and fictions. J. Sound Vib. 2007, 304, 497–529. [Google Scholar] [CrossRef]
- Schoen, R.R.; Habetler, T.G.; Kamran, F.; Bartheld, R.G. Motor bearing damage detection using stator current monitoring. IEEE Trans. Ind. Appl. 1995, 31, 1274–1279. [Google Scholar] [CrossRef]
- Tavner, P.J. Review of condition monitoring of rotating electrical machines. Iet Electr. Power Appl. 2008, 2, 215–247. [Google Scholar] [CrossRef]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Dron, J.P.; Bolaers, F.; Rasolofondraibe, I. Improvement of the sensitivity of the scalar indicators (crest factor, kurtosis) using a denoising method by spectral subtraction: Application to the detection of defects in ball bearings. J. Sound Vib. 2004, 270, 61–73. [Google Scholar] [CrossRef]
- Abdelkader, R.; Derouiche, Z.; Kaddour, A.; Zergoug, M. Rolling Bearing Faults Diagnosis Based on Empirical Mode Decomposition: Optimized Threshold De-noising Method. In Proceedings of the 8th International Conference on Modelling, Identification and Control (ICMIC), Algiers, Algeria, 15–17 November 2016; pp. 186–191. [Google Scholar]
- Zhang, Z.Y.; Zhang, X.; Zhang, P.P.; Wu, F.B.; Li, X.H. Compound fault extraction method via self-adaptively determining the number of decomposition layers of the variational mode decomposition. Rev. Sci. Instrum. 2018, 89, 7. [Google Scholar] [CrossRef]
- Ambrokiewicz, B.; Syta, A.; Meier, N.; Litak, G.; Georgiadis, A. Radial internal clearance analysis in ball bearings. Eksploat. I Niezawodn. Maint. Reliab. 2021, 23, 42–54. [Google Scholar] [CrossRef]
- Takens, F. Determing strange attractors in turbence. Lect. Notes Math 1981, 898, 361–381. [Google Scholar]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2003; pp. 30–47. [Google Scholar]
- Cao, L. Practical method for determining the minimum embedding dimension of a scalar time series. Phys. D Nonlinear Phenom. 1997, 110, 43–50. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Jia, J.; Gao, M.; Han, X. Study on the parameters determination for reconstructing phase-space in chaos time series. Acta Phys. Sin. 2010, 59, 1576–1582. [Google Scholar] [CrossRef]
- Kim, H.S.; Eykholt, R.; Salas, J.D. Nonlinear dynamics, delay times, and embedding windows. Physica D 1999, 1271, 48–60. [Google Scholar] [CrossRef]
- Kugiumtzis, D. State space reconstruction parameters in the analysis of chaotic time series—The role of the time window length. Phys. D Nonlinear Phenom. 1996, 95, 13–28. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.Z.; Wei, X. A hybrid wind speed forecasting model based on phase space reconstruction theory and Markov model: A case study of wind farms in northwest China. Energy 2015, 91, 556–572. [Google Scholar] [CrossRef]
- Chen, X.G.; Liu, D.; Xu, G.H.; Jiang, K.S.; Liang, L. Application of Wavelet Packet Entropy Flow Manifold Learning in Bearing Factory Inspection Using the Ultrasonic Technique. Sensors 2015, 15, 341–351. [Google Scholar] [CrossRef]
- Fu, X.W.; Wang, H.; Li, B.; Gao, X.G. An Efficient Sampling-Based Algorithms Using Active Learning and Manifold Learning for Multiple Unmanned Aerial Vehicle Task Allocation under Uncertainty. Sensors 2018, 18, 2645. [Google Scholar] [CrossRef] [PubMed]
- Leon-Medina, J.X.; Anaya, M.; Pozo, F.; Tibaduiza, D. Nonlinear Feature Extraction Through Manifold Learning in an Electronic Tongue Classification Task. Sensors 2020, 20, 4834. [Google Scholar] [CrossRef] [PubMed]
- Shah, M.; Zainal, A.; Ghaleb, F.A.; Al-Qarafi, A.; Saeed, F. Prototype Regularized Manifold Regularization Technique for Semi-Supervised Online Extreme Learning Machine. Sensors 2022, 22, 3113. [Google Scholar] [CrossRef] [PubMed]
- Yao, B.B.; Zhen, P.; Wu, L.F.; Guan, Y. Rolling Element Bearing Fault Diagnosis Using Improved Manifold Learning. IEEE Access 2017, 5, 6027–6035. [Google Scholar] [CrossRef]
- Zhang, T.H.; Yang, J.; Zhao, D.L.; Ge, X.L. Linear local tangent space alignment and application to face recognition. Neurocomputing 2007, 70, 1547–1553. [Google Scholar] [CrossRef]
- Tang, G.J.; Wang, X.L.; He, Y.L. A Novel Method of Fault Diagnosis for Rolling Bearing Based on Dual Tree Complex Wavelet Packet Transform and Improved Multiscale Permutation Entropy. Math. Probl. Eng. 2016, 2016, 13. [Google Scholar] [CrossRef]
- He, Q.B.; Liu, Y.B.; Long, Q.; Wang, J. Time-Frequency Manifold as a Signature for Machine Health Diagnosis. IEEE Trans. Instrum. Meas. 2012, 61, 1218–1230. [Google Scholar] [CrossRef]
- Noman, K.; He, Q.B.; Peng, Z.K.; Wang, D. A scale independent flexible bearing health monitoring index based on time frequency manifold energy & entropy. Meas. Sci. Technol. 2020, 31, 20. [Google Scholar] [CrossRef]
- Cao, X.W.; Cheng, Y.Q.; Wu, H.; Wang, H.Q. Nonstationary Moving Target Detection in Spiky Sea Clutter via Time-Frequency Manifold. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5. [Google Scholar] [CrossRef]
- He, Q.B.; Liu, Y.B.; Wang, J.; Wang, J.J.; Gong, C. Time-Frequency Manifold for Gear Fault Signature Analysis. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Hangzhou, China, 10–12 May 2011; pp. 491–495. [Google Scholar]
- Li, B.C. Time-Frequency Manifold Representation for Separating and Classifying Frequency Modulation Signals. In Proceedings of the Conference on Radar Sensor Technology XXV, Electr Network, online, 12–16 April 2021. [Google Scholar]
- Kumar, A.; Kumar, R. Manifold Learning Using Linear Local Tangent Space Alignment (LLTSA) Algorithm for Noise Removal in Wavelet Filtered Vibration Signal. J. Nondestruct. Eval. 2016, 35, 10. [Google Scholar] [CrossRef]
- Qin, Y. A New Family of Model-Based Impulsive Wavelets and Their Sparse Representation for Rolling Bearing Fault Diagnosis. IEEE Trans. Ind. Electron. 2018, 65, 2716–2726. [Google Scholar] [CrossRef]
- He, G.L.; Ding, K.; Lin, H.B. Fault feature extraction of rolling element bearings using sparse representation. J. Sound Vibr. 2016, 366, 514–527. [Google Scholar] [CrossRef]
- He, Q.B. Time-Frequency Manifold Histogram Matching for Transient Signal Detection. In Proceedings of the 32nd Annual IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Pisa, Italy, 11–14 May 2015; pp. 584–587. [Google Scholar]
- Zhang, D.Q.; Ding, X.X.; Huang, W.B.; He, Q.B. Transient Signal Analysis Using Parallel Time-Frequency Manifold Filtering for Bearing Health Diagnosis. IEEE Access 2019, 7, 175277–175289. [Google Scholar] [CrossRef]
- Tang, H.F.; Chen, J.; Dong, G.M. Sparse representation based latent components analysis for machinery weak fault detection. Mech. Syst. Signal Proc. 2014, 46, 373–388. [Google Scholar] [CrossRef]
- Zheng, W.B.; Jin, X.; Deng, F.; Mo, S.C.; Qu, Y.L.; Fan, Z.Y.; Zhou, J.W.; Zou, R.; Shuai, J.; Xie, Z.F.; et al. Face Recognition Based on Weighted Multi-channel Gabor Sparse Representation and Optimized ExtremeLearning Machines. In Proceedings of the 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 13–16 December 2017; pp. 1616–1620. [Google Scholar]
- Fan, W.; Zhu, Z.K.; Huang, W.G.; Cai, G.G. Sparse Representation De-noising Based on Morlet Wavelet Basis and its Application for Transient Feature Extraction. In Proceedings of the International Conference on Mechanical Engineering and Instrumentation (ICMEI), Brisbane, Australia, 31 December–2 January 2013; pp. 200–204. [Google Scholar]
- Zhou, H.T.; Chen, J.; Dong, G.M.; Wang, R. Detection and diagnosis of bearing faults using shift-invariant dictionary learning and hidden Markov model. Mech. Syst. Signal Proc. 2016, 72–73, 65–79. [Google Scholar] [CrossRef]
- Ren, L.K.; Lv, W.M. Sparse Representation Based Fault Diagnosis of Bearings. In Proceedings of the Prognostics and System Health Management Conference (PHM-Chengdu), Chengdu, China, 19–21 October 2016. [Google Scholar]
- Kong, Y.; Wang, T.Y.; Feng, Z.P.; Chu, F.L. Discriminative dictionary learning based sparse representation classification for intelligent fault identification of planet bearings in wind turbine. Renew. Energy 2020, 152, 754–769. [Google Scholar] [CrossRef]

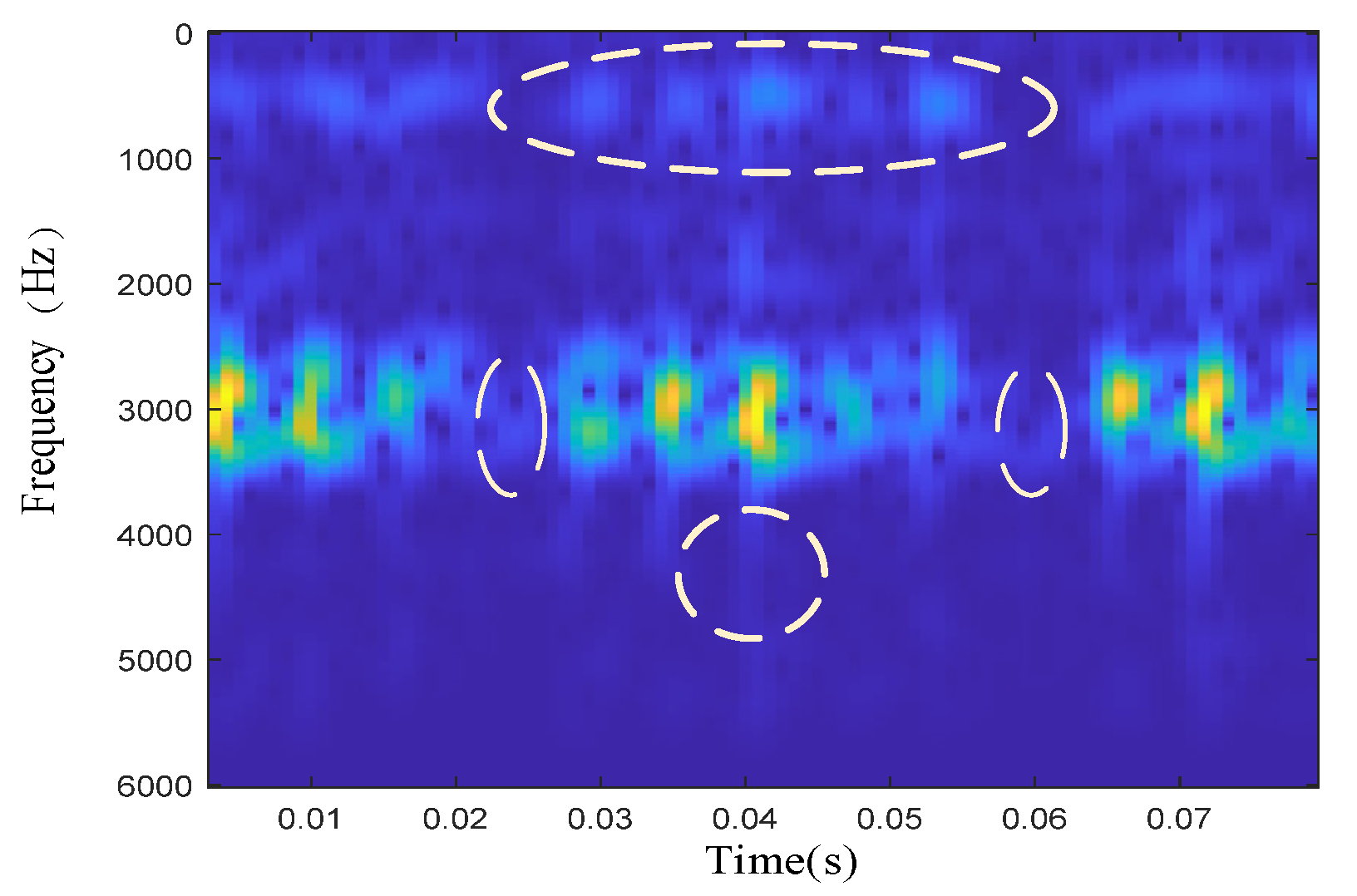
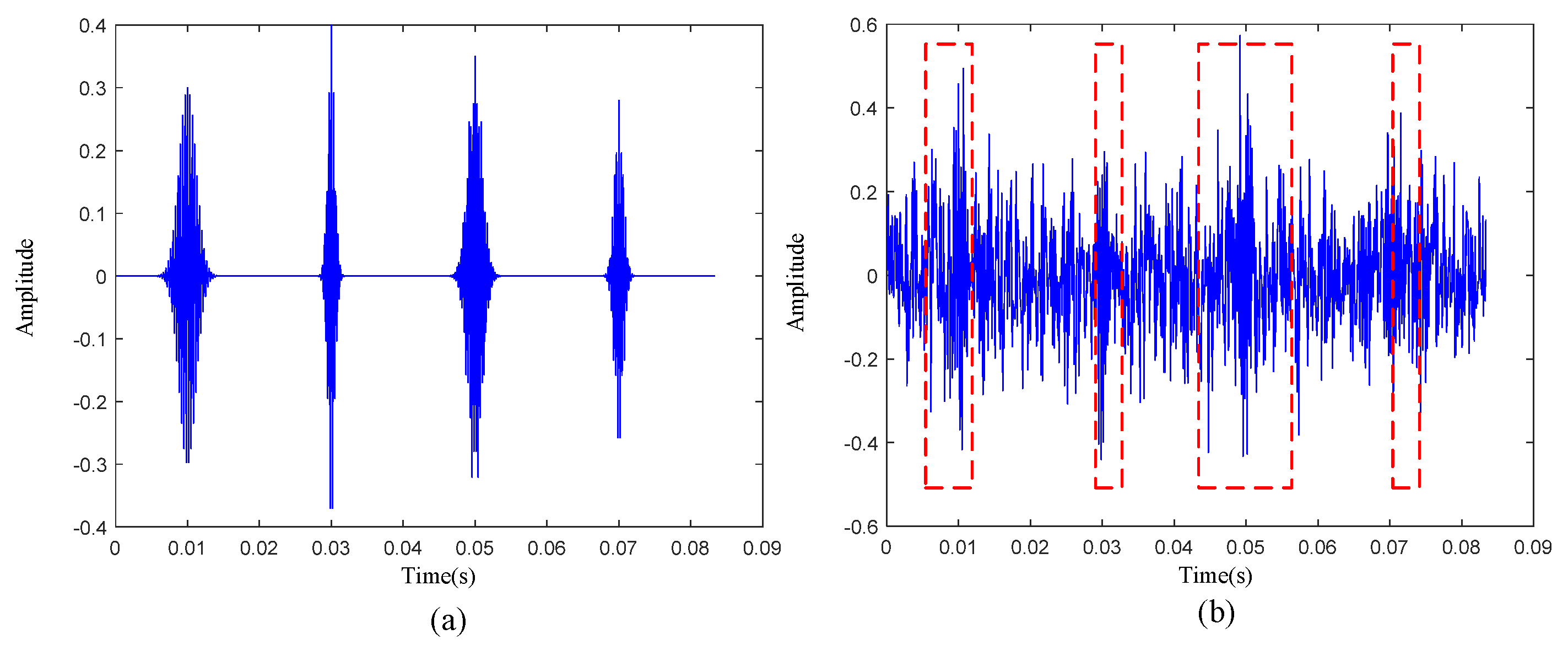


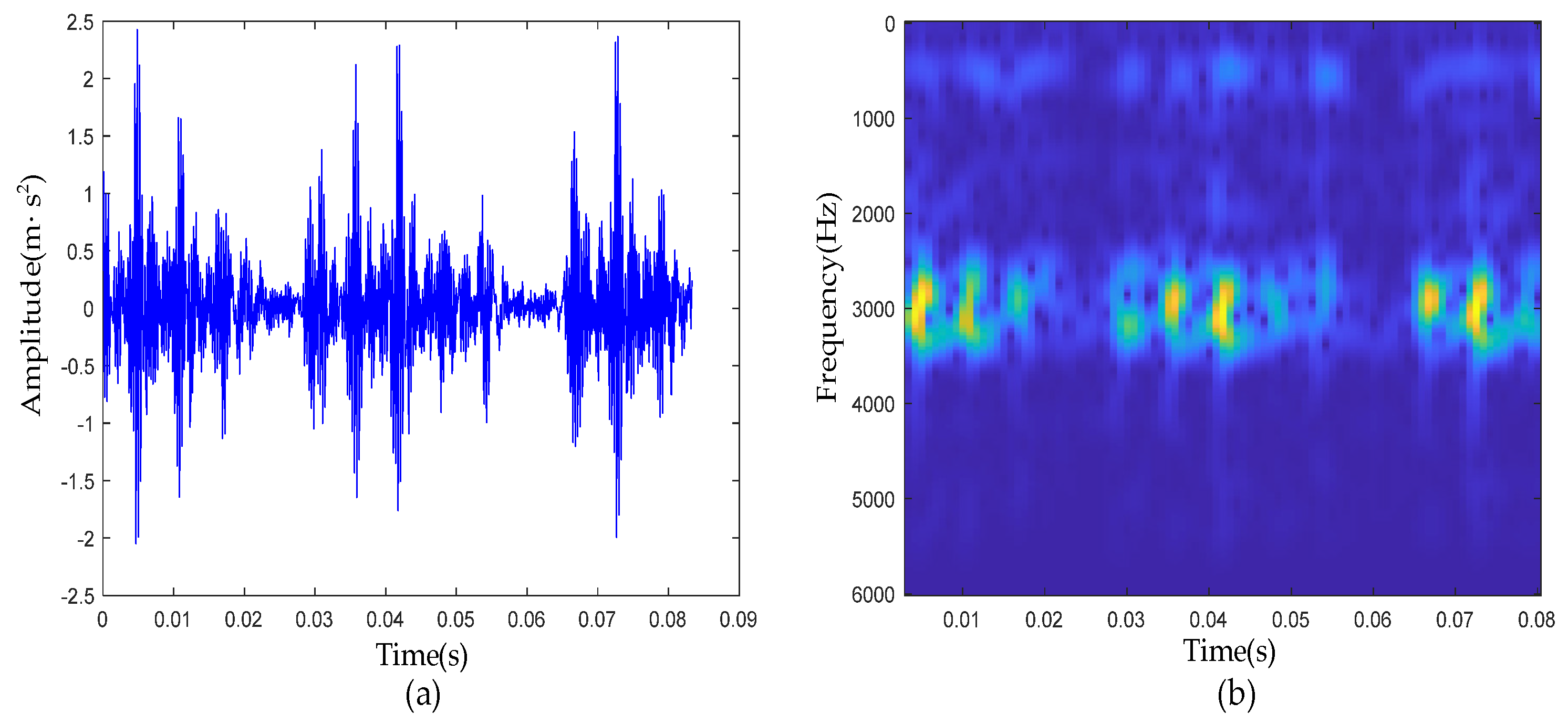






| Defect Type | Inner-Race | Outer-Race | Rolling Element |
|---|---|---|---|
| Defect size | 0.5334 mm | 0.3556 mm | 0.1778 mm |
| RPM | 1797 | 1750 | 1750 |
| Characteristic Frequency | 162 Hz | 105 Hz | 60 Hz |
| Control Parameters | C-C | Cao | C-C + Cao |
|---|---|---|---|
| Fuzzy entropy | 0.2641 | 0.2657 | 0.2619 |
| MSE | 0.2494 | 1.0324 | 0.2479 |
| Control Parameters | Raw Signal | ETFM | LLTSA-TFM | LTSA-TFM |
|---|---|---|---|---|
| Renyi entropy | 8.211 | 8.033 | 8.192 | 8.201 |
| Methods | MSE | Reconstructed Signal Energy | Reconstructed Signal Renyi Entropy |
|---|---|---|---|
| The proposed method | 0.0214 | 12.267 | 14.476 |
| Method 1 | 0.0213 | 12.471 | 15.666 |
| Method 2 | 0.0213 | 13.845 | 15.750 |
| Algorithms | Renyi Entropy | Kurtosis of the Reconstructed Signal |
|---|---|---|
| The proposed method | 7.648 | 12.266 |
| DWT | 8.283 | 7.307 |
| CWT | 7.697 | 6.350 |
| WPT | 8.227 | 5.419 |
| EMD | 7.931 | 6.464 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, Q.; Liu, Z.; Lu, F.; Feng, Z.; Wan, Q. A New De-Noising Method Based on Enhanced Time-Frequency Manifold and Kurtosis-Wavelet Dictionary for Rolling Bearing Fault Vibration Signal. Sensors 2022, 22, 6108. https://doi.org/10.3390/s22166108
Tong Q, Liu Z, Lu F, Feng Z, Wan Q. A New De-Noising Method Based on Enhanced Time-Frequency Manifold and Kurtosis-Wavelet Dictionary for Rolling Bearing Fault Vibration Signal. Sensors. 2022; 22(16):6108. https://doi.org/10.3390/s22166108
Chicago/Turabian StyleTong, Qingbin, Ziyu Liu, Feiyu Lu, Ziwei Feng, and Qingzhu Wan. 2022. "A New De-Noising Method Based on Enhanced Time-Frequency Manifold and Kurtosis-Wavelet Dictionary for Rolling Bearing Fault Vibration Signal" Sensors 22, no. 16: 6108. https://doi.org/10.3390/s22166108
APA StyleTong, Q., Liu, Z., Lu, F., Feng, Z., & Wan, Q. (2022). A New De-Noising Method Based on Enhanced Time-Frequency Manifold and Kurtosis-Wavelet Dictionary for Rolling Bearing Fault Vibration Signal. Sensors, 22(16), 6108. https://doi.org/10.3390/s22166108






