Vibration Prediction of the Robotic Arm Based on Elastic Joint Dynamics Modeling
Abstract
:1. Introduction
2. The Dynamic Modeling of the Prediction Function
2.1. Vibration Modeling of the Articulated Robot Arm under Electromagnetic Torque
2.2. Parameters Identification Model under the External Torque
2.2.1. The Single-Degree-of-Freedom Systems
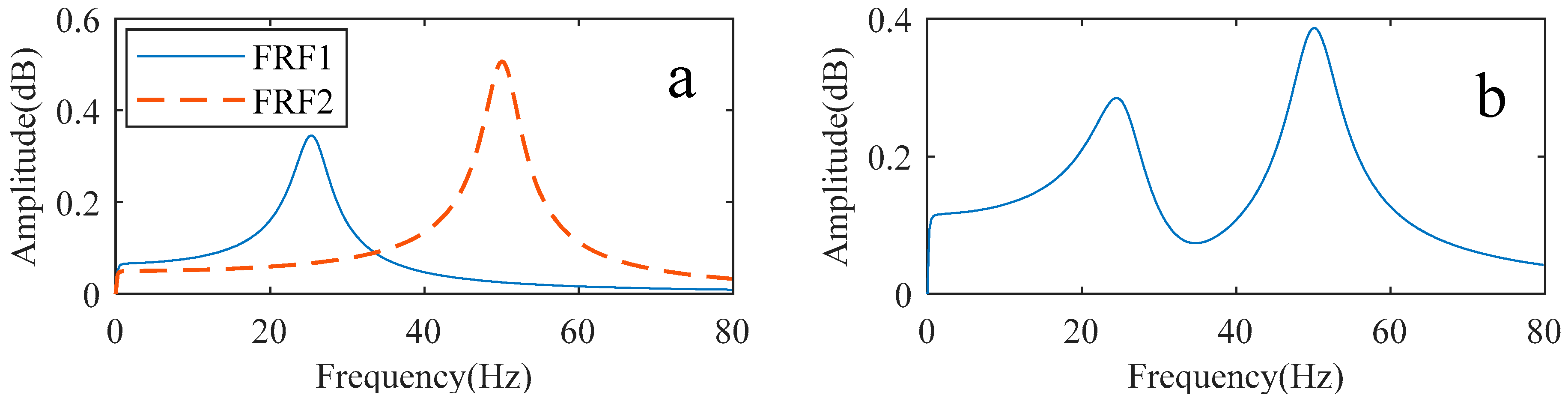
2.2.2. The Multi-Degree-of-Freedom Systems
2.3. Summary
- (1)
- The dynamics model of the servo system is established under the action of external forces when the motor is stationary and holding the brake.
- (2)
- Using the shock signal to excite the system of stationary holding brake to obtain the system frequency response function (FRF).
- (3)
- The unknown parameters of the system are determined by the direct parameter method.
- (4)
- The transfer relationship from the electromagnetic torque of the motor to the vibration acceleration of the load when the motor is in motion is determined. Additionally, the vibration prediction function is established according to this transfer relationship.
- (5)
- When the servo system moves, the electromagnetic torque signal of the motor is obtained.
- (6)
- The vibration prediction function is determined based on the identification parameters and known parameters.
- (7)
- The spectrum of predicted vibration is determined by the motor’s electromagnetic torque signal and the vibration prediction function.
3. Experiments on a Single-Joint Test Bench
3.1. Experimental Setup
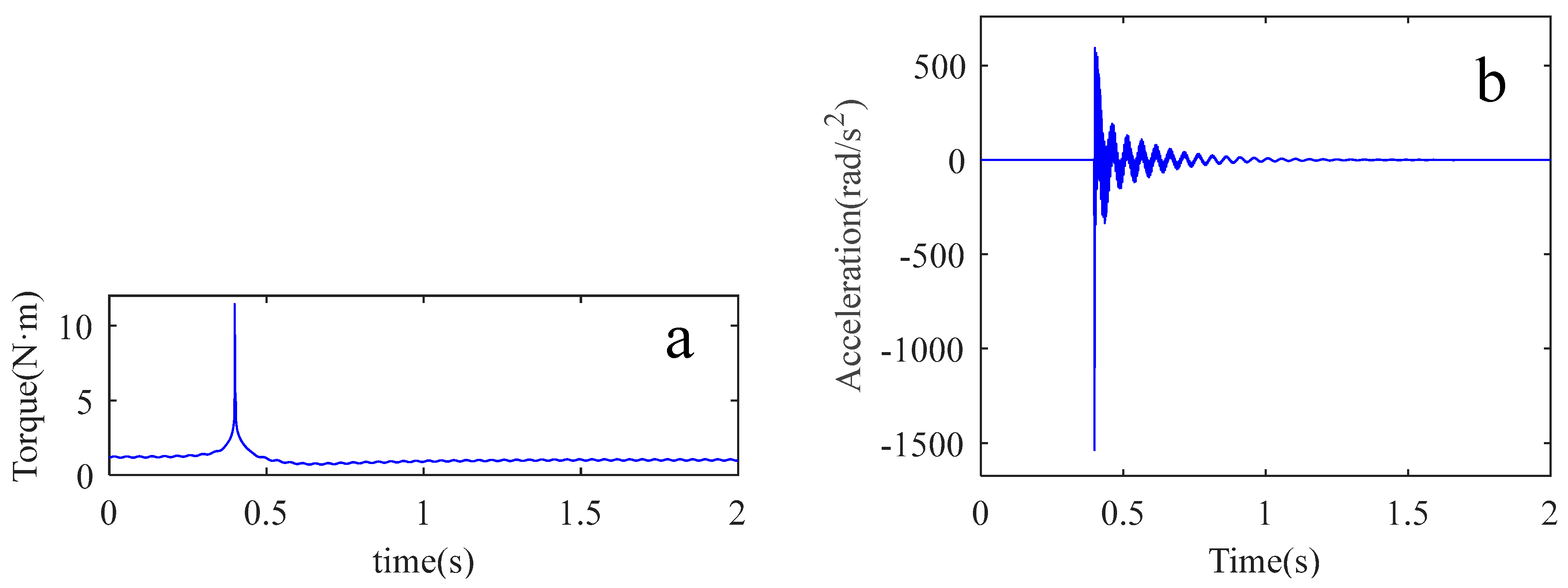
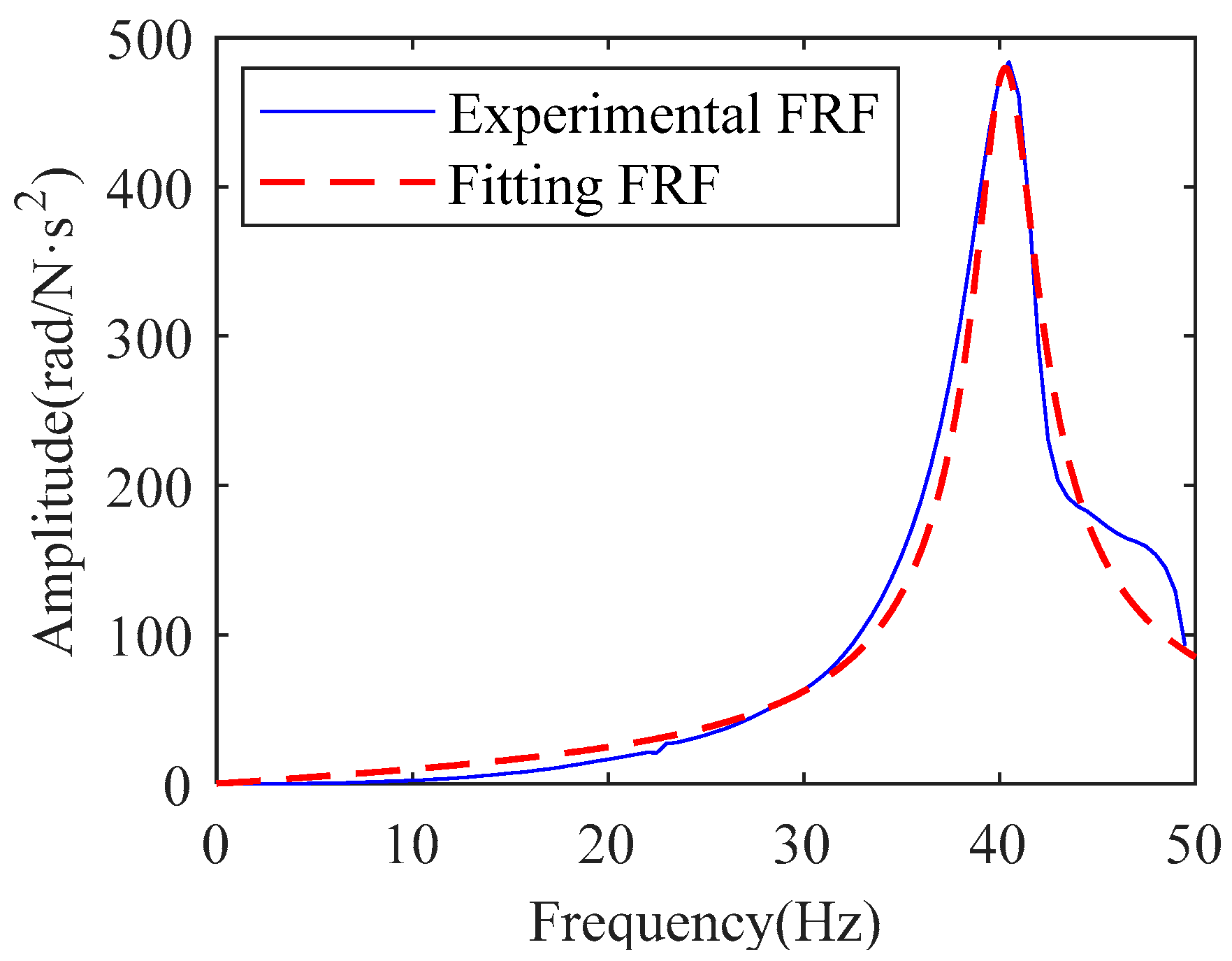
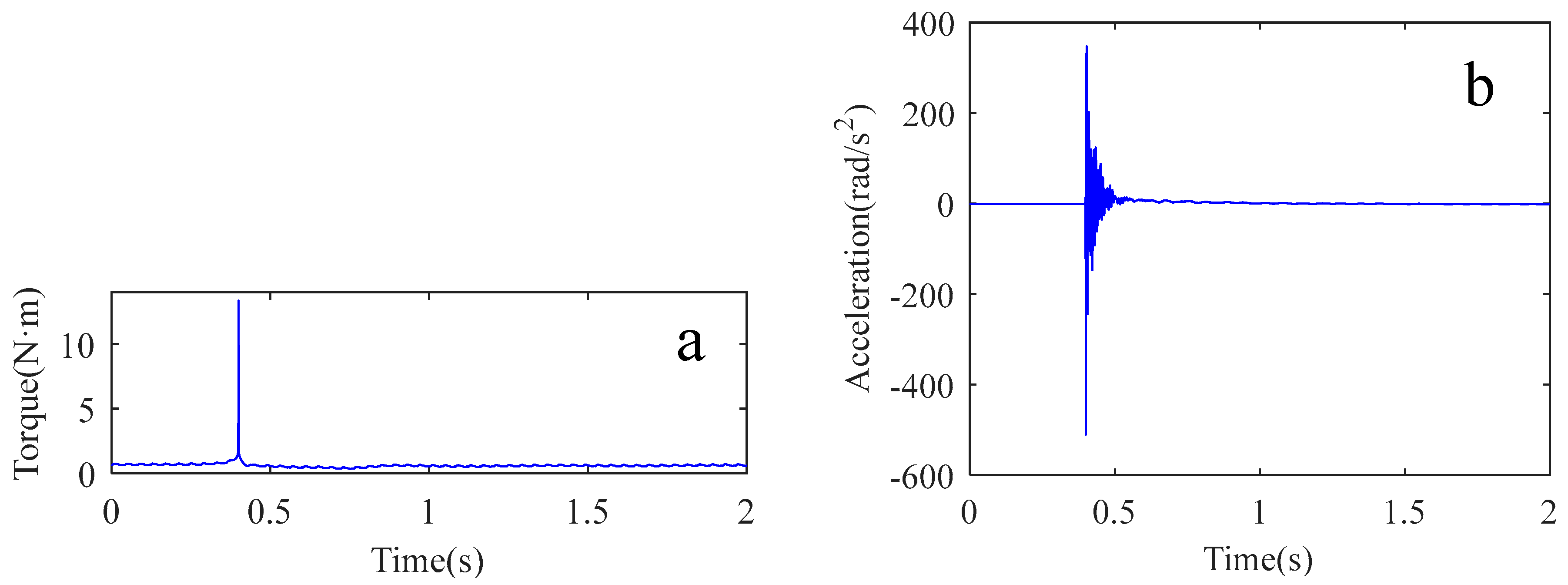
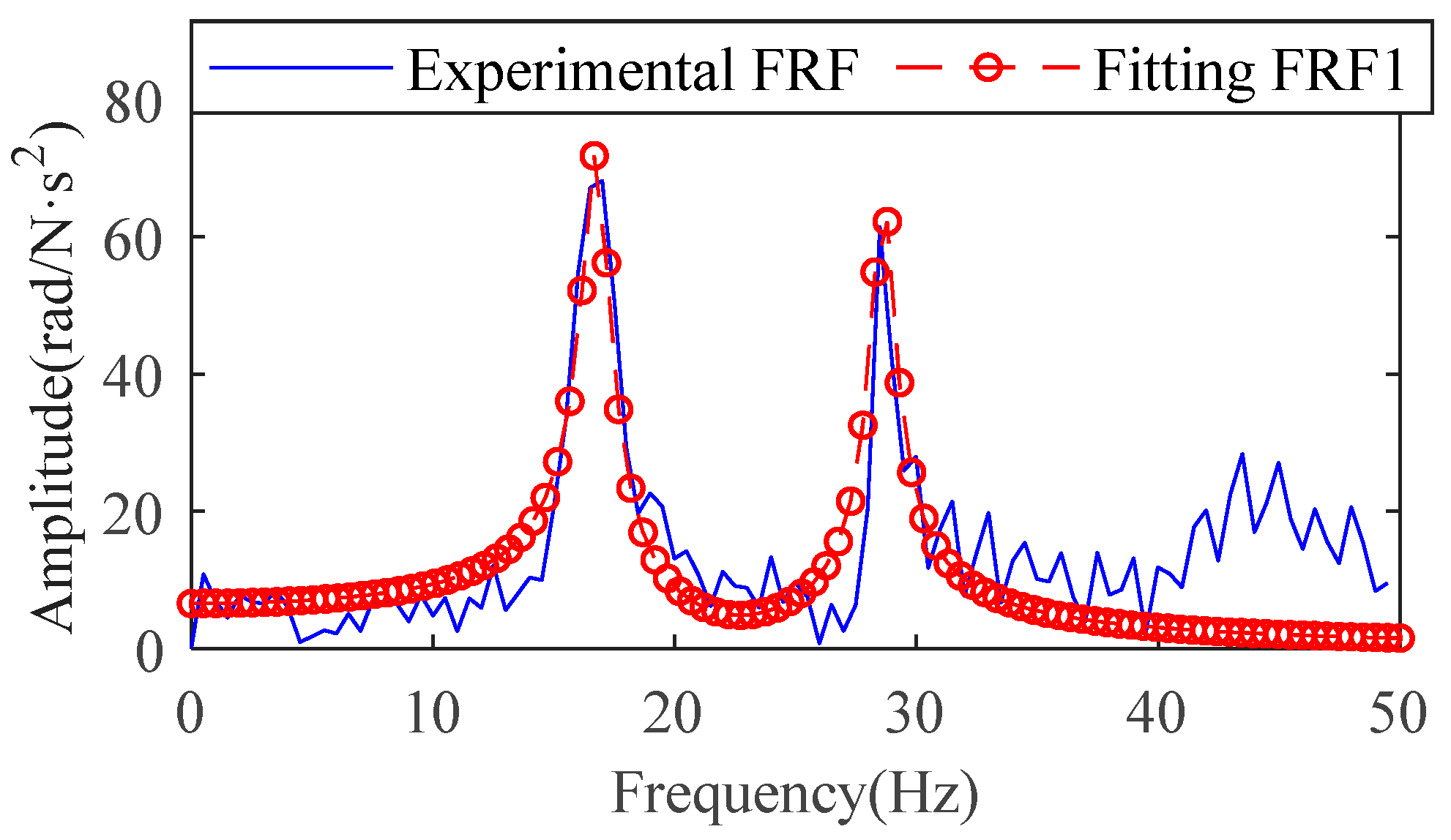
3.2. Identify Stiffness and Load Inertia by Impact Test
3.3. Prediction Experiment of Swing Arm Vibration
3.3.1. Vibration Prediction under Torque Control
3.3.2. Vibration Prediction under Speed Control
4. Experiments on the Articulated Robot
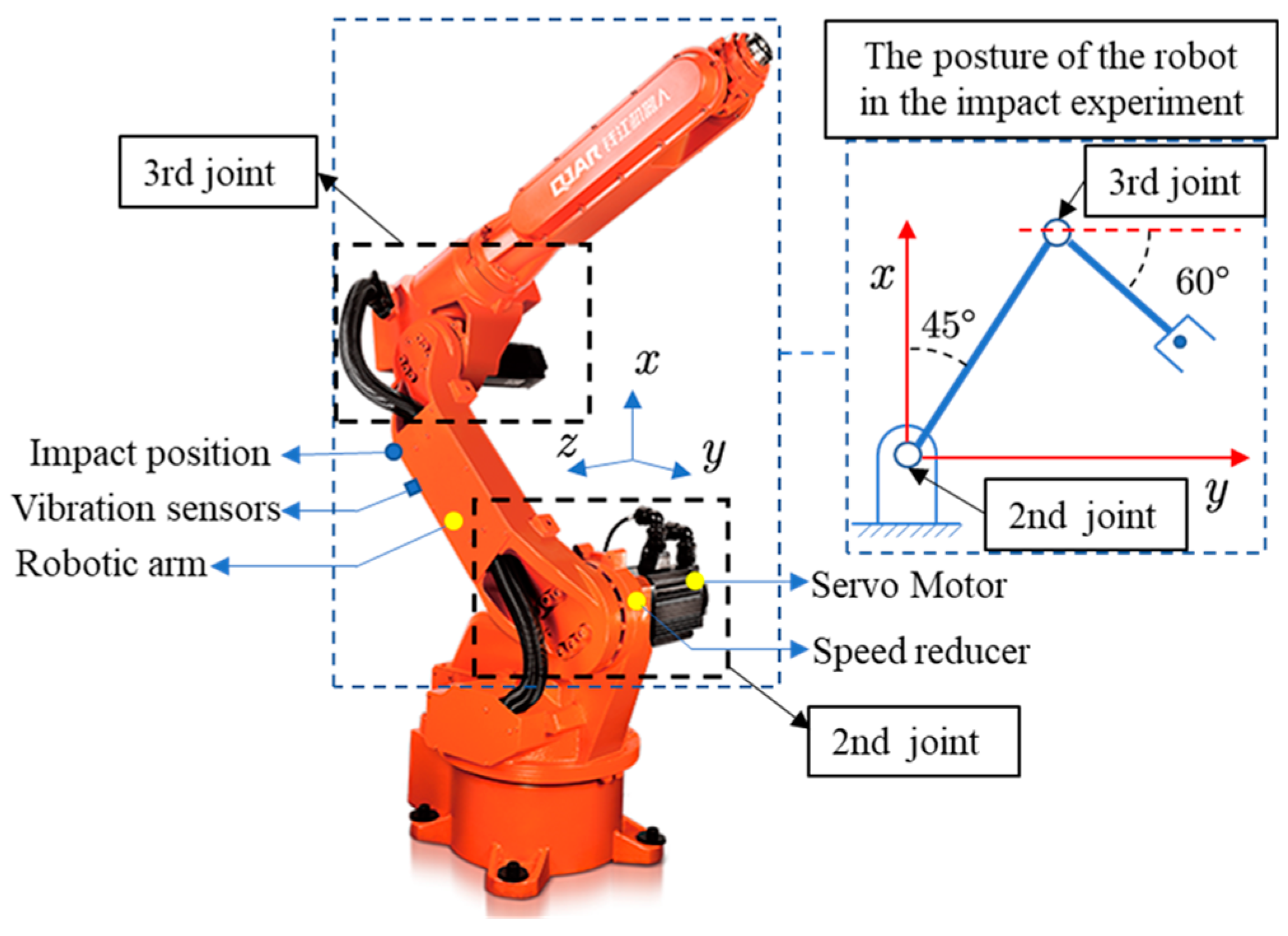
4.1. Experimental Setup
4.2. Experimental Setup
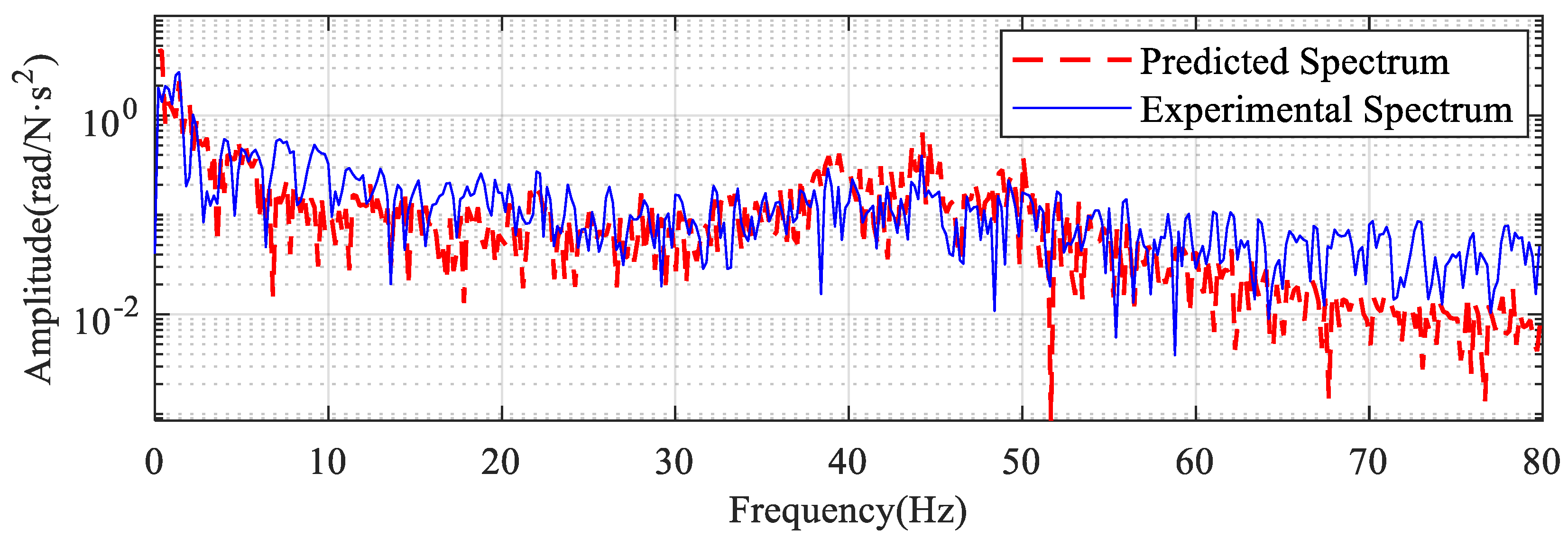
4.3. Vibration Prediction of the Second Joint
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nakayama, Y.; Fujikawa, K.; Kobayashi, H. A torque control method of three-inertia torsional system with backlash. In Proceedings of the 6th International Workshop on Advanced Motion Control. Proceedings (Cat. No. 00TH8494), Nagoya, Japan, 30 March–1 April 2000; pp. 193–198. [Google Scholar]
- Li, X.; Cao, L.; Tiong, A.M.H.; Phan, P.T.; Phee, S.J. Distal-end force prediction of tendon-sheath mechanisms for flexible endoscopic surgical robots using deep learning. Mech. Mach. Theory 2019, 134, 323–337. [Google Scholar] [CrossRef]
- Yang, S.-M.; Wang, S.-C. The detection of resonance frequency in motion control systems. IEEE Trans. Ind. Appl. 2014, 50, 3423–3427. [Google Scholar] [CrossRef]
- Surpatane, R.S. Detection and suppression of resonance frequency in motion control system. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 4528–4533. [Google Scholar]
- Thomsen, D.K.; Søe-Knudsen, R.; Balling, O.; Zhang, X. Vibration control of industrial robot arms by multi-mode time-varying input shaping. Mech. Mach. Theory 2021, 155, 104072. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, W.; Mu, Z. Dynamic modeling and vibration properties study for flexible-joint space manipulators. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics (ROBIO 2014), Bali, Indonesia, 5–10 December 2014; pp. 2443–2448. [Google Scholar]
- Moberg, S.; Wernholt, E.; Hanssen, S.; Brogårdh, T. Modeling and parameter estimation of robot manipulators using extended flexible joint models. J. Dyn. Syst. Meas. Control 2014, 136, 031005. [Google Scholar] [CrossRef]
- Zaher, M.H.; Megahed, S.M. Joints flexibility effect on the dynamic performance of robots. Robotica 2015, 33, 1424–1445. [Google Scholar] [CrossRef]
- Giorgio, I.; Del Vescovo, D. Energy-based trajectory tracking and vibration control for multilink highly flexible manipulators. Math. Mech. Complex Syst. 2019, 7, 159–174. [Google Scholar] [CrossRef]
- Singh, V.P.; Kishor, N.; Samuel, P.; Singh, N. Small-signal stability analysis for two-mass and three-mass shaft model of wind turbine integrated to thermal power system. Comput. Electr. Eng. 2019, 78, 271–287. [Google Scholar] [CrossRef]
- Yabuki, A.; Ohishi, K.; Miyazaki, T.; Yokokura, Y. Quick reaction force control for three-inertia resonant system. IEEJ J. Ind. Appl. 2019, 8, 941–952. [Google Scholar] [CrossRef]
- Sato, H.; Miyazaki, T.; Hojo, Y. Vibration Amplitude Suppression Control of Industrial Machine Driven at Resonance Frequency. In Proceedings of the 2020 IEEE 16th International Workshop on Advanced Motion Control (AMC), Kristiansand, Norway, 14–16 September 2020; pp. 337–342. [Google Scholar]
- Guo, Y.; Huang, L.; Muramatsu, M. Research on inertia identification and auto-tuning of speed controller for AC servo system. In Proceedings of the Power Conversion Conference-Osaka 2002 (Cat. No. 02TH8579), Osaka, Japan, 2–5 April 2002; pp. 896–901. [Google Scholar]
- Lian, C.; Xiao, F.; Gao, S.; Liu, J. Load torque and moment of inertia identification for permanent magnet synchronous motor drives based on sliding mode observer. IEEE Trans. Power Electron. 2018, 34, 5675–5683. [Google Scholar] [CrossRef]
- Ke, C.; Wu, A.; Bing, C. Mechanical parameter identification of two-mass drive system based on variable forgetting factor recursive least squares method. Trans. Inst. Meas. Control 2019, 41, 494–503. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; You, Z. An overview of dynamic parameter identification of robots. Robot. Comput.-Integr. Manuf. 2010, 26, 414–419. [Google Scholar] [CrossRef]
- Miranda-Colorado, R.; Moreno-Valenzuela, J. Experimental parameter identification of flexible joint robot manipulators. Robotica 2018, 36, 313–332. [Google Scholar] [CrossRef]
- Beineke, S.; Schutte, F.; Wertz, H.; Grotstollen, H. Comparison of parameter identification schemes for self-commissioning drive control of nonlinear two-mass systems. In Proceedings of the IAS’97. Conference Record of the 1997 IEEE Industry Applications Conference Thirty-Second IAS Annual Meeting, New Orleans, LA, USA, 5–9 October 1997; pp. 493–500. [Google Scholar]
- Östring, M.; Gunnarsson, S.; Norrlöf, M. Closed-loop identification of an industrial robot containing flexibilities. Control Eng. Pract. 2003, 11, 291–300. [Google Scholar] [CrossRef]
- Pacas, M.; Villwock, S.; Szczupak, P.; Zoubek, H. Methods for commissioning and identification in drives. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2010, 29, 53–71. [Google Scholar] [CrossRef]
- Villwock, S.; Pacas, M. Application of the Welch-method for the identification of two-and three-mass-systems. IEEE Trans. Ind. Electron. 2008, 55, 457–466. [Google Scholar] [CrossRef]
- van Zutven, P.; Kostić, D.; Nijmeijer, H. Parameter identification of robotic systems with series elastic actuators. IFAC Proc. Vol. 2010, 43, 350–355. [Google Scholar] [CrossRef]
- Zollo, L.; Lopez, E.; Spedaliere, L.; Garcia Aracil, N.; Guglielmelli, E. Identification of dynamic parameters for robots with elastic joints. Adv. Mech. Eng. 2015, 7, 843186. [Google Scholar] [CrossRef]
- Spong, M.W. Modeling and control of elastic joint robots. J. Dyn. Syst. Meas. Control 1987, 109, 310–319. [Google Scholar] [CrossRef]
- Avitabile, P. Modal Testing: A Practitioner’s Guide; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Łuczak, D.; Nowopolski, K. Identification of multi-mass mechanical systems in electrical drives. In Proceedings of the 16th International Conference on Mechatronics-Mechatronika 2014, Brno, Czech Republic, 3–5 December 2014; pp. 275–282. [Google Scholar]
- Östring, M. Closed Loop Identification of the Physical Parameters of an Industrial Robot; Linköping University Electronic Press: Linköping, Sweden, 2000. [Google Scholar]
- Zirn, O. Machine Tool Analysis: Modelling, Simulation and Control of Machine Tool Manipulators; ETH Zürich: Zürich, Switzerland, 2008; pp. 99–100. [Google Scholar]
- Saarakkala, S.E.; Hinkkanen, M. Identification of two-mass mechanical systems in closed-loop speed control. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 2905–2910. [Google Scholar]
- Saarakkala, S.E.; Hinkkanen, M. Identification of two-mass mechanical systems using torque excitation: Design and experimental evaluation. IEEE Trans. Ind. Appl. 2015, 51, 4180–4189. [Google Scholar] [CrossRef]
- Xu, K.; Wu, X.; Liu, X.; Wang, D. Identification of Robot Joint Torsional Stiffness Based on the Amplitude of the Frequency Response of Asynchronous Data. Machines 2021, 9, 204. [Google Scholar] [CrossRef]
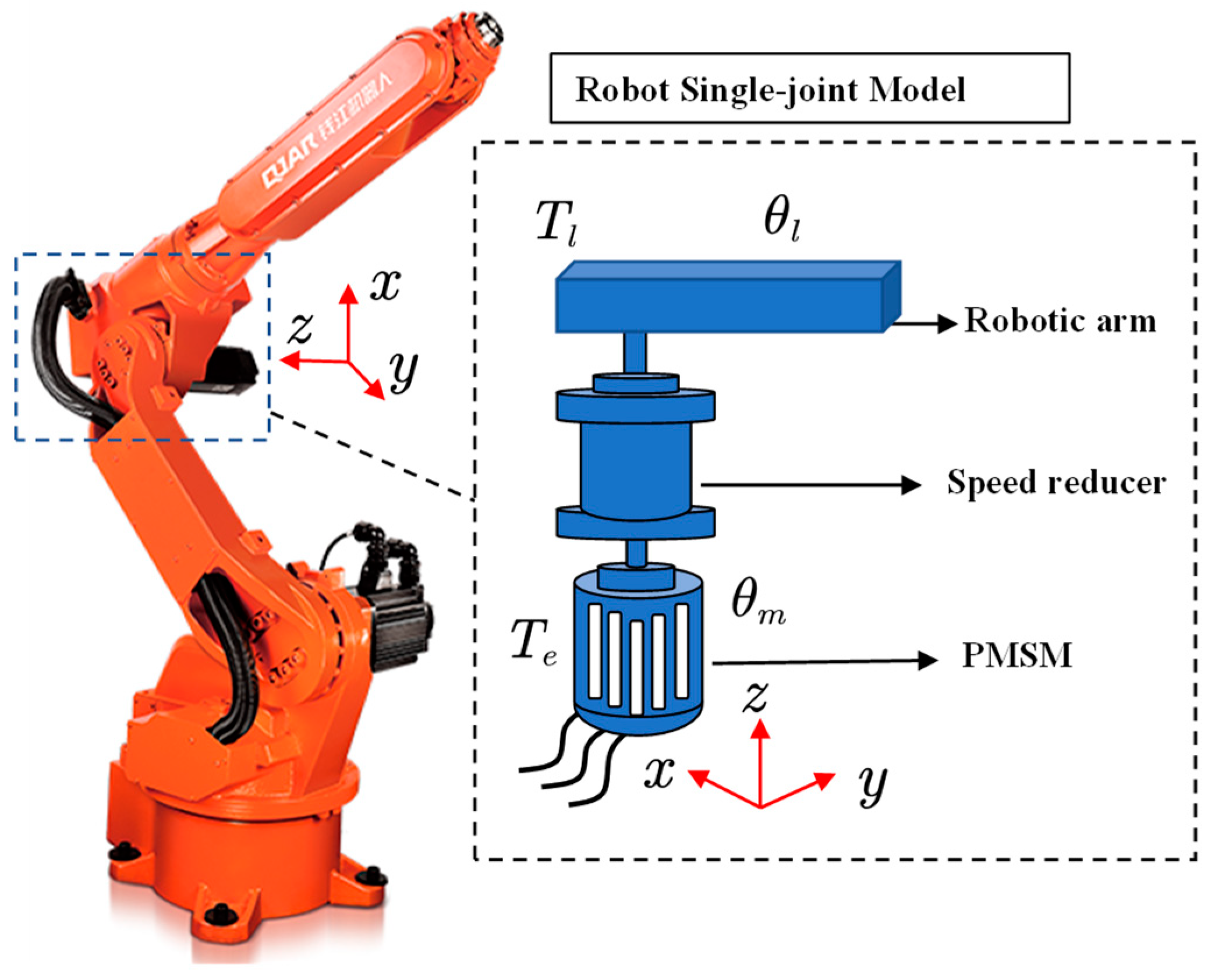


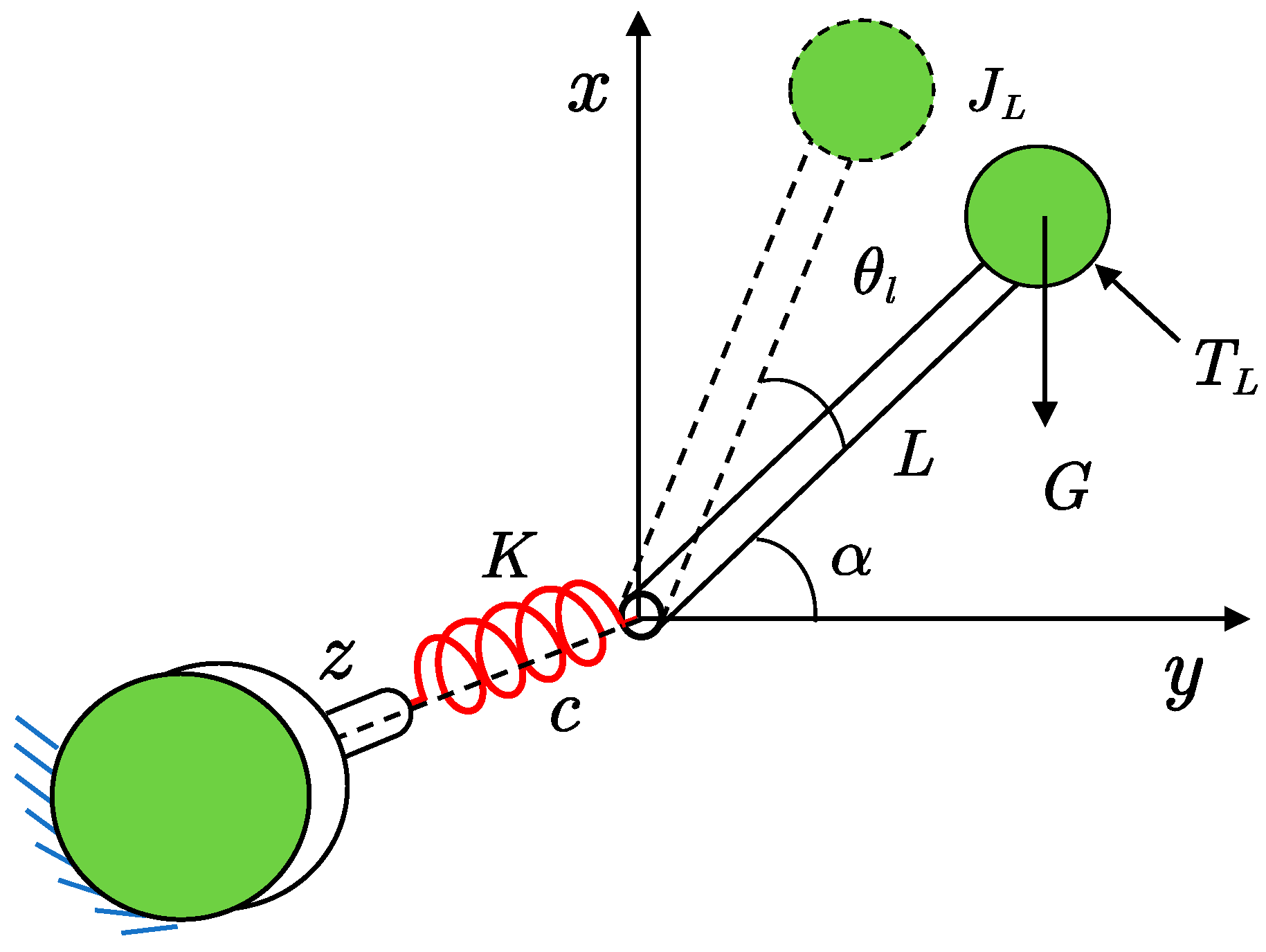




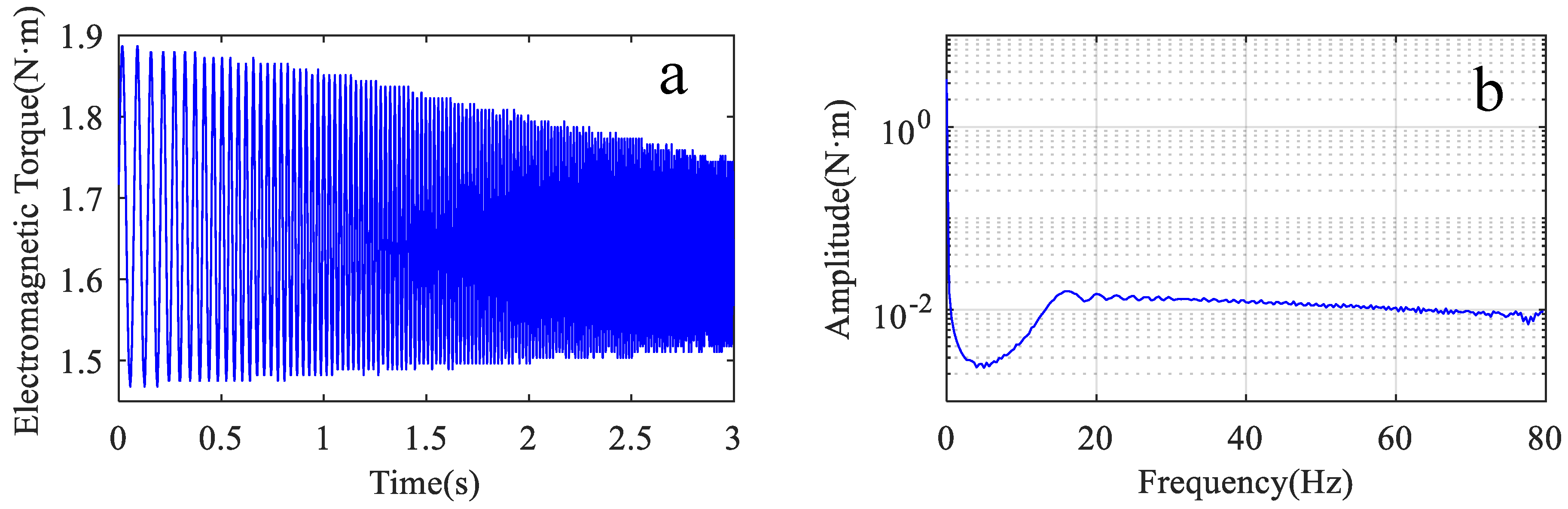
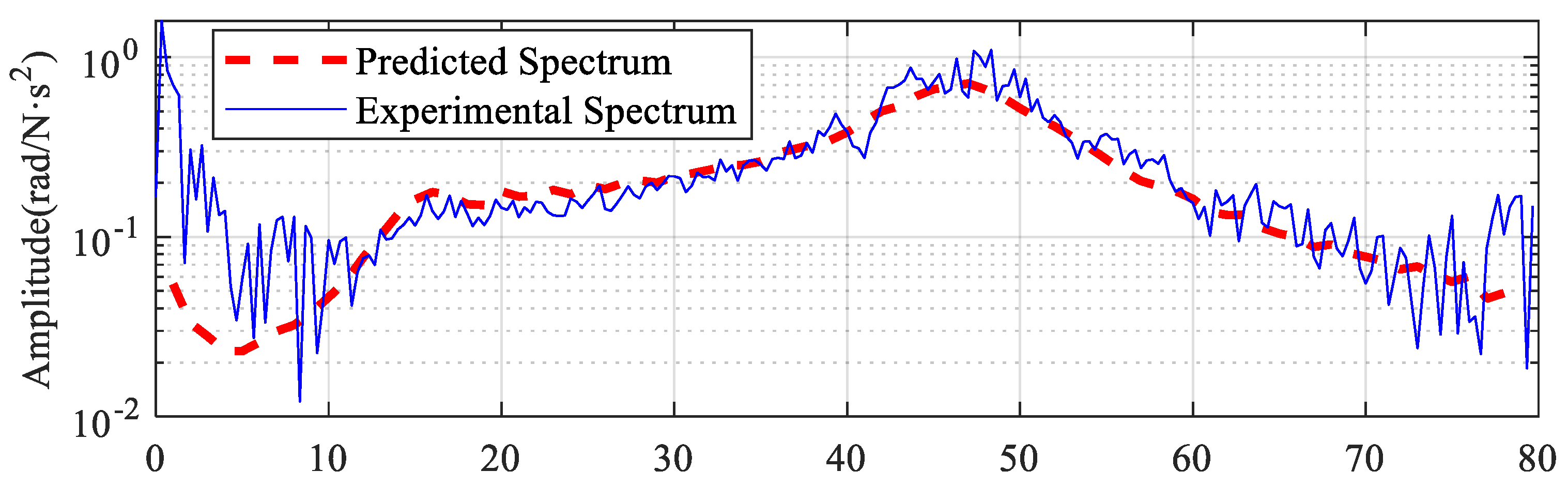
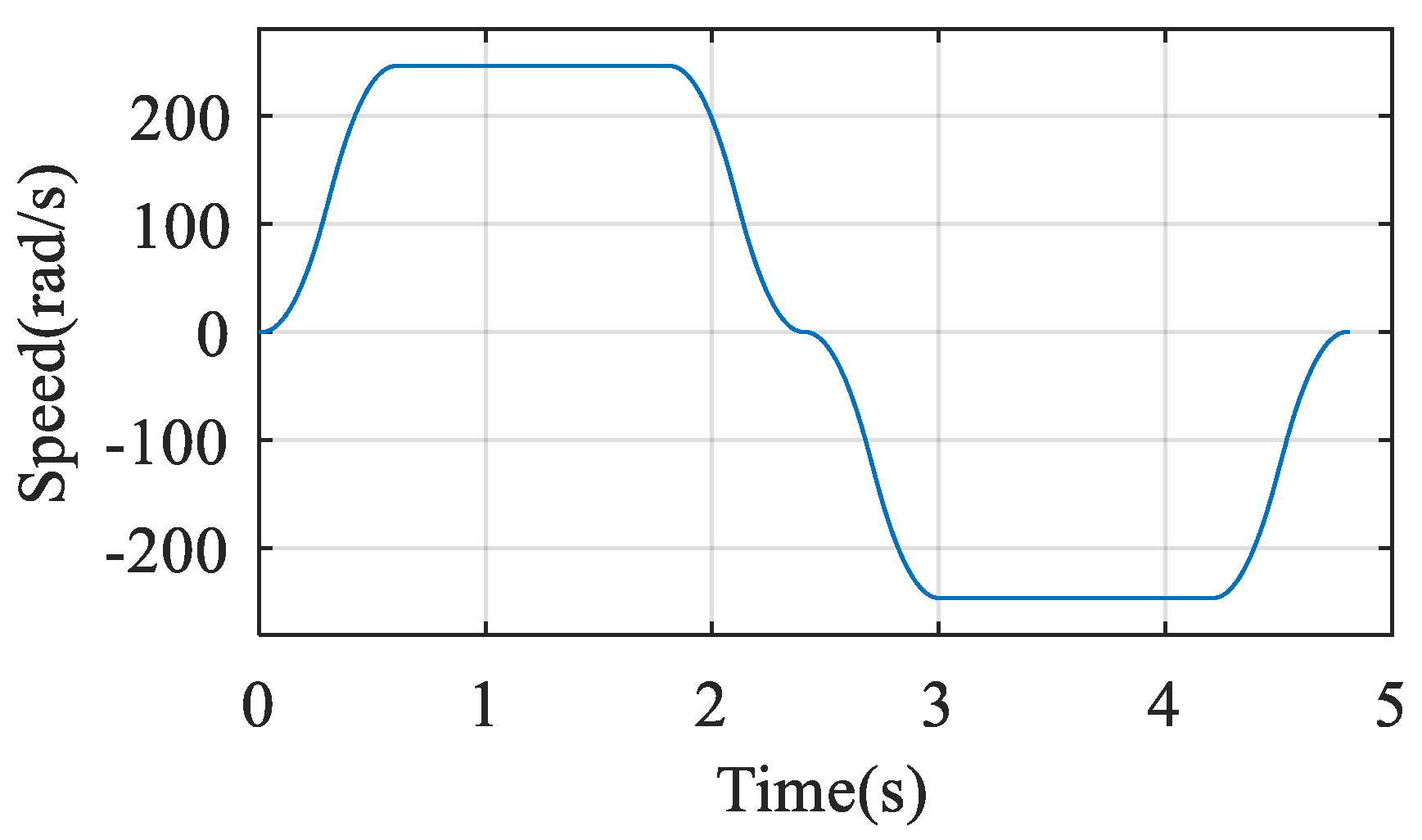
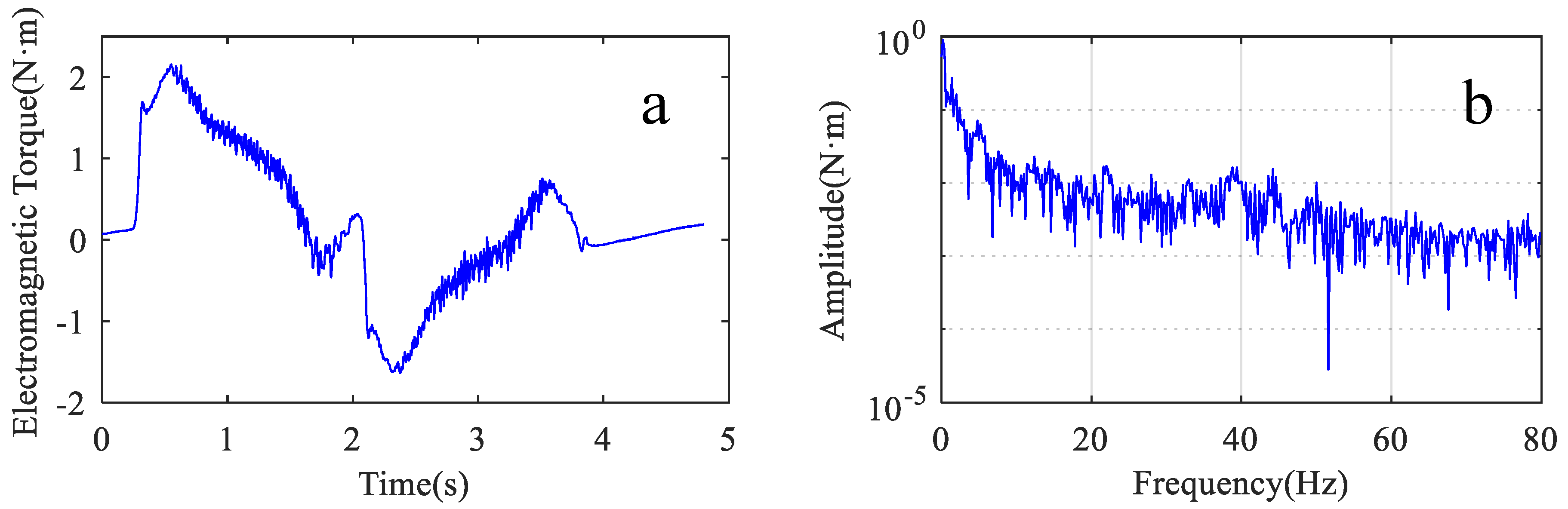




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| PMSM rated power | 1 | Swing arm length | 1 |
| Rotational inertia of PMSM Rotational inertia of reducer | 0.00021 0.000248 | Reducer stiffness Swing arm mass | 168,449.59 12 |
| Parameters | Identifying Value | Reference Value |
|---|---|---|
| Stiffness | 193,665 | 168,449 |
| Inertia | 3.02 | 3.4 |
| Damping | 59.76 | 30.27 |
| The Parameters of the Second Joint | Value |
|---|---|
| PMSM rated power | 2 |
| Rotational inertia of PMSM | 0.001 |
| Rotational inertia of reducer | 0.00032 |
| Number of motor pole pairs | 5 |
| Torque constant of the motor | 0.458 |
| Parameter | Identifying Value | Identifying Value |
|---|---|---|
| Stiffness | ||
| Inertia Damping |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wang, D.; Wu, X.; Xu, K.; Liu, X. Vibration Prediction of the Robotic Arm Based on Elastic Joint Dynamics Modeling. Sensors 2022, 22, 6170. https://doi.org/10.3390/s22166170
Li J, Wang D, Wu X, Xu K, Liu X. Vibration Prediction of the Robotic Arm Based on Elastic Joint Dynamics Modeling. Sensors. 2022; 22(16):6170. https://doi.org/10.3390/s22166170
Chicago/Turabian StyleLi, Jianlong, Dongxiao Wang, Xing Wu, Kai Xu, and Xiaoqin Liu. 2022. "Vibration Prediction of the Robotic Arm Based on Elastic Joint Dynamics Modeling" Sensors 22, no. 16: 6170. https://doi.org/10.3390/s22166170
APA StyleLi, J., Wang, D., Wu, X., Xu, K., & Liu, X. (2022). Vibration Prediction of the Robotic Arm Based on Elastic Joint Dynamics Modeling. Sensors, 22(16), 6170. https://doi.org/10.3390/s22166170









