OFDM Network Optimization Using a QPSK Based on a Wind-Driven Genetic Algorithm
Abstract
:1. Introduction
2. Materials and Methods
2.1. Related Work
2.2. Research Questions
- How can the QPSK based on the GAWDO be further modified to eliminate carrier offset drift?
3. GAWDO for OFDM Network Optimization
3.1. The Proposed GAWDO
- To continuously influence the number and quality of individuals that can be created and given the responsibility of reproduction at every evolution stage. This would reduce the loss of good genetic material. Since the GA is a multipath search algorithm, this would reduce the chances of trapping in suboptimal minima [26,27].
- To select parents based on their expectations. The best parents with high expectation values would be given more reproduction chances in descending order. This would mitigate stalling which greatly exists in the conventional GA when scores or expectation values are similar because they are chosen using probabilities [10,26,29].
3.2. Quadrature Phase-Shift Keying Enhancement
4. Performance Evaluation
4.1. Simulation Settings
4.2. Testing of the Algorithms
4.3. Simulation Settings
5. Results
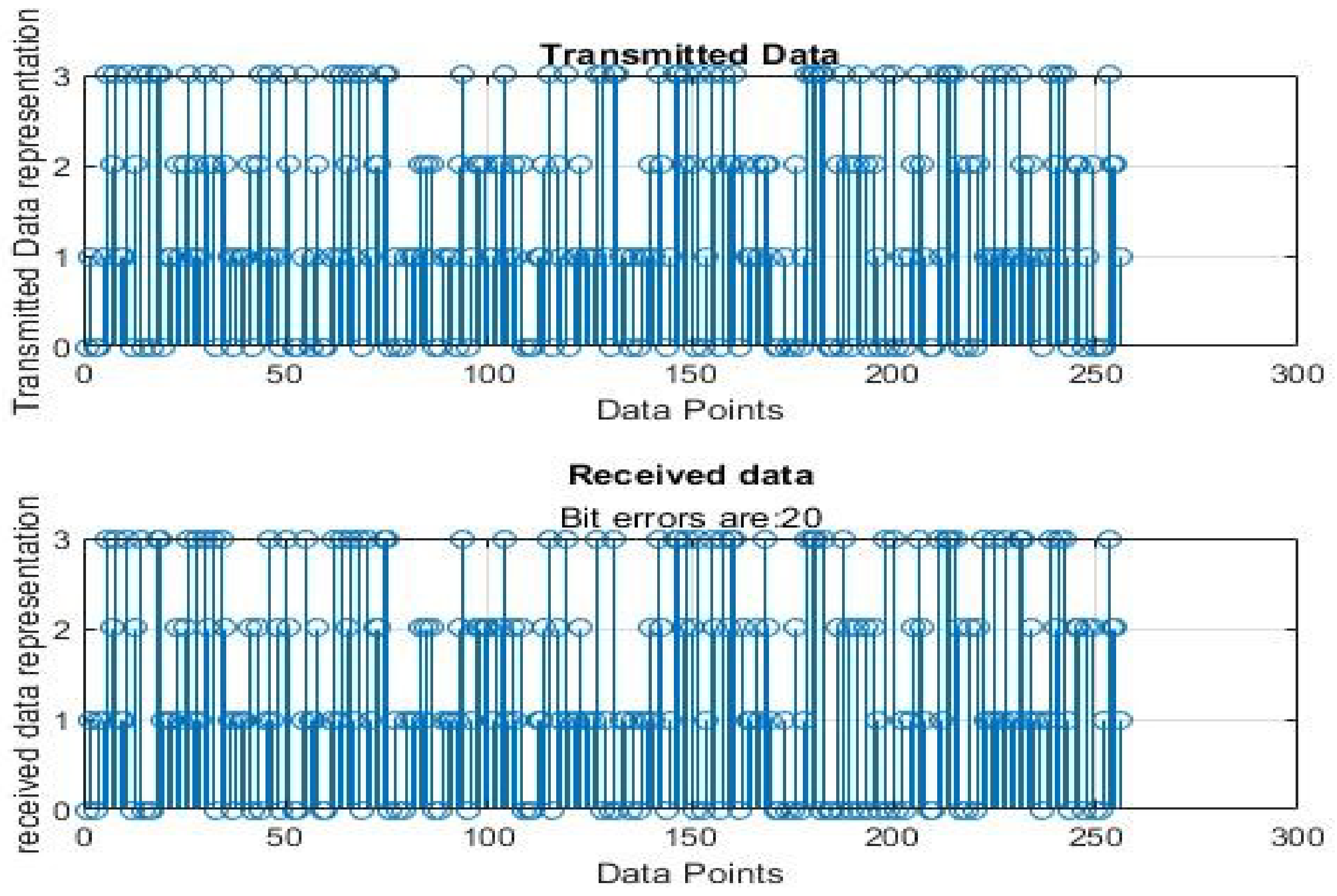
5.1. Noiseless Channel Simulation Outputs
5.2. Noisy Channel Simulation Outputs
5.3. Results Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Tiwari, S.; Das, S.S. Circularly Pulse-shaped Orthogonal Time Frequency Space Modulation. Electron. Lett. 2020, 56, 157–160. [Google Scholar] [CrossRef]
- Kuppusamy, V.; Mahapatra, R. Primary User Detection in OFDM Based MIMO Cognitive Radio. In Proceedings of the 2008 3rd International Conference on Cognitive Radio Oriented Wireless Networks and Communications (CrownCom 2008), Singapore, 15–17 May 2008; pp. 1–5. [Google Scholar]
- Gupta, R.; Majhi, S.; Dobre, O.A. Blind Modulation Classification of Different Variants of QPSK and 8-PSK for Multiple-Antenna Systems with Transmission Impairments. In Proceedings of the 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018; pp. 1–5. [Google Scholar]
- Cho, Y.S.; Kim, J.; Yang, W.Y.; Kang, C.G. MIMO-OFDM Wireless Communication with Matlab; John Wiley & Sons: Singapore, 2010; pp. 294–307. [Google Scholar]
- Zhao, F.; Yao, W.; Logothetis, C.C.; Song, Y. Comparison of superresolution algorithms for TOA estimation in indoor IEEE 802.11 wireless LANs. In Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing, Wuhan, China, 22–24 September 2006; pp. 1–5. [Google Scholar]
- Hu, Z.; Chen, F.; Wen, M.; Ji, F.; Yu, H. Low-Complexity LLR Calculation for OFDM With Index Modulation. IEEE Wirel. Commun. Lett. 2019, 7, 618–621. [Google Scholar] [CrossRef]
- Başar, E.; Aygölü, Ü.; Panayırcı, E.; Poor, H.V. Orthogonal Frequency Division Multiplexing with Index Modulation. IEEE Trans. Signal Process. 2013, 61, 5536–5549. [Google Scholar] [CrossRef]
- Pancaldi, F.; Vitetta, G.M. Equalization algorithms in the frequency domain for continuous phase modulations. IEEE Trans. Commun. 2006, 54, 648–658. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, C.; Min, T.; Xu, B.; Pan, Q.; Yue, C.M. Design and Co-Simulation of QPSK and NRZ/PAM-4/PAM-8 VCSEL-Based Optical Links Utilizing an Integrated System Evaluation Engine. In Proceedings of the IEEE 14th International Conference on ASIC (ASICON), Kunming, China, 26–29 October 2021; pp. 1–4. [Google Scholar]
- Verma, S.; Sood, N.; Sharma, A.K. Genetic algorithm-based optimized CH selection for single and multiple data sinks in heterogeneous wireless sensor network. Appl. Soft Comput. 2019, 85, 105788. [Google Scholar] [CrossRef]
- Wang, C.; Liu, X.; Hu, H.; Han, Y.; Yao, M. Energy-Efficient and Load-Balanced Clustering Routing Protocol for Wireless Sensor Networks Using a Chaotic Genetic Algorithm. IEEE Access 2020, 8, 158082–158096. [Google Scholar] [CrossRef]
- Le, T.T.H.; Tran, X.N.; Ngo, V.-D.; Le, M.-T. Repeated Index Modulation-OFDM With Coordinate Interleaving: Performance Optimization and Low-Complexity Detectors. IEEE Syst. J. 2020, 15, 3673–3681. [Google Scholar] [CrossRef]
- Akan, A.; Chaparro, L. Modeling and Estimation of Wireless OFDM Channels by Using Time-Frequency Analysis. Circuits Syst. Signal Process. 2006, 25, 389–403. [Google Scholar] [CrossRef]
- Selmy, H.; Shalaby, H.M.H.; Kawasaki, Z. Performance enhancement of QPSK modulation using hybrid QPSK-modified MPPM in optical fiber communications. In Proceedings of the Second International Japan-Egypt Conference on Electronics, Communications and Computers (JEC-ECC), Cairo, Egypt, 17–19 December 2013; pp. 140–142. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, C.; Cui, G.; Wang, W.; Zhang, Y. Phase noise estimation scheme based on linear interpolation for constant envelop OFDM system. In Proceedings of the 2017 9th International Conference on Advanced Infocomm Technology (ICAIT), Chengdu, China, 22–24 November 2017; pp. 279–284. [Google Scholar] [CrossRef]
- Robert, J.; Zoellner, J.; Slimani, M. Adaptive Windowing for OFDM with Dense Subcarrier Spacing in Mobile Channels. OFDM. In Proceedings of the 17th International OFDM Workshop 2012 (InOWo’12), Essen, Germany, 29–30 August 2012; pp. 1–6. [Google Scholar]
- Kishore, G.S.; Rallapalli, H. Performance Assessment of M-ary ASK, FSK, PSK, QAM and FQAM in AWGN Channel. In Proceedings of the 2019 International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, India, 4–6 April 2019; pp. 273–277. [Google Scholar] [CrossRef]
- Suhartomo, A.; Vincent, V. Comparison of BER Performance for M-ary QAM and PSK on DWT-based OFDM System with PTS Technique Through AWGN Channel. In Proceedings of the 2020 IEEE International Conference on Sustainable Engineering and Creative Computing (ICSECC), Bandung, Indonesia, 16–17 December 2020; pp. 5–10. [Google Scholar] [CrossRef]
- Taherkhani, N.; Kiasaleh, K. Subcarrier-Index Modulation for Reed Solomon Encoded OFDM-Based Visible Light Communication. In Proceedings of the 2019 16th IEEE Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 11–14 January 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Nasraoui, L.; Atallah, L.N.; Siala, M. Encoding sequence design for a reduced complexity time synchronization approach for OFDM systems. In Proceedings of the 2012 19th IEEE International Conference on Electronics, Circuits and Systems (ICECS 2012), Seville, Spain, 9–12 December 2012; pp. 913–916. [Google Scholar] [CrossRef]
- Ma, K.; Mou, S.; Wang, Y.; Yan, J.; Yeo, K.S.; Lim, W.M. A miniaturized 28mW 60GHz differential quadrature sub-harmonic QPSK modulator in 0.18 um SiGe BiCMOS. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS2014), Tampa, FL, USA, 1–6 June 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Dassa, K.; Recioui, A. Demand Side Management and Dynamic Economic Dispatch Using Genetic Algorithms. Eng. Proc. 2022, 14, 12. [Google Scholar] [CrossRef]
- Di Barba, P.; Mognaschi, M.E.; Wiak, S.; Przybylski, M.; Slusarek, B. Wind-driven optimization for the design of switched reluctance motors. In Proceedings of the 2017 18th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering (ISEF) Book of Abstracts, Łódź, Poland, 14–16 September 2017; pp. 1–2. [Google Scholar] [CrossRef]
- Sun, G.; Liu, Y.H.; Liang, S.; Chen, Z.Y.; Wang, A.M.; Ju, Q.A.; Zhang, Y. A sidelobe and energy optimization array node selection algorithm for collaborative beamforming in wireless sensor networks. IEEE Access 2018, 6, 2515–2530. [Google Scholar] [CrossRef]
- Jesenik, M.; Mernik, M.; Črepinšek, M.; Ravber, M.; Trlep, M. Searching for soil models’ parameters using metaheuristics. Appl. Soft Comput. 2018, 69, 131–148. [Google Scholar] [CrossRef]
- Corus, D.; Oliveto, P.S. Standard Steady State Genetic Algorithms Can Hillclimb Faster Than Mutation-Only Evolutionary Algorithms. IEEE Trans Evol. Comput. 2018, 22, 720–732. [Google Scholar] [CrossRef]
- Shi, Y.; Lu, X.; Gao, K.; Zhu, J.; Wang, S. Genetic Algorithm Aided OFDM With All Index Modulation. IEEE Commun. Lett. 2019, 23, 2192–2195. [Google Scholar] [CrossRef]
- Jafari, A.; Khalili, T.; Babaei, E.; Bidram, A. A Hybrid Optimization Technique Using Exchange Market and Genetic Algorithms. IEEE Access 2020, 8, 2417–2427. [Google Scholar] [CrossRef]
- Souza, M.G.; Vallejo, E.E.; Estrada, K. Detecting Clustered Independent Rare Variant Associations Using Genetic Algorithms. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 18, 932–939. [Google Scholar] [CrossRef] [PubMed]
- Bayraktar, Z.; Komurcu, M.; Jiang, Z.H.; Werner., D.H.; Werner, P.L. Stub-loaded inverted-F antenna synthesis via Wind Driven Optimization. In Proceedings of the IEEE International Symposium on Antennas and Propagation (APSURSI), Spokane, WA, USA, 3–8 July 2011; pp. 2920–2923. [Google Scholar] [CrossRef]
- Mahto, S.K.; Choubey, A.; Suman, S. Linear array synthesis with minimum side lobe level and null control using wind driven optimization. In Proceedings of the International Conference on Signal Processing and Communication Engineering Systems, Chengdu, China, 10–11 October 2015; pp. 191–195. [Google Scholar] [CrossRef]
- Yao, R.; Zhang, Y.; Zuo, X.; Zhang, X.; Li, J.; Liu, P.; Wu, Q. A Shifted Constellation of QPSK: Constellation Design and Dynamic Demodulation Threshold Optimization. In Proceedings of the 11th International Conference on Wireless Communications and Signal Processing (WCSP), Xi’an, China, 23–25 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Alhalabi, M.; El-Nahal, F.I.; Taşpinar, N. Comparison of different modulation techniques for optical OFDM Intensity Modulation and Direct Detection IM/DD system. In Proceedings of the IEEE 7th Palestinian International Conference on Electrical and Computer Engineering (PICECE), Gaza, Palestine, 26–27 March 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Khashirunnisa, S.; Chand, B.K.; Kumari, B.L. Performance analysis of Kalman filter, fuzzy Kalman filter and wind driven optimized Kalman filter for tracking applications. In Proceedings of the 2nd International Conference on Communication Control and Intelligent Systems (CCIS), Mathura, India, 18–20 November 2016; pp. 170–174. [Google Scholar] [CrossRef]
- Ho, S.L.; Yang, S.; Bai, Y. A wind driven optimization-based methodology for robust optimizations of electromagnetic devices under interval uncertainty. In Proceedings of the IEEE Conference on Electromagnetic Field Computation (CEFC), Miami, FL, USA, 13–16 November 2016. [Google Scholar] [CrossRef]
- Xuan, G.; Zhang, Z.; Liu, C. Design of QPSK Sequences for M-Ary Spread Spectrum OFDM Systems. In Proceedings of the 2019 12th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Huaqiao, China, 19–21 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Khan, M.S.A.; Iqbal, M.M.; Mahmood, K.S.; Anee, A.A.; Rahman, M.S.; Mahmud, S. Differential Quadrature Phase Shift Keying Modulation in Optical Fiber Communication—Modelling, Design, Case Implementation and Limitation. In Proceedings of the Fourth International Conference on Advances in Computing, Communication & Automation (ICACCA), Subang Jaya, Malaysia, 26–28 October 2018; pp. 1–6. [Google Scholar] [CrossRef]















| Parameter | Settings |
|---|---|
| Creation function | Uniform |
| Crossover function | Single point, 0.8 |
| Population type | Double vector |
| Population size | 1000 |
| Pareto fraction | 0.4 |
| Selection function | WDO |
| Penalty factor | 100 |
| Migration fraction | 0.2 |
| Migration interval | 20 |
| Fitness scaling function | Top |
| Migration direction | Both |
| Mutation function | Uniform |
| Stall test | Geometric weighted |
| Stall time limit | 60 |
| Non-linear solver | Augmented Lagrangian |
| Title 1 | Title 2 | Title 3 | Title 4 | Title 5 | |
|---|---|---|---|---|---|
| (X1; X2) | (X1; X2) | (X1; X2) | (X1; X2) | (X1; X2) | |
| GA | (0; 0.5) | (0; 0) | (−1; 3) | (0; 0) | (0; 0) |
| WDO | (0; 0) | (0; 1.5) | (0; 0) | (0; 0.06) | (0; 0) |
| GAWDO | (0; 0) | (0; 0.4) | (0; 0) | (0; 0) | (0; 0) |
| Title 1 | Title 2 | Title 3 | Title 4 | Title 5 | |
|---|---|---|---|---|---|
| (X1; X2) | (X1; X2) | (X1; X2) | (X1; X2) | (X1; X2) | |
| GA | (0; 0) | (0; 0) | (0; 0) | (0; 0) | (0; 0) |
| WDO | (0; 0) | (0; 0) | (0; 0) | (0; 0) | (0; 0) |
| GAWDO | (0; 0) | (0; 0) | (0; 0) | (0; 0) | (0; 0) |
| Data Points | GAWDO QPSK % Error | Customary QPSK % Error |
|---|---|---|
| 64 | 0 | 4.69 |
| 256 | 0 | 7.81 |
| 1024 | 0 | 4.2 |
| Data Points | GAWDO QPSK % Error | Customary QPSK % Error |
|---|---|---|
| 64 | 1.56 | 9.38 |
| 256 | 3.51 | 17.58 |
| 1024 | 7.52 | 12.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Shambare, C.; Imoru, O. OFDM Network Optimization Using a QPSK Based on a Wind-Driven Genetic Algorithm. Sensors 2022, 22, 6174. https://doi.org/10.3390/s22166174
Sun Y, Shambare C, Imoru O. OFDM Network Optimization Using a QPSK Based on a Wind-Driven Genetic Algorithm. Sensors. 2022; 22(16):6174. https://doi.org/10.3390/s22166174
Chicago/Turabian StyleSun, Yanxia, Chikomborero Shambare, and OdunAyo Imoru. 2022. "OFDM Network Optimization Using a QPSK Based on a Wind-Driven Genetic Algorithm" Sensors 22, no. 16: 6174. https://doi.org/10.3390/s22166174






