Monocular Depth Estimation: Lightweight Convolutional and Matrix Capsule Feature-Fusion Network
Abstract
:1. Introduction
- A fusion block that can simultaneously obtain the matrix capsule feature and CNN feature of the same scene;
- A method for generating depth images by integrating the three-feature information in the encoder stage, decoder stage, and fusion block;
- A triple loss function is designed with depth difference, gradient difference, and structural similarity.
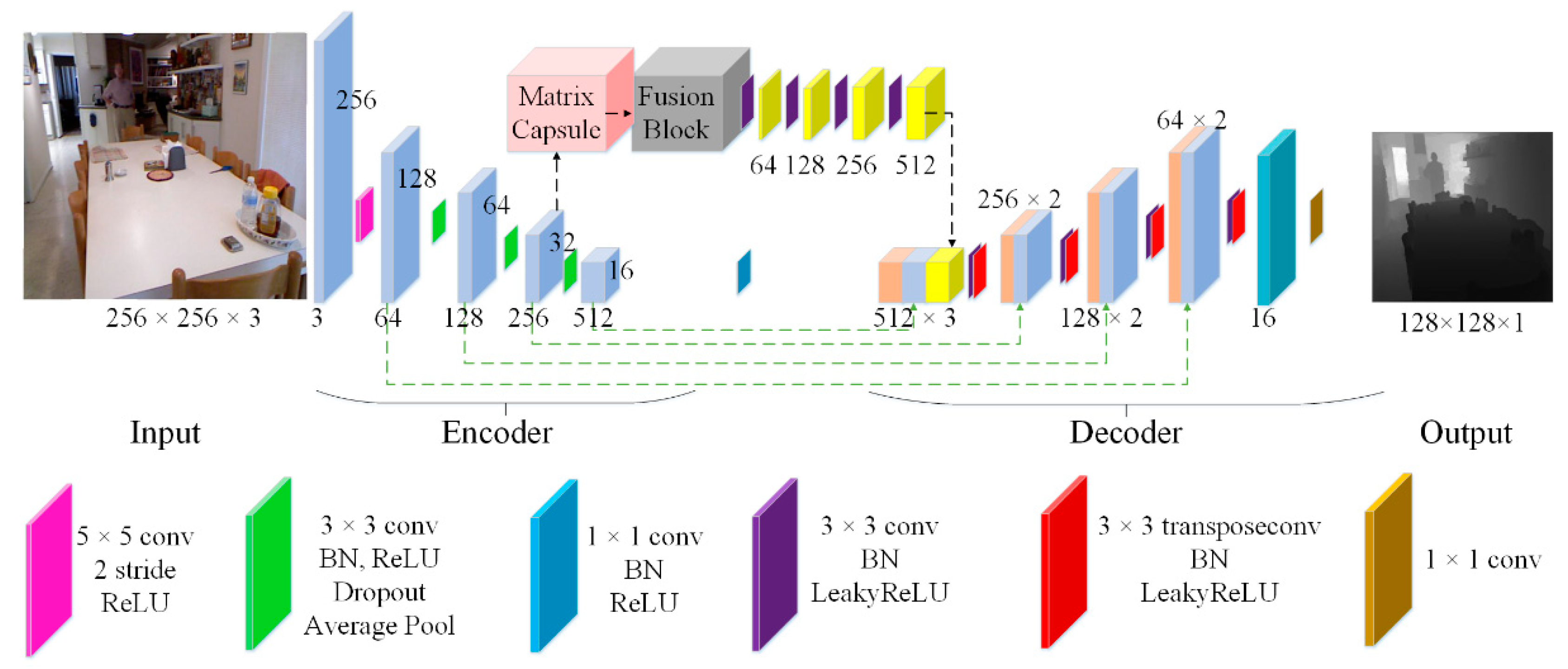
2. Convolutional Capsule Feature-Fusion Network (CNNapsule)
2.1. CNNapsule Network
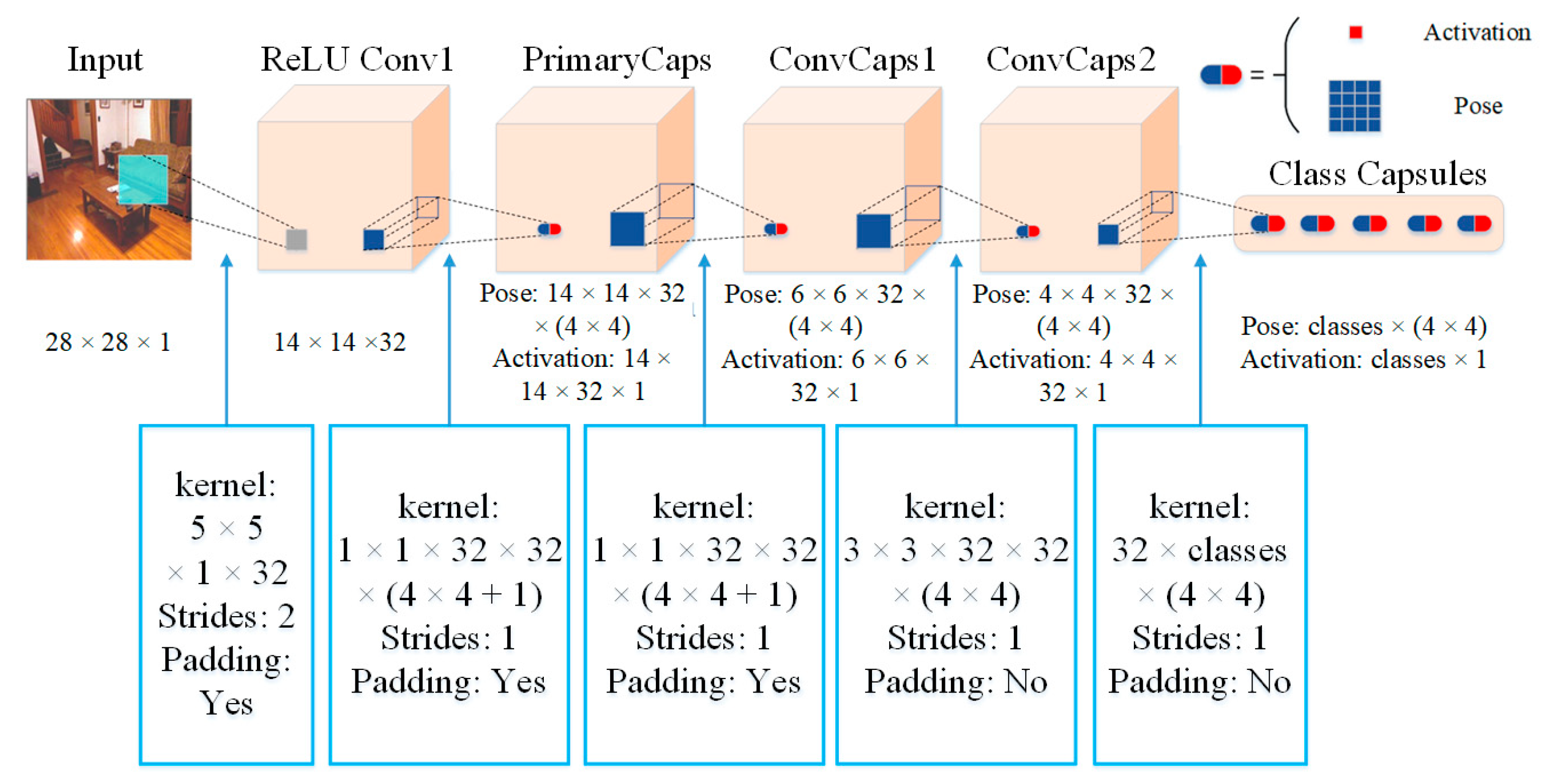
2.2. Matrix Capsule Feature Description
| Algorithm 1. EM algorithm |
| Procedure EM algorithm returns activation and pose of the capsules in layer l + 1 based on activations and poses of capsules in layer l. is the dimension of the vote from capsule i with activation in layer l to capsule j in layer L + 1. is the hth dimension of the pose from capsule j. is initialized to . |
| M-STEP for one higher-level capsule , , , E-STEP for one lower-level capsule , , |
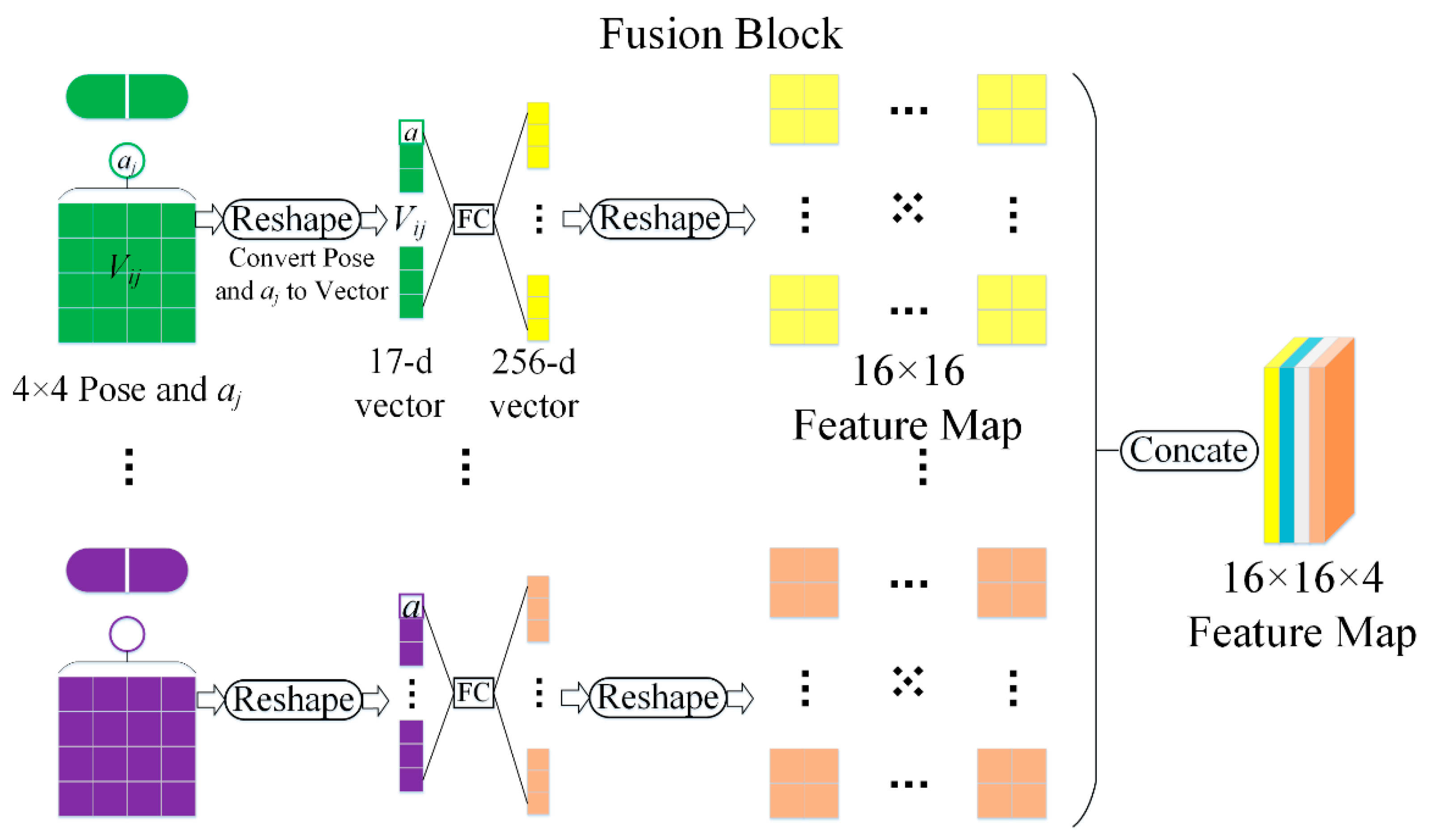
2.3. Fusion Block
2.4. Loss Function
3. Evaluation Indicators
4. Experimental Results and Analysis
4.1. Data Augmentation
- Brightness: The input image’s brightness was changed with a probability of 0.5, in the brightness range of [0.5, 1.5];
- Contrast: The contrast of the input image was 0.5, with a probability of changing the contrast to 0.5;
- Saturation: The input image’s saturation was changed with a probability of 0.5. The saturation range was [0.4, 1.2];
- Color: The R and G channels of the input image were exchanged with a probability of 0.25;
- Flip: The input and depth images were flipped horizontally with a probability of 0.5;
- Pan: The input image was randomly cropped to 224 × 224. To adapt to the network structure, the input image was scaled to 256 × 256, and the true depth map was scaled to 128 × 128.
4.2. Experiments on NYU Depth V2
4.3. Experiments in KITTI
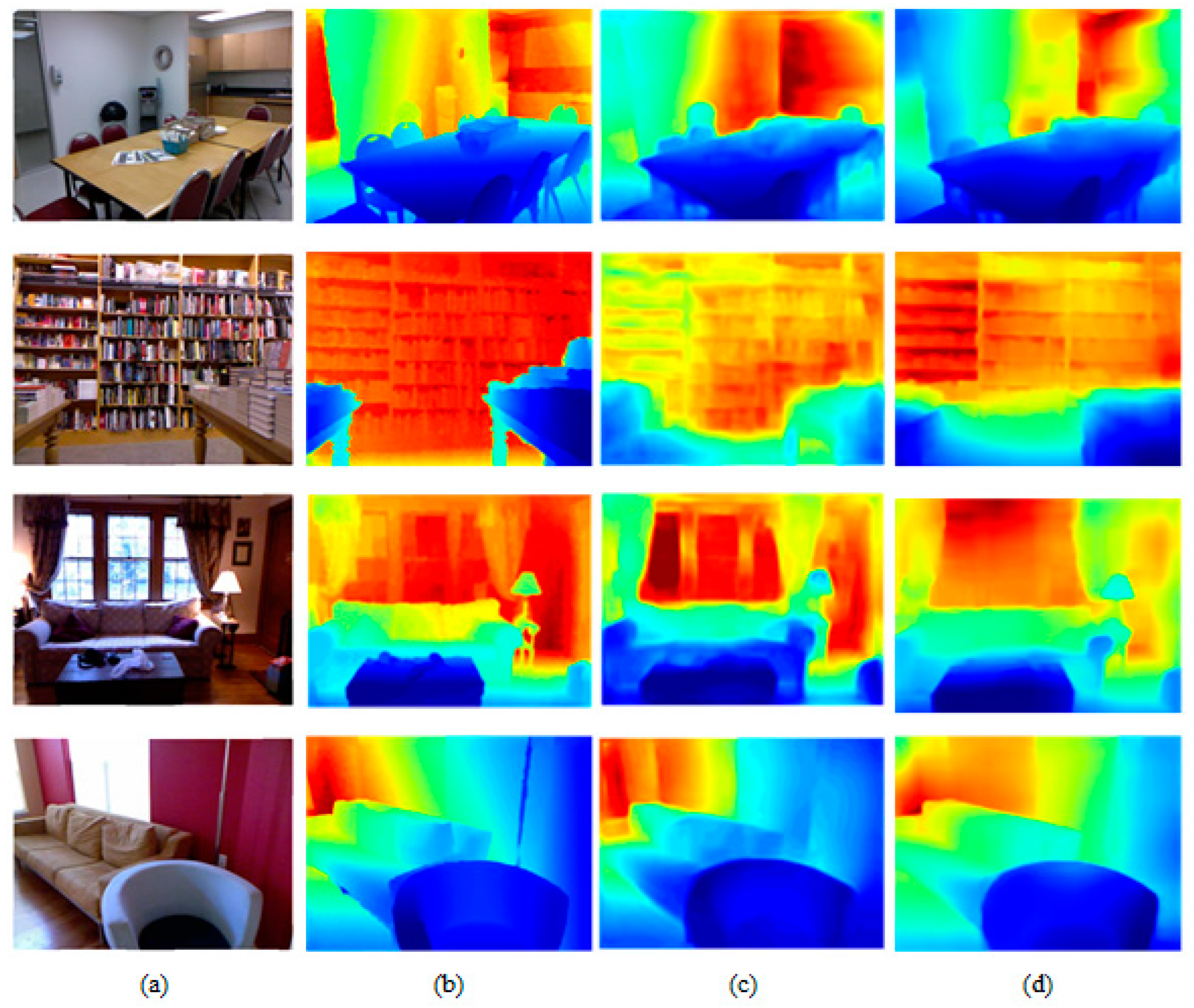
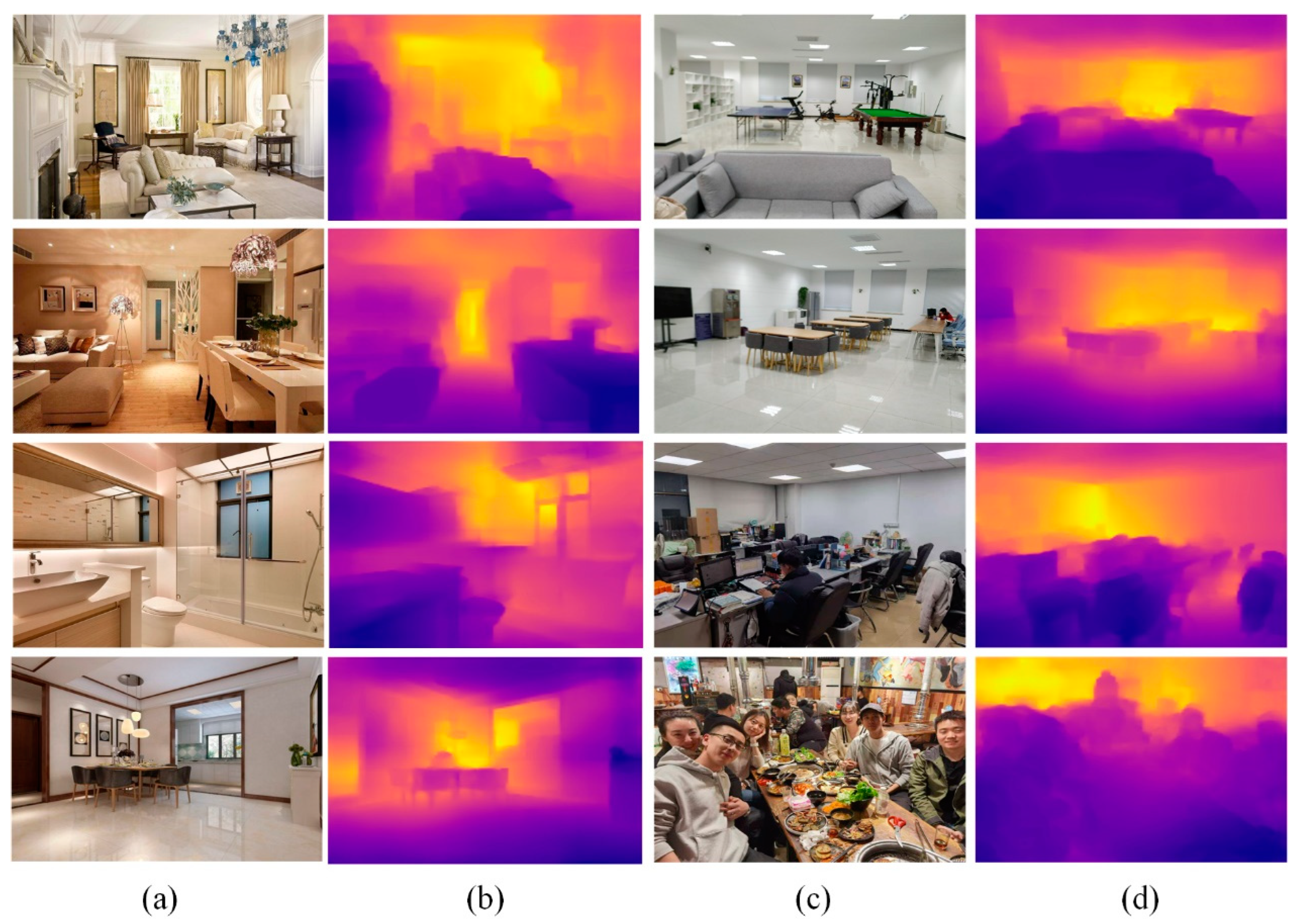
4.4. Experiments on Collected Images
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, W.; Wang, K.; Ding, W.; Gao, F.; Qin, T.; Shen, S. Autonomous aerial robot using dual-fisheye cameras. J. Robot. Syst. 2020, 37, 497–514. [Google Scholar] [CrossRef]
- Saleem, N.H.; Chien, H.J.; Rezaei, M.; Rezaei, M.; Klette, R. Effects of ground manifold modeling on the accuracy of stixel calculations. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3675–3687. [Google Scholar] [CrossRef] [Green Version]
- Civera, J.; Davison, A.J.; Montiel, J.M.M. Inverse Depth parameterization for monocular SLAM. IEEE Trans. Robot. 2008, 24, 932–945. [Google Scholar] [CrossRef] [Green Version]
- Ping, J.; Thomas, B.H.; Baumeister, J.; Guo, J.; Weng, D.; Liu, Y. Effects of shading model and opacity on depth perception in optical see-through augmented reality. J. Soc. Inf. Disp. 2020, 28, 892–904. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, L.; Jiang, H.; Tang, Z.; Wang, Y.; Bao, H.; Zhang, G. Mobile3DRecon: Real-time Monocular 3D Reconstruction on a Mobile Phone. IEEE Trans. Vis. Comput. Graph. 2020, 26, 3446–3456. [Google Scholar] [CrossRef] [PubMed]
- Hazirbas, C.; Ma, L.; Domokos, C.; Cremers, D. Fusenet: Incorporating depth into semantic segmentation via fusion-based CNN architecture. In Proceedings of the ACCV, Taipei, Taiwan, 21–23 November 2016. [Google Scholar]
- Yang, F.; Ding, X.; Cao, J. 3D reconstruction of free-form surface based on color structured light. Acta Opt. Sin. 2021, 41, 0212001. [Google Scholar] [CrossRef]
- May, S.; Droeschel, D.; Holz, D.; Wiesen, C. 3D pose estimation and mapping with time-of-flight cameras. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 120–125. [Google Scholar]
- Wang, X.; Liu, H.; Niu, Y. Binocular stereo matching combining multi-scale local features and depth features. Acta Opt. Sin. 2020, 40, 0215001. [Google Scholar] [CrossRef]
- Atapour-Abarghouei, A. Real-time monocular depth estimation using synthetic data with domain adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision & Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Ji, R.R.; Li, K.; Wang, Y.; Sun, X.S.; Guo, F.; Guo, X.W.; Wu, Y.J.; Huang, F.Y.; Luo, J.B. Semi-Supervised adversarial monocular depth estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2410–2422. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, M.L.; Ye, X.C.; Xin, F. Unsupervised detail-preserving network for high quality monocular depth estimation. Neurocomputing 2020, 404, 1–13. [Google Scholar] [CrossRef]
- Huang, K.; Qu, X.; Chen, S.; Chen, Z.; Zhang, W.; Qi, H.; Zhao, F. Superb Monocular Depth Estimation Based on Transfer Learning and Surface Normal Guidance. Sensors 2020, 20, 4856. [Google Scholar] [CrossRef] [PubMed]
- Ding, M.; Jiang, X. Scene depth estimation method based on monocular vision in advanced driving assistance system. Acta Opt. Sin. 2020, 40, 1715001. [Google Scholar] [CrossRef]
- Zheng, C.; Cham, T.J.; Cai, J. T2net: Synthetic-to-realistic translation for solving single-image depth estimation tasks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 767–783. [Google Scholar]
- Yeh, C.H.; Huang, Y.P.; Lin, C.Y.; Chang, C.Y. Transfer2Depth: Dual attention network with transfer learning for monocular depth estimation. IEEE Access 2020, 8, 86081–86090. [Google Scholar] [CrossRef]
- Konrad, J.; Wang, M.; Ishwar, P. 2d-to-3d image conversion by learning depth from examples. In Proceedings of the 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Providence, RI, USA, 16–21 June 2012; pp. 16–22. [Google Scholar]
- Li, B.; Shen, C.; Dai, Y.; den Hengel, A.V.; He, M. Depth and surface normal estimation from monocular images using regression on deep features and hierarchical CRFs. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1119–1127. [Google Scholar]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. In Proceedings of the NIPS, Montréal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Laina, I.; Rupprecht, C.; Belagiannis, V.; Tombari, F.; Navab, N. Deeper depth prediction with fully convolutional residual networks. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 239–248. [Google Scholar]
- Xu, D.; Ricci, E.; Ouyang, W.; Wang, X.; Sebe, N. Multi-scale continuous crfs as sequential deep networks for monocular depth estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5354–5362. [Google Scholar]
- Hao, Z.; Li, Y.; You, S.; Lu, F. Detail preserving depth estimation from a single image using attention guided networks. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 304–313. [Google Scholar]
- Fu, H.; Gong, M.; Wang, C.; Batmanghelich, N.; Tao, D. Deep ordinal regression network for monocular depth estimation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2002–2011. [Google Scholar]
- Ye, X.C.; Chen, S.D.; Xu, R. DPNet: Detail-preserving network for high quality monocular depth estimation. Pattern Recognit. 2021, 109, 107578. [Google Scholar] [CrossRef]
- Alhashim, I.; Wonka, P. High Quality Monocular Depth Estimation via Transfer Learning. arXiv 2018, arXiv:1812.11941. Available online: http://arxiv.org/abs/1812.11941 (accessed on 6 June 2022).
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic Routing Between Capsules. Neural Inf. Process. Syst. 2017, 30, 3856–3866. [Google Scholar]
- Hinton, G.; Sabour, S.; Frosst, N. Matrix capsules with EM routing. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Ribeiro, F.D.S.; Leontidis, G.; Kollias, S. Capsule routing via variational bayes. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Gu, J.; Tresp, V. Interpretable graph capsule networks for object recognition. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Ribeiro, F.D.S.; Leontidis, G.; Kollias, S. Introducing routing uncertainty in capsule networks. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; Volume 33, pp. 6490–9502. [Google Scholar]
- Sabour, S.; Tagliasacchi, A.; Yazdani, S.; Hinton, G.; Fleet, D.J. Unsupervised part representation by flow capsules. In Proceedings of the International Conference on Machine learning, Virtual, 18–24 July 2021; pp. 9213–9223. [Google Scholar]
- Ribeiro, F.D.S.; Duarte, K.; Everett, M.; Leontidis, G.; Shah, M. Learning with capsules: A survey. Computer Vision and Pattern Recognition (CVPR). arXiv 2022, arXiv:2206.02664. [Google Scholar]
- Jiao, J.; Cao, Y.; Song, Y.; Lau, R. Look Deeper into Depth: Monocular Depth Estimation with Semantic Booster and Attention-Driven Loss; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Ummenhofer, B.; Zhou, H.; Uhrig, J.; Mayer, N.; Ilg, E.; Dosovitskiy, A.; Brox, T. Demon: Depth and motionnetwork for learning monocular stereo. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5622–5631. [Google Scholar]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor segmentation and support inference from rgbd images. In Proceedings of the ECCV, Florence, Italy, 7–13 October 2012. [Google Scholar]
- Uhrig, J.; Schneider, N.; Schneider, L.; Franke, U.; Brox, T.; Geiger, A. Sparsity Invariant CNNs. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 11–20. [Google Scholar]
- Liu, M.; Salzmann, M.; He, X. Discrete-continuous depth estimation from a single image. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 716–723. [Google Scholar]
- Wang, P.; Shen, X.; Lin, Z.; Cohen, S.; Price, B.; Yuille, A.L. Towards unified depth and semantic prediction from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2800–2809. [Google Scholar]
- Zhou, J.; Wang, Y.; Qin, K.; Zeng, W. Moving indoor: Unsupervised video depth learning in challenging environments. In Proceedings of the ICCV, Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Lin, X.; Sánchez-Escobedo, D.; Casas, J.R.; Pardàs, M. Depth estimation and semantic segmentation from a single RGB image using a Hybrid convolutional neural network. Sensors 2019, 19, 1795. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saxena, A.; Chung, S.H.; Ng, A.Y. Learning depth from single monocular images. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2005; pp. 1–5. [Google Scholar]


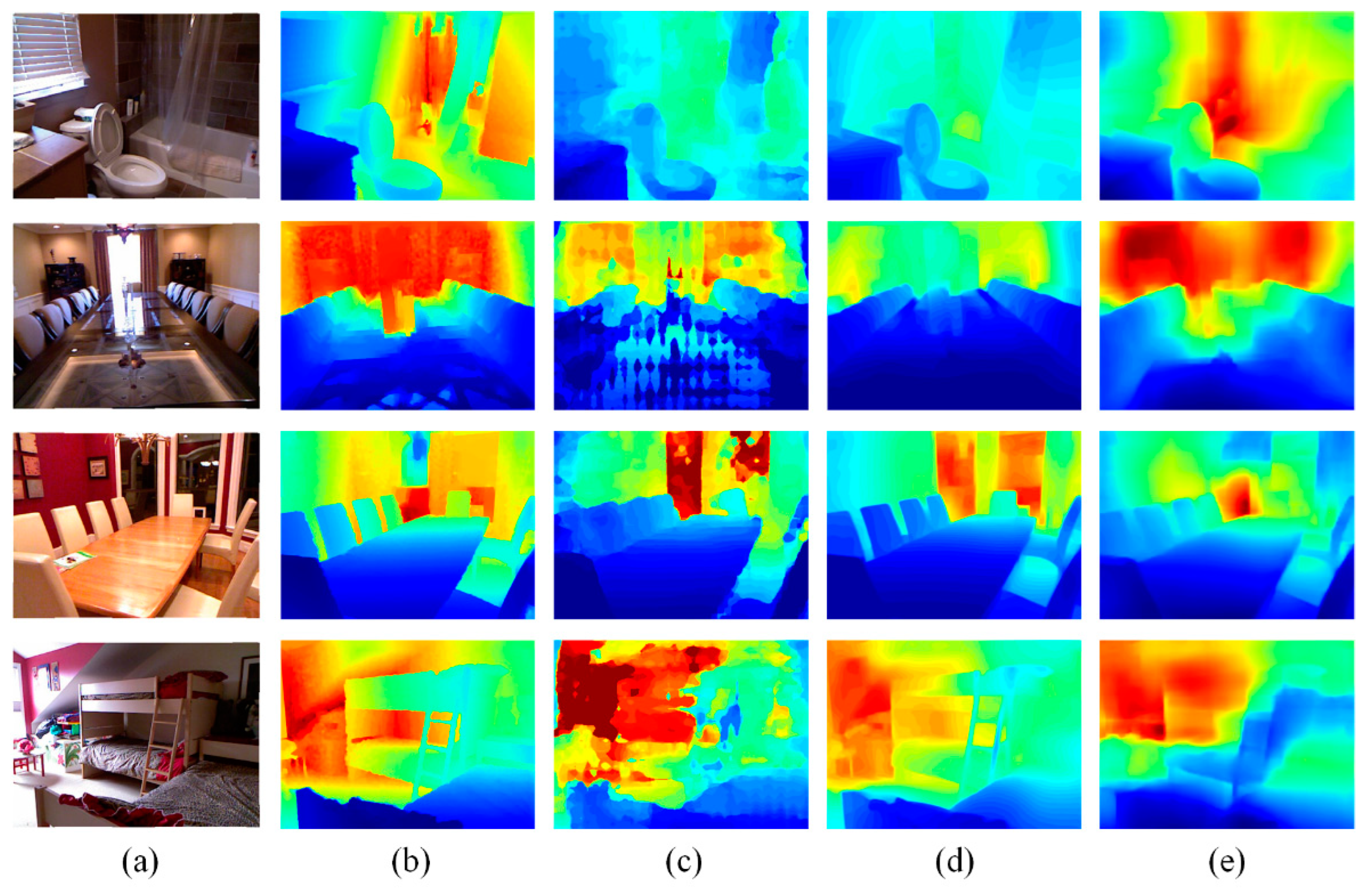


| Method | FB | bs | Loss | C1 Indices | C2 Indices | Output | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| AbsRel↓ | RMSE↓ | log10 | δ1↑ | δ2↑ | δ3↑ | |||||
| Zheng [15] | × | 6 | - | 0.257 | 0.915 | 0.305 | 0.540 | 0.832 | 0.948 | 256 × 192 |
| Liu [37] | × | - | - | 0.230 | 0.824 | 0.095 | 0.614 | 0.883 | 0.971 | - |
| Wang [38] | × | - | - | 0.220 | 0.745 | 0.094 | 0.605 | 0.890 | 0.970 | - |
| Zhou [39] | × | × | - | 0.208 | 0.712 | 0.086 | 0.674 | 0.900 | 0.968 | - |
| Lin [40] | × | × | - | 0.279 | 0.942 | - | 0.501 | - | - | - |
| Eigen [19] | × | 32 | 0.215 | 0.907 | - | 0.637 | 0.887 | 0.971 | 80 × 60 | |
| Ours | × | 4 | Lcost | 0.226 | 0.792 | 0.092 | 0.637 | 0.887 | 0.970 | 128 × 128 |
| Ours | √ | 2 | Lcost | 0.216 | 0.757 | 0.088 | 0.657 | 0.897 | 0.973 | 128 × 128 |
| Ours | √ | 4 | Ldepth | 0.229 | 0.817 | 0.094 | 0.605 | 0.883 | 0.971 | 128 × 128 |
| Ours | √ | 4 | Lcost | 0.214 | 0.760 | 0.087 | 0.663 | 0.900 | 0.973 | 128 × 128 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhu, H. Monocular Depth Estimation: Lightweight Convolutional and Matrix Capsule Feature-Fusion Network. Sensors 2022, 22, 6344. https://doi.org/10.3390/s22176344
Wang Y, Zhu H. Monocular Depth Estimation: Lightweight Convolutional and Matrix Capsule Feature-Fusion Network. Sensors. 2022; 22(17):6344. https://doi.org/10.3390/s22176344
Chicago/Turabian StyleWang, Yinchu, and Haijiang Zhu. 2022. "Monocular Depth Estimation: Lightweight Convolutional and Matrix Capsule Feature-Fusion Network" Sensors 22, no. 17: 6344. https://doi.org/10.3390/s22176344
APA StyleWang, Y., & Zhu, H. (2022). Monocular Depth Estimation: Lightweight Convolutional and Matrix Capsule Feature-Fusion Network. Sensors, 22(17), 6344. https://doi.org/10.3390/s22176344






