Attitude Solving Algorithm and FPGA Implementation of Four-Rotor UAV Based on Improved Mahony Complementary Filter
Abstract
:1. Introduction
- (1)
- Mathematical concepts and formulas in attitude solving are introduced to provide the theoretical basis for the key steps in the attitude solving system, such as the representation of the attitude matrix, the derivation of the theoretical field vectors, and the quaternion update of the attitude kinematic equations.
- (2)
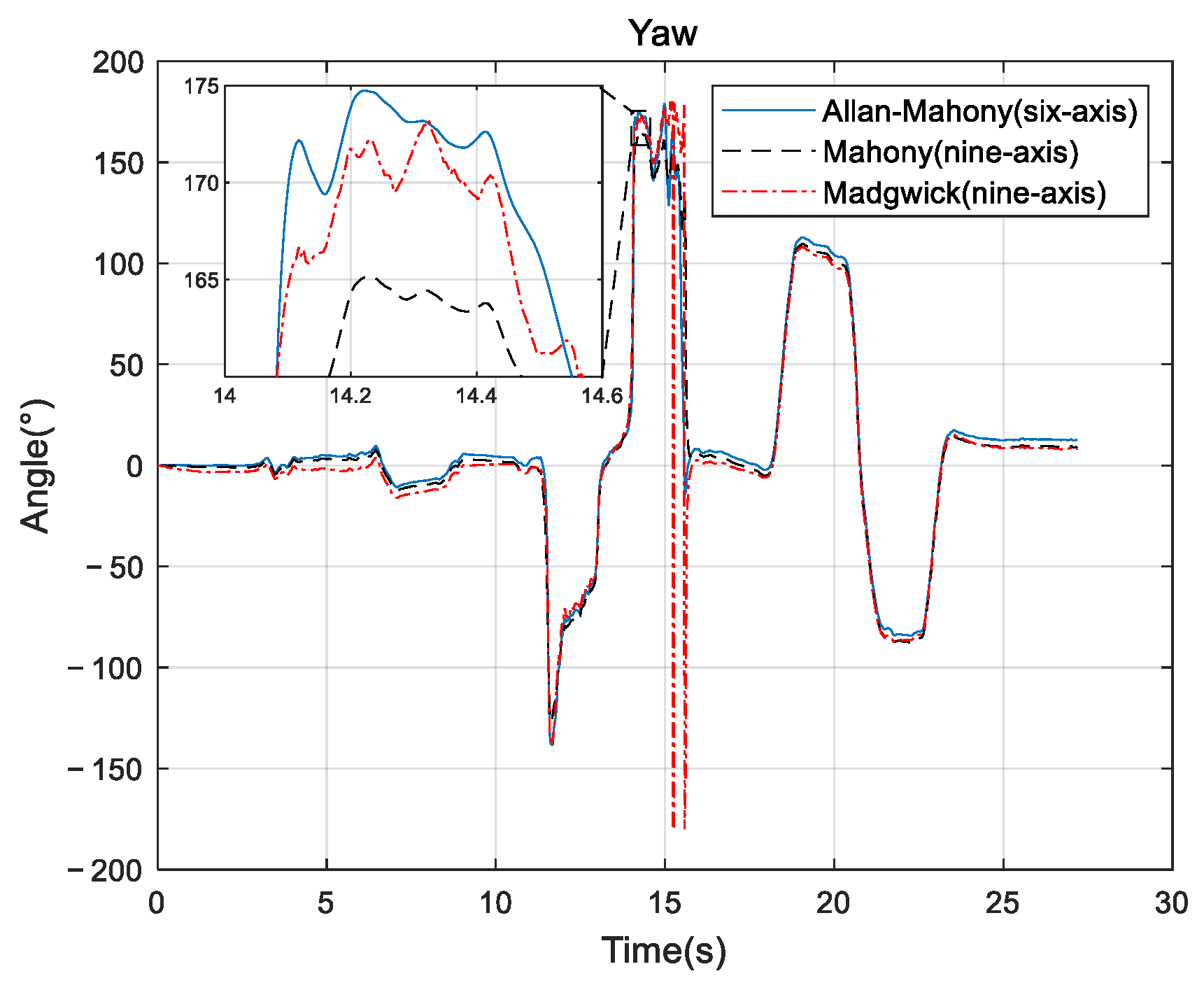
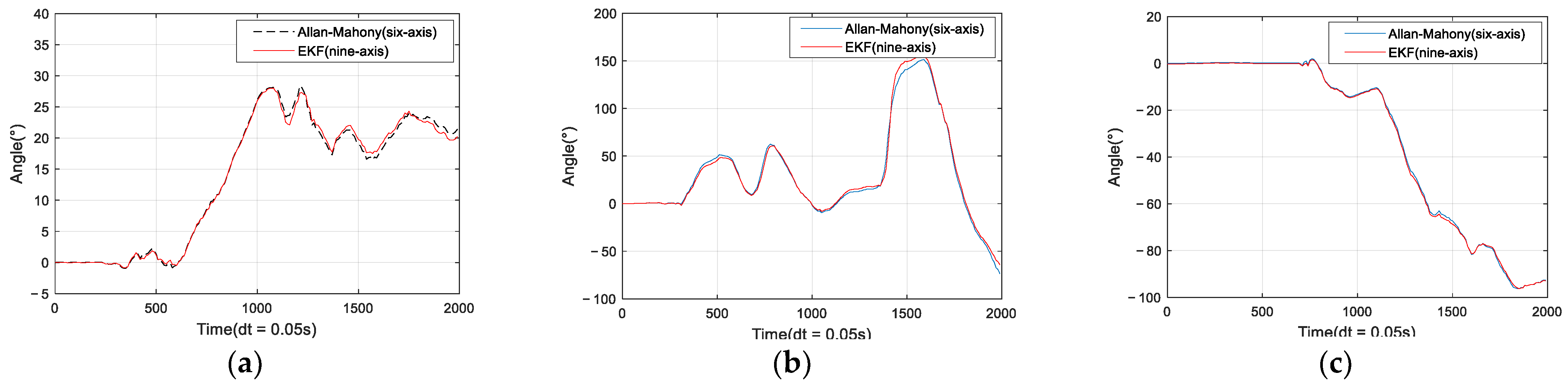
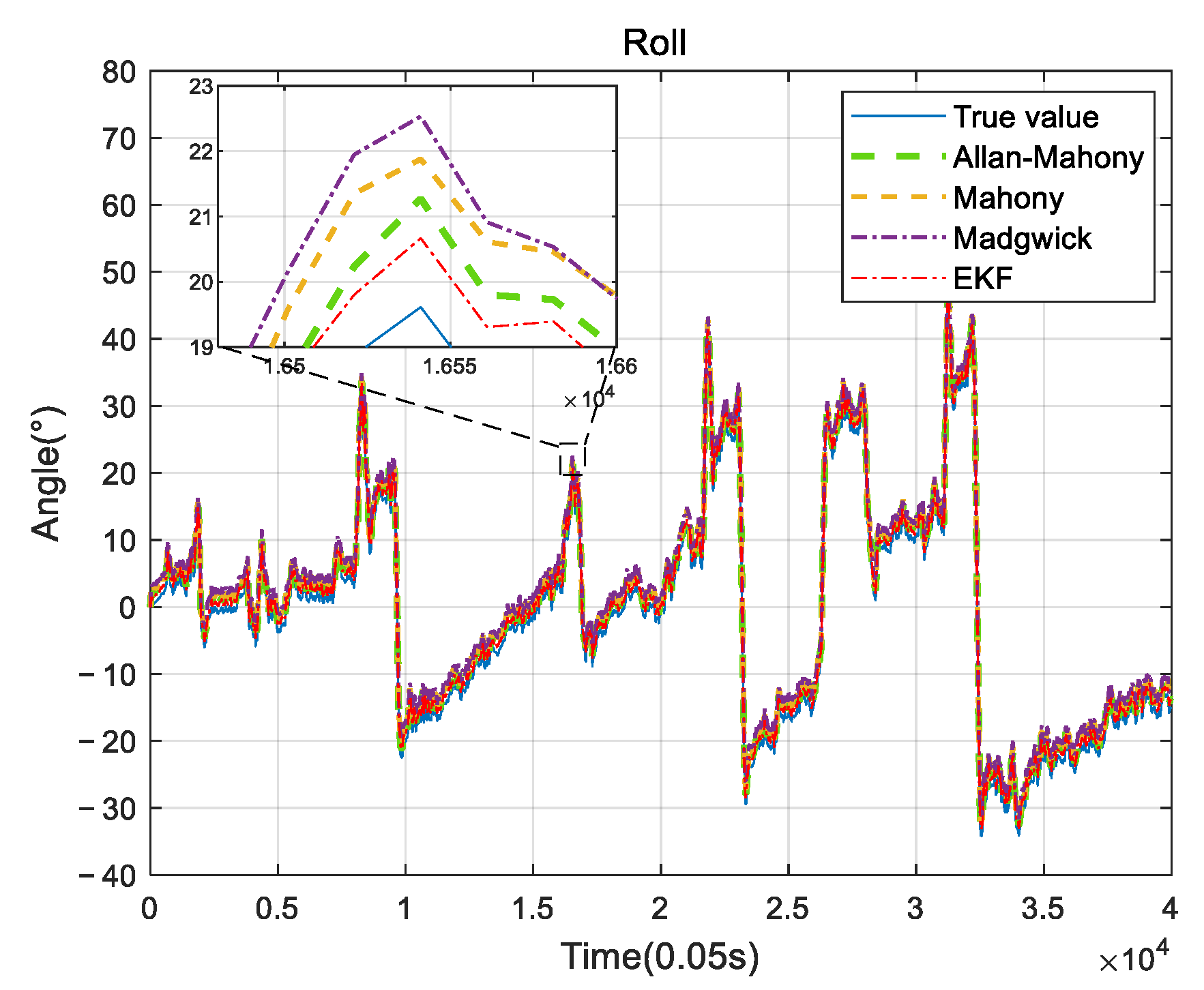
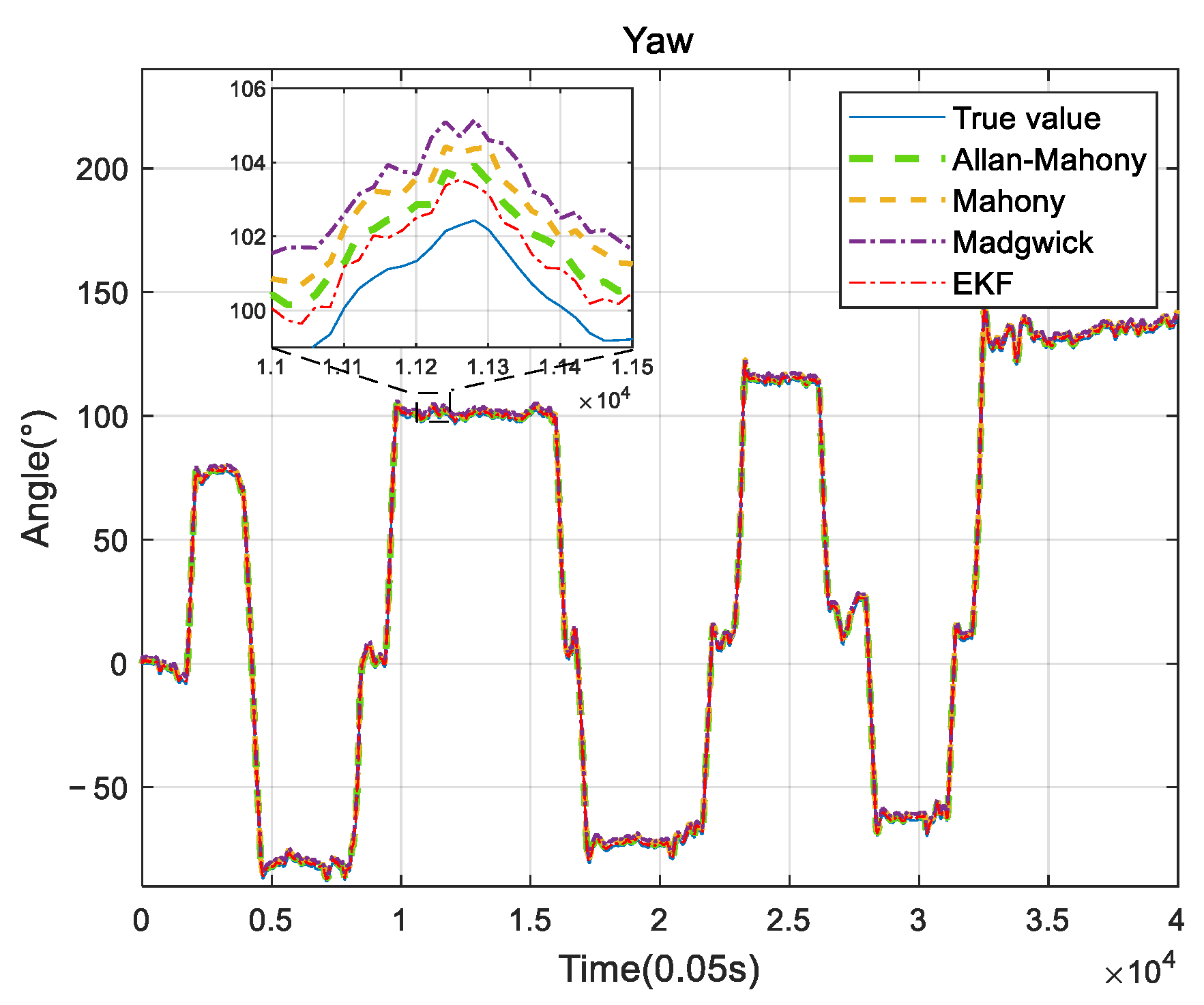
- Based on Allan variance, an improved Mahony complementary filtering using IMU six-axis data is proposed. Compared with the nine-axis data solving methods, i.e., Mahony and Madgwick, the accuracy of the proposed algorithm is comparable but has lower complexity.
- (3)
- The proposed algorithm is implemented on an FPGA platform. There are three steps to build the attitude solving system on the FPGA platform: data reading, data processing, and data sending, among which data processing as the focus of attitude solving contains key elements, such as floating-point operation, transcendental function operation, and system framework. The error analysis of the actual UAV test results is carried out.
2. Principle of Attitude Solution
2.1. Common Coordinate Systems and Representation of Attitude Matrix
2.2. Equations of Attitude Kinematics Based on Quaternions
3. Design and Simulation of the Attitude Solution Algorithm
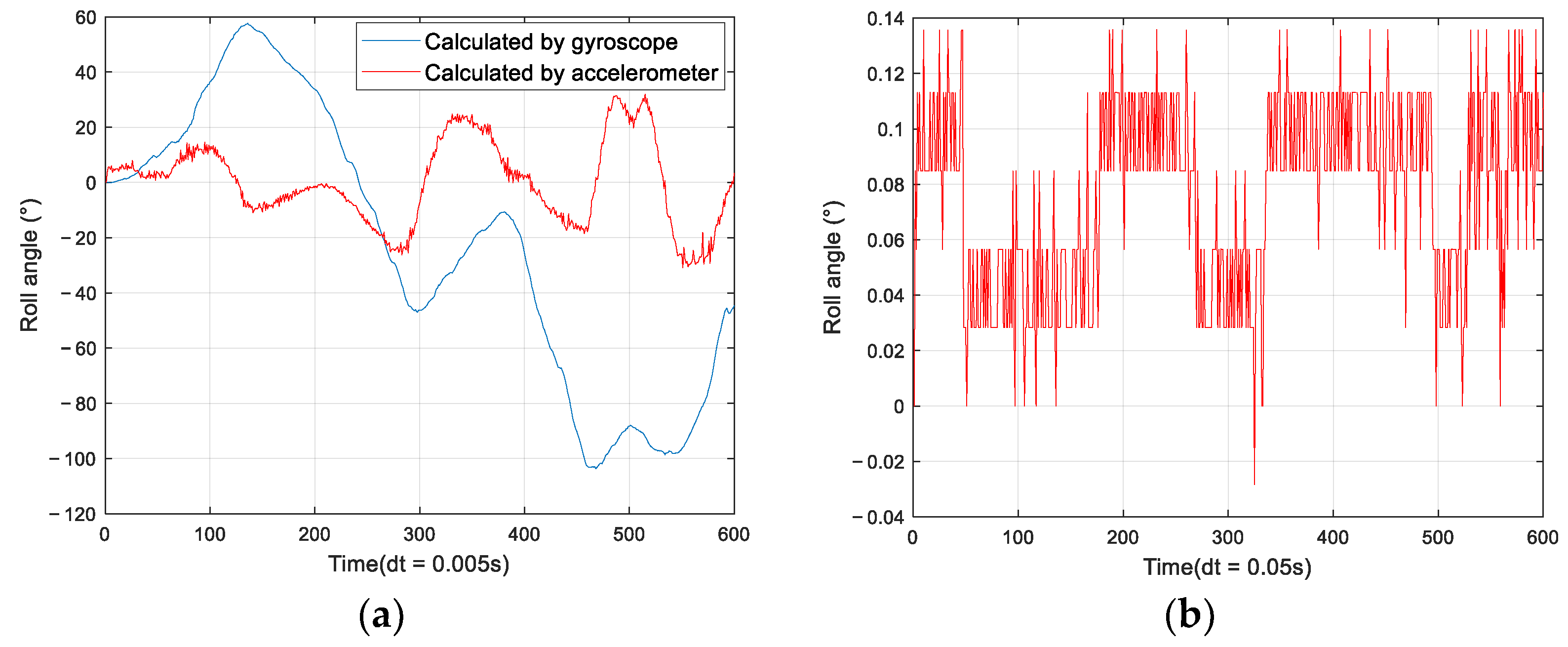
3.1. Inertial Sensor Error Analysis
- ①
- The gyroscope’s zero bias is serious, that is, the gyroscope has angular velocity output even when it is stationary, which is amplified by integrating zero bias, resulting in serious angular drift over time. Zero bias can be seen as a low-frequency noise with large amplitude and slow change.
- ②
- The accelerometer has good low-frequency characteristics, but there is high-frequency noise, and the operating principle causes the accelerometer to be unable to sense horizontal rotation, so the measured yaw angle accuracy is insufficient.
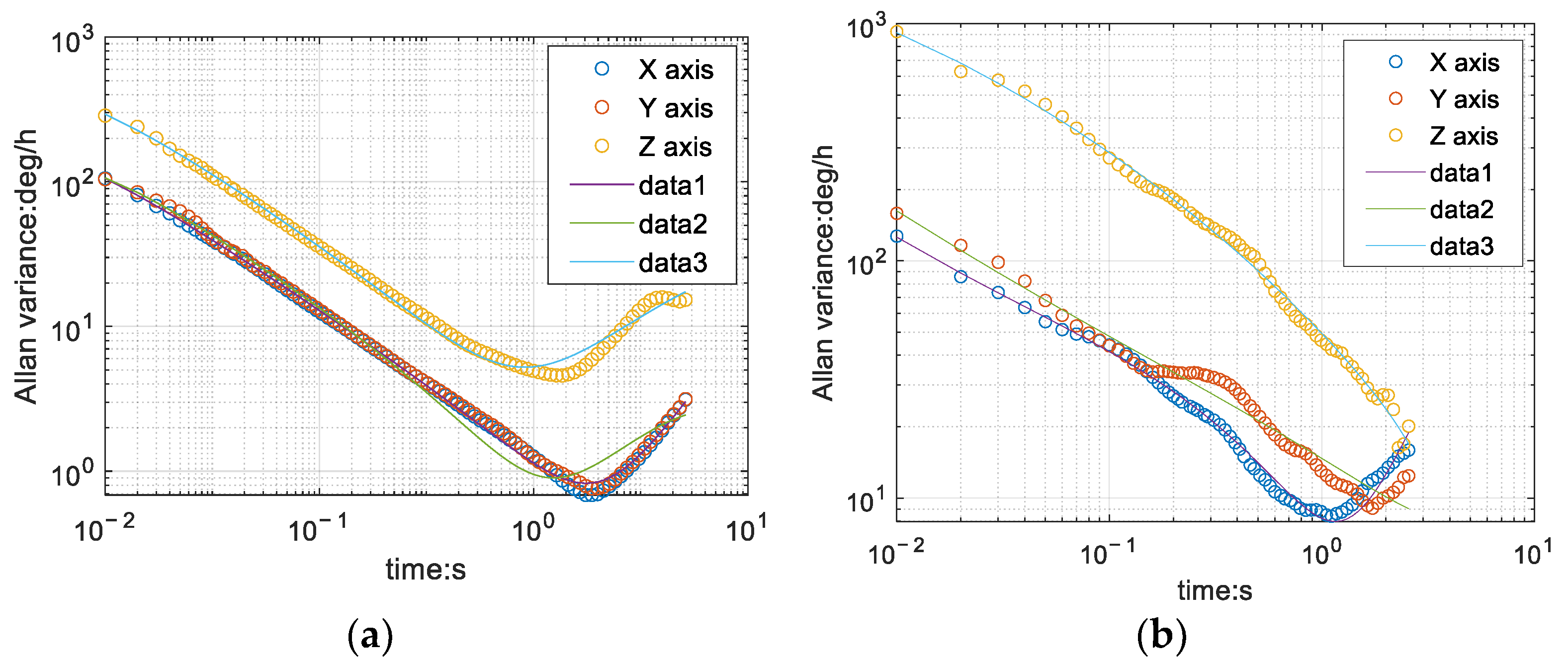
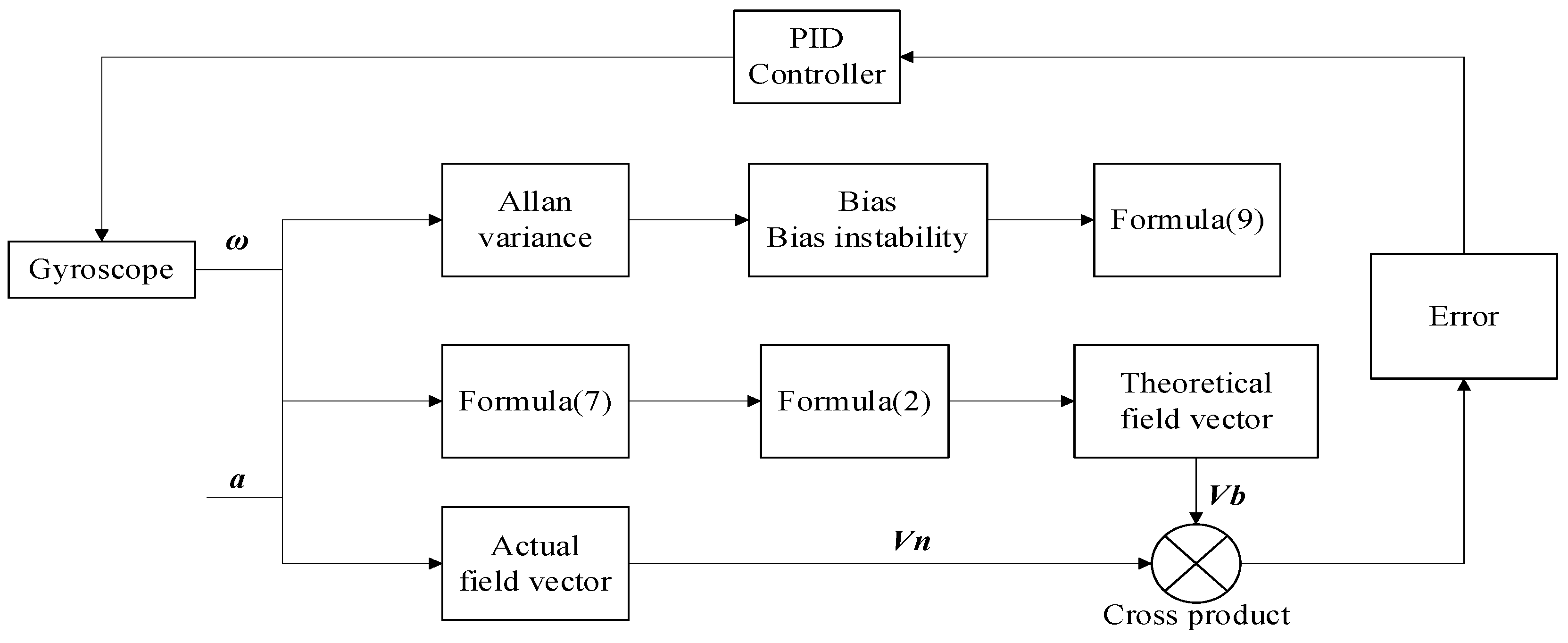
3.2. Improved Mahony Complementary Filtering Based on Allan Variance
- Step 1:
- Gyroscope and accelerometer measure angular velocity and acceleration respectively;
- Step 2:
- According to α = Vb ⊗ Vn, calculate the accelerometer error α; Based on Formula (9), calculate Allan variance δ2. The system error vector is ;
- Step 3:
- Use the error vector as an input to the PID controller. Obtain the correction value for the angular velocity: ;
- Step 4:
- Calculate the corrected angular velocity vector: ;
- Step 5:
- Update the quadratic q using Equation (7), and then update Vb using Equation (2);
- Step 6:
- Start a new round of calculations from step 1.
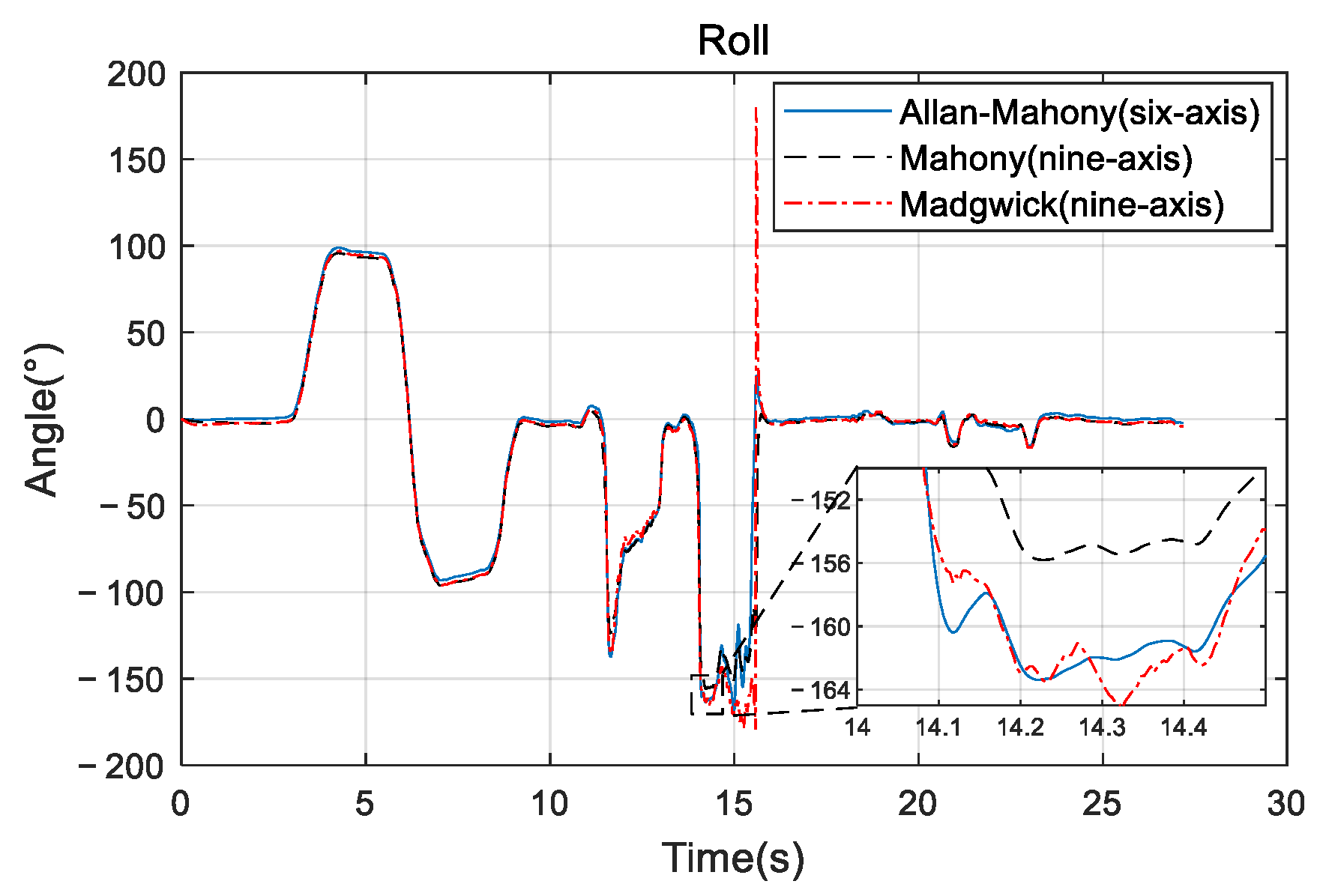
3.3. Simulation of Attitude Solution
4. Implementation of Attitude Calculation on FPGA Hardware Platform
4.1. FPGA System Implementation and Test
4.2. UAV Measurement System
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Holness, C.; Matthews, T.; Satchell, K.; Swindell, E.C. Remote sensing archeological sites through Unmanned Aerial Vehicle (UAV) imaging. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 6695–6698. [Google Scholar] [CrossRef]
- Ammann, N.; Theil, S. Using an UAV for testing an autonomous terrain-based optical navigation system for lunar landing. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Aslan, M.F.; Durdu, A.; Sabanci, K.; Ropelewska, E.; Gültekin, S.S. A Comprehensive Survey of the Recent Studies with UAV for Precision Agriculture in Open Fields and Greenhouses. Appl. Sci. 2022, 12, 1047. [Google Scholar] [CrossRef]
- Biçici, S.; Zeybek, M. An approach for the automated extraction of road surface distress from a UAV-derived point cloud. Autom. Constr. 2021, 122, 103475. [Google Scholar] [CrossRef]
- Avola, D.; Cinque, L.; Diko, A.; Fagioli, A.; Foresti, G.L.; Mecca, A.; Pannone, D.; Piciarelli, C. MS-Faster R-CNN: Multi-Stream Backbone for Improved Faster R-CNN Object Detection and Aerial Tracking from UAV Images. Remote Sens. 2021, 13, 1670. [Google Scholar] [CrossRef]
- Marantos, P.; Koveos, Y.; Kyriakopoulos, K.J. UAV State Estimation Using Adaptive Complementary Filters. IEEE Trans. Control Syst. Technol. 2016, 24, 1214–1226. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, J.; Liang, X.; Liu, N. A Coupling Method of Geomagnetic Aided Inertial Attitude Errors. IEEE Sensors J. 2020, 20, 14282–14289. [Google Scholar] [CrossRef]
- Djerida, A.; Zhao, Z.; Zhao, J. Development of scale and illumination invariant feature detector with application to UAV attitude estimation. J. Vis. Commun. Image Represent. 2021, 79, 103258. [Google Scholar] [CrossRef]
- Kamesh, R.; Rani, K.Y. Iterative EKF as a controller in novel MPC formulation: First principles model based IEKF-MPC for SISO systems. Comput. Chem. Eng. 2022, 163, 107833. [Google Scholar] [CrossRef]
- Guan, L.; Sun, P.; Xu, X.; Zeng, J.; Rong, H.; Gao, Y. Low-cost MIMU based AMS of highly dynamic fixed-wing UAV by maneuvering acceleration compensation and AMCF. Aerosp. Sci. Technol. 2021, 117, 106975. [Google Scholar] [CrossRef]
- Xia, Q.; Liu, S.; Guo, M.; Wang, H.; Zhou, Q.; Zhang, X. Multi-UAV trajectory planning using gradient-based sequence minimal optimization. Robot. Auton. Syst. 2021, 137, 103728. [Google Scholar] [CrossRef]
- Deibe, Á.; Nacimiento, J.A.A.; Cardenal, J.; Peña, F.L. A Kalman Filter for Nonlinear Attitude Estimation Using Time Variable Matrices and Quaternions. Sensors 2020, 20, 6731. [Google Scholar] [CrossRef]
- Bangura, M.; Hou, X.; Allibert, G.; Mahony, R.; Michael, N. Supervisory Control of Multirotor Vehicles in Challenging Conditions Using Inertial Measurements. IEEE Trans. Robot. 2018, 34, 1490–1501. [Google Scholar] [CrossRef]
- Wu, B.; Wang, D.; Poh, E.K. Decentralized attitude coordinated control without velocity measurements for spacecraft formation. In Proceedings of the IEEE ICCA 2010, Xiamen, China, 9–11 June 2010; pp. 667–672. [Google Scholar] [CrossRef]
- Mayhew, C.G.; Sanfelice, R.G.; Teel, A.R. Quaternion-Based Hybrid Control for Robust Global Attitude Tracking. IEEE Trans. Autom. Control 2011, 56, 2555–2566. [Google Scholar] [CrossRef]
- Wang, R.; Zhao, C.; Bai, Y.; Du, W.; Wang, J. An Actuator Fault Detection and Reconstruction Scheme for Hex-Rotor Unmanned Aerial Vehicle. IEEE Access 2019, 7, 93937–93951. [Google Scholar] [CrossRef]
- Bessaad, N.; Qilian, B.; Yuding, D.; Lin, L. An Adaptive Multi-Sample SINS Attitude Algorithm. In Proceedings of the 2018 IEEE International Conference on Information and Automation (ICIA), Wuyishan, China, 11–13 August 2018; pp. 888–892. [Google Scholar] [CrossRef]
- Dan, L.; Guowei, G. Design of Attitude and Heading Reference System Based on DSP and STM32. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 2733–2738. [Google Scholar] [CrossRef]
- Zhang, K.; Bi, F.H.; Li, K.L.; Liang, Y.; Yang, J. Design and Implementation of a Dual-IP Core UAV Flight Control System Based on Qsys. Procedia Comput. Sci. 2020, 166, 180–186. [Google Scholar] [CrossRef]
- Liu, J.; Xu, W.; Jiang, T.; Han, X. Development of an Attitude Transformation Method From the Navigation Coordinate System to the Projection Coordinate System. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1318–1322. [Google Scholar] [CrossRef]
- Piovan, G.; Bullo, F. On Coordinate-Free Rotation Decomposition: Euler Angles About Arbitrary Axes. IEEE Trans. Robot. 2012, 28, 728–733. [Google Scholar] [CrossRef]
- Bar-Itzhack, I.Y.; Bar-Itzhack, I.Y. Extension of Euler’s theorem to n-dimensional spaces. IEEE Trans. Aerosp. Electron. Syst. 1989, 25, 903–909. [Google Scholar] [CrossRef]
- Kinsey, J.C.; Whitcomb, L.L. Adaptive Identification on the Group of Rigid-Body Rotations and its Application to Underwater Vehicle Navigation. IEEE Trans. Robot. 2007, 23, 124–136. [Google Scholar] [CrossRef]
- Jahanchahi, C.; Mandic, D.P. A Class of Quaternion Kalman Filters. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 533–544. [Google Scholar] [CrossRef]
- Chou, J.C.K. Quaternion kinematic and dynamic differential equations. IEEE Trans. Robot. Autom. 1992, 8, 53–64. [Google Scholar] [CrossRef]
- Li, J.; Fang, J. Not Fully Overlapping Allan Variance and Total Variance for Inertial Sensor Stochastic Error Analysis. IEEE Trans. Instrum. Meas. 2013, 62, 2659–2672. [Google Scholar] [CrossRef]
- Hiller, T.; Pentek, Z.; Liewald, J.; Buhmann, A.; Roth, H. Origins and Mechanisms of Bias Instability Noise in a Three-Axis Mode-Matched MEMS Gyroscope. J. Microelectromechanical Syst. 2019, 28, 586–596. [Google Scholar] [CrossRef]
- Rahardjo, J.; Rizqi, M.; Prasetya, N.I.; Prima, D.A.; Rachman, A.; Wibowo, A.T.; Winardi, S.; Widodo, A.; Gumelar, A.B. Combination of Hardware and Microservices-based VR Game Controller using Mahony Filter. In Proceedings of the 2020 Inter-national Seminar on Application for Technology of Information and Communication (iSemantic), Semarang, Indonesia, 19–20 September 2020; pp. 614–619. [Google Scholar] [CrossRef]
- Dharmawan, A.; Ashari, A.; Aprilia, A.G.; Handayani, A.M. Auto VTOL System on Quadrotor Using Madgwick Quaternion Kalman Filter and LQR. In Proceedings of the 4th International Conference on Science and Technology (ICST), Yogyakarta, Indonesia, 7–8 August 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Heo, S.; Cha, J.; Park, C.G. EKF-Based Visual Inertial Navigation Using Sliding Window Nonlinear Optimization. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2470–2479. [Google Scholar] [CrossRef]
- Wang, M.; Guan, L.; Gao, Y.; Xu, X.; Chen, X.; Xiong, D. UAV Attitude Measurement based on Enhanced Mahony Complementary Filter. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 545–550. [Google Scholar] [CrossRef]






| Average Error Data Source | Roll (°) | Pitch (°) | Yaw (°) |
|---|---|---|---|
| This paper | 1.2383 | 0.8641 | 2.6764 |
| Madgwick | 2.4425 | 5.8539 | 5.8096 |
| Mahony | 2.1871 | 1.3685 | 5.1719 |
| EKF | 0.3195 | 0.3019 | 0.7315 |
| Maximum Error Data Source | Roll (°) | Pitch (°) | Yaw (°) |
|---|---|---|---|
| This paper | 3.152 | 3.364 | 5.012 |
| Ref. [31] | 6 | 5 | 4.5 |
| MTi-G-710 | 10 | 10 | 15 |
| Algorithm | Time (s) |
|---|---|
| This paper | 0.1568 |
| Madgwick | 0.2080 |
| Mahony | 0.1782 |
| EKF | 0.2895 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Liu, J.; Yu, R.; Mu, Z.; Huang, L.; Chen, J.; Chen, J. Attitude Solving Algorithm and FPGA Implementation of Four-Rotor UAV Based on Improved Mahony Complementary Filter. Sensors 2022, 22, 6411. https://doi.org/10.3390/s22176411
Zhu Y, Liu J, Yu R, Mu Z, Huang L, Chen J, Chen J. Attitude Solving Algorithm and FPGA Implementation of Four-Rotor UAV Based on Improved Mahony Complementary Filter. Sensors. 2022; 22(17):6411. https://doi.org/10.3390/s22176411
Chicago/Turabian StyleZhu, Yanping, Jing Liu, Ran Yu, Zijian Mu, Lei Huang, Jinli Chen, and Jianan Chen. 2022. "Attitude Solving Algorithm and FPGA Implementation of Four-Rotor UAV Based on Improved Mahony Complementary Filter" Sensors 22, no. 17: 6411. https://doi.org/10.3390/s22176411
APA StyleZhu, Y., Liu, J., Yu, R., Mu, Z., Huang, L., Chen, J., & Chen, J. (2022). Attitude Solving Algorithm and FPGA Implementation of Four-Rotor UAV Based on Improved Mahony Complementary Filter. Sensors, 22(17), 6411. https://doi.org/10.3390/s22176411






