A Novel Prediction Model for Malicious Users Detection and Spectrum Sensing Based on Stacking and Deep Learning
Abstract
:1. Introduction
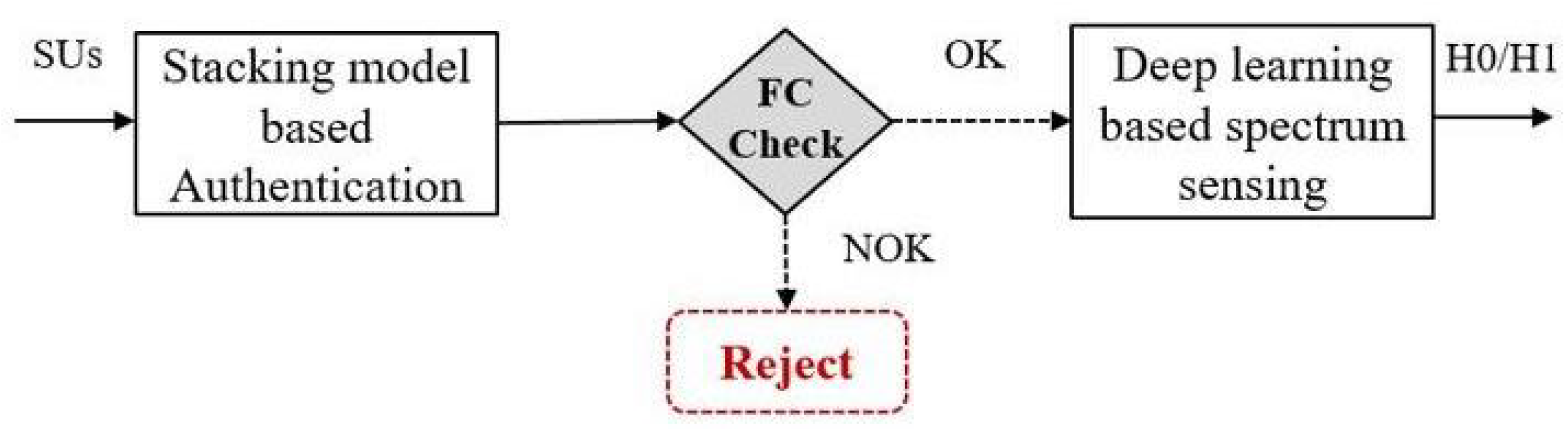
2. Materials and Methods
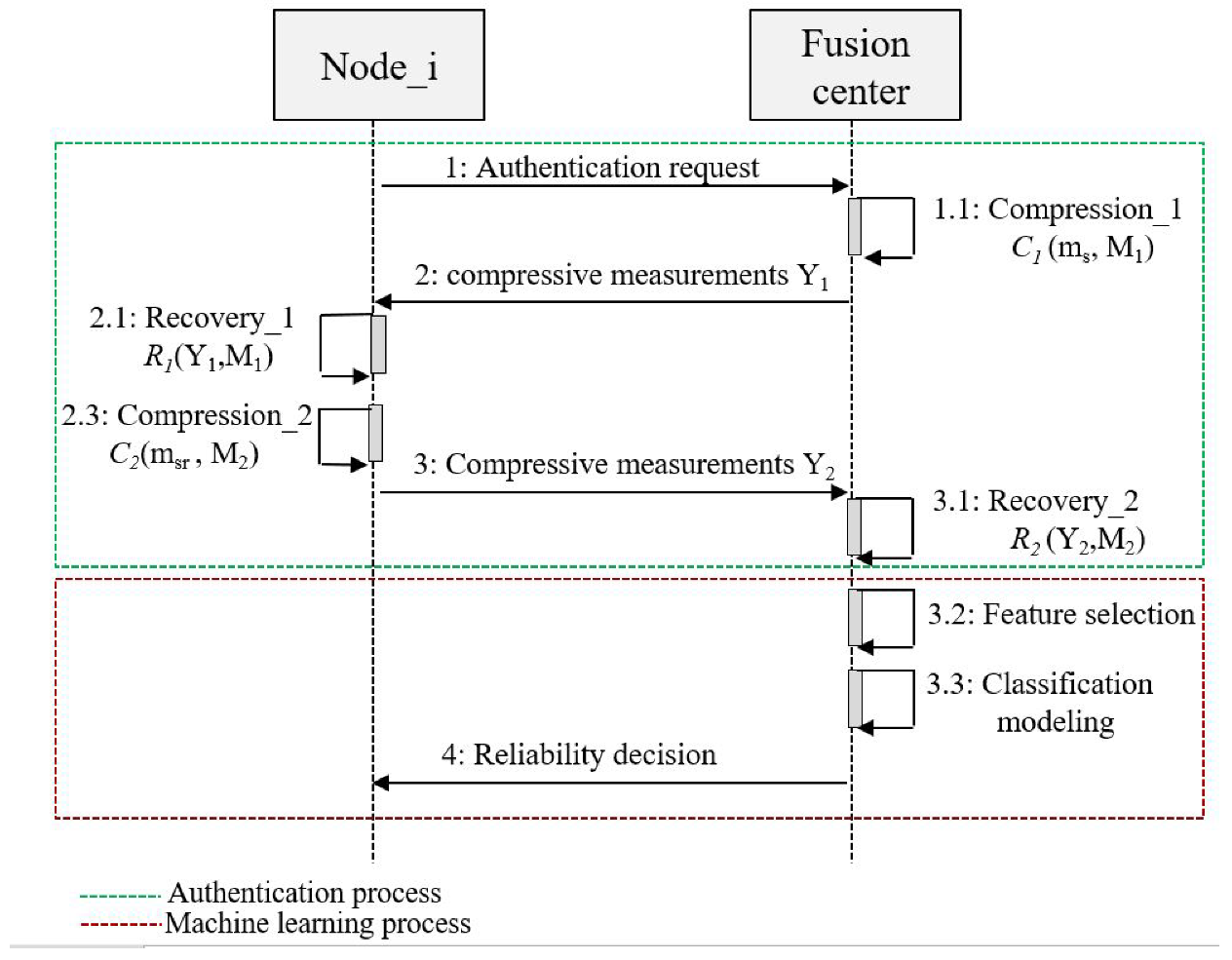
2.1. A Stacking Model-Based Malicious Users Detection
2.1.1. Features Selection
- Recovery error:Also denoted by reconstruction error, this is a metric used to measure the error level between the original signal and the recovered signal according to the distance between the two signals. It can be formulated mathematically aswhere is the recovery error, m is the original signal, and r is the recovered signal.
- Spikes error rate (SER):It estimates the error rate of a recovered signal in terms of its spikes. It is calculated as a function of missed and false spikes. It can be described as follows,where and are the number of false and missed recovered spikes, respectively, and N is the length of the original signal.
- Sparsity error:The sparsity of a signal defines the number of significant samples included in a signal. This characteristic takes a crucial function in the process of a compressive sensing technique to achieve a perfect recovery of a sparse signal. Thus, the sparsity error metric can be defined as the rate of failure between the original signal and the recovery signal in terms of their sparsity level. The sparsity error of a recovered signal r can be expressed as follows,where denotes the sparsity level of the recovered signal r and denotes the sparsity level of the original signal m.
- Magnitude squared coherence (MSC):It evaluates the similarities of two signals in terms of frequency. It uses a linear model to determine at which degree a signal can be predicted from another signal. The MSC between two signals m and r is a real-valued function that can be defined aswhere denotes the cross-spectral density between m and r, and and denote the auto-spectral density of m and r, respectively.
- Mean squared error (MSE):It aims at computing the squared error based on the measures of the square of each element of the error signal resulting from the difference between two signals. It measures the extent to which a reconstructed signal and an original signal are different. It also usually used as a performance metric for predictive modeling. The MSE between two signals m and r can be expressed aswhere m is the original signal, r is the recovered signal, and N denotes the number of samples.
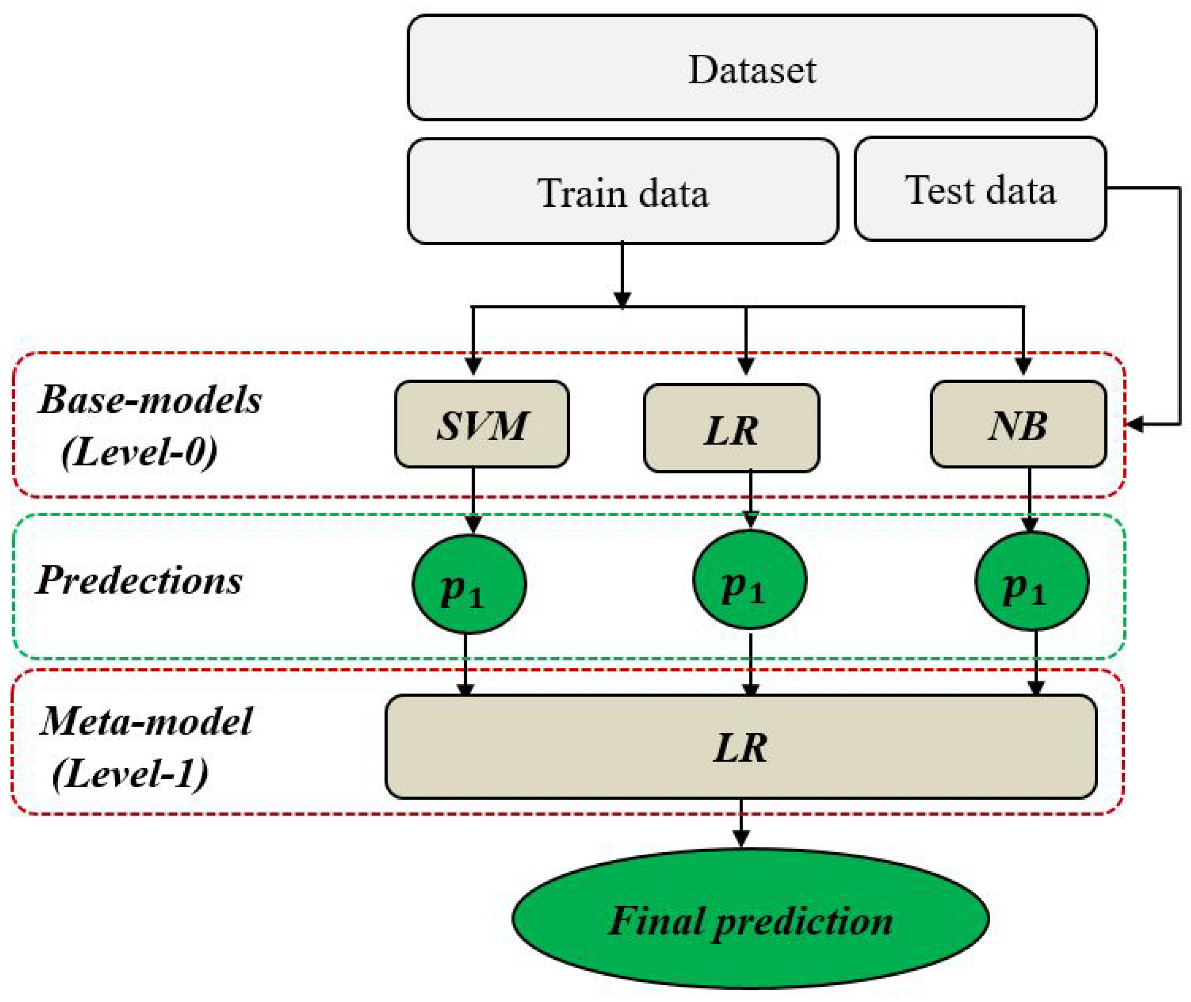
2.1.2. Classification Modeling
| Algorithm 1 Stacking model |
Input: Training data D = (, ) Level-0 classifiers , , Level-1 classifier C Output: Final prediction P Step 1: Train level-0 classifiers for t = 1 to 3 do = (D) % train a base model based on D end Step 2: Generate new inputs to meta-model for i = 1 to m do = (, ) with = (,, ) end Step 3: Train level-1 classifier = C() % train a meta model C based on Step 4: Take final prediction P P(X) = ( ,,) |
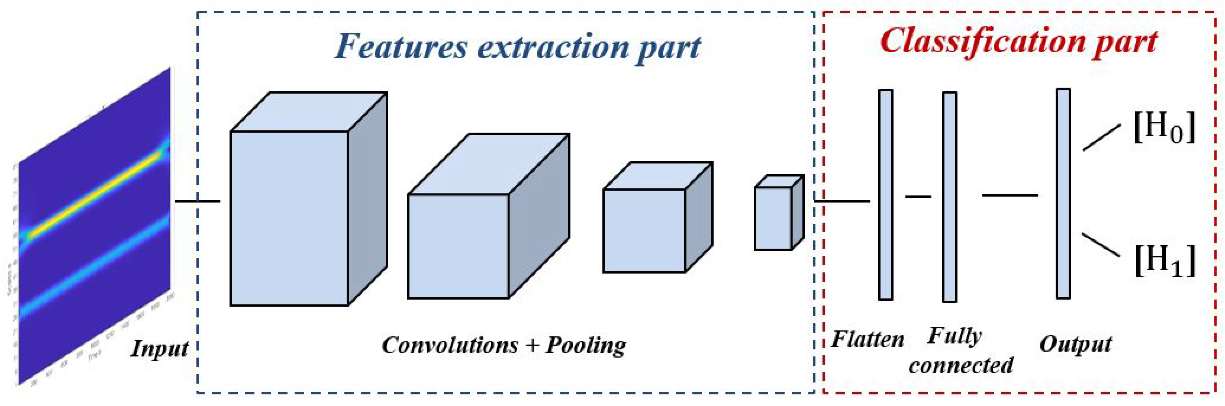
2.2. Scalogram-Based CNN Models for Spectrum Sensing
2.2.1. Continuous Wavelet Transform
2.2.2. CNN Models
- Simple CNN model: Includes an input layer, three convolution layers, three max-pooling layers, three dropout layers, one fully connected layer, and an output layer. The input layer takes images of size 128 × 128, and three channels. The three convolution layers used filters of small size, 3 × 3, stride 1, and max pooling layers with filters of 2 × 2 and stride 2. The first convolution layer contains 16 filters, while the second and the third convolution layer contain 64 filters. For all hidden layers, the ReLU activation function is used and a dropout rate of 0.2 is performed. Finally, a fully connected layer with 16 neurons and an output layer with sigmoid activation function are implemented for the final classification decision.
- Model A: is a combination of the features extraction part of the pre-trained VGG-16 model and the new proposed classification part. The VGG-16 model has a sequential architecture with various number of filters. It includes 13 convolution layers, five pooling layers, three fully connected layers, and an output layer. The input layer takes images of size 224 × 224, and three channels. Each convolution layer used filters of size 3 × 3, stride 1, and the same padding and max pooling layers as the filters of 2 × 2 and stride 2. Convolution layer 1 contains 64 filters, convolution layer 2 contains 128 filters, convolution layer 3 contains 256 filters, and convolution layer 4 and 5 contain 512 filters. For all hidden layers, the ReLU activation function is performed. The first two fully connected layers contain 4096 neurons each, and the third contains 1000. The output layer of VGG-16 used softmax activation function for the final classification decision.
- Model B: is a combination of the features extraction part of the pre-trained InceptionV3 model and the new proposed classification part. InceptionV3 is an advanced version of the standard InceptionV1 model that was released under the name GoogLeNet in 2014. Compared to the other CNN model, the most important property of the InceptionV3 model is the integration of the inception module, which has a sparsely connected architecture. This module performs multi-convolution at the input with different filters sizes and pooling layers simultaneously, which therefore leads to more complex features extraction. Overall, the InceptionV3 model includes 42 layers arranged under several symmetric and asymmetric components, including convolutions, average pooling, max pooling, concatenations, dropouts, fully connected layers, and an output layer with softmax activation function.
- Model C: is a combination of the features extraction part of the pre-trained EfficientNetB0 model and the new proposed classification part. The key concept of EfficientNetB0 is the implementation of a new scaling method, unlike the conventional one. This method scales the three dimensions of an input, namely width, depth, and resolution with a compound coefficient; i.e., it carries out the scaling using fixed coefficients. The EfficientNetB0 architecture is organized as a seven mobile-inverted bottleneck convolution, also known as MBConv block, which uses an inverted residual structure for an improved performance of the CNN model. Each block has two inputs: data and arguments. The data inputs are the output data from the previous block, and the argument inputs are a set of attributes such as squeeze ratio, input filters, and expansion ratio.
- Model D: is a combination of the features extraction part of the pre-trained DenseNet201 model, and the new proposed classification part. DenseNet201 architecture includes four dense blocks using the concept of dense connections between the different layers. To achieve this connection, each layer exploits the feature maps of all previous layers as inputs. The input layer of DenseNet201 takes images with a size of 224 × 224 and three channels. Each two dense blocks are separated by a transition layer, which contains a convolution layer with a filter of 1 × 1, followed by an average-pooling layer with a filter of 2 × 2. At the end, a fully connected layer with 1000 neurons and an output layer with softmax activation function are implemented for the final classification decision.
3. Results and Discussion
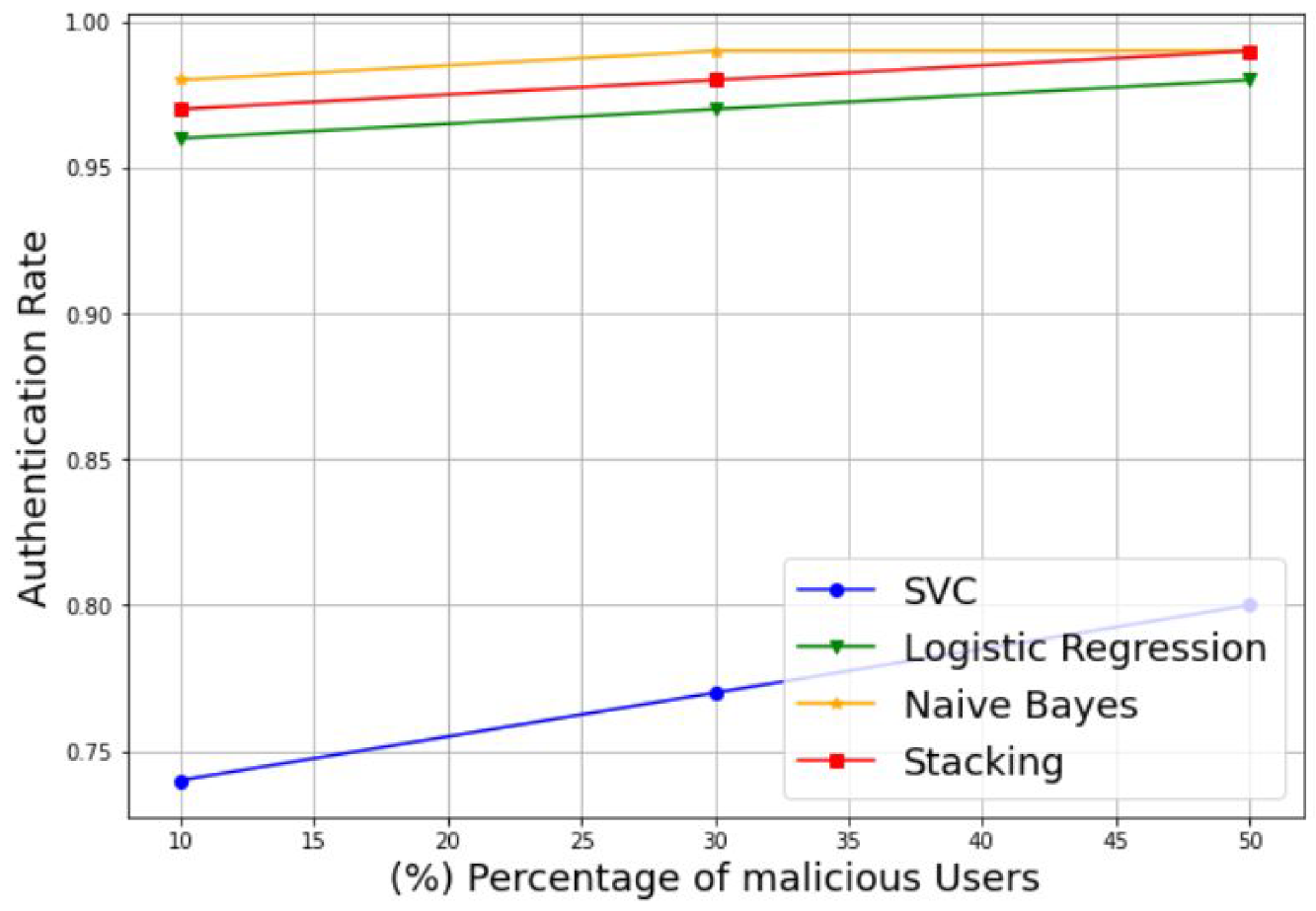
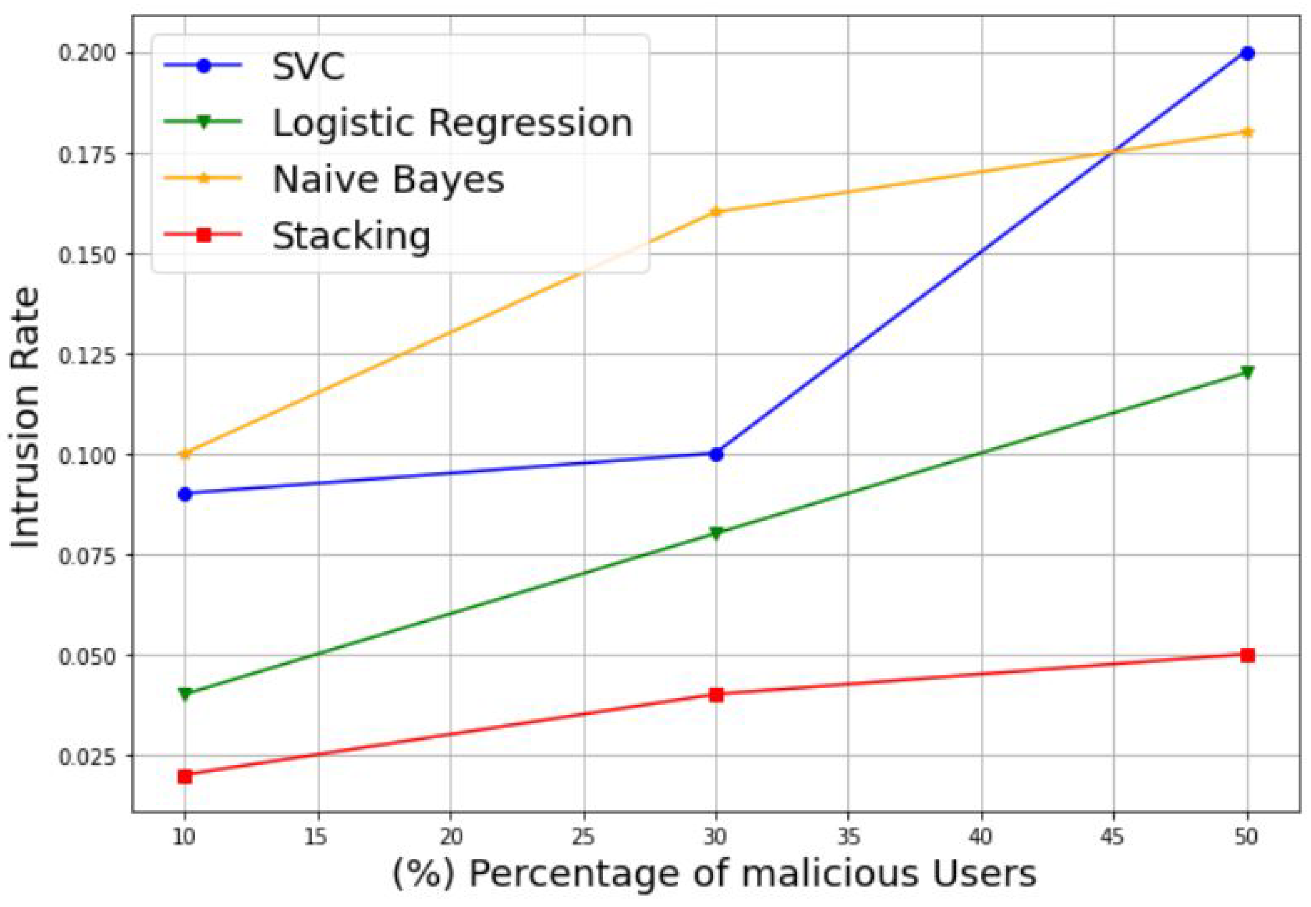
3.1. Simulation of Stacking Model-Based MUs Detection
- •
- True Positive (TP): Malicious users successfully recognized as malicious users.
- •
- True Negative (TN): Normal users successfully recognized as normal users.
- •
- False Negative (FN): Normal users wrongly recognized as malicious users.
- •
- False Positive (FP): Malicious users wrongly recognized as normal users.
- -
- Accuracy: This refers to the percentage of successfully classified nodes over the global number of nodes assessed. It can be defined as
- -
- Precision: This can be used as a quality metric to evaluate a machine leaning model. It measures the degree of accuracy of the model on positive predictions. It can be described as
- -
- Recall: It can be used as a quantity metric to evaluate a machine learning model. It quantifies the total number of correct positive predictions performed from all positive predictions that could have been performed. It can be described as
- -
- Authentication Rate (AR): This refers to the rate of the SUs detection. It can be described as
- -
- Intrusion Rate (IR): This refers to the rate of the MUs misdetection. It can be described asThe second category evaluates the model performances based on a direct comparison between the true values tested by the model and the final predicted values of the same model. Examples of these evaluation metrics include the Log loss score, Hamming loss score, and the Jaccard score.
- -
- Log loss score: Also denoted by cross-entropy loss, it shows the extent to which the prediction probability is approximately close to the related true value. A high log loss score corresponds to a large divergence between the prediction probability and the true value. It can be expressed aswhere denotes the input vector, the corresponding target, and is the probability that the ith sample is classified in the class c.
- -
- Hamming loss score: refers to the amount of incorrect labels relative to the total number of labels. It can be defined aswhere is the predicted value, y is the corresponding true value, and presents the number of classes.
- -
- Jaccard score: Also called the Jaccard similarity coefficient, it is used to evaluate the similarity between the predicted values and the true values. It is computed as the result of the quotient of the dimension of the intersection by the dimension of the union of two labels. The Jaccard score can be expressed aswhere y and are the true value and the corresponding predicted value, respectively.
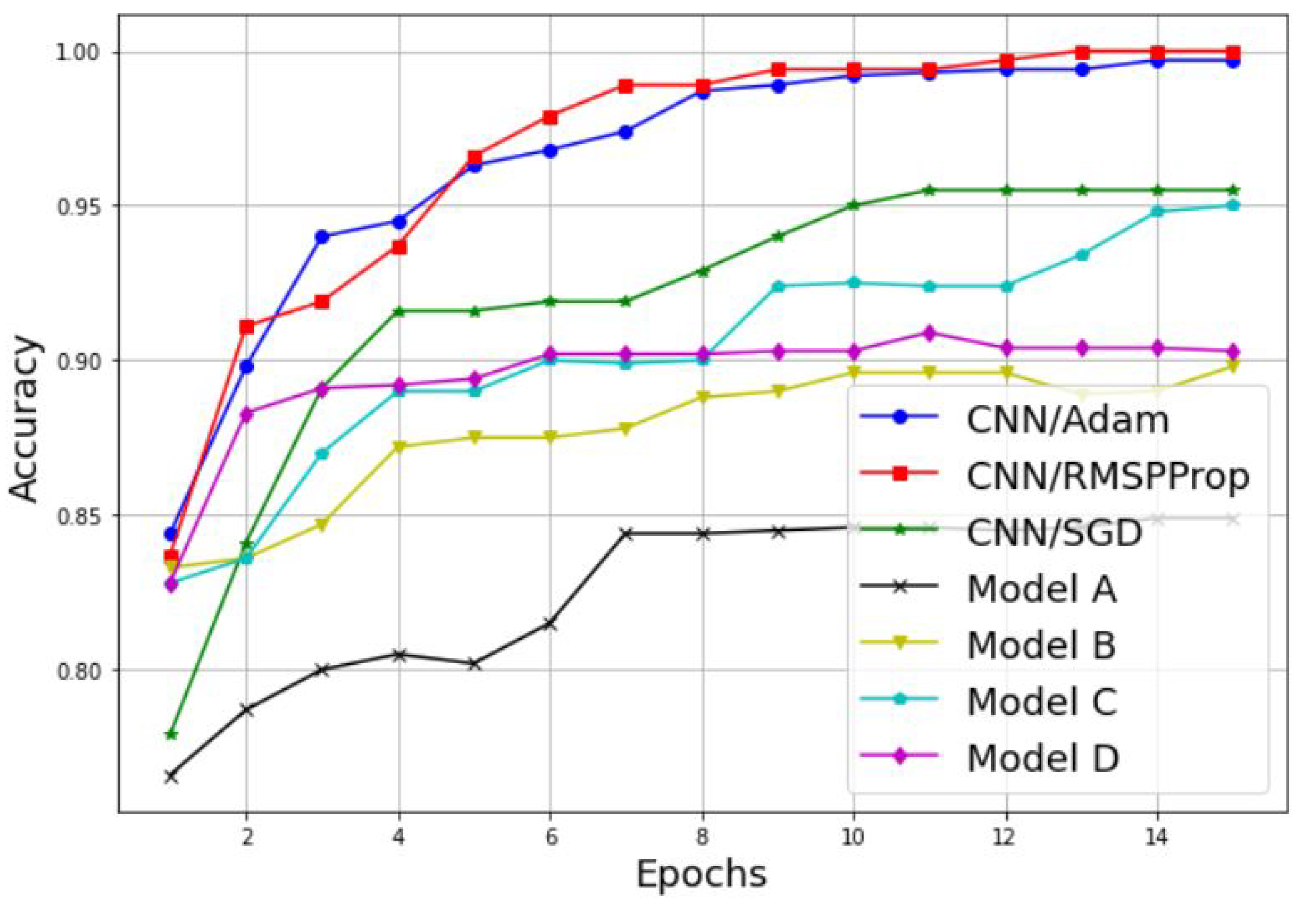
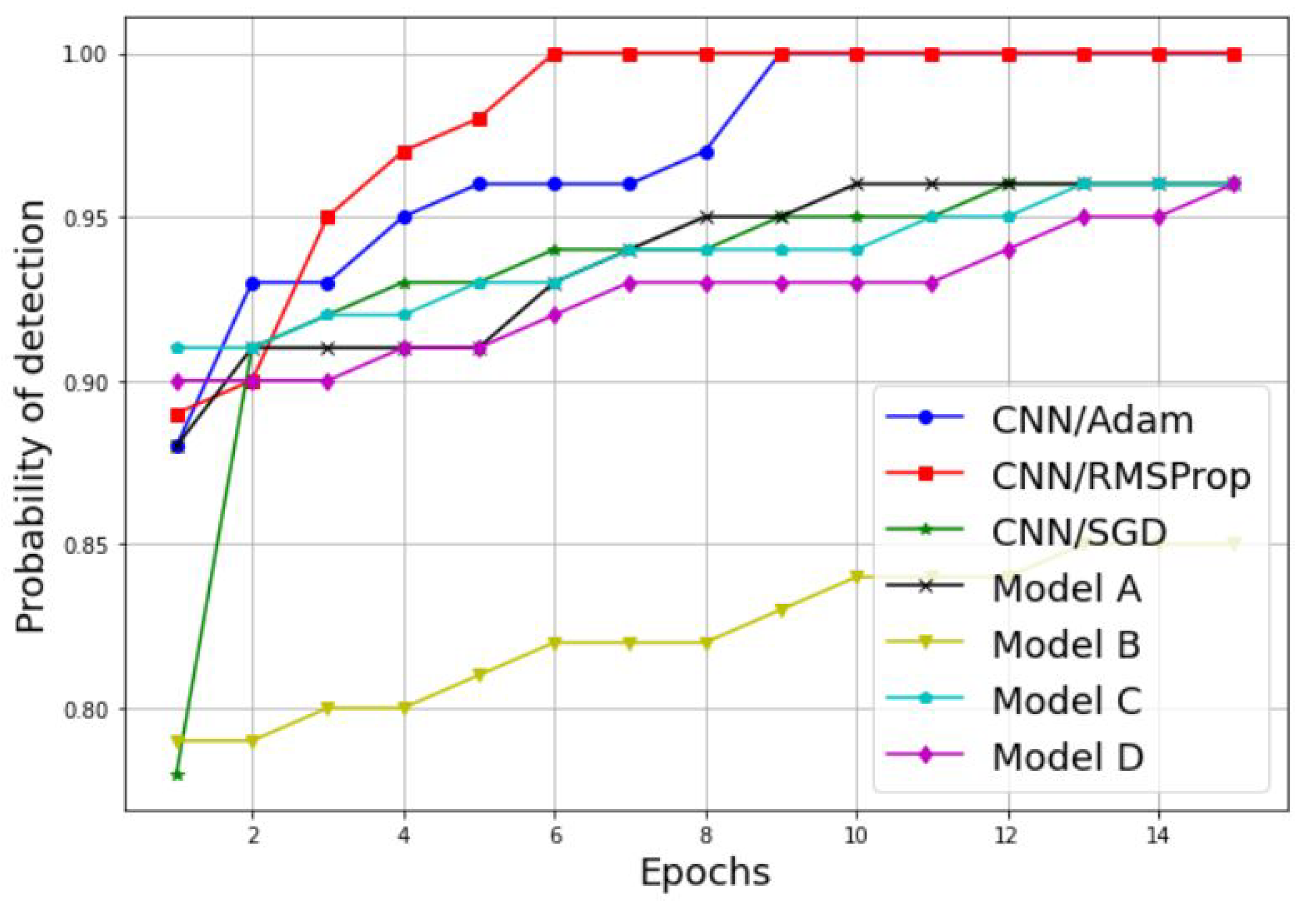
3.2. Simulation of a Scalogram-Based CNN Model for Spectrum Sensing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ridouani, M.; Hayar, A.; Haqiq, A. Relaxed constraint at cognitive relay network under both the outage probability of the primary system and the interference constrain. In Proceedings of the 2015 European Conference on Networks and Communications (EuCNC), Paris, France, 29 June–2 July 2015; pp. 311–316. [Google Scholar]
- Ridouani, M.; Hayar, A.; Haqiq, A. Perform sensing and transmission in parallel in cognitive radio systems: Spectrum and energy efficiency. Digit. Signal Process. 2017, 62, 65–80. [Google Scholar] [CrossRef]
- Salahdine, F.; Ghribi, N.K.E.; Kaabouch, N. A Cooperative Spectrum Sensing Scheme Based on Compressive Sensing for Cognitive Radio Networks. Int. J. Digit. Inf. Wirel. Commun. 2019, 9, 124–136. [Google Scholar] [CrossRef]
- Salahdine, F.; Kaabouch, N. Security threats, detection, and countermeasures for physical layer in cognitive radio networks: A survey. Phys. Commun. 2020, 39, 101001. [Google Scholar] [CrossRef]
- Khan, M.S.; Faisal, M.; Kim, S.M.; Ahmed, S.; St-Hilaire, M.; Kim, J. A Correlation-Based Sensing Scheme for Outlier Detection in Cognitive Radio Networks. Appl. Sci. 2021, 11, 2362. [Google Scholar] [CrossRef]
- Sajjad Khan, M.; Jibran, M.; Koo, I.; Kim, S.M.; Kim, J. A Double Adaptive Approach to Tackle Malicious Users in Cognitive Radio Networks. Wirel. Commun. Mob. Comput. 2019, 2019, 2350694. [Google Scholar]
- Chakraborty, A.; Banerjee, J.S.; Chattopadhyay, A. Malicious node restricted quantized data fusion scheme for trustworthy spectrum sensing in cognitive radio networks. J. Mech. Contin. Math. Sci. 2020, 15, 39–56. [Google Scholar] [CrossRef]
- Salahdine, F.; El Ghazi, H.; Kaabouch, N.; Fihri, W.F. Matched filter detection with dynamic threshold for cognitive radio networks. In Proceedings of the International Conference on Wireless Networks and Mobile Communications (WINCOM), Marrakech, Morocco, 20–23 October 2015; pp. 1–6.
- Benazzouza, S.; Ridouani, M.; Salahdine, F.; Hayar, A. Chaotic Compressive Spectrum Sensing Based on Chebyshev Map for Cognitive Radio Networks. Symmetry 2021, 13, 429. [Google Scholar] [CrossRef]
- Arjoune, Y.; Kaabouch, N. Wideband Spectrum Sensing: A Bayesian Compressive Sensing Approach. Sensors 2018, 18, 1839. [Google Scholar] [CrossRef]
- Jiang, T.; Gradus, J.L.; Rosellini, A.J. Supervised Machine Learning: A Brief Primer. Behav. Ther. 2020, 51, 675–687. [Google Scholar] [CrossRef]
- Usama, M.; Qadir, J.; Raza, A.; Arif, H.; Yau, K.L.; Elkhatib, Y.; Hussain, A.; Al-Fuqaha, A. Unsupervised Machine Learning for Networking: Techniques, Applications and Research Challenges. IEEE Access 2019, 7, 65579–65615. [Google Scholar] [CrossRef]
- Pak, M.S.; Kim, S.H. A review of deep learning in image recognition. In Proceedings of the International Conference on Computer Applications and Information Processing Technology, Kuta Bali, Indonesia, 8–10 August 2017; pp. 1–3. [Google Scholar]
- Hossain, M.S.; Miah, M.S. Machine learning-based malicious user detection for reliable cooperative radio spectrum sensing in Cognitive Radio-Internet of Things. Mach. Learn. Appl. 2021, 5, 100052. [Google Scholar] [CrossRef]
- Miah, M.S.; Hossain, M.A.; Ahmed, K.M.; Rahman, M.M.; Calhan, A.; Cicioglu, M. Machine Learning-Based Malicious User Detection in Energy Harvested Cognitive Radio-Internet of Things. TechRxiv, 2021; preprint. [Google Scholar] [CrossRef]
- Albehadili, A.; Ali, A.; Jahan, F.; Javaid, A.Y.; Oluochy, J.; Devabhaktuniz, V. Machine Learning-based Primary User Emulation Attack Detection In Cognitive Radio Networks using Pattern Described Link-Signature (PDLS). In Proceedings of the 2019 Wireless Telecommunications Symposium (WTS), New York, NY, USA, 9–12 April 2019; pp. 1–7. [Google Scholar]
- Furqan, H.M.; Aygül, M.A.; Nazzal, M.; Arslan, H. Primary user emulation and jamming attack detection in cognitive radio via sparse coding. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 141. [Google Scholar] [CrossRef]
- Arjoune, Y.; Kaabouch, N. On Spectrum Sensing, a Machine Learning Method for Cognitive Radio Systems. In Proceedings of the 2019 IEEE International Conference on Electro Information Technology (EIT), Brookings, SD, USA, 20–22 May 2019; pp. 333–338. [Google Scholar]
- Prasad, V.V.; Rao, P.T. Adaptive cooperative sensing in cognitive radio networks with ensemble model for primary user detection. Int. J. Commun. Syst. 2022, 35, e4247. [Google Scholar] [CrossRef]
- Han, D.; Charles Sobabe, C.; Zhang, C.; Bai, X.; Wang, Z.; Liu, S.; Guo, B. Spectrum sensing for cognitive radio based on convolution neural network. In Proceedings of the 10th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Shanghai, China, 14–16 October 2017; pp. 1–6. [Google Scholar]
- Yang, K.; Huang, Z.; Wang, X.; Li, X. A blind spectrum sensing method based on deep learning. Sensors 2019, 19, 2270. [Google Scholar] [CrossRef]
- Ridouani, M.; Benazzouza, S.; Salahdine, F.; Hayar, A. A novel secure cooperative cognitive radio network based on Chebyshev map. Digit. Signal Process. 2022, 126, 103482. [Google Scholar] [CrossRef]
- Benazzouza, S.; Ridouani, M.; Salahdine, F.; Hayar, A. A Survey on Compressive Spectrum Sensing for Cognitive Radio Networks. In Proceedings of the IEEE International Smart Cities Conference (ISC2), Casablanca, Morocco, 14–17 October 2019; pp. 535–541. [Google Scholar]
- Salahdine, F.; Kaabouch, N.; El Ghazi, H. A survey on compressive sensing techniques for cognitive radio networks. Phys. Commun. 2016, 20, 61–73. [Google Scholar] [CrossRef]
- Gan, H.; Li, Z.; Li, J.; Wang, X.; Cheng, Z. Compressive sensing using chaotic sequence based on Chebyshev map. Nonlinear Dyn. 2014, 78, 2429–2438. [Google Scholar] [CrossRef]
- Benazzouza, S.; Ridouani, M.; Salahdine, F.; Hayar, A. A Secure Bayesian Compressive Spectrum Sensing Technique Based Chaotic Matrix for Cognitive Radio Networks. In Proceedings of the 12th International Conference on Soft Computing and Pattern Recognition (SoCPaR 2020), Virtual, 15–18 December 2020; Advances in Intelligent Systems and Computing. Springer: Cham, Switzerland, 2021; Volume 1383, pp. 658–668. [Google Scholar]
- Zounemat-Kermani, M.; Batelaan, O.; Fadaee, M.; Hinkelmann, R. Ensemble machine learning paradigms in hydrology: A review. J. Hydrol. 2021, 598, 126266. [Google Scholar] [CrossRef]
- Salahdine, F.; Ghribi, E.; Kaabouch, N. Metrics for Evaluating the Efficiency of Compressing Sensing Techniques. In Proceedings of the International Conference on Information Networking (ICOIN), Barcelona, Spain, 7–10 January 2020; pp. 562–567. [Google Scholar]
- Rabbah, J.; Ridouani, M.; Hassouni, L. A New Classification Model Based on Stacknet and Deep Learning for Fast Detection of COVID 19 Through X Rays Images. In Proceedings of the 2020 Fourth International Conference on Intelligent Computing in Data Sciences (ICDS), Fez, Morocco, 21–23 October 2020; pp. 1–8. [Google Scholar]
- Stacking Ensemble Machine Learning with Python. Available online: https://machinelearningmastery.com/stacking-ensemble-machine-learning-with-python/ (accessed on 20 July 2022).
- Chauhan, V.K.; Dahiya, K.; Sharma, A. Problem formulations and solvers in linear SVM: A review. Artif. Intell. Rev. 2019, 52, 803–855. [Google Scholar] [CrossRef]
- Nusinovici, S.; Tham, Y.C.; Yan, M.Y.; Ting, D.S.; Li, J.; Sabanayagam, C.; Wong, T.Y.; Cheng, C.Y. Logistic regression was as good as machine learning for predicting major chronic diseases. J. Clin. Epidemiol. 2020, 122, 56–69. [Google Scholar] [CrossRef]
- Yang, F.J. An implementation of naive bayes classifier. In Proceedings of the International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 13–15 December 2018. [Google Scholar]
- Salahdine, F. Spectrum sensing techniques for cognitive radio networks. arXiv 2017, arXiv:1710.02668. [Google Scholar]
- Malhotra, M.; Aulakh, I.K.; Vig, R. A review on energy based spectrum sensing in Cognitive Radio Networks. In Proceedings of the International Conference on Futuristic Trends on Computational Analysis and Knowledge Management (ABLAZE), Noida, India, 25–27 February 2015; pp. 561–565. [Google Scholar]
- Lees, W.M.; Wunderlich, A.; Jeavons, P.J.; Hale, P.D.; Souryal, M.R. Deep learning classification of 3.5-GHz band spectrograms with applications to spectrum sensing. IEEE Trans. Cogn. Commun. Netw. 2019, 5, 224–236. [Google Scholar] [CrossRef]
- Sri, K. Advanced analysis of biomedical signals. In Biomedical Signal Analysis for Connected Healthcare; Academic Press: Cambridge, MA, USA, 2021; pp. 157–222. [Google Scholar]
- Li, T.; Zhou, M. ECG classification using wavelet packet entropy and random forests. Entropy 2016, 18, 285. [Google Scholar] [CrossRef]
- MorseWavelets. Available online: https://in.mathworks.com/help/wavelet/ug/morse-wavelets.htmlbvgfke1 (accessed on 15 November 2018).
- Elaanba, A.; Ridouani, M.; Hassouni, L. Automatic detection Using Deep Convolutional Neural Networks for 11 Abnormal Positioning of Tubes and Catheters in Chest X-ray Images. In Proceedings of the 2021 IEEE World AI IoT Congress (AIIoT), Virtual Conference, 10–13 May 2021; pp. 7–12. [Google Scholar]
- Rabbah, J.; Ridouani, M.; Hassouni, L. A New Churn Prediction Model Based on Deep Insight Features Transformation for Convolution Neural Network Architecture and Stacknet. Int. J. Web Based Learn. Teach. Technol. (IJWLTT) 2022, 17, 1–18. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Mascarenhas, S.; Agarwal, M. A comparison between VGG16, VGG19 and ResNet50 architecture frameworks for Image Classification. In Proceedings of the 2021 International Conference on Disruptive Technologies for Multi-Disciplinary Research and Applications (CENTCON), Bengaluru, India, 19–21 November 2021; pp. 96–99. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. Int. Conf. Mach. Learn. 2019, 97, 6105–6114. [Google Scholar]
- Attallah, O. MB-AI-His: Histopathological diagnosis of pediatric medulloblastoma and its subtypes via AI. Diagnostics 2021, 11, 359. [Google Scholar] [CrossRef]
- Salahdine, F.; Kaabouch, N.; El Ghazi, H. Techniques for dealing with uncertainty in cognitive radio networks. In Proceedings of the IEEE 7th Annual Computing and Communication Workshop and Conference, Las Vegas, NV, USA, 9–11 January 2017; pp. 1–6. [Google Scholar]
- Al-jabery, K.K.; Obafemi-Ajayi, T.; Olbricht, G.R.; Wunsch Ii, D.C. Data analysis and machine learning tools in MATLAB and Python. In Computational Learning Approaches to Data Analytics in Biomedical Applications; Academic Press: Cambridge, MA, USA, 2020; pp. 231–290. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]






| References | Approach | Machine Learning Algorithms | Features | Evaluation Metrics |
|---|---|---|---|---|
| Ref. [14] | MU detection | SVM | Energy feature | Accuracy/ROC/ |
| and | ||||
| Ref. [15] | MU detection | LR/KNN/SVM | Energy feature | Accuracy |
| Sum rate | ||||
| Network lifetime | ||||
| Ref. [16] | MU detection | LR/KNN/SVM/ | SNR feature | Accuracy/Recall |
| LDA/DTC/NB | Entropy feature | Precision/F-score | ||
| PU state | ||||
| Ref. [17] | MU detection | Feed-forward network | Energy decay rate | ROC |
| Gradient vectors | Area under ROC | |||
| Ref. [18] | PU detection | SVM/KNN/DCT/ | Energy feature | Accuracy |
| NB/LR | / | |||
| Ref. [19] | PU detection | DTC/SVM/KNN/ | Energy feature | Accuracy/Pd |
| Weighted ensemble | Wavelet feature | ROC/Training time | ||
| SNR feature | Predection speed | |||
| Ref. [20] | PU detection | CNN | Cyclostationary feature | Loss function |
| Energy feature | ||||
| Ref. [21] | PU detection | CNN/LSTM/ | Automatic features | ROC |
| Fully connected neural network | extraction |
| Models | SVM | LR | NB | Stacking |
|---|---|---|---|---|
| Accuracy | 0.70 | 0.93 | 0.94 | 0.97 |
| Precision | 0.66 | 0.87 | 0.89 | 0.96 |
| Recall | 0.75 | 0.99 | 0.99 | 0.98 |
| Log loss | 10.2 | 2.37 | 2.07 | 0.86 |
| Hamming loss | 0.3 | 0.07 | 0.06 | 0.02 |
| Jaccard score | 0.55 | 0.87 | 0.88 | 0.94 |
| Processing time | 0.09 | 0.05 | 0.12 | 0.2 |
| CNN Model | Optimizer | Transfer Learning | Training Accuracy | Testing Accuracy | Classification Time |
|---|---|---|---|---|---|
| Simple CNN | Adam | No | 99.74 | 100 | 135 s |
| Simple CNN | RMSProp | No | 100 | 100 | 132 s |
| Simple CNN | SGD | No | 95.55 | 98.18 | 137 s |
| Model A | Adam | Yes | 84.90 | 93.35 | 1218 s |
| Model B | Adam | Yes | 89.87 | 93.94 | 278 s |
| Model C | Adam | Yes | 95.06 | 96.36 | 165 s |
| Model D | Adam | Yes | 90.39 | 96.97 | 950 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benazzouza, S.; Ridouani, M.; Salahdine, F.; Hayar, A. A Novel Prediction Model for Malicious Users Detection and Spectrum Sensing Based on Stacking and Deep Learning. Sensors 2022, 22, 6477. https://doi.org/10.3390/s22176477
Benazzouza S, Ridouani M, Salahdine F, Hayar A. A Novel Prediction Model for Malicious Users Detection and Spectrum Sensing Based on Stacking and Deep Learning. Sensors. 2022; 22(17):6477. https://doi.org/10.3390/s22176477
Chicago/Turabian StyleBenazzouza, Salma, Mohammed Ridouani, Fatima Salahdine, and Aawatif Hayar. 2022. "A Novel Prediction Model for Malicious Users Detection and Spectrum Sensing Based on Stacking and Deep Learning" Sensors 22, no. 17: 6477. https://doi.org/10.3390/s22176477
APA StyleBenazzouza, S., Ridouani, M., Salahdine, F., & Hayar, A. (2022). A Novel Prediction Model for Malicious Users Detection and Spectrum Sensing Based on Stacking and Deep Learning. Sensors, 22(17), 6477. https://doi.org/10.3390/s22176477









