Over-Two-Octave Supercontinuum Generation of Light-Carrying Orbital Angular Momentum in Germania-Doped Ring-Core Fiber
Abstract
:1. Introduction
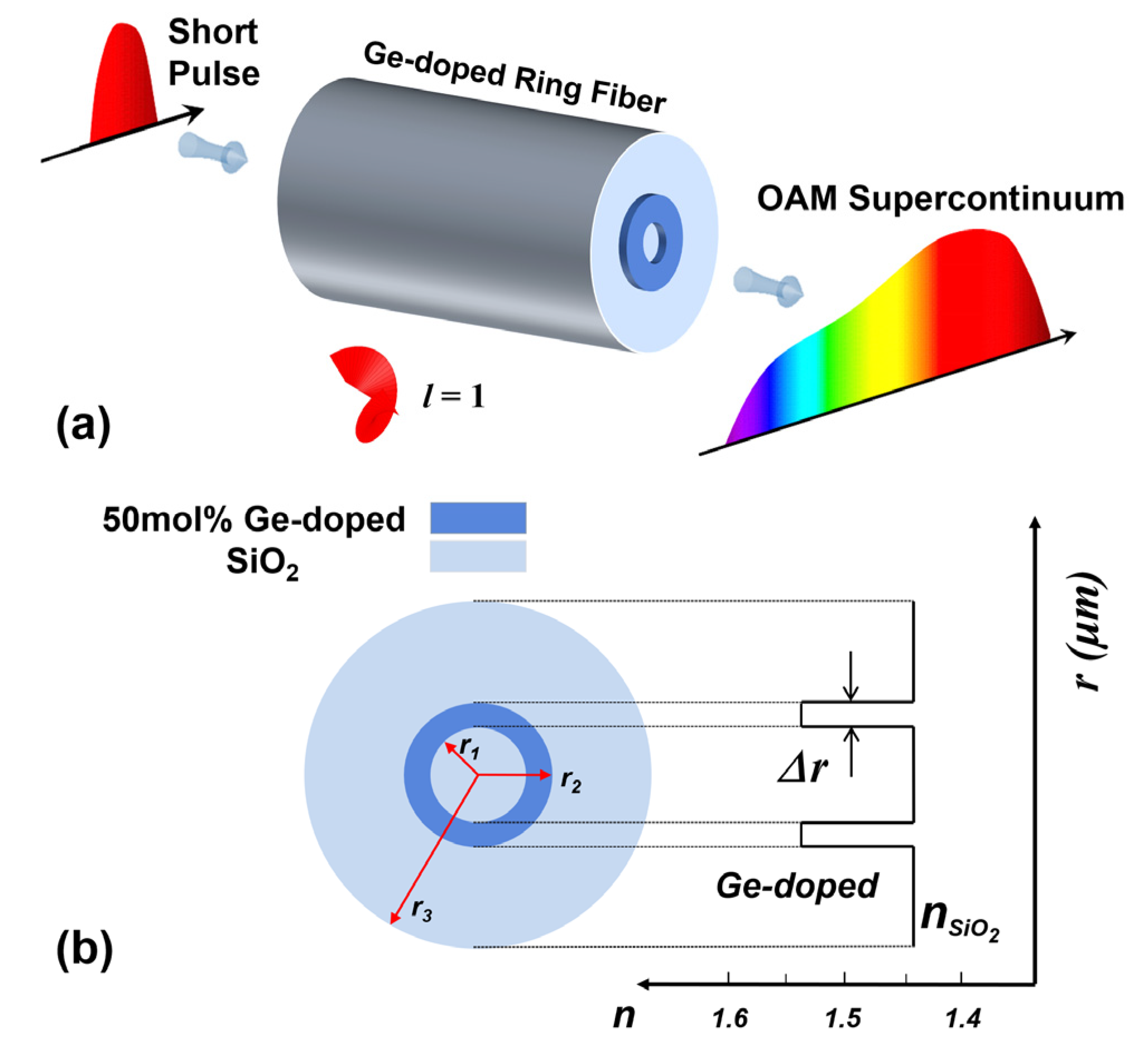
2. Concept and Fiber Structure
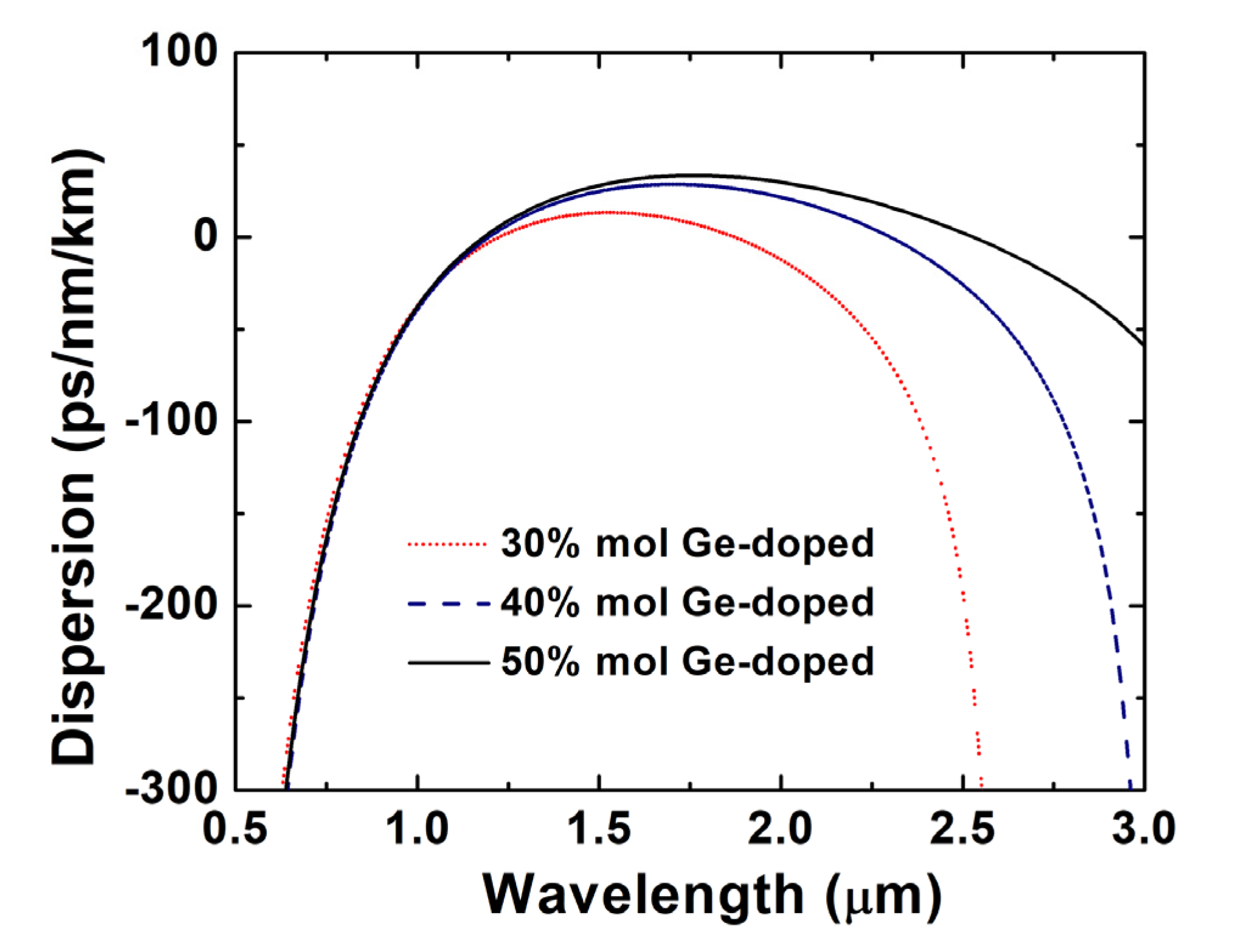
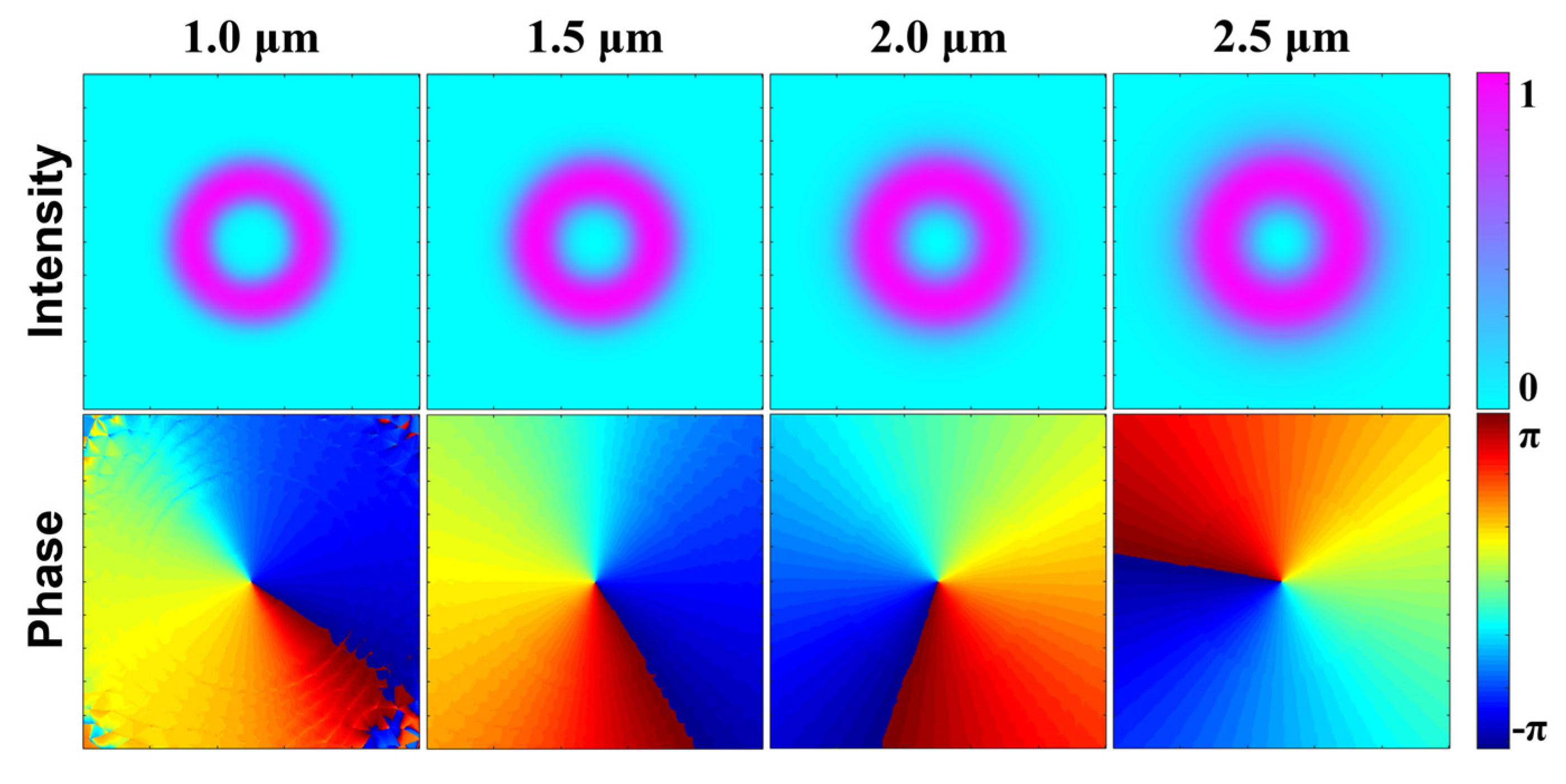
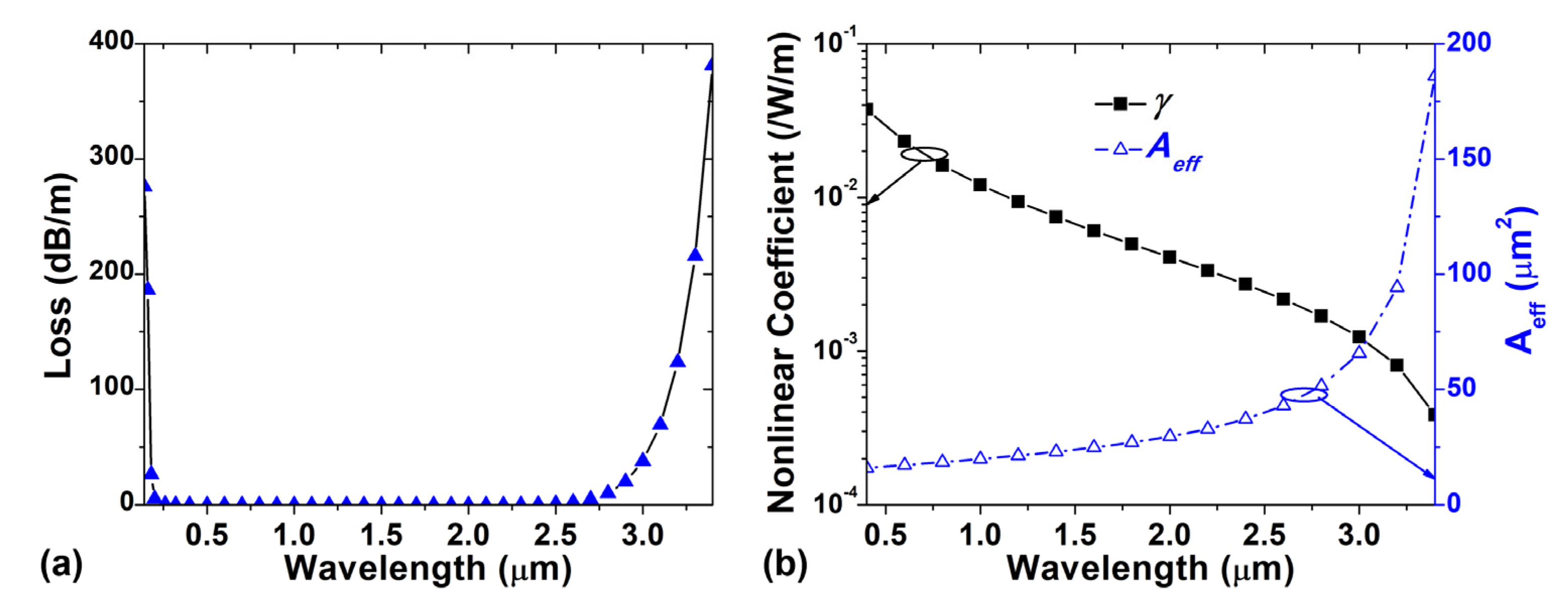
3. Fiber Properties and Dispersion Optimization
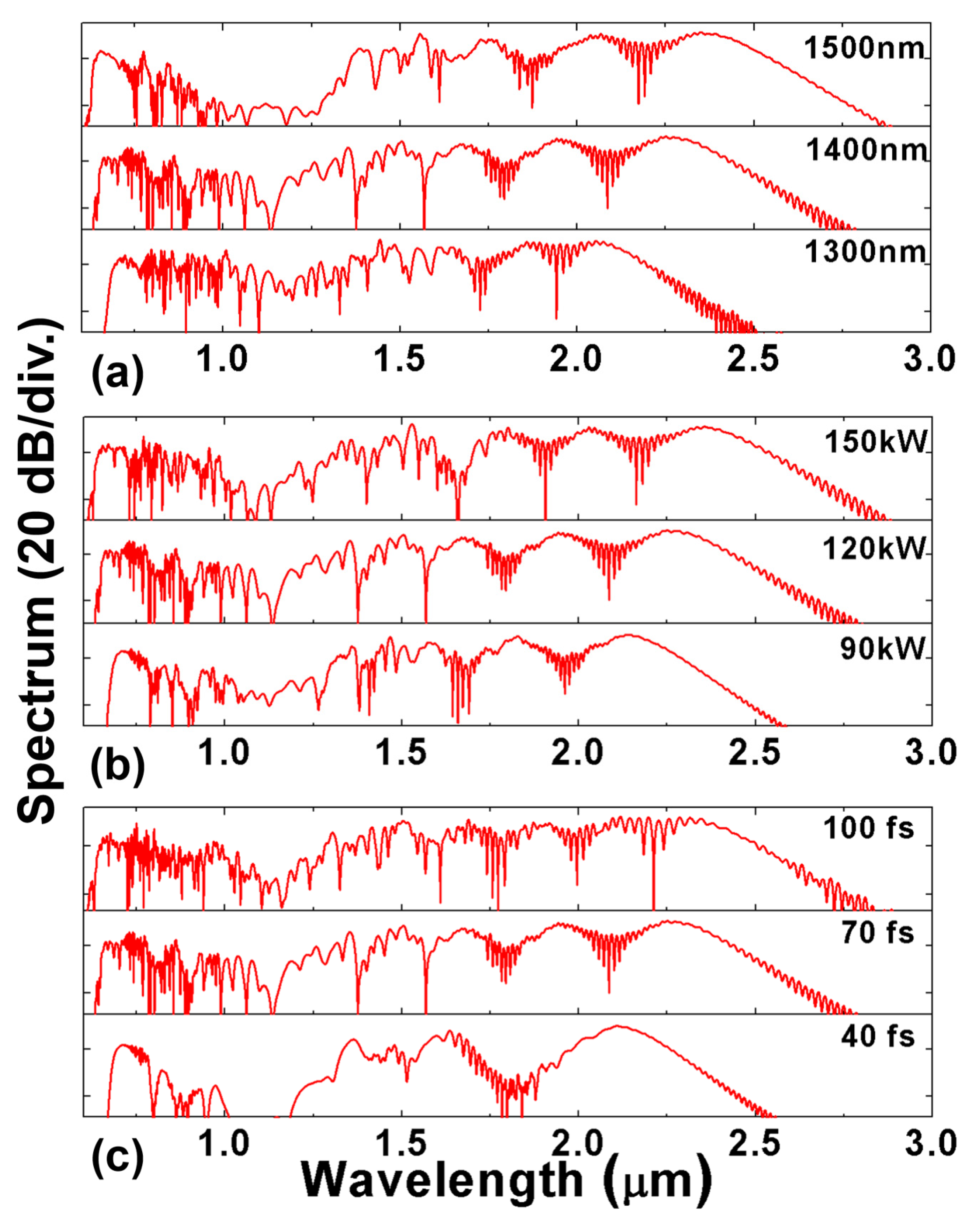
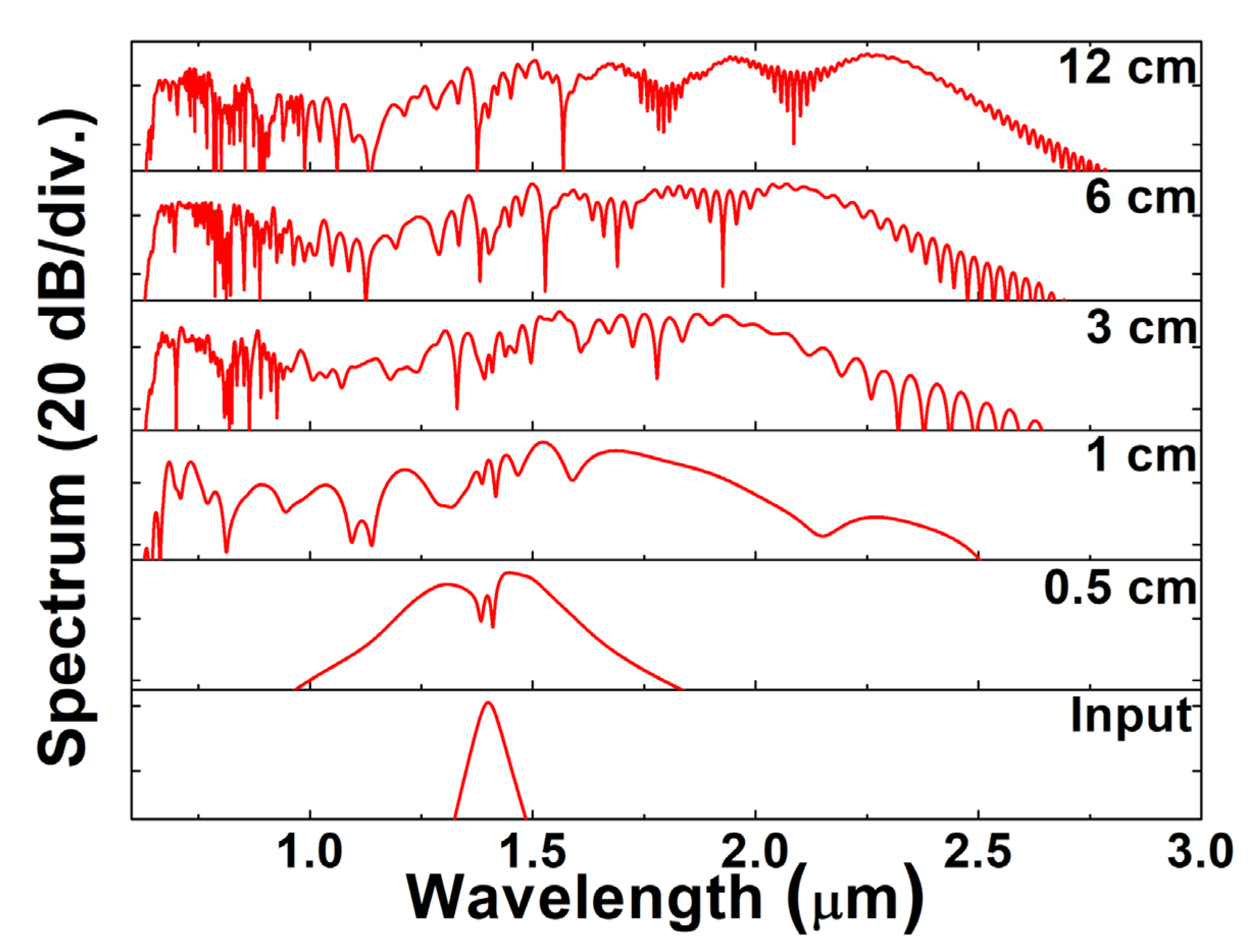
4. Supercontinuum Generation
5. Conclusions and Perspective
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-Scale Orbital Angular Momentum Mode Division Multiplexing in Fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, J.-Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Yan, Y.; Xie, G.; Lavery, M.; Huang, H.; Ahmed, N.; Bao, C.; Ren, Y.; Cao, Y.; Li, L.; Zhao, Z.; et al. High-capacity millimetre-wave communications with orbital angular momentum multiplexing. Nat. Commun. 2014, 5, 4876. [Google Scholar] [CrossRef] [PubMed]
- Djordjevic, I.B. Deep-space and near-Earth optical communications by coded orbital angular momentum (OAM) modulation. Opt. Express 2011, 19, 14277–14289. [Google Scholar] [CrossRef]
- Deng, D.; Li, Y.; Zhao, H.; Han, Y.; Ye, J.; Qu, S. High-capacity spatial-division multiplexing with orbital angular momentum based on multi-ring fiber. J. Opt. 2019, 21, 055601. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M.; Wang, D.; Wu, S.; Zhan, Y. Joint atmospheric turbulence detection and adaptive demodulation technique using the CNN for the OAM-FSO communication. Opt. Express 2018, 26, 10494–10508. [Google Scholar] [CrossRef]
- Yu, W.; Ji, Z.; Dong, D.; Yang, X.; Xiao, Y.; Gong, Q.; Xi, P.; Shi, K. Super-resolution deep imaging with hollow Bessel beam STED microscopy. Laser Photonics Rev. 2015, 10, 147–152. [Google Scholar] [CrossRef]
- Yan, L.; Kristensen, P.; Ramachandran, S. Vortex fibers for STED microscopy. APL Photonics 2019, 4, 022903. [Google Scholar] [CrossRef]
- Niederriter, R.D.; Siemens, M.E.; Gopinath, J.T. Fiber Optic Sensors Based on Orbital Angular Momentum. In Proceedings of the 2015 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 10–15 May 2015. [Google Scholar]
- Xie, G.; Song, H.; Zhao, Z.; Milione, G.; Ren, Y.; Liu, C.; Zhang, R.; Bao, C.; Li, L.; Wang, Z.; et al. Using a complex optical orbital-angular-momentum spectrum to measure object parameters. Opt. Lett. 2017, 42, 4482–4485. [Google Scholar] [CrossRef]
- Liu, K.; Cheng, Y.; Li, X.; Gao, Y. Microwave-Sensing Technology Using Orbital Angular Momentum: Overview of Its Advantages. IEEE Veh. Technol. Mag. 2019, 14, 112–118. [Google Scholar] [CrossRef]
- Knöner, G.; Parkin, S.; Nieminen, T.A.; Loke, V.L.Y.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Integrated optomechanical microelements. Opt. Express 2007, 15, 5521–5530. [Google Scholar] [CrossRef]
- Duocastella, M.; Arnold, C. Bessel and annular beams for materials processing. Laser Photonics Rev. 2012, 6, 607–621. [Google Scholar] [CrossRef]
- Liu, K.; Cheng, Y.; Gao, Y.; Li, X.; Qin, Y.; Wang, H. Super-resolution radar imaging based on experimental OAM beams. Appl. Phys. Lett. 2017, 110, 164102. [Google Scholar] [CrossRef]
- Swartzlander, G.A.; Ford, E.L.; Abdul-Malik, R.S.; Close, L.M.; Peters, M.A.; Palacios, D.M.; Wilson, D.W.; Swartzlander, J.G.A. Astronomical demonstration of an optical vortex coronagraph. Opt. Express 2008, 16, 10200–10207. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Liu, K.; Cheng, Y.; Wang, H. Microwave Vortex Imaging Based on Dual Coupled OAM Beams. IEEE Sens. J. 2019, 20, 806–815. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Wang, J.; Liu, K.; Wang, H. Electromagnetic Vortex Enhanced Imaging Using Fractional OAM Beams. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 948–952. [Google Scholar] [CrossRef]
- Wang, X.; Nie, Z.; Liang, Y.; Wang, J.; Li, T.; Jia, B. Recent advances on optical vortex generation. Nanophotonics 2018, 7, 1533–1556. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, J. A review of multiple optical vortices generation: Methods and applications. Front. Optoelectron. 2019, 12, 52–68. [Google Scholar] [CrossRef]
- Yue, Y.; Yan, Y.; Ahmed, N.; Yang, J.Y.; Zhang, L.; Ren, Y.; Huang, H.; Birnbaum, K.M.; Erkmen, B.I.; Dolinar, S.; et al. Mode Properties and Propagation Effects of Optical Orbital Angular Momentum (OAM) Modes in a Ring Fiber. IEEE Photon. J. 2012, 4, 535–543. [Google Scholar]
- Rumala, Y.S.; Milione, G.; Nguyen, T.A.; Pratavieira, S.; Hossain, Z.; Nolan, D.; Slussarenko, S.; Karimi, E.; Marrucci, L.; Alfano, R.R. Tunable supercontinuum light vector vortex beam generator using a q-plate. Opt. Lett. 2013, 38, 5083–5086. [Google Scholar] [CrossRef]
- Wu, R.; Torres-Company, V.; Leaird, D.E.; Weiner, A.M. Supercontinuum-based 10-GHz flat-topped optical frequency comb generation. Opt. Express 2013, 21, 6045–6052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lamb, E.S.; Carlson, D.R.; Hickstein, D.D.; Stone, J.R.; Diddams, S.A.; Papp, S.B. Optical-Frequency Measurements with a Kerr Microcomb and Photonic-Chip Supercontinuum. Phys. Rev. Appl. 2018, 9, 024030. [Google Scholar] [CrossRef]
- Humbert, G.; Wadsworth, W.J.; Leon-Saval, S.G.; Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Lederer, M.J.; Kopf, D.; Wiesauer, K.; Breuer, E.I.; et al. Supercontinuum generation system for optical coherence tomography based on tapered photonic crystal fibre. Opt. Express 2006, 14, 1596–1603. [Google Scholar] [CrossRef] [PubMed]
- Ferhat, M.L.; Cherbi, L.; Haddouche, I. Supercontinuum generation in silica photonic crystal fiber at 1.3 μm and 1.65 μm wavelengths for optical coherence tomography. Optik 2018, 152, 106–115. [Google Scholar] [CrossRef]
- Morioka, T.; Mori, K.; Saruwatari, M. More than 100-wavelength-channel picosecond optical pulse generation from single laser source using supercontinuum in optical fibres. Electron. Lett. 1993, 29, 862–864. [Google Scholar] [CrossRef]
- Oda, S.; Maruta, A. A novel quantization scheme by slicing supercontinuum spectrum for all-optical analog-to-digital conversion. IEEE Photon. Technol. Lett. 2005, 17, 465–467. [Google Scholar] [CrossRef]
- Sotobayashi, H.; Chujo, W.; Kitayama, K.-I. Photonic gateway: TDM-to-WDM-to-TDM conversion and reconversion at 40 Gbit/s (4 channels × 10 Gbits/s). J. Opt. Soc. Am. B 2002, 19, 2810–2816. [Google Scholar] [CrossRef]
- Neshev, D.N.; Dreischuh, A.; Maleshkov, G.; Samoc, M.; Kivshar, Y.S. Supercontinuum generation with optical vortices. Opt. Express 2010, 18, 18368–18373. [Google Scholar] [CrossRef]
- Prabhakar, G.; Gregg, P.; Rishoj, L.; Kristensen, P.; Ramachandran, S. Octave-wide supercontinuum generation of light-carrying orbital angular momentum. Opt. Express 2019, 27, 11547–11556. [Google Scholar] [CrossRef]
- Yue, Y.; Zhang, L.; Yan, Y.; Ahmed, N.; Yang, J.-Y.; Huang, H.; Ren, Y.; Dolinar, S.; Tur, M.; Willner, A.E. Octave-spanning supercontinuum generation of vortices in an As2S3 ring photonic crystal fiber. Opt. Lett. 2012, 37, 1889–1891. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Y.; Geng, W.; Jiang, J.; Wang, Z.; Zhang, H.; Bao, C.; Huang, H.; Ren, Y.; Pan, Z.; et al. Beyond Two-Octave Coherent OAM Supercontinuum Generation in Air-Core As2S3 Ring Fiber. IEEE Access 2020, 8, 96543–96549. [Google Scholar] [CrossRef]
- Geng, W.; Bao, C.; Fang, Y.; Wang, Y.; Li, Y.; Wang, Z.; Liu, Y.-G.; Huang, H.; Ren, Y.; Pan, Z.; et al. 1.6-Octave Coherent OAM Supercontinuum Generation in As2S3 Photonic Crystal Fiber. IEEE Access 2020, 8, 168177–168185. [Google Scholar] [CrossRef]
- Wang, Y.; Bao, C.; Jiang, J.; Fang, Y.; Geng, W.; Wang, Z.; Zhang, W.; Huang, H.; Ren, Y.; Pan, Z. Two-octave supercontinuum generation of high-order OAM modes in air-core As2S3 ring fiber. IEEE Access 2020, 8, 114135–114142. [Google Scholar] [CrossRef]
- Shiryaev, V.; Kosolapov, A.; Pryamikov, A.; Snopatin, G.; Churbanov, M.; Biriukov, A.; Kotereva, T.; Mishinov, S.; Alagashev, G.; Kolyadin, A.N. Development of technique for preparation of As2S3 glass preforms for hollow core microstructured optical fibers. J. Optoelectron. Adv. Mater. 2014, 16, 1020–1025. [Google Scholar]
- Sakaguchi, S.; Todoroki, S.-I. Optical properties of GeO2 glass and optical fibers. Appl. Opt. 1997, 36, 6809–6814. [Google Scholar] [CrossRef]
- Dianov, E.; Mashinsky, V.; Neustruev, V.; Sazhin, O.; Guryanov, A.; Khopin, V.; Vechkanov, N.; Lavrishchev, S. Origin of Excess Loss in Single-Mode Optical Fibers with High GeO2-Doped Silica Core. Opt. Fiber Technol. 1997, 3, 77–86. [Google Scholar] [CrossRef]
- Brunet, C.; Ung, B.; Wang, L.; Messaddeq, Y.; LaRochelle, S.; Rusch, L.A. Design of a family of ring-core fibers for OAM transmission studies. Opt. Express 2015, 23, 10553–10563. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 195–211. [Google Scholar]
- Wang, C.C.; Wang, M.H.; Wu, J. Heavily Germanium-Doped Silica Fiber with a Flat Normal Dispersion Profile. IEEE Photon. J. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Dianov, E.; Mashinsky, V. Germania-based core optical fibers. J. Light. Technol. 2005, 23, 3500–3508. [Google Scholar] [CrossRef]
- Lægsgaard, J.; Tu, H. How long wavelengths can one extract from silica-core fibers? Opt. Lett. 2013, 38, 4518–4521. [Google Scholar] [CrossRef]
- Rottwitt, K.; Povlsen, J.H. Analyzing the fundamental properties of Raman amplification in optical fibers. J. Light. Technol. 2005, 23, 3597–3605. [Google Scholar] [CrossRef]
- Yatsenko, Y.; Mavritsky, A. D-scan measurement of nonlinear refractive index in fibers heavily doped with GeO2. Opt. Lett. 2007, 32, 3257–3259. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, L.; Agarwal, A.M.; Kimerling, L.C.; Michel, J. Nonlinear Group IV photonics based on silicon and germanium: From near-infrared to mid-infrared. Nanophotonics 2014, 3, 247–268. [Google Scholar] [CrossRef]
- Afshar, S.; Monro, T.M. Monro. A full vectorial model for pulse propagation in emerging waveguides with subwavelength structures part I: Kerr nonlinearity. Opt. Express 2009, 17, 2298–2318. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen comparison of the refractive index of fused silica. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Barnes, N.P.; Piltch, M.S. Temperature-dependent Sellmeier coefficients and nonlinear optics average power limit for germanium. J. Opt. Soc. Am. 1979, 69, 178–180. [Google Scholar] [CrossRef]
- Chen, B.; Hong, L.; Hu, C.; Li, Z. White Laser Realized via Synergic Second- and Third-Order Nonlinearities. Research 2021, 2021, 1539730. [Google Scholar] [CrossRef]
- Heidt, A.M.; Hartung, A.; Bosman, G.; Krok, P.; Rohwer, E.; Schwoerer, H.; Bartelt, H. Coherent octave spanning near-infrared and visible supercontinuum generation in all-normal dispersion photonic crystal fibers. Opt. Express 2011, 19, 3775–3787. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Wang, Y.; Fang, Y.; Geng, W.; Zhao, W.; Bao, C.; Ren, Y.; Wang, Z.; Liu, Y.; Pan, Z.; et al. Over-Two-Octave Supercontinuum Generation of Light-Carrying Orbital Angular Momentum in Germania-Doped Ring-Core Fiber. Sensors 2022, 22, 6699. https://doi.org/10.3390/s22176699
Yang J, Wang Y, Fang Y, Geng W, Zhao W, Bao C, Ren Y, Wang Z, Liu Y, Pan Z, et al. Over-Two-Octave Supercontinuum Generation of Light-Carrying Orbital Angular Momentum in Germania-Doped Ring-Core Fiber. Sensors. 2022; 22(17):6699. https://doi.org/10.3390/s22176699
Chicago/Turabian StyleYang, Jian, Yingning Wang, Yuxi Fang, Wenpu Geng, Wenqian Zhao, Changjing Bao, Yongxiong Ren, Zhi Wang, Yange Liu, Zhongqi Pan, and et al. 2022. "Over-Two-Octave Supercontinuum Generation of Light-Carrying Orbital Angular Momentum in Germania-Doped Ring-Core Fiber" Sensors 22, no. 17: 6699. https://doi.org/10.3390/s22176699
APA StyleYang, J., Wang, Y., Fang, Y., Geng, W., Zhao, W., Bao, C., Ren, Y., Wang, Z., Liu, Y., Pan, Z., & Yue, Y. (2022). Over-Two-Octave Supercontinuum Generation of Light-Carrying Orbital Angular Momentum in Germania-Doped Ring-Core Fiber. Sensors, 22(17), 6699. https://doi.org/10.3390/s22176699







