Modeling, Simulation and Implementation of All Terrain Adaptive Five DOF Robot
Abstract
:1. Introduction
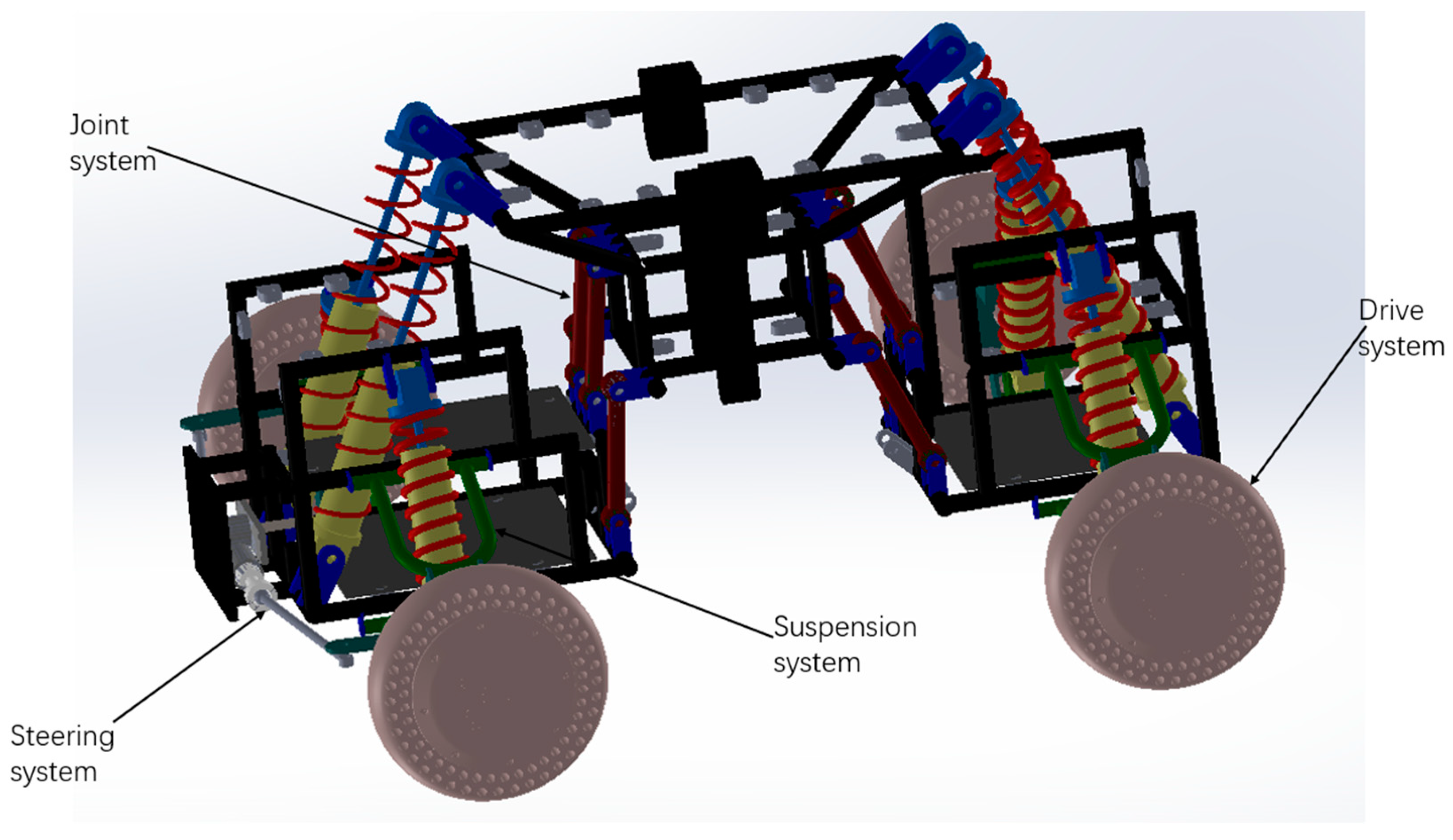
2. Mechanical Structure Design
2.1. Steering System
2.2. Suspension System
2.3. Joint System
2.4. Drive System
3. Mathematical Model
3.1. Forward Kinematics Analysis
3.2. Inverse Kinematic Analysis
4. Adams Simulation Analysis
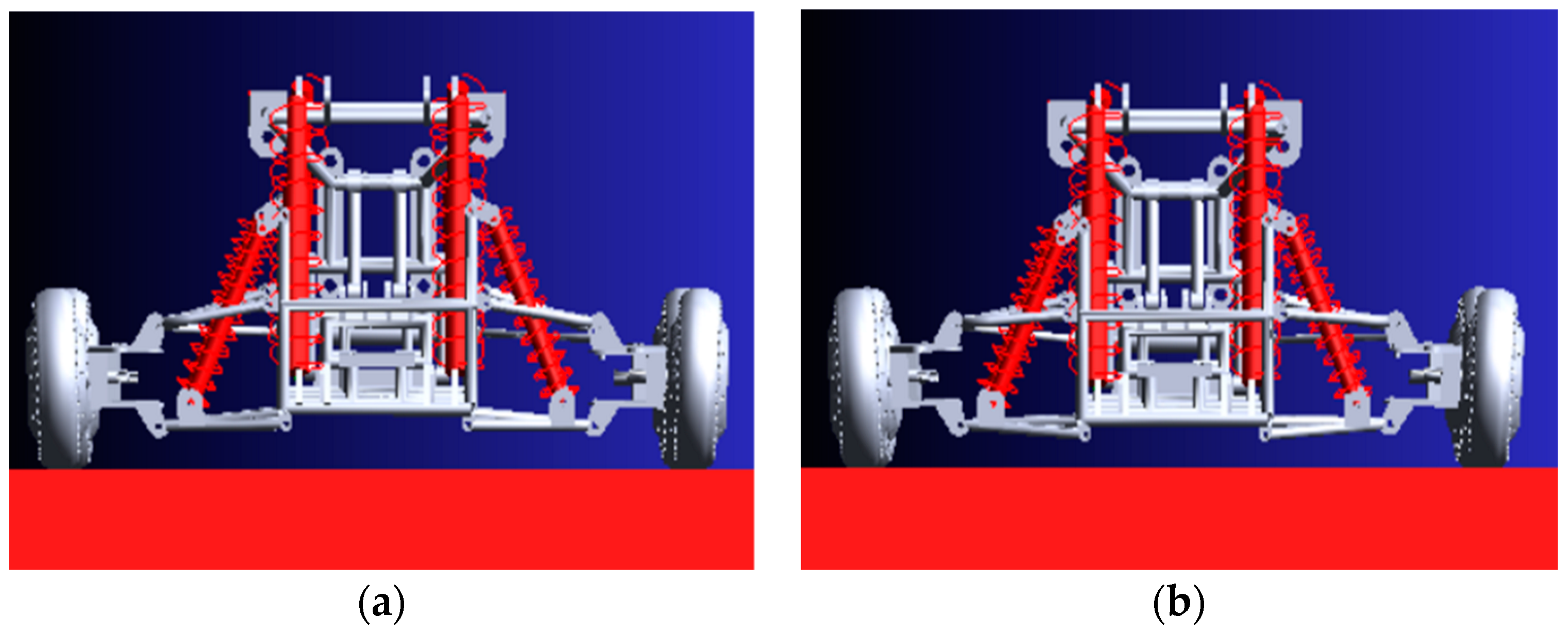
4.1. Statics Analysis (Loading Experiment)
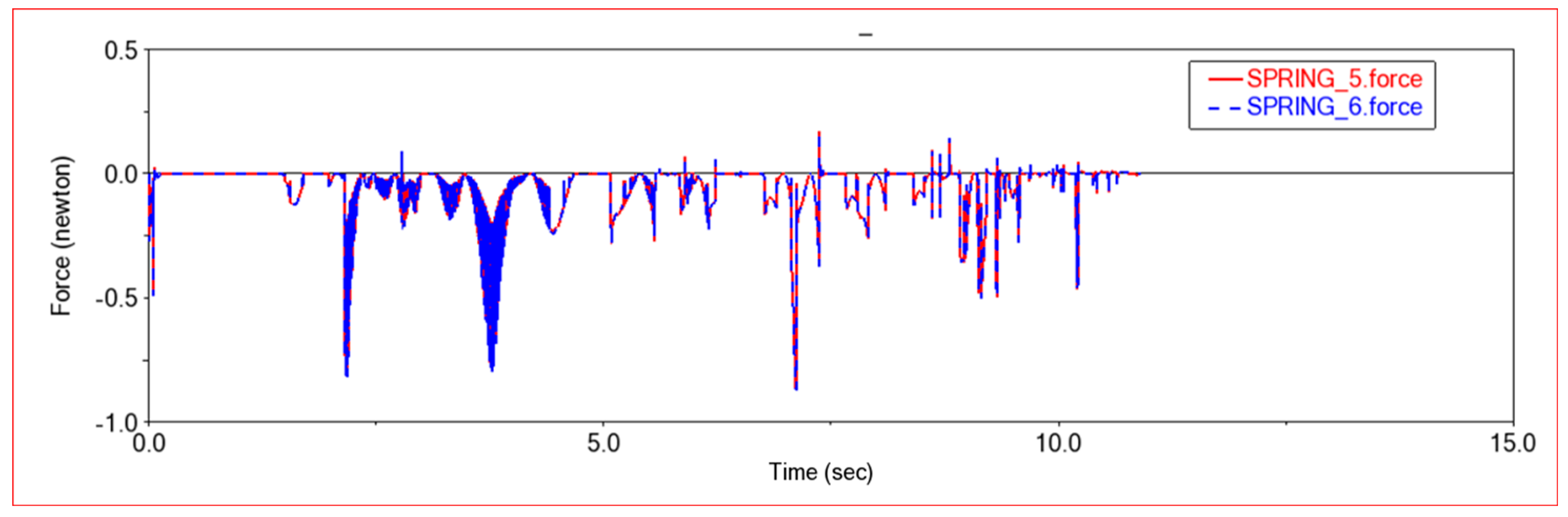
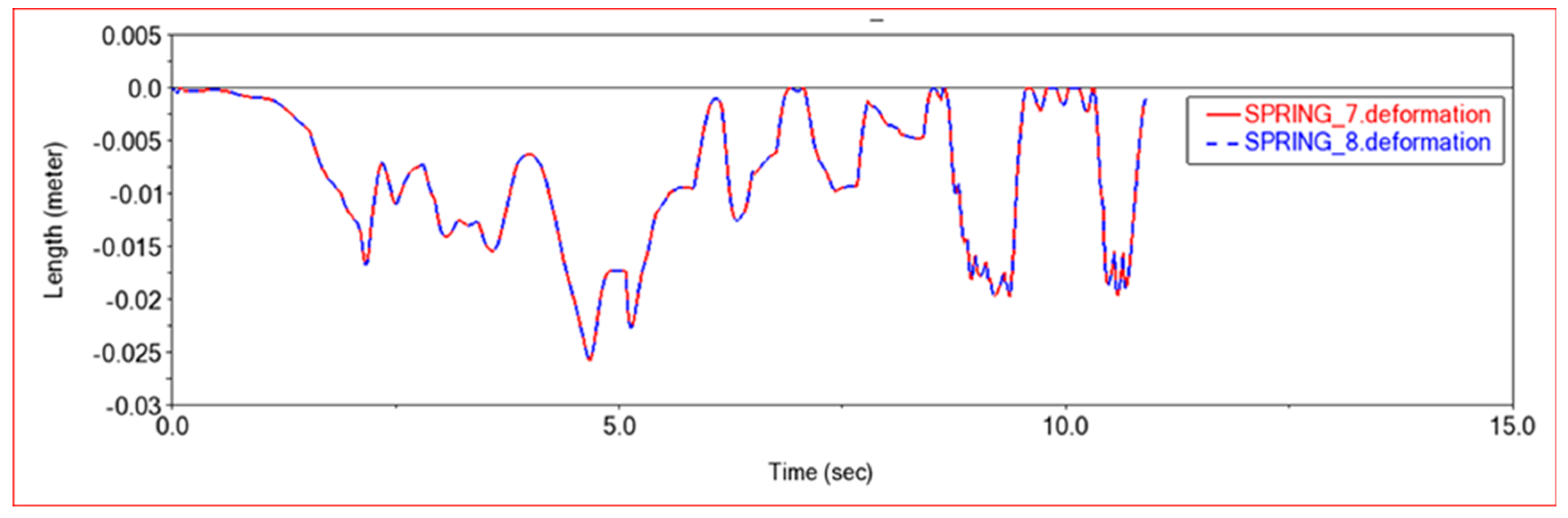
4.2. Dynamic Simulation
4.2.1. Terrain Construction
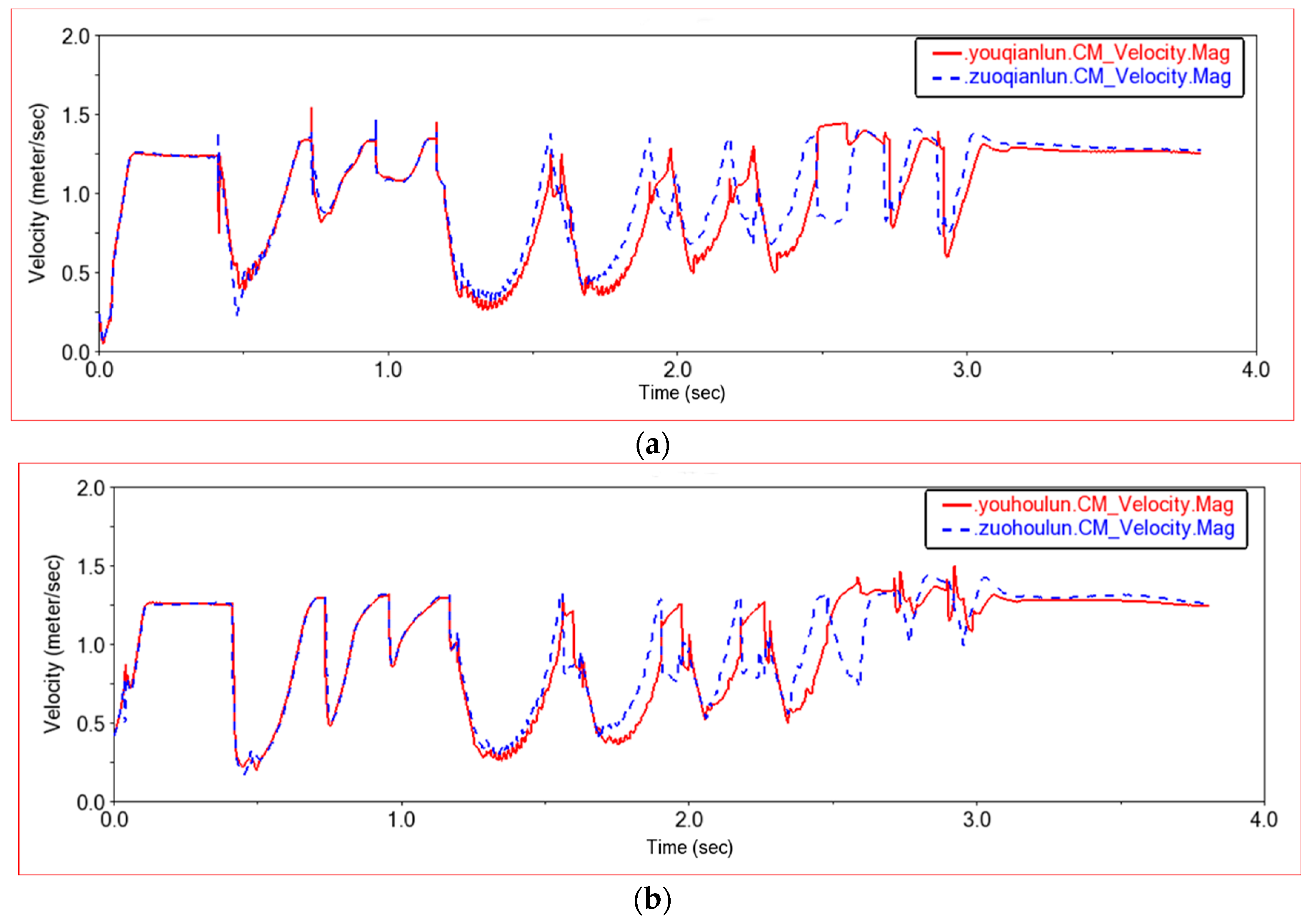
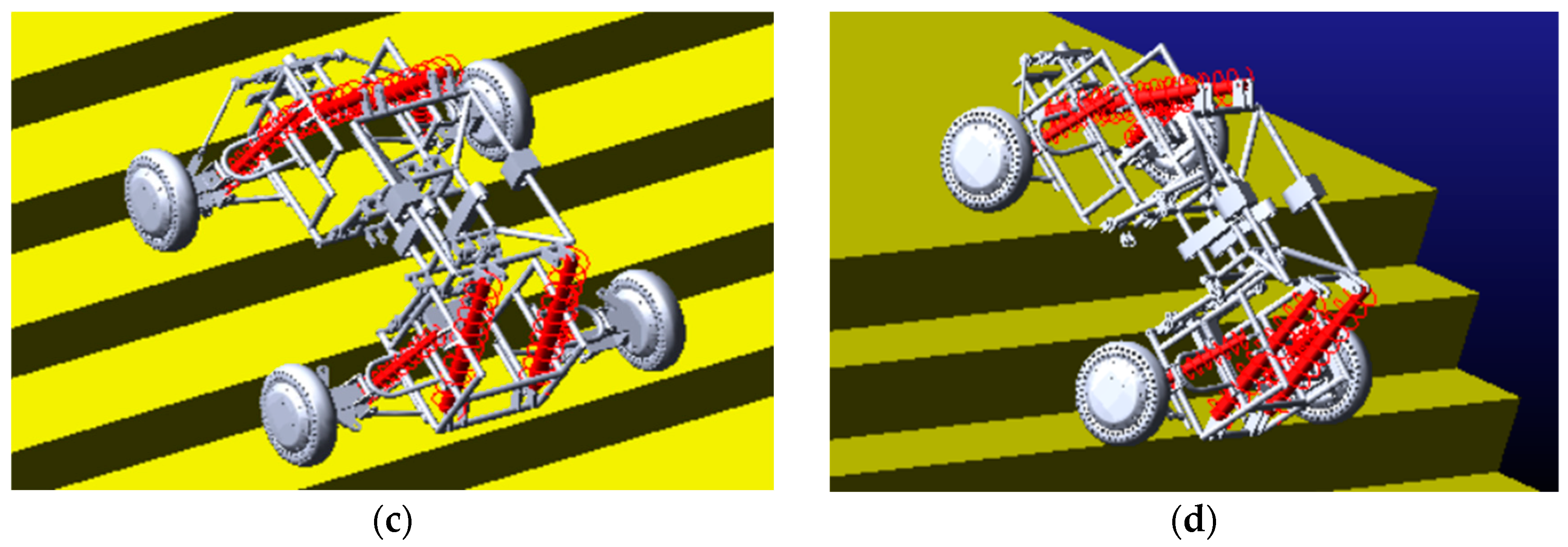
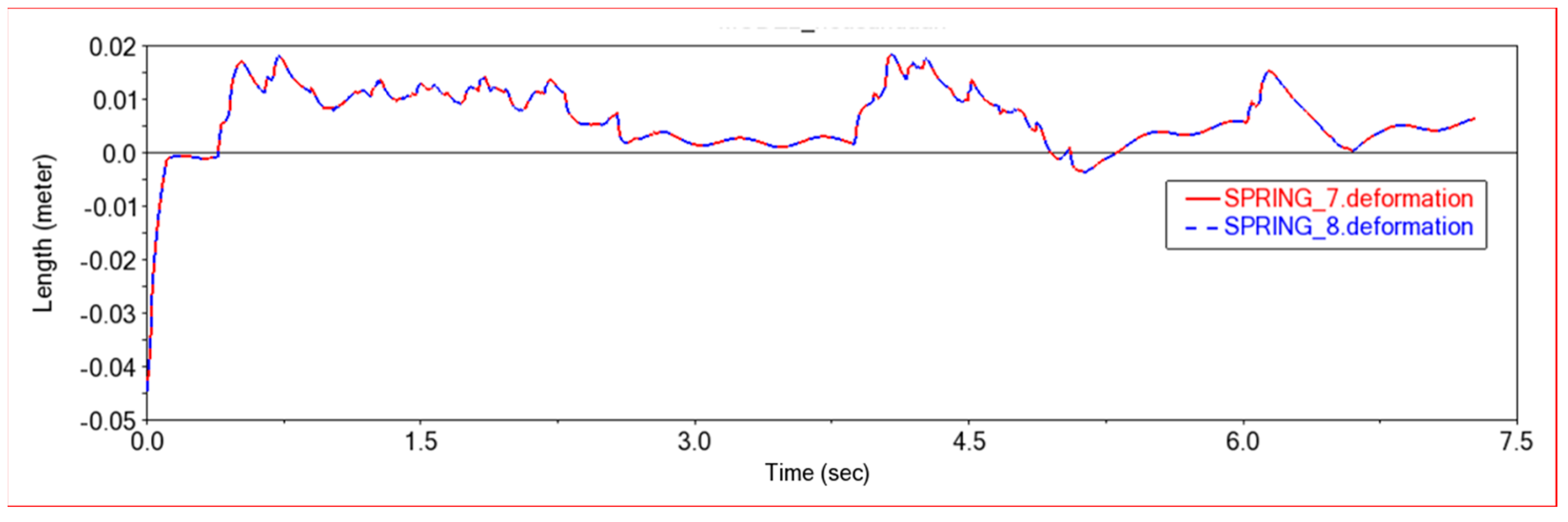
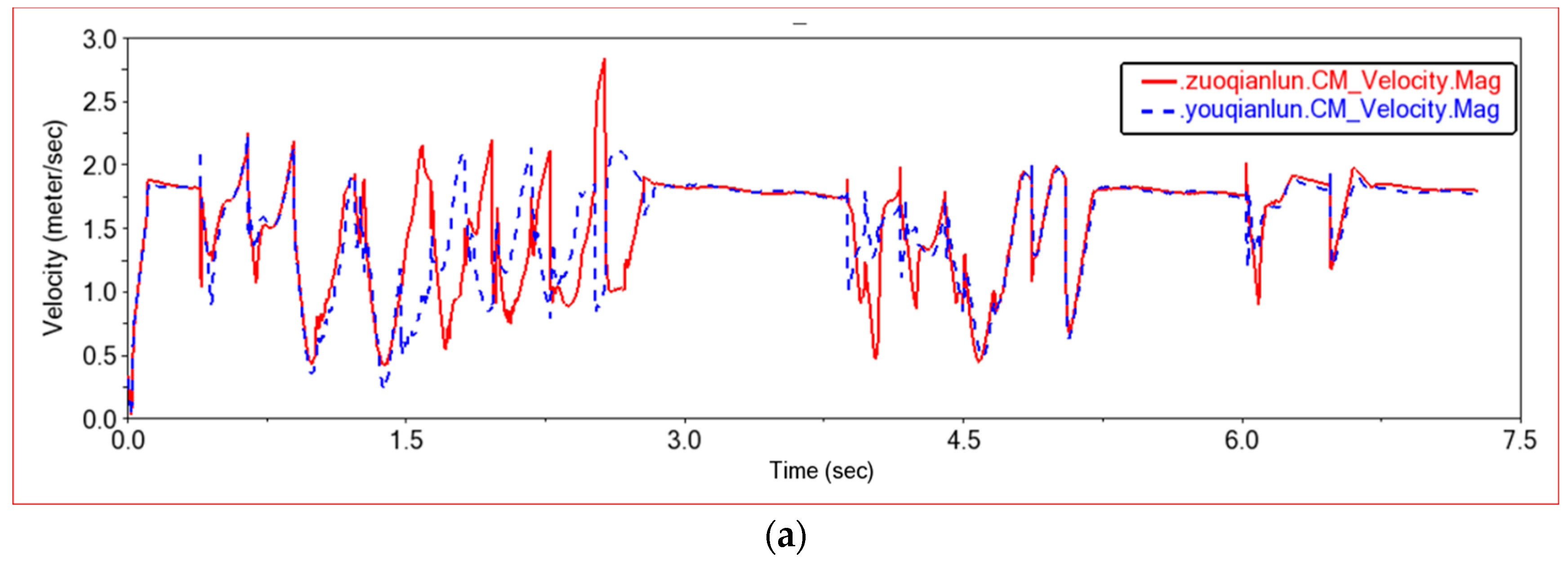
4.2.2. Obstacle Crossing Experiment 1
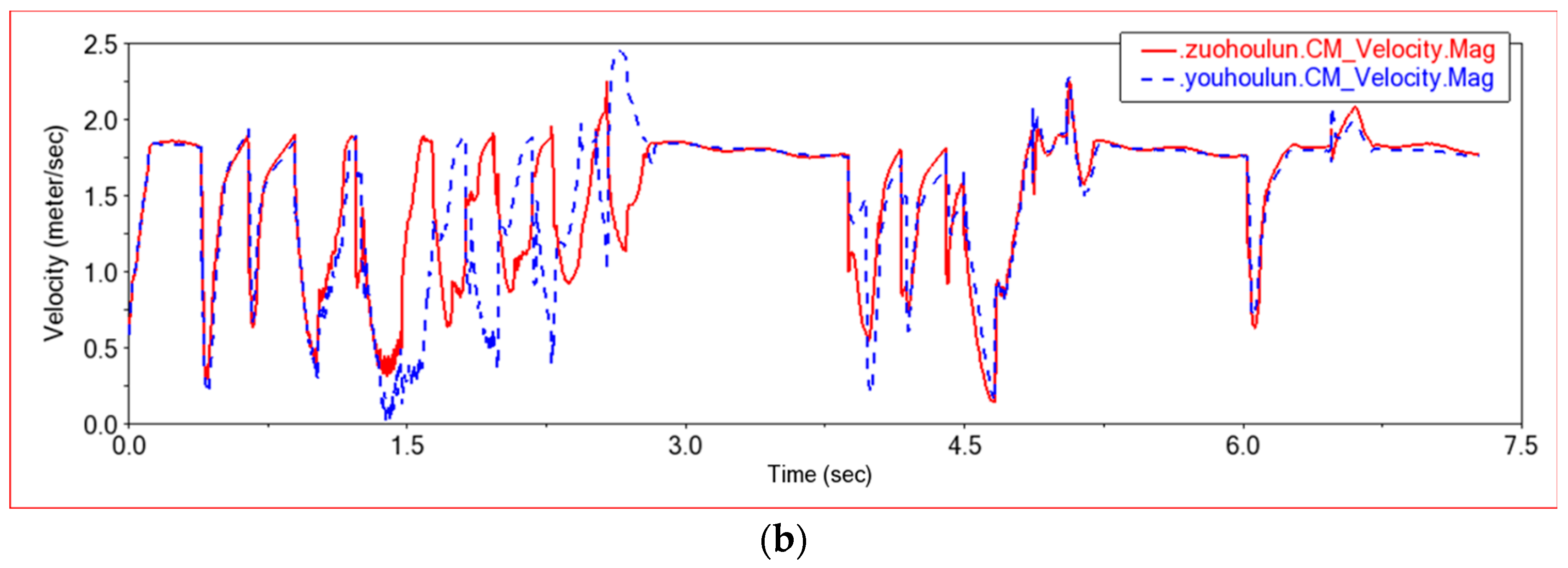
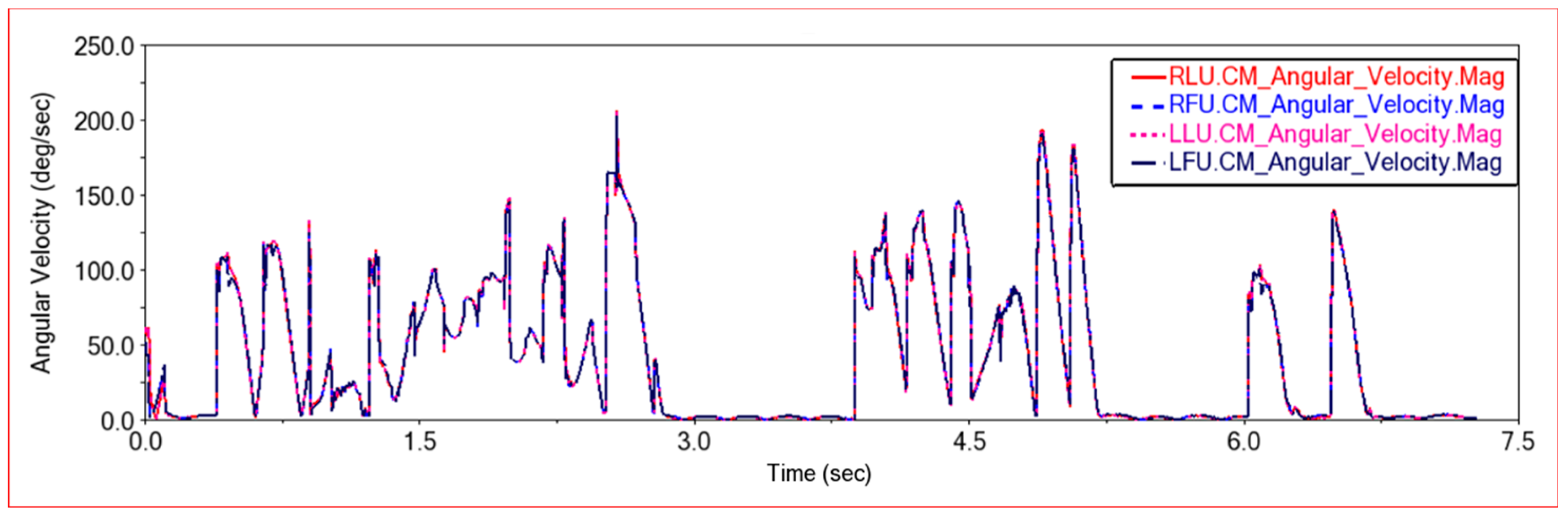
4.2.3. Obstacle Crossing Experiment 2
4.2.4. Obstacle Crossing Experiment 3
5. Ansys Analysis
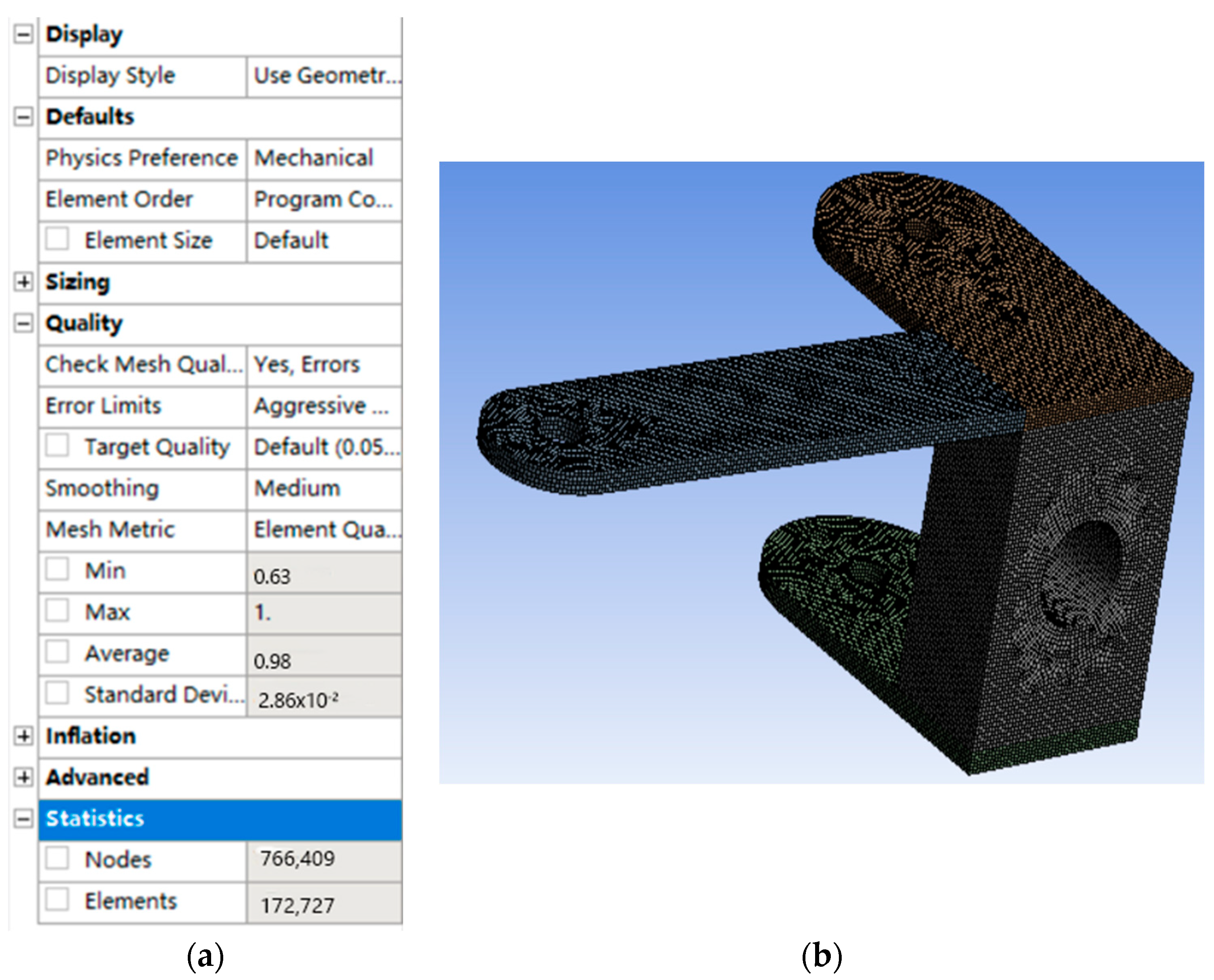
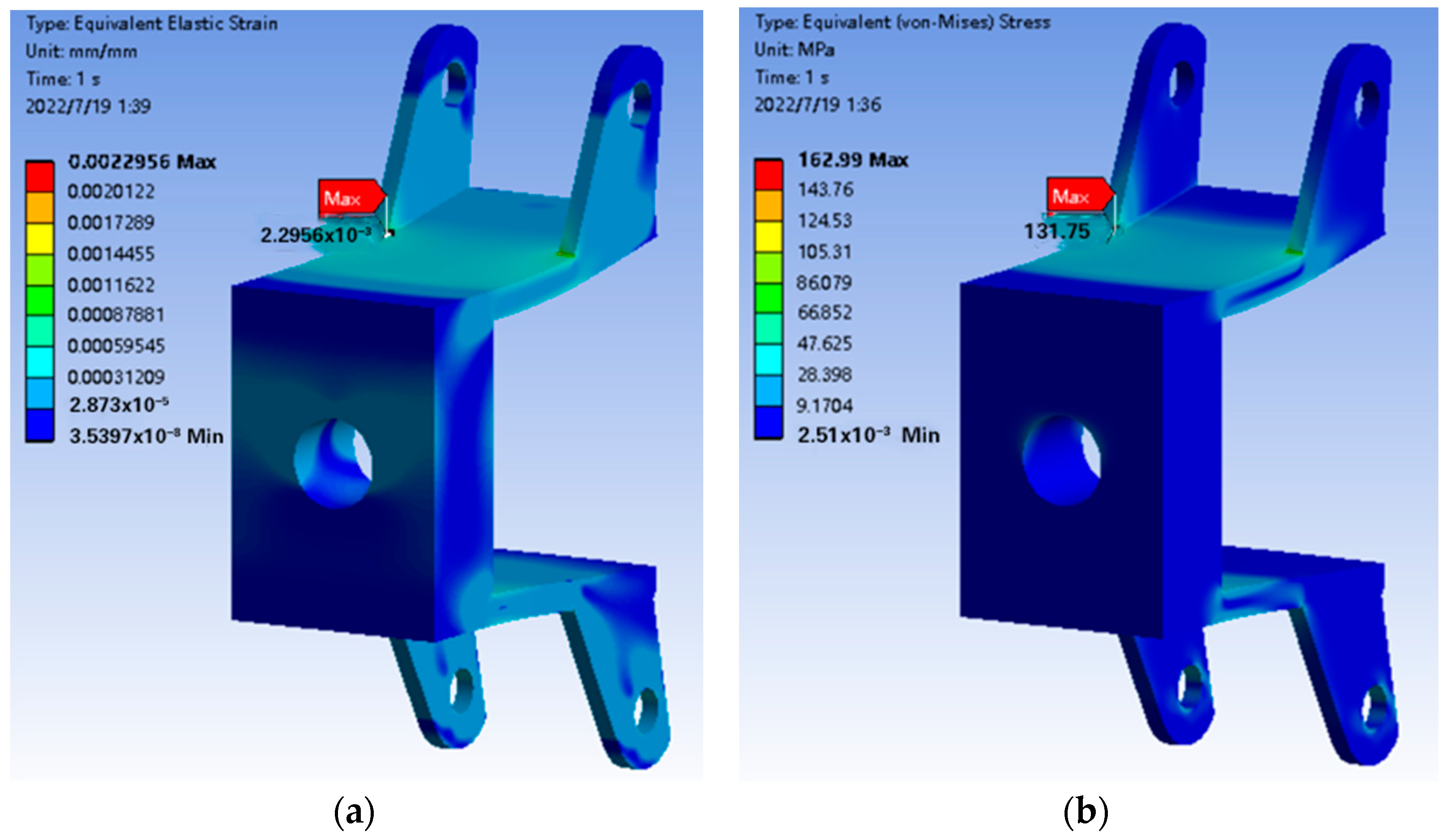
5.1. Finite Element Analysis of Front Wheel Connector
5.2. Finite Element Analysis of Rear Wheel Connector
6. Real Vehicle Test and Analysis
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dulemba, J.F. Excising a Large Bladder Endometrioma Using the Flexible CO2 Laser Fiber and Robot. J. Minim. Invasive Gynecol. 2018, 25, 7. [Google Scholar] [CrossRef]
- Fahmi, S.; Mastalli, C.; Focchi, M.; Semini, C. Passive whole-body control for quadruped robots: Experimental validation over challenging terrain. IEEE Robot. Autom. Lett. 2019, 4, 2553–2560. [Google Scholar] [CrossRef]
- Li, Z.; Huang, B.; Ajoudani, A.; Yang, C.; Su, C.-Y.; Bicchi, A. Asymmetric bimanual control of dual-arm exoskeletons for human-cooperative manipulations. IEEE Trans. Robot. 2017, 34, 264–271. [Google Scholar] [CrossRef]
- Kececi, E.F.; Ceccarelli, M. Mobile Robots for Dynamic Environments; ASME Press: New York, NY, USA, 2015; ISBN 978-0791860526. [Google Scholar]
- Chung, W.; Iagnemma, K. Wheeled robots. In Springer Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 575–594. [Google Scholar]
- Bruzzone, L.; Berselli, G.; Bilancia, P.; Fanghella, P. Design Issues for Tracked Boat Transporter Vehicles. In Advances in Mechanismand Machine Science; IFToMM WC 2019. Mechanisms and Machine Science; Springer: Cham, Switzerland, 2019; Volume 73, pp. 3671–3679. [Google Scholar]
- Raibert, M.; Blankespoor, K.; Nelson, G.; Playter, R. BigDog, the Rough-Terrain Quadruped Robot. IFAC Proc. Vol. 2008, 41, 10822–10825. [Google Scholar] [CrossRef]
- Zhi, Y.M. Research on Moving Performance of 3-PUU Wheel-Legged Mobile Robot. Master’s Thesis, North University of China, Taiyuan, China, 2018. [Google Scholar]
- Zhu, J.M.; Li, F.C.; Li, H.W.; Zhai, D.T. Design and Motion Analysis of Wheel-legged Step-climbing Mobile Robot. Chin. J. Mech. Eng. 2013, 20, 2722–2729. [Google Scholar]
- Zhao, J.; Han, T.; Wang, S.; Liu, C.; Fang, J.; Liu, S. Design and Research of All-Terrain Wheel-Legged Robot. Sensors 2021, 21, 5367. [Google Scholar] [CrossRef]
- Alamdari, A.; Krovi, V.N. Design of articulated leg–wheel subsystem by kinetostatic optimization. Mech. Mach. Theory 2016, 100, 222–234. [Google Scholar] [CrossRef]
- Xiao, J.; Sadegh, A.; Elliot, M.; Calle, A.; Persad, A.; Chiu, H.M. Design of mobile robots with wall climbing capability. In Proceedings of the IEEE AIM, Monterey, CA, USA, 24–28 July 2005; pp. 438–443. [Google Scholar] [CrossRef]
- Takita, Y.; Shimoi, N.; Date, H. Development of a wheeled mobile robot” octal wheel” realized climbing up and down stairs. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No.04CH37566), Sendai, Japan, 28 September–2 October 2004; pp. 2440–2445. [Google Scholar] [CrossRef]
- Luo, R.C.; Hsiao, M.; Lin, T.-W. Erect wheel-legged stair climbing robot for indoor service applications. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 2731–2736. [Google Scholar] [CrossRef]
- Joshi, V.A.; Banavar, R.N.; Hippalgaonkar, R. Design and analysis of a spherical mobile robot. Mech. Mach. Theory 2010, 45, 130–136. [Google Scholar] [CrossRef]
- Ni, L.; Wu, L.; Zhang, H. Parameters uncertainty analysis of posture control of a four-wheel-legged robot with series slow active suspension system. Mech. Mach. Theory 2022, 175, 104966. [Google Scholar] [CrossRef]
- Hirai, K. Current and future perspective of honda humamoid robot. In Proceedings of the 1997 IEEE/RSJ International Conference on Intelligent Robot and Systems. Innovative Robotics for Real-World Applications. IROS ‘97, Grenoble, France, 11 September 1997; pp. 500–508. [Google Scholar] [CrossRef]
- Kaneko, K.; Harada, K.; Kanehiro, F.; Miyamori, G.; Akachi, K. Humanoid robot hrp-3. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 2471–2478. [Google Scholar] [CrossRef]
- Kim, S.; Spenko, M.; Trujillo, S.; Heyneman, B.; Mattoli, V.; Cutkosky, M.R. Whole body adhesion: Hierarchical, directional and distributed control of adhesive forces for a climbing robot. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 1268–1273. [Google Scholar] [CrossRef]
- Bjelonic, M.; Kottege, N.; Homberger, T.; Borges, P.; Beckerle, P.; Chli, M. Weaver: Hexapod robot for autonomous navigation on unstructured terrain. J. Field Robot. 2018, 35, 1063–1079. [Google Scholar] [CrossRef]
- Parween, P.; Muthugala, M.A.V.J.; Heredia, M.V.; Elangovan, K.; Elara, M.R. Collision Avoidance and Stability Study of a Self-Reconfigurable Drainage Robot. Sensors 2021, 21, 3744. [Google Scholar] [CrossRef] [PubMed]
- Gogu, G. Mobility of mechanisms: A critical review. Mech. Mach. Theory 2005, 40, 1068–1097. [Google Scholar] [CrossRef]
- Cully, A.; Clune, J.; Tarapore, D.; Mouret, J.-B. Robots that can adapt like animals. Nature 2015, 521, 503. [Google Scholar] [CrossRef] [PubMed]
- Transeth, A.A.; Pettersen, K.Y.; Liljebäck, P. A survey on snake robot modeling and locomotion. Robotica 2009, 27, 999–1015. [Google Scholar] [CrossRef]
- Bayraktaroglu, Z.Y. Snake-like locomotion: Experimentations with a biologically inspired wheel-less snake robot. Mech. Mach. Theory 2009, 44, 591–602. [Google Scholar] [CrossRef]
- Transeth, A.A.; Leine, R.I.; Glocker, C.; Pettersen, K.Y. Non-smooth 3d modeling of a snake robot with external obstacles. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006; pp. 1189–1196. [Google Scholar] [CrossRef]
- Transeth, A.A.; Leine, R.I.; Glocker, C.; Pettersen, K.Y.; Liljebäck, P. Snake robot obstacle-aided locomotion: Modeling, simulations, and experiments. IEEE Trans. Robot. 2008, 24, 88–104. [Google Scholar] [CrossRef]
- Wright, C.; Buchan, A.; Brown, B.; Geist, J.; Schwerin, M.; Rollinson, D.; Tesch, M.; Choset, H. Design and architecture of the unified modular snake robot. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 4347–4354. [Google Scholar] [CrossRef]
- Kamegawa, T.; Harada, T.; Gofuku, A. Realization of cylinder climbing locomotion with helical form by a snake robot with passive wheels. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3067–3072. [Google Scholar] [CrossRef]
- Wright, C.; Johnson, A.; Peck, A.; McCord, Z.; Naaktgeboren, A.; Gianfortoni, P.; Gonzalez-Rivero, M.; Hatton, R.; Choset, H. Design of a modular snake robot. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 9 October–2 November 2007; pp. 2609–2614. [Google Scholar] [CrossRef]
- Sugiyama, Y.; Hirai, S. Crawling and jumping by a deformable robot. Int. J. Robot. Res. 2006, 25, 603–620. [Google Scholar] [CrossRef]
- Sugiyama, Y.; Shiotsu, A.; Yamanaka, M.; Hirai, S. Circular/spherical robots for crawling and jumping. In Proceedings of the Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 3595–3600. [Google Scholar] [CrossRef]
- Shibata, M.; Saijyo, F.; Hirai, S. Crawling by body deformation of tensegrity structure robots. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 4375–4380. [Google Scholar] [CrossRef]
- Shibata, M.; Hirai, S. Moving strategy of tensegrity robots with semiregular polyhedral body. In Emerging Trends in Mobile Robotics; World Scientific: Washington, DC, USA, 2010; pp. 359–366. [Google Scholar] [CrossRef]
- Koizumi, Y.; Shibata, M.; Hirai, S. Rolling tensegrity driven by pneumatic soft actuators. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 1988–1993. [Google Scholar] [CrossRef]
- Arsenault, M.; Gosselin, C.M. Kinematic and static analysis of a three-degree-of-freedom spatial modular tensegrity mechanism. Int. J. Robot. Res. 2008, 27, 951–966. [Google Scholar] [CrossRef]
- Hirai, S.; Imuta, R. Dynamic simulation of six-strut tensegrity robot rolling. In Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangzhou, China, 11–14 December 2012; pp. 198–204. [Google Scholar] [CrossRef]
- Sabelhaus, A.P.; Bruce, J.; Caluwaerts, K.; Manovi, P.; Firoozi, R.F.; Dobi, S.; Agogino, A.M.; SunSpiral, V. System design and locomotion of superball, an untethered tensegrity robot. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2867–2873. [Google Scholar] [CrossRef]
- Zhang, F.; Yu, Y.; Wang, Q.; Zeng, X.; Niu, H. A terrain-adaptive robot prototype designed for bumpy-surface exploration. Mech. Mach. Theory 2019, 141, 213–225. [Google Scholar] [CrossRef]
- Hu, C.; Wang, R.; Yan, F.; Karimi, H. Robust composite nonlinear feedback path following control for independently actuated autonomous vehicles with differential steering. IEEE Trans. Transp. Electrif. 2016, 2, 312–321. [Google Scholar] [CrossRef]
- Jagirdar, V.V.; Dadar, M.S.; Sulakhe, V.P. Wishbone Structure for Front Independent Suspension of a Military Truck. Def. Sci. J. 2010, 60, 178–183. [Google Scholar] [CrossRef]
- Singh, A.; Singla, A.; Soni, S. D-H parameters augmented with dummy frames for serial manipulators containing spatial links. In Proceedings of the 23rd IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN 2014), Edinburgh, UK, 25–29 August 2014; pp. 975–980. [Google Scholar]
- Nguyen, S.D.; Choi, S.B. A novel minimum-maxi-mum data-clustering algorithm for vibration control of asemi-active vehicle suspension system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2013, 227, 1242–1254. [Google Scholar] [CrossRef]
- Chen, L.; Wang, J.; Wu, X.; Wang, S. Analysing kinetic characteristic of multi-link rear suspension based on Adams/Car. Automob. Appl. Technol. 2015, 1–2. [Google Scholar] [CrossRef]











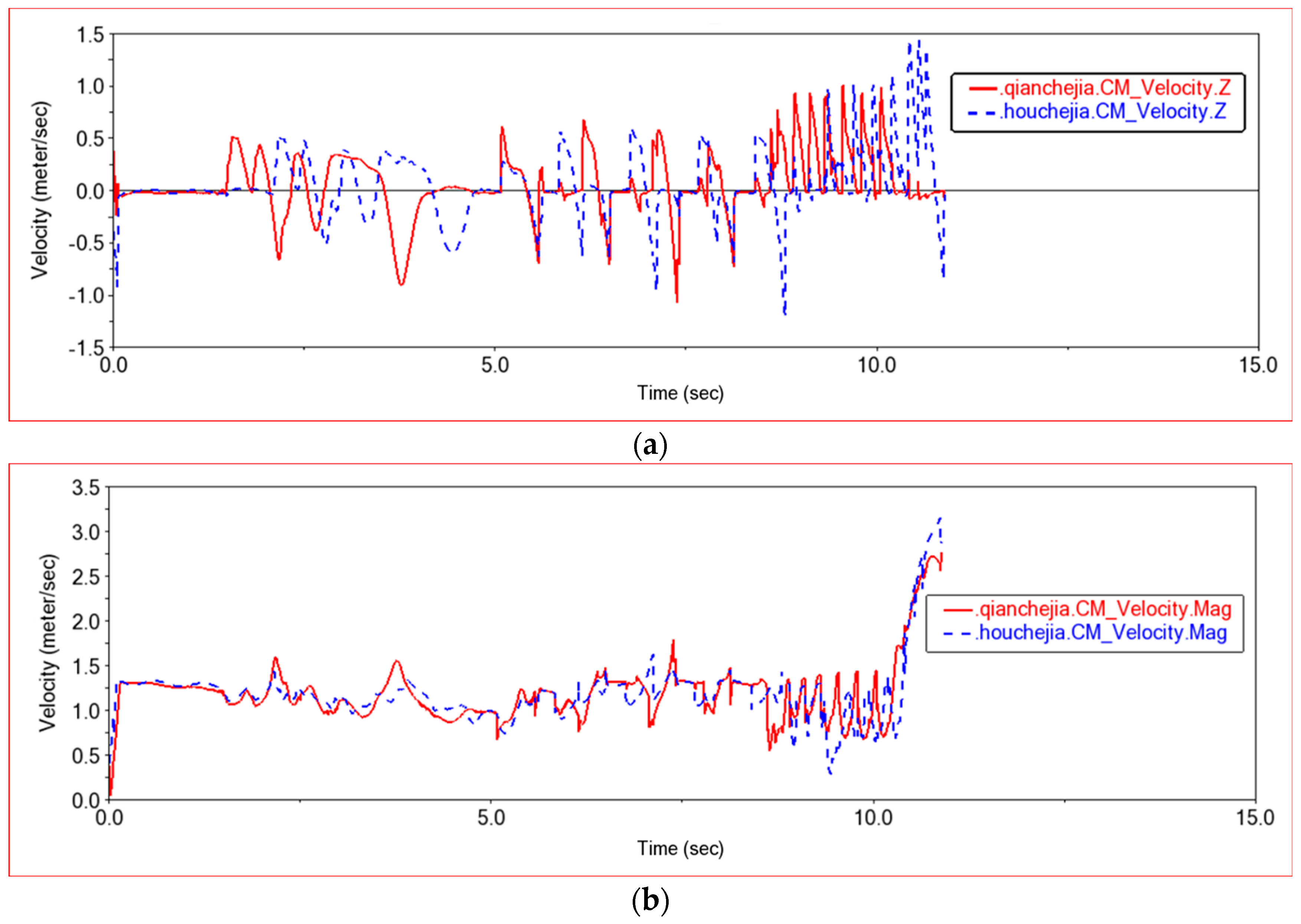
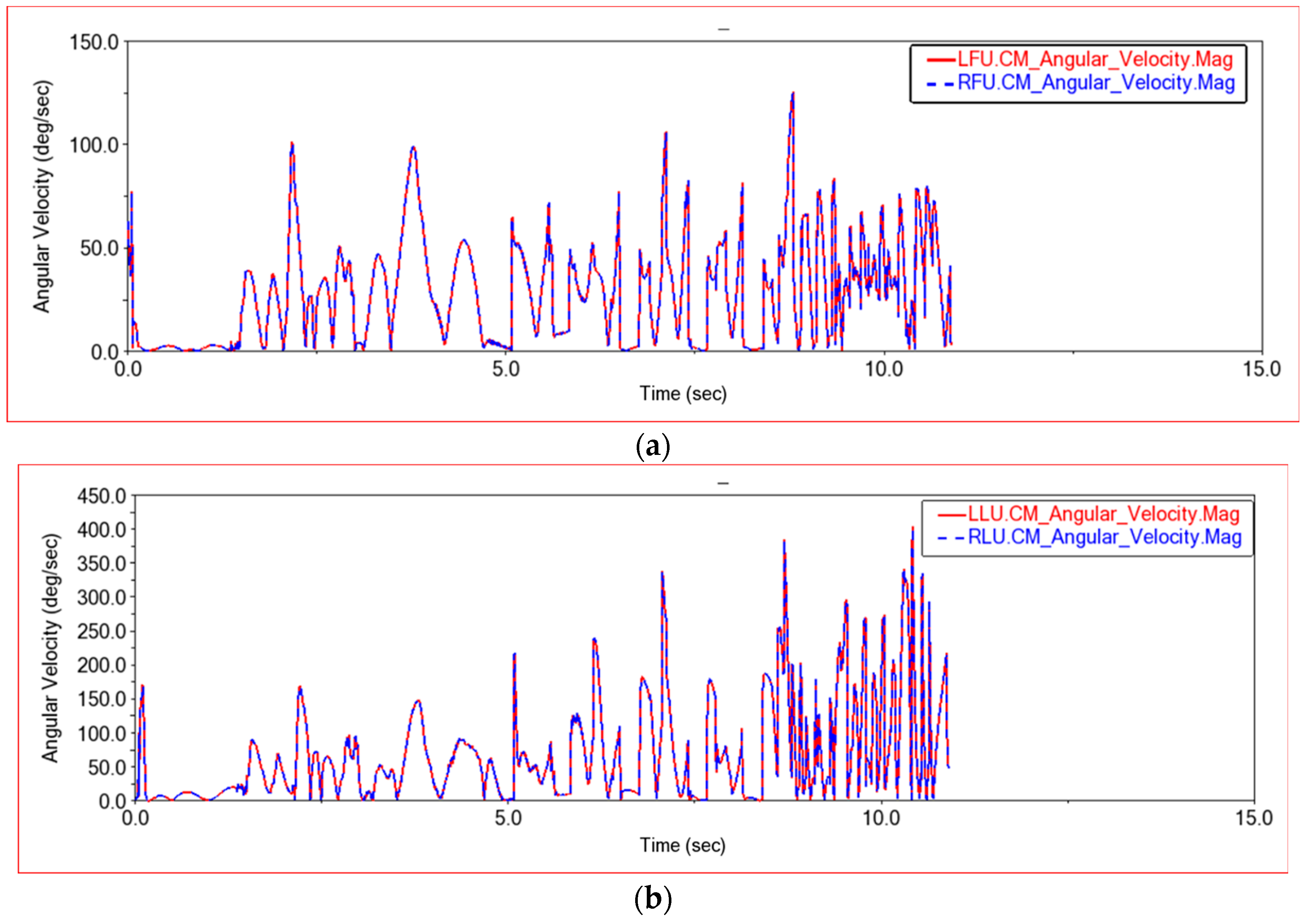



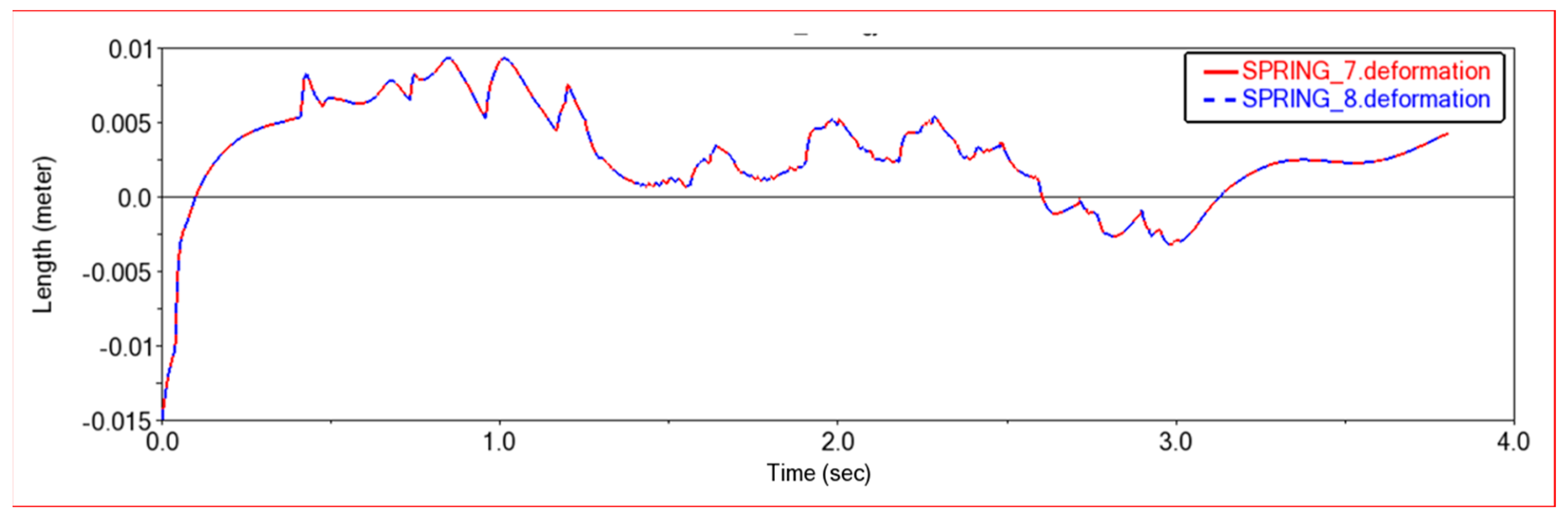
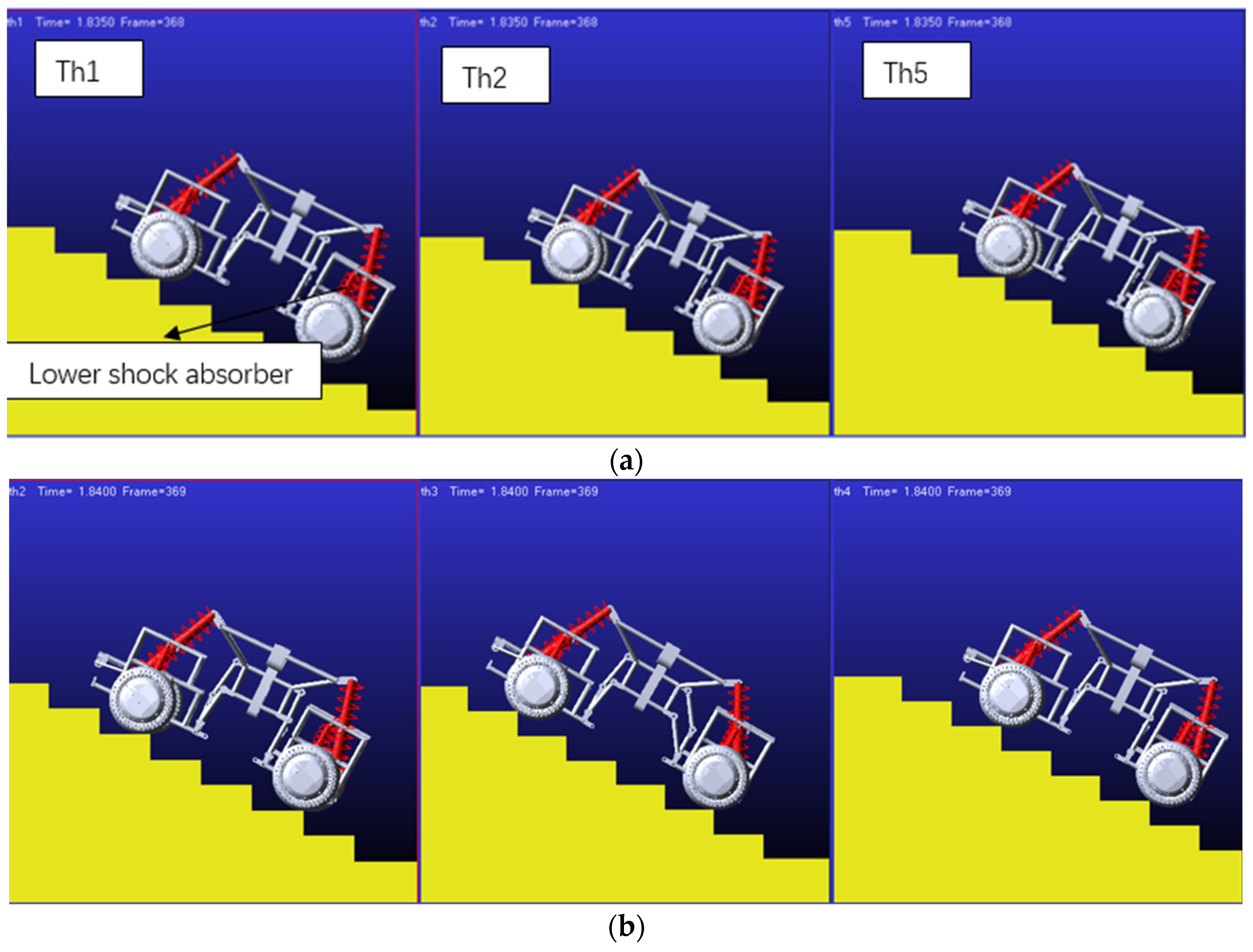








| 0 | 0 | 0 | ||
| 0 | 0 | |||
| 0 | 0 | |||
| 0 | 0 |
| Kinematic Pair | Resultant Force | |||
|---|---|---|---|---|
| Upper rotating pair | 0 | 185 | −500 | 533.128 |
| Middle rotating pair | −500 | 0 | 0 | 500 |
| Lower rotational pair | 0 | −150 | 550 | 570.088 |
| Upper plane pair | 600 | 0 | 0 | 600 |
| Lower plane pair | −600 | 0 | 0 | 600 |
| Kinematic Pair | Resultant Force | |||
|---|---|---|---|---|
| Left upper rotational pair | 0 | 325 | −20 | 325.615 |
| Right upper rotation pair | 0 | 325 | −20 | 325.615 |
| Middle rotating pair | 600 | 0 | 0 | 600 |
| Left lower rotational pair | 0 | −325 | −275 | 425.735 |
| Right lower rotational pair | 0 | −325 | −275 | 425.735 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhao, J.; Zeng, G. Modeling, Simulation and Implementation of All Terrain Adaptive Five DOF Robot. Sensors 2022, 22, 6991. https://doi.org/10.3390/s22186991
Wang Z, Zhao J, Zeng G. Modeling, Simulation and Implementation of All Terrain Adaptive Five DOF Robot. Sensors. 2022; 22(18):6991. https://doi.org/10.3390/s22186991
Chicago/Turabian StyleWang, Zhe, Jianwei Zhao, and Gang Zeng. 2022. "Modeling, Simulation and Implementation of All Terrain Adaptive Five DOF Robot" Sensors 22, no. 18: 6991. https://doi.org/10.3390/s22186991
APA StyleWang, Z., Zhao, J., & Zeng, G. (2022). Modeling, Simulation and Implementation of All Terrain Adaptive Five DOF Robot. Sensors, 22(18), 6991. https://doi.org/10.3390/s22186991







