Rotating Single-Antenna Spoofing Signal Detection Method Based on IPNN
Abstract
:1. Introduction
2. Rotating Single-Antenna Carrier-Phase Differential Spoofing Detection Model
2.1. Model Description
2.2. Detection Principle
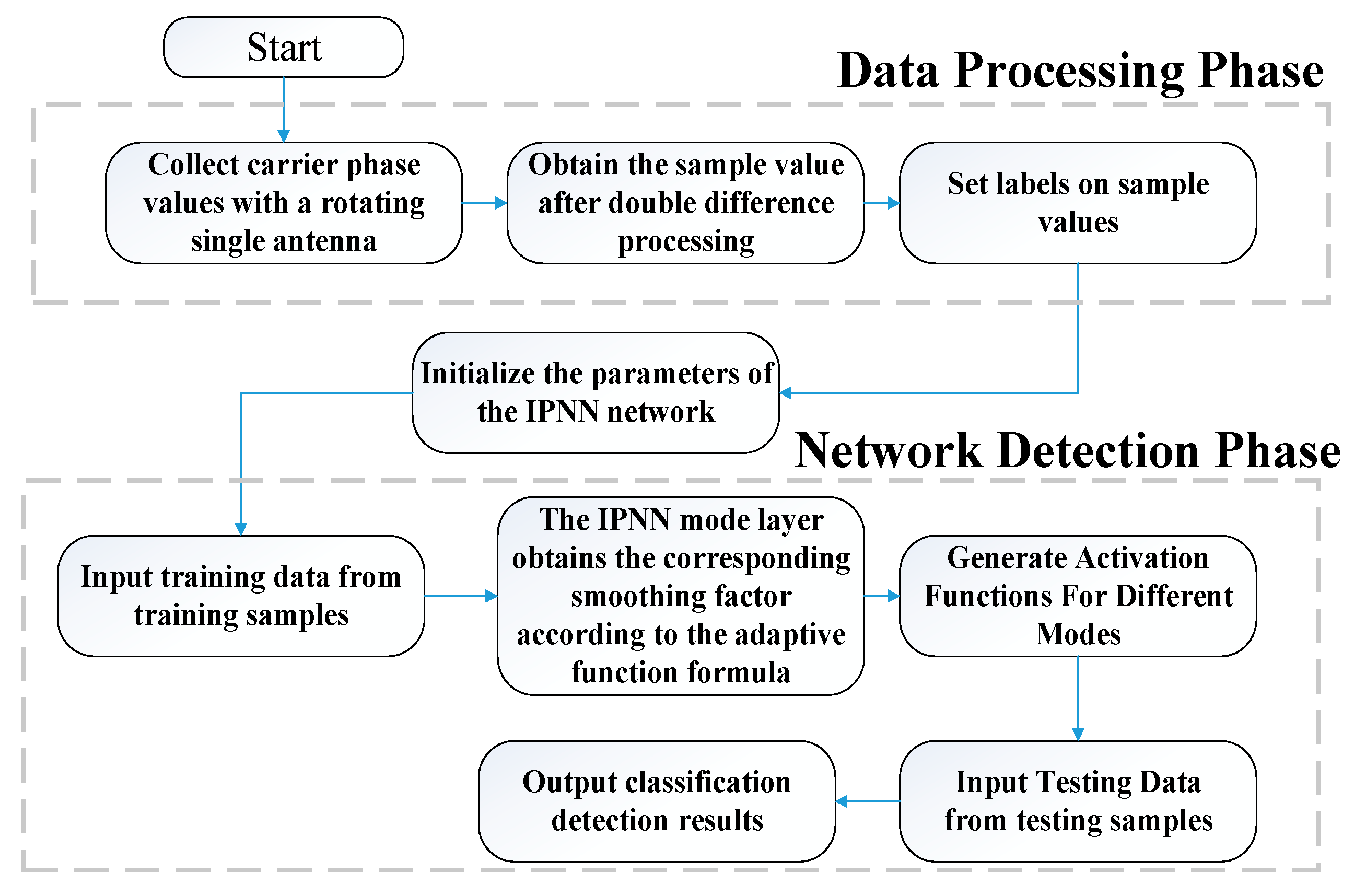
3. Rotating Single-Antenna Spoofing Signal Detection Method Based on IPNN
3.1. PNN Network Model
3.2. IPNN Basic Principles
3.3. Spoofing Jamming Detection Process
- (1)
- Using the rotating single-antenna model, the carrier-phase observations under the real signal and the spoofed signal are collected respectively, and the double-difference processing is performed on them:
- (2)
- The double-difference observations under the real signal are mainly affected by the values of and , while the double-difference observations under the deceptive signal are only related to the noise term. According to this feature, the sample label is set. The real signal label is 1, and the deception signal label is 2;
- (3)
- Initialize the network weights, input the training samples, that is, the carrier-phase double-difference observations, and send the sample feature vectors to the pattern layer after normalization;
- (4)
- Analyze and calculate the errors of the samples under different deception models, obtain the smoothing factors under different sample labels by (14), and then establish the corresponding Gaussian kernel function as the node activation function of the network;
- (5)
- Input the test sample, use the trained IPNN network for deception detection, and get the deception detection result;
- (6)
- Simulate the real situation where the satellite is deceived and interfered, and through the IPNN classification and detection results, the abnormal satellite signals can be eliminated.
4. Experimental Analysis
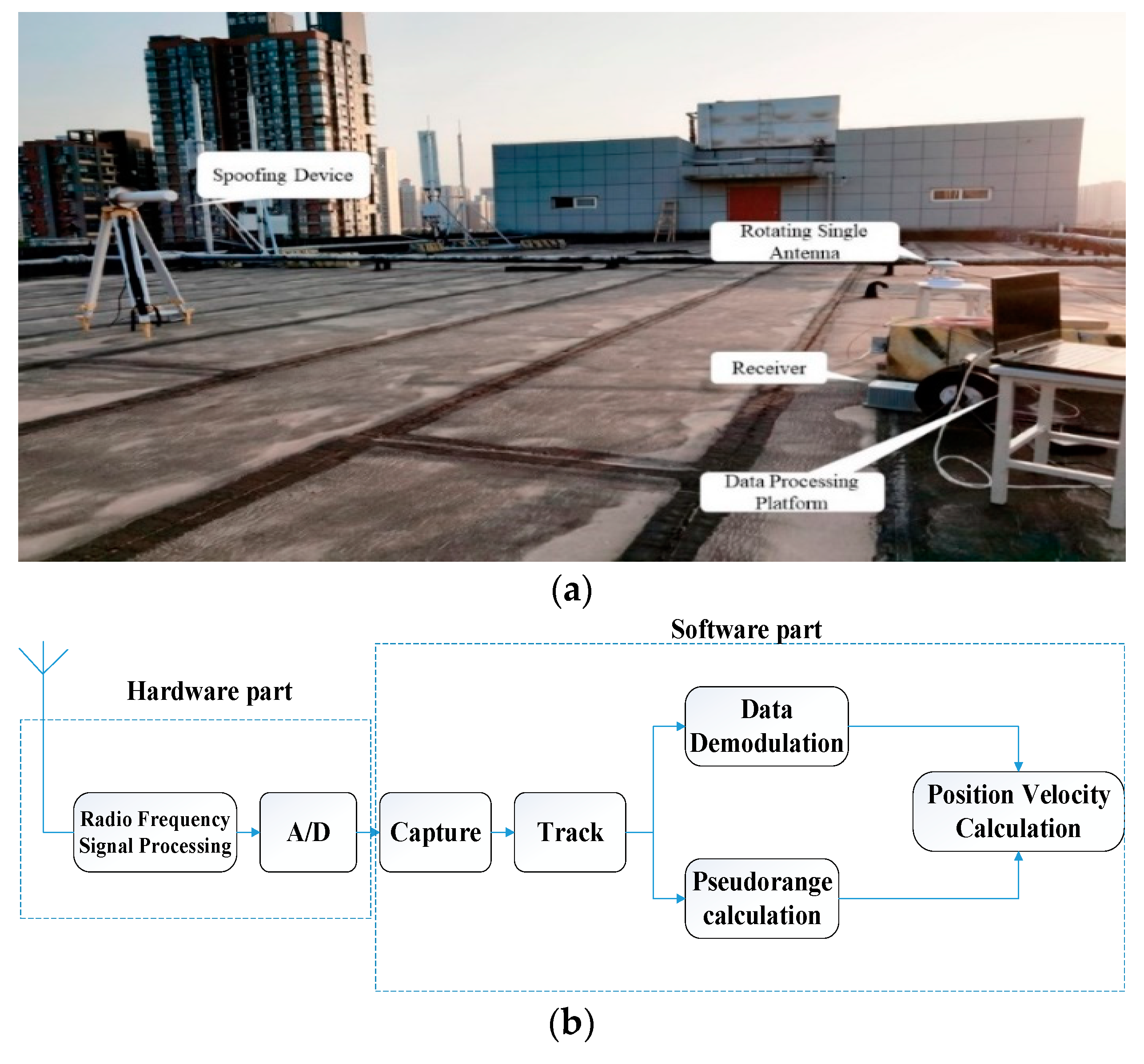
4.1. Data Collection and Processing
- (a)
- Turn on the receiving device; all received satellite signals are real signals;
- (b)
- The receiving device is placed in the house, and the signal is received by the receiving antenna placed outdoors. After being processed by the signal transponder, it is transmitted to the receiver by the transmitting antenna indoors for collection, thus, ensuring that the data collected by the receiver are all spoofing signals.
- (a)
- The receiving device is working normally, the GNSS signal transponder is not working, and the receiver receives the real signal at this time;
- (b)
- Turn on the signal transponder and keep the receiving device working normally. At this time, the collected data are changed from real signal to spoofing signal.
4.2. Analysis of Experimental Results
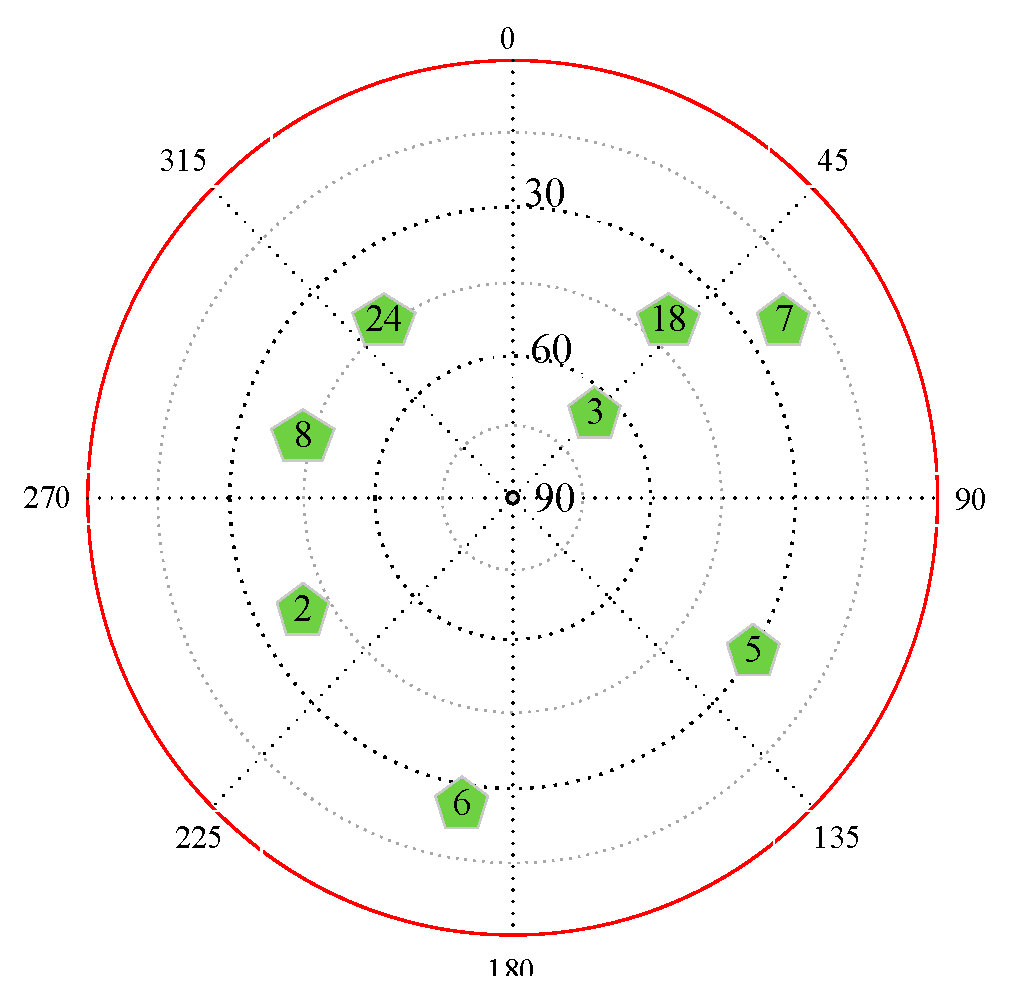
5. Application Verification
6. Conclusions
- (1)
- When using the rotating single-antenna carrier-phase differential detection model to obtain double-difference observations, there is no need to rely on traditional antenna array technology, which reduces the cost of observation.
- (2)
- The IPNN model can accurately classify different differential signal types, and its detection accuracy and detection rate are significantly better than the BPNN model and the traditional PNN model.
- (3)
- Under the premise of detecting spoofing interference, the classification and detection results of the IPNN model can accurately determine the satellites containing spoofing signals, which is suitable for forwarding spoofing interference detection of fixed-site receivers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Psiaki, M.L.; Humphreys, T.E. GNSS spoofing and detection. Proc. IEEE 2016, 104, 1258–1270. [Google Scholar] [CrossRef]
- Troglia Gamba, M.; Truong, M.D.; Motella, B.; Falletti, E.; Ta, T.H. Hypothesis testing methods to detect spoofing attacks: A test against the TEXBAT datasets. GPS Solut. 2017, 21, 577–589. [Google Scholar] [CrossRef]
- Formaggio, F.; Tomasin, S.; Caparra, G.; Ceccato, S.; Laurenti, N. Authentication of Galileo GNSS signal by super-imposed signature with artificial noise. In Proceedings of the 26th European Signal Processing Conference, Rome, 3–7 September 2018; pp. 2573–2577. [Google Scholar]
- Li, J.; Zhu, X.; Ouyang, M.; Li, W.; Chen, Z.; Dai, Z. Research on multi-peak detection of small delay spoofing signal. IEEE Access 2020, 8, 151777–151787. [Google Scholar] [CrossRef]
- Miralles, D.; Bornot, A.; Rouquette, P.; Levigne, N.; Akos, D.M.; Chen, Y.H.; Lo, S.; Walter, T. An assessment of GPS spoofing detection via radio power and signal quality monitoring for aviation safety operations. IEEE Intell. Transp. Syst. Mag. 2020, 12, 136–146. [Google Scholar] [CrossRef]
- Tao, H.; Wu, H.; Li, H.; Lu, M. GNSS spoofing detection based on consistency check of velocities. Chin. J. Electron. 2019, 28, 437–444. [Google Scholar] [CrossRef]
- Gross, J.N.; Kilic, C.; Humphreys, T.E. Maximum-likelihood power-distortion monitoring for GNSS signal authentication. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 469–475. [Google Scholar] [CrossRef]
- Jafarnia-Jahromi, A.; Broumandan, A.; Nielsen, J.; Lachapelle, G. GPS vulnerability to spoofing threats and a review of anti-spoofing techniques. Int. J. Navig. Obs. 2012, 2012, 127072. [Google Scholar]
- Zhang, X.; Pang, J.; Su, Y.; Ou, G. Spoofing detection technique on antenna array carrier phase double difference. J. Natl. Univ. Def. Technol. 2014, 36, 55–60. [Google Scholar]
- Huang, L.; Yong, L.; Xu, B.; Wang, F. Analysis of carry phase difference detection for satellite navigation receivers anti-spoofing. J. Natl. Univ. Def. Technol. 2016, 38, 103–106. [Google Scholar]
- Zhenglin, G.; Junwei, N.; Baiyu, L. Carrier phase double difference GNSS spoofing detection technique based on multi-direction measurements. J. Natl. Univ. Def. Technol. 2016, 38, 32–38. [Google Scholar]
- Lu, D.; Bai, T. Global Navigation Satellite System Deception Jam Suppression Method Using Signal Reconstruction. J. Electron. Inf. 2020, 42, 1268–1273. [Google Scholar]
- Nielsen, J.; Broumandan, A.; Lachapelle, G. Spoofing detection and mitigation with a moving handheld receiver. GPS World Mag. 2010, 21, 27–33. [Google Scholar]
- Nielsen, J.; Broumandan, A.; Lachapelle, G. GNSS spoofing detection for single antenna handheld receivers. Navigation 2012, 58, 335–344. [Google Scholar] [CrossRef]
- Broumandan, A.; Jafarnia-Jahromi, A.; Dehghanian, V.; Nielsen, J.; Lachapelle, G. GNSS spoofing detection in handheld receivers based on signal spatial correlation. In Proceedings of the Position Location and Navigation Symposium (PLANS), IEEE/ION, Myrtle Beach, SC, USA, 23–26 April 2012; pp. 479–487. [Google Scholar]
- Zhang, Z.J.; Zhan, X.Q. GNSS spoofing network monitoring based on differential pseudorange. Sensors 2016, 16, 1771. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Wu, W.Q.; Tang, K.H.; Wu, Z.J.; Zhang S, H. GNSS dual-receiver anti-spoofing jamming detection algorithm based on pseudorange information. Syst. Eng. Electron. Technol. 2017, 39, 2393–2398. [Google Scholar]
- Chen, P. Attitude Determination Algorithms for Spinning Satellites Using Single Antenna GPS Receiver and MEMS Gyro. Aerosp. Sci. Technol. 2013, 26, 10–15. [Google Scholar]
- Zhang, X.; Chen, H.; Huang, Y.; Zhang, G.; Ou, G. Spoofing Detection Technology Based on Carrier Phase Double Difference of Spin-Antenna. Geomat. Inf. Sci. Wuhan Univ. 2012, 41, 529–534. [Google Scholar]
- Wang, F.; Li, H.; Lu, M.Q. GNSS Spoofing Countermeasure with a Single Rotating Antenna. IEEE Access 2017, 5, 8039–8046. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, Y.; Wu, W.; Su, X.; Shi, X. Application of probabilistic neural network to typical fault diagnosis of vehicle gearbox. Automot. Eng. 2020, 42, 972–977. [Google Scholar]
- Zhu, H.; Lu, L.; Yao, J.; Dai, S.; Hu, Y. Fault diagnosis approach for photovoltaic arrays based on unsupervised sample clustering and probabilistic neural network model. Sol. Energy 2018, 176, 395–405. [Google Scholar] [CrossRef]
- Romesis, C.; Mathioudakis, K. Setting Up of a Probabilistic Neural Network for Sensor Fault Detection Including Operation with Component Faults. J. Eng. Gas Turbines Power 2003, 3, 125. [Google Scholar] [CrossRef]
- Yi, J.H.; Wang, J.; Wang, G.G. Improved probabilistic neural networks with self-adaptive strategies for transformer fault diagnosis problem. Adv. Mech. Eng. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Wang, Z.M.; Zhou, P.; Li, C.N. Fault Diagnosis of Roller Bearing Based on an Improved Probabilistic Neural Network. Mech. Sci. Technol. Aerosp. Eng. 2013, 32, 730–732. [Google Scholar]
- Song, H.; Yuan, H. Simulation of GPS IF Signal in a Spinning State. Comput. Simul. 2009, 26, 87–90. [Google Scholar]
- Specht, D.F. Probabilistic neural network. Neural Netw. 1990, 3, 109–118. [Google Scholar] [CrossRef]
- Pang, C.L.; Guo, Z.H.; Zhang, L.; Zhai, D.; Zhang, C. BDS against repeater deception jamming detection algorithm based on PNN. J. Chin. Inert. Technol. 2021, 29, 554–559. [Google Scholar]







| Species | Authentic Signal | Spoofing Signal |
|---|---|---|
| Tag | 1 | 2 |
| The size of training sample | 445 | 522 |
| The size of testing sample | 512 | 428 |
| Signal Type | Detection Accuracy Rate(%) | |
|---|---|---|
| Training Samples | Testing Samples | |
| Real signal | 93.48 | 95.65 |
| Spoofing signal | 97.63 | 97.46 |
| Model | Parameter Setting |
|---|---|
| BPNN | Network structure: 3-7-1 |
| PNN | Network structure: 3-300-2-1, |
| IPNN | Network structure: 3-300-2-1 , |
| Detection Accuracy Rate (%) | Detection Time (10−2 s) | ||||||
|---|---|---|---|---|---|---|---|
| BPNN | PNN | IPNN | BPNN | PNN | IPNN | ||
| Epoch | 5 | 83.67 | 91.98 | 96.03 | 17.8 | 7.59 | 5.14 |
| 10 | 84.78 | 93.47 | 97.31 | 21.8 | 8.52 | 5.97 | |
| 20 | 85.17 | 93.95 | 97.71 | 30.1 | 10.35 | 6.24 | |
| 30 | 85.38 | 94.07 | 97.93 | 36.9 | 11.87 | 6.57 | |
| 40 | 85.54 | 94.15 | 98.03 | 45.1 | 13.05 | 7.03 | |
| 50 | 85.71 | 94.26 | 98.14 | 52.6 | 14.14 | 7.39 | |
| 60 | 85.88 | 94.39 | 98.22 | 60.1 | 15.12 | 7.84 | |
| 70 | 86.02 | 94.55 | 98.34 | 66.5 | 16.32 | 8.17 | |
| 80 | 86.14 | 94.67 | 98.45 | 71.5 | 17.38 | 8.69 | |
| 90 | 86.09 | 94.81 | 98.61 | 78.6 | 18.43 | 9.05 | |
| 100 | 86.42 | 94.99 | 98.84 | 84.4 | 19.58 | 9.63 | |
| Groups | Signal Settings | ||||
|---|---|---|---|---|---|
| S02 | S03 | S05 | S08 | S18 | |
| G1 | R | R | S | R | R |
| G2 | S | R | R | S | R |
| G3 | R | S | R | R | S |
| Intersatellite Difference Combination | Detection Results | ||
|---|---|---|---|
| G1 | G2 | G3 | |
| S02 and S05 | 2 | 2 | 1 |
| S02 and S03 | 1 | 2 | 2 |
| S02 and S08 | 1 | 2 | 1 |
| S02 and S18 | 1 | 2 | 2 |
| S03 and S05 | 2 | 1 | 2 |
| S03 and S08 | 1 | 2 | 2 |
| S03 and S18 | 1 | 1 | 2 |
| S05 and S08 | 2 | 2 | 1 |
| S05 and S18 | 2 | 1 | 2 |
| S08 and S18 | 1 | 2 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, H.; Pang, C.; Zhang, L.; Guo, Z. Rotating Single-Antenna Spoofing Signal Detection Method Based on IPNN. Sensors 2022, 22, 7141. https://doi.org/10.3390/s22197141
Chang H, Pang C, Zhang L, Guo Z. Rotating Single-Antenna Spoofing Signal Detection Method Based on IPNN. Sensors. 2022; 22(19):7141. https://doi.org/10.3390/s22197141
Chicago/Turabian StyleChang, Haowei, Chunlei Pang, Liang Zhang, and Zehui Guo. 2022. "Rotating Single-Antenna Spoofing Signal Detection Method Based on IPNN" Sensors 22, no. 19: 7141. https://doi.org/10.3390/s22197141
APA StyleChang, H., Pang, C., Zhang, L., & Guo, Z. (2022). Rotating Single-Antenna Spoofing Signal Detection Method Based on IPNN. Sensors, 22(19), 7141. https://doi.org/10.3390/s22197141





