A Contemporary Design Process for Single-Phase Voltage Source Inverter Control Systems
Abstract
:1. Introduction
- Presentation of the full process of design–from a theoretical background, through the simulation, using real time interface (RTI) and dSpace libraries up to the final stage of the design process–programming the microprocessor that will control the VSI. Using real time interface creates design much more flexible.
- Definition of requirements of the design process final success:
- (a)
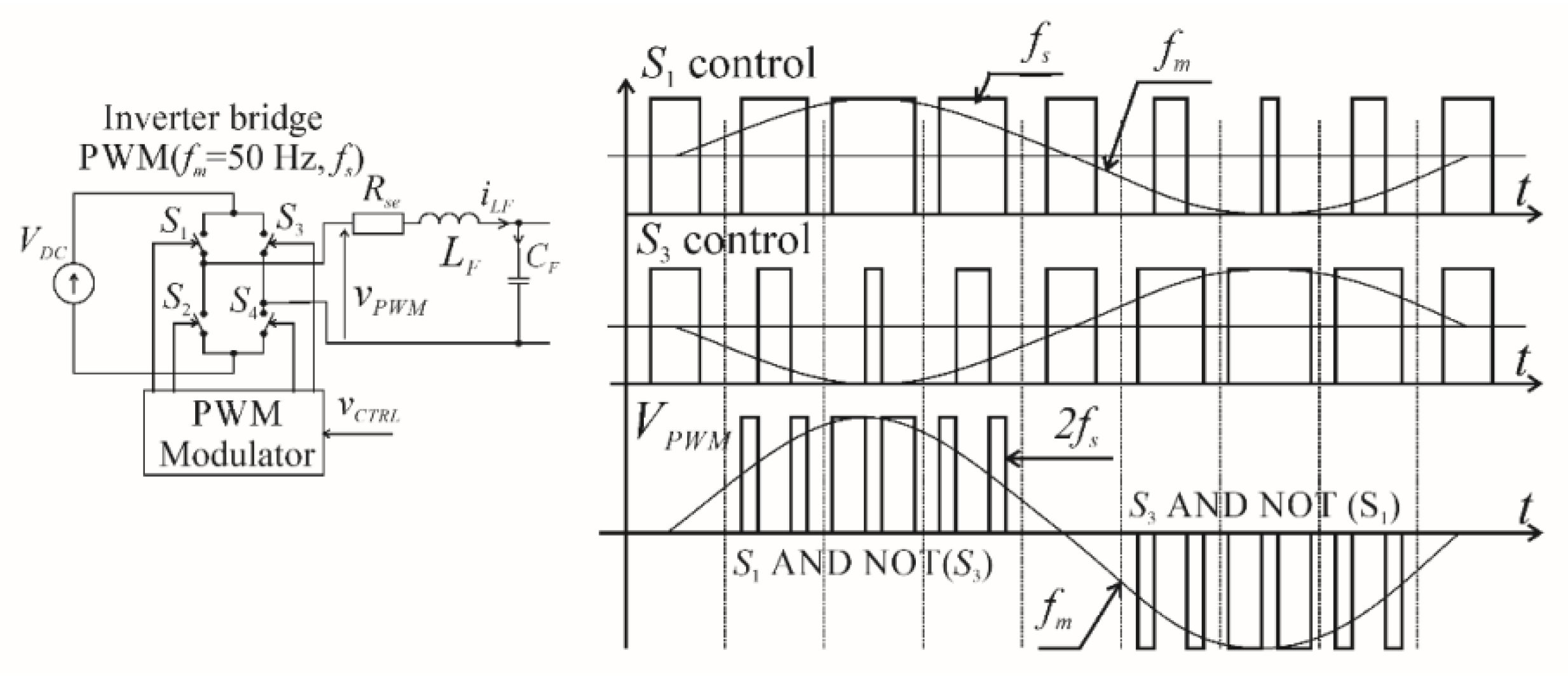
- The control law should be realized in a similar way in all the stages of the design process. It means that in the simulation the input controller data and supply of the reference waveform was measured using a sample time equal to the switching period. The PWM modulator should have the sample time equal to the period of the waveform on the input of the microprocessor PWM unit comparator (the much higher frequency than the switching frequency).
- (b)
- The real time interface and the microprocessor should use the same software architecture based on interrupts (trigger events in case of the RTI) from the PWM modulator.
- (c)
- The scaling procedure is crucial because wrong scaling changes the control law coefficients. In none of the referred papers [2,3,4] concerning the RTI usage, the scaling procedure of voltages and currents is presented. In [3] where the RTI–MicroLabBox and dSpace software was used there is nothing about using ControlDesk–the software that enables scaling.
2. Theoretical Background of SISO CDM Control Materials
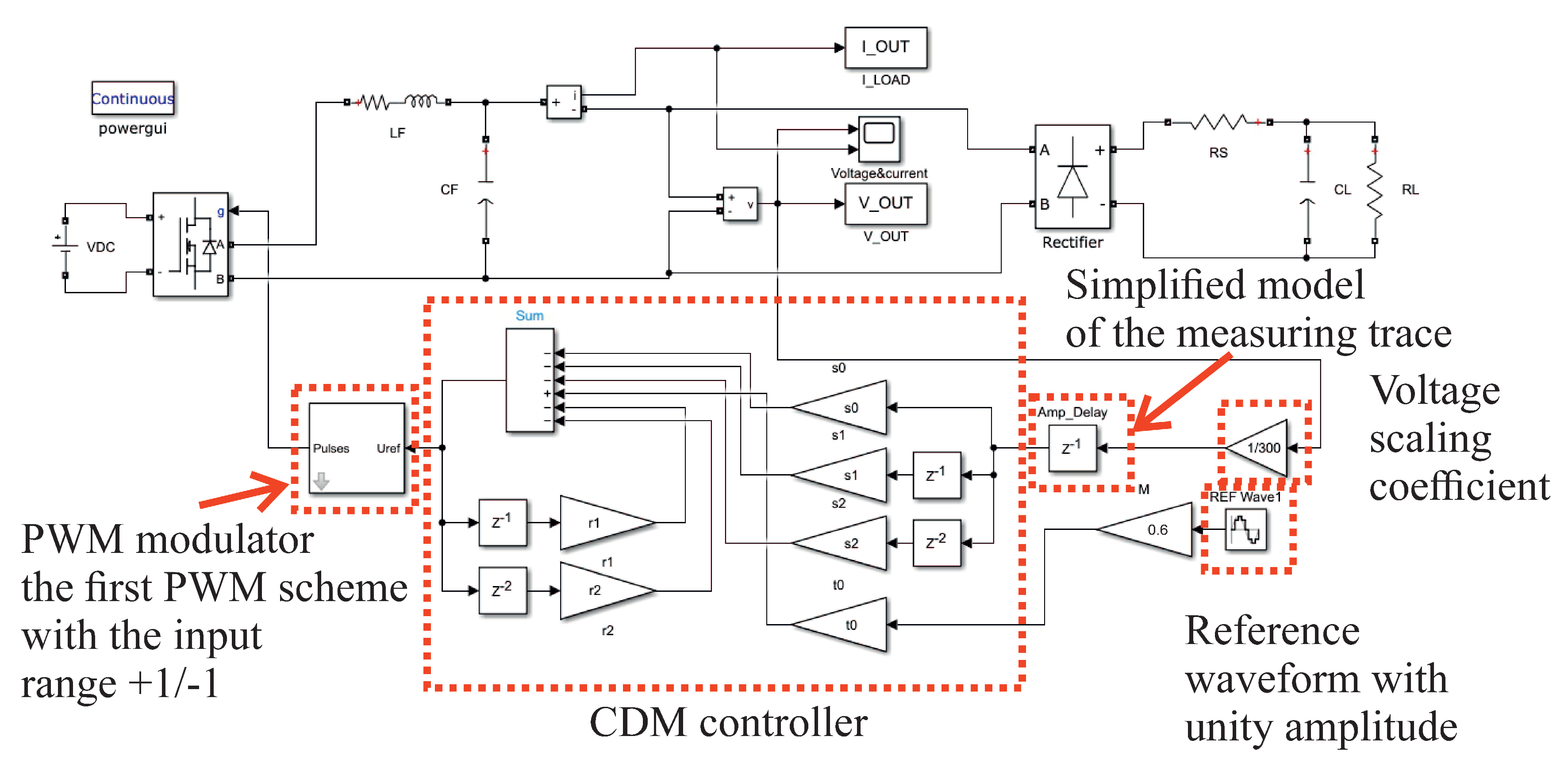
3. MATLAB’s Simulink Simulation of SISO CDM Control
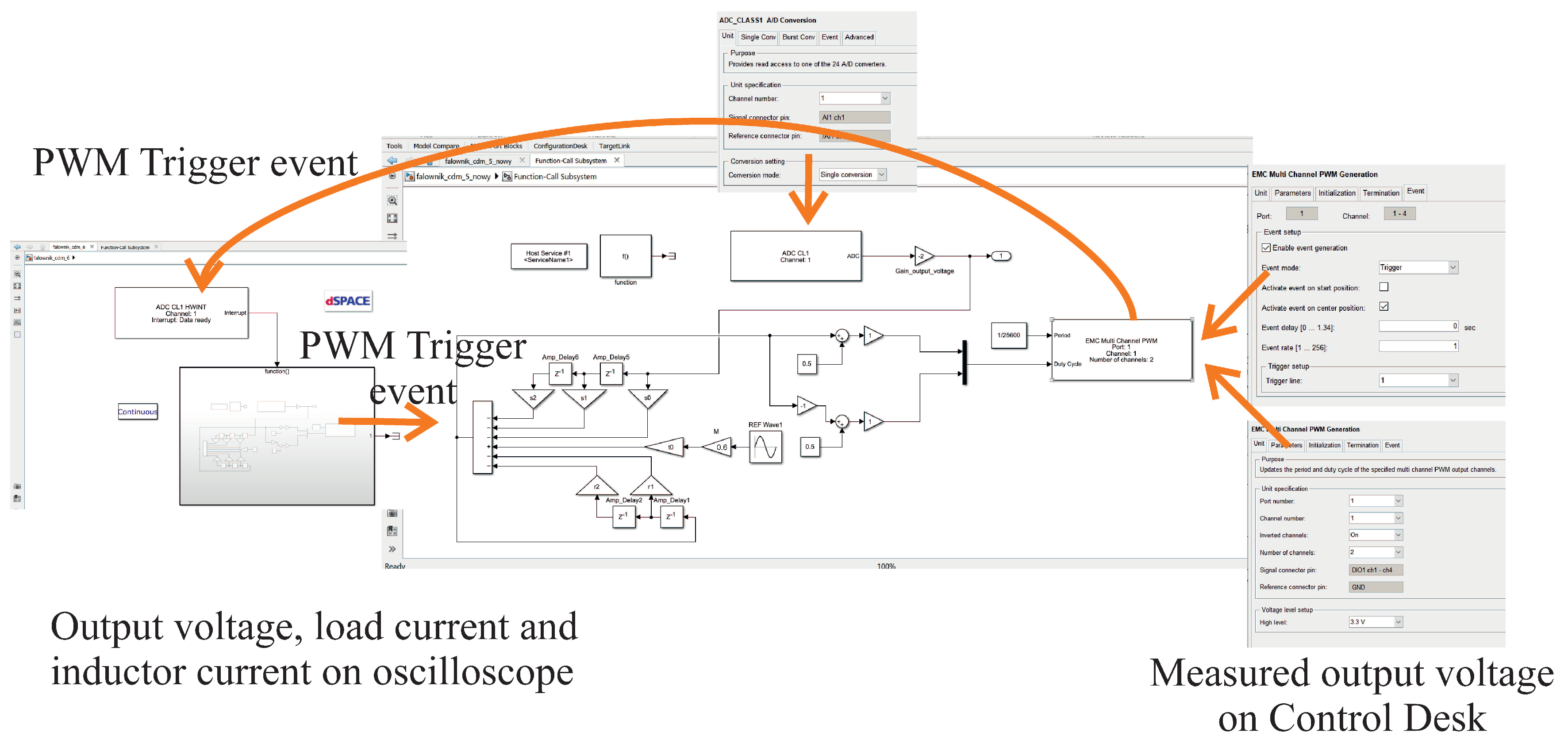
4. Interfacing MATLAB’s Simulink and dSpace Simulation of the SISO CDM Controller with the Experimental Model
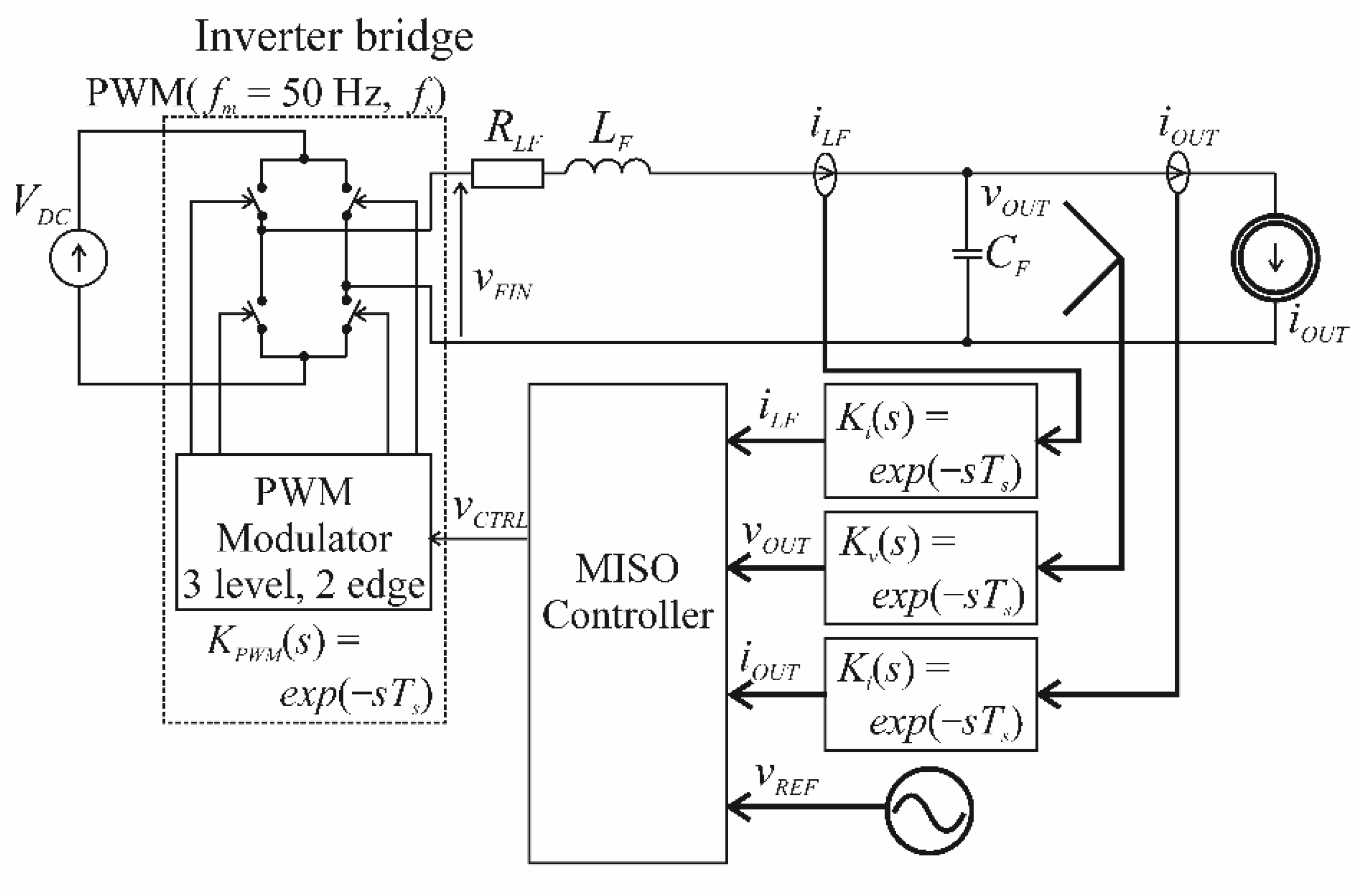
5. Implementation of the CDM Controller in the VSI Microprocessor
6. Theoretical Background of MISO PCB Control
7. MATLAB’s Simulink Simulation of MISO PBC Control
8. Interfacing MATLAB’s Simulink and dSpace Simulation of the MISO PBC Controller with the Experimental Model
9. Implementation of the MISO PBC Controller in the VSI Microprocessor
10. Results
11. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rymarski, Z. The analysis of output voltage distortion minimization in the 3-phase VSI for the nonlinear rectifier R0C0 load. Prz. Elektrotechniczny 2009, 85, 127–132. [Google Scholar]
- Bossoufi, B.; Karim, M.; Taoussi, M.; Aroussi, H.A.; Bouderbala, M.; Deblecker, O.; Motahhir, S.; Nayyar, A.; Alzain, M.A. Rooted Tree Optimization for the Backstepping Power Control of a Doubly Fed Induction Generator Wind Turbine: dSPACE Implementation. IEEE Access 2021, 9, 26512–26522. [Google Scholar] [CrossRef]
- Grgic, I.; Vukadinovic, D.; Bašic, M.; Bubalo, M. Efficiency Boost of a Quasi-Z-Source Inverter: A Novel Shoot-Through Injection Method with Dead-Time. Energies 2021, 14, 4216. [Google Scholar] [CrossRef]
- Kamalesh, M.S.; Senthilnathan, N.; Bharatiraja, C.; Mihet-Popa, L. Mitigation of circulating current with effective energy management in low-power PV-FC-battery-microgrid. Int. Trans. Electr. Energy Syst. 2021, 31, e12899. [Google Scholar] [CrossRef]
- Van der Broeck, H.W.; Miller, M. Harmonics in DC to AC converters of single phase uninterruptible power supplies. In Proceedings of the 17th International Telecommunications Energy Conference 1995, INTELEC’95, The Hague, The Netherlands, 29 October–1 November 1995; pp. 653–658. [Google Scholar]
- Rymarski, Z. The discrete model of the power stage of the voltage source inverter for UPS. Int. J. Electron. 2011, 98, 1291–1304. [Google Scholar] [CrossRef]
- Bernacki, K.; Rymarski, Z. Electromagnetic compatibility of voltage source inverters for uninterruptible power supply system depending on the pulse-width modulation scheme. IET Power Electron. 2015, 8, 1026–1034. [Google Scholar] [CrossRef]
- Rymarski, Z. Measuring the real parameters of single-phase voltage source inverters for UPS systems. Int. J. Electron. 2017, 104, 1020–1033. [Google Scholar] [CrossRef]
- Rymarski, Z.; Bernacki, K.; Dyga, L. Measuring the power conversion losses in voltage source inverters. AEU-Int. J. Electron. Commun. 2020, 124, 153359. [Google Scholar] [CrossRef]
- Bernacki, K.; Rymarski, Z. The Effect of Replacing Si-MOSFETs with WBG Transistors on the Control Loop of Voltage Source Inverters. Energies 2022, 15, 5316. [Google Scholar] [CrossRef]
- Rymarski, Z.; Bernacki, K. Different Features of Control Systems for Single-Phase Voltage Source Inverters. Energies 2020, 13, 4100. [Google Scholar] [CrossRef]
- Rymarski, Z.; Bernacki, K. Technical Limits of Passivity-Based Control Gains for a Single-Phase Voltage Source Inverter. Energies 2021, 14, 4560. [Google Scholar] [CrossRef]
- Manabe, S. Coefficient diagram method. IFAC Proc. Vol. 1998, 31, 211–222. [Google Scholar] [CrossRef]
- Manabe, S. Importance of coefficient diagram in polynomial method. In Proceedings of the 42nd IEEE Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003; pp. 3489–3494. [Google Scholar] [CrossRef]
- Coelho, J.P.; Pinho, T.M.; Boaventura-Cunha, J. Controller system design using the coefficient diagram method. Arab. J. Sci. Eng. 2016, 41, 3663–3681. [Google Scholar] [CrossRef]
- Hamamci, S.E.; Kaya, I.; Koksal, M. Improving performance for a class of processes using coefficient diagram method. In Proceedings of the 9th Mediterranean Conference on Control and Automation, MED’01, Dubrovnik, Croatia, 27–29 June 2001; pp. 1–6. [Google Scholar]
- Serra, F.M.; De Angelo, C.H.; Forchetti, D.G. IDA-PBC control of a DC–AC converter for sinusoidal three-phase voltage generation. Int. J. Electron. 2016, 104, 93–110. [Google Scholar] [CrossRef]
- Komurcugil, H. Improved passivity-based control method and its robustness analysis for single-phase uninterruptible power supply inverters. IET Power Electron. 2015, 8, 1558–1570. [Google Scholar] [CrossRef]
- Wang, Z.; Goldsmith, P. Modified energy-balancing-based control for the tracking problem. IET Control Theory Appl. 2008, 2, 310–312. [Google Scholar] [CrossRef]
- Ortega, R.; Garcıa-Canseco, E. Interconnection and Damping Assignment Passivity-Based Control: A Survey. Eur. J. Control. 2004, 10, 432–450. [Google Scholar] [CrossRef]
- Wang, X.; Loh, P.C.; Blaabjerg, F. Stability Analysis and Controller Synthesis for Single-Loop Voltage-Controlled VSIs. IEEE Trans. Power Electron. 2017, 32, 7394–7404. [Google Scholar] [CrossRef]
- Sun, X.; Liu, Y.; Ren, B.; Yu, M. Research on control strategy of a single-phase inverter with good output voltage quality. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 2068–2071. [Google Scholar] [CrossRef]
- Gattamaneni, M.; Gudey, S.K. Design and Stability Analysis of Single-Loop Voltage Control of Voltage Source Inverter. In Proceedings of the 6th International Conference on Computing, Communication and Automation (ICCCA), New Delhi, India, 17–19 December 2021; pp. 249–253. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; Wang, P.; Zhu, H.; Liu, C.; Gao, F. Single-Loop Digital Control of High-Power 400-Hz Ground Power Unit for Airplanes. IEEE Trans. Ind. Electron. 2010, 57, 532–543. [Google Scholar] [CrossRef]
- IEC 62040-3:2021; Uninterruptible Power Systems (UPS)—Part 3: Method of Specifying the Performance and Test Requirements. IEC: Geneva, Switzerland, 2021.


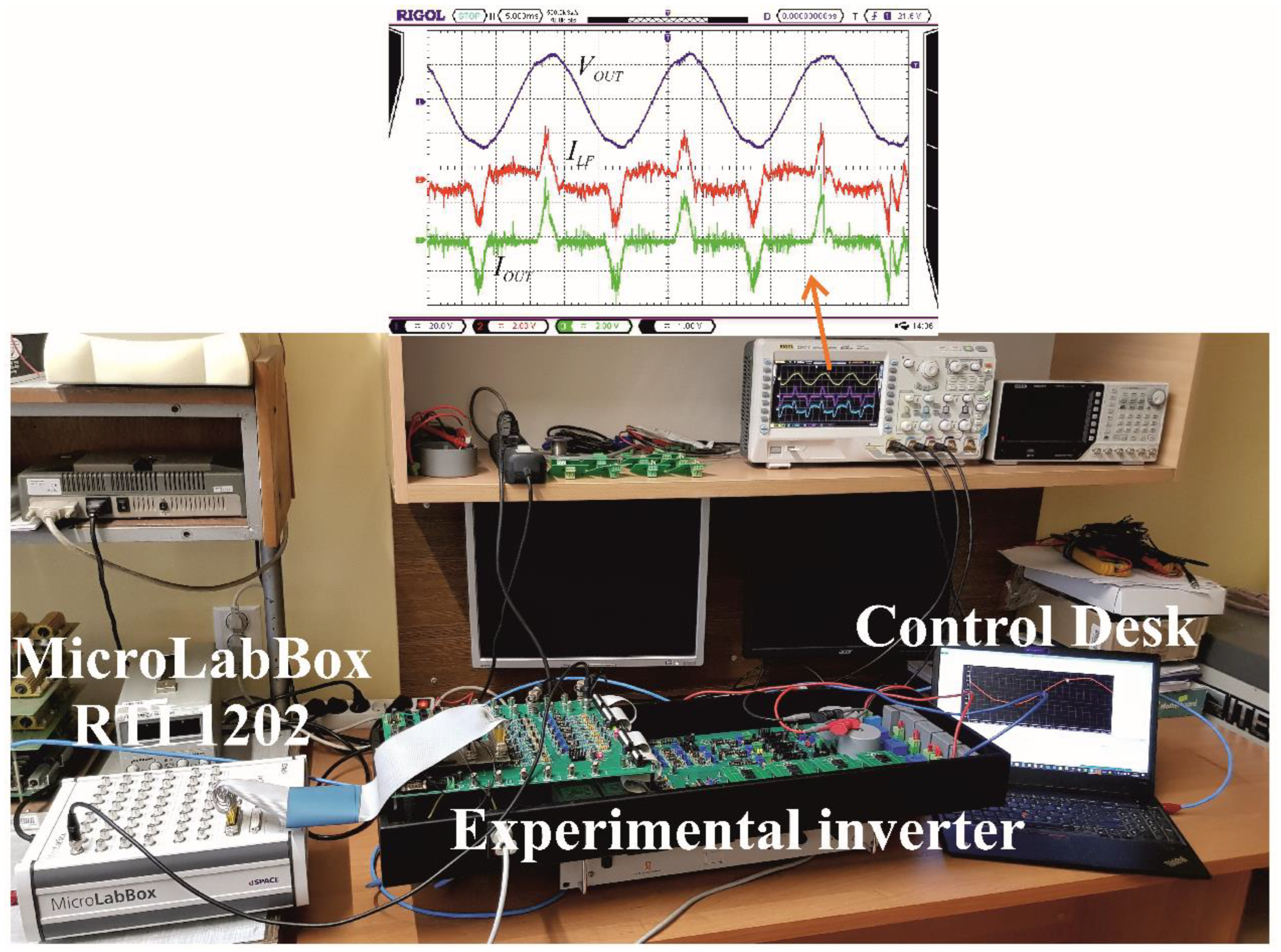


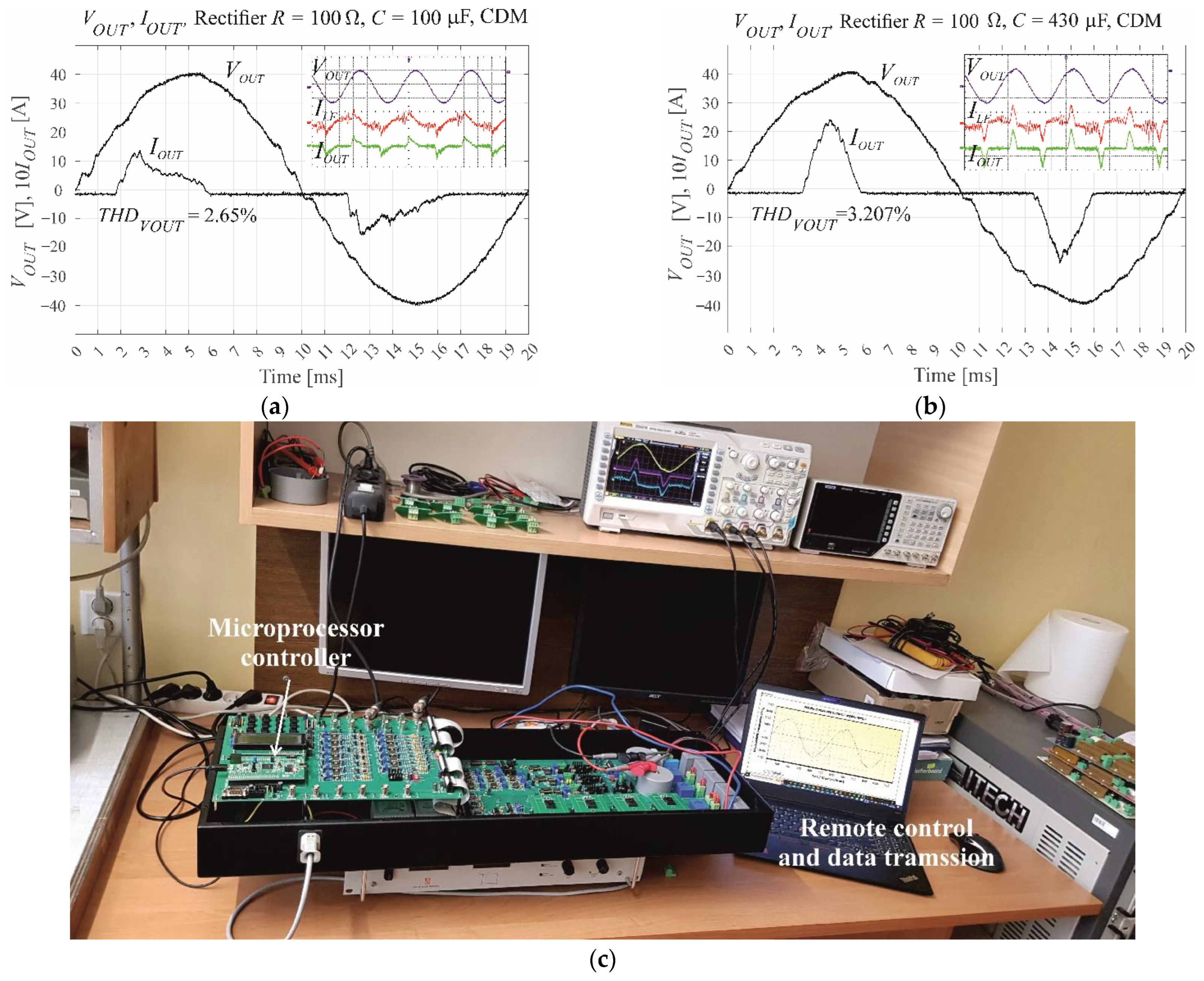



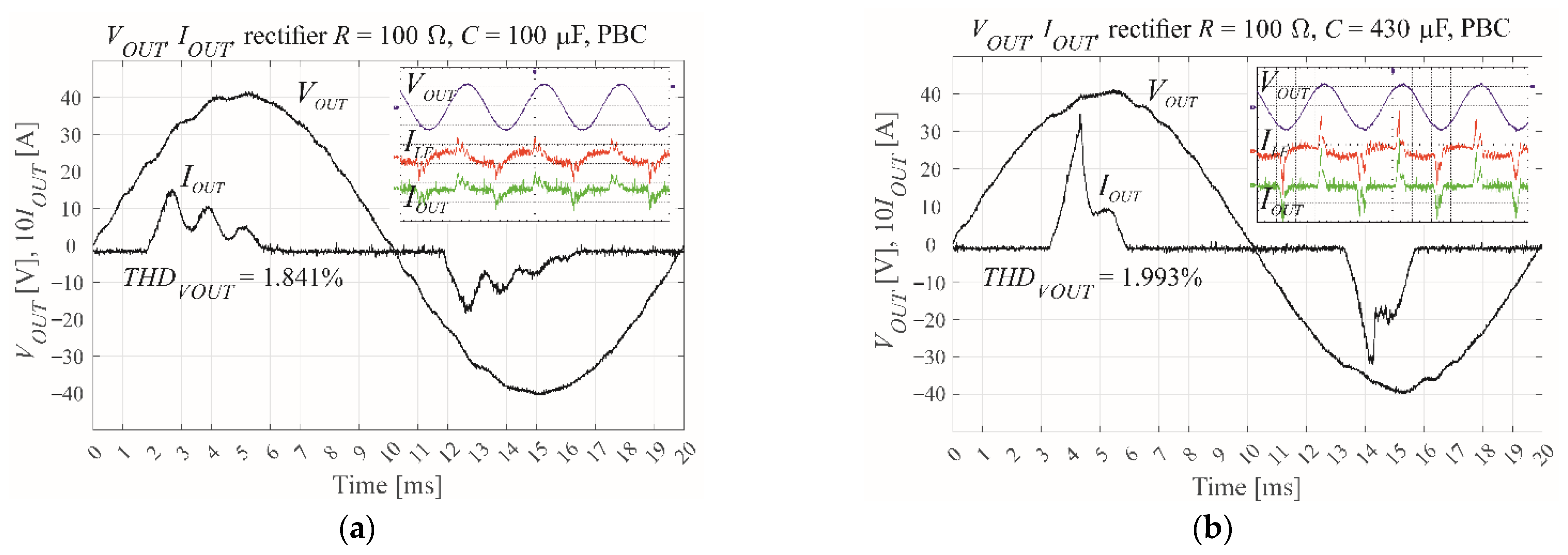
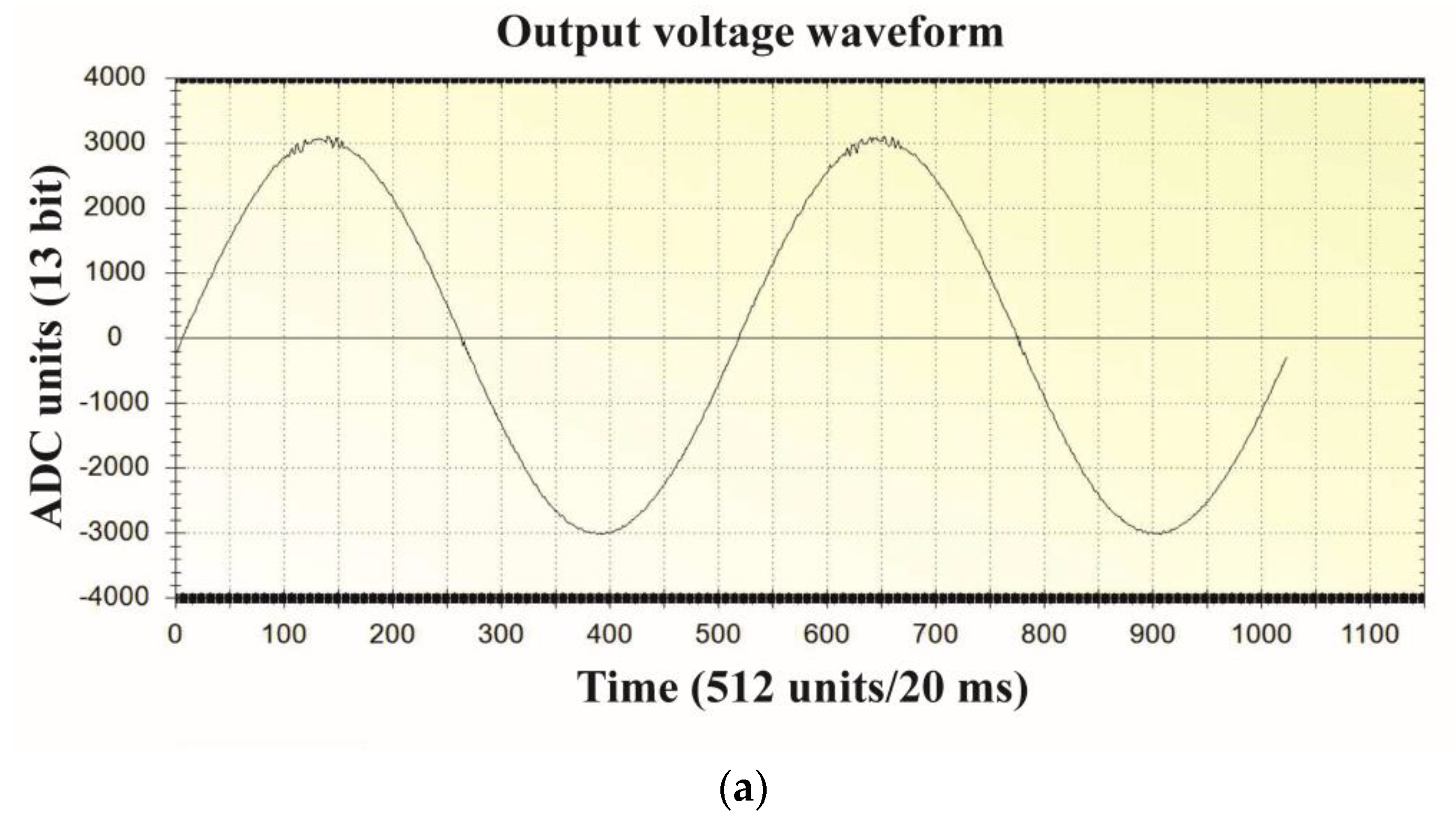
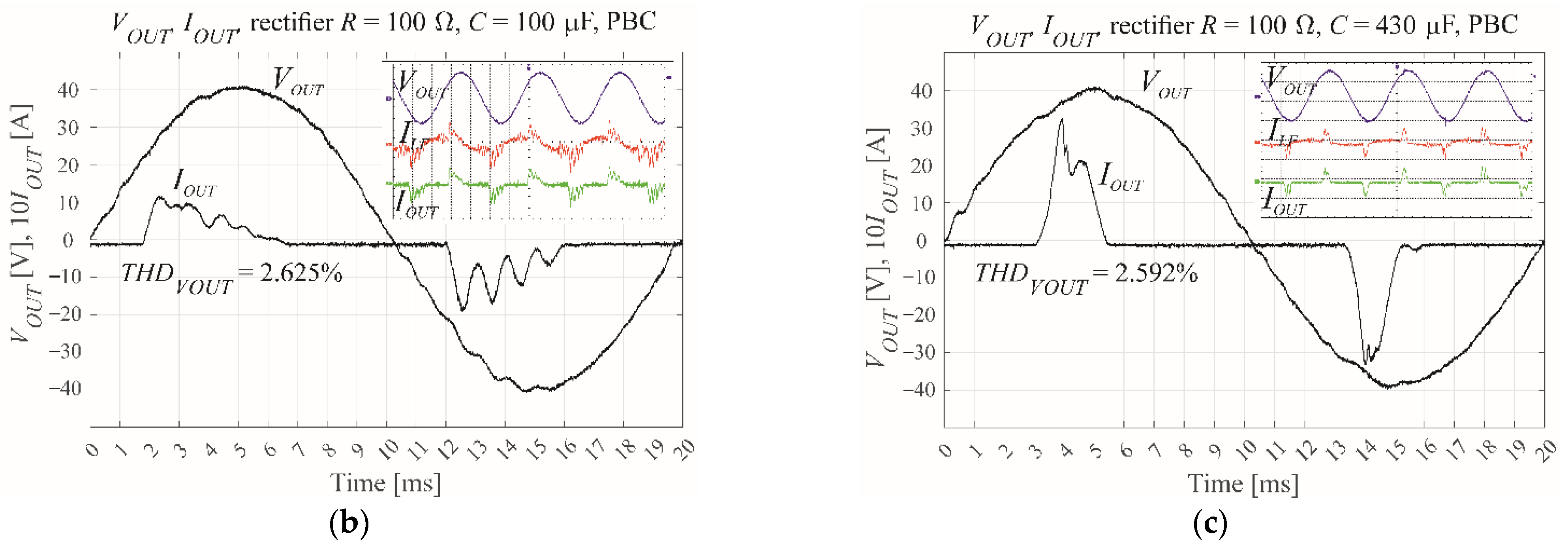
| Control Type; Nonlinear Rectifier Load RC Parameters Modulation Index M | Simulation | MicroLabBox and Experimental Model | Microprocessor and Experimental Model |
|---|---|---|---|
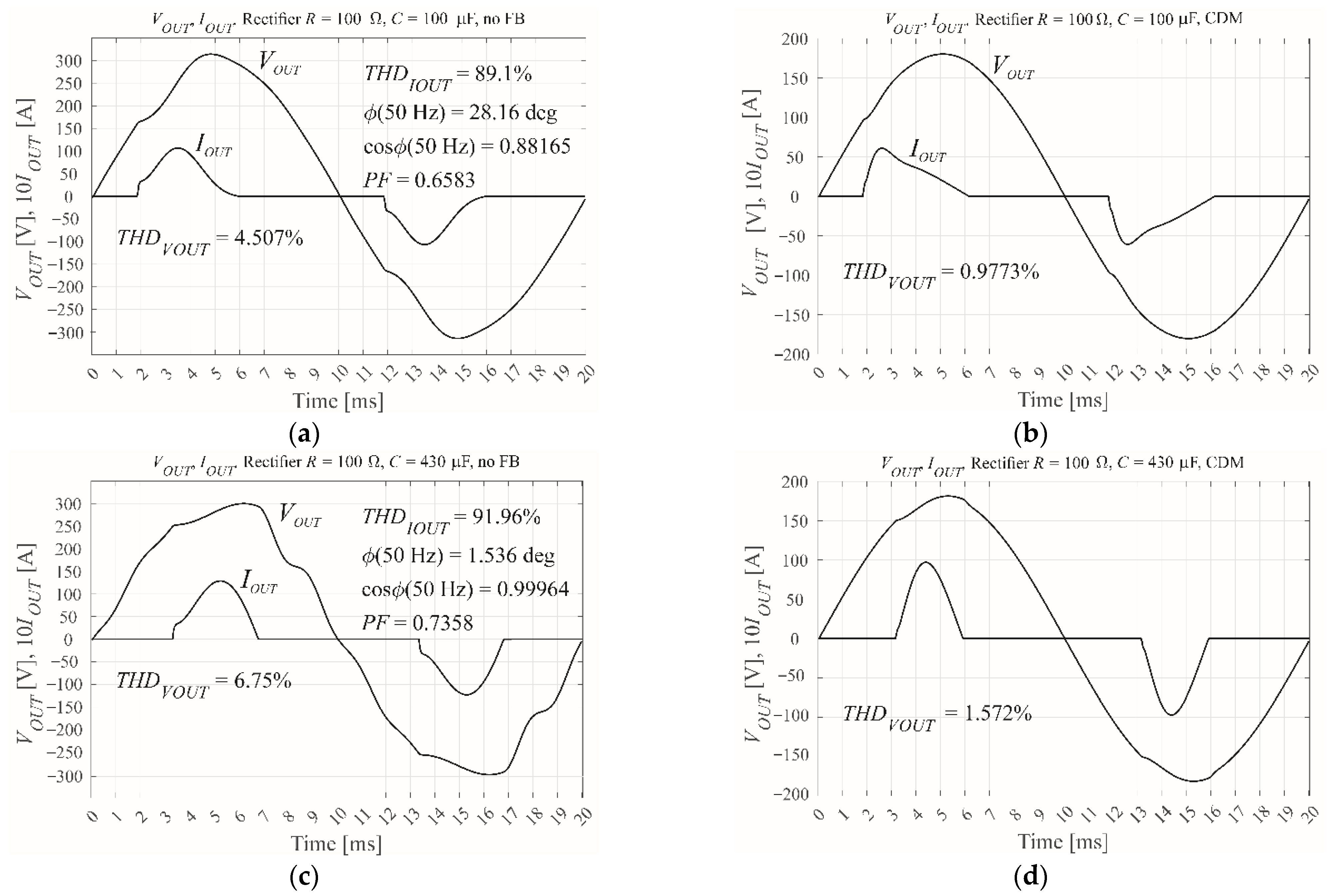
| Open loop, R = 100 Ω, C = 100 μF | 4.51% | 4.35% | - |
| Open loop, R = 100 Ω, C = 430 μF | 6.75% | 6.96% | - |
| CDM, R = 100 Ω, C = 100 μF, M = 0.6 | 0.98% | 2.01% | 2.65% |
| CDM, R = 100 Ω, C = 430 μF, M = 0.6 | 1.57% | 3.44% | 3.21% |
| PBC, R = 100 Ω, C = 100 μF, M = 0.6 | 0.37% | 1.84% | 2.63% |
| PBC, R = 100 Ω, C = 430 μF, M = 0.6 | 0.34% | 1.99% | 2.59% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernacki, K.; Rymarski, Z. A Contemporary Design Process for Single-Phase Voltage Source Inverter Control Systems. Sensors 2022, 22, 7211. https://doi.org/10.3390/s22197211
Bernacki K, Rymarski Z. A Contemporary Design Process for Single-Phase Voltage Source Inverter Control Systems. Sensors. 2022; 22(19):7211. https://doi.org/10.3390/s22197211
Chicago/Turabian StyleBernacki, Krzysztof, and Zbigniew Rymarski. 2022. "A Contemporary Design Process for Single-Phase Voltage Source Inverter Control Systems" Sensors 22, no. 19: 7211. https://doi.org/10.3390/s22197211
APA StyleBernacki, K., & Rymarski, Z. (2022). A Contemporary Design Process for Single-Phase Voltage Source Inverter Control Systems. Sensors, 22(19), 7211. https://doi.org/10.3390/s22197211







