Dynamic Compensation Method for Humidity Sensors Based on Temperature and Humidity Decoupling
Abstract
:1. Introduction
2. Coupling Effect of Temperature on Humidity Sensing
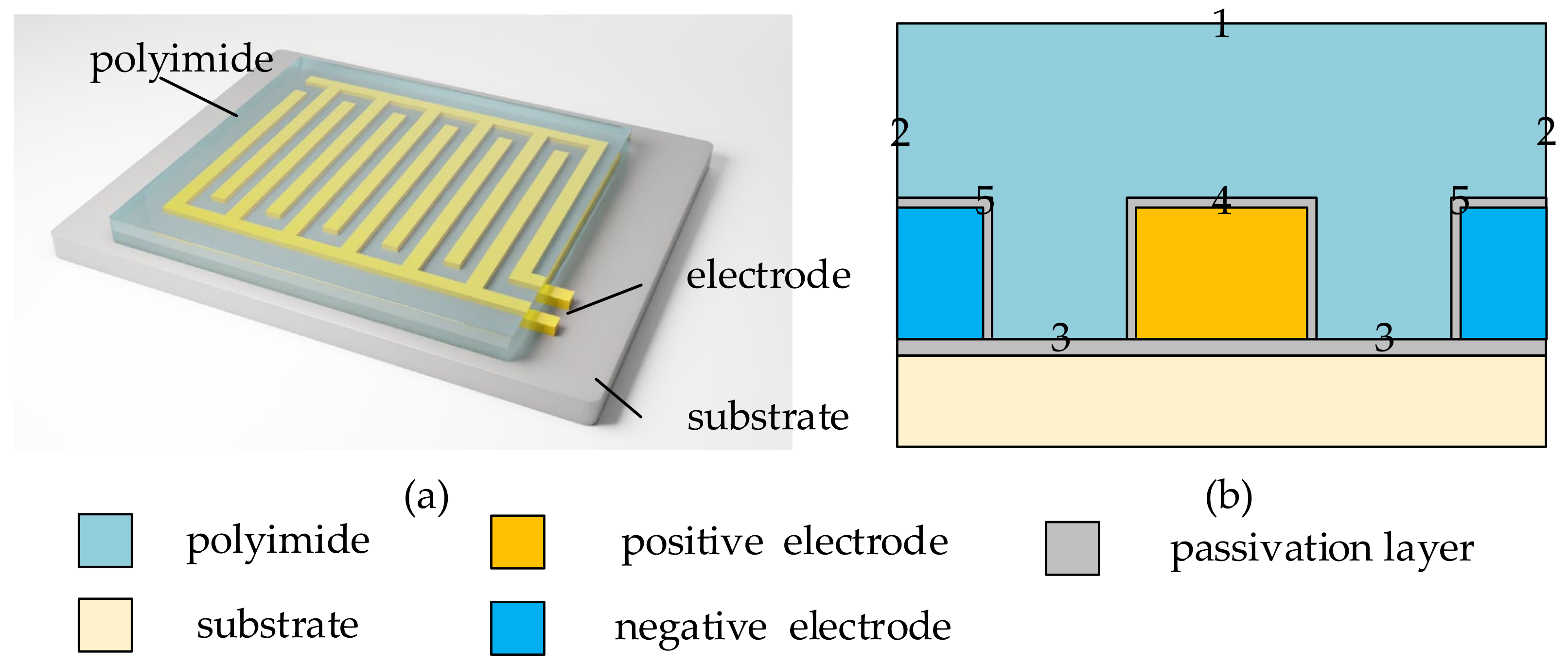
2.1. Humidity-Sensing Mechanism
- i.
- Medium is homogeneous. A polyimide probe is a uniformly isotropic porous medium with the same porosity. The change in diffusivity is consistent with temperature. Gases, including water vapor in the medium, are ideal gases that do not react with the polyimide medium. Ignoring the diffusion resistance of the film surface, the water vapor concentration at the contact position between the medium and the air is uniform and the same as those in the ambient air.
- ii.
- The temperature is uniform. In polyimide probes, the diffusion equations for temperature transfer and water molecule transfer take the same form. However, the thermal diffusivity in polyimide and silicon wafers is much greater than the water molecule diffusivity in polyimide. As shown in Table 1, some materials have thermal diffusivities that are 106 times higher than the diffusivity of water molecules. Assuming a response time of 10 s for the humidity sensor, the thermal diffusion time is less than 1 ms. Therefore, when modeling the dynamic process of water molecule diffusion, the temperature in the sensor Tsensors can be considered to be uniform.
- iii.
- Signal processing time can be ignored. This is because the time required for signal amplification and digitization of the probe is milliseconds.
2.2. Coupling Effect of Temperature on Sensing Humidity
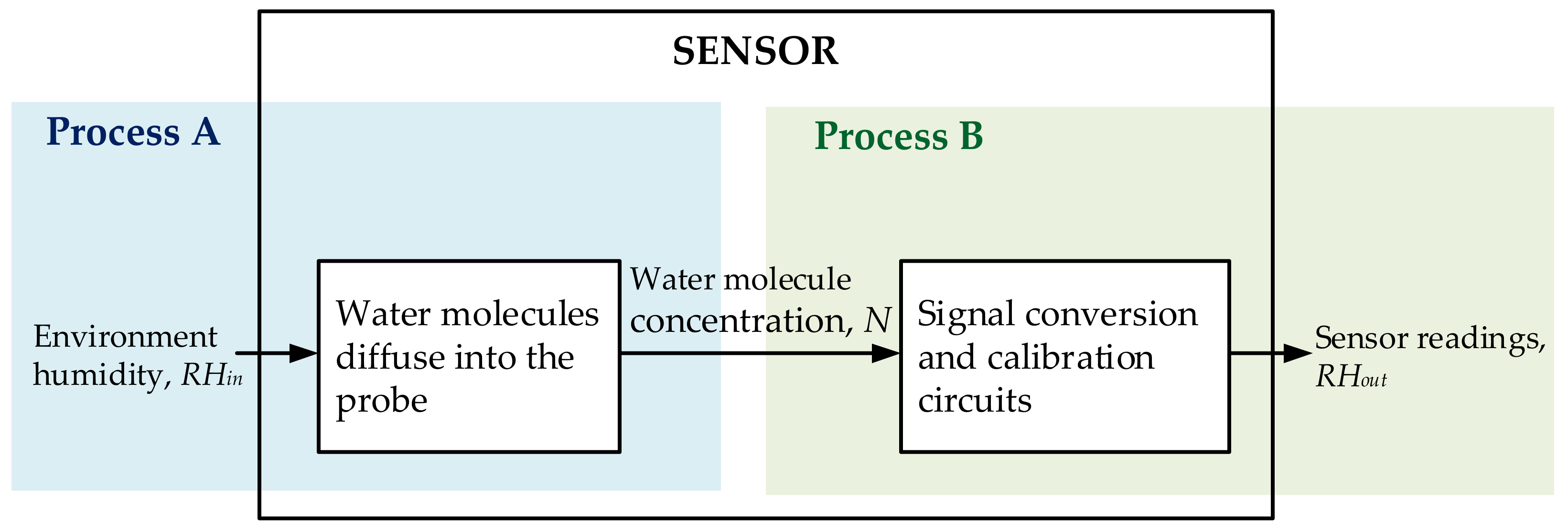
2.2.1. Process A
- i.
- According to Equation (1), RHin is affected by both temperature and Nin.
- ii.
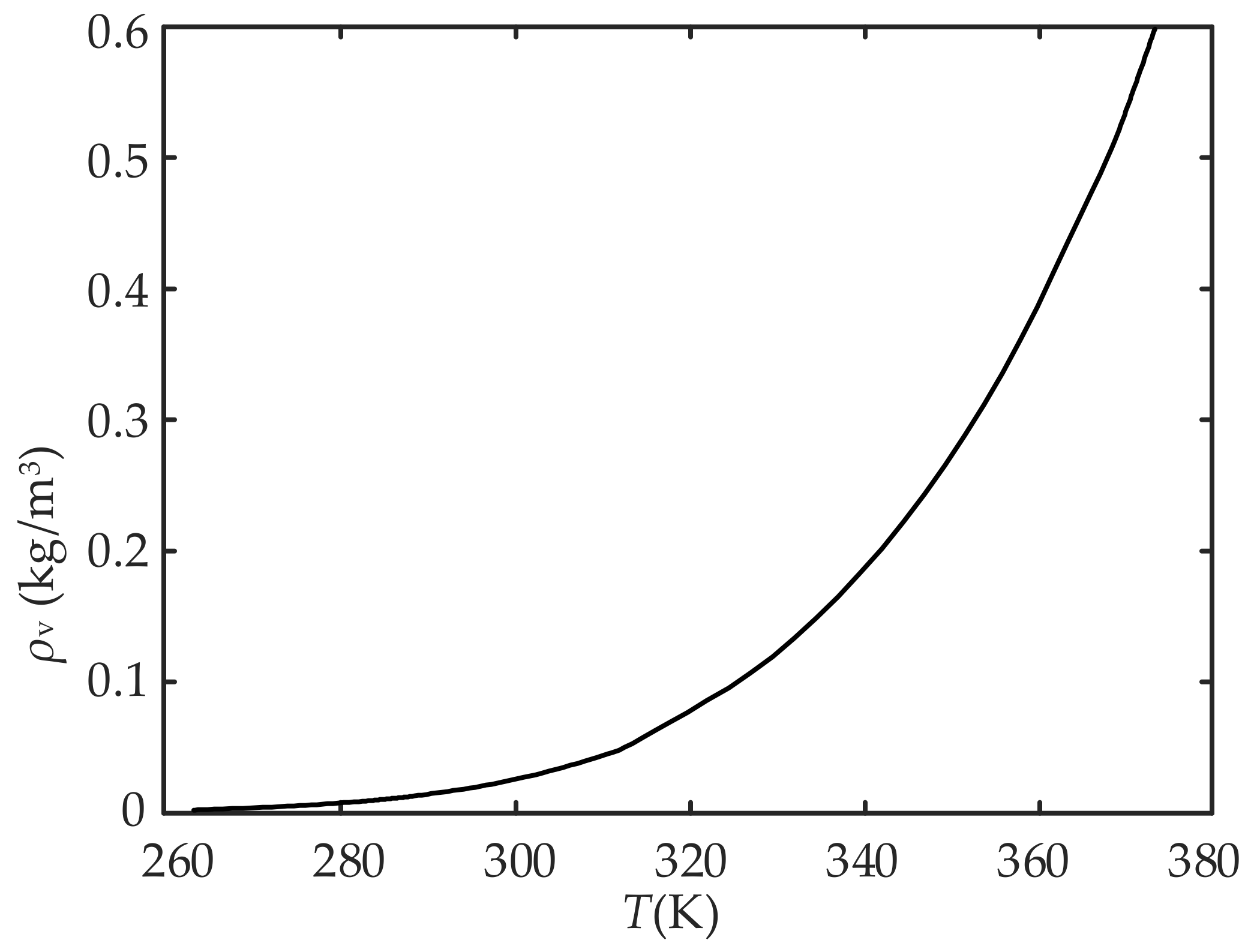
- Since De is affected by temperature, the diffusion Equation (2) is coupled with temperature. The relationship between De and temperature is written as follows [25]:
2.2.2. Process B
3. Decoupling-Based Dynamic Compensation Method
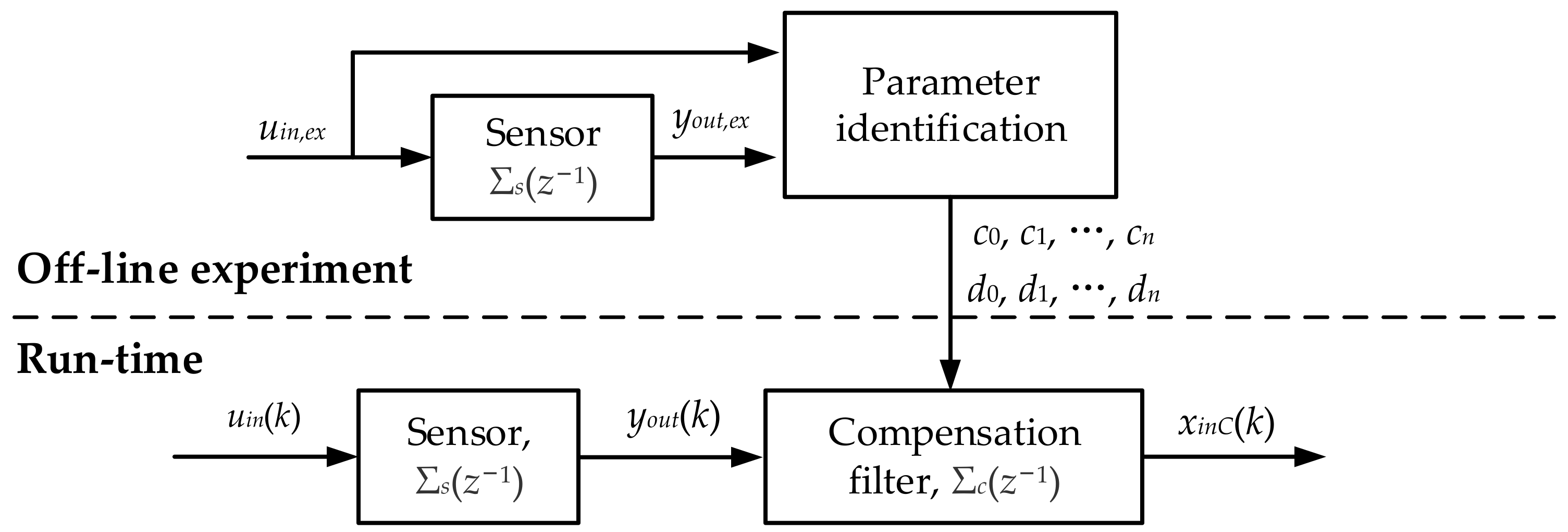
3.1. The Principle of Dynamic Compensation for LTI System
3.2. Solving the Compensation System
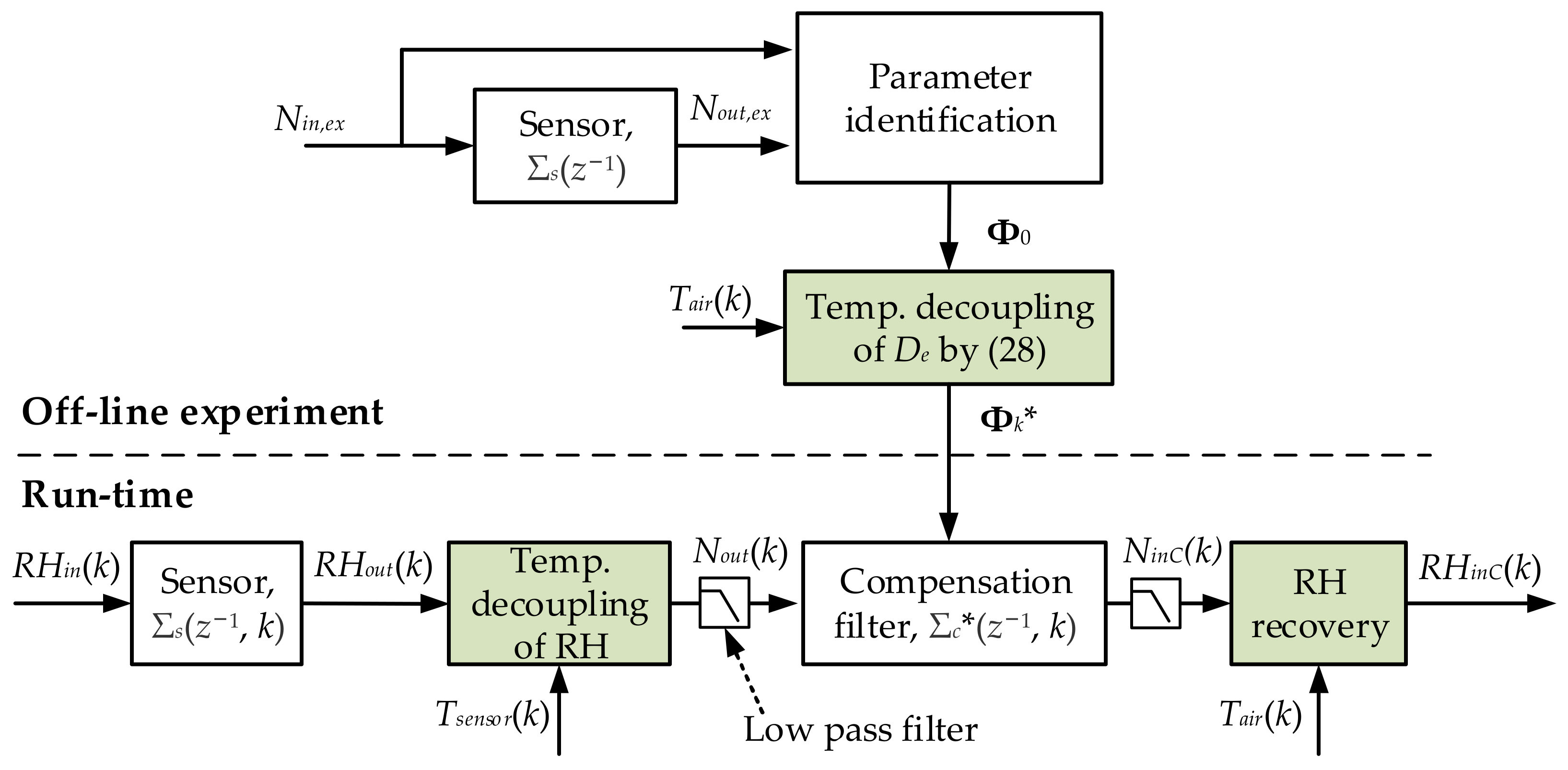
3.3. Dynamic Compensation Based on Temperature and Humidity Decoupling
3.3.1. Temperature Decoupling of RH
3.3.2. Temperature Decoupling of De
4. Simulations and Experiments
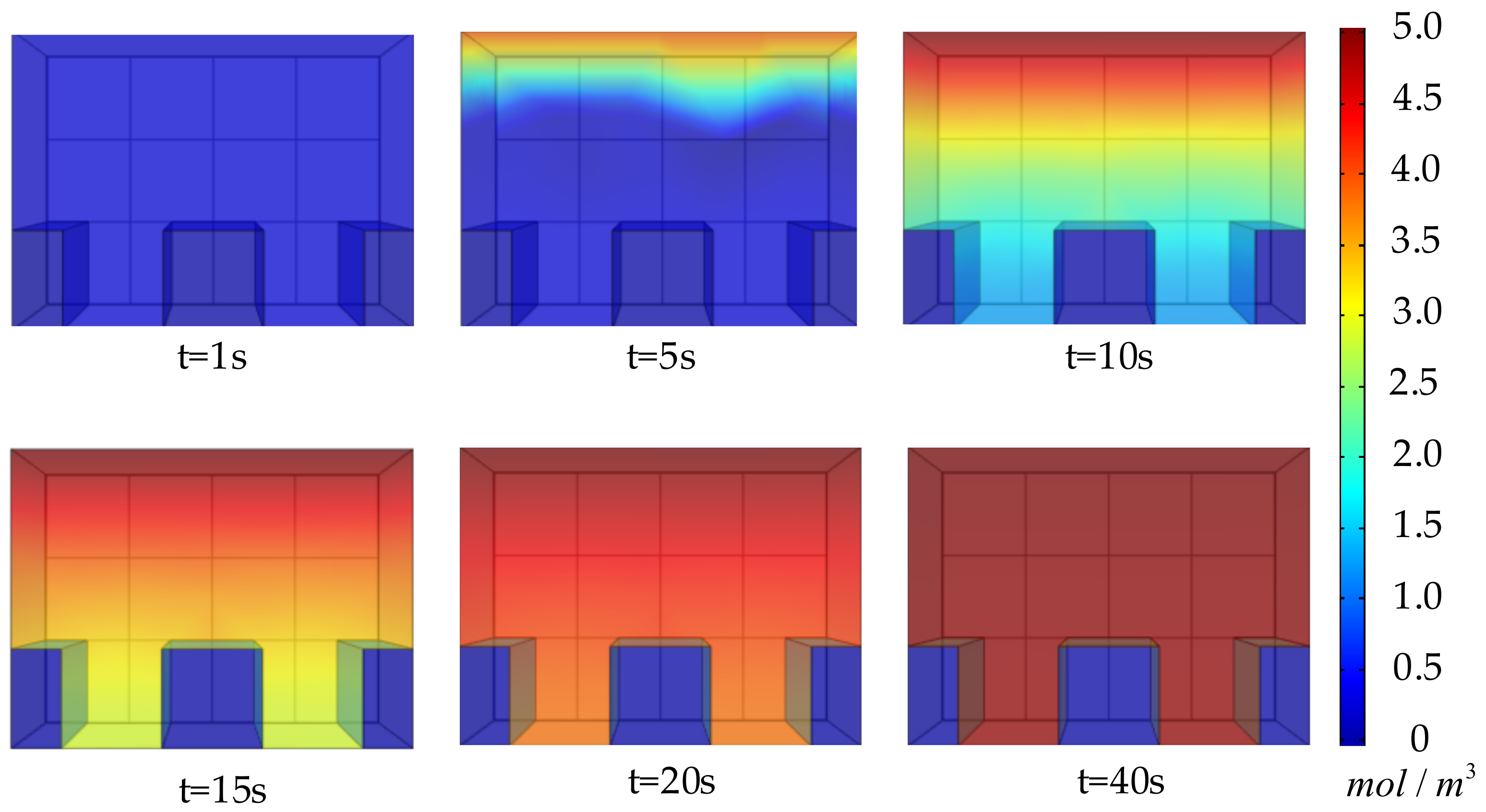
4.1. Simulations
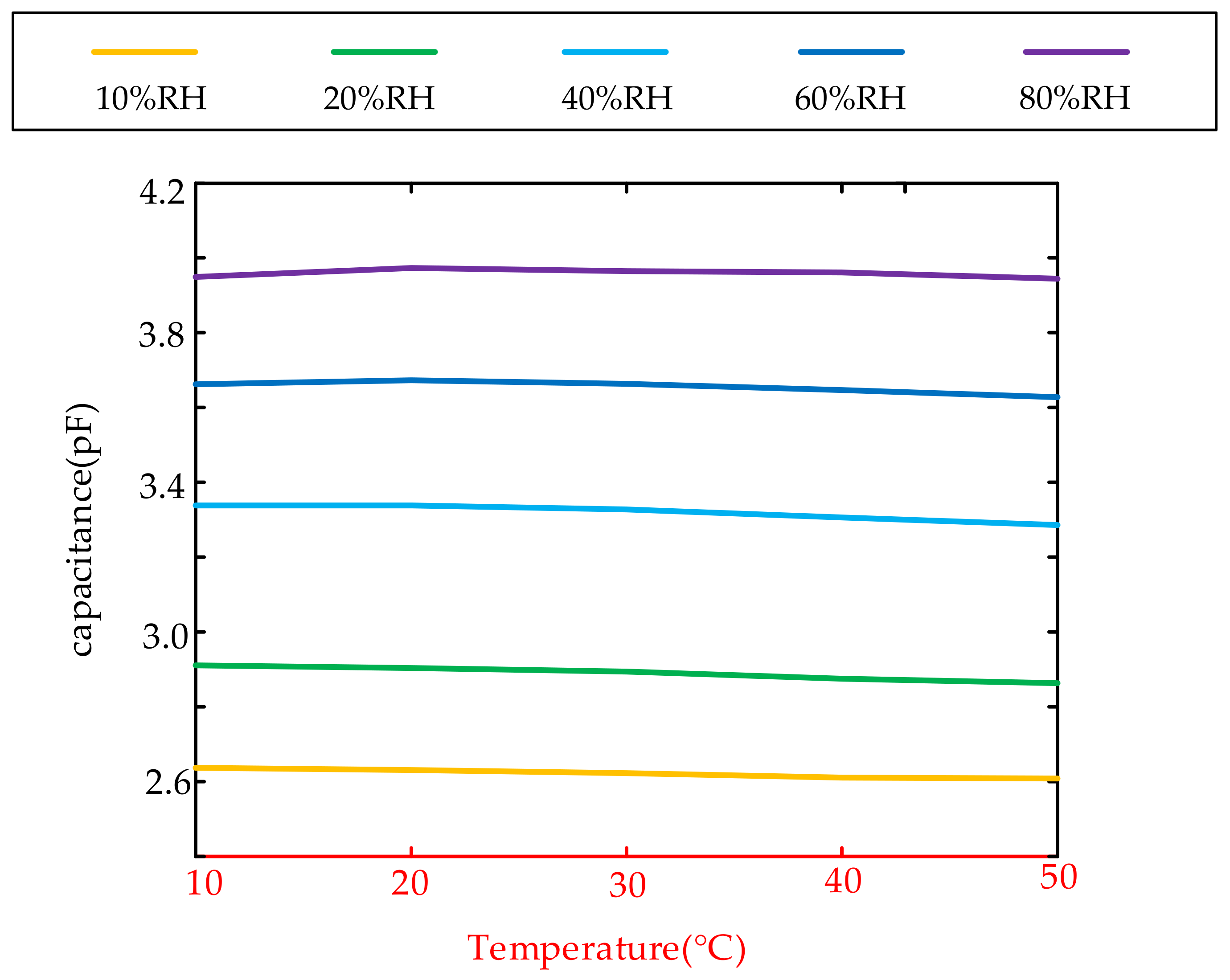
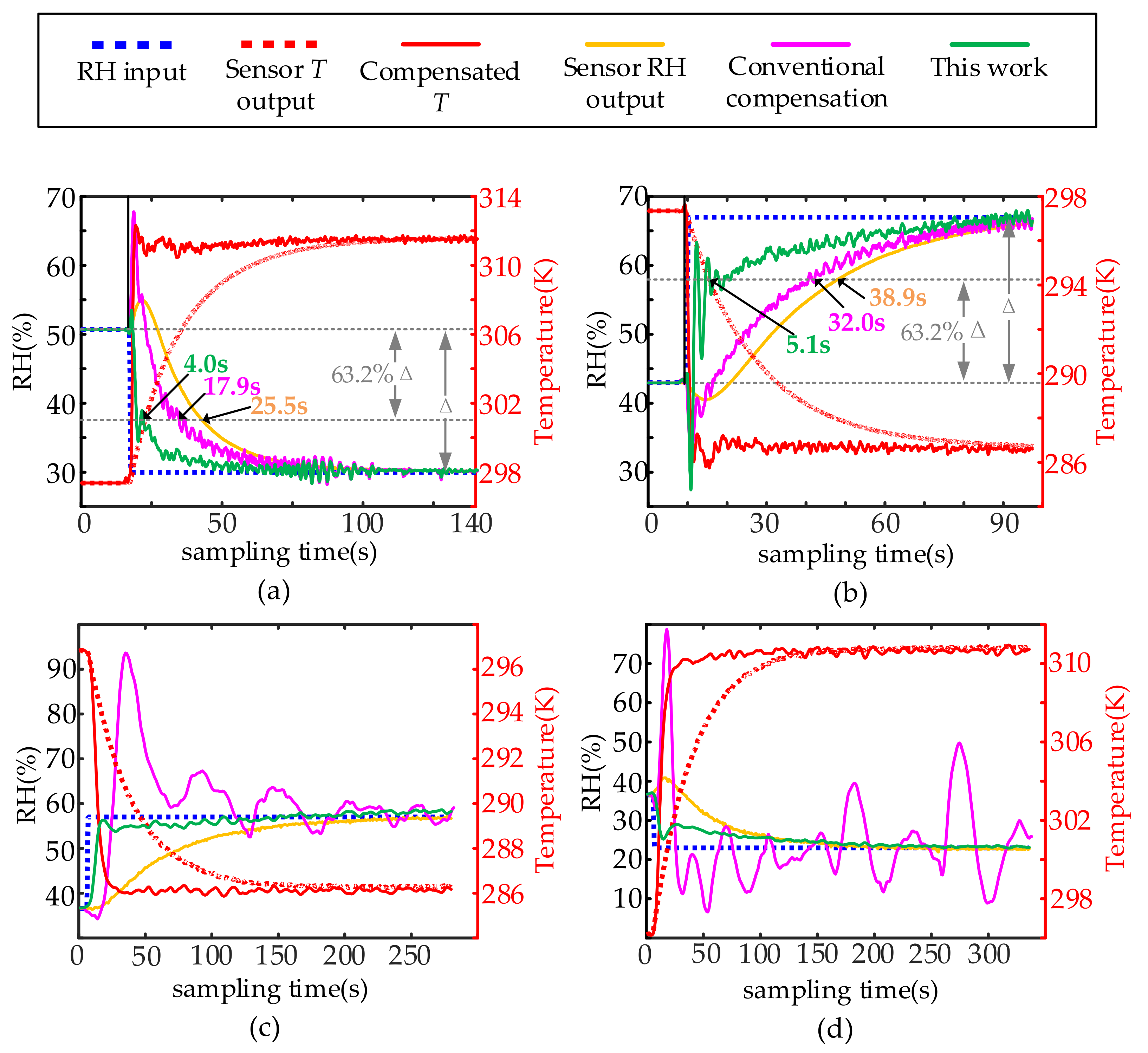
4.2. Experiments
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farahani, H.; Wagiran, R.; Hamidon, M. Humidity Sensors Principle, Mechanism, and Fabrication Technologies: A Comprehensive Review. Sensors 2014, 14, 7881–7939. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.Q.; Wang, C.; Kim, N.Y. High-Sensitivity and Low-Hysteresis Porous MIM-Type Capacitive Humidity Sensor Using Functional Polymer Mixed with TiO2 Microparticles. Sensors 2017, 17, 0284. [Google Scholar]
- Saeidi, N.; Strutwolf, J.; Marechal, A.; Demosthenous, A.; Donaldson, N. A capacitive humidity sensor suitable for cmos integration. IEEE Sens. J. 2013, 13, 4487–4495. [Google Scholar] [CrossRef]
- Jamila, B.; Matthias, S.; Hanns-Erik, E.; Andreas, D.; Ignaz, E.; Christoph, K.; Peter, M.B. Polyimide-based capacitive humidity sensor. Sensors 2018, 18, 1516. [Google Scholar]
- Dokmeci, M.; Najafi, K. A high-sensitivity polyimide capacitive relative humidity sensor for monitoring anodically bonded hermetic micropackages. J. Microelectromech. Syst. 2001, 10, 197–204. [Google Scholar] [CrossRef]
- Kalkan, A.K.; Li, H.; O’Brien, C.J.; Fonash, S.J. A rapid-response, high-sensitivity nanophase humidity sensor for respiratory monitoring. IEEE Electron Device Lett. 2004, 25, 526–528. [Google Scholar] [CrossRef]
- Qi, Q.; Tong, Z.; Wang, S.; Zheng, X. Humidity sensing properties of KCl-doped ZnO nanofibers with super-rapid response and recovery. Sens. Actuators B Chem. 2009, 137, 649–655. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, X.; Tang, N.; Fang, Y.; Zhang, H.; Duan, X. Rapid response flexible humidity sensor for respiration monitoring using nano-confined strategy. Nanotechnology 2020, 31, 125302. [Google Scholar] [CrossRef]
- Shen, D.; Xiao, M.; Xiao, Y.; Zou, G.; Hu, L.; Zhao, B.; Liu, L.; Duley, W.W.; Zhou, Y.N. Self-Powered, Rapid-Response and Highly Flexible Humidity Sensors Based on Moisture-Dependent Voltage Generation. ACS Appl. Mater. Interfaces 2019, 11, 14249–14255. [Google Scholar] [CrossRef]
- Dai, J.; Zhao, H.; Lin, X.; Liu, S.; Liu, Y.; Liu, X.; Fei, T.; Zhang, T. Ultrafast Response Polyelectrolyte Humidity Sensor for Respiration Monitoring. ACS Appl. Mater. Interfaces 2019, 11, 6483–6490. [Google Scholar] [CrossRef]
- Kang, U.; Wise, K.D. A high-speed capacitive humidity sensor with on-chip thermal reset. IEEE Trans. Electron Devices 1999, 47, 702–710. [Google Scholar] [CrossRef]
- Mittal, U.; Islam, T.; Nimal, A.T.; Sharma, M.U. A Novel Sol-Gel γ-Al2O3 Thin-Film-Based Rapid SAW Humidity Sensor. IEEE Trans. Electron Devices 2015, 62, 4242–4250. [Google Scholar] [CrossRef]
- Tomer, V.K.; Nishanthi, S.T.; Gahlot, S.; Kailasam, K. Cubic mesoporous Ag@CN: A high performance humidity sensor. Nanoscale 2016, 8, 19794–19803. [Google Scholar] [CrossRef]
- Itoh, E.; Takada, A. Fabrication of fast, highly sensitive all-printed capacitive humidity sensors with carbon nanotube/polyimide hybrid electrodes. Jpn. J. Appl. Phys. 2016, 55, 02BB10. [Google Scholar] [CrossRef]
- Subbarao, N.; Gedda, M.; Iyer, P.K.; Goswami, D.K. Organic field-effect transistors as high performance humidity sensors with rapid response, recovery time and remarkable ambient stability. Org. Electron. 2016, 32, 169–178. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, Y.; Li, Z.; Huang, J.; Wang, Y.; Wu, J.; He, H. Rapid response and recovery humidity sensor based on CoTiO3 thin film prepared by RF magnetron co-sputtering with post annealing process. Ceram. Int. 2015, 41, 15176–15184. [Google Scholar] [CrossRef]
- Lyubchik, L.M. Dynamic Sensors Distortion Compensation by Means of Input Estimation Algorithms. In Intelligent Components and Instruments for Control Applications; Pergamon: Oxford, UK, 1994; pp. 211–216. [Google Scholar]
- Schoen, M.P. Dynamic Compensation of Intelligent Sensors. IEEE Trans. Instrum. Meas. 2007, 56, 1992–2001. [Google Scholar] [CrossRef]
- Jafaripanah, M.; Al-Hashimi, B.M.; White, N.M. Application of Analog Adaptive Filters for Dynamic Sensor Compensation. IEEE Trans. Instrum. Meas. 2005, 54, 245–251. [Google Scholar] [CrossRef]
- Yu, D.; Fang, L.; Lai, P.Y.; Wu, A. Nonlinear Dynamic Compensation of Sensors Using Inverse-Model-Based Neural Network. IEEE Trans. Instrum. Meas. 2008, 57, 2364–2376. [Google Scholar]
- Zimmerschied, R.; Isermann, R. Nonlinear time constant estimation and dynamic compensation of temperature sensors. Control. Eng. Pract. 2010, 18, 300–310. [Google Scholar] [CrossRef]
- Yang, S.L.; Yang, R.; Zha, F.Y.; Liu, H.D.; Xu, K.J. Dynamic compensation method based on system identification and error-overrun mode correction for strain force sensor. Mech. Syst. Signal Processing 2020, 140, 106649. [Google Scholar] [CrossRef]
- Fan, Y.; Kong, D.; Lin, K. Accurate measurement of high-frequency blast waves through dynamic compensation of miniature piezoelectric pressure sensors. Sens. Actuators A Phys. 2018, 280, 14–23. [Google Scholar]
- Xu, K.J.; Cheng, L.; Zhu, Z.N. Dynamic Modeling and Compensation of Robot Six-Axis Wrist Force/Torque Sensor. IEEE Trans. Instrum. Meas. 2007, 56, 2094–2100. [Google Scholar] [CrossRef]
- Wanga, L.B.; Wakayama, N.I.; Okada, T. Numerical simulation of enhancement of mass transfer in the cathode electrode of a PEM fuel cell by magnet particles deposited in the cathode-side catalyst layer. Chem. Eng. Sci. 2005, 60, 4453–4467. [Google Scholar] [CrossRef]
- Shibata, H.; Ito, M.; Asakursa, M.; Watanabe, K. A Digital Hygrometer Using a Polyimi Film Relative Humiditv Sensor. IEEE Trans. Instrum. Meas. 1996, 45, 564–569. [Google Scholar] [CrossRef] [Green Version]




| Materials | Thermal Diffusivity (m2/s) | Water Molecular Diffusivity (m2/s) |
|---|---|---|
| Polyimide | 6.55 × 10−8 | 2.20 × 10−14 |
| Silicon | 9.07 × 10−5 | - |
| Silicon oxide | 3.60 × 10−6 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Li, W.; Lu, H.; Liu, J.; Zhang, T. Dynamic Compensation Method for Humidity Sensors Based on Temperature and Humidity Decoupling. Sensors 2022, 22, 7229. https://doi.org/10.3390/s22197229
Yang W, Li W, Lu H, Liu J, Zhang T. Dynamic Compensation Method for Humidity Sensors Based on Temperature and Humidity Decoupling. Sensors. 2022; 22(19):7229. https://doi.org/10.3390/s22197229
Chicago/Turabian StyleYang, Wenxuan, Wenchang Li, Huaxiang Lu, Jian Liu, and Tianyi Zhang. 2022. "Dynamic Compensation Method for Humidity Sensors Based on Temperature and Humidity Decoupling" Sensors 22, no. 19: 7229. https://doi.org/10.3390/s22197229
APA StyleYang, W., Li, W., Lu, H., Liu, J., & Zhang, T. (2022). Dynamic Compensation Method for Humidity Sensors Based on Temperature and Humidity Decoupling. Sensors, 22(19), 7229. https://doi.org/10.3390/s22197229




