Modeling and Performance Analysis of Large-Scale Backscatter Communication Networks with Directional Antennas
Abstract
:1. Introduction
- In contrast to prior related studies focusing on the performance of Omn-BackCom Nets, we first identify Dir-BackCom Nets. Then, we establish a theoretical model to analyze the performance of Dir-BackCom Nets. This model is general for BackCom Nets equipped with omn-directional antennas or directional antennas.
- We derive both the connectivity and the spatial throughput of Dir-BackCom Nets. Results indicate that the spatial throughput can be maximized by selecting an optimal density of BTs.
- We make a comparison of the performance among Dir-BackCom Nets, Omn-BackCom Nets, and networks in which BTs and BRs are equipped with directional antennas and omni-directional antennas, respectively, called Dir-Omn-BackCom Nets. Our results indicate that equipping directional antennas at BTs or BR can improve network performance. Moreover, we perform a comparison of performance among Dir-BackCom Nets equipped with different directional antennas with varied antenna beamwidths and antenna gains. Results show that the performance of Dir-BackCom Nets can be improved by choosing suitable directional antennas with proper antenna beamwidths and gains of the main lobe.
2. System Models
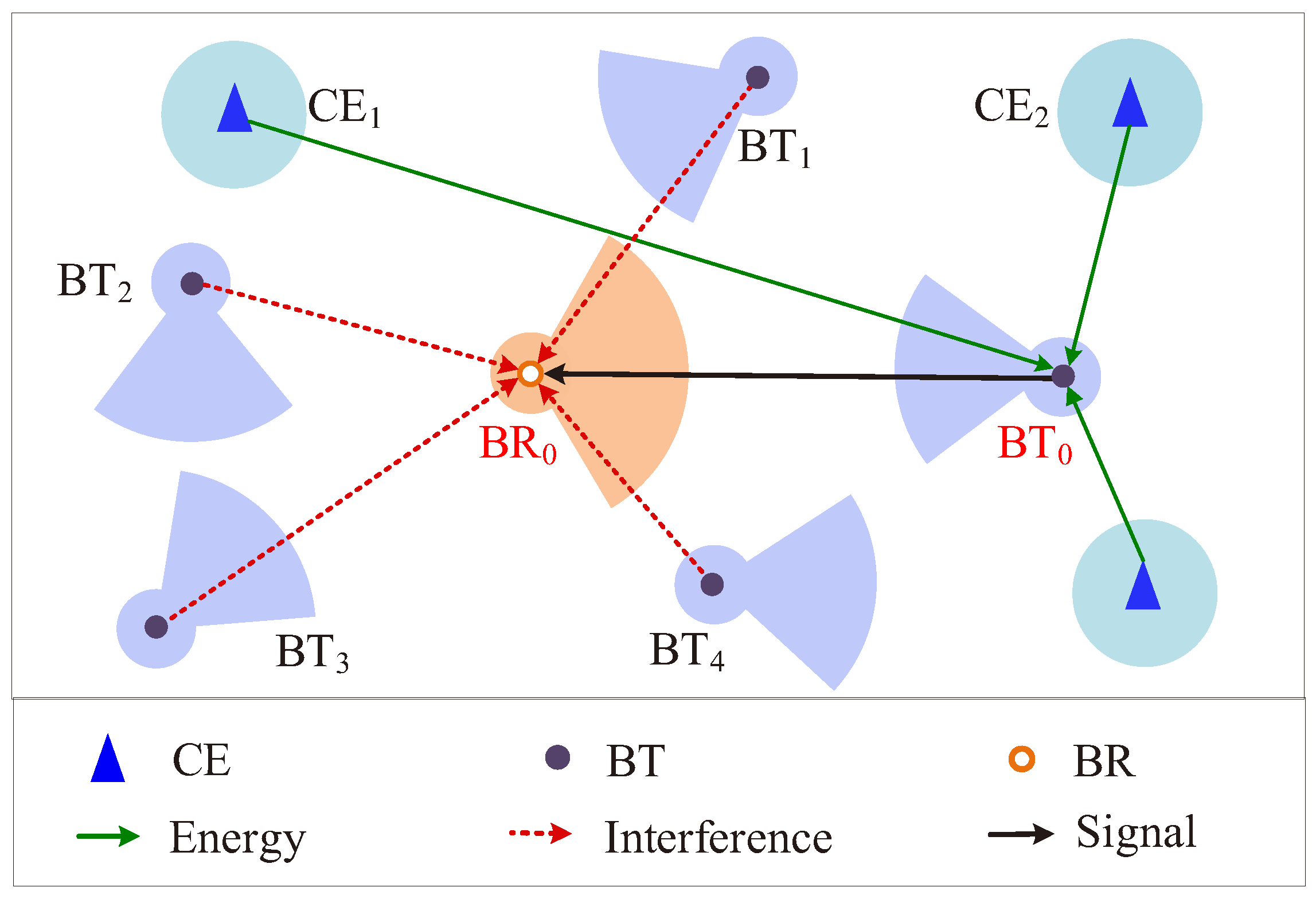
2.1. Network Model
2.2. Channel Model
2.3. Antenna Model
2.4. Backscatter Communication Model
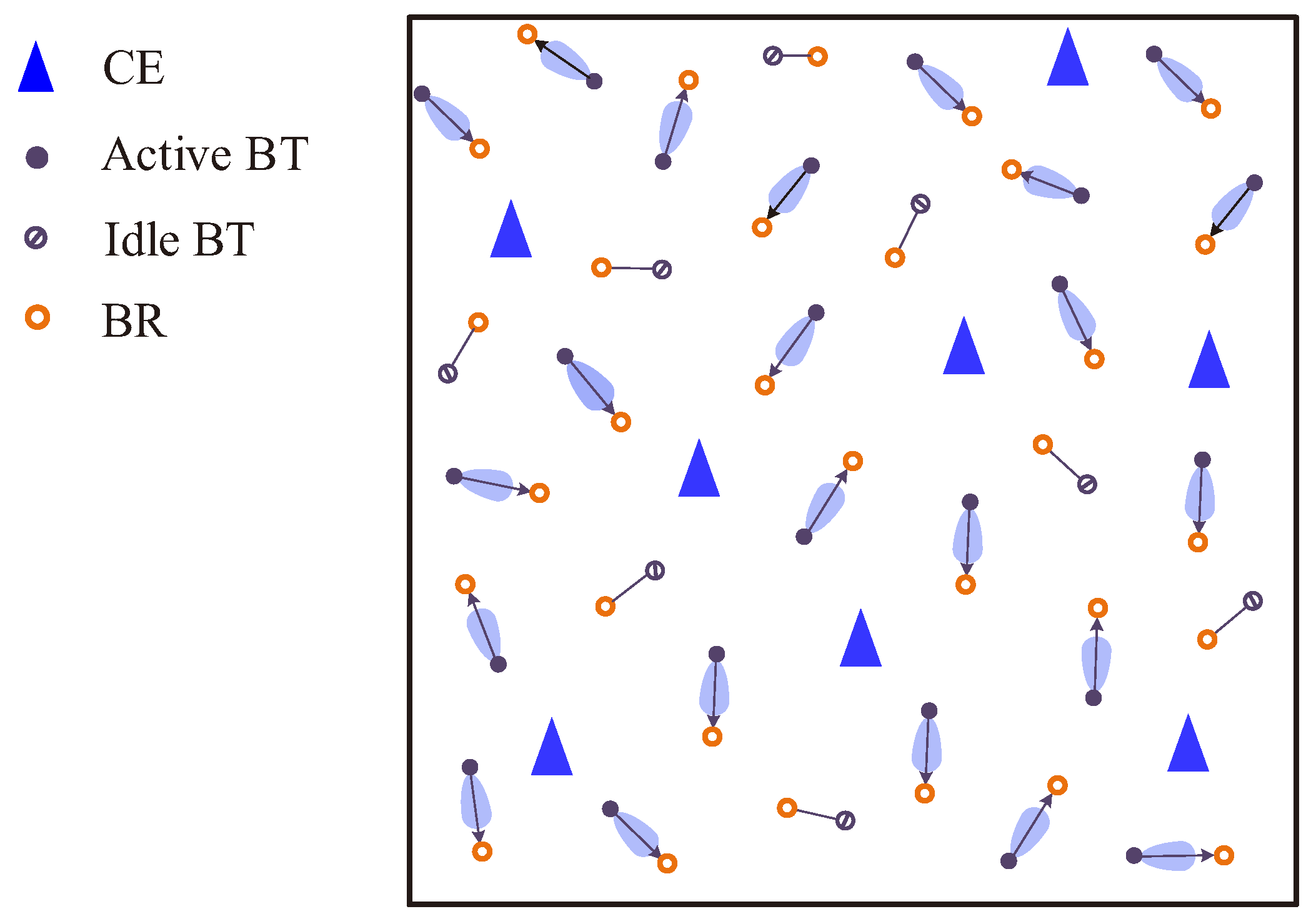
3. Connectivity
- The BT can receive sufficient power to activate backscatter communications.
- The signal reflected from the BT can be successfully received by the BR.
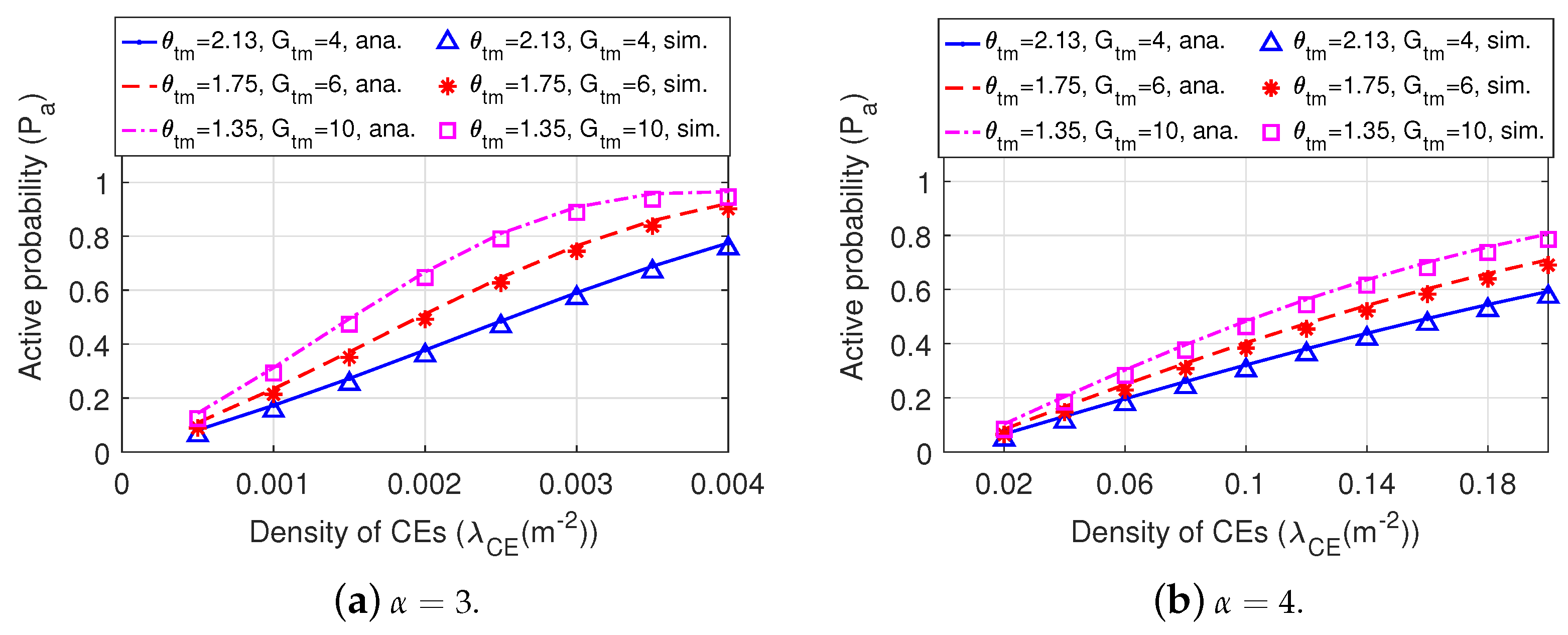
3.1. Active Probability
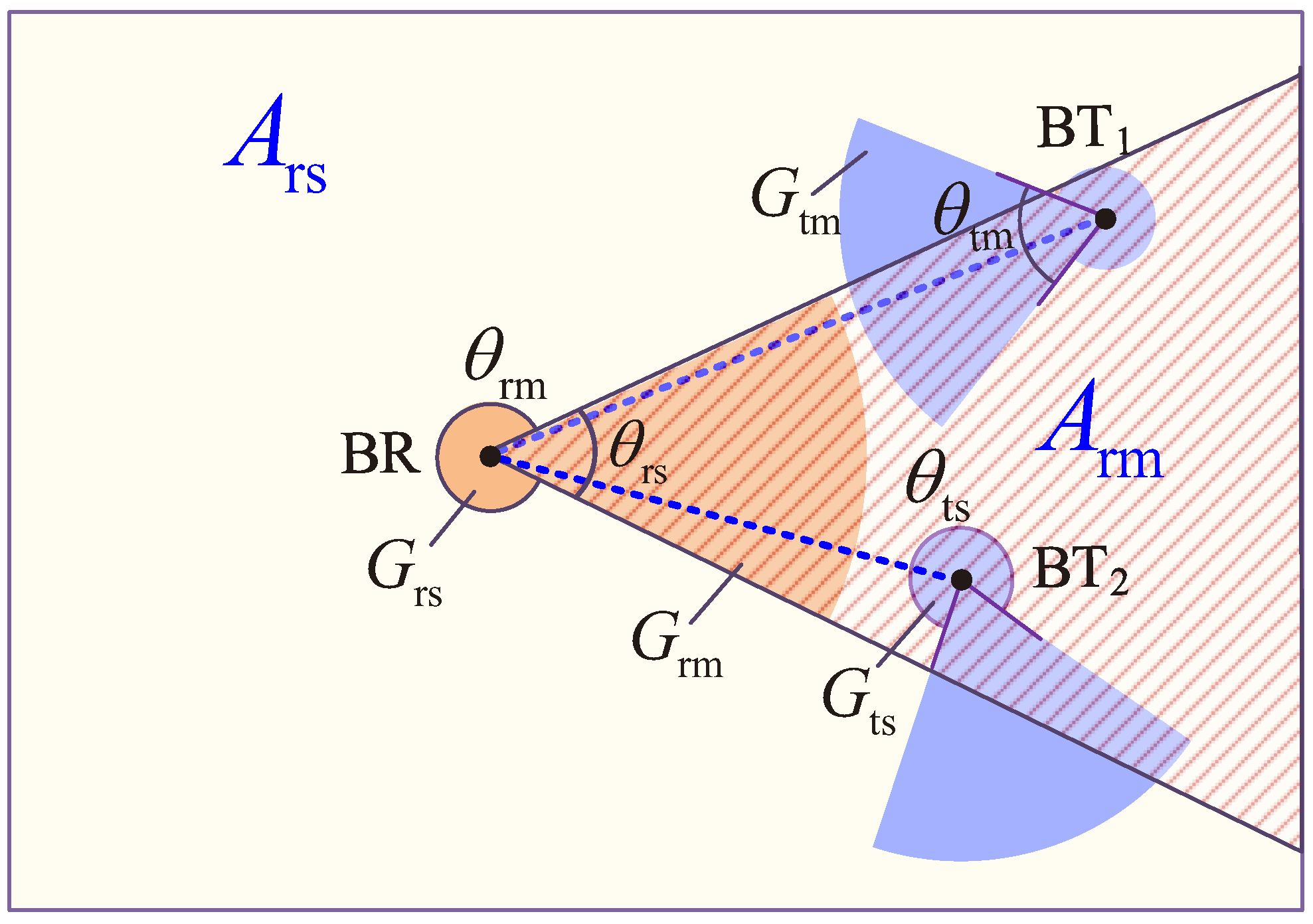
- The region in which a BT receives signals by the main lobe (the shadowed region in Figure 5), named region .
- The region in which a BT receives signals by the side lobe, named region .
3.2. Connectivity
- The region where a BR receives interference by the main lobe within (the shadowed region in Figure 6), named region ;
- The region where a BR receives interference by the side lobe within , named region .
4. Network Throughput
5. Simulations and Numerical Results
5.1. Comparison among Dir-BackCom Nets, Dir-Omn-BackCom Nets, and Omn-BackCom Nets
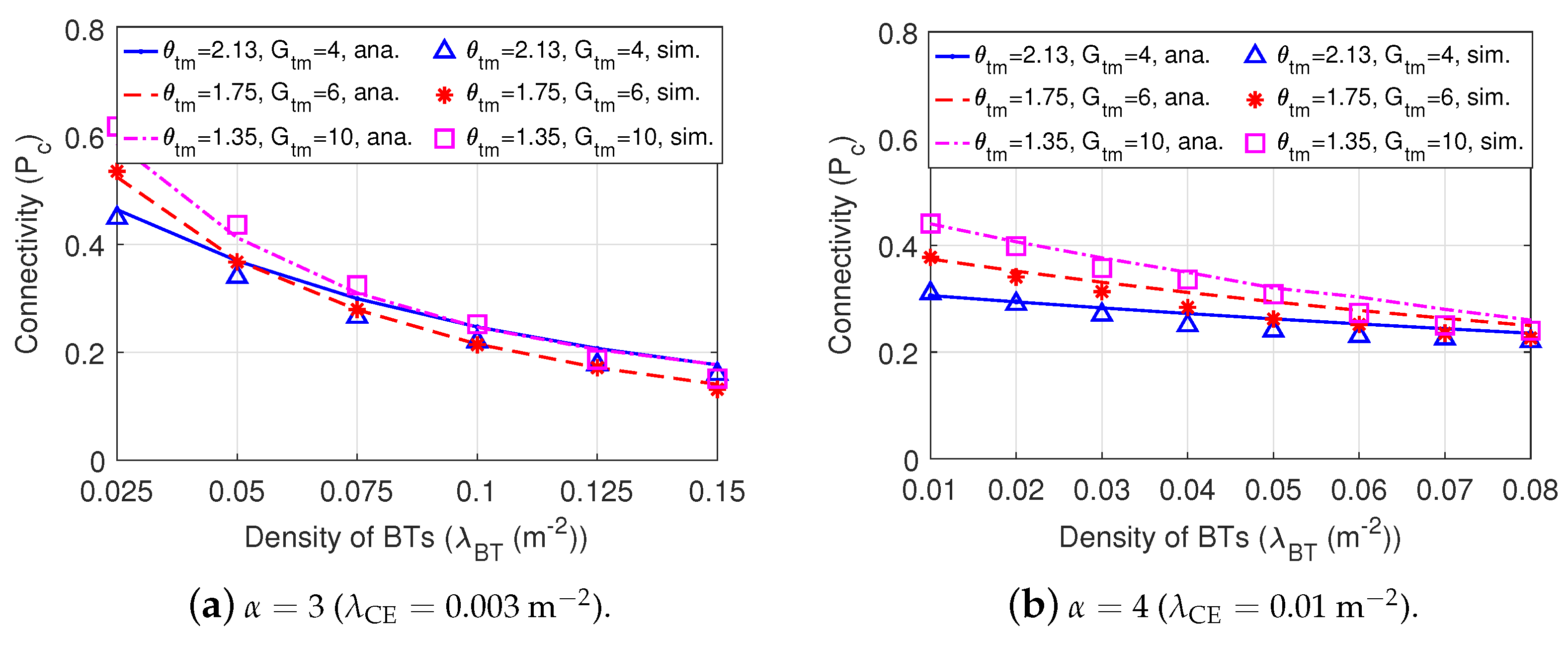
5.2. Comparison among Dir-BackCom Nets with Different Directional Antennas
6. Conclusions
- Equipping directional antennas instead of omni-directional antenna at BTs can improve the active probability.
- Employing directional antennas at either BTs or BRs can improve the connectivity and spatial throughput of BackCom Nets.
- The spatial throughput can be maximized by choosing an optimal density of BTs.
- Both the connectivity and spatial throughput of BackCom Nets can be improved by choosing a directional antenna with a proper antenna beamwidth and gain of the main lobe.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BackCom | Backscatter communication; |
| BackCom Net | Backscatter communication network; |
| RF | Radio frequency; |
| IoT | Internet of things; |
| BT | Backscatter transmitter; |
| CE | Carrier emitter; |
| BR | Backscatter receiver; |
| WPT | Wireless power transfer; |
| RFID | Radio frequency identification; |
| HPPP | Homogeneous Poisson point process; |
| UCA | Uniform circular array; |
| HPBW | Half-power beamwidth; |
| CDF | Cumulative distribution function; |
| Probability density function; | |
| SINR | Signal-to-interference-noise-ratio; |
| PGFL | Probability generating functional; |
Appendix A. Deviation of the Antenna Gain of the Keyhole Antenna Model
Appendix B. Proof of Proposition 1
Appendix C. Proof of Proposition 2
Appendix D. Proof of Lemma 1
Appendix E. Proof of Theorem 2
References
- Toro, U.S.; Wu, K.; Leung, V.C.M. Backscatter Wireless Communications and Sensing in Green Internet of Things. IEEE Trans. Green Commun. Netw. 2022, 6, 37–55. [Google Scholar] [CrossRef]
- Rayhana, R.; Xiao, G.G.; Liu, Z. Printed Sensor Technologies for Monitoring Applications in Smart Farming: A Review. IEEE Trans. Instrum. Meas. 2021, 70, 1–19. [Google Scholar] [CrossRef]
- Liu, W.; Huang, K.; Zhou, X.; Durrani, S. Next generation backscatter communication: Systems, techniques, and applications. EURASIP J. Wirel. Commun. Netw. 2019, 69. [Google Scholar] [CrossRef]
- Ye, Y.; Shi, L.; Chu, X.; Lu, G. On the Outage Performance of Ambient Backscatter Communications. IEEE Internet Things J. 2020, 7, 7265–7278. [Google Scholar] [CrossRef]
- Daskalakis, S.N.; Assimonis, S.D.; Kampianakis, E.; Bletsas, A. Soil Moisture Scatter Radio Networking with Low Power. IEEE Trans. Microw. Theory Tech. 2016, 64, 2338–2346. [Google Scholar] [CrossRef]
- Shi, L.; Hu, R.Q.; Ye, Y.; Zhang, H. Modeling and Performance Analysis for Ambient Backscattering Underlaying Cellular Networks. IEEE Trans. Veh. Technol. 2020, 69, 6563–6577. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, Y.; Dai, H.N.; Zhang, G.; Zhang, W. Performance on Cluster Backscatter Communication Networks with Coupled Interferences. IEEE Internet Things J. 2022. [Google Scholar] [CrossRef]
- Lu, X.; Jiang, H.; Niyato, D.; Kim, D.I.; Han, Z. Wireless-Powered Device-to-Device Communications with Ambient Backscattering: Performance Modeling and Analysis. IEEE Trans. Wirel. Commun. 2018, 17, 1528–1544. [Google Scholar] [CrossRef]
- Han, K.; Huang, K. Wirelessly Powered Backscatter Communication Networks: Modeling, Coverage, and Capacity. IEEE Trans. Wirel. Commun. 2017, 16, 2548–2561. [Google Scholar] [CrossRef]
- Han, D.; Minn, H. Coverage Probability Analysis Under Clustered Ambient Backscatter Nodes. IEEE Wirel. Commun. Lett. 2019, 8, 1713–1717. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Salehi, M.; Haenggi, M.; Hossain, E.; Jiang, H. Stochastic Geometry Analysis of Spatial-Temporal Performance in Wireless Networks: A Tutorial. IEEE Commun. Surv. Tutor. 2021, 23, 2753–2801. [Google Scholar] [CrossRef]
- Hmamouche, Y.; Benjillali, M.; Saoudi, S.; Yanikomeroglu, H.; Renzo, M.D. New Trends in Stochastic Geometry for Wireless Networks: A Tutorial and Survey. Proc. IEEE 2021, 109, 1200–1252. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, H.M.; Zheng, T.X.; Han, Z.; Lee, M.H. Wireless Powered Asynchronous Backscatter Networks With Sporadic Short Packets: Performance Analysis and Optimization. IEEE Internet Things J. 2018, 5, 984–997. [Google Scholar] [CrossRef]
- Zhu, K.; Xu, L.; Niyato, D. Distributed Resource Allocation in RF-Powered Cognitive Ambient Backscatter Networks. IEEE Trans. Green Commun. Netw. 2021, 5, 1657–1668. [Google Scholar] [CrossRef]
- Xu, L.; Zhu, K.; Wang, R.; Gong, S. Performance analysis of ambient backscatter communications in RF-powered cognitive radio networks. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar]
- Balanis, C.A. Antenna Theory: Analysis and Design, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2005. [Google Scholar]
- Wang, Q.; Dai, H.N.; Zheng, Z.; Imran, M.; Vasilakos, A.V. On Connectivity of Wireless Sensor Networks with Directional Antennas. Sensors 2017, 17, 134. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Dai, H.N.; Georgiou, O.; Shi, Z.; Zhang, W. Connectivity of Underlay Cognitive Radio Networks With Directional Antennas. IEEE Trans. Veh. Technol. 2018, 67, 7003–7017. [Google Scholar] [CrossRef]
- Shafi, M.; Molisch, A.F.; Smith, P.J.; Haustein, T.; Zhu, P.; De Silva, P.; Tufvesson, F.; Benjebbour, A.; Wunder, G. 5G: A Tutorial Overview of Standards, Trials, Challenges, Deployment, and Practice. IEEE J. Sel. Areas Commun. 2017, 35, 1201–1221. [Google Scholar] [CrossRef]
- Vaezi, M.; Azari, A.; Khosravirad, S.R.; Shirvanimoghaddam, M.; Azari, M.M.; Chasaki, D.; Popovski, P. Cellular, Wide-Area, and Non-Terrestrial IoT: A Survey on 5G Advances and the Road Towards 6G. IEEE Commun. Surv. Tutor. 2022, 24, 1117–1174. [Google Scholar] [CrossRef]
- Nitsche, T.; Cordeiro, C.; Flores, A.; Knightly, E.W.; Perahia, E.; Widmer, J.C. IEEE 802.11ad: Directional 60 GHz communication for multi-Gigabit-per-second Wi-Fi. IEEE Commun. Mag. 2014, 52, 132–141. [Google Scholar] [CrossRef]
- Bettstetter, C. On the Connectivity of Ad Hoc Networks. Comput. J. 2004, 47, 432–447. [Google Scholar] [CrossRef] [Green Version]
- Jeon, Y.; Gil, G.T.; Lee, Y.H. Design and Analysis of LoS-MIMO Systems With Uniform Circular Arrays. IEEE Trans. Wirel. Commun. 2021, 20, 4527–4540. [Google Scholar] [CrossRef]
- Kornprobst, J.; Mittermaier, T.J.; Mauermayer, R.A.M.; Hamberger, G.F.; Ehrnsperger, M.G.; Lehmeyer, B.; Ivrlaŏ, M.T.; Imberg, U.; Eibert, T.F.; Nossek, J.A. Compact Uniform Circular Quarter-Wavelength Monopole Antenna Arrays with Wideband Decoupling and Matching Networks. IEEE Trans. Antennas Propag. 2021, 69, 769–783. [Google Scholar] [CrossRef]
- Hu, D.; Zhang, Y.; He, L.; Wu, J. Low-Complexity Deep-Learning-Based DOA Estimation for Hybrid Massive MIMO Systems With Uniform Circular Arrays. IEEE Wirel. Commun. Lett. 2020, 9, 83–86. [Google Scholar] [CrossRef]
- Wang, Q.; Dai, H.N.; Wang, Q.; Shukla, M.K.; Zhang, W.; Soares, C.G. On Connectivity of UAV-Assisted Data Acquisition for Underwater Internet of Things. IEEE Internet Things J. 2020, 7, 5371–5385. [Google Scholar] [CrossRef]
- Azimi-Abarghouyi, S.M.; Makki, B.; Nasiri-Kenari, M.; Svensson, T. Stochastic Geometry Modeling and Analysis of Finite Millimeter Wave Wireless Networks. IEEE Trans. Veh. Technol. 2019, 68, 1378–1393. [Google Scholar] [CrossRef]
- Bai, T.; Heath, R.W. Coverage and Rate Analysis for Millimeter-Wave Cellular Networks. IEEE Trans. Wirel. Commun. 2015, 14, 1100–1114. [Google Scholar] [CrossRef]
- Van Huynh, N.; Hoang, D.T.; Lu, X.; Niyato, D.; Wang, P.; Kim, D.I. Ambient Backscatter Communications: A Contemporary Survey. IEEE Commun. Surv. Tutor. 2018, 20, 2889–2922. [Google Scholar] [CrossRef]
- Song, X.; Chin, K.W. A Novel Hybrid Access Point Channel Access Method for Wireless-Powered IoT Networks. IEEE Internet Things J. 2021, 8, 12329–12338. [Google Scholar] [CrossRef]
- Zargari, S.; Khalili, A.; Wu, Q.; Robat Mili, M.; Ng, D.W.K. Max-Min Fair Energy-Efficient Beamforming Design for Intelligent Reflecting Surface-Aided SWIPT Systems With Non-Linear Energy Harvesting Model. IEEE Trans. Veh. Technol. 2021, 70, 5848–5864. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, X. Secure Resource Allocation for Polarization-Based Non-Linear Energy Harvesting over 5G Cooperative Cognitive Radio Networks. In Proceedings of the IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Boshkovska, E.; Ng, D.W.K.; Zlatanov, N.; Schober, R. Practical Non-Linear Energy Harvesting Model and Resource Allocation for SWIPT Systems. IEEE Commun. Lett. 2015, 19, 2082–2085. [Google Scholar] [CrossRef] [Green Version]
- Haenggi, M. Stochastic Geometry for Wireless Networks, 1st ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Lee, S.; Zhang, R.; Huang, K. Opportunistic Wireless Energy Harvesting in Cognitive Radio Networks. IEEE Trans. Wirel. Commun. 2013, 12, 4788–4799. [Google Scholar] [CrossRef]
- Konstantopoulos, C.; Koutroulis, E.; Mitianoudis, N.; Bletsas, A. Converting a Plant to a Battery and Wireless Sensor with Scatter Radio and Ultra-Low Cost. IEEE Trans. Instrum. Meas. 2016, 65, 388–398. [Google Scholar] [CrossRef]
- Rezaei, O.; Naghsh, M.M.; Rezaei, Z.; Zhang, R. Throughput Optimization for Wireless Powered Interference Channels. IEEE Trans. Wirel. Commun. 2019, 18, 2464–2476. [Google Scholar] [CrossRef]
- Bettstetter, C.; Hartmann, C.; Moser, C. How does randomized beamforming improve the connectivity of ad hoc networks? In Proceedings of the IEEE International Conference on Communications (ICC 2005), Seoul, Korea, 16–20 May 2005; Volume 5, pp. 3380–3385. [Google Scholar]
- Andrews, J.G.; Baccelli, F.; Ganti, R.K. A Tractable Approach to Coverage and Rate in Cellular Networks. IEEE Trans. Commun. 2011, 59, 3122–3134. [Google Scholar] [CrossRef]
- Cohen, A.M. Numerical Methods for Laplace Transform Inversion, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 5. [Google Scholar]
- Sakr, A.H.; Hossain, E. Cognitive and Energy Harvesting-Based D2D Communication in Cellular Networks: Stochastic Geometry Modeling and Analysis. IEEE Trans. Commun. 2015, 63, 1867–1880. [Google Scholar] [CrossRef] [Green Version]
- Chiu, S.N.; Stoyan, D.; Kendall, W.S.; Mecke, J. Stochastic Geometry and Its Applications, 3rd ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]







| Parameters | Values |
|---|---|
| The number of available frequency channels (N) | 5 |
| The transmitted power of CEs () | dBm [7] |
| The reflection coefficient () | [7,8] |
| The power of noise () | dBm [7,8] |
| The threshold of SINR () | 5 dB [7] |
| The power threshold for activating the circuits | |
| of backscatter communications () | W [36] |
| The saturated energy power at the energy harvester () | W [37] |
| The factors in the energy harvester | , [37] |
| Dir-BackCom Nets | Dir-Omn-BackCom Nets | Omn-BackCom Nets | |
|---|---|---|---|
| BTs | Directional antennas | Directional antennas | Omni-directional antennas |
| BRs | Directional antennas | Omni-directional antennas | Omni-directional antennas |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Zhou, Y. Modeling and Performance Analysis of Large-Scale Backscatter Communication Networks with Directional Antennas. Sensors 2022, 22, 7260. https://doi.org/10.3390/s22197260
Wang Q, Zhou Y. Modeling and Performance Analysis of Large-Scale Backscatter Communication Networks with Directional Antennas. Sensors. 2022; 22(19):7260. https://doi.org/10.3390/s22197260
Chicago/Turabian StyleWang, Qiu, and Yong Zhou. 2022. "Modeling and Performance Analysis of Large-Scale Backscatter Communication Networks with Directional Antennas" Sensors 22, no. 19: 7260. https://doi.org/10.3390/s22197260
APA StyleWang, Q., & Zhou, Y. (2022). Modeling and Performance Analysis of Large-Scale Backscatter Communication Networks with Directional Antennas. Sensors, 22(19), 7260. https://doi.org/10.3390/s22197260





