Research on Monocular-Vision-Based Finger-Joint-Angle-Measurement System
Abstract
1. Introduction
2. Biological Structure of Human Fingers and Their Movement Characteristics
2.1. Structural Composition of the Human Hand
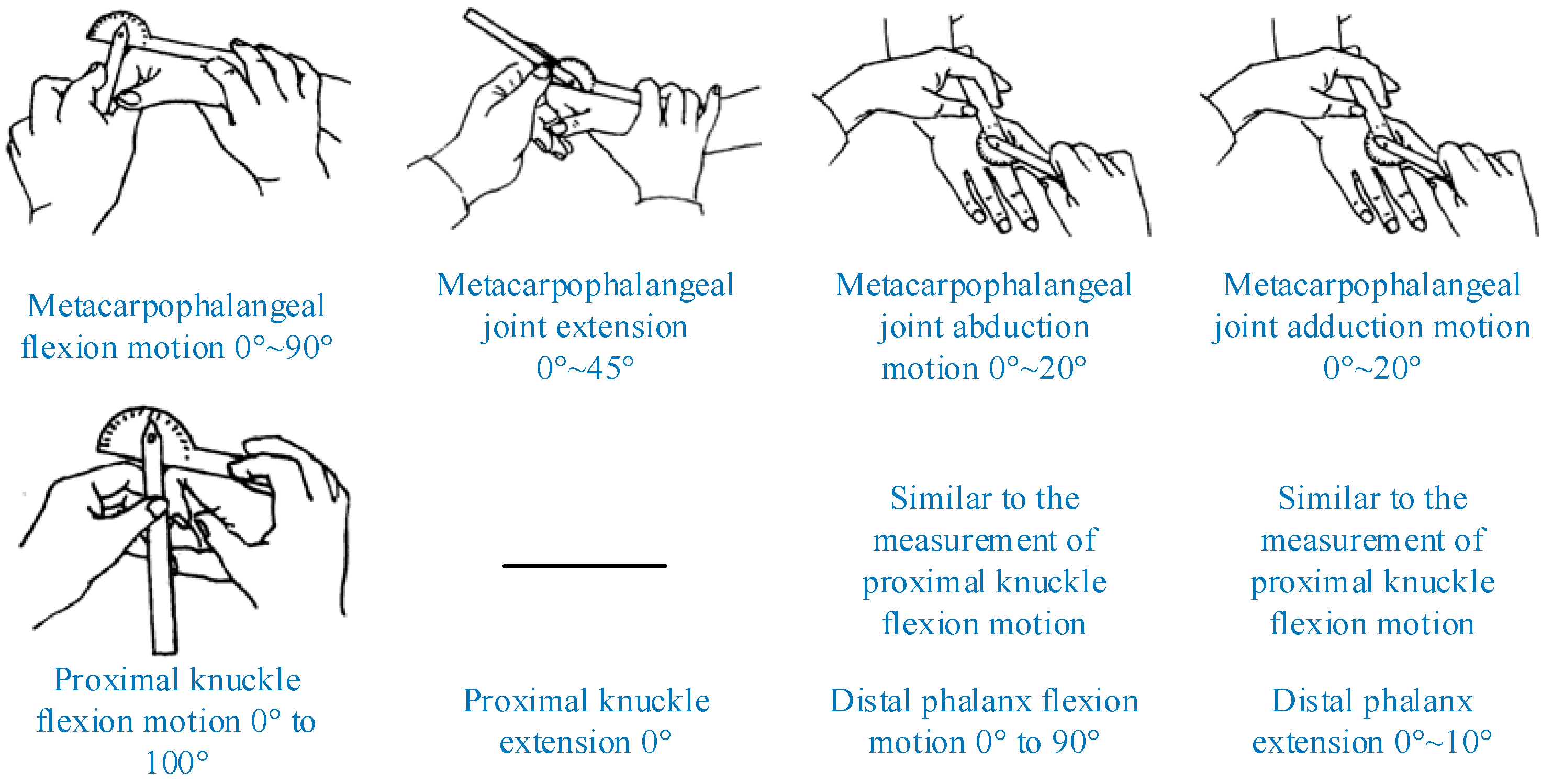
2.2. Finger-Movement Characteristics
3. Experimental-Platform Construction
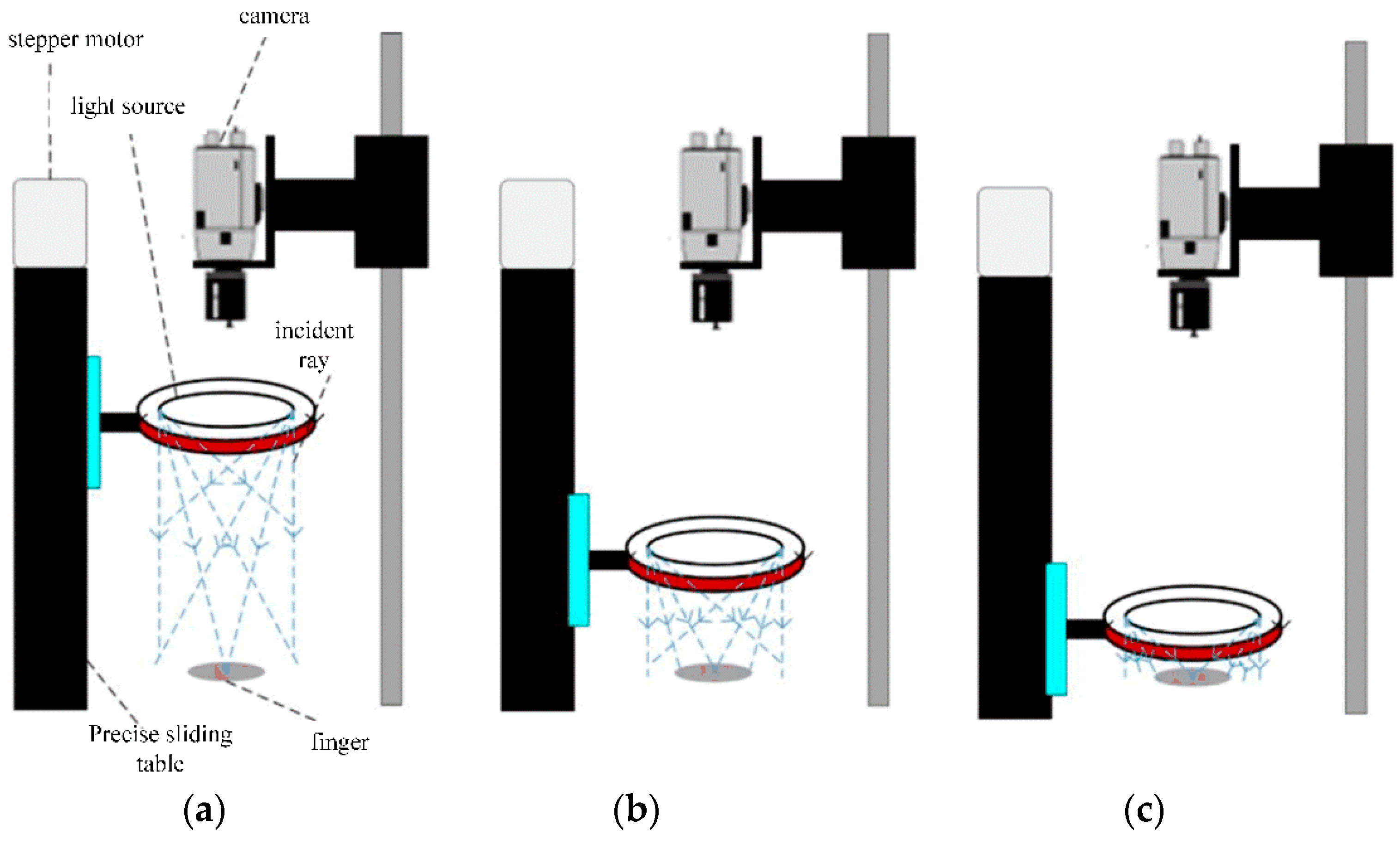
3.1. Design of Experimental Platform
3.2. Light-Source Selection and Solution of the Single-Reflection Matrix
4. Vision-Based Finger-Joint-Angle-and-Length-Detection Method
4.1. Vision-Based Finger-Joint-Angle-and-Length-Detection Method
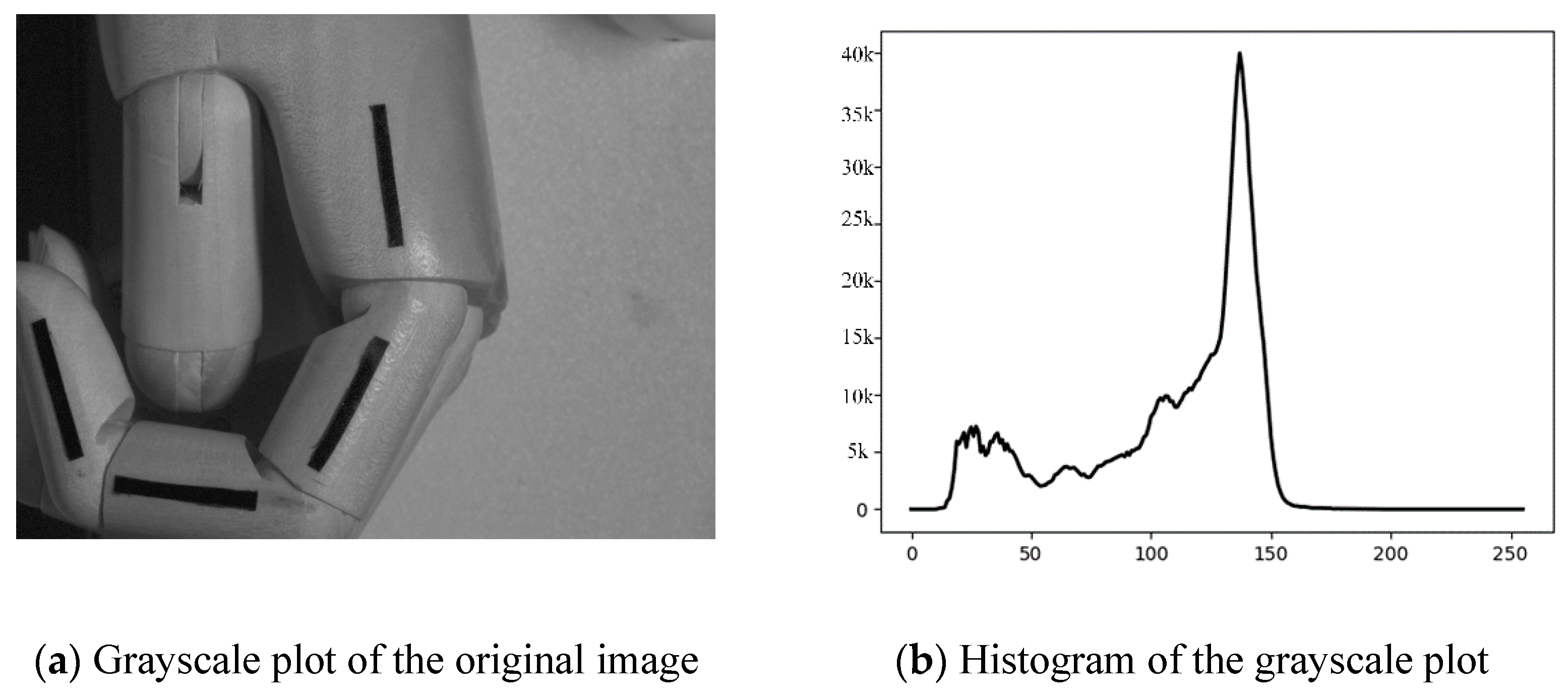
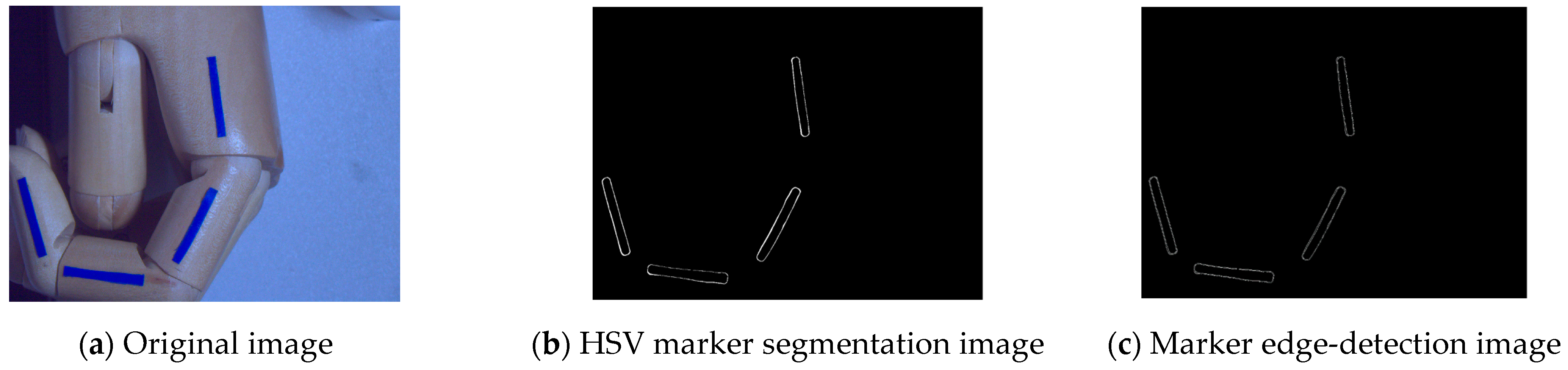
4.2. Visual Marker Segmentation Methods
- (1)
- HSV color-space-marker-segmentation extraction with Canny edge detection
- (2)
- Image thresholding method with edge-contour extraction
4.3. Joint-Angle-Calculation Method Based on Different Joint Identifiers of the Finger
- (1)
- Hough straight-line detection method for inner and outer edges
- (2)
- Least-squares fitting of the target identifier profile
- (3)
- Finger-joint-angle-calculation method
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Okuyama, T.; Kobayashi, K.; Otsuki, M.; Tanaka, M. Measurement of finger joint angle using a flexible polymer sensor. Int. J. Appl. Electromagn. Mech. 2016, 52, 951–957. [Google Scholar] [CrossRef]
- Park, W.; Ro, K.; Kim, S.; Bae, J. A soft sensor-based three-dimensional (3-D) finger motion measurement system. Sensors 2017, 17, 420. [Google Scholar] [CrossRef] [PubMed]
- Kawaguchi, J.; Yoshimoto, S.; Kuroda, Y.; Oshiro, O. Estimation of finger joint angles based on electromechanical sensing of wrist shape. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 25, 1409–1418. [Google Scholar] [CrossRef] [PubMed]
- Kitano, K.; Ito, A.; Tsujiuchi, N.; Wakida, S. Estimation of joint center and measurement of finger motion by inertial sensors. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 5668–5671. [Google Scholar]
- Zheng, Y.; Peng, Y.; Wang, G.; Liu, X.; Dong, X.; Wang, J. Development and evaluation of a sensor glove for hand function assessment and preliminary attempts at assessing hand coordination. Measurement 2016, 93, 1–12. [Google Scholar] [CrossRef]
- Veber, M.; Bajd, T.; Munih, M. Assessing joint angles in human hand via optical tracking device and calibrating instrumented glove. Meccanica 2007, 42, 451–463. [Google Scholar] [CrossRef]
- Lu, S.; Chen, D.; Liu, C.; Jiang, Y.; Wang, M. A 3-D finger motion measurement system via soft strain sensors for hand rehabilitation. Sens. Actuators A Phys. 2019, 285, 700–711. [Google Scholar] [CrossRef]
- Park, Y.; Lee, J.; Bae, J. Development of a wearable sensing glove for measuring the motion of fingers using linear potentiometers and flexible wires. IEEE Trans. Ind. Inform. 2014, 11, 198–206. [Google Scholar] [CrossRef]
- Park, Y.; Bae, J. A three-dimensional finger motion measurement system of a thumb and an index finger without a calibration process. Sensors 2020, 20, 756. [Google Scholar] [CrossRef] [PubMed]
- Jang, M.; Kim, J.S.; Kang, K.; Kim, J.; Yang, S. Towards Finger Motion Capture System Using FBG Sensors. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 3734–3737. [Google Scholar]
- Metcalf, C.D.; Robinson, R.; Malpass, A.J.; Bogle, T.P.; Dell, T.A.; Harris, C.; Demain, S.H. Markerless motion capture and measurement of hand kinematics: Validation and application to home-based upper limb rehabilitation. IEEE Trans. Biomed. Eng. 2013, 60, 2184–2192. [Google Scholar] [CrossRef] [PubMed]
- Pham, T.; Pathirana, P.N.; Trinh, H.; Fay, P. A non-contact measurement system for the range of motion of the hand. Sensors 2015, 15, 18315–18333. [Google Scholar] [CrossRef] [PubMed]
- Simon, T.; Joo, H.; Matthews, I.; Sheikh, Y. Hand keypoint detection in single images using multiview bootstrapping. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4645–4653. [Google Scholar]
- Mathis, A.; Mamidanna, P.; Cury, K.M.; Abe, T.; Murthy, V.N.; Mathis, M.W.; Bethge, M. Deeplabcut: Markerless pose estimation of user-defined body parts with deep learning. Nat. Neurosci. 2018, 21, 1281–1289. [Google Scholar] [CrossRef] [PubMed]
- Oikonomidis, P.I.; Argyros, A. Using a single rgb frame for real time 3d hand pose estimation in the wild. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 436–445. [Google Scholar]
- Tung, J.Y.; Lulic; Gonzalez, D.A.; Tran, J.; Dickerson, C.R.; Roy, A.E.A. Evaluation of a portable markerless finger position capture device: Accuracy of the leap motion controller in healthy adults. Physiol. Meas. 2015, 36, 1025–1035. [Google Scholar] [CrossRef] [PubMed]
- Nizamis, K.; Rijken, N.H.M.; Mendes, A.; Janssen, M.M.H.P.; Bergsma, A.; Koopman, B.F.J.M. A novel setup and protocol to measure the range of motion of the wrist and the hand. Sensors 2018, 18, 3230. [Google Scholar] [CrossRef] [PubMed]
- Lim, G.M.; Jatesiktat, P.; Kuah, C.W.K.; Ang, W.T. Camera-based hand tracking using a mirror-based multi-view setup. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 5789–5793. [Google Scholar]
- Lee, J.W.; Rim, K. Measurement of finger joint angles and maximum finger forces during cylinder grip activity. J. Biomed. Eng. 1991, 13, 152–162. [Google Scholar] [CrossRef]
- Zhu, J.J.; Ji, W.; Hua, Q. An automatic vision inspection system for detecting surface cracks of welding joint. J. Comput. Methods Sci. Eng. 2019, 19, 635–646. [Google Scholar] [CrossRef]
- Zhang, H. Mechanical and Control System Design of Finger Training Rehabilitation Apparatus; Yanshan University: Qinhuangdao, China, 2016. [Google Scholar]
- Zotin, A. Fastalgorithm of image enhancement based on nulti-scale retinex. Procedia Comput. Sci. 2018, 131, 6–14. [Google Scholar] [CrossRef]
- Kruseaw, A.W.; Alenin, A.S.; Vaughni, I.J.; Tyo, J.S. Perceptually uniform color space for visualizing trivariate linear polarization imaging data. Opt. Lett. 2018, 43, 2426–2429. [Google Scholar] [CrossRef] [PubMed]
- Abbas, A.K.; Bassam, R. Phonocardiography signal processing. Morgan Claypool 2009, 4, 218. [Google Scholar]
- Papadaniil, C.D.; Hadjileontiadis, L.J. Efficient heart sound segmentation and extraction using ensemble empirical mode decomposition and kurtosis features. IEEE J. Biomed. Health Inform. 2014, 18, 1138–1152. [Google Scholar] [CrossRef]






| HSV + Hough Outer- and Inner-Straight-Line Method | HSV + Least-Squares-Fitting Linear-Knuckle-Angle-Detection Method | Threshold Segmentation + Hough Outer Medial Linear-Detection Method | Threshold-Segmentation + Least-Squares-Fitting-Line Method | Traditional Knuckle-Angle Measurement | |
|---|---|---|---|---|---|
| MCP | 145.02° | 144.76° | 144.95° | 144.59° | 145° |
| PIP | 111.03° | 109.38° | 110.48° | 111.26° | 110° |
| DIP | 111.83° | 114.07° | 112.09° | 112.34° | 112° |
| Length of proximal phalanx | 26.94 mm | 28.24 mm | 27.37 mm | 27.32 mm | 27 mm |
| Length of middle phalanx | 25.53 mm | 25.53 mm | 25.64 mm | 25.26 mm | 26 mm |
| Mean Angle deviation | 0.407° | 0.967° | 0.207° | 0.670° |
| MCP (°) | PIP (°) | DIP (°) | |
|---|---|---|---|
| Knuckle-hold angle under each marker | 145 | 110 | 115 |
| 160 | 130 | 110 | |
| 150 | 165 | 130 |
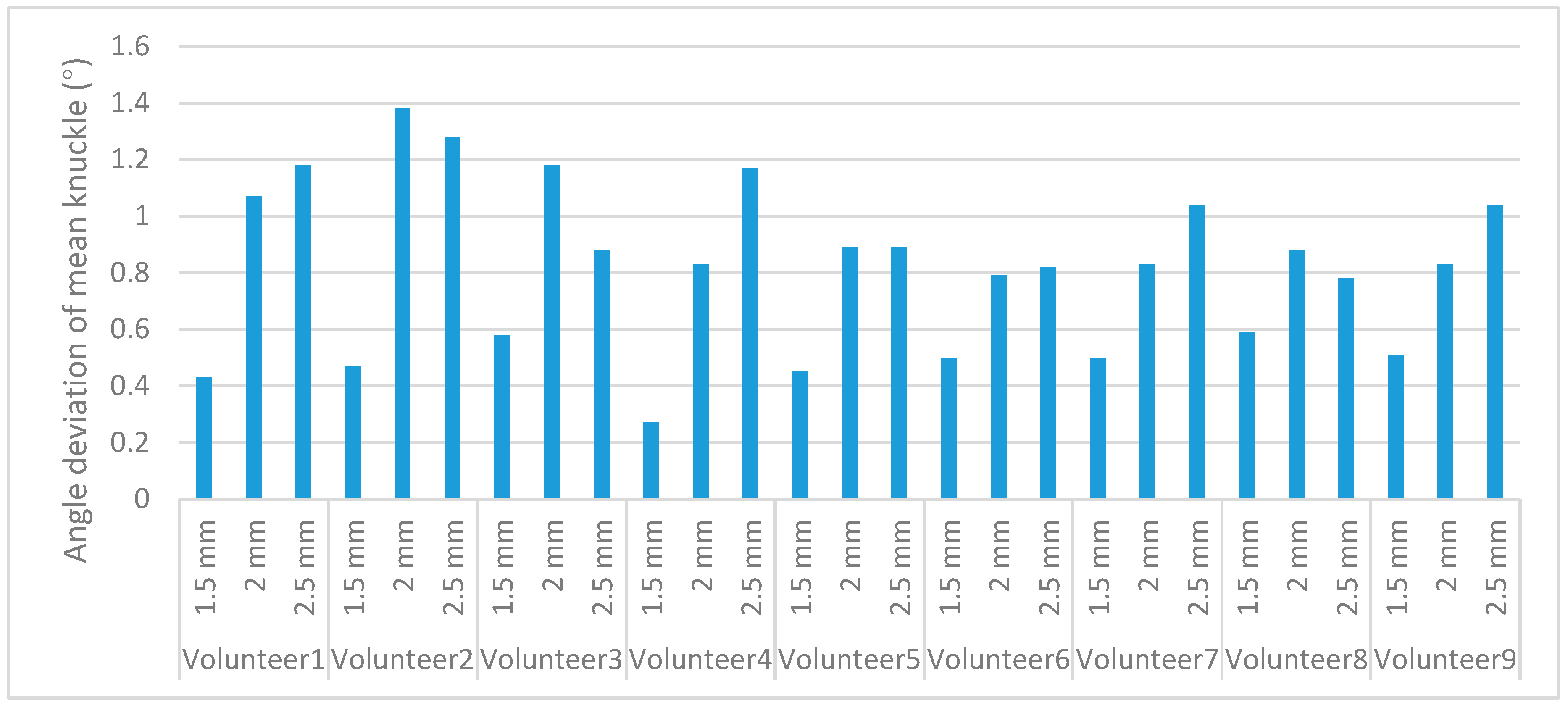
| Volunteer | Mark on the Scale | MCP (°) | PIP (°) | DIP (°) | Length of Proximal Phalanx (mm) | Length of Middle Phalanx (mm) |
|---|---|---|---|---|---|---|
| volunteer 1 | 1.5 mm | 144.72 | 109.31 | 115.42 | 45.52 | 30.23 |
| 160.10 | 130.12 | 109.21 | 44.07 | 31.45 | ||
| 149.48 | 165.72 | 130.31 | 45.31 | 30.21 | ||
| 2 mm | 145.21 | 109.10 | 114.42 | 46.21 | 31.03 | |
| 161.71 | 132.22 | 109.71 | 44.71 | 30.15 | ||
| 151.31 | 167.28 | 130.02 | 45.49 | 29.24 | ||
| 2.5 mm | 144.72 | 108.91 | 115.92 | 46.71 | 29.02 | |
| 160.40 | 128.93 | 109.27. | 43.93 | 30.51 | ||
| 147.32 | 164.89 | 133.22 | 46.44 | 29.91. | ||
| volunteer 2 | 1.5 mm | 145.31 | 110.21 | 114.71 | 47.22 | 33.47 |
| 159.27 | 130.31 | 111.31 | 47.31 | 32.17 | ||
| 150.32 | 164.44 | 139.74 | 46.28 | 31.95 | ||
| 2 mm | 143.31 | 110.72 | 116.71 | 46.93 | 33.36 | |
| 160.44 | 129.10 | 110.23 | 47.32 | 32.78 | ||
| 150.77 | 165.69 | 131.21 | 48.91 | 34.19 | ||
| 2.5 mm | 146.21 | 110.79 | 114.49 | 48.31 | 35.66 | |
| 162.99 | 131.44 | 111.22 | 47.76 | 34.54 | ||
| 150.55 | 167.21 | 131.59 | 47.77 | 31.22 | ||
| volunteer 3 | 1.5 mm | 144.81 | 110.47 | 115.69 | 43.17 | 27.49 |
| 160.77 | 130.21 | 110.48 | 44.21 | 26.36 | ||
| 150.06 | 165.56 | 131.81 | 42.89 | 28.91 | ||
| 2 mm | 144.31 | 111.81 | 114.01 | 44.33 | 29.36 | |
| 161.17 | 130.79 | 112.58 | 46.96 | 27.22 | ||
| 150.97 | 163.84 | 130.91 | 45.89 | 26.54 | ||
| 2.5 mm | 146.79 | 110.11 | 115.98 | 43.22 | 27.77 | |
| 160.89 | 129.33 | 111.39 | 45.10 | 29.99 | ||
| 150.34 | 166.79 | 130.44 | 45.78 | 26.53 | ||
| volunteer 4 | 1.5 mm | 145.32 | 110.17 | 114.87 | 45.17 | 30.24 |
| 160.17 | 130.22 | 109.97 | 44.54 | 29.77 | ||
| 150.27 | 164.90 | 131.07 | 45.98 | 29.31 | ||
| 2 mm | 146.32 | 110.54 | 115.94 | 43.33 | 27.45 | |
| 159.12 | 130.84 | 110.95 | 44.54 | 26.79 | ||
| 149.71 | 165.55 | 128.77 | 42.59 | 26.34 | ||
| 2.5 mm | 146.71 | 110.21 | 116.19 | 43.24 | 28.79 | |
| 160.77 | 131.44 | 108.22 | 45.77 | 27.32 | ||
| 151.45 | 165.99 | 130.97 | 43.35 | 28.23 | ||
| volunteer 5 | 1.5 mm | 145.21 | 109.55 | 115.94 | 40.22 | 23.33 |
| 160.56 | 129.53 | 109.84 | 41.57 | 24.35 | ||
| 150.41 | 165.77 | 129.92 | 43.98 | 23.47 | ||
| 2 mm | 145.99 | 109.21 | 116.31 | 42.22 | 25.22 | |
| 160.77 | 131.74 | 109.55 | 41.31 | 24.51 | ||
| 150.22 | 166.33 | 130.44 | 39.45 | 23.91 | ||
| 2.5 mm | 145.97 | 109.22 | 115.33 | 40.58 | 25.33 | |
| 161.44 | 130.55 | 110.89 | 41.32 | 24.56 | ||
| 148.97 | 165.33 | 131.75 | 43.77 | 22.22 | ||
| volunteer 6 | 1.5 mm | 145.31 | 109.12 | 114.33 | 40.12 | 30.21 |
| 160.33 | 130.22 | 109.22 | 44.45 | 29.22 | ||
| 150.22 | 165.72 | 130.33 | 43.43 | 27.34 | ||
| 2 mm | 145.33 | 110.47 | 115.33 | 39.65 | 28.79 | |
| 161.43 | 130.99 | 109.44 | 41.76 | 30.33 | ||
| 150.67 | 165.33 | 131.65 | 42.22 | 30.67 | ||
| 2.5 mm | 146.12 | 110.22 | 115.48 | 45.97 | 30.15 | |
| 158.91 | 130.21 | 110.77 | 42.71 | 31.33 | ||
| 149.23 | 163.47 | 131.22 | 42.45 | 29.78 | ||
| volunteer 7 | 1.5 mm | 145.33 | 110.32 | 116.12 | 36.45 | 27.13 |
| 159.31 | 130.07 | 110.77 | 36.84 | 26.56 | ||
| 150.21 | 165.22 | 129.22 | 37.32 | 26.32 | ||
| 2 mm | 146.71 | 110.42 | 113.41 | 34.78 | 25.72 | |
| 160.12 | 130.65 | 110.89 | 37.77 | 28.23 | ||
| 151.14 | 164.31 | 130.22 | 37.96 | 27.45 | ||
| 2.5 mm | 145.42 | 110.31 | 114.21 | 39.03 | 29.81 | |
| 161.31 | 128.64 | 109.01 | 39.76 | 25.33 | ||
| 152.12 | 166.21 | 129.13 | 38.78 | 25.91 | ||
| volunteer 8 | 1.5 mm | 145.32 | 110.77 | 114.57 | 43.15 | 27.49 |
| 160.74 | 129.22 | 110.10 | 41.33 | 28.27 | ||
| 151.12 | 165.33 | 129.38 | 44.54 | 27.39 | ||
| 2 mm | 145.72 | 110.31 | 116.66 | 42.56 | 29.72 | |
| 159.21 | 131.72 | 110.07 | 42.33 | 27.59 | ||
| 150.56 | 166.77 | 130.33 | 41.12 | 28.23 | ||
| 2.5 mm | 145.32 | 110.07 | 115.21 | 44.45 | 30.02 | |
| 157.42 | 131.72 | 110.99 | 41.75 | 29.67 | ||
| 150.22 | 166.23 | 129.25 | 45.39 | 28.37 | ||
| volunteer 9 | 1.5 mm | 145.31 | 110.23 | 115.76 | 35.46 | 23.57 |
| 160.22 | 130.74 | 110.55 | 34.90 | 24.88 | ||
| 159.31 | 165.21 | 130.90 | 37.04 | 24.42 | ||
| 2 mm | 146.13 | 111.31 | 114.31 | 36.24 | 25.56 | |
| 158.91 | 129.10 | 110.12 | 39.35 | 23.78 | ||
| 149.01 | 165.12 | 131.14 | 37.67 | 24.33 | ||
| 2.5 mm | 143.21 | 109.22 | 115.33 | 38.91 | 24.89 | |
| 160.33 | 131.55 | 107.32 | 37.33 | 26.33 | ||
| 151.33 | 165.77 | 129.22 | 37.57 | 23.91 |
| Volunteer | Knuckle-Angle Measurement | Measuring Angle (°) | Mean Knuckle-Angle Deviation (°) | ||
|---|---|---|---|---|---|
| volunteer 1 | Vmm | 25.73 | 39.21 | 40.39 | 0.63 |
| Tmm | 25 | 40 | 40 | ||
| volunteer 2 | Vmm | 24.32 | 39.03 | 40.41 | 0.68 |
| Tmm | 25 | 40 | 40 | ||
| volunteer 3 | Vmm | 23.91 | 40.71 | 40.51 | 0.77 |
| Tmm | 25 | 40 | 40 | ||
| volunteer 4 | Vmm | 24.41 | 39.93 | 40.33 | 0.33 |
| Tmm | 25 | 40 | 40 | ||
| volunteer 5 | Vmm | 25.22 | 39.35 | 40.61 | 0.49 |
| Tmm | 25 | 40 | 40 | ||
| volunteer 6 | Vmm | 24.12 | 38.77 | 41.12 | 0.61 |
| Tmm | 25 | 40 | 40 | ||
| volunteer 7 | Vmm | 24.52 | 39.79 | 40.22 | 0.30 |
| Tmm | 25 | 40 | 40 | ||
| volunteer 8 | Vmm | 24.91 | 38.54 | 40.89 | 0.81 |
| Tmm | 25 | 40 | 40 | ||
| volunteer 9 | Vmm | 24.33 | 40.95 | 40.87 | 0.83 |
| Tmm | 25 | 40 | 40 | ||
| Method of Knuckle-Angle Detection | Time Taken to Measure and Record Knuckle Angles for 30 Times (s) |
|---|---|
| TMM | 51.75 |
| VMM | 421.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Zhong, M.; Dong, F. Research on Monocular-Vision-Based Finger-Joint-Angle-Measurement System. Sensors 2022, 22, 7276. https://doi.org/10.3390/s22197276
Feng Y, Zhong M, Dong F. Research on Monocular-Vision-Based Finger-Joint-Angle-Measurement System. Sensors. 2022; 22(19):7276. https://doi.org/10.3390/s22197276
Chicago/Turabian StyleFeng, Yongfei, Mingwei Zhong, and Fangyan Dong. 2022. "Research on Monocular-Vision-Based Finger-Joint-Angle-Measurement System" Sensors 22, no. 19: 7276. https://doi.org/10.3390/s22197276
APA StyleFeng, Y., Zhong, M., & Dong, F. (2022). Research on Monocular-Vision-Based Finger-Joint-Angle-Measurement System. Sensors, 22(19), 7276. https://doi.org/10.3390/s22197276





