1. Introduction
The interaction between the sea water and atmosphere in the South China Sea (SCS) can cause inhomogeneity in time and space of the refractive rate over the sea, which brings about the refractive error of radar measurement. A special phenomenon called evaporation duct often occurs, owing to rapid decrease in humidity, and it possesses an anomalous atmospheric refractive index structure [
1,
2,
3,
4]. Without the consideration of other influencing factors such as rainfall, the propagation of electromagnetic waves in the atmosphere is mainly determined by the structures of the refractive index, so propagation models (e.g., the terrain parabolic equation model (TPEM)) require a refractivity profile to make their calculations. It is now well established that the evaporation duct is the dominant propagation mechanism, resulting in over-the-horizon radar detection or causing a radar-blind area for microwaves at frequencies above the L-band [
5,
6,
7,
8]. Therefore, the measurement of the evaporation duct is of extreme importance because it affects most of the radar, radio communication, and navigation systems when they are operating under that condition.
Results show that the evaporation duct mainly depends on the atmospheric refractivity profile of the vertical direction. The minimum of the atmospheric refractivity responds to the evaporation duct height (EDH) [
9,
10]. There are many methods employed for measuring evaporation ducts. Conventionally, the evaporation duct is measured using a microwave refraction instrument [
11,
12], sounding balloon [
13,
14], or a gradient meteorological instrument (GMI) based on the tower platform [
15,
16], and it is predicted by the meteorological models. The refractivity from the clutter technique has recently been developed, deducing the duct height using the inversion algorithm including the genetic algorithm [
17,
18], the Bayesian–Markov chain Monte Carlo method (MCMC) [
19,
20], and the support vector machine (SVM) [
21,
22], among others. However, these methods have many drawbacks, such as low detecting precision, high costs, real time nature, and vulnerability to electromagnetic interference or electromagnetic exposure, which precludes them from practice in application.
Research shows that the probability of occurrence for an evaporation duct reaches 80% in the SCS due to conditions there being apt for its formation [
23,
24]. Thus, the height and intensity of the evaporation duct is measured by building a 0~40 m high tower platform. This platform measures the atmospheric temperature, humidity, air pressure, and other parameters at different heights and obtains the modified atmospheric refractive index profile. In general, the detection of the evaporation duct using the GMI on the basis of the tower platform has attracted individuals’ attention and is widely employed in practice. However, to obtain a high-resolution refractive index profile, it is necessary to study the evaporation duct model. Many scholars have proposed the following models based on the Monin–Obukhov similarity theory in the near-surface layer. In 1973, Jeske proposed an evaporation duct model for the propagation of the radio waves on the sea surface [
25], which was later improved and revised by Paulus to form the Paulus–Jeske (PJ) model [
26]. On the basis of the mesoscale forecast system, Musson-Genon et al. calculated the EDH using an analytical method and proposed the Musson-Genon–Gauthier–Bruth (MGB) model [
27]. In 2000, Frederickson et al. proposed the Naval Postgraduate School (NPS) model [
28]. The Non-Iterative Air–Sea Flux (NAF) model was proposed by Li et al. in 2014 and 2015 [
29,
30]. Although many domestic scholars have proposed many calculation methods based on the Monin–Obukhov similarity theory, due to the influence of the geographical environment factors, the adaptability of the models is not consistent. The algorithm of the PJ model is simple and fast, but it assumes that the potential refractive index, potential temperature, and potential humidity meet the Monin Obukhov similarity theory. When the actual conditions are stable, the potential refractive index does not meet the Monin–Obukhov similarity theory, so its calculation results may be wrong under the stable conditions. Moreover, its parameters are often derived from the terrestrial measurement results, so the PJ model cannot provide completely correct results. The EDH calculated by the MGB model is zero under many meteorological conditions, and the number of non-zero values will increase when the wind speed is large enough. The NPS model ignores the influence of the changes of the sea surface attachment parameters on the gradient coefficients of each parameter, and also has certain limitations. Compared with the aforementioned model, the NAF model adopts an advanced air–sea flux algorithm and extends the Monin–Obukhov similarity theory to low-wind-speed conditions. It is a relatively perfect evaporative duct prediction model in theory.
At present, to obtain the profile of the atmospheric refractive index, the GMI needs to carry a body of hydrological and meteorological sensors. Each sensor requires a cable to provide the electric energy and to transmit data though the aviation plug [
31,
32]. Further, when the battery of each sensor runs out and needs to be replaced, cables can let the GMI be more complicated, which can lead to high cost, short life, and hard maintenance in the high temperature and high humidity environment such as the SCS [
33,
34]. Inductively coupled power transfer (ICPT) technology is based on the principle of electromagnetics [
35,
36,
37,
38]. There is no direct connection between the power source and the load. On the basis of the ICPT system, the data can be transferred by using the same principle. In order to prevent the collected important data from being lost due to the interruption of monitoring during the process of replacing the sensor battery, a newly developed easy maintenance and high resistance system for measuring the evaporation duct on the basis of the magnetic coupling principle was introduced, which only required a closed steel ring (CSR) for power feeding and data transmission in the paper. In order to reduce the proportion of the reactive power and improve the overall efficiency of the non-contact power transmission system, the resonant principle was used to compensate the inductive reactance on the CSR. At the same time, the super capacitor was introduced as the energy temporary storage device of the sensor system to solve the problem of normal data acquisition after the power supply of the sensor was stopped. The built meteorological gradient meter testing equipment based on contactless power and data transmission technology was found to be suitable for the evaporation duct detection environment and was able to obtain a body of the marine hydrological and meteorological data. Since the current iterative calculation of the existing evaporative duct models requires a large number of operations, the efficiency and calculation stability of the prediction and diagnosis of the evaporative duct in a large range and multiple times was reduced. To avoid the iterative calculation by setting the initial value and to further improve the calculation stability of the existing evaporative duct models for long-term and large-scale atmospheric duct simulation prediction, the K-theory flux observation method based on the NAF model was introduced into the atmospheric refractive index equation to obtain the EDH in this paper. This paper will proceed in the following manner. First, the proposed system for detecting the evaporation duct is briefly introduced, including the structure of the proposed system and the design of inductive couplers and a sensing unit. Second, the magnetic coupling principle for power feeding and data transmission was further represented. The magnetic coupling system for power feeding and data transmission was tested. Third, according to the collected hydrological and meteorological data, the effects of the air pressure (AP), air temperature (AT), relative humidity (RH), air-sea temperature difference (ASTD), and wind speed (WS) on the EDH were analyzed by means of the NAF model. Last, the adaptability of the NAF model for predicting the evaporation duct was studied. The research results of the NAF model were compared with the NPS model. Experimental results showed that the detection of the evaporation duct was able to demonstrate the capability of the proposed system. The feasibility of the NAF model in the prediction of the EDH in the SCS was verified.
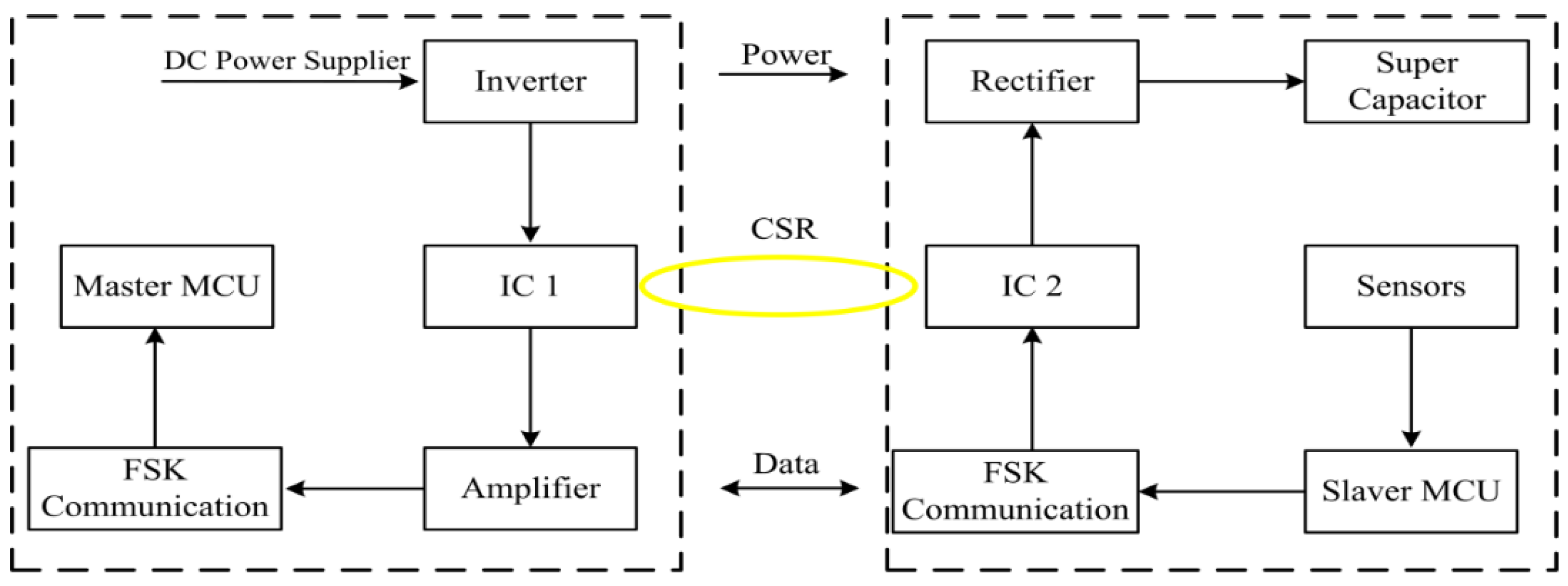
3. The Magnetic Coupling Principle for Power Feeding and Data Transmission
A schematic diagram of the power feeding and data transmission is shown in
Figure 6. The structure of the double transformer was devised to actualize the contactless power feeding and data transmission on the basis of the principle of the electromagnetic coupling. The CSR was not only the secondary coil of the transformer A but also the primary coil of the transformer B. According to the electromagnetic induction law [
39,
40,
41,
42], the input voltage
ui of the transformer A is given by
where
N1 is the turns number of the coil 1,
L1 is the self-inductance of the coil 1,
φ11 is the main flux of the coupler, and
i1 is the current following through the coil 1. Two coils cannot be fully coupled in actuality, and the coupling coefficient
k1 is computed by [
43,
44,
45,
46]
where
M is the mutual inductance of the two coils, and
L2 is the self-inductance of the coil 2. The relationship between the changes of the magnetic flux in the two-layer coils is as follows [
39,
40]:
where
φ12 is the flux of the coil 2, and the voltage
u2 of the coil 2 can be obtained according to the above equation.
where
N2 is the turns number of the coil 2, and its value is 1 (single turn). Likewise, the voltage relationship of the transformer B can be obtained in the same way. Finally, the output voltage
u3 is expressed by
where
N3 is the turns number of the coil 3, and
k2 is the coupling coefficient of the transformer B.
The block diagram of the system circuit is shown in
Figure 7. For the electromagnetic coupler, the principle of resonance is used to compensate the inductive reactance on the CSR. The supercapacitor is used as the energy temporary storage device of the sensor system, and the GMI is charged when it needs to work. After the power supply is stopped, the sensor uses the energy stored in the supercapacitor to collection and transmit data. At the same time, a simple and effective dual-power automatic switching circuit structure is proposed, which solves the contradiction between the direct power supply and the super capacitor power supply and becomes the core of the GMI high-efficiency power supply system. In the power transmission, the input signal of the primary coil (IC 1) is the obtained high frequency AC signal by a DC-AC inverter, and the power is transmitted to the CSR by electromagnetic coupling. The CRS is the secondary coil of the IC 1 and the primary coil of the IC 2 at the same time. Moreover, the electrical energy is transmitted to the sensing unit that provides the power for sensors.
5. Test Experiment of the Magnetic Coupling System for Power Feeding and Data Transmission
In order to verify whether the system can meet the performance requirements of the actual evaporation duct observation, the inductive couplers were used for power feeding and data transmission. The power feeding and data transmission test experiment is shown in
Figure 8. The test system included the electronic load, closed steel ring, master circuit, inductive couplers, multiple sensing unit, compensation capacitance, and analog resistance. The preset indicators of the power feeding and data transmission system were as follows: the transmission power was 5~20 W; the power transmission efficiency reached 50%; the communication accuracy rate exceeded 99%.
The secondary coil of the inductive couplers converts AC energy into DC energy through a full bridge rectifier and capacitor filter, and then connects to the DC electronic load. The electronic load can simulate the load in the real environment. It has the working modes of the constant current, constant resistance, constant voltage, and constant power. It can set the load size by itself and automatically in order to stabilize at the set value; it is thus convenient for the testing of the system, since the sensing unit of the evaporation duct measurement system has an operating voltage range of 5~24 V and a power range of 1~15 W. During the experimental test, the measurement system provides square waves with amplitudes of ±24 V, ±12 V, and ±5 V. The electronic load of the simulation system was set to the constant power mode, and the range of the power was 1 W to 15 W. The voltage and current output were recorded by the stabilized voltage source every 1 W. The relationship between the transmission power and the transmission efficiency obtained by the experimental test is shown in
Figure 9. The overall non-contact power transmission experiment showed that the overall power transmission efficiency of the system was about 57%, and the system transmission power reached 22.8 W, which essentially realizes the low-power transmission of non-contact power.
In order to verify the reliability of the communication, 1000 frames of data were sent by the sensing unit nodes to each other for 10 tests. There were three frames with the verification errors, and the correct reception rate was 99.7%. In addition, all error frames were automatically retransmitted. There was no check error after retransmission, and the communication continued smoothly. It can be seen that the communication was relatively stable and reliable. The communication error may have been caused by the residual magnetism accumulated in the magnetic core of the communication waveform of the previous frame, which affected the communication waveform of this frame, and the transmitted waveform was distorted, resulting in data error. The experimental test results showed that the system met the design requirements of the stable and reliable energy supply and data transmission, and also met the working requirements of the evaporation duct measurement system.
6. Results of the Evaporation Duct Measurement System
In order to measure the atmospheric refractive index profile, the atmospheric duct was calculated. The experiment was performed from 31 October 2021 to 5 November 2021 in the SCS. The data of the marine hydrological and meteorological sensors were obtained every three minutes in the experiment process. Each set of the experiment data contained five groups of data, which were mainly as follows: wind speed (WP), air temperature (AT), relative humidity (RH), air pressure (AP), and sea surface temperatures (SST). Considering the strong turbulence characteristics near the sea surface, the EDH needs to be determined by applying the Dybye theory to process and analyze the measured data.
6.1. A Sensitivity Study of Meteorological Data on EDH Based on the NAF Model
Research shows that the EDH is mainly influenced by the ASTD, AT, RH, WP, and AP. The research on the adaptability of the model for predicting the evaporation duct propagation of the electromagnetic wave has an extremely important significance in radar communication and tactical guidance. To study the impact of the meteorological sensors on the EDH, the influence of the AT, RH, ASTD/and WP on the EDH is mainly analyzed by using the NAF model. The sensitivity of the meteorological sensors was simulated on the basis of the NAF model, as shown in
Figure 10,
Figure 11 and
Figure 12. The horizontal axis is the ASTD, and the vertical axis is the EDH. The ASTD was less than or equal to or greater than zero, which is described as the instability, neutral, and stability conditions of the atmosphere, respectively. As the EDH is generally less than 40 m, it would be limited to 40 m, although it is greater than 40 m.
It can be seen from
Figure 10 that under the unstable condition, with the ASTD increasing, the EDH essentially remained unchanged. When the ASTD remained unchanged, the EDH increased with the WS increasing; when the ASTD remained constant, the EDH increased slightly with the SST increasing. When transitioning from the unstable condition to the stable condition, the EDH rose rapidly and reached the maximum value as the ASTD continued to increase. When the WS decreased, the EDH increased faster. It shows that the evaporative duct was very sensitive to the change of the ASTD under the stable condition of the low WS. When the ASTD was constant, the EDH increased with the SST increasing under the stable condition.
As shown in
Figure 11, under the unstable condition, the EDH decreased slowly with the RH increasing. Under the stable condition, when the RH was 95%, the EDH decreased rapidly to zero, and it can be interpreted as the trend of the rapid decline in the RH. When the RHs were 65% and 75% under the unstable condition in
Figure 11a,b, respectively, the EDH rose rapidly to 40 m. When the RH was lower than 75% and the WS was 1 m/s or 4 m/s, the EDH increased rapidly to 40 m and remained unchanged at the EDH of 40 m with the ASTD increasing. When the RH was greater than 85%, the EDH also decreased rapidly with the ASTD increasing.
It can be seen from
Figure 12a,b that when the RHs were 65% and 75%, respectively, and the ASTD was constant, and the EDH increased with the AT increasing under the unstable condition; when the AT was constant, the EDH was essentially stable under the stable condition, that is, the EDH was only somewhat affected by the ASTD when it was not stable. Under the stable condition, the EDH rapidly reached the maximum value with the ASTD increasing. In this case, the EDH was greatly affected by the SST. As shown in
Figure 12c, when the RH was 85%, the EDH remained essentially unchanged under the unstable condition and the SST changed in the range of −3 °C to −0.8 °C; under the stable condition, the EDH first increased and then decreased with the ASTD increasing. When the ASTD was 1.2 °C, the EDH reached the maximum value. As shown in
Figure 12d, when the RH was 95%, under the unstable condition, the EDH decreased slowly with the ASTD increasing; under the stable condition, the EDH decreased with the ASTD increasing. It decreased rapidly to zero, that is, there was no evaporative duct phenomenon under the stable condition.
According to the sensitivity study of the meteorological data in
Figure 10,
Figure 11 and
Figure 12, under the unstable condition, when the ASTD was less than 0, the EDH was less affected by the ASTD. As the AT and SST rose, the WS increased higher, and as the RH decreased, the sea water evaporation became more favorable, a strong evaporative duct was formed, and the EDH was larger. However, under the stable condition, when the ASTD was greater than 0, the EDH was greatly affected by the ASTD. When the WS was relatively low, the RH was small and the ASTD was high, and it was easy to form a strong evaporation duct. In addition, it can also be seen that under the unstable condition, the sensitivity of the hydro meteorological sensor had little influence on the EDH. When the unstable condition was transited to the stable condition, the small mutation of the hydro meteorological parameters can cause the EDH to reach 40 m instantaneously, which would bring a great error to the prediction of the EDH. Thus, the meteorological data inaccuracies can bring up some huge errors under the stable condition. When the NAF model is used to predict the EDH, the prediction accuracy of the model can be improved by improving the sensitivity of the hydro meteorological sensor.
6.2. The Experiment of EDH Measurement in the South China Sea
In order to obtain the measured M values at each level of the tower platform, under the assumption of the static balance and ideal gas, the pressure at 8 m was converted to other levels by using the pressure height formula. Then, according to the Debye theory, the M values at different levels were able to be calculated by using Equation (6). Furthermore, the modified refractive index of the six layers can be fitted by using Equation (7) to perform the nonlinear least square fitting. The modified atmospheric refractive index profile and EDH were determined.
The EDH that varied from 4 to 14 m in a day is shown in
Figure 13. The EDH first remained steady, then considerably mounted and levelled off, and finally decreased gradually; it can be interpreted as the evaporation of the sea water. In the morning, the air and sea water temperature were lower, which led to the weaker evaporation of the sea water and weaker EDH. The EDH increased rapidly with the air temperature and sea water temperature increasing. This phenomenon can be explained according to the aforementioned sensitivity study. Moreover, the EDH was small, and the occurrence probability of the evaporation duct was more than 95% in the SCS. The mean value of the EDH was 8.7 m, which was lower than the mean EDH of the SCS. The EDH trend of a day was in good agreement though the two methods. The modified refractive index profile as the function of the height is shown in
Figure 13b. As shown in the black line, the EDH was identical, but there was a significant difference between the black solid line and black broken line. Because the black solid line was described by a log-linear function, it was obtained by Equation (7). However, the black broken line was obtained according to Equation (6). Sometimes, the shape of the modified refractive index profile was almost the same as that shown in the red line, but the value of the EDH showed an enormous difference, showing that the accuracy of the model requires further research.
7. Discussion
Since the NPS model has been used to evaluate the adaptability of the evaporation duct in the SCS [
31,
52], in order to verify the superiority of the NAF model in diagnosing the evaporation duct in the SCS, the sensitivity analysis results of the NAF model were effectively compared with the NPS model. For the variation of the WS, when the RH was 85% and the WS was less than 7 m/s, the EDH calculated by the NPS model and NAF model had a fast-rising trend with the ASTD changing. When the WS was greater than 7 m/s, the EDH calculated by the NPS model maintained a fast growth rate with the ASTD changing, while the NAF model showed a slightly decreasing trend with the ASTD changing, and the growth rate of the EDH tended to be flat. For the variation of the RH, when the SST was 25 °C, and the RH was less than 85%, the EDH calculated by the NPS model and NAF model had a fast-rising trend with the ASTD changing. When the RH was more than 85%, the decreasing rate of the EDH calculated by the NPS model and NAF model was obviously accelerated, and then tended to be flat. For the variation of the AT, when the WS was 5 m/s and the RH was 75%, the EDH calculated by the NPS model had a fast-rising trend with the ASTD changing, and the EDH calculated by the NAF model quickly rose to the EDH of 40 m and then tended to be flat. When the WS was 5 m/s and the RH was greater than 85%, the EDH calculated by the two models was kept consistent with the overall change trend, but the EDH calculated by the NPS model was slightly higher than that calculated by the NAF model.
According to the aforementioned analysis, the overall average EDH calculated by the NAF model was slightly lower than that calculated by the NPS model [
31,
52]. The sensitivity of the NAF model to the RH and WS under the unstable atmospheric stratification condition was consistent with that of the NPS model; under the stable atmospheric stratification condition, the NAF model had an obvious response to the variation of the ASTD, RH, and WS. The diagnosis effect of the NAF model was better than that of the NPS model, mainly because the NAF model adopts a more optimized and reasonable non-iterative flux parameterization scheme, and its calculation results are close to the Babin model and the NPS model using the latest algorithm COARE3.0 [
31,
52]. It can be seen that the computational stability of the NAF model was better, the probability of extreme values was lower, and the diagnostic results were relatively reliable. In general, the simulation effect of the NAF model was more stable when different meteorological elements changed.
8. Conclusions
A novel system for the measurement of the evaporation duct on the basis of the magnetic coupling technology for the power feeding and data transmission was proposed in this paper. No direct connection between the power source and load was realized. The stability of the system, especially in high humidity and high salt fog conditions, can be improved. The magnetic coupling system was designed by some simulations and experiments in detail. The sensitivity of the NAF model was analyzed, and the EDH was compared with the measured value on the basis of the experiment data in the SCS. The EDH was detected by not only the direct measurement but also the indirect prediction based on the NAF model. The results show that the system for measuring the evaporation duct using the magnetic coupling technology for the power feeding and data transmission was feasible in practice. The overall efficiency of the power transmission reached 57%, and the transmission power was 22.8 W, which realized the low-power transmission of GMI non-contact power. The communication of the whole system was stable and reliable, and the correct rate of data communication for 1000 frames in the experiment reached 99.7%. On the basis of the analysis of the experimental data of the SCS, it was found that the prediction trend of the EDH by the NAF model was essentially consistent with the measured value. The mean value of the EDH was 8.7 m, which was lower than the mean EDH of the SCS. The EDH calculated by the NAF model in the unstable air–sea stratification state was slightly lower than that calculated by the NPS model. The diagnosis of the EDH by the NAF model was similar to that of the NPS model, but the calculation stability of the NAF model was better.
Although a novel gradient observation system was proposed in this paper, the atmospheric refractive rate profile was obtained by using the NAF model. It verified the fact that the model can perform an effective evaporative duct diagnosis and prediction under the unstable air–sea stratification in the SCS. However, the electromagnetic coupler with a toroidal core was only used as the non-contact power transmission structure of the GMI. In the future, the non-contact power transmission efficiency can be further improved by studying the influence of other special-shaped electromagnetic coupler structures on the system transmission efficiency.
The prediction of the EDH by a single NAF model under the neutral or the unstable state would bring about large errors to the experimental results. In view of this problem, in the follow-up study of the NAF model, a variety of model fusion methods (PJ, Babin, NPS, and other models) can be used to perform the data fusion joint prediction according to different weights. It reduces the large error caused by a single NAF model to the height diagnosis results of the evaporation duct. When the linear relationship is selected under the stable condition of the NAF model, it would lead to unreasonable EDH results. This unreasonable phenomenon can be improved by developing some new universal functions under stable conditions. Moreover, due to the limited experimental data at sea and the inconsistent horizontal distribution characteristics of the different sea areas, a large number of empirical formulas and assumptions were used in the prediction of the NAF model, and the accuracy of the NAF model was not the same. To apply the NAF model to the actual sea environment, a long-term comparative analysis test needs to be carried out. In later research, the capacitive refractometer can be considered to obtain the atmospheric refractive rate profile by measuring the resonant frequency of the resonator. Similarly, the lidar system can also be used to obtain atmospheric water vapor pressure parameters by emitting electromagnetic waves in different bands, and then the atmospheric refractive rate profile is obtained. The accuracy of the atmospheric refractive rate profile of the NAF model is further verified.