The Clutter Simulation of a Known Terrain by the 3D Parabolic Equation and RCS Computation
Abstract
:1. Introduction
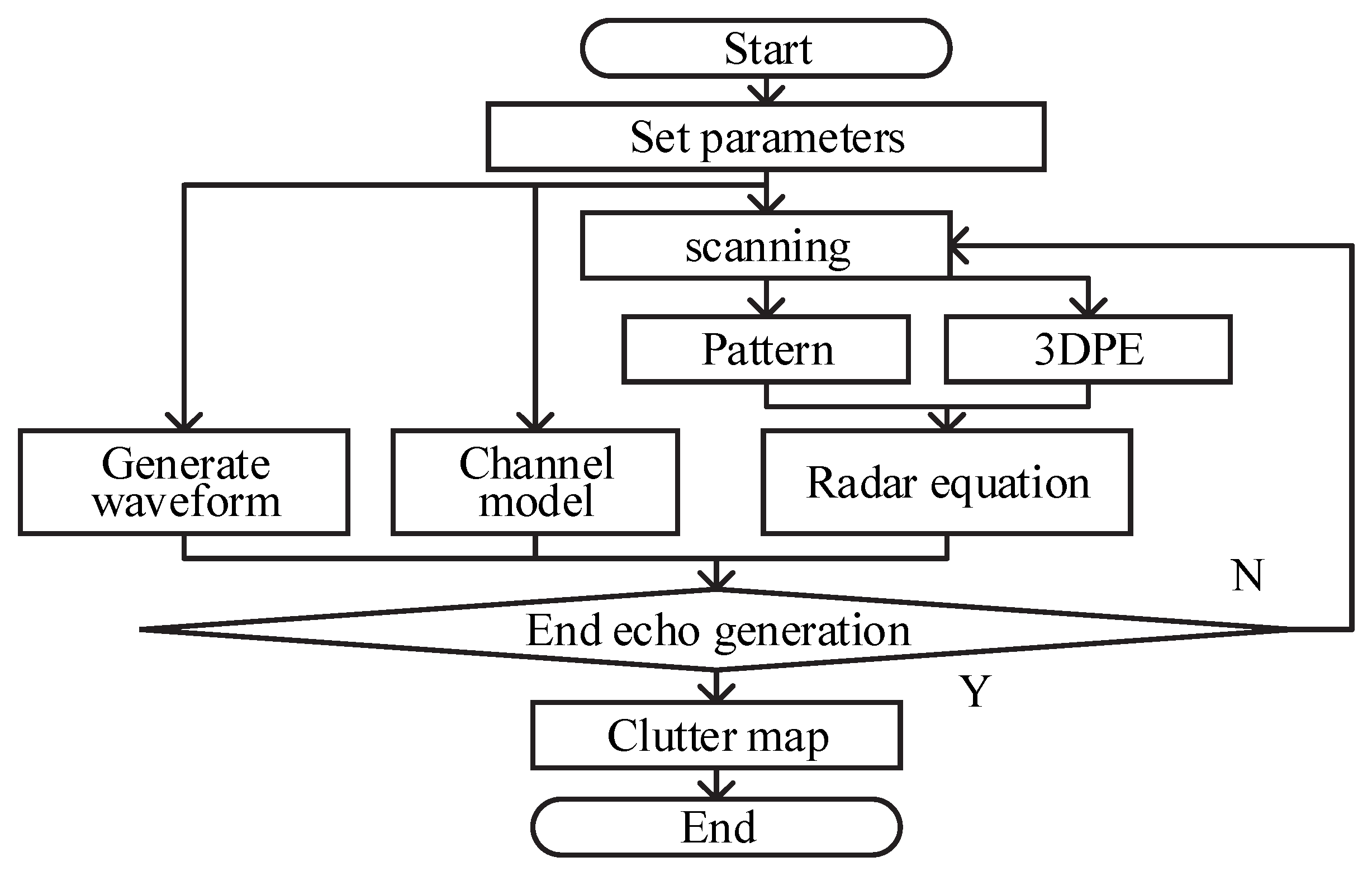
2. The Simulation Scheme
2.1. The Radar Echo Model
2.2. The Proposed Simulation Scheme
3. The 3D Parabolic Equation and RCS Computation
3.1. The Parabolic Equation Model
3.2. 3D-SSFT
3.2.1. The Initial Field
3.2.2. Boundary Conditions (BC)
3.2.3. 3D-SSFT
3.3. Computation of RCS Based on the Cell
| Algorithm 1: The pseudo-code of our scheme. | |
| Input: Radar Parameters, Known Terrain Data Output: the Clutter Map | |
| 1: | Initialize , the azimuth of beam , , , . |
| 2: | while |
| 3: | for do |
| 4: | ; |
| 5: | ; |
| 6: | according to reflection coefficients, is calculated by ; |
| 7: | ; |
| 8: | end for where is the nonzero subset of in all space cells |
| 9: | for do |
| 10: | ; |
| 11: | end for |
| 12: | ; |
| 13: | as the antenna scans increases; |
| 14: | end while |
| 15: | after pulse compression to obtain the clutter map from |
4. Simulation Results and Discussion
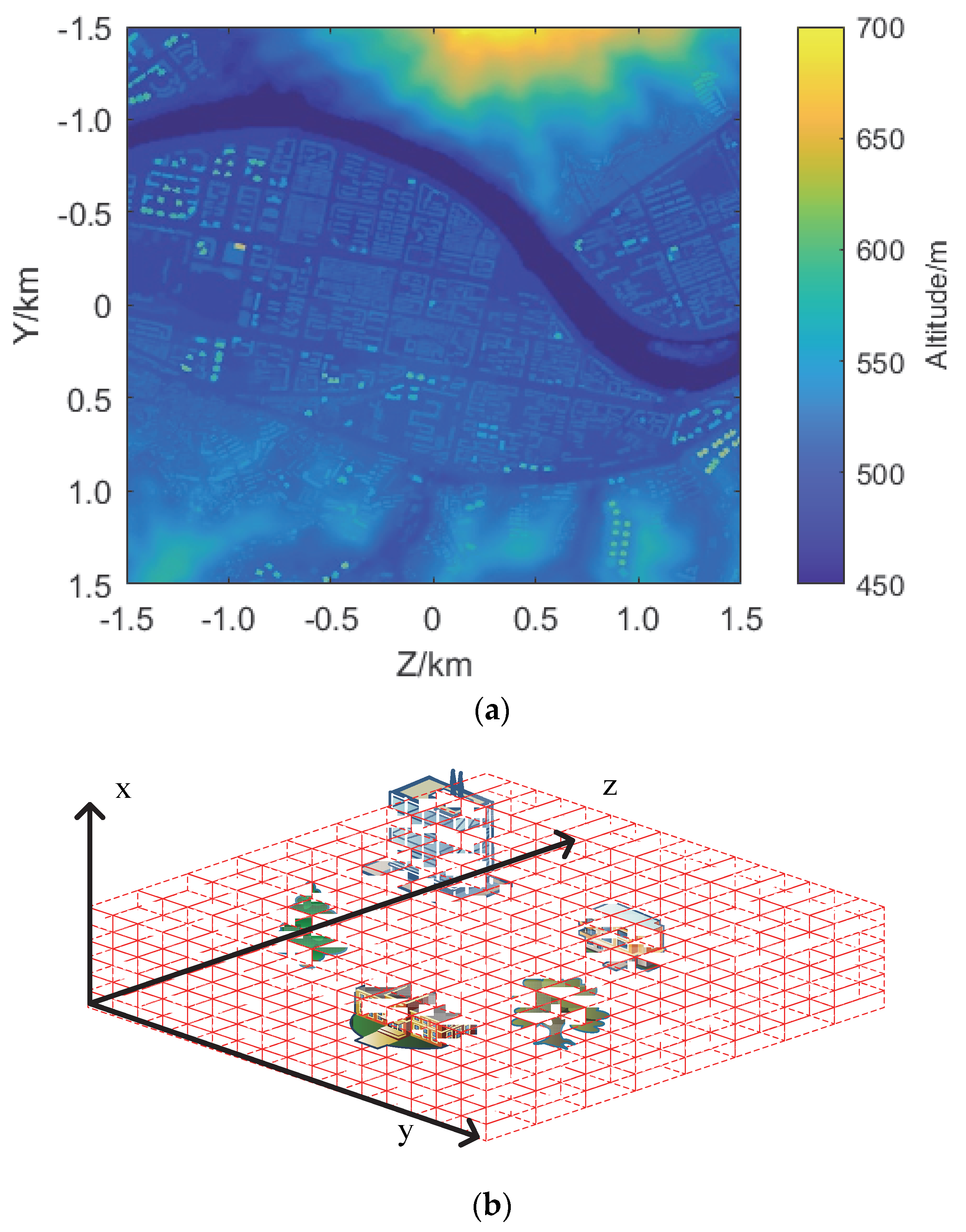
4.1. The Influence of Buildings on 3D-SSFT
4.2. Comparisons with Different Sizes of Cell
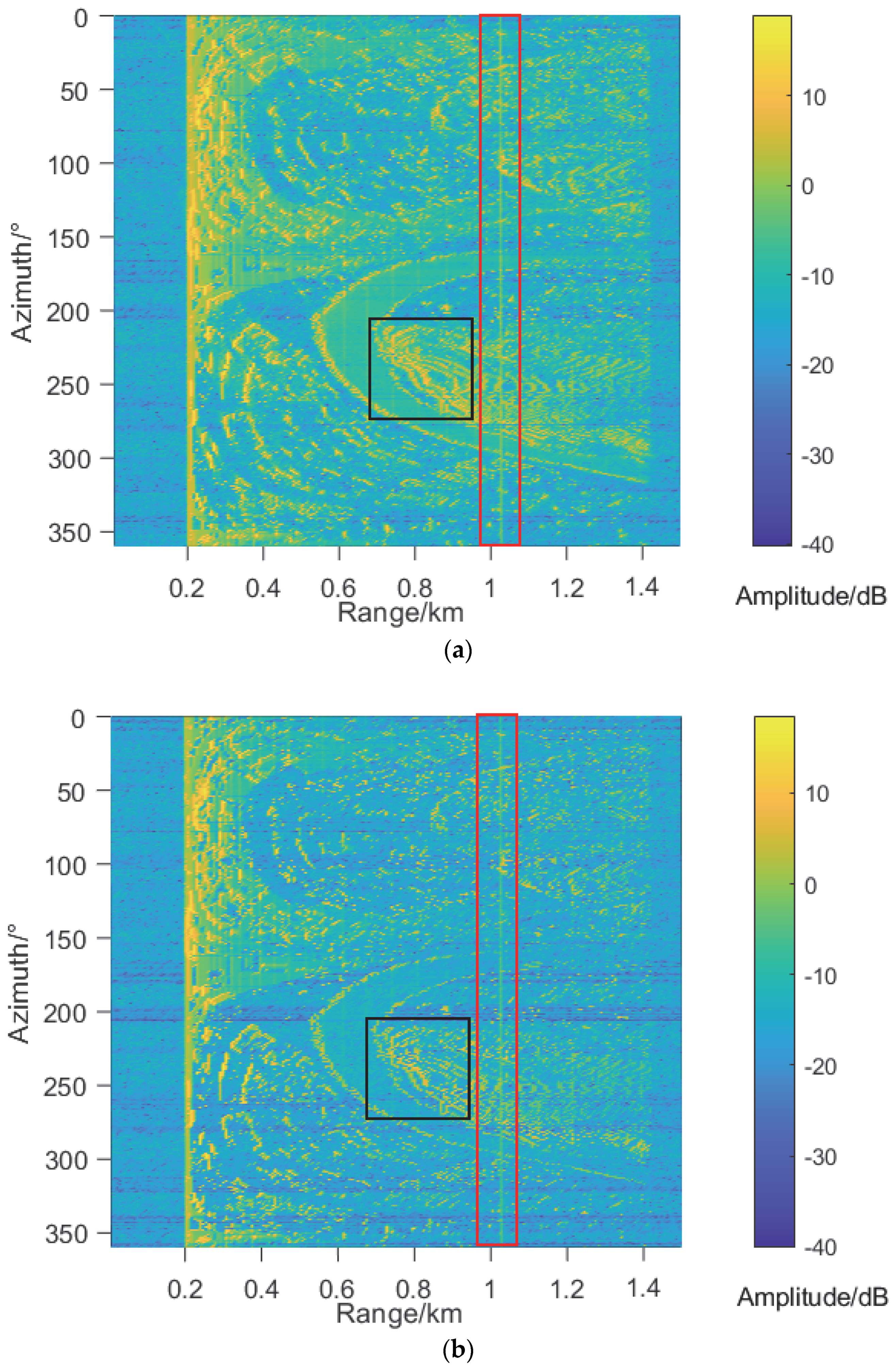
4.3. Clutter Maps and Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | two-dimensional |
| 3D | three-dimensional |
| RCS | radar cross section |
| PE | parabolic equation |
| ZMNL | Zero-Memory Non-Linear |
| SIRP | Spherically Invariant Random Processes |
| SSFT | step-by-step Fourier transform |
| BC | Boundary Conditions |
| PML | the perfectly matched layer |
| FDTD | finite difference time domain method |
References
- Marier, L.J. Correlated K-distributed clutter generation for radar detection and track. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 568–580. [Google Scholar] [CrossRef]
- Rangaswamy, M.; Weiner, D.D.; Ozturk, A. Non-Gaussian random vector identification using spherically invariant random processes. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 111–124. [Google Scholar] [CrossRef]
- Wu, G.; Fan, J.; Zhang, F.; Lu, F. A semi-empirical model of sea clutter based on zero memory nonlinearity. IEEE Access 2019, 7, 18125–18137. [Google Scholar] [CrossRef]
- Conte, E.; Longo, M.; Lops, M. Modelling and simulation of non-Rayleigh radar clutter. In IEE Proceedings F (Radar and Signal Processing); IET: London, UK, 1991; Volume 138, pp. 121–130. [Google Scholar]
- Rangaswamy, M.; Weiner, D.; Ozturk, A. Computer generation of correlated non-Gaussian radar clutter. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 106–116. [Google Scholar] [CrossRef]
- Mallahzadeh, A.R.; Soleimani, M.; Rashed-Mohassel, J. RCS computation of airplane using parabolic equation. In Proceedings of the 2005 Asia-Pacific Microwave Conference Proceedings, Suzhou, China, 4–7 December 2005; Volume 4, p. 4. [Google Scholar]
- Mallahzadeh, A.R.; Rashed-Mohassel, J.; Soleimani, M. Monostatic RCS computation of reflector antennas using parabolic equation. In Proceedings of the 6th International Conference on Computational Electromagnetics, Aachen, Germany, 4–6 April 2006; pp. 1–2. [Google Scholar]
- Levy, M. Parabolic Equation Methods for Electromagnetic Wave Propagation; IET: London, UK, 2000. [Google Scholar]
- Chiou, M.-M.; Kiang, J.-F. PWE-based radar equation to predict backscattering of millimeter-wave in a sand and dust storm. IEEE Trans. Antennas Propag. 2016, 65, 785–793. [Google Scholar] [CrossRef]
- Guo, Q.; Zhou, C.; Long, Y. Greene approximation wide-angle parabolic equation for radio propagation. IEEE Trans. Antennas Propag. 2017, 65, 6048–6056. [Google Scholar] [CrossRef]
- He, Z.; Zeng, H.; Chen, R.S. Two-way propagation modeling of expressway with vehicles by using the 3-D ADI-PE method. IEEE Trans. Antennas Propag. 2018, 66, 2156–2160. [Google Scholar] [CrossRef]
- Thomson, D.J.; Chapman, N.R. A wide-angle split-step algorithm for the parabolic equation. J. Acoust. Soc. Am. 1983, 74, 1848–1854. [Google Scholar] [CrossRef]
- Barrios, A.E. A terrain parabolic equation model for propagation in the troposphere. IEEE Trans. Antennas Propag. 1994, 42, 90–98. [Google Scholar] [CrossRef]
- Li, A.; Yin, C.; Zhang, Q. Predicting spatial field values under undulating terrain with 2W-PE based on machine learning. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 222–226. [Google Scholar] [CrossRef]
- He, Z.; Chen, R.S. A novel parallel parabolic equation method for electromagnetic scatterings. IEEE Trans. Antennas Propag. 2016, 64, 4777–4784. [Google Scholar] [CrossRef]
- Guo, Q.; Long, Y. Two-way parabolic equation method for radio propagation over rough sea surface. IEEE Trans. Antennas Propag. 2020, 68, 4839–4847. [Google Scholar] [CrossRef]
- Deng, X.; Liao, C.; Zhang, D.; Feng, J.; Shang, Y.; Zhou, H. A novel PE/FDTD hybrid model for predicting echo signals of radar targets in large-scale complex environments. IEEE Access 2020, 8, 28450–28461. [Google Scholar] [CrossRef]
- Wang, D.-D.; Xi, X.-L.; Pu, Y.-R.; Zhang, J.-S.; Zhou, L.-L. LF groundwave propagation modeling over irregular terrain by the hybrid two-way parabolic equation method. IEEE Trans. Antennas Propag. 2019, 67, 6596–6601. [Google Scholar] [CrossRef]
- Gao, Y.; Shao, Q.; Yan, B.; Li, Q.; Guo, S. Parabolic equation modeling of electromagnetic wave propagation over rough sea surfaces. Sensors 2019, 19, 1252. [Google Scholar] [CrossRef] [Green Version]


| Num | RCS/dBm | Num | RCS/dBm |
|---|---|---|---|
| 1 | −251.27 | 6 | −235.04 |
| 2 | −247.48 | 7 | −241.65 |
| 3 | −250.04 | 8 | −246.30 |
| 4 | −255.91 | 9 | −241.37 |
| 5 | −252.25 | 10 | −242.60 |
| RCS/dBm | A 100 m Cube | 1000 Cubes |
|---|---|---|
| >−248 | 45 | 45 |
| −248~−265 | 108 | 108 |
| −265~−282 | 169 | 169 |
| −282~−299 | 401 | 401 |
| −299~−316 | 364 | 364 |
| −316~−333 | 380 | 380 |
| −333~−350 | 1960 | 1960 |
| −350~−368 | 3800 | 3800 |
| −368~−385 | 2140 | 2140 |
| <−385 | 529 | 529 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Ding, J.; Wang, M.; Yang, S. The Clutter Simulation of a Known Terrain by the 3D Parabolic Equation and RCS Computation. Sensors 2022, 22, 7452. https://doi.org/10.3390/s22197452
Wang Z, Ding J, Wang M, Yang S. The Clutter Simulation of a Known Terrain by the 3D Parabolic Equation and RCS Computation. Sensors. 2022; 22(19):7452. https://doi.org/10.3390/s22197452
Chicago/Turabian StyleWang, Zhiyi, Jieru Ding, Min Wang, and Shuyuan Yang. 2022. "The Clutter Simulation of a Known Terrain by the 3D Parabolic Equation and RCS Computation" Sensors 22, no. 19: 7452. https://doi.org/10.3390/s22197452
APA StyleWang, Z., Ding, J., Wang, M., & Yang, S. (2022). The Clutter Simulation of a Known Terrain by the 3D Parabolic Equation and RCS Computation. Sensors, 22(19), 7452. https://doi.org/10.3390/s22197452






