A Height Nonlinear Velocity Field Algorithm for CORS Station Based on GARCH Model
Abstract
:1. Introduction
2. Nonlinear Fitting of CORS Station Elevation
2.1. The Principle of Nonlinear Fitting of the Signal Term
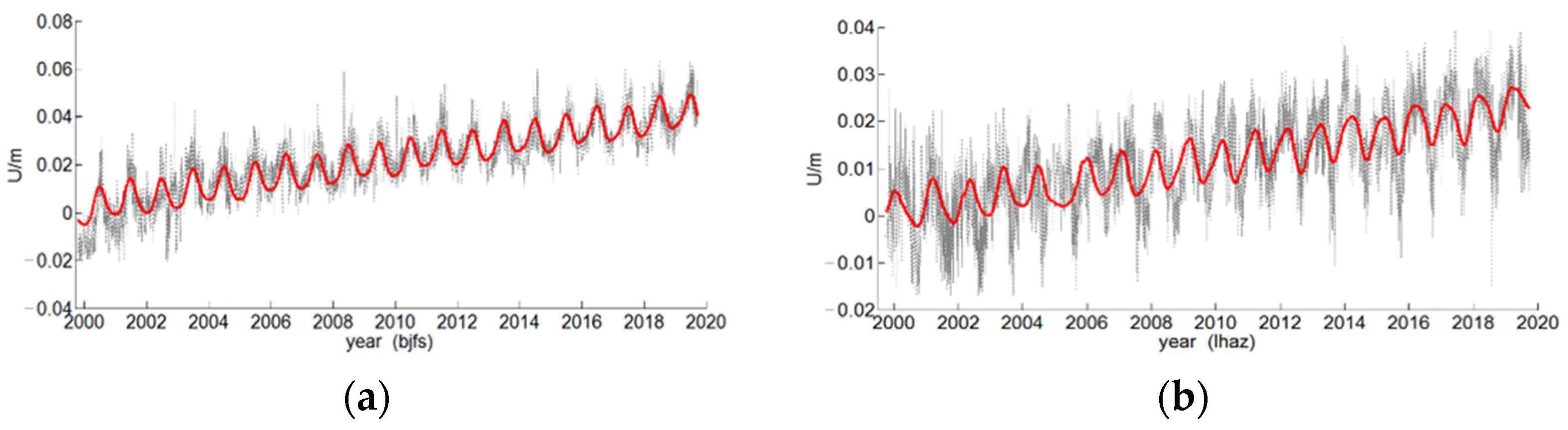
2.2. Nonlinear Fitting Experiment
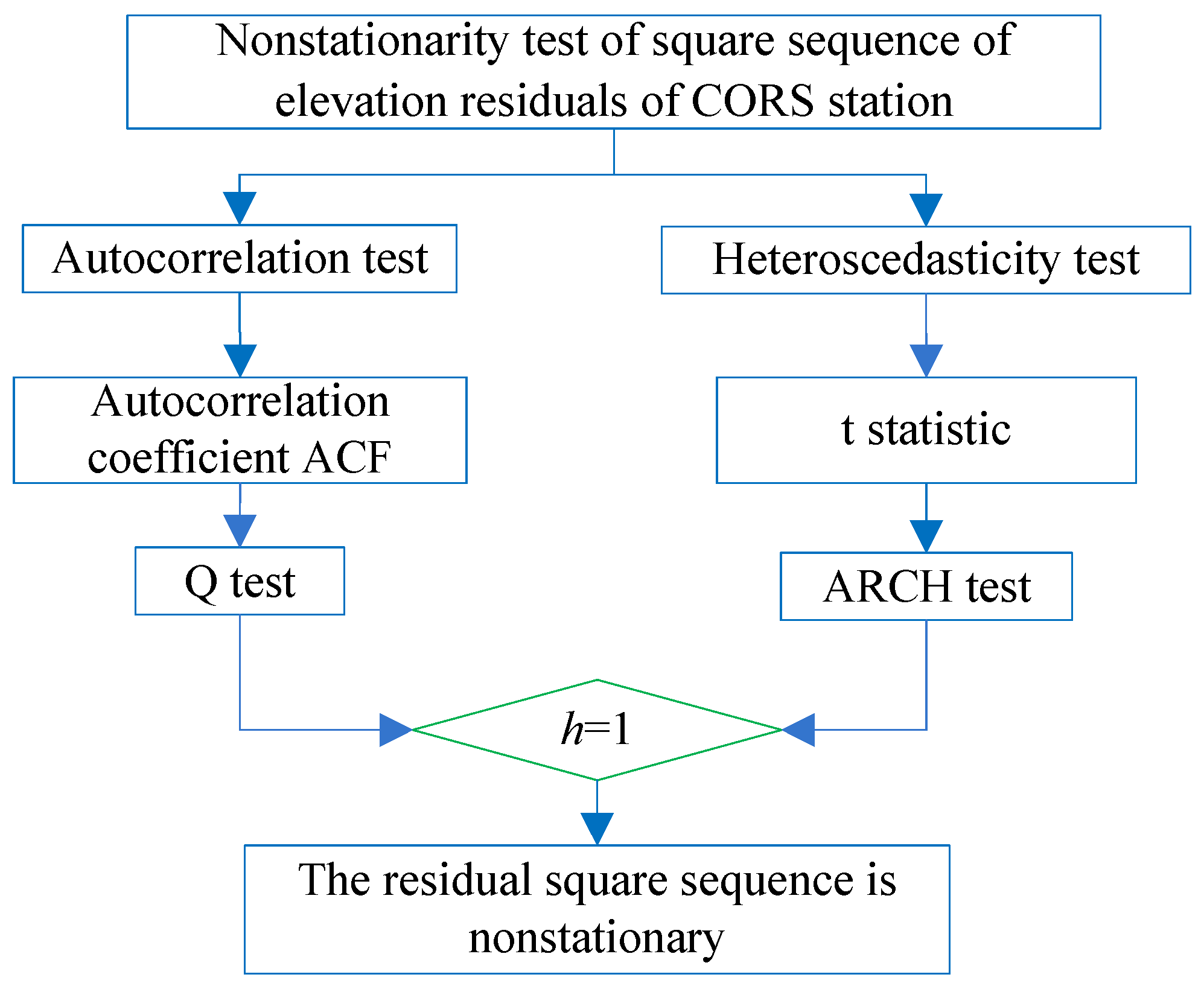
3. Non-Stationary Determination Method of Residual Squared Sequence
3.1. ARCH Effect Test Method
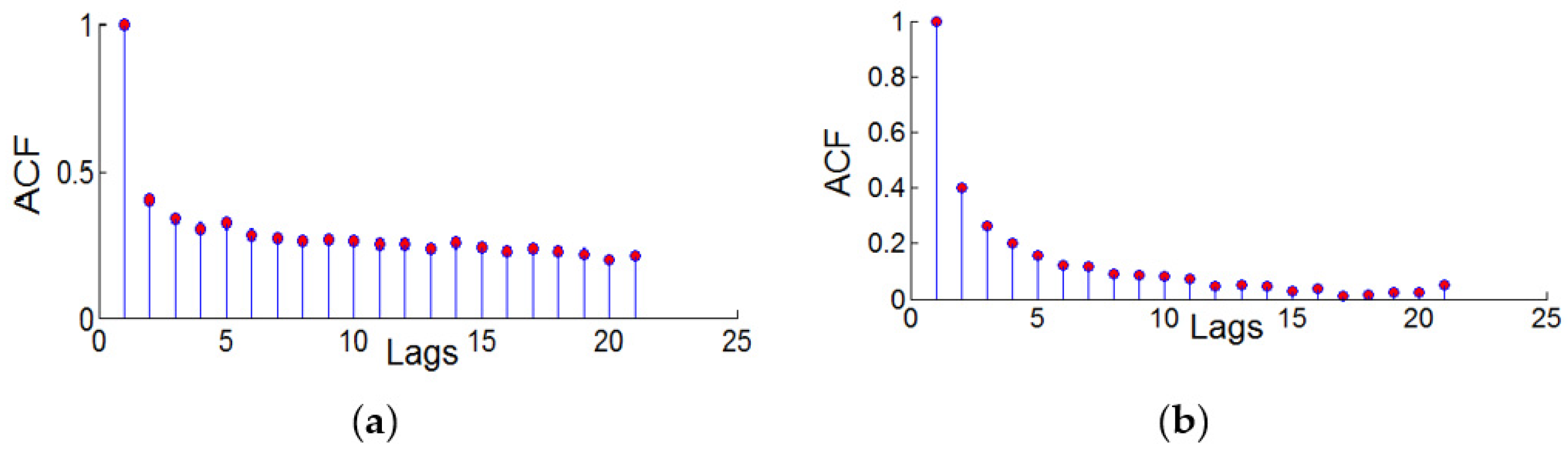
3.2. Autocorrelation Test of Residual Squared Series
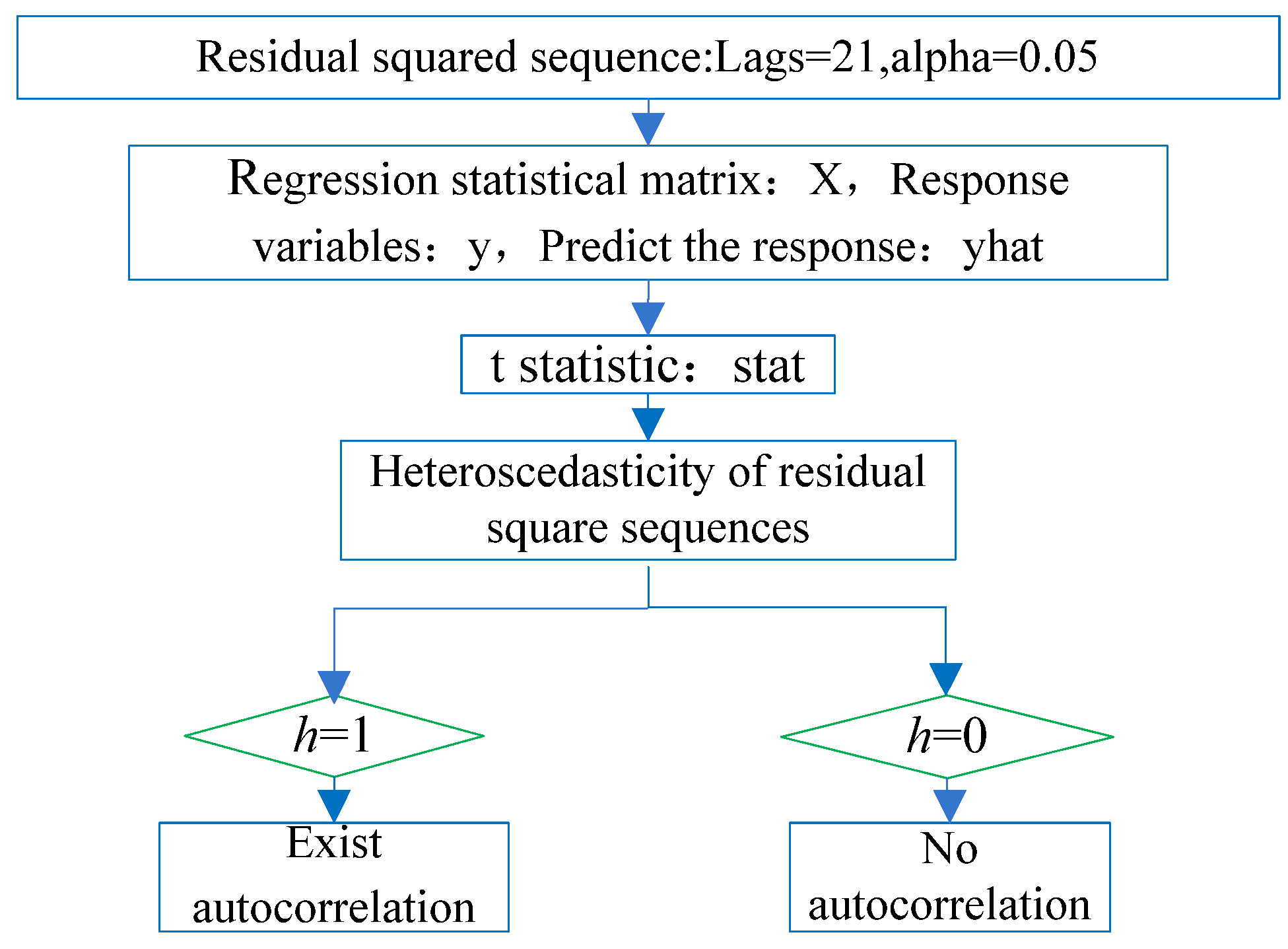
3.3. Heteroskedasticity Test of Residual Squared Sequence
4. GARCH Modeling of Non-Stationary Residual Series
5. Modeling of CORS Station Elevation Nonlinear Velocity Field
5.1. Prediction Experiment of Elevation Velocity Field at Four CORS Stations
5.2. Prediction of the Elevation Velocity Field of 25 CORS Stations around the World
6. Conclusions
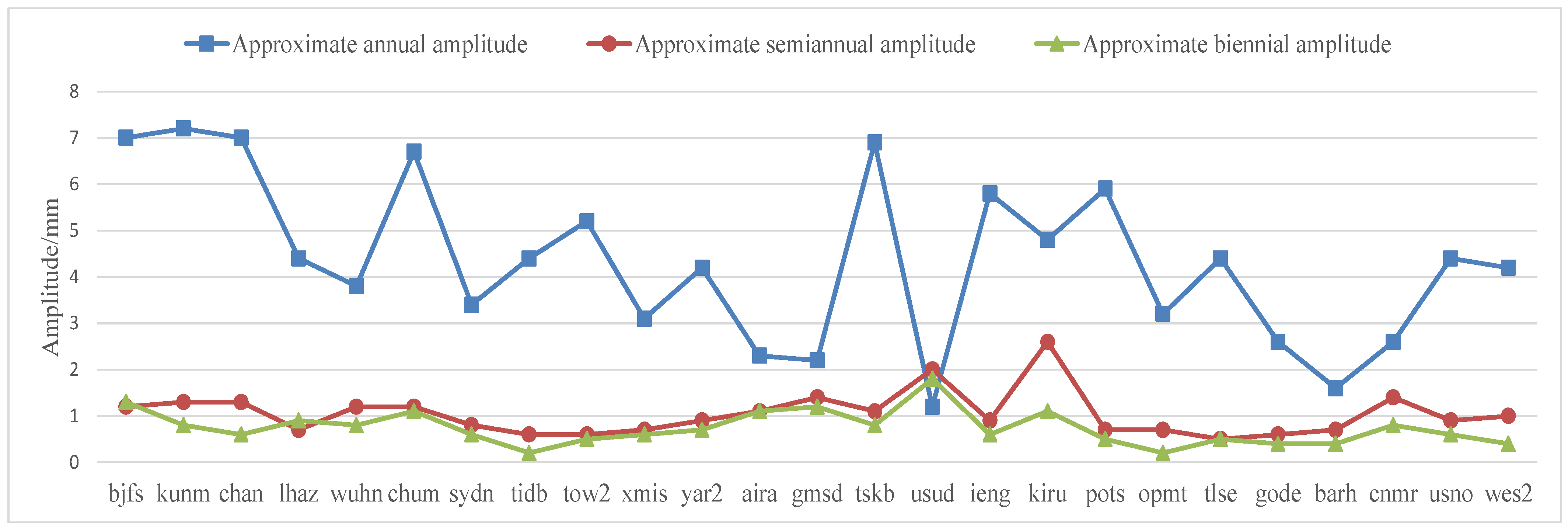
- We established a nonlinear fitting model for CORS station elevation time series data including approximate one-year, half-year, and two-year cycle terms. The annual period motion was the main contribution, and its amplitude was 3–7 mm, the half year and two-year were 1–2 mm and less than 1 mm, respectively. The median error of nonlinear fitting results of 25 CORS stations compared with SOPAC showed that the difference of velocity field was 0.73 mm/a, and the difference of annual period and half year period were 0.94 mm and 0.51 mm, respectively.
- The GARCH fitting model of the CORS station elevation residual sequence was established, and the nonlinear velocity field of the CORS station elevation was obtained. After reconstructing the nonlinear velocity field of the elevation of the CORS station, the half-year prediction error was 7 mm. At present, the highest accuracy of the elevation coordinate component of the CORS station was 3–5 mm, and the difference between the two was about 3 mm.
- The prediction results of different interval lengths showed that the prediction accuracy of the nonlinear velocity field model based on GARCH was better than the traditional nonlinear prediction model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, P.F. Theory and Method for Establishment of the China Geodetic Coordinate System 2000; Surveying and Mapping Press: Beijing, China, 2014. [Google Scholar]
- Altamimi, Z.; Rebischung, P.; Metivier, L.; Collilieux, X.; Chanard, K.; Teyssendier-de-la-Serve, M. Preparatory analysis and development for the ITRF2020. In Proceedings of the 23rd EGU General Assembly, Online, 19–30 April 2021. [Google Scholar]
- Dong, D. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. 2002, 107, 2075. [Google Scholar] [CrossRef] [Green Version]
- Williams, S.D.P. The effect of coloured noise on the uncertainties of rates estimated from geodetic time series. J. Geod. 2003, 76, 483–494. [Google Scholar] [CrossRef]
- Williams, S.D.P. Error analysis of continuous GPS position time series. J. Geophys. Res. 2004, 109, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Williams, S.D.P. CATS: GPS coordinate time series analysis software. GPS Solut. 2008, 12, 147–153. [Google Scholar] [CrossRef]
- Tregoning, P. Effects of atmospheric pressure loading and seven-parameter transformations on estimates of geocenter motion and station heights from space geodetic observations. J. Geophys. Res. Solid Earth 2005, 110, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Amiri-Simkooei, A.R. Noise in multivariate GPS position time-series. J. Geod. 2009, 83, 175–187. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Li, Z.; Liu, W.; Zhou, X. Some Thoughts on Establishment and Maintenance of Terrestrial Reference Frame Considering Non-linear Variation. Geomat. Inf. Sci. Wuhan Univ. 2010, 35, 665–669. [Google Scholar]
- Jiang, Z.H.; Peng, Z.; Bei, J.Z.; Li, Z.C. Characteristics of the non-linear movement of CORS network in China based on the CGCS2000 frame. Chin. J. Geophys. 2012, 55, 841–850. [Google Scholar]
- Zhang, H.J. Nonlinear Time-Varying Study of GPS Height Time Series of National CORS Stations. Ph.D. Thesis, Liaoning Technical University, Fuxin, China, 2013. [Google Scholar]
- Liang, T.; Sun, F.; Niu, D. The Study on Phase Rule of Global GNSS Coordinate Annual Non-Linear Motion. J. Geod. Geodyn. 2016, 36, 154–157. [Google Scholar]
- Fu, Y.; Sun, F.; Zhu, X.; Liu, J. Establishment of Statistical Correction Model for Vertical Annual Variations of Global GPS Stations. Acta Geod. Cartogr. Sin. 2018, 47, 1337–1345. [Google Scholar]
- Mao, A. Noise in GPS coordinate times series. J. Geophys. Res 1999, 104, 2797–2816. [Google Scholar] [CrossRef] [Green Version]
- Georgiev, I.; Dimitrov, D.; Briole, P.; Botev, E. Velocity field in Bulgaria and northern Greece from GPS campaigns spanning 1993–2008. In Proceedings of the 2nd INQUA-IGCP-567 International Workshop on Active Tectonics, Earthquake Geology, Archaeology and Engineering, Corinth, Greece, 19–24 September 2011; pp. 54–56. [Google Scholar]
- Holden, L.; Silcock, D.; Fournier, N.; Choy, S.; Cas, R. Evaluating a campaign GNSS velocity field derived from an online precise point positioning service. Geophys. J. Int. 2017, 208, 246–256. [Google Scholar] [CrossRef]
- Tsanovski, Y.; Danchev, T. Horizontal intraplate velocity field model for the territory of Bulgaria derived from GNSS solution. In Proceedings of the SGEM 2019 Conference, Albena, Bulgaria, 28 June–7 July 2019. [Google Scholar]
- Li, Z.; Jiang, W.P.; Liu, H.F. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series inside China. Acta Geod. Cartogr. Sin. 2012, 41, 496–503. [Google Scholar]
- Wang, X.; Cheng, Y.; Jiang, Z.; Wang, F.; Li, X. The Study on Movement Characteristics and Non-Linear Model of CGCS2000 Framework; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zhang, H.J.; Cui, D.D.; Cheng, P.F. Height nonlinear velocity field and variance fluctuation model construction method for CORS station. Acta Geod. Cartogr. Sin. 2019, 48, 1096–1106. [Google Scholar] [CrossRef]
- Engle, R.E. Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Tim, B. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar]
- Zakoian, J.M. Threshold heteroskedastic models. J. Econ. Dyn. Control 1994, 18, 931–955. [Google Scholar] [CrossRef]
- Chen, M.; An, H. A test of conditional heteroscedasticity in time series. Sci. China Ser. A Math. 1999, 42, 26–37. [Google Scholar] [CrossRef]
- Lin, Z. Modelling and forecasting the stock market volatility of SSE Composite Index using GARCH models. Future Gener. Comput. Syst. 2018, 79, 960–972. [Google Scholar] [CrossRef]
- Cerovecki, C.; Francq, C.; Hörmann, S.; Zakoïan, J.M. Functional GARCH models: The quasi-likelihood approach and its applications. J. Econom. 2019, 209, 353–375. [Google Scholar] [CrossRef]
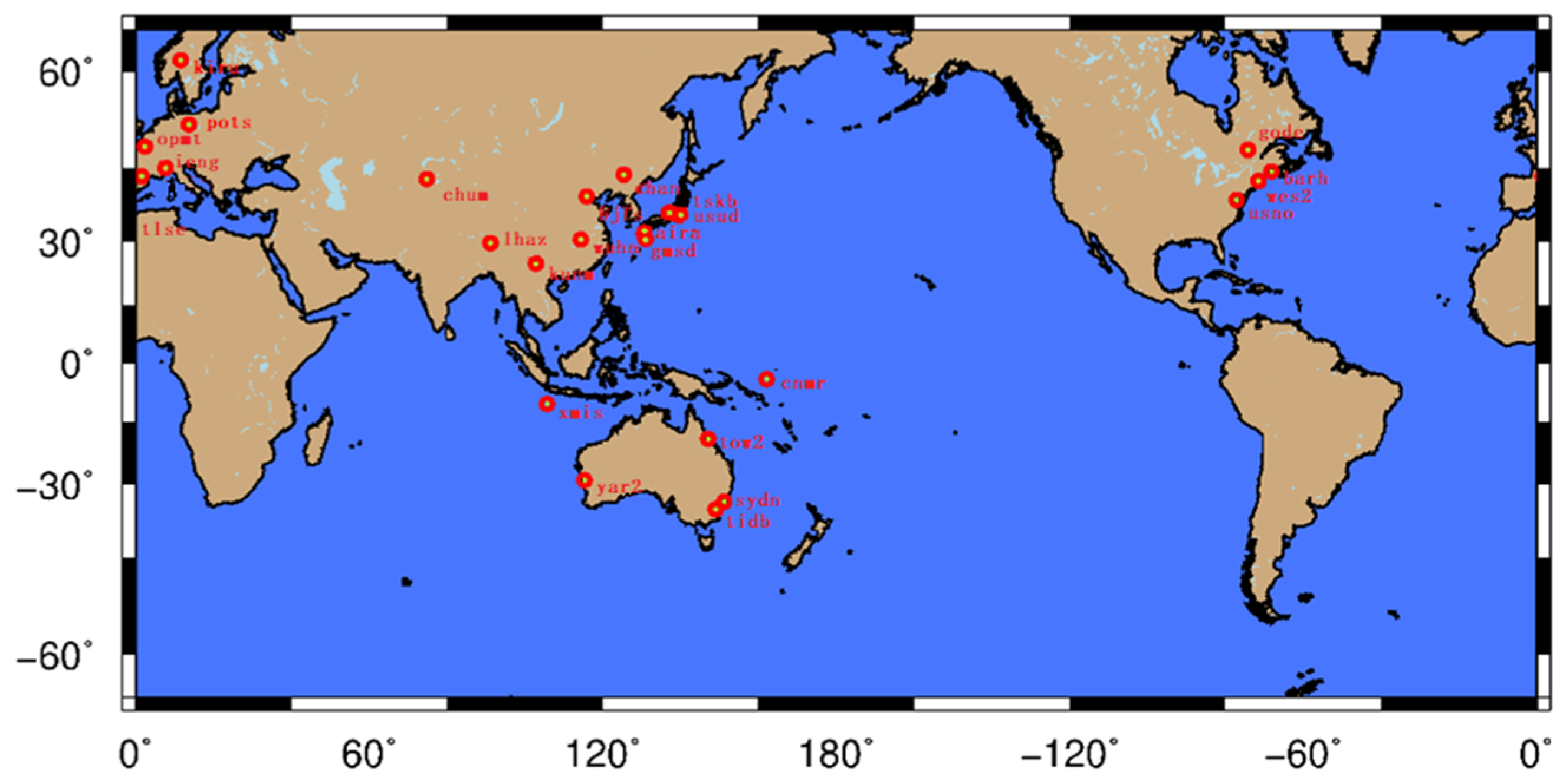



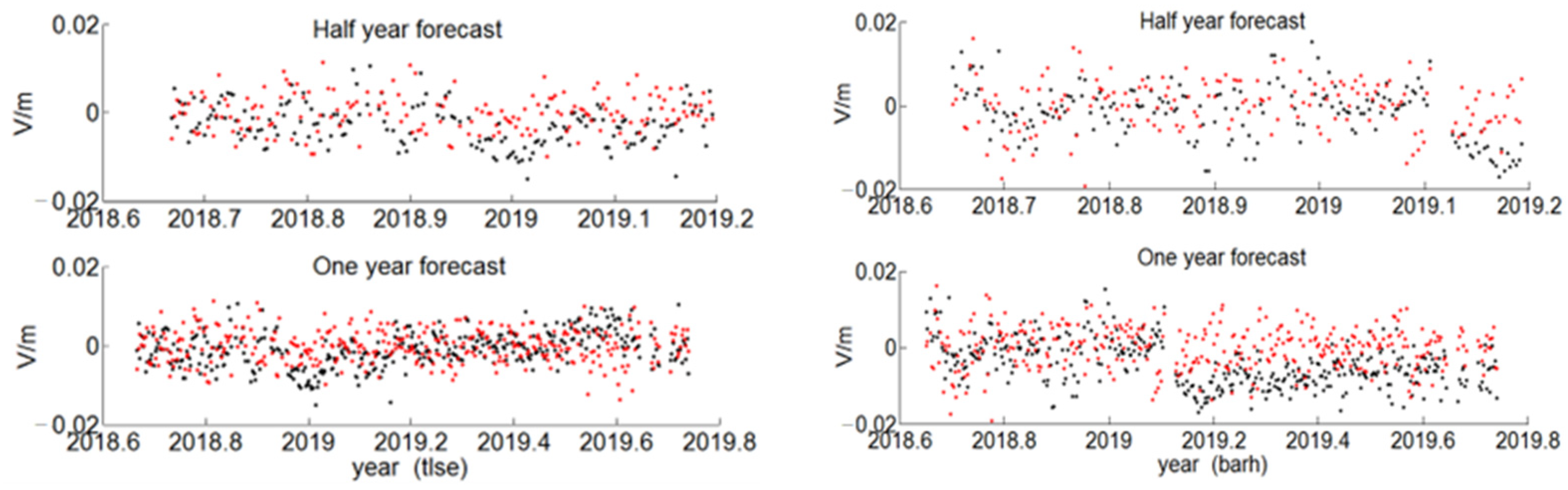
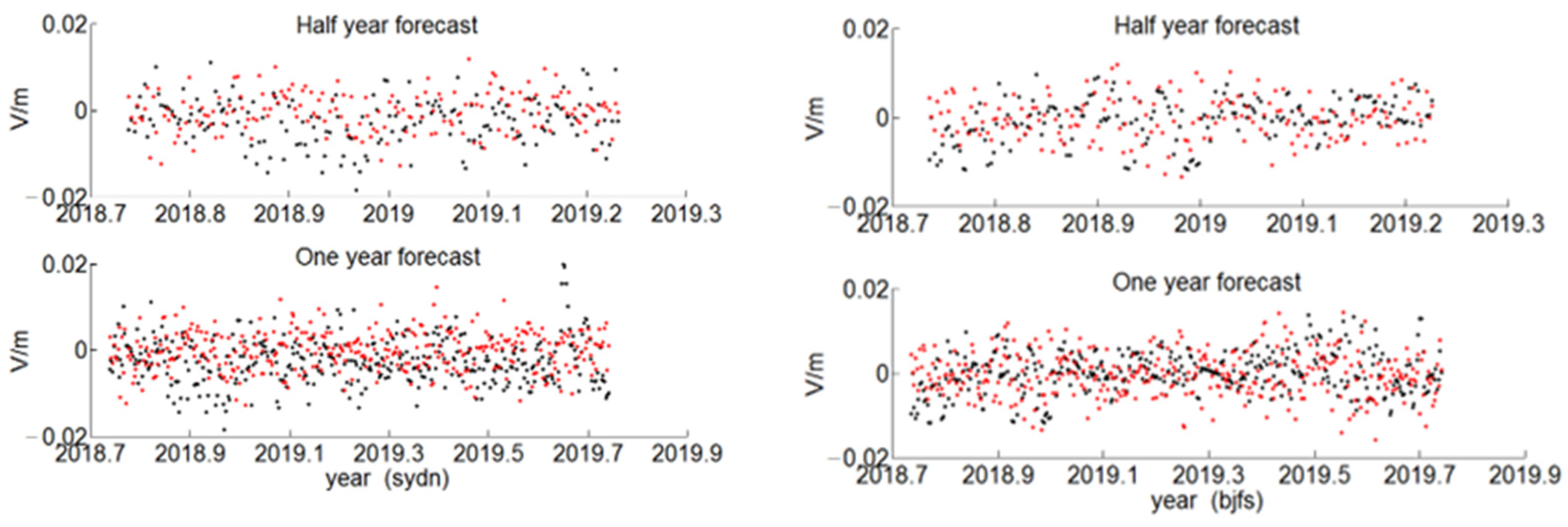

| Location | Station Name | |||||
|---|---|---|---|---|---|---|
| China and its surroundings | bjfs | kunm | chan | lhaz | wuhn | chum |
| Australia | sydn | tidb | tow2 | xmis | yar2 | |
| Japan | aira | gmsd | tskb | usud | ||
| Europe | ieng | kiru | pots | opmt | tlse | |
| U.S. | gode | barh | cnmr | usno | wes2 | |
| Parameters | bjfs | lhaz | ||
|---|---|---|---|---|
| Linear | Nonlinear | Linear | Nonlinear | |
| 2.60 | 2.70 | 0.44 | 0.32 | |
| 2.00 | 2.00 | 1.20 | 1.20 | |
| 4.50 | 6.80 | 4.60 | 5.70 | |
| 1.10 | 1.30 | 1.60 | 2.10 | |
| 0.72 | 0.91 | 0.41 | 0.52 | |
| 1.0 | 1.01 | 2.0 | 1.01 | |
| 0.5 | 0.48 | 0.5 | 0.52 | |
| 2.0 | 2.08 | 2.0 | 2.09 | |
| 1.85 | 0.48 | |||
| 6.79 | 0.29 | |||
| 4.50 | 4.78 | |||
| Model | bjfs (mm) | lhaz (mm) |
| Linear model | 7.9 | 6.0 |
| Nonlinear model | 6.0 | 5.4 |
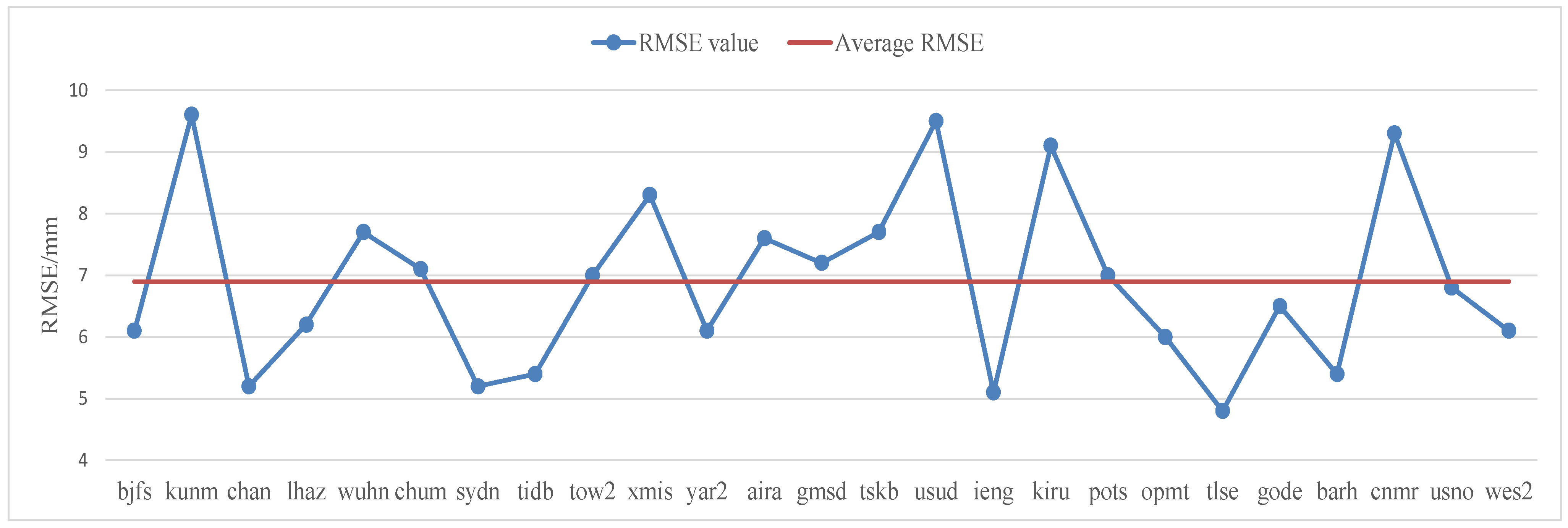
| Station Name | bjfs | kunm | chan | lhaz | wuhn | chum | sydn | tidb | tow2 |
| RMSE/mm | 6.1 | 9.6 | 5.2 | 6.2 | 7.7 | 7.1 | 5.2 | 5.4 | 7.0 |
| Station Name | xmis | yar2 | aira | gmsd | tskb | usud | ieng | kiru | pots |
| RMSE/mm | 8.3 | 6.1 | 7.6 | 7.2 | 7.7 | 9.5 | 5.1 | 9.1 | 7.0 |
| Station Name | opmt | tlse | gode | barh | cnmr | usno | wes2 | ||
| RMSE/mm | 6.0 | 4.8 | 6.5 | 5.4 | 9.3 | 6.8 | 6.1 |
| Station Name/ Amplitude | bjfs | kunm | chan | lhaz | wuhn | chum | sydn | tidb | tow2 |
| one year | 7 | 7.2 | 7 | 4.4 | 3.8 | 6.7 | 3.4 | 4.4 | 5.2 |
| half year | 1.2 | 1.3 | 1.3 | 0.7 | 1.2 | 1.2 | 0.8 | 0.6 | 0.6 |
| two years | 1.3 | 0.8 | 0.6 | 0.9 | 0.8 | 1.1 | 0.6 | 0.2 | 0.5 |
| Station Name/ Amplitude | xmis | yar2 | aira | gmsd | tskb | usud | ieng | kiru | pots |
| one year | 3.1 | 4.2 | 2.3 | 2.2 | 6.9 | 1.2 | 5.8 | 4.8 | 5.9 |
| half year | 0.7 | 0.9 | 1.1 | 1.4 | 1.1 | 2 | 0.9 | 2.6 | 0.7 |
| two years | 0.6 | 0.7 | 1.1 | 1.2 | 0.8 | 1.8 | 0.6 | 1.1 | 0.5 |
| Station Name/ Amplitude | opmt | tlse | gode | barh | cnmr | usno | wes2 | ||
| one year | 3.2 | 4.4 | 2.6 | 1.6 | 2.6 | 4.4 | 4.2 | ||
| half year | 0.7 | 0.5 | 0.6 | 0.7 | 1.4 | 0.9 | 1 | ||
| two years | 0.2 | 0.5 | 0.4 | 0.4 | 0.8 | 0.6 | 0.4 |
| Station Name | Modeling Speed (mm/a) | Modeling Year Amplitude (mm) | Modeling Half Year Amplitude (mm) | SOPAC Speed (mm/a) | SOPAC Year Amplitude (mm) | SOPAC Half Year Amplitude (mm) | Speed Difference | Year Amplitude Difference | Half-Year Amplitude Difference |
|---|---|---|---|---|---|---|---|---|---|
| bjfs | 2 | 7 | 1.2 | 2.43 | 6.97 | 0.95 | −0.43 | 0.03 | 0.25 |
| kunm | −0.9 | 7.2 | 1.3 | 1.31 | 8.12 | 0.33 | −2.21 | −0.92 | 0.97 |
| chan | −0.4 | 7 | 1.3 | −0.23 | 7.49 | 0.74 | −0.17 | −0.49 | 0.56 |
| lhaz | 1.2 | 4.4 | 0.7 | 1.17 | 6.02 | 1.63 | 0.03 | −1.62 | −0.93 |
| wuhn | 0.1 | 3.8 | 1.2 | 0.19 | 4.12 | 0.17 | −0.09 | −0.32 | 1.03 |
| chum | 0.4 | 6.7 | 1.2 | 0.4 | 7.72 | 1.83 | 0 | −1.02 | −0.63 |
| sydn | −0.6 | 3.4 | 0.8 | −0.75 | 3.54 | 0.26 | 0.15 | −0.14 | 0.54 |
| tidb | −1.1 | 4.4 | 0.6 | −0.77 | 2.52 | 0.23 | −0.33 | 1.88 | 0.37 |
| tow2 | −0.6 | 5.2 | 0.6 | −0.64 | 2.9 | 0.96 | 0.04 | 2.3 | −0.36 |
| xmis | −0.1 | 3.1 | 0.7 | −0.09 | 3.46 | 0.63 | −0.01 | −0.36 | 0.07 |
| yar2 | 0.3 | 4.2 | 0.9 | 0.19 | 3.04 | 0.44 | 0.11 | 1.16 | 0.46 |
| aira | −0.5 | 2.3 | 1.1 | 1.13 | 2.89 | 1.26 | −1.63 | −0.59 | −0.16 |
| gmsd | −0.8 | 2.2 | 1.4 | 0.56 | 2.18 | 0.74 | −1.36 | 0.02 | 0.66 |
| tskb | 0.3 | 6.9 | 1.1 | 0.64 | 6.66 | 0.76 | −0.34 | 0.24 | 0.34 |
| usud | −0.5 | 1.2 | 2 | −0.99 | 1.64 | 2.15 | 0.49 | −0.44 | −0.15 |
| ieng | 0.2 | 5.8 | 0.9 | 0.25 | 5.98 | 1.29 | −0.05 | −0.18 | −0.39 |
| kiru | 6.8 | 4.8 | 2.6 | 6.76 | 5.02 | 2.28 | 0.04 | −0.22 | 0.32 |
| pots | 0.3 | 5.9 | 0.7 | 0.42 | 5.86 | 0.27 | −0.12 | 0.04 | 0.43 |
| opmt | 0.1 | 3.2 | 0.7 | 0.02 | 4.74 | 0.47 | 0.08 | −1.54 | 0.23 |
| tlse | 0 | 4.4 | 0.5 | 0 | 4.33 | 0.63 | 0 | 0.07 | −0.13 |
| gode | −1.3 | 2.6 | 0.6 | −1.2 | 3.1 | 0.89 | −0.1 | −0.5 | −0.29 |
| barh | 0.3 | 1.6 | 0.7 | 0.25 | 2.53 | 1.04 | 0.05 | −0.93 | −0.34 |
| cnmr | −2.3 | 2.6 | 1.4 | −1.91 | 1.66 | 0.69 | −0.39 | 0.94 | 0.71 |
| usno | 0.8 | 4.4 | 0.9 | −0.78 | 3.87 | 0.79 | 1.58 | 0.53 | 0.11 |
| wes2 | 0.2 | 4.2 | 1 | 0.27 | 3.38 | 1.05 | −0.07 | 0.82 | −0.05 |
| Parameter | Value | Standard Error | t Statistic |
|---|---|---|---|
| Constant | 0.0000010 | 0.0000003 | 4.0329500 |
| GARCH(1) | 0.9015880 | 0.0055081 | 163.68300 |
| ARCH(2) | 0.0703840 | 0.0048549 | 14.497700 |
| Offset | 0.0001350 | 0.0000712 | 1.8952600 |
| Parameter | Value | Standard Error | t Statistic |
|---|---|---|---|
| Constant | 0.0000117 | 0.0000059 | 19.896500 |
| GARCH(1) | 0.2877190 | 0.0297679 | 9.6654300 |
| ARCH(1) | 0.3148980 | 0.0230891 | 13.638400 |
| Offset | 0.0000204 | 0.0000673 | 0.0302618 |
| RMSE/mm | tlse | barh | sydn | bjfs |
|---|---|---|---|---|
| Half a year | 5.3 | 6.7 | 5.6 | 6.2 |
| A year | 5.9 | 7.0 | 5.9 | 6.6 |
| Method of Prediction | bjfs | sydn | barh | tlse | ||||
|---|---|---|---|---|---|---|---|---|
| Half a Year | One Year | Half a Year | One Year | Half a Year | One Year | Half a Year | One Year | |
| Nonlinear LS | 7.2 | 7.5 | 6.4 | 6.8 | 7.4 | 7.7 | 6.0 | 6.8 |
| nonlinear LS based GARCH | 6.2 | 6.6 | 5.6 | 5.9 | 6.7 | 7.0 | 5.3 | 5.9 |
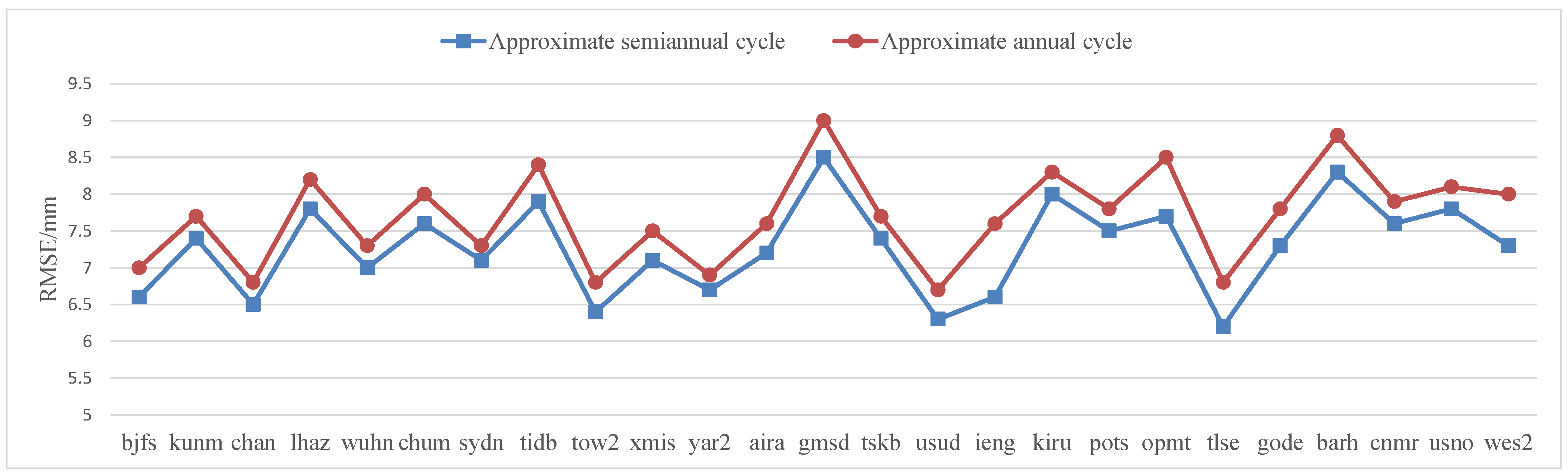
| Station Name/Section | bjfs | kunm | chan | lhaz | wuhn | chum | sydn | tidb | tow2 |
| half a year | 6.6 | 7.4 | 6.5 | 7.8 | 7 | 7.6 | 7.1 | 7.9 | 6.4 |
| one year | 7 | 7.7 | 6.8 | 8.2 | 7.3 | 8 | 7.3 | 8.4 | 6.8 |
| Station Name/Section | xmis | yar2 | aira | gmsd | tskb | usud | ieng | kiru | pots |
| half a year | 7.1 | 6.7 | 7.2 | 8.5 | 7.4 | 6.3 | 6.6 | 8 | 7.5 |
| one year | 7.5 | 6.9 | 7.6 | 9 | 7.7 | 6.7 | 7.6 | 8.3 | 7.8 |
| Station Name/Section | opmt | tlse | gode | barh | cnmr | usno | wes2 | ||
| half a year | 7.7 | 6.2 | 7.3 | 8.3 | 7.6 | 7.8 | 7.3 | ||
| one year | 8.5 | 6.8 | 7.8 | 8.8 | 7.9 | 8.1 | 8 |
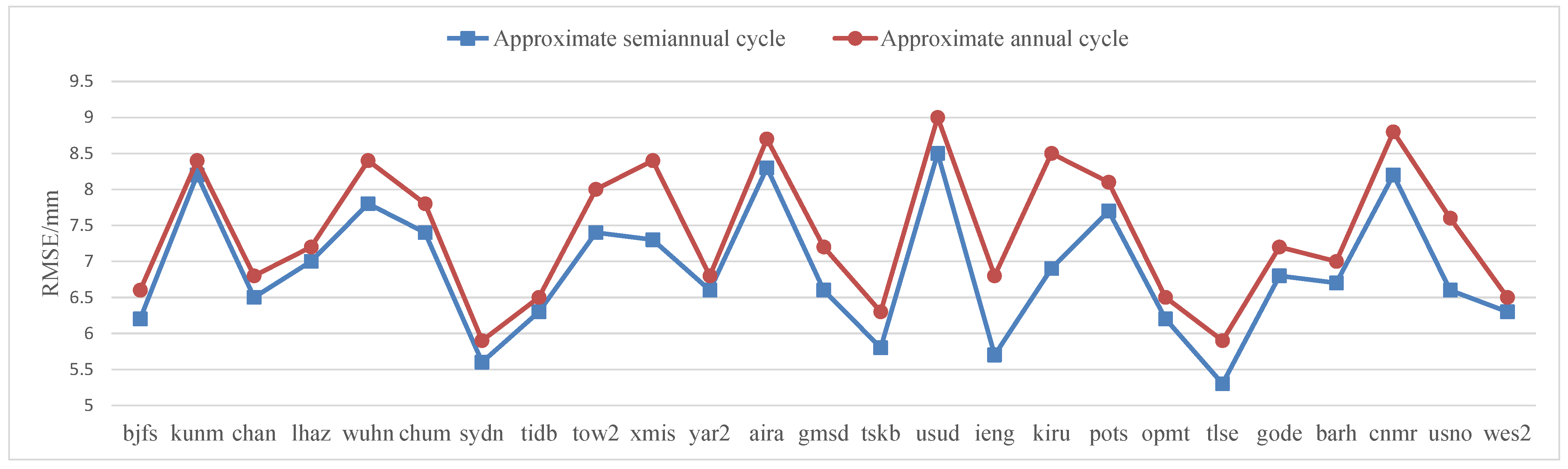
| Station Name/ Section | bjfs | kunm | chan | lhaz | wuhn | chum | sydn | tidb | tow2 |
| half a year | 6.2 | 8.2 | 6.5 | 7 | 7.8 | 7.4 | 5.6 | 6.3 | 7.4 |
| one year | 6.6 | 8.4 | 6.8 | 7.2 | 8.4 | 7.8 | 5.9 | 6.5 | 8 |
| Station Name/ Section | xmis | yar2 | aira | gmsd | tskb | usud | ieng | kiru | pots |
| half a year | 7.3 | 6.6 | 8.3 | 6.6 | 5.8 | 8.5 | 5.7 | 6.9 | 7.7 |
| one year | 8.4 | 6.8 | 8.7 | 7.2 | 6.3 | 9 | 6.8 | 8.5 | 8.1 |
| Station Name/ Section | opmt | tlse | gode | barh | cnmr | usno | wes2 | ||
| half a year | 6.2 | 5.3 | 6.8 | 6.7 | 8.2 | 6.6 | 6.3 | ||
| one year | 6.5 | 5.9 | 7.2 | 7 | 8.8 | 7.6 | 6.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Liu, H.; Cui, D.; Zhang, F. A Height Nonlinear Velocity Field Algorithm for CORS Station Based on GARCH Model. Sensors 2022, 22, 7589. https://doi.org/10.3390/s22197589
Zhang H, Liu H, Cui D, Zhang F. A Height Nonlinear Velocity Field Algorithm for CORS Station Based on GARCH Model. Sensors. 2022; 22(19):7589. https://doi.org/10.3390/s22197589
Chicago/Turabian StyleZhang, Hengjing, Huanling Liu, Dongdong Cui, and Fang Zhang. 2022. "A Height Nonlinear Velocity Field Algorithm for CORS Station Based on GARCH Model" Sensors 22, no. 19: 7589. https://doi.org/10.3390/s22197589
APA StyleZhang, H., Liu, H., Cui, D., & Zhang, F. (2022). A Height Nonlinear Velocity Field Algorithm for CORS Station Based on GARCH Model. Sensors, 22(19), 7589. https://doi.org/10.3390/s22197589








